(2: 江西师范大学地理与环境学院,南昌 330022)
(2: School of Geography and Environment, Jiangxi Normal University, Nanchang 330022, P.R.China)
鄱阳湖是我国最大的淡水湖,是长江水系中的两大通江湖泊之一,具有调蓄洪水和保护生物多样性等特殊生态功能,对维系区域和国家生态安全具有重要作用.鄱阳湖高动态的水位特征,形成了独特的湖泊湿地景观和生态格局[1].然而,自2003年以来受鄱阳湖水系入湖径流量减少以及长江水资源形势变化等多种因素影响,鄱阳湖枯水期出现了时间提前、水位偏低、持续时间延长等现象,引起国内学者和有关政府部门的高度关注.建设鄱阳湖水利枢纽工程的构想再次进入人们的视野.上升为国家战略的鄱阳湖生态经济区建设,推动了地方政府对这一工程的规划实施和进一步深化,并基于生态角度提出了“控枯不控洪,动态调整”的新设计方案与运行思路,国内专家与学者也从江湖关系、生态环境与经济社会效益等方面进行了大量研究和论证[2-4],但仍引发了众多争鸣[5].
湖泊是水系的重要组成部分,由江湖水系所支撑的江湖生态系统是地表最富生产力和生物多样性的生态系统类型之一,也是陆地生态系统中物质循环和生命支持的动脉.水利枢纽工程作为人类社会的重要基础设施之一,不仅具有“调节丰枯、抵御洪涝”的生态服务功能,而且还有促进区域经济发展的重要社会功能.然而,构建在自然江湖水系中的水利枢纽工程必然会造成江湖生态系统连续性和流动性的破坏,从而导致水流情势的变化,引发不同的生态环境效应[6-8].水量与水动力是河湖生态系统的重要基础变量,水流情势变化是河湖生态系统演变最主要的驱动力[9].因此,湖泊水量与水动力及其对营养盐循环和生物生长及优势种群演替的影响是浅水湖泊现代过程研究的核心内容之一[10].而水动力模型是定量分析水流情势变化的重要而有效工具[11],它可以在短时间内模拟单变量或多变量组合对河湖系统水流情势变化的影响.因此,应用具有物理意义的水动力学模型,通过单变量或多变量组合的敏感性模拟和情景模拟,开展水利枢纽工程对河湖系统水文水动力的影响研究,是人类定量理解和认识湖泊演变的人文作用机理、江湖关系改变及其生态环境效应的有效方法,也是人类进一步认识与评估水利枢纽工程对水生态环境的影响及调控、江湖关系优化调整的重要基础.
近年来随着计算机技术、计算流体力学、数值计算和GIS技术等方面的快速发展,国际上开发了大量有影响的水动力模型,如EFDC、MIKE、SMS、Delft3d、ANUGA、CCHE等[12].国内外学者利用这些具有动力机制的模型,在数值模拟的基础上,开展了对河、库、湖和河口海岸等水体的水动力、富营养化、生态修复和重大水利工程影响分析等众多领域的大量研究. Obeysekera、Onnish及Endon等[11, 13-14]通过湖泊水动力模型,进行了湖泊开发利用和修复保护等有关水动力学方面的模拟;Ferrari等应用三维水动力数值模拟,研究水库溃坝过程中不同点位压力场的温度变化、水深和铅垂速度分布[15];我国学者利用水动力模型或耦合的生态动力学模型,在重大水利工程对库湖水动力和水环境的影响方面已进行一定探讨,如陈江应用二维水动力模型,对长江水源地现状及假设淤积状态下的流场进行了情景模拟,探讨了引江济太对水源地安全的影响[16];李云良等[17-18]以鄱阳湖湖泊流域系统为研究对象,构建了鄱阳湖湖泊流域联合模拟模型.该模型基于自主研发的流域分布式水文模型WATLAC和湖滨平原区产流模型以及水动力模型MIKE21等3个不同功能子模型的连接来实现该复杂系统的模拟,利用构建的模型模拟了湖泊水位对流域入湖径流量的响应.在三峡工程方面,国内学者马超、陈栋和辛小康等利用MIKE、CE-QUAL-W2、ECOMSED等模型分别进行了不同维数的模拟研究,探讨了三峡水库日调节调度方案、运行方式、不同水位蓄放方式的水动力和水质效应及对支流水动力与水质的影响及其效果[4, 19-20].
虽然拟建的鄱阳湖水利枢纽工程在学术界引起了较多争论,许多学者也开展了这方面的研究,但目前的研究多局限在定性方面[2-3],虽有学者利用具有动力机制的模型开展了这方面的研究,如胡春华等应用EFDC建立了鄱阳湖二维的水动力和水质模型,进行鄱阳湖水利枢纽工程对主湖区氮、磷营养盐的影响模拟[21];杜彦良等[22]采用水深平均的二维水动力-水质模型,在相同入流边界和现状污染负荷条件下,通过鄱阳湖有枢纽和无枢纽的情景模拟,研究水动力和水质状态差异,结果表明:枯水期大部分区域的水质浓度下降,但尾闾等部分区域有所升高,开闸泄水期前后,水质较现状水质下降,敞泄期的大部分时间,较现状水质基本相似,蓄水期水质变化不大;余启辉等[23]在充分考虑鄱阳湖与长江之间的相互作用、湖区区间汇流对水动力的作用以及湖区复杂的河湖交替形态的条件下,采用江湖连通一、二维耦合水文-水动力模型,研究了鄱阳湖水利枢纽调度对湖区枯期水位与流速的影响.但这些研究对于建设一个具有重大影响的水利枢纽工程来说,深度和广度仍显不足.
针对拟建的鄱阳湖水利枢纽工程,在EFDC模型基础上,建立了二维的湖泊水动力模拟模型,通过对典型年份的情景模拟,探讨拟建的水利枢纽工程对鄱阳湖水文水动力的影响.作为研究的一部分,文献[24]主要探讨了鄱阳湖水利枢纽工程运行对主湖区及鄱阳湖两大自然保护区水位变化的时间节律影响.本文在文献[24]的基础上,进一步探讨不同情景年型中鄱阳湖水利枢纽工程调度方案的低枯水期11m最低控制水位对主湖区不同空间位置水位的抬升程度,并进而分析鄱阳湖水利枢纽工程对湖泊流场和湖泊换水周期的可能影响,为定量分析鄱阳湖水利枢纽工程对湖泊水质和生态系统演化造成的可能影响提供必要的基础支撑.
1 鄱阳湖水利枢纽工程设计及调度方案概况拟建的鄱阳湖水利枢纽工程坝址选定于鄱阳湖入江水道(29°32′N,116°07′E),介于庐山区长岭与湖口县屏峰山之间,两山之间湖面宽约2.8km,为鄱阳湖入长江通道最窄之处.该处上距星子县城约12km,下至长江汇合口约27km.规划中的鄱阳湖水利枢纽工程以“一湖清水”为建设目标,坚持“江湖两利”的原则,按“调枯不控洪”方式运行,按生态保护和综合利用要求控制相对稳定的鄱阳湖枯水位,提高鄱阳湖枯水季节水环境容量,达到保护水生态环境、根本解决湖区干旱及生态缺水问题、改善湿地环境、消灭钉螺、提高航道等级、发展湖区旅游及渔业等方面的综合效益.鄱阳湖水利枢纽工程调度规划方案见表 1.
| 表 1 鄱阳湖水利枢纽工程规划调度方案* Tab.1 The scheme of water level regulation of the Lake Poyang hydraulic project for ecological control-water operations |
鄱阳湖二维水动力模型以EFDC(Environmental Fluid Dynamics Code,EFDC)模型为基础水动力模型.EFDC是由威廉玛丽大学维吉尼亚海洋科学研究所(Virginia Institute of Marine Science at the College of William and Mary,VIMS)John Hamrick等开发的综合模型,可实现河流、湖泊、水库、湿地系统、河口和海洋等水体的一维至三维水动力、泥沙淤积与水质模拟.该模型在水平方向采用直角坐标或正交曲线坐标,垂直方向采用σ坐标.动力学方程采用有限差分法求解,水平方向采用交错网格离散,时间积分采用二阶精度的有限差分法以及内外模式分裂技术(即采用剪切应力或斜压力的内部模块和自由表面重力波或正压力的外模块分开计算).外模块采用半隐式计算方法,允许较大的时间步长,且可采用自适应时间步长模式.内模块采用了垂直扩散的隐式格式,期间水陆漫滩带区域采用干湿格网技术.此外,该模型由Fortran语言开发而成,源代码开放,易于根据不同的应用目标进行适当的修改,有较大的适用性.EFDC模型是美国环保署(US EPA)首推的水动力模型,目前在国际上有大量的应用[25-26].
2.1 EFDC水动力模型的控制方程 2.1.1 动量方程、连续方程和状态方程EFDC模型的动力学方程是基于三维不可压缩的、变密度紊流边界层方程组,为了便于处理由于密度差而引起的浮升力项,采用Boussinesq假设.在水平方向上采用曲线正交坐标变换和在垂直方向上采用σ坐标变换:
| $ \left\{ \begin{array}{l} x = \varphi ({x^ * }, {y^ * })\\ y = \phi ({x^ * }, {y^ * })\\ z = ({z^ * } + h)/(\xi + h) = H(\xi + h) \end{array} \right. $ | (1) |
式中,(x*,y*,z*)为任意点P的直角坐标,(x,y,z)为P点的正交曲线σ坐标,ξ为水位,h为湖底高程,H为水深.坐标经过这两种变换后的动量方程和连续方程如下:
动量方程为:
| $ \begin{array}{*{20}{l}} {\frac{{\partial (mHu)}}{{\partial t}} + \frac{{\partial ({m_y}Huu)}}{{\partial x}} + \frac{{\partial ({m_x}Hvu)}}{{\partial y}} + \frac{{\partial (mwu)}}{{\partial z}} - \left( {mf + v\frac{{\partial {m_x}}}{{\partial x}} - u\frac{{\partial {m_x}}}{{\partial y}}} \right)Hv}\\ { = - {m_y}H\frac{{\partial (g\zeta + p)}}{{\partial x}} - {m_y}(\frac{{\partial h}}{{\partial x}} - z\frac{{\partial H}}{{\partial z}})\frac{{\partial p}}{{\partial z}} + \frac{\partial }{{\partial z}}\left( {m\frac{1}{H}{A_V}\frac{{\partial U}}{{\partial z}}} \right) + {Q_u}} \end{array} $ | (2) |
| $ \begin{array}{*{20}{l}} {\frac{{\partial (mHv)}}{{\partial t}} + \frac{{\partial ({m_y}Huv)}}{{\partial x}} + \frac{{\partial ({m_x}Hvv)}}{{\partial y}} + \frac{{\partial (mwv)}}{{\partial z}} - \left( {mf + v\frac{{\partial {m_y}}}{{\partial x}} - u\frac{{\partial {m_x}}}{{\partial y}}} \right)Hu}\\ { = - {m_x}H\frac{{\partial (g\zeta + p)}}{{\partial y}} - {m_y}(\frac{{\partial h}}{{\partial y}} - z\frac{{\partial H}}{{\partial y}})\frac{{\partial p}}{{\partial z}} + \frac{\partial }{{\partial z}}\left( {m\frac{1}{H}{A_V}\frac{{\partial U}}{{\partial z}}} \right) + {Q_v}} \end{array} $ | (3) |
| $ \frac{{\partial p}}{{\partial z}} = - gH\frac{{\rho - {\rho _0}}}{{{\rho _0}}} = - gHb $ | (4) |
连续方程为:
| $ \frac{{\partial (m\zeta )}}{{\partial t}} + \frac{{\partial ({m_y}Hu)}}{{\partial x}} + \frac{{\partial ({m_x}Hv)}}{{\partial y}} + \frac{{\partial (mw)}}{{\partial z}} = 0 $ | (5) |
| $ \frac{{\partial (m\zeta )}}{{\partial t}} + \frac{{\partial ({m_y}H\int_0^1 {u{\rm{d}}z} )}}{{\partial x}} + \frac{{\partial ({m_x}H\int_0^1 {v{\rm{d}}z} )}}{{\partial y}} = 0 $ | (6) |
| $ \rho = \rho (p, S, T) $ | (7) |
式中,u、v、w分别为边界拟合正交曲线坐标x、y和z方向上的水平速度分量,mx和my为水平坐标变换尺度因子,m=mxmy是度量张量行列式的平方根,Av为垂向紊动粘滞系数,Ab垂向紊动扩散系数,f为科里奥利系数,p为压力,ρ为混合密度,ρ0为参考密度,S为盐度,T为温度,Qu和Qv为动量的源汇项.
2.1.2 边界条件和初始条件自由水表面动力学边界条件为:
| $ w(x, y, 1, t) = 0 $ | (8) |
| $ \frac{{{K_{\rm{v}}}}}{H}\frac{{\partial u}}{{\partial z}}\left| {\begin{array}{*{20}{l}} {}\\ {z = 1} \end{array}} \right. = 0;\frac{{{K_{\rm{v}}}}}{H}\frac{{\partial v}}{{\partial z}}\left| {\begin{array}{*{20}{l}} {}\\ {z = 1} \end{array}} \right. = 0 $ | (9) |
水底动力学边界条件为:
| $ w(x, y, 0, t) = 0 $ | (10) |
| $ \frac{{{K_{\rm{v}}}}}{H}\frac{{\partial u}}{{\partial z}}\left| {\begin{array}{*{20}{l}} {}\\ {z = 1} \end{array}} \right. = {\tau _{{\rm{b}}x}};\frac{{{K_{\rm{v}}}}}{H}\frac{{\partial v}}{{\partial z}}\left| {\begin{array}{*{20}{l}} {}\\ {z = 0} \end{array}} \right. = {\tau _{{\rm{b}}y}} $ | (11) |
式中,τbx和τby分别为风应力τb在x和y方向上的分量.
湖岸边界条件为:
| $ {u_{{\rm{boundary}}}}(x, y, z, t) = 0 $ | (12) |
| $ \frac{{\partial S}}{{\partial x}}\left| {\begin{array}{*{20}{l}} {}\\ {{x_{{\rm{boundary}}}}} \end{array}} \right. = 0;\frac{{\partial C}}{{\partial x}}\left| {\begin{array}{*{20}{l}} {}\\ {{x_{{\rm{boundary}}}}} \end{array}} \right. = 0 $ | (13) |
入口和出口的边界条件分别为:
| $ \begin{array}{l} {u_{in}}(x,y,z,t) = 0;{v_{in}}(x,y,z,t) = {\psi _1}(t);{u_{out}}(x,y,z,t) = 0;{v_{out}}(x,y,t)\\ = {\psi _2}(t);w(x,y,z,t) = 0 \end{array} $ | (14) |
式中,ψ1(t)和ψ2(t)分别为入口和出口的流量函数.模型的初始条件为:
| $ u(x, y, z, 0) = 0;v(x, y, z, 0) = 0;w(x, y, z, 0) = 0;\xi (x, y, 0) = C $ | (15) |
式中,C为常数.
2.2 鄱阳湖二维水动力模型的构建以1998年鄱阳湖洪水期间的遥感影像为参照,结合鄱阳湖圩堤GIS数据,对圩堤外与湖区水体不能自由流通的水体予以排除,以此来确定鄱阳湖的最大水面范围和模型的计算域.并在此基础上,采用正交曲线格网对模型的鄱阳湖计算域进行格网化;格网总数为96004,格网分辨率参数介于178~205m之间,格网的正交性参数小于0.2(图 1a、b).由于格网为非正方形格网,其长宽不等,故格网分辨率参数是用每个格网面积的平方根来表示的.在构建计算格网时,在一定程度上考虑了湖盆地形的高程变差,从图 1b可以看出,在湖泊北部和东部,由于高程变差较大,因而采用较小的格网来反映地形高程变差,而在高程变差小的湖泊漫滩部分(湖泊中部)采用了较大的格网,以控制格网总数,减小计算耗时.
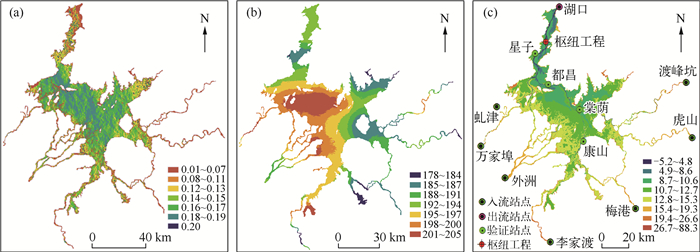
|
图 1 鄱阳湖水动力模型的格网正交性(a)和分辨率(b)参数,入湖与出湖的控制站点和验证站点位置(c) Fig.1 Parameters of grid orthogonality(a)and resolution(b) of Lake Poyang hydrodynamic modeling, positions of control cross section for lake inlets/outlet and verification points(c) |
鄱阳湖水底地形采用1998年实测的数据,比例尺为1:2.5万,由长江水利委员会提供.模型的上边界为鄱阳湖虬津、万家埠、外洲、李家渡、梅港、虎山、渡峰坑等“五河七口”的逐日实测流量数据(m3/s),下边界为湖口的逐日实测水位数据(m,黄海高程),为了进行鄱阳湖水利枢纽工程的情景模拟,在水利枢纽工程位址处设置了一个下边界(图 1c),其边界条件为水位强迫,水位数据由无枢纽模拟时在工程位址处获取,具体见情景模拟方案部分.
2.3 模型的率定与验证由于模拟比较耗费时间,所以模型的参数率定时期选取了1999年11月1日-2000年7月31日间的9个月,该时段包含了鄱阳湖的丰水期和枯水期,这有利于提高参数率定过程中模型对高水位和低水位的模拟效果及模型参数率定的效率.模型的验证时期选2000年8月1日-2001年7月31日,这个时段包括了一个完整水文年.模型验证分别选取鄱阳湖南北方向不同部位的星子、都昌、棠荫和康山4个站点的实测水位与模拟水位来进行.图 2绘制了模型参数率定以后模拟的1999年11月1日—2001年7月31日4个验证站点的实测水位与模拟水位对照图,表 2给出了其间的平均绝对误差、平均相对误差、RMS误差和Nash-Stucliffe效率系数[27],各误差参数由EFDC模型提供的EFDC-Explorer程序自动计算得出.
| 表 2 模型验证的误差分析表 Tab.2 Error analysis table of model for validation |
4个验证点的平均误差在0.160~0.351m之间,相对误差在1.523%~2.792%之间,RMS误差在0.229~0.459之间,Nash-Stucliffe效率系数在0.852~0.988之间(图 2、表 2).其中星子、都昌、棠荫3个验证点的误差比较接近,康山误差相对较大,究其原因,应与康山的水底地形及计算格网的相对大小有关,康山水底比其它验证点的地形复杂,表现在高程上即其变率较大(图 1c),而模型的计算格网大小在康山位置上却较其它验证位置上的格网分辨率大(图 1b),这就造成了计算格网的分辨率没有很好地反映实际地形的高程变率.此外,图 2康山水位验证中在1999年11月1日到2000年3月1日、2000年12月1日到2001年3月1日实测值呈波动状而模拟值基本不变,这可能与插值后地形被拉平有关.这两方面因素综合作用造成了康山验证点实测值与模拟值之间较大的误差.

|
图 2 参数率定和模型验证的逐日水位实测值与模拟值 Fig.2 Observed and simulated daily water levels for parameter calibration and model validation |
为了更好地验证模拟结果的可靠性,尤其是验证模拟的湖泊水面与实际湖泊水面的对应情况,图 3呈示了枯水期(1999年12月10日)和丰水期(2005年9月29日)模拟的湖泊水面(图 3a、c)与遥感影像中的湖泊水面(图 3b、d)对照.由于模拟过程中干湿判断参数网格为干的水深为0.16m,图 3a和3c图例中的第一等级水深为0~0.16m,因此,两图的模拟水面实际上是水深0.17m以上的水深分布区域.对照图 3a、b和图 3c、d可以看出,模拟水面与实际水面有较好的对应关系.

|
图 3 模拟的湖泊水面与遥感影像中的水面对照(a、b分别为1999年12月10日的模拟水面和遥感水面,c、d分别为2005年9月29日的模拟水面和遥感水面) Fig.3 Comparison of simulated water surface with images of remote sensing(a, b represent simulated water surface and remote sensing image in December 10th, 1999, respectively; c, d represent simulated water surface and remote sensing image in September 29th, 2005, respectively) |
依据鄱阳湖水利枢纽工程的调度方案,本文根据项目组长江水利委员会参加单位对长江中下游“丰、平、枯”水文年型的研究界定,选择2000年作为平水年、2004年作为枯水年、2010年作为丰水年,进行典型情景年份的模拟;根据EFDC模型的原理,在工程位址上,将网格边界条件设置为“Open BC”类型,并定义此“Open BC”的控制类型为“指定的水位”作为其强迫条件.“指定的水位”以枢纽工程调度方案定义的水位和排控方案及过程为依据来确定;以工程位址的控制水位作为边界条件输入,由于该位址上水文部门没有建相应的水位站,因此,其水位以模型来模拟,在模拟结果的基础上,结合工程调度方案的控制水位,作为边界条件输入.
模型的干湿判断参数为:格网为湿的水深为0.10m,格网为干的水深为0.15m,格网为干的时间步长为16s.模型在参数率定和模拟期间均采用自适应时间步长.
3 模拟结果分析 3.1 水利枢纽工程调度方案11m低枯水期最低控制水位对湖泊水位抬升的程度分析自2003年以来受鄱阳湖水系入湖径流量减少以及长江水资源形势变化等多种因素影响,鄱阳湖出现了枯水时间提前、水位偏低、持续时间延长等现象,对湖泊生态系统造成了一定的影响.为了减缓这些影响,鄱阳湖水利枢纽工程的调度方案设计了11月底或12月初至次年3月底或4月初低枯水期的11m最低控制水位.
由不同情景年型鄱阳湖水利枢纽工程低枯位生态调节期(12月1日至3月底4月初)中11m控制水位对该时期湖泊平均水位的抬升程度及其空间分布可以看出(图 4),2010年(丰水年)11m控制水位对枯水期湖泊平均水位的最大抬升为2.59m,2000年(平水年)枯水期湖泊的平均水位最大抬升为2.68m,而2004(枯水年)枯水期湖泊的平均水位最大抬升为4.35m.由此可以看出,鄱阳湖水利枢纽工程11.0m的控制水位对不同年型湖泊枯水期的水位起到一定的调节作用,尤其是枯水年型.枯水期的水位抬升在某种程度上可以解决湖泊出现的枯水时间提前、水位偏低、持续时间延长等问题,从而缓解湖泊旱情.
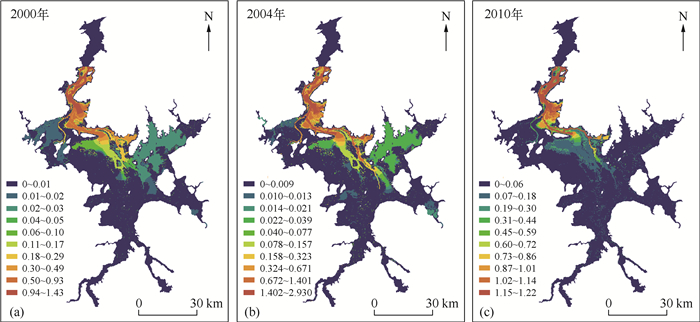
|
图 4 不同情景年型枯水期11m控制水位对枯水期湖泊平均水位的抬升程度 Fig.4 Uplift distribution of average water level of Lake Poyang during dry season in different hydro-year scenario due to the controlled water level of 11 m according to the scheme of water level regulation of the Lake Poyang hydraulic project |
为了对比分析水利枢纽对鄱阳湖流场流速的影响,在鄱阳湖选择了50个观测点,对有枢纽工程和无枢纽工程的模拟结果进行分析,所选观测点的分布见图 5.

|
图 5 观测点分布 Fig.5 Distribution of observation points |
修河与主河道汇合点以北为入江河道观测点,共8个观测点;重点湖区分吴城国家级自然保护区和南矶山湿地国家级自然保护区,主要选择核心区的观测点,共10个观测点;两个保护区及入江河道之外的观测点为主湖区观测点,共32个观测点.主湖区观测点的选择原则:以有枢纽模拟时星子11.0m控制水位所形成的鄱阳湖水陆分界线为依据.枯水期与丰水期的划分以星子水位低于10.22m为枯水期,高于13.39m为丰水期.
根据有枢纽和无枢纽模拟结果绘制的鄱阳湖入江河道、主湖区、吴城自然保护区和南矶山自然保护区年平均流速、枯水期平均流速和丰水期平均流速对比表明,枢纽工程的控水过程降低了入江河道的年平均流速,2000、2004和2010年分别由原来的0.31、0.26和0.41m/s降为0.26、0.18和0.32m/s,其降速的影响因素主要为枯水期间的水位抬升,因此枯水期的平均流速变化较大,2000、2004和2010年分别由原来的0.46、0.32和0.45m/s降为0.24、0.15和0.25m/s,分别降低了48%、53%和44%.
枢纽控水过程对主湖区平均流速的影响相对于入江河道来说比较小,2000年的平均流速没有变化,但最大流速由无枢纽时的1.34m/s到有枢纽的1.18m/s,降低了0.16m/s.2004和2010年分别由原来的0.075和0.11m/s到有枢纽时的0.061和0.09m/s(图 6b).
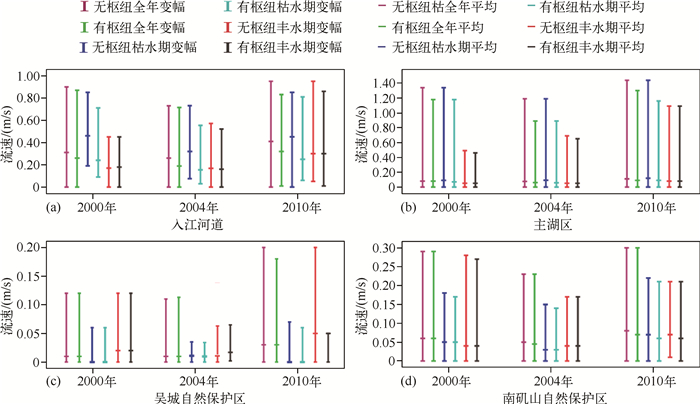
|
图 6 几个重要区域有无枢纽流速全年、枯水期、丰水期的最大值、最小值及平均值 Fig.6 Maximum, minimum and average of velocities in several import regions under both situations with hydraulic project and without hydraulic project in the whole year, low-water level and high-water level period |
枢纽控水过程对主湖区最大流速的降低作用比入江河道明显,尤其是对2000年和2004年最大流速的降低作用最为明显,这两年的最大流速分别从1.38和1.19m/s降到了1.18和0.89m/s,降幅分别达14%和25%(图 6).
枢纽工程对入江河道、主湖区和两大保护区的枯水期平均流速、最大流速和最小流速都有不同程度的影响,其中以入江河道最大,对两大保护区的影响则较小,主要影响表现在降低了两大保护区枯水期的流速变幅,但减小程度不明显(图 6).
鄱阳湖是一个吞吐型湖泊,其湖流的主要形态为吞吐流,密度流和异重流较为少见.在吞吐流中,根据流势、流向及江湖水文关系可分为重力型、倒灌型和顶托型3种湖流类型.而在上述的3种湖流中,又以重力流为主.倒灌型湖流常发生在“五河”汛期基本结束,长江水位迅速上涨并高于鄱阳湖水位,且鄱阳湖水面比降较小的7-10月.而顶托型湖流多发生在汛期,此时鄱阳湖处于“五河”与长江同时涨水,或“五河”大汛已结束,长江涨水尚未达到倒灌条件的情况下[28].按照表 1的水利枢纽工程调度方案,控水过程主要作用于当年的9月1日至次年的3月底4月初,这一时期未包含汛期.因此,水利枢纽工程对顶托型湖流不会造成影响.倒灌型湖流发生的时间与控水过程的作用时间尽管有部分重叠(9-10月),但由于水利枢纽工程调度方案主要基于“控枯不控洪”的原则,且2000、2004年倒灌发生的实际水位多半高于水利枢纽的调度水位,而2010年没有发生倒灌.为此,本文讨论水利枢纽工程对湖泊流场的影响,只考虑对湖泊重力流流场的影响.
为了进一步分析和讨论水利枢纽工程对湖泊重力流流场的影响,选取了反差最大的无枢纽最低水位流场与有枢纽时的湖流流场进行对比.图 7呈示了典型年份无枢纽最低水位时的流场与同期有枢纽的流场格局(矢量与标量).其中图 7a、b和c分别代表 2000、2004和2010年无枢纽最低水位时的湖泊流场(具体时间分别是1月7日、1月12日和1月2日,对应的星子模拟水位分别为6.72、6.65和5.80m),而图 7d、e和f分别代表对应年份同一天有枢纽流场.
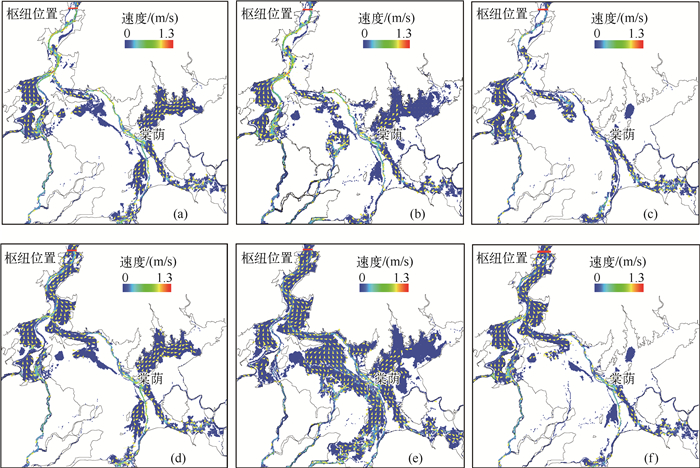
|
图 7 典型年份无枢纽最低水位时的流场与同期有枢纽的流场对比(a、b和c分别代表 2000、2004和2010年无枢纽流场,d、e和f分别代表 2000、2004和2010年有枢纽流场) Fig.7 The flow fields of typical years under both situations with hydraulic project in lowest water level and without hydraulic project in the same day(a, b and c represent without hydraulic project in the year of 2000, 2004 and 2010, respectively; d, e and f represent with hydraulic project in the year of 2000, 2004 and 2010, respectively) |
从图 7a、b和c可以看出,尽管无枢纽时不同年型的最低水位有所不同,但流场格局基本相似;棠荫东北附近湖区由于两江合流,当两江来水较大时,易在棠荫东北方向湖区出现回流场(图 7a);2010年虽为丰水年,但最低水位为5.80m,棠荫附近东北方向湖区水面比2000年及2004年的水面小很多,流场呈现较大的差异.有枢纽时由于低枯水期的11m水位控制,棠荫以北尤其是入江河道的流场与无枢纽时的流场表现出明显的不同;棠荫以南的湖区,2000年和2010年无枢纽与有枢纽的流场格局相似,但2004年由于赣江中支和赣江南支的来水较大,由于11m水位的“顶托”,在棠荫附近及松门山以南的湖区会呈现出较大的水面.对比图 7a和图 7b还可以发现,棠荫东北方向湖区出现回流场在无枢纽与有枢纽时都存在,且差异不明显,由此可以说明,枢纽工程低枯水期的11m控制水位对棠荫东北方向湖区由于局部来水较大出现的回流没有明显的增强作用.
3.3 水利枢纽工程对湖泊换水周期的影响分析利用2000、2004和2010年的模拟结果,根据换水周期的概念,计算了逐日的换水周期,其计算公式如下:
| $ {p_l} = \frac{{\sum\limits_{i = 1}^T {\sum\limits_{j = 1}^n {{\xi _j}{H_{ij}}} } }}{{86400\sum\limits_{i = 1}^T {\sum\limits_{k = 1}^m {{Q_{ik}}} } }},if\;\;{Q_{ik}} < 0,{Q_{ik}} = 0 $ | (16) |
式中,Pl为第l月的换水周期,ξ为格网j的面积(m2),H为格网j第i天的平均水深(m),n为整个湖泊计算域的格网数量(大小为96004),Q为出口断面处格网k的流量(m3/s),m为出口断面处格网数量,T为第l月的天数.86400为将时间单位“秒”转换为“天”的转换系数.发生倒灌时,出口断面流量Qik为负值,而此时的湖泊库容
从有枢纽与无枢纽条件下月换水周期可以看出(图 8),在江湖连通的4-8月期间,枢纽工程对月换水周期没有影响,但在1-3月及9-12月期间,湖泊水位由枢纽工程控制,明显增加了这些月份的换水周期.其中,月换水周期相差最大的为丰水年型(2010年)的11月,其差值为14.5d,有枢纽与无枢纽相比增加了43.4%;其次为枯水年型(2004年),最大相差天数为9.6d(10月),有枢纽与无枢纽相比增加了59.5%;平水年型(2000年)的月换水周期相差最大的为8.0d(1月),有枢纽与无枢纽相比增加了55.7%.

|
图 8 平、枯、丰年型下无、有枢纽工程时月换水周期 Fig.8 Monthly water exchange period under both situations with hydraulic project and without hydraulicproject in normal water level year,low water level year and high water level year |
从不同年型有无水利枢纽工程时年换水周期及枢纽控制期间换水周期可以看出(表 3),枢纽工程的控水过程导致了年换水周期的增加,2000、2004和2010年分别增加了2.1、3.2和1.9d,其增加比例分别为14.4%、12.4%和10.9%.
| 表 3 不同年型无、有水利枢纽工程时年换水周期及控水期间换水周期对照 Tab.3 Comparison of water-exchange periods in both whole year and control-water period under the situations with hydraulic project and without hydraulic project in three hydro-scenario years |
枢纽工程实际控水期间的换水周期变化体现了枢纽工程对湖泊换水周期的实际影响,从表 3可以看出,枢纽工程实际控水期间使2000、2004和2010年的换水周期分别增加了3.5、5.6和3.3d,增加的比例分别为24.2%、26.1%和13.1%.其中对枯水年型(2004年)影响最大.
平水年(2000年)的平均流量为4502.4m3/s,丰水年(2010年)的平均流量为7031.3m3/s,枯水年的平均流量为2934.4m3/s,从平均流量看符合“平”、“丰”、“枯”年型的标准,但从枯水期的天数来看,2000年星子水位低于10.22m的天数为100d,2010年星子水位低于10.22m的天数为148d,而2004年为172d.由此可以看出,枢纽工程对换水周期的影响与星子水位低于10.22m的枯水期天数及期间的平均水位密切相关.
4 结语本文针对拟建的鄱阳湖水利枢纽工程,在EFDC模型基础上,建立了二维的湖泊水动力模型,通过对丰、平、枯典型年份的情景模拟,探讨了鄱阳湖水利枢纽工程对不同情景年型丰水期和枯水期湖区不同空间位置水位及其抬升、流速和湖泊换水周期的可能影响,结果表明:
1) 不同情景年型鄱阳湖水利枢纽工程低枯水位生态调节期(12月1日至3月底4月初)中11m控制水位对该时期湖泊平均水位的抬升程度明显,2010年(丰水年)11m控制水位对枯水期湖泊平均水位的最大抬升为2.59m,2000年(平水年)枯水期湖泊的平均水位最大抬升为2.68m,而2004年(枯水年)枯水期湖泊的平均水位最大抬升为4.35m,因此11m控制水位对不同年型湖泊枯水期的水位可以起到有效的调节作用,尤其是枯水年型.枯水期的水位抬升在某种程度上可以解决湖泊出现的枯水时间提前、水位偏低、持续时间延长等问题,从而缓解湖泊的旱情.
2) 鄱阳湖水利枢纽工程通过控制湖泊的水位,抬升了枯水期的最低水位,使不同年型入江河道、主湖区和两大保护区的枯水期平均流速、最大流速和最小流速都有不同程度的减小,其中以入江河道为最大,2000年平水年和2010年丰水年枯水期平均流速降幅在44%以上,2004年(枯水年)枯水期的平均降速范围在50%以上.对两大保护区的影响则较小,主要影响表现在降低了两大保护区枯水期的流速变幅,但减小程度不明显.
3) 有枢纽时由于低枯水期的11m水位控制,棠荫以北尤其是入江河道的流场与无枢纽时的流场表现出明显的不同;棠荫以南的湖区,当赣江中支和赣江南支的来水较大时,在棠荫附近及松门山以南的湖区会呈现出较大的水面;但11m控制水位造成的“顶托”对棠荫东北方向湖区由于局部来水较大出现的回流没有明显的增强作用.
4) 由于湖泊水位抬升、库容增加,且流速相对减小,水利枢纽工程对湖泊换水周期的作用明显,不同年型的换水周期都受到不同程度的影响,2004年(枯水年份)枢纽工程的调度方案使低枯水位生态调节期的平均换水周期增加了5.6d,影响程度达26.1%.换水周期的增加,对湖泊水质带来一定影响.但同时也应看到,湖泊库容的增加是换水周期增加的主要因素,该因素的增加在某种程度上又将导致湖泊环境容量的增加.因此,水利枢纽工程对湖泊换水周期所造成的影响,最终给湖泊水质带来何种程度的影响,有待进一步的研究.
| [1] |
谢冬明, 郑鹏, 邓红兵等. 鄱阳湖湿地水位变化的景观响应. 生态学报, 2011, 31(5): 1269-1276. |
| [2] |
洪峰, 陈文静, 周辉明等. 鄱阳湖水利枢纽工程对水生生物影响的探讨. 江西科学, 2010, 28(4): 555-558. |
| [3] |
葛刚, 纪伟涛, 刘成林等. 鄱阳湖水利枢纽工程与湿地生态保护. 长江流域资源与环境, 2010, 19(6): 606-613. |
| [4] |
马超, 练继建. 人控调度方案对库区支流水动力和水质的影响机制初探. 天津大学学报, 2011, 44(3): 202-209. |
| [5] |
Li J. Scientists line up against dam that would alter protected wetlands. Science, 2009, 326: 508-509. DOI:10.1126/science.326_508 |
| [6] |
Humborg C, Ittekkot V, Cociasu A et al. Effect of Danube River dam on Black Sea biogeochemistry and ecosystem structure. Nature, 1997, 386(6626): 385-388. |
| [7] |
Wang B, Uwe B. Potential impacts of Three Gorges Dam in China on the ecosystem of East China Sea. Acta Oceanologica Sinica, 2008, 27(1): 67-76. |
| [8] |
傅开道, 黄河清, 钟荣华等. 水库下游水沙变化与河床演变研究综述. 地理学报, 2011, 66(9): 1239-1250. DOI:10.11821/xb201109009 |
| [9] |
Nikora V. Hydrodynamics of aquatic ecosystems: An interface between ecology, biomechanics and environmental fluid mechanics. River Research and Applications, 2010, 26(4): 367-384. DOI:10.1002/rra.v26:4 |
| [10] |
冷疏影, 杨桂山, 刘正文等. 湖泊及流域科学重点发展领域与方向. 中国科学基金, 2003(2): 82-85. |
| [11] |
Obeysekera J, Kuebler L, Ahmed S et al. Use of hydrologic and hydrodynamic modeling for ecosystem restoration. Critical Reviews in Environmental Science and Technology, 2011, 41(supp.1): 447-488. |
| [12] |
潘晓东, 王伟卓, 唐健生等. 哈达山水库水动力与水质模拟研究. 人民黄河, 2010, 32(8): 61-62. |
| [13] |
Onnish Y, Imasato N. Study on the currents in Lake Biwa(Ⅲ). Journal of the Oceanographical Society of Japan, 1979(9): 53-60. |
| [14] |
Endoh S. Diagnostic study on the vertical circulation and the maintenance mechanisms of the cyclonic gyre in Lake Biwa. Journal of Geophysical Research, 1986, 91(C1): 869-876. DOI:10.1029/JC091iC01p00869 |
| [15] |
Ferrari A, Fraccarollo L, Dumbser M et al. Three-dimensional flow evolution after a dam break. Journal of Fluid Mechanics, 2010, 663: 456-477. DOI:10.1017/S0022112010003599 |
| [16] |
陈江. 引江济太长江水源地岸线稳定性与河床演变研究[学位论文]. 南京: 河海大学, 2007. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-SLSW201212001165.htm
|
| [17] |
李云良, 张奇, 姚静等. 鄱阳湖湖泊流域系统水文水动力联合模拟. 湖泊科学, 2013, 25(2): 227-235. DOI:10.18307/2013.0208 |
| [18] |
Li Y, Zhang Q, Yao J et al. Hydrodynamic and hydrological modeling of the Lake Poyang catchment system in China. American Society of Civil Engineers, 2014, 19: 607-616. |
| [19] |
陈栋. 三峡水库非汛期水动力及水质模拟研究[学位论文]. 济南: 山东大学, 2008.
|
| [20] |
辛小康, 尹炜, 叶闽. 水动力调控三峡库区支流水华方案初步研究. 水电能源科学, 2011, 29(7): 16-18. |
| [21] |
胡春华, 施伟, 胡龙飞等. 鄱阳湖水利枢纽工程对湖区氮磷营养盐影响的模拟研究. 长江流域资源与环境, 2012, 21(6): 749-755. |
| [22] |
杜彦良, 周怀东, 毛战坡等. 鄱阳湖水利枢纽工程对水质环境影响研究. 中国水利水电科学研究院学报, 2011, 9(4): 249-256. |
| [23] |
余启辉, 马强, 游中琼. 鄱阳湖水利枢纽调度对湖区枯期水位与流速影响. 人民长江, 2013, 44(17): 18-21. DOI:10.3969/j.issn.1001-4179.2013.17.005 |
| [24] |
王鹏, 赖格英, 黄小兰. 鄱阳湖水利枢纽工程对湖泊水位变化影响的模拟. 湖泊科学, 2014, 26(1): 29-36. DOI:10.18307/2014.0104 |
| [25] |
Zhou J, Pan S, Falconer RA et al. Effects of open boundary location on the far-field hydrodynamics of a Severn Barrage. Ocean Modelling, 2014, 73: 19-29. DOI:10.1016/j.ocemod.2013.10.006 |
| [26] |
Scott CJ, Vijayasarathi J, David TH et al. Simulating pH effects in an algal-growth hydrodynamics model. Journal of Phycology, 2013, 49(3): 606-615. |
| [27] |
Krause1 P, Boyle DP, Base F. Comparison of different efficiency criteria for hydrological model assessment. Advances in Geosciences, 2005, 5: 89-97. DOI:10.5194/adgeo-5-89-2005 |
 2015, Vol. 27
2015, Vol. 27 
