水体中叶绿素a含量的高低直接影响水体的光学特性,也是表征水体富营养化程度的主要参数,所以叶绿素a浓度已经成为水体水质评价的重要指标.叶绿素浓度的反演方法主要有经验方法、半经验/半分析方法和分析方法,对于叶绿素浓度反演方法,目前国内外已有众多学者对其进行了深入的研究.李素菊等[1]根据地面实测高光谱数据和同步水质采样分析,分别利用反射率比值法和一阶微分法建立了叶绿素浓度的遥感定量模型,结果表明反射率比值法及一阶微分法与叶绿素a浓度均有较好的相关性,且反射率比值法估算叶绿素a浓度效果较好.旷达等[2]综合环境一号小卫星的CCD数据和同步地面水质监测数据,发现近红外波段与红波段比值的模型用于太湖地区叶绿素a浓度反演的精度良好.乐成峰等[3]基于季节分异对太湖叶绿素浓度反演模型进行研究,结果表明春季和秋季选用波段比值算法精度较高,夏季选用微分算法最好.Kahru等[4]结合MODIS真彩色影像,利用红波段、近红外波段叶绿素反射特征的差异建立红、近红外波段反射率差值模型,成功检测了秘鲁帕拉卡斯湾赤潮的发生.Gitelson等[5]首次提出用于估算陆地植被叶绿素含量的三波段式半分析模型,Zimba、Dall’Olmo等[6-7]将该方法应用于水体叶绿素a浓度反演,提高了反演精度.周冠华等[8]利用太湖实测的高光谱遥感数据建立三波段模型并进行波段优化,得到较高的反演精度.杨煜等[9]通过地面实测数据,建立太湖叶绿素a浓度反演模型,对比各模型反演效果,认为三波段模型反演精度最高.徐京萍等[10]利用2004年5-9月的吉林省新庙泡实测高光谱数据和实验室分析数据,建立了基于三波段的叶绿素a浓度反演模型,并优化组合了3个特征波长,结果表明用该方法建立的模型反演精度较高,适合于内陆水体叶绿素a含量的定量提取.2012年El-Alem等[11]提出了一种新的叶绿素浓度反演模型APPEL模型(APProach by ELimination),结合南魁北克4个湖泊的9年实测数据和同步MODIS影像数据对叶绿素浓度进行反演,决定系数达到0.95.
差值模型、比值模型以及三波段模型已成功应用于内陆水体的叶绿素浓度反演研究并取得较好的效果,成为内陆水体叶绿素浓度反演最常用的模型.APPEL模型是以MODIS传感器波段数据为参数,以叶绿素在红波段强吸收、近红外波段高反射的光谱特征为原理,以不同波段组合来去除悬浮物、CDOM和后向散射的影响,最终构建而成的叶绿素浓度反演模型.它是一种新的半分析模型,目前并未用于内陆水体的叶绿素浓度反演研究,所以其精度与稳定性如何,适不适合内陆水质参数的反演,这些问题还需要进一步验证.
在叶绿素浓度遥感估算方面,各国已相继发射了多种水色遥感传感器,这些卫星无疑为叶绿素浓度遥感估算提供了良好的数据源.例如美国海洋水色卫星(SeaStar)携带的海洋宽视场扫描仪SeaWiFS、搭载在美国Aqua和Terra卫星上的中分辨率光谱成像仪(MODIS)、搭载于Envisat-1卫星平台上的中等分辨率成像频谱仪(MERIS)、日本ADEOS-2卫星平台上的全球成像仪(GLI)、印度遥感卫星IRS平台上的海洋水色监测仪(OCM)、韩国发射的静止海洋观测卫星成像仪(GOCI)等.其中,MODIS于1999年12月18日发射,拥有9个为水色遥感专门设计的通道,其最大空间分辨率为250m,一天可过境4次,对各种突发性、快速变化的自然灾害有更强的实时监测能力;MERIS传感器于2002年3月发射,在可见光/近红外区域(309~1040nm)有15个水色波段,可见光波段平均带宽为10nm,中心波段位置更精细,其空间分辨率为300m,重返周期为2~3d,适用于二类水体各组分的反演;GOCI为世界首次发射的静止海洋观测卫星成像仪,发射时间为2011年4月,其具有可见光到近红外8个波段,空间分辨率为500m,其最突出的特点是从8:0015:00提供每小时的遥感影像,由于GOCI影像较高的时间分辨率和光谱分辨率,并且对于东北亚地区相对静止,其影像数据可有效用于我国东部湖泊富营养化情况的实时监测.
但是,目前的水色遥感传感器主要是为海洋遥感服务的,在内陆水体中是否适用,其稳定性如何还有待验证.此外,我国于2008年发射了环境一号卫星,该卫星由两颗光学小卫星(HJ-1A、HJ-1B)组成双星星座,时间分辨率为2d,虽然其传感器波段不是专门针对水体设置,但是,其较高的时间分辨率和30m的空间分辨率,使得该数据在内陆水环境的遥感监测中具有突出的优势.
结合以上两点,在内陆水体叶绿素浓度反演过程中,反演模型的选择和卫星数据的选择是非常重要的,二者直接影响水体叶绿素浓度的反演结果,因此基于卫星数据的叶绿素浓度反演模型适宜性分析具有十分重要的研究意义.
本文基于太湖2007年11月、2009年4月和2011年8月实测数据,选择差值模型、比值模型、三波段模型以及APPEL模型,针对HJ-CCD、MODIS、MERIS以及GOCI传感器波段设置,分别构建太湖水体叶绿素a浓度的估算模型,并分析模型的适宜性,以期确定最适合太湖水体叶绿素的反演算法,为同类卫星数据的建模和应用提供参考.
1 材料与方法 1.1 实验区概况太湖位于江苏省南部,长江三角洲中部,是中国第三大淡水湖,湖面面积、平均海拔和平均水深分别为2338.1km2、3.33m和1.9m.2007年11月、2009年4月和2011年8月分别对太湖水体进行样点采集,并去除异常数据,光谱数据的采集和水体采样同步进行.
1.2 数据获取与预处理 1.2.1 水体光谱数据的获取水体光谱数据采用美国分析光谱仪器公司(Analytical Spectral Devices)制造的ASD FieldSpec Pro便携式光谱辐射计测量,该仪器波段范围为350~1050nm,光谱分辨率为2nm.选择水面平静,天空晴朗时测量.具体按照唐军武等[12]提出的关于内陆二类水体水面以上光谱测量的方法进行测量,并最终计算出水面遥感反射率参数.地面实验于2007年11月、2009年4月和2011年8月在太湖进行,共获得有效数据88个.
1.2.2 叶绿素浓度的测量叶绿素浓度采用陈宇炜等[13]提出的浮游植物叶绿素a测定的“热乙醇法”进行测量.首先用GF/F滤膜过滤200ml水样,然后加入热乙醇水浴2min后避光萃取4~6h,萃取结束后,用25mm玻璃纤维滤膜过滤萃取液并定容至10ml,将10ml叶绿素样品萃取液在UV-2550紫外分光光度计上用90%乙醇作为参比液进行比色,先后在665nm和750nm波长处测消光率E665和E750,然后在样品比色皿中加1滴1mol/L的盐酸进行酸化,加盖摇匀,1min后重新在665nm和750nm波长处测消光率A665和A750.叶绿素a浓度计算公式为:
| $ {\rm{Chl}}.{\rm{a = 27.9}}{V_{乙醇}}[({E_{665}} - {E_{750}}) - ({A_{665}} - {A_{750}})]/{V_{样品}} $ | (1) |
式中,Chl.a为叶绿素a浓度(mg/m3),V乙醇为萃取液定容的体积(ml),V样品为过滤水样的体积(m3).
1.3 叶绿素浓度反演模型构建首先,利用水面实测光谱以波段均值法模拟HJ-CCD、MODIS、MERIS以及GOCI传感器波段光谱,HJ-CCD波段1、2、3、4的波宽分别为430~520、520~600、630~690、760~900nm; MODIS波段1、2、3、4的波宽分别为620~670、841~876、459~479、545~565nm; MERIS波段2、5、7、9、12的波宽分别为437.5~447.5、555~565、660~670、703.75~713.75、771.25~786.25nm; GOCI波段2、4、6、7、8的波宽分别为433~453、545~565、675~685、735~755、845~885nm.其次,针对各传感器波段设置,分别建立差值模型、比值模型、三波段模型和APPEL模型等叶绿素浓度反演模型.建模数据为88个太湖实测数据中随机选择的68个样点数据.
1.3.1 差值模型差值模型是根据红波段和近红外波段叶绿素的光谱特性差异建立的半分析模型[4].该模型将红、近红外波段的差值作为相关变量,进行叶绿素浓度量化反演.针对HJ-CCD、MODIS、MERIS以及GOCI传感器波段设置,太湖叶绿素浓度反演对应的量化波段如下:
| $ {\rm{HJ}} - {\rm{CCD}};[{\rm{Chl}}{\rm{.a}}] \propto R({b_4}) - R({b_3}) $ | (2) |
| $ {\rm{MODIS}};[{\rm{Chl}}{\rm{.a}}] \propto R({b_2}) - R({b_1}) $ | (3) |
| $ {\rm{MERIS}};[{\rm{Chl}}{\rm{.a}}] \propto R({b_9}) - R({b_7}) $ | (4) |
| $ {\rm{COCI}};[{\rm{Chl}}{\rm{.a}}] \propto R({b_7}) - R({b_6}) $ | (5) |
式中, R(bi)为第i波段的遥感反射率,[Chl.a]为叶绿素a浓度.
1.3.2 比值模型比值模型根据叶绿素在近红外波段高反射与红波段强吸收的特性,选用两波段比值作为光谱指数进行叶绿素浓度反演,对于不同传感器选取的波段如下:
| $ {\rm{HJ - CCD:[Chl}}{\rm{.a]}} \propto R({b_4})/R({b_3}) $ | (6) |
| $ {\rm{MODIS:[Chl}}{\rm{.a]}} \propto R({b_2})/R({b_1}) $ | (7) |
| $ {\rm{MERIS:[Chl}}{\rm{.a]}} \propto R({b_9})/R({b_7}) $ | (8) |
| $ {\rm{GOCI:[Chl}}{\rm{.a]}} \propto R({b_7})/R({b_6}) $ | (9) |
三波段模型使用1个红光波段、2个近红外波段的组合来构建叶绿素反演模型[5],定义如下:
| $ [{\rm{CH1}}.{\rm{a}}] \propto ({R^{ - 1}}({\lambda _1}) - {R^{ - 1}}({\lambda _2})) \cdot R({\lambda _3}) $ | (10) |
| $ {\rm{MERIS}}:[{\rm{Chl}} \bullet {\rm{a}}] \propto [{{\rm{R}}^{ - 1}}({b_7}) - {R^{ - 1}}({b_9})] \cdot R({b_{12}}) $ | (11) |
| $ {\rm{GOCI}}:[{\rm{Chl}} \bullet {\rm{a}}] \propto [{{\rm{R}}^{ - 1}}({b_6}) - {R^{ - 1}}({b_7})] \cdot R({b_8}) $ | (12) |
由于HJ-CCD和MODIS传感器波段设置不能完全包含理想的三波段范围,因此,无法直接采用上述方法建立三波段模型.El-Alem等[11]提出,对于MODIS数据,可采用波段1(红光波段)代替λ1叶绿素a吸收的敏感波段,选用波段1、3、4的组合代替λ2去除悬浮物和CDOM的影响[18-19],同时选用波段2近红外波段代替λ3去除后向散射的影响.由于HJ-CCD波段设置类似于MODIS的1~4波段,因此,本研究采用El-Alem等提出的方法设置MODIS和HJ-CCD数据的三波段模型参数:
| $ {\rm{HJ - CCD}}:[{\rm{Chl}}{\rm{.a}}] \propto [{{\rm{R}}^{ - 1}}({b_3}) - {R^{ - 1}}({b_1} + \frac{{\Delta {b_1}}}{{\Delta {b_2}}})] \cdot R({b_4}) $ | (13) |
| $ {\rm{MODIS}}:[{\rm{Chl}}{\rm{.a}}] \propto [{{\rm{R}}^{ - 1}}({b_1}) - {R^{ - 1}}({b_3} + \frac{{\Delta {b_3}}}{{\Delta {b_4}}})] \cdot R({b_2}) $ | (14) |
式中,对于
APPEL模型是由El-Alem等[11]针对MODIS传感器数据提出,由于近红外波段叶绿素光谱特征表现出高反射,而水体在此波段强吸收,因此可以用来获取最大的叶绿素信息量.在此波段仍有悬浮物、CDOM和后向散射的影响,因此,选用CDOM反射最强的蓝波段来去除CDOM的影响[20],同时选取近红外波段作为叶绿素的敏感波段来去除CDOM敏感波段中的叶绿素信息,近红外波段由于水体强吸收也用来去除蓝波段后向散射的影响.红波段可以作为悬浮物敏感波段的研究,来最小化悬浮物的影响,并用近红外波段去除红波段叶绿素的信息,在红、近红外波段,水体表现为强吸收特征,因此后向散射可以忽略.综上,最终得到的APPEL光谱指数为:
| $ {\rm{APPEL = }}R({b_{{\rm{NIR}}}}) - [(R({b_{{\rm{BLUE}}}}) - R({b_{{\rm{NIR}}}})) \cdot R({b_{{\rm{NIR}}}}) + (R({b_{\rm{R}}}) - R({b_{{\rm{NIR}}}}))] $ | (15) |
APPEL模型用于不同传感器的叶绿素浓度反演光谱指数如下所示:
| $ {\rm{HJ - CCD}}:[{\rm{Chl}}.{\rm{a}}] \propto R({b_4}) - [(R({b_1}) - R({b_4})) \cdot R({b_4}) + (R({b_3}) - R({b_4}))] $ | (16) |
| $ {\rm{MODIS}}:[{\rm{Chl}}.{\rm{a}}] \propto R({b_2}) - [(R({b_3}) - R({b_2})) \cdot R({b_2}) + (R({b_1}) - R({b_2}))] $ | (17) |
| $ {\rm{MERIS}}:[{\rm{Chl}}.{\rm{a}}] \propto R({b_9}) - [(R({b_2}) - R({b_9})) \cdot R({b_9}) + (R({b_7}) - R({b_9}))] $ | (18) |
| $ {\rm{COCI}}:[{\rm{Chl}}.{\rm{a}}] \propto R({b_7}) - [(R({b_2}) - R({b_7})) \cdot R({b_7}) + (R({b_6}) - R({b_7}))] $ | (19) |
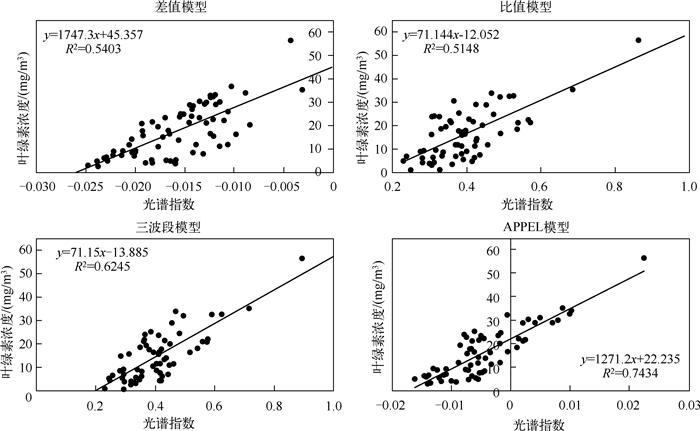
利用实测数据模拟HJ-CCD传感器波段数据,构建叶绿素反演模型的拟合结果, 可以看出4个模型的光谱指数与叶绿素浓度均呈现较好的线性关系,其中APPEL模型拟合效果最好,决定系数为0.7434,其次为三波段模型,决定系数为0.6245,两波段差值模型和比值模型的拟合结果决定系数分别为0.5403和0.5148,模型拟合精度由高到低分别为APPEL模型、三波段模型、差值模型、比值模型(图 1).
|
图 1 基于HJ-CCD波段数据模型拟合结果 Fig.1 Fitting results of the models based on the band data of HJ-CCD sensor |
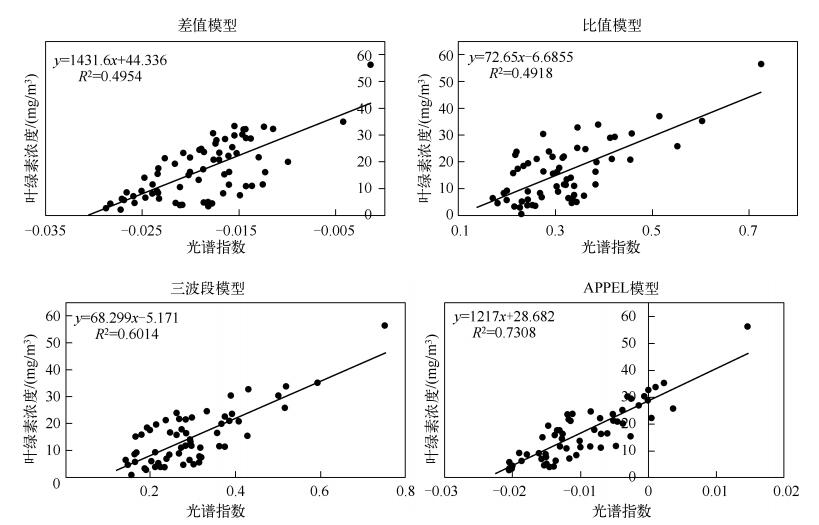
利用实测数据模拟MODIS传感器波段数据,构建叶绿素反演模型的拟合结果, 可以看出APPEL模型拟合结果最好,决定系数为0.7308,三波段模型决定系数为0.6014,差值模型和比值模型拟合结果决定系数均在0.5以下,分别为0.4954和0.4918,模型拟合精度由高到低分别为APPEL模型、三波段模型、差值模型、比值模型(图 2).
|
图 2 基于MODIS波段数据模型拟合结果 Fig.2 Fitting results of the models based on the band data of MODIS sensor |
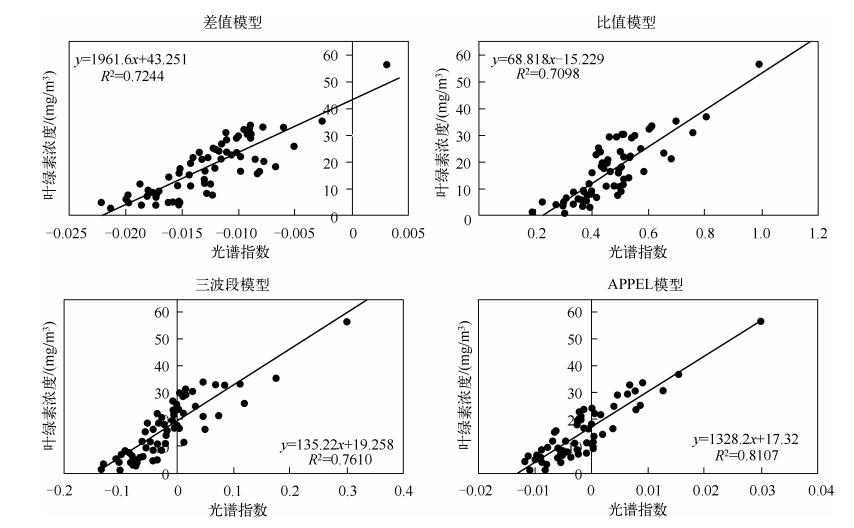
利用实测数据模拟MERIS传感器波段数据,构建叶绿素反演模型的拟合结果, 可以看出三波段模型和APPEL模型拟合的光谱指数与叶绿素浓度呈现出很好的线性相关,决定系数分别为0.7610和0.8107,差值模型和比值模型拟合的光谱指数与叶绿素浓度也有较好的线性相关,并且模型决定系数都在0.7以上,模型拟合精度由高到低分别为APPEL模型、三波段模型、差值模型、比值模型(图 3).
|
图 3 基于MERIS波段数据模型拟合结果 Fig.3 Fitting results of the models based on the band data of MERIS sensor |
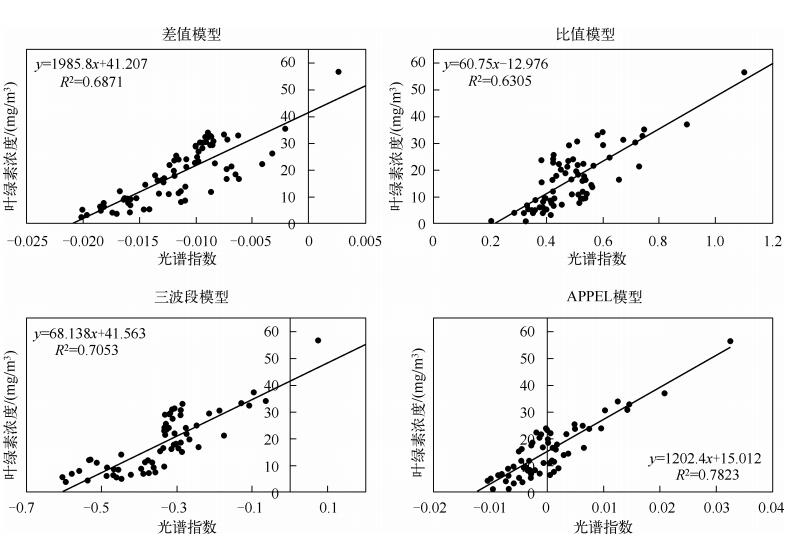
利用实测数据模拟GOCI传感器波段数据,构建叶绿素反演模型的拟合结果, 可知APPEL模型拟合结果的决定系数为0.7823,三波段模型决定系数为0.7053,差值模型和比值模型的决定系数分别为0.6871和0.6305,模型拟合精度由高到低分别为APPEL模型、三波段模型、差值模型、比值模型(图 4).
|
图 4 基于GOCI波段数据模型拟合结果 Fig.4 Fitting results of the models based on the band data of GOCI sensor |
基于水色遥感传感器的太湖水体叶绿素浓度反演模型拟合结果可以看出,APPEL模型拟合结果决定系数都在0.73以上.三波段模型拟合结果决定系数都在0.6以上,其精度与稳定性都较APPEL模型差.差值模型和比值模型对于不同的传感器波段设置,模型拟合结果有一定的波动,差值模型拟合决定系数为0.4954~0.7244,比值模型拟合决定系数为0.4918~0.7098.这是因为差值模型和比值模型均为两波段模型,二者建模原理是基于红、近红外波段叶绿素光谱特性的差异,构建红、近红外波段的差值和比值作为光谱参数,并未去除悬浮物、CDOM以及后向散射等的影响,降低了模型适用性与稳定性.而三波段模型和APPEL模型考虑到了悬浮物、CDOM以及后向散射等的影响并对其进行了去除,一定程度上提高了模型的精度.
从模型拟合结果还可以看出,对于同一叶绿素浓度反演模型,基于MERIS传感器波段设置的模型模拟结果精度最好,其次分别为基于GOCI传感器波段设置拟合结果、基于HJ-CCD传感器波段设置拟合结果、基于MODIS传感器波段设置拟合结果.
2.2 模型外推适应性分析利用未参与建模的数据,对所建模型的外推适应性进行分析.在此,分别采用相对误差(Er)和相对均方根误差(RMSEr)两个指标对模型反演结果进行评价:
| $ Er = \left| {\left( {\frac{{E{s_i} - {O_i}}}{{{O_i}}}} \right)} \right| $ | (20) |
| $ RMSEr = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {\frac{{E{s_i} - {O_i}}}{{{O_i}}}} \right)}^2}} } $ | (21) |
式中,n是样点数目,Oi和Esi分别为第i个样点的实测值和模型估算值.
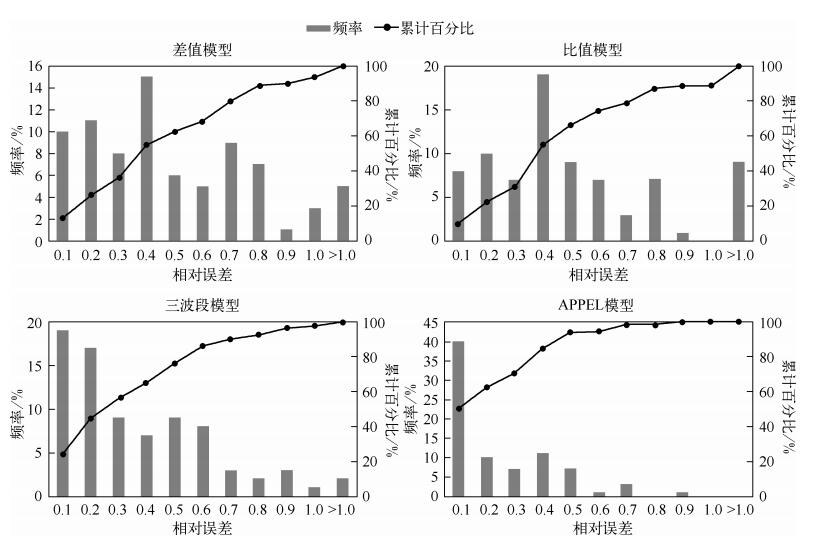
图 5为基于不同传感器波段数据的4个模型验证结果相对误差频率分布直方图,差值模型有36%的样点相对误差小于0.3,并且有7%的样点相对误差大于1.比值模型相对误差小于0.3的样点数占31%,有11%的样点相对误差大于1.三波段模型外推验证结果56%的样点相对误差小于0.3,相对误差大于1的样点数占3%.APPEL模型接近一半的样点相对误差小于0.1,占总样点数的48%,71%的样点相对误差小于0.3.
|
图 5 模型验证结果相对误差频率分布直方图 Fig.5 Frequency distribution and cumulative percentage of the relative errors |
对4种模型反演叶绿素a浓度的反演值和实测值进行相对误差统计和相对均方根误差统计,结果如表 1所示.整体来说,APPEL模型的外推结果最好,具有很高的稳定性,对于不同传感器波段设置和不同的传感器波段宽度,模型敏感度较低,叶绿素浓度反演值与实测值的相对误差与相对均方根误差均较小,相对误差为15%~24%,相对均方根误差为21%~32%.三波段模型对于不同传感器波段数据,模型外推结果的相对误差为28%~36%,相对均方根误差为39%~46%.差值模型验证结果相对误差为39%~53%,相对均方根误差为51%~72%,比值模型验证结果相对误差为41%~55%,相对均方根误差为56%~75%.外推验证结果显示模型外推性由高到低分别为APPEL模型、三波段模型、差值模型、比值模型.
| 表 1 模型相对误差与均方根误差统计 Tab.1 Relative error and relative root mean square error of these models |
综合对4种叶绿素浓度反演模型的精度分析可知,APPEL模型在不同传感器拟合结果中和模型外推适宜性分析结果中都显示出很好的精度与稳定性,三波段模型在不同传感器数据叶绿素浓度反演过程中精度有小范围的波动,模型外推适宜性分析结果显示三波段模型的稳定性较APPEL模型低,差值模型和比值模型不论在拟合结果还是外推适宜性分析当中都表现出较大的精度波动,模型的稳定性相对较差.所以APPEL模型因其较好的稳定性与外推性,可以推广到遥感水色卫星反演太湖水体叶绿素浓度.
2.3 基于不同传感器波段参数的APPEL模型适应性分析APPEL模型拟合结果决定系数均在0.73以上,对于不同的水色传感器波段数据模型的稳定性较强.其中,基于MERIS传感器数据的模型拟合精度为0.8107,基于GOCI传感器数据的模型拟合精度为0.7823,基于HJ-CCD传感器数据的模型拟合精度为0.7434,基于MODIS传感器数据的模型拟合精度为0.7308.在模型外推适宜性验证结果当中,基于MERIS传感器数据建模的验证结果相对误差和相对均方根误差分别为15%和21%,基于GOCI传感器数据建模的验证结果相对误差和相对均方根误差分别为19%和23%,基于HJ-CCD传感器数据建模的验证结果相对误差和相对均方根误差分别为22%和27%,基于MODIS传感器数据建模的验证结果相对误差和相对均方根误差分别为24%和32%.可以看出基于不同传感器波段设置的APPEL模型精度与稳定性由高到低分别为基于MERIS传感器波段设置、基于GOCI传感器波段设置、基于HJ-CCD传感器波段设置、基于MODIS传感器波段设置.不同传感器参数建立的模型精度不同的原因主要是,建模所用实测数据的光谱曲线显示红波段的叶绿素吸收峰和近红外波段的叶绿素反射峰分别位于677和707nm附近,且CDOM的敏感波段位于440nm附近,而建模所用的遥感传感器波段设置与这些特征波长均有不同程度的偏离,不能最大程度地获取特征信息.并且不同传感器的光谱分辨率不同,也会影响特征信息的获取.这些问题都会对模型精度产生不同程度的影响.
2.4 传感器波段设置对模型精度的影响分析从模型拟合结果和外推性验证结果可以看出,对于不同模型,基于MERIS传感器波段数据的模型拟合结果精度和外推性都是最好的,其次为GOCI、HJ-CCD、MODIS.分析实测数据遥感反射率和叶绿素浓度之间的相关性可以看出,相关系数最小值出现在叶绿素吸收波段677nm,相关系数最大值出现在叶绿素反射峰值附近的707nm,通过循环迭代方法得出三波段最佳位置分别为677、706、730nm.结合建模使用的传感器波段参数,对于叶绿素强吸收的红波段HJ-CCD、MODIS、MERIS、GOCI对应的波段中心波长分别为660、645、665、680nm,分别和特征波长相差17、32、12、3nm.对于叶绿素高反射的近红外波段HJ-CCD、MODIS、MERIS、GOCI对应的波段中心波长分别为830、858.5、708.75、745nm,分别和特征波长相差123、151.5、1.75、38nm.对于730nm波段MERIS、GOCI对应的波段中心波长分别为778.75、865nm,分别和特征波长相差48.75、135nm,而基于HJ-CCD和MODIS传感器的三波段建模使用了波段组合代替近红外波段.对于CDOM敏感波段440nm,HJ-CCD、MODIS、MERIS、GOCI对应的波段中心波长分别为475、469、442.5、443nm,和特征波长分别相差35、29、2.5、3nm.MERIS和GOCI的波段设置都较为接近特征波长,相比较之下,HJ-CCD和MODIS的波段设置和特征波长有较大偏离.另一方面,不同传感器的光谱分辨率不同,这些因子都会对叶绿素浓度模型反演的最终效果产生影响.
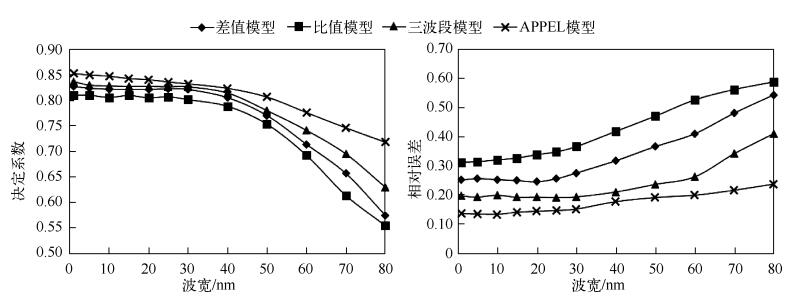
2.4.1 波段宽度的影响为了检验波段宽度对叶绿素浓度反演模型的影响,以实测数据分析出的特征波长作为中心波长,分别拟合出1、5、10、15、20、25、30、40、50、60、70、80nm波宽的各特征波段,然后构建叶绿素浓度反演差值模型、比值模型、三波段模型和APPEL模型.从图 6可以看出,模型拟合精度和验证精度由高到低分别为APPEL模型、三波段模型、差值模型和比值模型.当波宽在1~30nm之间变化时,4个模型拟合结果决定系数呈现比较稳定的趋势,在0.81~0.86之间略微变动;当波段宽度大于30nm时,模型拟合结果决定系数呈现降低趋势,并在40nm之后明显降低;当波宽为80nm时,差值模型、比值模型、三波段模型和APPEL模型的决定系数分别为0.57、0.55、0.63和0.70.模型验证结果与拟合结果一致,波宽小于30nm时,验证结果相对误差和相对均方根误差波动不明显,波宽大于30nm时,验证结果相对误差和相对均方根误差开始逐渐增大.模型的精度随波宽的增加而逐渐降低的原因主要是当波宽较小时,叶绿素特征波长处的信息可以最大程度被获取,模型的信噪比高,而当波宽变大,较大的波段宽度包含更多的噪声,对叶绿素特征信息产生一定程度的模糊,降低了模型的信噪比.另外,由于红、近红外波段比较接近,当波段过宽时,两个波段的光谱信息会出现互相包含现象,这都会影响模型的精度与稳定性.从上述分析可以看出在特征波长处,当波段宽度小于30nm时,波宽的变化对4个模型的精度不会产生较大的影响.
|
图 6 以特征波长为中心不同波段宽度模型拟合结果与验证结果 Fig.6 Fitting and validation results of the models based on different band widths centering around the characteristics wavelengths |
为了验证波段位置对叶绿素浓度反演模型精度的影响,以HJ-CCD、MODIS、MERIS、GOCI各波段中心波长作为中心波长,分别拟合出1、5、10、20、30、40、50、60、70、80nm波宽的各特征波段,构建叶绿素浓度反演差值模型、比值模型、三波段模型和APPEL模型,模型拟合结果和验证结果如图 7、图 8所示.

|
图 7 以传感器波段中心波长为中心的不同波段宽度模型拟合结果 Fig.7 Fitting results of the models based on different band widths centering around the center wavelengths of the sensor bands |
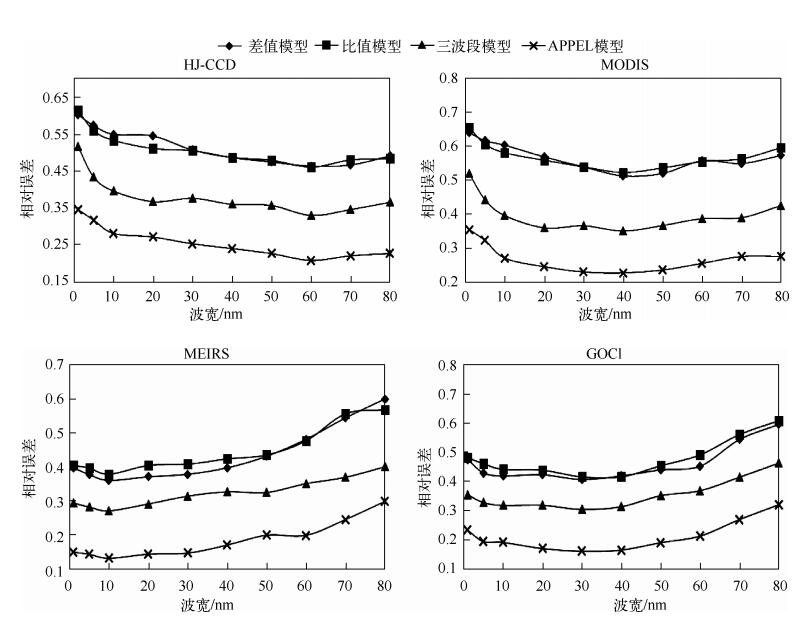
|
图 8 以传感器波段中心波长为中心的不同波段宽度模型验证结果 Fig.8 Validation results of the models based on different band widths centering around the center wavelengths of the sensor bands |
从模型拟合结果与验证结果可以看出,对于不同的波段位置与波段宽度,APPEL模型的精度最高,其次是三波段模型,差值模型和比值模型反演精度相对较低.
对于HJ-CCD传感器,波段宽度从1~60nm变化时,各模型的拟合结果决定系数呈现逐渐增大的趋势,并且模型验证结果相对误差逐渐减小.波宽为60nm处各模型的反演精度最好,差值模型、比值模型、三波段模型和APPEL模型拟合结果决定系数分别为0.6、0.58、0.66、0.77,验证结果相对误差分别为0.44、0.46、0.32、0.20.当波段宽度大于60nm之后,各模型的精度开始呈现下降趋势.对于MODIS传感器,当波段宽度从1~40nm逐渐增加,各模型的精度逐渐升高.对于MODIS传感器波段设置来说,波段宽度为40nm时,各模型的反演精度最优,差值模型、比值模型、三波段模型和APPEL模型拟合结果决定系数分别为0.57、0.56、0.64、0.75,验证结果相对误差分别为0.51、0.52、0.35、0.23,波宽大于40nm后模型精度开始下降.对于MERIS传感器波段位置设置,当波段宽度为10nm时,各模型反演精度最高,差值模型、比值模型、三波段模型和APPEL模型拟合结果决定系数分别为0.74、0.74、0.79、0.84,验证结果相对误差分别为0.36、0.38、0.27、0.13,当波宽由10nm逐渐增加时,模型的精度逐渐降低.对于GOCI传感器波段设置,波段宽度从1~30nm,模型反演精度逐渐升高,30nm处各模型的精度最高,差值模型、比值模型、三波段模型和APPEL模型拟合结果决定系数分别为0.72、0.68、0.75、0.80,验证结果相对误差分别为0.41、0.42、0.30、0.17,30nm之后模型精度开始降低.
综上所述,传感器波段的光谱范围对叶绿素浓度反演模型的精度产生一定影响,由于不同传感器波段位置设置并不相同,对于相同的叶绿素浓度反演模型,其最优的光谱范围也不相同.例如MERIS传感器的波段位置比较接近叶绿素的特征波长,因此较小的波谱范围即可包含大量特征信息,而波宽增加时,噪声也相应增加,模型的信噪比降低.而HJ-CCD传感器的波段位置离叶绿素特征波长较远,所以波段光谱范围较窄时,波段包含的叶绿素特征信息较少,影响模型反演精度,当波段宽度增加到一定范围时,波段内信噪比增大,模型精度得到提高.所以对于不同的波段设置,特定宽度的光谱范围才能够最大程度地增加模型的信噪比,得到最为理想的反演结果.
3 结论本文利用太湖水体实测水质参数和同步光谱数据,结合HJ-CCD、MODIS、MERIS、GOCI传感器波段参数,分别建立差值模型、比值模型、三波段模型和APPEL模型反演太湖水体叶绿素浓度,并对反演结果进行比较分析.
太湖叶绿素浓度反演模型精度由高到低分别是APPEL模型、三波段模型、差值模型、比值模型,对于同一模型,按反演精度由高到低顺序,模型使用的传感器数据分别为MERIS、GOCI、HJ-CCD、MODIS.APPEL模型具有相对较好的稳定性与外推性,可以推广到遥感水色卫星反演太湖水体叶绿素浓度.
不同的波段宽度与波段位置对叶绿素浓度反演模型有一定影响,相对而言,波段位置的设置对叶绿素浓度反演具有更加重要的影响,当波段位置接近叶绿素特征波长时,较窄的波宽有利于提高模型的精度,波段位置和叶绿素浓度特征波长相差较大时,合理地增加波谱范围有利于叶绿素特征信息的获取.
| [1] |
李素菊, 吴倩, 王学军等. 巢湖浮游植物叶绿素含量与反射光谱特征的关系. 湖泊科学, 2002, 14(3): 230-233. |
| [2] |
旷达, 韩秀珍, 刘翔等. 基于环境一号卫星的太湖叶绿素a浓度提取. 中国环境科学, 2010, 30(9): 1268-1273. |
| [3] |
乐成峰, 李云梅, 孙德勇等. 基于季节分异的太湖叶绿素浓度反演模型研究. 遥感学报, 2007, 11(4): 473-480. DOI:10.11834/jrs.20070466 |
| [4] |
Kahru M, Michell BG, Diaz A et al. MODIS detects a devastating algal bloom in Paracas Bay, Peru. EOS, 2004, 85(45): 465-472. |
| [5] |
Gitelson AA, Merzlyak MN. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. Journal of Plant Physiology, 2003, 160(3): 271-282. DOI:10.1078/0176-1617-00887 |
| [6] |
Zimba PV, Gitelson A. Remote estimation of chlorophyll concentration in hyper-eutrophic aquatic systems: Model tuning and accuracy optimization. Aquaculture, 2006, 256(1): 272-286. |
| [7] |
Dall'Olmo G, Gitelson AA. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: experimental results. Applied Optics, 2005, 44(3): 412-422. DOI:10.1364/AO.44.000412 |
| [8] |
周冠华, 柳钦火, 马荣华等. 基于半分析模型的波段最优化组合反演混浊太湖水体叶绿a. 湖泊科学, 2008, 20(2): 153-159. DOI:10.18307/2008.0203 |
| [9] |
杨煜, 李云梅, 王桥等. 富营养化的太湖水体叶绿素a浓度模型反演. 地球信息科学学报, 2009, 11(5): 597-603. |
| [10] |
徐京萍, 张柏, 宋开山等. 基于半分析模型的新庙泡叶绿素a浓度反演研究. 红外与毫米波学报, 2008, 27(3): 197-201. |
| [11] |
El-Alem A, Chokmani K, Laurion I et al. Comparative analysis of four models to estimate chlorophyll-a concentration in case-2 waters using MODerate Resolution Imaging Spectroradiometer(MODIS) Imagery. Remote Sensing, 2012, 4(8): 2373-2400. DOI:10.3390/rs4082373 |
| [12] |
唐军武, 田国良, 汪小勇等. 水体光谱测量与分析(Ⅰ):水面以上测量法. 遥感学报, 2004, 8(1): 37-44. DOI:10.11834/jrs.20040106 |
| [13] |
陈宇炜, 陈开宁, 胡耀辉. 浮游植物叶绿素a测定的"热乙醇法"及其测定误差的探讨. 湖泊科学, 2006, 18(5): 550-552. DOI:10.18307/2006.0519 |
| [14] |
Dall'Olmo G, Gitelson AA. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: experimental results. Applied Optics, 2005, 44(3): 412-422. DOI:10.1364/AO.44.000412 |
| [15] |
Gitelson AA, Schalles JF, Hladik CM. Remote chlorophyll-a retrieval in turbid, productive estuaries: Chesapeake Bay case study. Remote Sensing of Environment, 2007, 109(4): 464-472. DOI:10.1016/j.rse.2007.01.016 |
| [16] |
Babin M, Stramski D. Light absorption by aquatic particles in the near-infrared spectral region. Limnology and Oceanography, 2002, 47(3): 911-915. DOI:10.4319/lo.2002.47.3.0911 |
| [17] |
Gons HJ. Optical teledetection of chlorophyll a in turbid inland waters. Environmental Science & Technology, 1999, 33(7): 1127-1132. |
| [18] |
Liu W, Liu Y, Mannaerts CM et al. Monitoring variation of water turbidity and related environmental factors in Poyang Lake National Nature Reserve, China. In: eoinformatics 2007. International Society for Optics and Photonics, 2007: 67541H-67541H-12.
|
| [19] |
Hu C, Chen Z, Clayton TD et al. Assessment of estuarine water-quality indicators using MODIS medium-resolution bands: Initial results from Tampa Bay, FL. Remote Sensing of Environment, 2004, 93(3): 423-441. DOI:10.1016/j.rse.2004.08.007 |
| [20] |
Luciani X. Analyse numérique des spectresde fluorescence 3D issus de mélanges non linéaires[Dissertation]. Toulon: Université du Sud Toulon Var, 2007.
|
| [21] |
金惠淑, 鱼京善, 孙文超等. 基于GOCI遥感数据的湖泊富营养化监测研究. 北京师范大学学报:自然科学版, 2013, 49(2/3): 271-274. |
| [22] |
刘小丽, 沈芳, 朱伟健等. MERIS卫星数据定量反演长江河口的悬沙浓度. 长江流域资源与环境, 2009, 18(11): 1026-1030. DOI:10.3969/j.issn.1004-8227.2009.11.006 |
| [23] |
李云梅, 黄家柱, 韦玉春等. 用分析模型方法反演水体叶绿素的浓度. 遥感学报, 2006, 10(2): 169-175. |
| [24] |
周正, 何连, 刘良明. 基于HJ-1A/B CCD数据的东湖叶绿素a浓度反演可行性研究. 测绘通报, 2011(3): 11-14. |
| [25] |
李云亮, 张运林. 基于TM影像的太湖夏季悬浮物和叶绿素a浓度反演. 遥感信息, 2008, 6(2): 22-27. |
| [26] |
杜聪, 王世新, 周艺等. 利用Hyperion高光谱数据的三波段法反演太湖叶绿素a浓度. 环境科学, 2009, 30(10): 2904-2910. DOI:10.3321/j.issn:0250-3301.2009.10.015 |
| [27] |
佘丰宁, 李旭立, 蔡启铭等. 水体叶绿素含量的遥感定量模型. 湖泊科学, 1996, 8(3): 201-207. DOI:10.18307/1996.0302 |
| [28] |
李伟, 殷为, 郑小慎等. 利用SeaDAS从SeaWiFS卫星数据反演中国东海叶绿素浓度. 海洋湖沼通报, 2009(4): 152-156. |
| [29] |
闻建光, 肖青, 杨一鹏等. 基于Hyperion数据的太湖水体叶绿素a浓度遥感估算. 湖泊科学, 2006, 18(4): 327-336. DOI:10.18307/2006.0402 |
| [30] |
黄昌春, 李云梅, 徐良将等. 内陆水体叶绿素反演模型普适性及其影响因素研究. 环境科学, 2013, 34(2): 525-531. |
| [31] |
李云亮, 张运林, 李俊生等. 不同方法估算太湖叶绿素a浓度对比研究. 环境科学, 2009, 30(3): 680-686. |
| [32] |
焦红波, 查勇, 李云梅等. 基于高光谱遥感反射比的太湖水体叶绿素a含量估算模型. 遥感学报, 2006, 10(2): 242-248. |
| [33] |
李莉, 尹球, 巩彩兰等. 太湖不同叶绿素a浓度水体荧光特征分析. 光谱学与光谱分析, 2011, 31(1): 136-140. |
 2015, Vol. 27
2015, Vol. 27 

