(2: 环保部卫星环境应用中心,北京 100029)
(2: Satellite Environment Application Center, Ministry of Environmental Protection, Beijing 100029, P.R.China)
太湖是我国第三大淡水湖,是长江中下游地区最典型的浅水湖泊,全湖水面面积2338 km2,湖泊长度69 km,平均宽度34 km,平均水深1.89m,平底水浅是太湖湖盆的一个显著特点[1].近年来太湖水体富营养化严重,蓝藻水华频繁暴发,严重危害了区域的可持续发展.叶绿素a浓度作为水体富营养化和水质评价的重要指标,一直是水环境监测的主要参数.目前,对其进行监测的方法主要有地面采样分析和遥感监测.常规采样监测主要存在取样点少和覆盖面积小的缺点,难以反映太湖区域全面、动态的信息.利用遥感技术对叶绿素a浓度进行监测,有着速度快、范围广、相对成本低的优势.但是受卫星的时间分辨率和天气状况的影响,遥感反演数据难以连续、动态地反映水体组分参数.
数据同化方法提供了将多源数据融合,结合模型和观测信息,进行数据连续模拟、预测的手段.数据同化技术已经广泛应用于气象、土壤、水文、海洋、生态等多个领域. Pathmathevan等[2-3]进行了土壤水分同化试验;Moradkhani等[4]基于Kalman滤波数据同化方法对水文模型的状态、参数同时进行估计;Gregg[5]利用三维全球海洋数值模型同化SeaWiFS海洋叶绿素数据,有效地提高了模型结果精度;Gu等[6]利用数据同化方法重构了高质量的MODIS NDVI数据.
数据同化方法主要分为两类:变分法和顺序同化法[7].近年来,以卡尔曼滤波为代表的顺序数据同化方法在很多领域都得到了广泛应用.而基于集合论和统计估计理论的集合卡尔曼滤波具有程序设计相对简单、不需要伴随或切线性算子、可以应用于非线性系统等优点,克服与弥补了传统卡尔曼滤波中的缺陷.集合卡尔曼滤波的方法首先是由Evensen在1994年引入的[8],由于其相对四维变分而言计算相对简单,可操作性强、计算成本相对较低,近年来引起了人们的广泛关注.该方法在气象、海洋方面都有广泛的应用[9].近年来,为了避免采样误差,确定性方法随之产生,这些方法主要包括集合均方根滤波、集合调整滤波、集合变换卡尔曼滤波等[10-15].
将数据同化模型引入太湖水环境监测中,可以利用遥感反演的水质参数信息,结合太湖水体动力学数值模型,模拟水质参数的扩散和运输,从而连续、动态地反映太湖水质情况.但是,模型的适用性、运行效率等都有待于进一步检验.本研究以叶绿素a浓度为监测指标,基于集合均方根滤波和太湖叶绿素扩散模型,利用2009年4月21日环境一号卫星的叶绿素a浓度场反演信息,研究和分析样本数目、同化时长、背景场误差、观测误差和模型误差对同化系统性能的影响.同时为同化系统在将来的实际应用寻求最佳的参数组合.
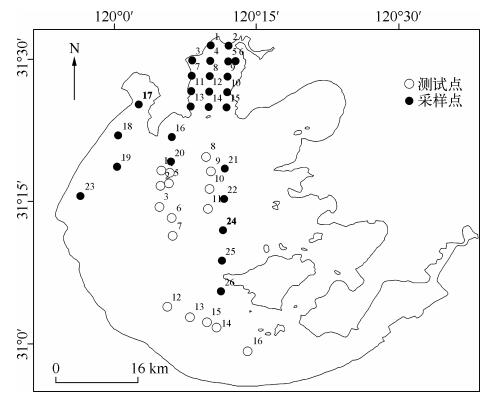
1 数据与方法 1.1 研究区与样点分布以太湖为实验区,2009年4月21日在太湖布设了26个采样点(图 1),对叶绿素a浓度及水面光谱进行了野外实地观测.此外,本课题组在太湖湖心区布设有浮标和平台水质监测站点,Taihu因此在太湖湖心区随机选取了16个同化系统敏感性分析的测试点(图 1).以这些测试点为例,分析和评价样本数目、同化时长、背景场误差、观测误差和模型误差对同化系统性能的影响.
|
图 1 太湖样点分布 Fig.1 The distribution of sample sites and test sites in Lake |
野外实测数据包括水面光谱的采集和26个样点的叶绿素a浓度测量.
水面的反射光谱采用美国ASD公司生产的ASD Handheld Spectroradiometer便携式光谱辐射计测量,其波段范围为350~1050nm,光谱分辨率为2nm.为了减少水体镜面反射和船体阴影的影响,更好地提取出反映水体信息的离水辐亮度Lw和遥感反射率Rrs,采用唐军武等[16]提出的关于内陆Ⅱ类水体水面以上光谱测量的方法.测量时,天空晴朗无云,湖面平静,待船停稳后,在甲板开阔处(距水面1m左右)分别测量标准灰板、遮挡标准灰板、水体和天空光的光谱信息,以上4个参数各测量10条光谱曲线,在测量水面反射光谱的同时记录各测点的GPS坐标和当时的风速、风向以及时间.遥感反射率通常利用式(1)进行计算[17]:
| $ {{R}_{\text{rs}}}=\frac{({{L}_{\text{sw}}}-r{{L}_{\text{sky}}}){{\rho }_{\text{p}}}}{\text{ }\pi \text{L}_{\text{p}}^{*}} $ | (1) |
式中,Lsw为总的辐亮度,Lsky为天空漫反射光,不带有任何水体信息,r参照唐军武等[17]的研究取值为0.025,Lp*为标准灰板实测值,ρp为参考板的反射率.
在光谱采集的同时采集表层水样,低温冷藏带回实验室测量叶绿素浓度.叶绿素浓度的测量采用常规的化学分析方法,用0.45μm的GF/F滤膜过滤,90%的热乙醇提取,然后利用分光光度计检测,叶绿素浓度获取的详细步骤见文献[18].
1.3 卫星数据及预处理环境一号卫星是由我国于2008年9月发射升空的,包括两颗光学卫星(HJ-1A卫星和HJ-1B卫星)和一颗雷达卫星(HJ-1C卫星),拥有光学、红外、超光谱多种探测手段,具有大范围、全天候、全天时、动态的环境和灾害监测能力[19].伴随着环境一号卫星的发射升空和遥感技术的不断发展,众多学者利用环境一号卫星在水体环境遥感监测方面取得了大量的研究成果[20-22].本文利用2009年4月21日环境一号卫星(HJ-1B CCD2)影像数据,结合野外实测叶绿素a浓度反演太湖叶绿素a浓度场信息.
图像预处理部分包括4步,第1步:辐射定标;第2步:几何校正;第3步:大气校正;第4步:水体提取.其中大气校正参考Freitas在2009年提出的校正方法.首先计算大气顶层的遥感反射率(RTOA),然后在地面实测点位中寻找在时间和空间上的准同步点位.利用该点位的实测遥感反射率(RBOA),计算同步的RTOA与RBOA之间的差值,认为该差值是大气贡献率.假设在研究区太湖上空大气状况均一,从而最终将该点的大气贡献率应用到整个太湖.具体校正方法参考文献[23].
1.4 初始背景场的生成本研究将使用HJ-1卫星的叶绿素a浓度反演结果作为基于风生流的叶绿素a扩散模型(见1.5节)的初始浓度场及太湖叶绿素a同化系统(见2.2节)的初始背景场.为此,首先利用经过数据预处理的环境一号卫星(HJ-1B CCD2)影像数据,结合地面实测叶绿素a浓度,构建叶绿素a浓度反演模型.在满足精度需求的条件下,遵循模型易于构建和易于业务化运行的原则,通过模型的构建与遴选,最终确定了单波段反演模型.构建的单波段反演模型为:
| $ y = - 42.67\ln x - 139.54 $ | (2) |
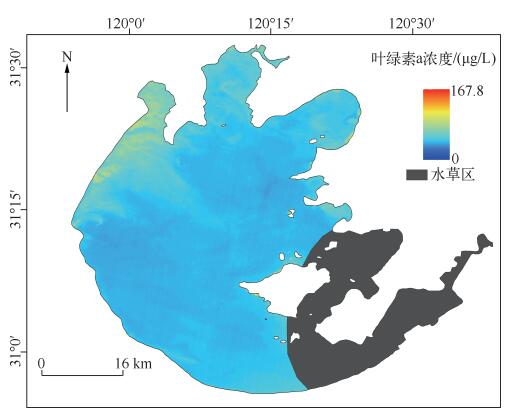
式中,x为环境一号卫星(HJ-1B)第4波段(760~900nm)的遥感反射率,y为叶绿素a浓度(μg/L).其中,野外实测26个样点的叶绿素a浓度数据,随机选取18个样点数据用来构建反演模型,剩余8个点用来进行模型精度验证.建模R2为0.938,验证数据与反演结果的散点图可以看出(图 2),验证数据较好地分布在1 :1线两侧,而且RMSE为4.1985μg/L,平均相对误差为29.3%,精度满足实验需求.基于单波段反演模型,结合HJ-1B卫星影像数据,反演了2009年4月21日太湖叶绿素a浓度,结果如图 3所示.

|
图 2 反演与实测叶绿素a浓度对比 Fig.2 Comparison of retrieved and measured chlorophyll-a concentrations |
|
图 3 太湖叶绿素a浓度分布 Fig.3 The distribution of chlorophyll-a concentration in Lake Taihu |
假设湖水为均匀不可压的流体,垂直方向服从静水压力分布,采用笛卡尔左手直角坐标系,x轴和y轴位于湖水的平均水平面上,x轴向东为正,y轴向北为正,z轴向上为正.流体动力学方程为[24-25]:
| $ \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} = fv - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {A_{\rm{h}}}\left[ {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right] + {A_z}\frac{{{\partial ^2}u}}{{\partial {z^2}}} $ | (3) |
| $ \frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} = fu - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {A_{\rm{h}}}\left[ {\frac{{{\partial ^2}v}}{{\partial {x^2}}}v + \frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right] + {A_z}\frac{{{\partial ^2}v}}{{\partial {z^2}}} $ | (4) |
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0 $ | (5) |
| $ p = {\rho _w}g(\eta + z) $ | (6) |
将连续方程垂向积分可得到自由面方程:
| $ \frac{\partial \eta }{\partial t}+\frac{\partial }{\partial x}[\int_{-h}^{\eta }{u\text{d}z}]+\frac{\partial }{\partial y}[\int_{-h}^{\eta }{v\text{d}z}]=0 $ | (7) |
式中,u、v、w分别为x、y、z轴上的流速分量;η为垂直方向上湖面相对于平均水面的高度;ρw是水体密度;Az和Ah分别是垂直和水平的涡粘系数;f为柯氏力,为7.23×10-5;g为重力加速度;p为水的压强.
叶绿素a浓度的控制方程为:
| $ \frac{{\partial c}}{{\partial t}} + \frac{{\partial uc}}{{\partial x}} + \frac{{\partial vc}}{{\partial y}} + \frac{{\partial wc}}{{\partial z}} = \frac{\partial }{{\partial z}}\left( {{v_c}\frac{{\partial c}}{{\partial z}}} \right) + {F_c} + S $ | (8) |
式中,c为叶绿素a浓度(μg/L).该模型的数值解法参考文献[24-25],可以有效地估算和预测叶绿素a浓度.
2 叶绿素数据同化模型构建 2.1 数据同化方案本研究中的太湖叶绿素a数据同化系统主要由数据同化算法(基于集合均方根滤波的数据同化方法)、叶绿素扩散模拟模型、数据(参数、观测数据、输出数据)及误差分析4部分组成(图 4).

|
图 4 叶绿素同化系统 Fig.4 Framework of chlorophyll-a assimilation |
卡尔曼滤波是一种典型的顺序数据同化方法,1960年,Kalman[26]针对随机过程状态估计提出了卡尔曼滤波的思想.Evensen等在1994年提出了集合卡尔曼滤波算法[8],克服了传统卡尔曼滤波的不足,并且具有计算成本低、运算效率高等优点[27].但是在标准的集合卡尔曼滤波中,观测值是被当做随机变量处理的,所以会在观测值上加扰动.近年来,为了避免采样误差,确定性方法随之产生. Whitaker等[13]提出确定性观测法的集合均方根滤波就是其中之一.该方法不需要对观测值进行扰动,减少了误差的引入.该算法利用蒙特卡罗方法的思想,用符合高斯分布的一组随机变量(设数目为N)去代表随机动态预报中的概率密度函数,通过向前积分,计算下一个时刻状态总体的概率密度,并得到该时刻的统计特性(如均值与协方差).
具体算法如下:
① 估计所有时刻的观测误差(Rn)和模式误差协方差矩阵(Qn).已知初始时刻的背景值x0f和相应的协方差矩阵B0,进行随机取样,即x0(k)f~N(x0f, B0),k=1, 2, …, K.假设样本总数为K.
② 计算卡尔曼增益矩阵Kn:
| $ {K_{\rm{n}}} = {B_{\rm{n}}}H{}_{\rm{n}}^{\rm{T}}{({H_{\rm{n}}}{B_{\rm{n}}}H{}_{\rm{n}}^{\rm{T}} + {R_{\rm{n}}})^{ - 1}} $ | (9) |
| $ {B_{\rm{n}}}H_{\rm{n}}^{\rm{T}} = \frac{1}{{K - 1}}\sum\limits_{k = 1}^K {[x_{{\rm{n}}({\rm{k}})}^{\rm{f}} - \overline {x_{\rm{n}}^{\rm{f}}} ]} {[{H_{\rm{n}}}(x_{{\rm{n}}({\rm{k}})}^{\rm{f}}) - \overline {{H_{\rm{n}}}(x_{{\rm{n}}({\rm{k}})}^{\rm{f}})} ]^T} $ | (10) |
| $ {H_{\rm{n}}}{B_{\rm{n}}}H_{\rm{n}}^{\rm{T}} = \frac{1}{{K - 1}}\sum\limits_{k = 1}^K {[{H_{\rm{n}}}(x_{{\rm{n}}({\rm{k}})}^{\rm{f}}) - \overline {{H_{\rm{n}}}(x_{{\rm{n}}({\rm{k}})}^{\rm{f}})} ]} {[{H_{\rm{n}}}(x_{{\rm{n}}({\rm{k}})}^{\rm{f}}) - \overline {{H_{\rm{n}}}(x_{{\rm{n}}({\rm{k}})}^{\rm{f}})} ]^{\rm{T}}} $ | (11) |
| $ \overline {x_{\rm{n}}^{\rm{f}}} = \frac{1}{K}\sum\limits_{k = 1}^K {x_{{\rm{n}}({\rm{k}})}^{\rm{f}}} $ | (12) |
在求解增益矩阵的过程中,采用了通过样本来计算增益矩阵的方法,这样可以达到降低计算机存储和提高运算效率的目的.在这里观测算子H可以不是线性的.
③ 进行分析场的观测更新:采用确定性观测的方法进行观测更新,分别对均值场
| $ x_{{\rm{n}}({\rm{k}})}^{\overline {\rm{a}} } = \overline {x_{\rm{n}}^{\rm{a}}} + x{}_{{\rm{n(k)}}}^{{\rm{'a}}} $ | (13) |
| $ \overline {x_{\rm{n}}^{\rm{a}}} = \overline {x_{\rm{n}}^{\rm{f}}} + {K_{\rm{n}}}[y_{\rm{n}}^{\rm{o}} - {H_{\rm{n}}}\overline {(x_{\rm{n}}^{\rm{f}})} ] $ | (14) |
| $ x{}_{{\rm{n(k)}}}^{{\rm{'a}}} = x{}_{{\rm{n(k)}}}^{{\rm{'f}}} - {\widetilde K_{\rm{n}}}{H_{\rm{n}}}x{}_{{\rm{n(k)}}}^{'{\rm{f}}} $ | (15) |
式中,
| $ {\widetilde K_{\rm{n}}} = {B_{\rm{n}}}{H_{\rm{n}}}{(Z{}_{\rm{d}}^{{\rm{ - 1}}})^{\rm{T}}}{({Z_{\rm{d}}} + {Z_{\rm{r}}})^{ - 1}} $ | (16) |
④ 进行预报,也就是进行状态的时间更新:
| $ x{}_{{\rm{n(k)}}}^{\rm{f}} = {M_{{\rm{n - 1}}}}(x{}_{{\rm{n(k)}}}^{\rm{a}}) + {\eta _{{\rm{n - 1(k)}}}} $ | (17) |
式中,
⑤ 回到步骤②,如此循环往复,直至没有新的观测资料加入或已满足同化时长需求.
2.3 误差统计对于同化后的结果,采用两种误差分析方法:(1)均方根误差(root mean square error, RMSE);(2)相对误差(relative error, RE).
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({\rm{ob}}{{\rm{s}}_i} - {X_i})}^2}} } $ | (18) |
| $ RE = \frac{{\left| {{\rm{ob}}{{\rm{s}}_i} - {X_i}} \right|}}{{{\rm{obs}}}} $ | (19) |
式中, N为整个观测时间,obsi为i时刻的“真值”,Xi为i时刻的叶绿素a扩散模拟值或同化结果.
3 敏感性分析从集合均方根滤波同化算法的设计过程可知,同化系统的性能会受到背景场误差、观测误差、样本数目和模型误差等因素的影响[28].为了研究这些参数对于同化结果的影响,我们将通过调整参数的变化,来观察这些参数对于同化系统性能的影响.目前,太湖叶绿素a同化系统基于Matlab软件实现,水体动力学模型是基于Fortran语言封装,在系统运行时,由Matlab调用水体动力学模型.
本次实验共分为5部分,分别是样本数目、同化时长、背景误差、观测误差和模型误差的敏感性分析.敏感性分析实验利用2009年4月21日环境一号卫星的叶绿素a浓度反演结果作为叶绿素a扩散模型的初值,结合叶绿素a扩散模型,在模拟时长内每小时输出一次模拟结果,并将该结果作为理论意义上的“真值”.因此,当我们把敏感性分析实验的同化结果与上述结果进行对比分析后,即可判断不同参数及其组合对太湖叶绿素a同化系统性能的影响.为了避免随机性误差因素的影响,关于每个变量的同化实验都重复了10次,以消除随机性因素的影响.最终的误差分析采用平均均方根误差(ARMSE),即以10次的均方根误差的均值为评价标准.
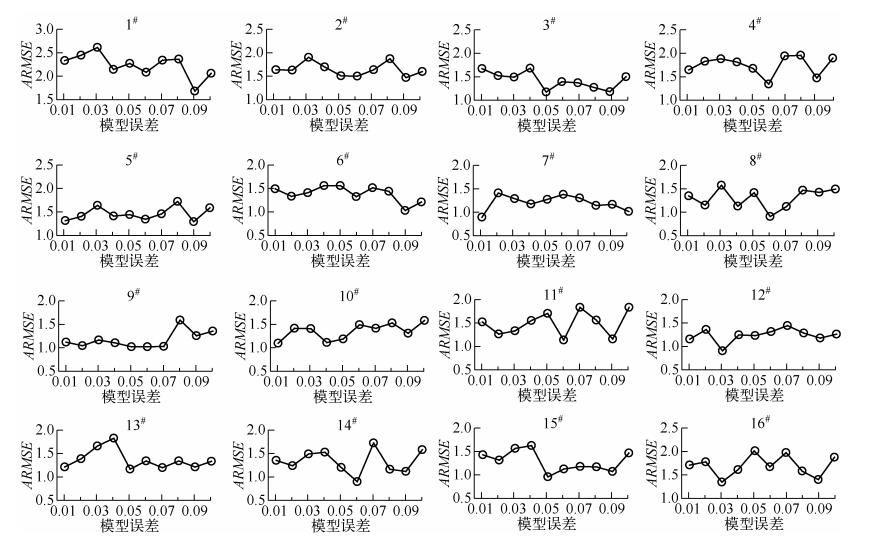
3.1 模型误差敏感性分析同化实验参数设置为:叶绿素a扩散模型误差:最小值为1%,步长1%,最大值为10%;同化时长12h;观测误差1%;背景场误差30%;样本数目为25.模型误差主要是由于模型本身无法精确描述和刻画水体动力学的变化而引起的系统误差,同时由于边界条件、模型参数等的不确定也会引起模型误差.图 5反映了模型误差对于同化系统的影响.不同点位对于模型误差敏感性是不同的,出现最小的ARMSE的模型误差的值各不相同(图 5).在集合卡尔曼滤波的时间更新方程中,如果忽略模型误差一项会导致低估预报误差协方差矩阵[29],从而引起预报的偏差.但本身对于模型误差的估计也是很难的一件事情.从敏感性分析的结果中可以看出,大部分的点位当模型误差为4%~6%时,ARMSE最小.这也说明,对于叶绿素a扩散模型而言,当模型误差在4%~6%之间的时候,同化效果较好.当模型误差较小时,会导致对预报误差协方差矩阵的低估;当模型误差较大时,又会导致预报精度下降.
|
图 5 模型误差敏感性分析结果 Fig.5 Sensitivity analysis results of the model error |
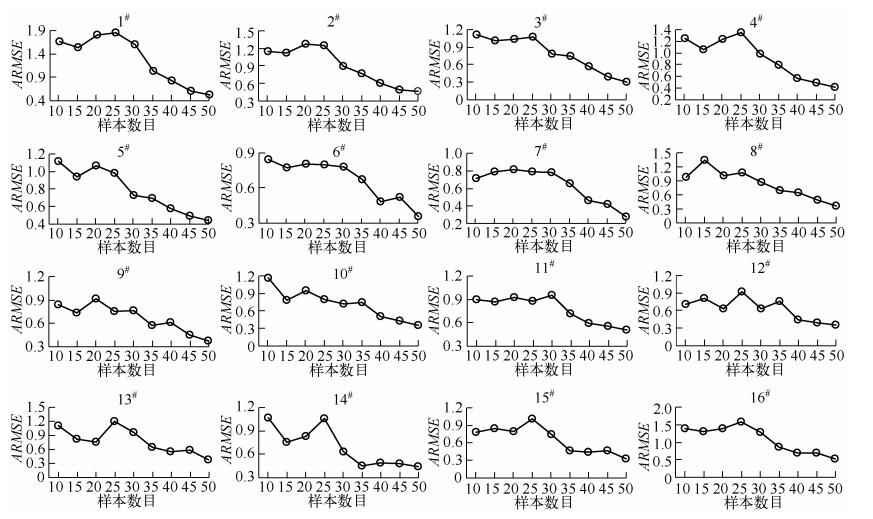
同化实验参数设置为:样本数目:最小值为10,步长5,最大值为50;背景场误差30%;观测误差1%;叶绿素a扩散模型误差为5%;同化时长为12h.样本数目的多少决定了通过这些样本是否能够更加准确地反映状态变量的空间分布,而样本数目过多又会增加系统运行的时间,所以分析样本数目对同化系统的敏感性就变得十分重要.考虑到时间的计算成本,目前实验中最大样本数目设计为50.样本的敏感性分析实验结果可以看出,随着集合样本数目的增加,ARMSE总体上呈现逐渐减小的趋势(图 6).当样本数目在10~25附近时,ARMSE会出现不同程度的轻微波动,当集合数目大于30后,ARMSE总体减小的趋势就很明显了.从系统运行时间和同化效果来看,当集合样本数目在30~40左右时,系统的运行效率和同化效果都取得了较好的效果.关于集合样本数目敏感性分析这一结果也符合了集合均方根滤波通过蒙特卡洛方法解决非线性问题的原理与方法.即大量样本可以更加准确地反映状态变量的空间分布,更加准确地反映和刻画状态变量在真实空间中的分布.但大量样本也会导致同化系统运行时间过长,增加计算成本.
|
图 6 样本数目敏感性分析结果 Fig.6 Sensitivity analysis results of the number of the ensemble |
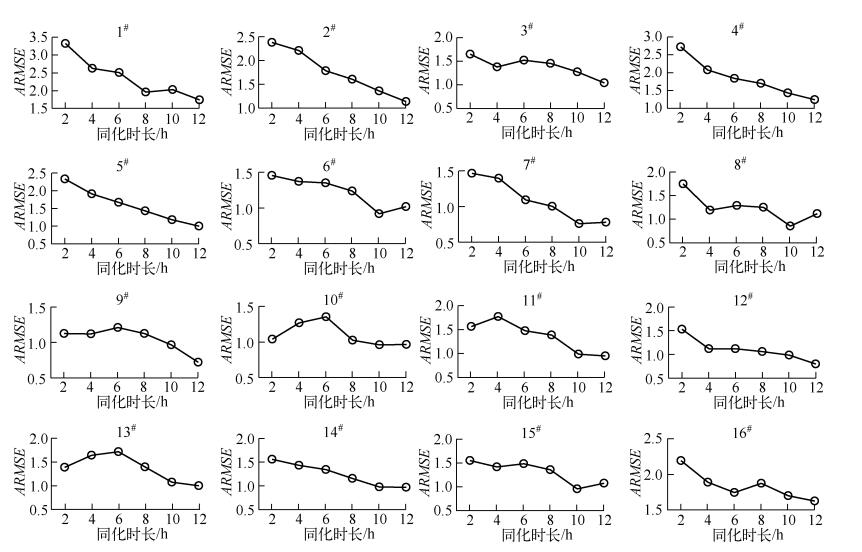
同化实验参数设置为:同化时长:最小值为2h,步长2h,最大值为12h;背景场误差30%;观测误差1%;叶绿素a扩散模型误差为5%;样本数目为25.同化时长决定了同化观测数据的周期长短与同化结果之间的关系,较长的同化时长需要更多的观测数据,同时系统的运行时间也会更长,但却能得到较好的结果.同化时长的确定往往与观测数据的采集频率、数据处理系统的配置等因素有关.同化时长的敏感性分析结果可以看出(图 7),随着同化时长的增加,ARMSE逐渐减小.其中,10#点位出现了一个上升的波动,其余点位都呈现整体下降的趋势. 10#点位在2~6h平均均方根误差上升,说明在该点位该同化时长的情况下,同化滤波出现了滤波发散的不稳定情况.说明在某些时段,同化时长因素对不同湖区的影响具有差异性.但整体趋势还是随着同化时长的增加,ARMSE逐渐减小.
|
图 7 同化时长敏感性分析结果 Fig.7 Sensitivity analysis results of the assimilation time |
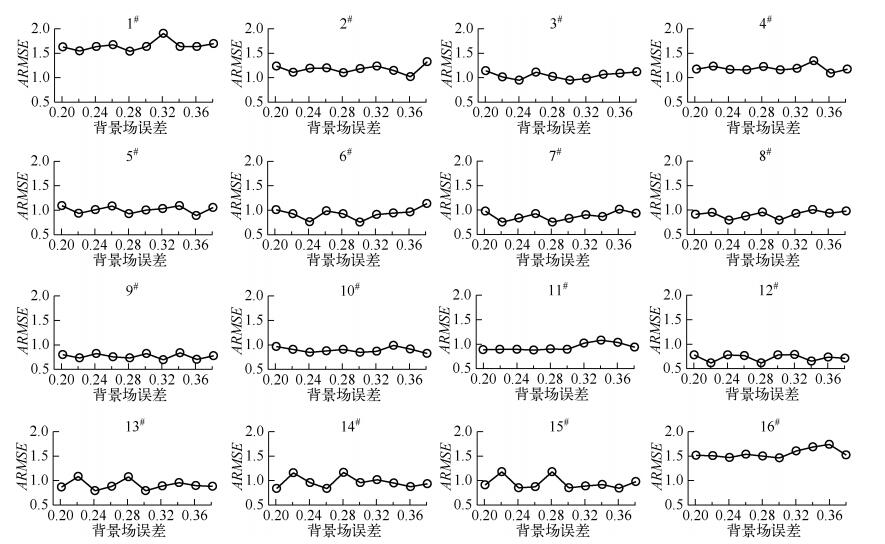
同化实验参数设置为:背景场误差:最小值为20%,步长2%,最大值为38%;同化时长12h;观测误差1%;叶绿素a扩散模型误差为5%;样本数目为25.背景场误差是在HJ-1卫星反演结果基础上加入了满足高斯正态分布的误差扰动.背景场误差反映了对状态变量空间的初始误差估计,决定了对状态空间的初始估计.背景场误差敏感性分析结果可以看出(图 8),当背景场误差被低估的时候,即背景场误差为20%~28%时,ARMSE基本都处于一个平稳的波动状态,没有明显的变化趋势.当背景场误差被高估的时候,即背景场误差为32%~38%时,不同的点位表现得有所不同.以3#、6#、11#、16#点位为代表,当背景场误差为32%~38%时,这些点位的ARMSE都呈上升趋势.以4#、5#、8#、9#点位为代表,当背景场误差为32%~38%时,这些点位的平均均方根误差仍表现为一平稳波动状态.但就整体而言,这些点位在背景场误差估计存在偏差的情况下,ARMSE变化不大.随着背景场误差的增大,ARMSE呈现一个有规律的波动状态.而这也符合顺序同化的特点,即使初始场的状态变量的估计存在较大误差,同化系统经过一段时间也会达到稳定.
|
图 8 背景场误差敏感性分析结果 Fig.8 Sensitivity analysis results of the background error |
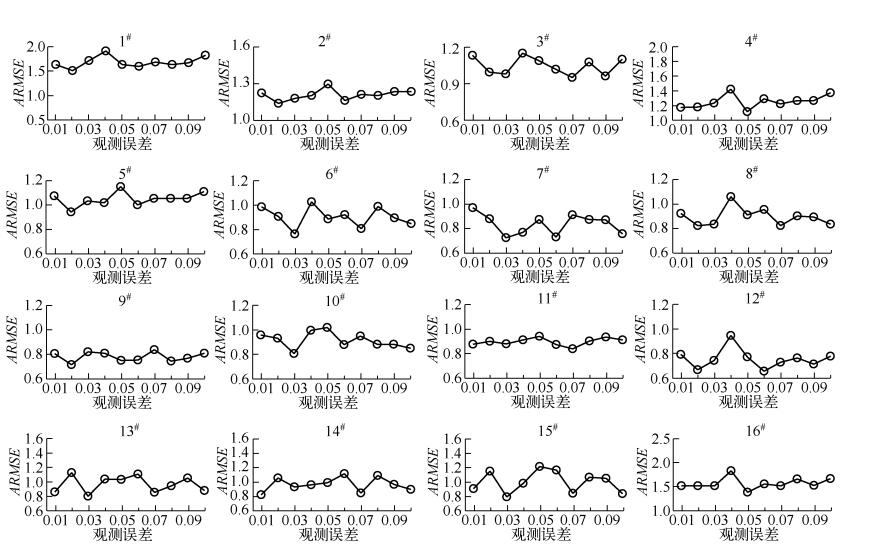
同化实验参数设置为:观测误差:最小值为1%,步长1%,最大值为10%;同化时长12h;背景场误差30%;叶绿素a扩散模型误差为5%;样本数目为25.观测误差是在模拟“真值”结果基础上加入了满足高斯正态分布的误差扰动.观测误差主要包括仪器采集数据时的仪器误差和代表性误差.观测误差敏感性分析结果可以看出(图 9),随着观测误差的增加,ARMSE主要分为两种情况.其一,以1#、2#、4#、5#、9#、16#点位为代表,随着观测误差的增加,ARMSE也在增加,整体呈上升的趋势.其二,剩余的点位随着观测误差的增加,ARMSE围绕某一均值处于一个波动状态.说明位于太湖不同区域的点位,由于水体动力学性质的不同,其同化效果随观测误差的变化而异.
|
图 9 观测误差敏感性分析结果 Fig.9 Sensitivity analysis results of the observation error |
模拟实验基于2009年4月21日环境一号卫星的反演叶绿素数据作为叶绿素扩散模型的“真实”初值.将该初值在叶绿素扩散模型下进行12h模拟,每1小时输出一次测试点位的模拟结果.同时在“真实”初值场上进行30%的扰动,作为同化系统的初始背景场信息.利用之前分析的敏感性参数,采用观测误差为1%,模型误差为5%,背景场误差为30%,集合样本数为50,同化时长12h参数设置同化系统,分析和评价太湖叶绿素a同化系统的同化效果.同化12h后的结果与“真实”初值在叶绿素a扩散模型作用下12h的预测结果作相对误差分析可以看出,全湖范围内大部分的区域都将误差控制在30%以下(图 10).由于在数值计算时,将全湖离散为2813个离散的网格点,通过统计得到全湖有56.5%网格点的误差控制在30%以下.即通过同化16个网格点数据,使得全湖56.5%的区域误差得到了改善.从同化的16个点位数据来看,相对误差分别为16.3%、4.7%、16.7%、13.7%、3.5%、18.4%、19.9%、15.1%、13.8%、25.9%、11.4%、17.2%、11.9%、20.6%、16.7%、18.1%.从单点的同化效果来看,精度平均提升了49.2%.但是,我们也发现在太湖西部部分区域同化效果不理想,一方面可能是由于目前同化系统还不够完善,在系统运行效率和计算成本方面有待进一步改善;另一方面,由于模拟实验中数据同化时长在1~12h之内,因此,未考虑藻类生长模型及水质模型.但是,从长时间尺度来看,叶绿素a浓度变化还会受到水温、营养盐含量、光照等因素的影响.因此,为了提高数据同化精度,在将来进一步的研究中还需要在基于风生流的太湖水体动力学模型基础上耦合藻类生长模型,从而更加全面准确地模拟和估算太湖叶绿素a浓度.就目前实际情况而言,由于太湖东部水质状况较好,所以大部分的浮标站点位于太湖中部和北部,其数目不少于20个.因此,利用这些浮标站点的连续动态观测数据,利用基于集合均方根的数据同化方法对于太湖叶绿素a浓度的估算是有效可行的.

|
图 10 全湖相对误差分析 Fig.10 Relative error analysis of Lake Taihu |
1) 集合样本数目越多、同化时长越长都可以越有效地降低同化系统的误差,但也会增加系统的计算成本和运算时间.当集合样本数目在30~40左右时,系统的运行效率和同化效果都取得了较好的效果.
2) 背景场误差对于同化系统的影响不是很大,即使背景场误差估计偏差较大,同化系统的平均均方根误差变化也不是很大.
3) 观测误差对于同化系统的影响较大,不同的点位呈现出的趋势有所不同.有的点位随着观测误差增大,同化系统的误差也会增大;有的点位则出现围绕某一均值上下波动.
4) 模型误差对于基于集合均方根滤波的数据同化方法较为重要,准确估计模型误差对于提高同化系统的性能至关重要.对于叶绿素a扩散模型而言,当模型误差在4%~6%之间时,同化效果较好.
| [1] |
秦伯强, 胡维平, 陈伟民. 太湖水环境演化过程与机理. 北京: 科学出版社, 2004, 1-296.
|
| [2] |
Pathmathevan M, Koilke T, Li X et al. A simplified land data assimilation scheme and its application to soil moisture experiments in 2002(SMEX02). Water Resources Research, 2003, 39(12): 1341. DOI:10.1029/2003WR002124 |
| [3] |
Pathmathevan M, Koilke T, Li X. A new satellite-based data assimilation algorithm to determine spatial and temporal variations of soil moisture and temperature profiles. Journal of the Meteorological Society of Japan, 2003, 81(5): 1111-1135. DOI:10.2151/jmsj.81.1111 |
| [4] |
Moradkhani H, Sorooshian S, Gupta HV et al. Dual state-parameter estimation ofhydrological models using ensemble Kalman filter. Advances in Water Resources, 2005, 28(2): 135-147. DOI:10.1016/j.advwatres.2004.09.002 |
| [5] |
Gregg WW. Assimilation of seawifs ocean chlorophyll data into a three-dimensional global ocean model. Journal of Marine Systems, 2008, 69(3/4): 205-225. |
| [6] |
Gu J, Li X, Huang CL et al. A simplified data assimilation method for reconstructing time-series MODIS NDVI data. Advances in Space Research, 2009, 44(4): 501-509. DOI:10.1016/j.asr.2009.05.009 |
| [7] |
Anderson LA, Robinson AR, Lozano CJ. Physical and biological modeling in the Gulf Stream region: I. Data assimilation methodology. Deep-sea Research Part I, 2000, 47: 1787-1827. DOI:10.1016/S0967-0637(00)00019-4 |
| [8] |
Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research, 1994, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
| [9] |
Evensen G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dynamics, 2003, 53(4): 343-367. DOI:10.1007/s10236-003-0036-9 |
| [10] |
Burgers G, Leeuwen PJV, Evensen G. Analysis scheme in the ensemble Kalman filter. Monthly Weather Review, 1998, 126(6): 1719-1724. DOI:10.1175/1520-0493(1998)126<1719:ASITEK>2.0.CO;2 |
| [11] |
Houtekamer PL, Mitchell HL. Data assimilation using an ensemble Kalman filter technique. Monthly Weather Review, 1998, 126(3): 796-811. DOI:10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2 |
| [12] |
Houtekamer PL, Mitchell HL. A sequential ensemble Kalman filter for atmospheric data assimilation. Monthly Weather Review, 2001, 129(1): 123-137. DOI:10.1175/1520-0493(2001)129<0123:ASEKFF>2.0.CO;2 |
| [13] |
Whitaker JS, Hamill TM. Ensemble data assimilation without perturbed observations. Monthly Weather Review, 2002, 130(7): 1913-1924. DOI:10.1175/1520-0493(2002)130<1913:EDAWPO>2.0.CO;2 |
| [14] |
Anderson JL. An ensemble adjustment Kalman filter for data assimilation. Monthly Weather Review, 2001, 129(12): 2884-2903. DOI:10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2 |
| [15] |
Tippett MK, Anderson JL, Bishop CH et al. Ensemble square root filters. Monthly Weather Review, 2003, 131(7): 1485-1490. DOI:10.1175/1520-0493(2003)131<1485:ESRF>2.0.CO;2 |
| [16] |
唐军武. 海洋光学特性模拟与遥感模型[学位论文]. 北京: 中国科学院遥感应用研究所, 1999: 107-110.
|
| [17] |
唐军武, 田国良, 汪小勇等. 水体光谱测量与分析Ⅰ水面以上测量法. 遥感学报, 2004, 8(1): 37-44. DOI:10.11834/jrs.20040106 |
| [18] |
Le CF, Li YM, Zha Y et al. Specific absorption coefficient and the phytoplankton package effect in Lake Taihu, China. Hydrobiologia, 2009, 619(1): 27-37. DOI:10.1007/s10750-008-9579-6 |
| [19] |
王桥, 吴传庆, 厉青. 环境一号卫星及其在环境监测中的应用. 遥感学报, 2010, 14(1): 104-121. |
| [20] |
徐祎凡, 李云梅, 王桥等. 基于环境一号卫星多光谱影像数据的三湖一库富营养化状态评价. 环境科学学报, 2011, 31(1): 81-92. |
| [21] |
旷达, 韩秀珍, 刘翔等. 基于环境一号卫星的太湖叶绿素a浓度提取. 中国环境科学, 2010, 30(9): 1269-1273. |
| [22] |
金焰, 张咏, 牛志春等. 环境一号CCD数据在太湖蓝藻水华遥感监测中的应用. 环境监测管理与技术, 2010, 22(5): 53-54. |
| [23] |
Freitas FH. Spectral merging of MODIS/MERIS Ocean Colour Data to improve monitoring of coastal water processes [Dissertation]. Enschede: International Institute for Geo-Information Science and Earth Observation, 2009.
|
| [24] |
Zhang Z, Song ZY, Lv GN. A new implicit scheme for solving 3-D shallow water flows. Journal of Hydrodynamics(Series B), 2009, 21(6): 790-798. |
| [25] |
Zhang Z, Song ZY. Three-dimensional numerical modeling for wind-driven circulation and pollutant transport in a large scale lake. International Conference of Bioinformatics and Biomedical Engineering. Chengdu: IEEE, 2010, 1-7. |
| [26] |
Kalman RE. A new approach to linear filtering and prediction problems. Journal of Fluids Engineering, 1960, 82(1): 35-45. |
| [27] |
刘成思. 集合卡尔曼滤波资料同化方案的设计和研究[学位论文]. 北京: 中国气象科学研究院, 2005: 13-14.
|
| [28] |
黄春林, 李新. 土壤水分同化系统的敏感性试验研究. 水科学进展, 2006, 17(4): 457-465. |
| [29] |
曾忠一. 大气科学中的反问题(上册). 台北: 国立编译馆, 2006.
|
 2015, Vol. 27
2015, Vol. 27 

