圩区是长江中下游广泛存在的一种地理单元,占太湖流域平原区面积的50 %以上,其建设初衷主要是抵御洪涝灾害[1],随着社会经济的发展,环境问题的日益突出,圩区作为太湖流域广大农村主要的单元,其非点源污染问题成为流域污染控制的重要方面[2-3],其中磷素作为太湖富营养化的重要限制性因子[4],受到众多研究者的关注.国内外学者在平原区开展了系列磷素流失监测[5-7]、磷素流失模拟[8-12]等方面的研究,分析了平原区农田磷素流失与环境因子之间的相互作用机制,构建了平原区磷素流失模拟的非点源污染模型,估算了磷素流失通量,为平原圩区的磷素流失模拟积累了宝贵的数据、参数与方法.
平原圩区通过节制闸或泵站实现圩区与外围河网的水量交换,与非圩区单元相比,平原圩区的磷素流失过程受到显著的人工干扰,影响因素众多,机理过程复杂,目前结合圩区水循环规律开展圩区磷素流失模拟的研究案例不多.本研究根据实际调研圩区的农田灌溉与洪涝排水规律,结合大量太湖流域平原区的研究案例,构建了日尺度的平原圩区磷素流失过程模型,估算了圩区磷素月流失量,分析了圩区磷素流失对环境因子的响应机制,对识别圩区磷素污染控制的关键环节、制定磷素削减优化方案、控制磷素污染具有重要实践意义.
1 研究区概况研究区——尖圩(图 1)位于溧阳市西北部(31°29′2″~31°29′13″N,119°25′17″~119°25′37″E),面积约为106000 m2,年降雨量为1168 mm(基于2003-2012年溧阳气象资料统计);圩区海拔较低,地势平坦,田地成块,农田多为水田、旱地,分别占圩区总面积的50.1 %、21.7 %;圩内沟渠、坑塘众多,占圩区总面积的9.0 %,排水沟呈网状分布,且水力梯度低;圩区四周均为河道,暴雨期间,圩外河道水位通常高于圩内水位,圩内水体通过圩区北部的排涝泵站排出;圩内有一自然村(尖圩村),人口约为100人,住宅用地面积占圩区总面积的19.2 %,无工业污染源,该圩区是太湖流域平原区的典型农村圩区.
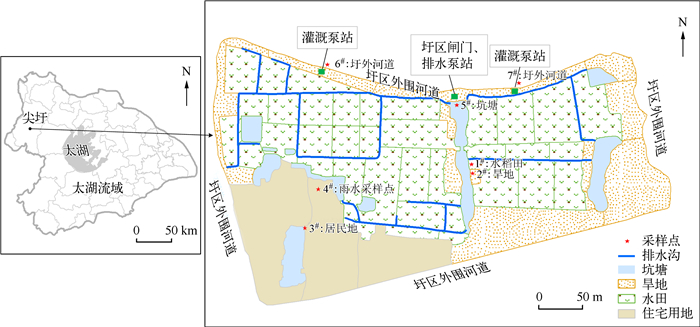
|
图 1 尖圩地理位置、土地利用及采样点分布 Fig.1 Location, land use and sampling sites of Polder Jian |
圩区磷素流失模型以尖圩为研究区,收集的数据包括土地利用、气象、水质数据(表 1).
| 表 1 圩区磷素流失模型构建的数据列表 Tab.1 Data list of the phosphorus loss model for polder |
1) 土地利用数据通过2010年12月31日的Spot卫星影像,采用监督分类解译获取.
2) 气象数据来自国家气象中心的溧阳站(站点编号:58345),该气象站与尖圩的水平距离仅为8.5 km,其气象数据能够代表尖圩的气象条件,收集的数据包括2009-2013年的逐日数据,包括7个气象指标:日平均气温、日最高气温、日最低气温、日平均相对湿度、日照时数、日平均风速、日降水量.
3) 水质数据为不同水体的总磷浓度,来源包括野外采样分析与参考文献.圩外河道的总磷浓度通过采集农田灌溉时段(2013年6-9月)的水样获取;雨水、圩区坑塘、不同土地利用类型(水稻田、旱地与居民区)降雨径流的总磷浓度通过采集降雨事件(2013年8月24日)的水样获取,该降雨事件持续2.5 h(16:30-19:00),累计降雨量为38 mm,采用钼酸铵分光光度法测定样品总磷浓度;考虑不同土地利用类型降雨径流的总磷浓度影响因素众多,为更好表征降雨径流的总磷浓度,收集了太湖流域平原圩区多个研究区不同土地利用类型的磷素流失数据;具体水质数据见表 2.
| 表 2 圩区磷素流失模型构建的总磷浓度数据 Tab.2 The data of total phosphorus for the phosphorus loss model for polder |
圩区磷素流失模型以水量平衡为基础,考虑了圩区内部水分与磷素迁移的相关过程(图 2),模型包含4个状态变量,即水域蓄水量、水田蓄水量、旱地蓄水量、坑塘总磷浓度,模拟时间步长(ΔT)为1天,模拟时长为4年(2009年10月1日-2013年9月30日),不同模块的计算方法阐述如下.
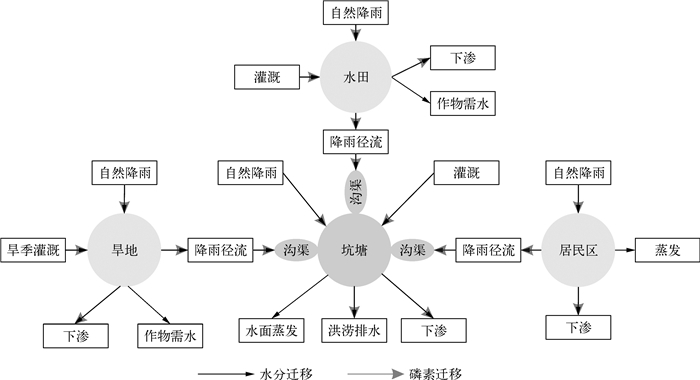
|
图 2 圩区水量平衡与磷素迁移 Fig.2 Conceptual diagram of water balance in polder system |
尖圩的水域包括坑塘与沟渠;强降雨过程中,居民区与农田的径流通过沟渠汇入坑塘;缺水季节,圩区通过泵站从外围河道抽水到沟渠,并输送到农田与坑塘.水域水量的影响要素包括:降雨、水田汇流、居民区汇流、旱地汇流、灌溉抽水、水面蒸发、水域渗漏、洪涝排水,计算公式如下:
| $ {H_{{\rm Pond}}^{T}} = {H_{{\rm Pond}}^{T - \Delta T}} + \Delta {H_{{\rm Pond}}^{T}} + {H_{{\rm PondIrr}}^{T}} - {H_{{\rm PondPump}}^{T}} $ | (1) |
| $ \begin{array}{l} \Delta {H_{{\rm Pond}}^{T}} = P{r^T} + {H_{{\rm TownQ}}}^{T} \cdot \frac{{{S_{{\rm Town}}}}}{{{S_{{\rm Pond}}}}} + {H_{{\rm PaddyQ}}^{T}} \cdot \\ \frac{{{S_{{\rm Paddy}}}}}{{{S_{{\rm Pond}}}}} + {H_{{\rm DryQ}}^{T}} \cdot \frac{{{S_{{\rm Dry}}}}}{{{S_{{\rm Pond}}}}} - {E_{{\rm Pond}}^{T}} - {H_{{\rm PondInf}}} \end{array} $ | (2) |
式中,HPondT为T时刻水域的蓄水量(mm),初始值为1000 mm;ΔT为模型时间步长;ΔHPondT为自然条件下水域蓄水量的变化速率(mm/d);HPondIrrT、HPondPumpT分别为单位时间灌溉、排涝引起的水域蓄水量变幅(mm/d);PrT为日降水量(mm/d);HTownQT、HPaddyQT、HDryQT分别为单位时间居民区、水田、旱地的径流深度(mm/d);SPond、SDry、SPaddy、STown分别为水域、旱地、水田与居民区的面积(m2);EPondT为水域蒸发速率(mm/d);HPondInf为水域水体的渗漏强度(mm/d).
3.2 居民区水量平衡居民区水量平衡的影响要素包括降雨径流、地表填洼、地面渗漏;单位时间内,居民区的输出水量采用径流深度(HTownQT)表示,其计算公式如下:
| $ {H_{{\rm TownQ}}}^{T} = \left\{ \begin{array}{l} {C_{{\rm Town}}} \cdot P{r^T} - {H_{{\rm TownInf}}^{T}}\;\;P{r_{{\rm Cum}}^T} \ge {H_{{\rm TownFill}}}\\ - {H_{{\rm TownInf}}^{T}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P{r_{{\rm Cum}}^T} < {H_{{\rm TownFill}}} \end{array} \right. $ | (3) |
式中,CTown为居民区的径流系数;模型基于该系数,将降雨量(PrT)折算成径流深度;地表填洼主要发生在降雨初期,当累计降雨量(PrCumT)达到最大地表填洼量(HTownFill)后,才能产生径流;HTownInfT为居民区的地面渗漏强度(mm/d);地面渗漏发生在降雨期间,在无降雨期间,折算为居民区对水域水体的少量消耗.
3.3 水田与旱地水量平衡水田水量平衡的影响要素包括自然降雨、人工灌溉、作物需水、渗漏、降雨径流,计算公式如下:
| $ {H_{{\rm Paddy}}^{T}} = {H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}} + {H_{{\rm PaddyIrr}}^{T}} - {H_{{\rm PaddyQ}}^{T}} $ | (4) |
| $ \Delta {H_{{\rm Paddy}}^{T}} = P{r^T} - {E_{{\rm Paddy}}^{T}} - {H_{{\rm PaddyInf}}^{T}} $ | (5) |
| $ {E_{{\rm Paddy}}^{T}} = K{c_{{\rm Paddy}}^T} \cdot {f_{{\rm Penman}}} $ | (6) |
| $ {H_{{\rm PaddyInf}}^{T}} = \left\{ \begin{array}{l} 2\;\;\;{H_{{\rm Paddy}}^{T - \Delta T}} + P{r^T} - {E_{{\rm Paddy}}^{T}} \ge {H_{{\rm PaddySat}}}\\ 0\;\;\;{H_{{\rm Paddy}}^{T - \Delta T}} + P{r^T} - {E_{{\rm Paddy}}^{T}} < {H_{{\rm PaddySat}}} \end{array} \right. $ | (7) |
| $ {H_{{\rm PaddyIrr}}^{T}} = \\\left\{ {\begin{array}{*{20}{l}} {{H_{{\rm PaddyMax}}^{T}} - ({H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}})}&{{H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}} < {H_{{\rm PaddyMin}}^{T}}}\\ 0&{{H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}} \ge {H_{{\rm PaddyMin}}^{T}}} \end{array}} \right. $ | (8) |
| $ {H_{{\rm PaddyQ}}^{T}} = \\\left\{ {\begin{array}{*{20}{l}} {({H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}}) - {H_{{\rm Paddy}}^{{\rm Flood}}}}&{{H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}} \ge {H_{{\rm Paddy}}^{{\rm Flood}}}}\\ 0&{{H_{{\rm Paddy}}^{T - \Delta T}} + \Delta {H_{{\rm Paddy}}^{T}} < {H_{{\rm Paddy}}^{{\rm Flood}}}} \end{array}} \right. $ | (9) |
式中,HPaddyT为T时刻水田的蓄水量(mm),其初始值为120 mm;ΔHPaddyT为自然条件下水田的蓄水量变化速率(mm/d);水田的作物需水量(EPaddyT,mm/d),采用彭曼公式(式6)计算[16-17],式中,KcPaddyT为水田作物的需水系数;水田渗漏发生在土壤含水饱和时段,在土壤含水未饱和的条件下,水田的渗漏强度(HPaddyInfT)为0,式中,HPaddySat为水田土壤的饱和含水量(mm);HPaddyIrrT为单位时间人工灌溉引起的水田蓄水量变幅(mm/d);人工灌溉发生在稻季,当水田蓄水量小于水田适宜蓄水量下限(HPaddyMinT)时,稻田通过坑塘取水灌溉(式8)[11];HPaddyQT为单位时间水田的径流深度(mm/d);当水田蓄水量大于水田的最大蓄水量(HPaddyFlood)时,产生径流(式9).
旱地的水量平衡模式与水田相似,主要区别在于没有发生灌溉过程,计算公式如下:
| $ H_{{\rm{Dry}}}^T = H_{{\rm{Dry}}}^{T - \Delta T} + \Delta H_{{\rm{Dry}}}^T - H_{{\rm{DryQ}}}^T $ | (10) |
| $ \Delta H_{{\rm{Dry}}}^T = P{r^T} - H_{{\rm{DryInf}}}^T - E_{{\rm{Dry}}}^T $ | (11) |
| $ E_{{\rm{Dry}}}^T = Kc_{{\rm{Dry}}}^T \cdot {f_{{\rm{Penman}}}} $ | (12) |
| $ H_{{\rm{DryInf}}}^T = \left\{ {\begin{array}{*{20}{l}} 2&{H_{{\rm{Dry}}}^{T - \Delta T} + P{r^T} - E_{{\rm{Dry}}}^T \ge {H_{{\rm{DrySat}}}}}\\ 0&{H_{{\rm{Dry}}}^{T - \Delta T} + P{r^T} - E_{{\rm{Dry}}}^T < {H_{{\rm{DrySat}}}}} \end{array}} \right. $ | (13) |
| $ H_{{\rm{DryQ}}}^T = \left\{ {\begin{array}{*{20}{l}} {(H_{{\rm{Dry}}}^{T - \Delta T} + \Delta H_{{\rm{Dry}}}^T) - H_{{\rm{Dry}}}^{{\rm{Flood}}}}&{H_{{\rm{Dry}}}^{T - \Delta T} + \Delta H_{{\rm{Dry}}}^T \ge H_{{\rm{Dry}}}^{{\rm{Flood}}}}\\ 0&{H_{{\rm{Dry}}}^{T - \Delta T} + \Delta H_{{\rm{Dry}}}^T < H_{{\rm{Dry}}}^{{\rm{Flood}}}} \end{array}} \right. $ | (14) |
式中,HDryT为T时刻旱地的蓄水量(mm),其初始值为100 mm;ΔHDryT为自然条件下旱地的蓄水量变化速率(mm/d);HDryQT为单位时间旱地的径流深度(mm/d);HDryInfT为旱地的水体渗漏强度(mm/d);EDryT为旱地的作物需水量(mm/d);KcDryT为旱地的作物需水系数;HDrySat为水田土壤的饱和含水量(mm);HDryFlood为旱地的最大蓄水量(mm).
3.4 灌溉抽水与洪涝排水圩区灌溉抽水与洪涝排水通过4个水位控制(图 3),即启动与关闭灌溉泵站的水域蓄水量(HPondStartIrr、HPondStopIrr)、启动与关闭排涝泵站的水域蓄水量(HPondStartExport、HPondStopExport).水田缺水时段,水田从坑塘取水灌溉,造成坑塘水面持续下降,当水域蓄水量小于HPondStartIrr时,启动灌溉泵站(式15),水域蓄水量到达HPondStopIrr时,关闭灌溉泵站,圩区的灌溉水量(VPolderIrrT)采用式16计算;强降雨期间,农田与居民区的大量径流汇入坑塘,造成坑塘水面迅速上升,当水域蓄水量到达HPondStartExport时,启动排涝泵站,水域蓄水量下降到HPondStopExport时,关闭排涝泵站(式17).
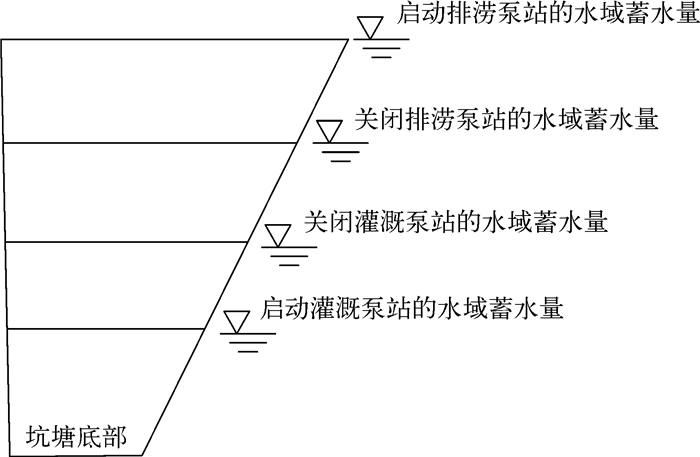
|
图 3 圩区灌溉与排涝的水域蓄水量 Fig.3 The water storage controlling irrigation and drainage for polder |
| $ H_{{\rm{PondIrr}}}^T =\\ \left\{ {\begin{array}{*{20}{l}} {H_{{\rm{Pond}}}^{{\rm{StopIrr}}} - (H_{{\rm{Pond}}}^{T - \Delta T} + \Delta H_{{\rm{Pond}}}^T)}&{H_{{\rm{Pond}}}^{T - \Delta T} + \Delta H_{{\rm{Pond}}}^T < H_{{\rm{Pond}}}^{{\rm{StartIrr}}}}\\ 0&{H_{{\rm{Pond}}}^{T - \Delta T} + \Delta H_{{\rm{Pond}}}^T \ge H_{{\rm{Pond}}}^{{\rm{StartIrr}}}} \end{array}} \right. $ | (15) |
| $ V_{{\rm{PolderIrr}}}^T = \\(H_{{\rm{PondIrr}}}^T \cdot {S_{{\rm{Pond}}}} + H_{{\rm{PaddyIrr}}}^T \cdot {S_{{\rm{Paddy}}}} + H_{{\rm{DryIrr}}}^T \cdot {S_{{\rm{Dry}}}})/{10^3} $ | (16) |
| $ H_{{\rm{PondPump}}}^T =\\ \left\{ {\begin{array}{*{20}{l}} {H_{{\rm{Pond}}}^{T - \Delta T} + \Delta H_{{\rm{Pond}}}^T - H_{{\rm{Pond}}}^{{\rm{StopExport}}}}&{H_{{\rm{Pond}}}^{T - \Delta T} + \Delta H_{{\rm{Pond}}}^T > H_{{\rm{Pond}}}^{{\rm{StopExport}}}}\\ 0&{H_{{\rm{Pond}}}^{T - \Delta T} + \Delta H_{{\rm{Pond}}}^T \le H_{{\rm{Pond}}}^{{\rm{StopExport}}}} \end{array}} \right. $ | (17) |
圩区系统磷素的输入途径主要包括人工灌溉与自然降雨,输出渠道主要包括排涝泵站排水与水体渗漏,圩区磷素流失总量(ΔTPPolderT,kg)的计算见式18,式中,TPRiverT、TPPrT分别为圩外河道、雨水的总磷浓度(mg/L),ΔTPinfT为地面渗漏导致的磷素流失量(kg),包括圩区不同土地利用类型(水域、居民区、水田、旱地)地面渗漏而导致的磷素流失量(式19);排涝泵站位于坑塘与外围河道的相连区域(图 1),因此T时刻圩区排出水体的总磷浓度为水域的总磷浓度(TPPondT),其初始值为0.2 mg/L;水域总磷浓度的主要影响因素包括自然降雨、人工灌溉、居民区与农田径流(式20),式中,TPTownQT、TPPaddyQT、TPDryQT分别为居民区、水田、旱地径流汇入坑塘时的总磷浓度(mg/L);沟渠对居民区与农田径流的磷素有一定的拦截效应,采用拦截系数方法计算(式21~23)[18],式中,TPTownT、TPPaddyT、TPDryT分别为居民区、水田、旱地径流的总磷浓度(mg/L),αDitchTown、αDitchPaddy、αDitchDry分别为沟渠对居民区、水田与旱地径流的磷素拦截系数.
| $ \Delta TP_{{\rm{Polder}}}^T = V_{{\rm{PolderIrr}}}^T \cdot \frac{{TP_{{\rm{River}}}^T}}{{{{10}^3}}} + \frac{{P{r^T}}}{{{{10}^3}}} \cdot {S_{{\rm{Polder}}}} \cdot \frac{{T{P_{{\rm Pr}}^{T}}}}{{{{10}^3}}} - \frac{{{H_{{\rm PondPump}}^{T}}}}{{{{10}^3}}} \cdot {S_{{\rm{Pond}}}} \cdot \frac{{T{P_{{\rm Pond}}^{T}}}}{{{{10}^3}}} - \Delta T{P_{{\rm Inf}}^{T}} $ | (18) |
| $ \begin{array}{l} \Delta T{P_{{\rm Inf}}^{T}} = \frac{{{H_{{\rm{PondInf}}}}}}{{{{10}^3}}} \cdot {S_{{\rm{Pond}}}}\cdot\frac{{T{P_{{\rm Pond}}^{T}}}}{{{{10}^3}}} + \frac{{{H_{{\rm TownInf}}^{T}}}}{{{{10}^3}}} \cdot {S_{{\rm{Town}}}} \cdot \frac{{T{P_{{\rm Town}}^{T}}}}{{{{10}^3}}}\\ + \frac{{{H_{{\rm PaddyInf}}^{T}}}}{{{{10}^3}}} \cdot {S_{{\rm{Paddy}}}} \cdot \frac{{T{P_{{\rm Paddy}}^{T}}}}{{{{10}^3}}} + \frac{{{H_{{\rm DryInf}}^{T}}}}{{{{10}^3}}} \cdot {S_{{\rm{Dry}}}}\cdot\frac{{T{P_{{\rm Dry}}^{T}}}}{{{{10}^3}}} \end{array} $ | (19) |
| $ \begin{array}{l} T{P_{{\rm Pond}}^{T}} = \frac{{T{P_{{\rm Pond}}^{{T - \Delta T}}} \cdot {H_{{\rm Pond}}^{{T - \Delta T}}} + T{P_{{\rm River}}^{T}} \cdot {H_{{\rm PondIrr}}^{T}} + T{P_{{\rm Pr}}^{T}} \cdot P{r_{{\rm Pond}}^{T}}}{{{H^T}}}} + \\ \frac{{T{P_{{\rm DryQ}}^{T}} \cdot {H_{{\rm Dry}}^{T}} \cdot {S_{{\rm{Dry}}}} + T{P_{{\rm PaddyQ}}^{T}} \cdot {H_{{\rm Paddy}}^{T}} \cdot {S_{{\rm{Paddy}}}} + T{P_{{\rm TownQ}}^{T}} \cdot {H_{{\rm TownQ}}^{T}} \cdot {S_{{\rm{Town}}}}}}{{{H_{{\rm Pond}}^{T}} \cdot {S_{{\rm{Pond}}}}}} \end{array} $ | (20) |
| $ T{P_{{\rm TownQ}}^{T}} = T{P_{{\rm Town}}^{T}} \cdot {\alpha _{{\rm Ditch}}^{{{\rm{Town}}}}} $ | (21) |
| $ T{P_{{\rm PaddyQ}}^{T}} = T{P_{{\rm Paddy}}^{T}} \cdot {\alpha _{{\rm Ditch}}^{{{\rm{Paddy}}}}} $ | (22) |
| $ T{P_{{\rm DryQ}}^{T}} = T{P_{{\rm Dry}}^{T}} \cdot {\alpha _{{\rm Ditch}}^{{{\rm{Dry}}}}} $ | (23) |
本研究构建的圩区磷素流失模型包括27个参数,各参数取值与来源详见表 3,其中5个参数(水域蒸发速率、水田与旱地作物需水系数、圩外河道总磷浓度、水田适宜蓄水量下限与上限)考虑了年内的差异(图 4).
| 表 3 圩区磷素流失模型参数 Tab.3 Parameters in the phosphorus loss model for polder |
参数取值通过3种方法获取:实地调研、野外监测、太湖流域平原区的已有研究成果.水域蒸发速率采用毛锐在太湖流域平原区的研究结果[19];沟渠对居民区与农田径流中磷素的拦截系数采用王岩等在宜兴平原区农田沟渠的实验结果[20],该研究的农田沟渠系统与尖圩沟渠系统的沟渠长度与气象条件极其接近;启动与关闭灌溉泵站的水域蓄水量、启动与关闭排涝泵站的水域蓄水量通过尖圩的实地调研获取,能够反映尖圩的实际灌溉与排水情况;水体(包括农田与居民区径流、圩外河道、降雨)总磷浓度的影响因素很多,为了更好反映不同时间的农田径流磷素流失差异,本研究采用尖圩的实地监测,结合太湖流域平原区的大量监测数据[13-15],采用上述研究案例不同水体总磷浓度的均值,共有46次降雨事件;圩外河道总磷浓度采用了2013年度的7次总磷监测结果,用于代表历年5-10月份的总磷变化过程,其它月份由于没有洪涝排水,无需输入这一参数.其余参数主要参考程文辉等[11]在太湖流域平原区的研究结果.
4 模拟结果与分析尖圩水域水体是洪涝排水的出水口,其总磷浓度对圩区系统磷素输出有重要影响,而圩区磷素流失量是导致区域水体污染的直接原因;基于构建的圩区磷素流失模型可模拟尖圩水域水体总磷浓度变化(式19)与磷素流失量(式18),模拟结果详述如下.
4.1 尖圩水域水体总磷浓度变化过程模拟结果表明,尖圩水域水体总磷浓度存在剧烈的变化(图 5),在夏季期间,水域的总磷浓度受人工灌溉与强降雨影响较大.人工灌溉对水域水体总磷浓度的影响主要通过大量抽水与水域水体混合,造成水域水体在短时间内大幅度波动.在降雨过程中,由于雨水的总磷浓度较低,圩区水域水体总磷含量得到稀释,与之相反,居民区的总磷含量较高,径流汇入水域中,造成水体总磷浓度升高.此外,在严重干旱期间(如:2011年4月8日-6月9日),水域蓄水量由于大量蒸发,持续减少,也会造成水体总磷浓度的大幅增加(图 5).

|
图 5 2009年10月-2013年9月圩区水域水体总磷浓度变化 Fig.5 Total phosphorus concentration in the water area of polder (Oct.2009-Sep.2013) |
水体总磷浓度也存在显著的年度差异,由于圩区水域的水深通常较浅,蓄水总量有限,总磷浓度容易受到外界干扰,年度气象、灌溉与排涝方案的差异极易造成水域水体总磷浓度的大幅波动.
4.2 圩区磷素流失量根据模型模拟结果,尖圩的年均磷素流失量为-0.17~0.54 kg/(hm2·a),这一磷素负荷显著低于太湖流域平原区的磷素负荷(4.5~10.5 kg/(hm2·a))[22-23],甚至存在磷素输入量大于输出量的年份,磷素流失量为负值,充分反映了圩区对磷素的拦截效应;其中人工灌溉与自然降雨是磷素输入的主要途径,人工灌溉的磷素输入量为0.27~0.69 kg/(hm2·a),自然降雨的磷素输入量为1.05~1.19 kg/(hm2·a);水体下渗与洪涝排水是磷素输出的主要途径,水体下渗的磷素输出量为1.04~1.06 kg/(hm2·a),洪涝排水的磷素输出量为0.65~0.93 kg/(hm2·a).尖圩磷素流失量的年度差异较大(图 6),以2010-2012年为例,尖圩年磷素流失量分别为0.73、5.79、-1.83 kg,即0.07、0.54、-0.17 kg/(hm2·a).本研究构建的模型考虑了灌溉、降雨过程而导致的磷素输入,体现了圩区对其周围河道水体营养盐的吸附能力,因此磷素流失量的估算结果远低于孙金华等对常州雪堰镇圩区磷素流失的估算结果(16.5 kg/(hm2·a))[24].
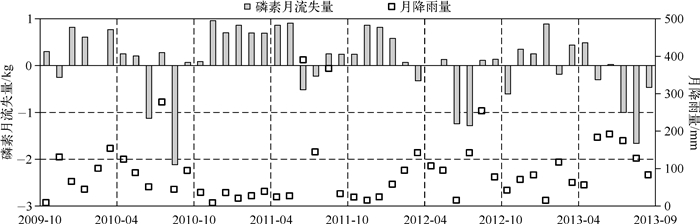
|
图 6 2009年10月-2013年9月圩区磷素月流失量与降雨量(其中正值与负值分别表示圩区排放与吸收磷素) Fig.6 Monthly phosphorus loss and precipitation of polder(Oct.2009-Sep.2013) |
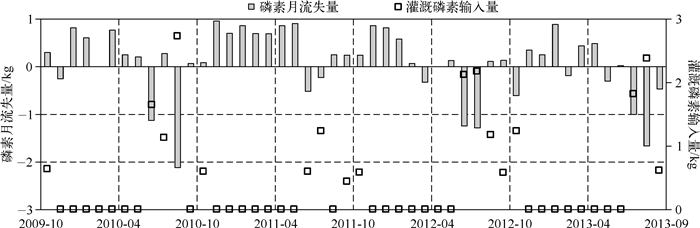
尖圩吸收外界磷素主要集中在历年夏季,其中灌溉是引起夏季磷素输入的重要渠道(图 7),春、秋、冬3季主要为磷素输出(图 6).同时,圩区磷素流失与降雨量、降雨分布均有密切关系,以2010年6-8月为例,2010年6月与8月,降雨量较少,而这一时间稻田需水量大,圩区通过人工灌溉吸收大量磷素;与此相反,2010年7月降雨充足(降雨量为277.3 mm),圩区通过农田灌溉输入磷素较少(图 7),同时有两场暴雨级别降雨(降雨量分别为92.5和85.3 mm),造成农田的大量磷素流失,而2011年7月、2012年7月、2013年7月,暴雨级别的降雨事件较少,因此圩区磷素月流失量均为负值,即圩区的磷素输入量大于输出量.
|
图 7 2009年10月-2013年9月圩区磷素月流失量与灌溉磷素输入量(其中正值与负值分别表示圩区排放与吸收磷素) Fig.7 Monthly phosphorus loss and phosphorus input due to irrigation of polder(Oct.2009-Sep.2013) |
综上所述,与非圩区集水单元相比[25],圩区系统对磷素具有显著的拦截效应,主要有3种途径:(1)夏季期间,水田需水量大,需要从圩外河道大量取水,而目前太湖流域平原区磷素污染严重,圩外河道磷素浓度较高,因此圩区通过灌溉吸收了外界大量磷素,这一途径是圩区吸收外界磷素的最重要渠道(图 6、7);(2)与非圩区区域相比,圩区水面率普遍较高,在降雨期间,水面区域能够接纳雨水中的大量磷素;(3)圩区内部沟渠广泛分布,对农田与居民区径流的磷素有一定的去除作用.
4.3 模型可靠性与不确定性本研究构建了圩区磷素流失过程模型,模型的结构与参数选择是合理的,具体阐述如下:
模型结构方面,基于圩区实地调研,模型描述了人工控制的灌溉抽水与洪涝排水过程,充分体现了圩区水文过程的独特性;同时参考了已有研究的相关模块:作物需水估算、农田与居民区径流估算、沟渠磷素拦截效应,而上述模块在平原区已有大量的应用[11, 17],计算方法是可靠的.因此,模型结构能够较好地表征圩区水量平衡与磷素流失过程.
模型参数方面,圩区磷素流失过程模型涉及大量参数,这些参数通过3种途径获取:(1)圩区实地调研资料:圩区灌溉与排涝过程受人工干预显著,与非圩区地区的差异较大,目前可借鉴的圩区磷素流失过程参数不多,采用实地调研的方法能够有效反映圩区的实际情况;(2)时间系列监测数据:圩区河道水体总磷浓度受到上游来水影响,时间上可能存在显著变化,采用时间系列的监测数据能够体现参数的时间变化过程;(3)太湖流域平原区的已有研究成果:目前已有大量研究集中于太湖流域平原区磷素流失,估算了磷素流失过程的相关参数[2, 5, 11, 18],上述案例的研究区与尖圩在地理位置、气象条件、农田耕作制度等方面都极其相似,这些参数已应用于相关的模拟研究,并得到不同程度的验证,具有较高的可靠性,对本研究的平原圩区磷素流失过程模型有重要参考价值.
目前模型尚存在多方面不足,有待于做以下几方面改进:(1)基于长时间系列的监测数据校正模型参数,并验证模型;本研究构建的圩区磷素流失过程模型涉及过程与参数较多,参数校正与模型验证需要长期监测数据的支持,而目前针对平原圩区非点源污染的监测有限,监测数据仍难以有效支持参数校正与模型验证,后期需要基于监测数据进一步优化模型参数,并分析模型的可靠性与不确定性;(2)考虑模型参数的时间与空间异质性;本研究仅考虑了6个参数的时间异质性(表 3),而事实上模型参数可能存在不同程度的时间与空间上的差异,因此需要通过深入研究圩区系统的机理过程,进一步校正模型参数;(3)考虑施肥对磷素流失过程的影响;本研究尚未考虑农田径流总磷浓度的动态变化过程,而农田径流总磷浓度在施肥后存在显著的波动现象,可能造成磷素流失总量的估算误差;(4)考虑工业点源对磷素流失的影响;尖圩是典型的农村圩区,没有工业污染源,因此模型应用于包含工业污染源的圩区时,需要进一步描述工业点源的磷素排放过程.
5 结论本研究开发了针对圩区系统的磷素流失模型,模型考虑了圩区人工灌溉与洪涝排水等过程,充分体现了圩区磷素流失过程的规律,可应用于预测不同降雨、灌溉与排涝情景下的磷素流失过程,进而估算圩区系统的磷素流失通量.模拟结果表明,与太湖流域平原非圩区相比,圩区的年度磷素流失通量较低(-0.17~0.54 kg/(hm2·a)),甚至存在磷素输入量大于输出量的年份,即磷素流失量为负值,表明圩区对磷素有一定的拦截效应;圩区磷素流失通量年度与年内均存在大幅度的波动,受降雨因子影响十分显著;农田灌溉、自然降雨是圩区磷素输入的主要渠道,其磷素输入量分别为0.27~0.69、1.05~1.19 kg/(hm2·a),而水体下渗和洪涝排水是圩区磷素输出的主要途径,其磷素输出量分别为1.04~1.06、0.65~0.93 kg/(hm2·a).
致谢: 感谢尹洪斌副研究员提供样品分析支持,感谢黄蔚博士、黄琪博士、闫人华博士在野外监测、实验室样品分析给予的帮助,感谢国家气象中心提供建模气象数据,感谢审稿人为本文提出的宝贵修改意见.| [1] |
高俊峰, 韩昌来. 太湖地区的圩及其对洪涝的影响. 湖泊科学, 1999, 11(2): 105-109. DOI:10.18307/1999.0203 |
| [2] |
崔广柏, 刘凌, 姚琪. 太湖流域富营养化控制机理研究. 北京: 中国水利水电出版社, 2009.
|
| [3] |
杨林章, 冯彦房, 施卫明等. 我国农业面源污染治理技术研究进展. 中国生态农业学报, 2013, 21(1): 96-101. |
| [4] |
Stone R. China aims to turn tide against toxic lake pollution. Science, 2011, 333: 1210-1211. DOI:10.1126/science.333.6047.1210 |
| [5] |
曹志洪, 林先贵, 杨林章等. 论"稻田圈"在保护城乡生态环境中的功能Ⅰ.稻田土壤磷素径流迁移流失的特征. 土壤学, 2005, 42(5): 799-804. DOI:10.11766/trxb200501030513 |
| [6] |
俞映倞, 薛利红, 杨林章. 太湖地区稻麦轮作系统不同氮肥管理模式对麦季氮素利用与流失的影响研究. 农业环境科学学报, 2011, 30(12): 2475-2482. |
| [7] |
徐爱兰, 王鹏. 太湖流域典型圩区农田磷素随地表径流迁移特征. 农业环境科学学报, 2008, 27(3): 1106-1111. |
| [8] |
夏军, 翟晓燕, 张永勇. 水环境非点源污染模型研究进展. 地理科学进展, 2012, 31(7): 941-952. DOI:10.11820/dlkxjz.2012.07.013 |
| [9] |
Daniel EB, Camp JV, LeBoeuf EJ et al. Watershed modeling and its applications: A state-of-the-art review. Open Hydrology Journal, 2011, 5: 26-50. DOI:10.2174/1874378101105010026 |
| [10] |
赖格英, 吴敦银, 钟业喜等. SWAT模型的开发与应用进展. 河海大学学报:自然科学版, 2012, 40(3): 243-251. |
| [11] |
程文辉, 王船海, 朱琰. 太湖流域模型. 南京: 河海大学出版社, 2006.
|
| [12] |
郝芳华, 杨胜天, 程红光等. 大尺度区域非点源污染负荷计算方法. 环境科学学报, 2006, 26(3): 375-383. |
| [13] |
曾远, 张永春, 范学平. 太湖流域典型平原河网区降雨径流氮磷流失特征分析. 水资源保护, 2007, 23(1): 25-27. |
| [14] |
张继宗, 张维理, 雷秋良等. 太湖平原农田区域地表水特征及对氮磷流失的影响. 生态环境学报, 2009, 18(4): 1497-1503. |
| [15] |
徐爱兰. 太湖流域典型圩区农业非点源污染产污规律及模型研究[学位论文]. 南京: 河海大学, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1031162
|
| [16] |
Cai J, Liu Y, Lei T et al. Estimating reference evapotranspiration with the FAO Penman-Monteith equation using daily weather forecast messages. Agricultural and Forest Meteorology, 2007, 145: 22-35. DOI:10.1016/j.agrformet.2007.04.012 |
| [17] |
Allen RG, Pereira LS, Raes D et al. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Rome, 1998, 300(9): 6541. |
| [18] |
王岩, 王建国, 李伟等. 三种类型农田排水沟渠氮磷拦截效果比较. 土壤, 2009, 41(6): 902-906. |
| [19] |
毛锐. 太湖、团氿湖水面蒸发的初步研究. 海洋与湖沼, 1978, 9(1): 26-35. |
| [20] |
王岩, 王建国, 李伟等. 生态沟渠对农田排水中氮磷的去除机理初探. 生态与农村环境学报, 2010, 26(6): 586-590. |
| [21] |
彭世彰, 黄万勇, 杨士红等. 田间渗漏强度对稻田磷素淋溶损失的影响. 节水灌溉, 2013(9): 36-39. |
| [22] |
章明奎, 王阳, 黄超. 水网平原地区不同种植类型农田氮磷流失特征. 应用生态学报, 2011, 22(12): 3211-3220. |
| [23] |
赖格英, 于革. 太湖流域营养物质输移的模拟评估研究. 河海大学学报:自然科学版, 2007, 35(2): 140-144. |
| [24] |
孙金华, 朱乾德, 练湘津等. 平原水网圩区非点源污染模拟分析及最佳管理措施研究. 长江流域资源与环境, 2013, 22(Z1): 75-82. |
| [25] |
赵广举, 田鹏, 穆兴民等. 基于PCRaster的流域非点源氮磷负荷估算. 水科学进展, 2012, 23(1): 80-86. |
 2015, Vol. 27
2015, Vol. 27 


