洪水作为一种自然灾害事件，每年造成的经济损失数以亿计，如何控制洪水并减少损失一直是灾害风险管理的重点.由于洪水事件发生的随机性，频率分析成为洪水风险评估的一种有效手段，重现期与设计值的定义与计算则是频率分析中的重点.同一个洪水事件前后两次发生的平均间隔时间即为该事件的重现期，若把该洪水事件造成的破坏和影响(以下称效应)作为洪水风险管理与工程设计的标准，重现期更大的洪水事件则可视为该标准下的危险事件.传统的单变量频率分析并不能满足洪水事件多个特征属性的特点，随着Copula函数在水文分析中的应用，多变量的洪水频率分析已成为近年来的研究热点^[1-4].与单变量重现期相比，多变量重现期的定义则要复杂得多，“或”和“且”定义法^[5]是目前最常用的两种多变量重现期定义方法，但在安全事件与危险事件的判定上，两者都存在局限性^[6].Salvadori等^[6]在“或”和“且”多变量重现期定义法的基础上，基于安全与危险域的概念提出了新的多变量重现期定义——二次重现期，相关概念与定义已在海岸工程设计的研究中有了初步的应用^[7-8].

本文以东江下游博罗站点为例，介绍多变量重现期新的定义与计算方法，通过分析传统重现期与二次重现期在安全与危险域识别的差异性，探讨二次重现期在洪水风险应用的合理性与可靠性.本文的目的在于理论方法的介绍与探讨，为洪水风险管理与工程设计的研究提供一种新的思路和方法.

1 洪水特征属性

洪水事件具有多个特征属性，其中最重要的是历时、洪峰和洪量.一场洪水的选取关键在于辨别洪水开始和结束的时间，当流量开始增加并超过了基流量时即可认为是洪水开始发生，当流量又退落到基流量时即意味着洪水的结束.然而，由于每一场洪水的基流量都不一样，实际上要准确地辨认出基流量是十分困难的，一般可以将流量突然并持续增加的时刻看作是洪水开始的时间，将流量突然下降并退落至起涨流量或稳定流量的时刻看作是洪水结束的时间^[9].

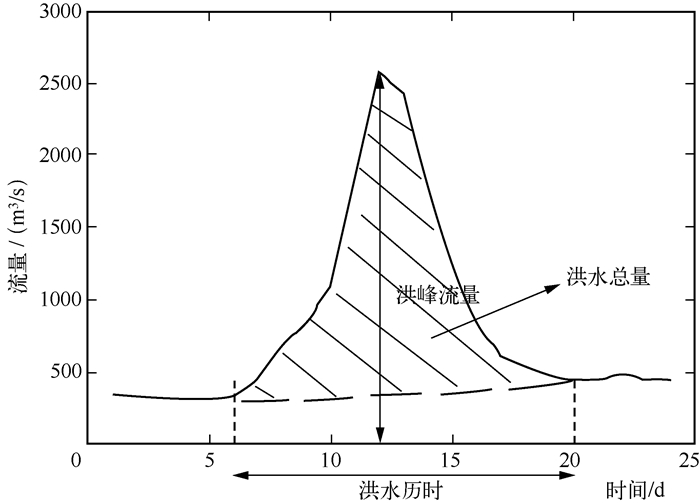
洪水的特征属性可以按照流量过程线来提取，如图 1所示，流量从突然增加到退落至稳定所经历的时间为洪水历时D(d)，其间最大的流量即为洪峰流量Q(m³/s)，所增加的水量为洪水总量(洪量)V(斜线部分面积，日m³/s).历时和洪量可分别根据下式计算^[9]：

$ D={{t}_{\text{e}}}-{{t}_{\text{s}}} $

(1)

$ V=\left[\sum\limits_{i={{t}_{\text{s}}}}^{{{t}_{\text{e}}}}{{{q}_{i}}-\frac{1}{2}}\left( {{q}_{{{t}_{\text{s}}}}}+{{q}_{{{t}_{\text{e}}}}} \right) \right]-\frac{1}{2}D\left( {{q}_{{{t}_{\text{s}}}}}+{{q}_{{{t}_{\text{e}}}}} \right) $

(2)

式中，t_s和t_e分别为洪水开始和结束的时间，q为日流量观测序列.

2 边缘分布与联合分布

洪水频率分析中的样本序列主要通过年最大抽样的方法从每年发生的洪水事件中选取，选取的年最大洪水事件可认为是极值事件，根据极值理论，极值事件应服从极值分布^[10].极值理论中的单元极值分布为广义极值分布(GEV)，其分布函数为：

$ F(x)=\left\{ \begin{align} &\text{exp}\left\{-{{\left[1-k\left( \frac{x-\mu }{\sigma } \right) \right]}^{\frac{1}{k}}} \right\}, k\ne 0 \\ &\text{exp}\left[-\text{exp}\left( \frac{x-\mu }{\sigma } \right) \right], k=0 \\ \end{align} \right. $

(3)

式中，μ、σ和k分别为位置、尺度和形状参数.

与传统的多变量分布函数相比，Copula函数具有简单灵活的结构特点，并且不受边缘分布的限制，是一种可以适用于多个变量间不同相关结构的多变量分布函数^[11].Archimedean copula是水文分析中最常用的Copula函数族，其基本形式为：

$ C({{\mathit{u}}_{1}}, \cdots, {{\mathit{u}}_{j}})=\varphi _{\theta }^{[-1]}\left[{{\varphi }_{\theta }}({{\mathit{u}}_{\text{1}}})+\cdots +{{\varphi }_{\theta }}({{\mathit{u}}_{j}}) \right] $

(4)

式中，u_j∈[0, 1](j＞1)为边缘分布，$φ$_θ为Archimedean copula生成元，θ为参数.当C满足下式时，则C是一个多变量极值分布^[13].

$ C({u}_1^t, \cdots ,{u}_j^t) = {\left[ {C({{u}_1}, \cdots ,{{u}_j})} \right]^t} $

(5)

可以证明Gumbel-Hougaard copula满足上式，并且是Archimedean copula中唯一的多变量极值copula^[12-13]，其结构形式为：

$ C({u_1}, \cdots ,{u_j}) = {{e}^{ - {{[{{({\rm{ln}}{{u}_1})}^\theta } + \cdots + {{( - {\rm{ln}}{{u}_j})}^\theta }]}^{\frac{1}{\theta }}}}} $

(6)

仅当边缘分布和Copula函数均具有极值性质时，构造的联合分布才是极值分布^[13]，可用于极值事件的频率分析中.

3 多变量重现期与分位值 3.1 传统多变量重现期

若以历时、洪峰和洪量来描述洪水事件，则洪水事件可以表示为E(D，Q，V).在单变量的洪水频率分析中，以洪峰作为特征变量，设定一个阈值q^*，洪峰大于q^*的任何洪水事件都被定义为危险事件，即E的危险域为$\Im$_E＝{q∈R：q＞q^*}.当考虑多个特征变量时，可以将以下两类洪水事件定义为危险事件：(1)历时、洪峰和洪量其中一个超过了设定的阈值(记为事件E^∨)；(2)历时、洪峰和洪量同时都超过了设定的阈值(记为事件E^∧).危险事件发生的概率即为危险率，若将E^∨作为危险事件，则危险率为P(D＞d^*∨Q＞q^*∨V＞v^*)，对应的危险域为$\Im$$_{\mathop E\limits^ \vee }$ ＝{(d，q，v)∈R³：d＞d^*∨q＞q^*∨v＞v^*}；若将E^∧作为危险事件，则危险率为P(D＞d^*∧ Q＞q^*∧V＞v^*)，对应的危险域为$\Im$$_{\mathop E\limits^ \wedge }$＝{(d，q，v)∈R³：d＞d^*∧ q＞q^*∧ v＞v^*}.

在传统的多变量重现期定义中，E^∨对应的重现期为“或”重现期T^∨，E^∧对应的重现期则为“且”重现期T^∧.年最大洪水事件的3变量“或”重现期和“且”重现期可分别由以下两式计算：

$ {{T}^{\vee }}=\frac{1}{P(\mathit{D>}{{\mathit{d}}^{*}}\vee \mathit{Q>}{{\mathit{q}}^{*}}\vee \mathit{V>}{{\mathit{v}}^{*}})}=\frac{1}{1-C({{\mathit{u}}_{d}}, {{\mathit{u}}_{q}}, {{\mathit{u}}_{v}})} $

(7)

$ {{T}^{\wedge }}=\frac{1}{P(\mathit{D>}{{\mathit{d}}^{*}}\wedge Q>{{q}^{*}}\wedge V>{{v}^{*}})}=\frac{1}{\hat{C}(1-{{u}_{d}}, 1-{{\mathit{u}}_{q}}, 1-{{\mathit{u}}_{v}})} $

(8)

式中，$\hat{C}$(1－u_d，1－u_q，1－u_v)为生存Copula函数^[12].

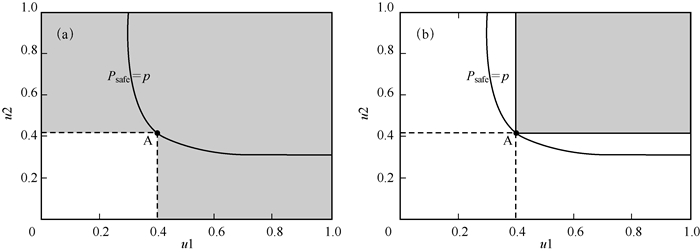
假设E的安全率为P_safe(危险率则为1－P_safe)，在P_safe＝p的条件下，以两变量的情形进行阐述，“或”重现期和“且”重现期对安全与危险域的识别如图 2所示.在相同安全率的情况下，“或”重现期和“且”重现期标准下不同的分位值组合对应的安全与危险域都不一样.

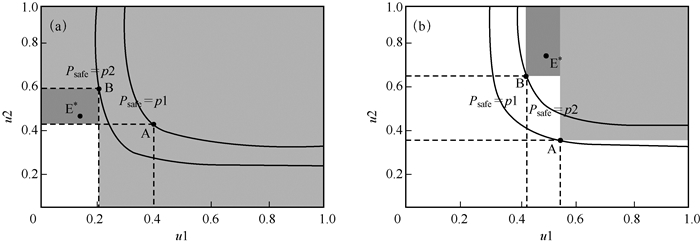
一般地，设计的重现期越大，相应的危险率就越小，设置的灾害防御标准遭遇的风险就越低.就此而言，“或”重现期和“且”重现期识别的安全与危险域显然具有局限性^[6].如图 3a所示，对于“或”重现期，A点处的重现期大于B点(p1＞p2)，而A点识别的危险域却有一部分在B点识别的危险域之外(深灰色部分)，即当事件E^*发生时，若以B点的组合值作为灾害防御的标准则可以认为E^*是安全的，E^*造成的效应在防御的标准之下；若以重现期更大的A点组合值作为灾害防御的标准则E^*显然是危险事件.高风险的防御标准识别的安全事件却被更低风险的防御标准识别为危险事件，这显然是矛盾的.对于“且”重现期(图 3b)，A点处的重现期小于B点(p1＜p2)，但A点识别的危险域并没有完全覆盖B点的危险域，即当事件E^*发生时，若以B点的组合值作为灾害防御的标准，E^*造成的效应超过了防御的标准，可认为E^*是危险事件；若以A点的组合值作为灾害防御的标准则E^*造成的效应在防御的标准下，E^*是安全事件.低风险的防御标准识别的危险事件在更高风险的防御标准里却是安全事件，这显然也是矛盾的.无论是“或”重现期还是“且”重现期，都会对安全事件与危险事件产生错误的识别，从而造成风险管理与工程设计的经济浪费或抵御风险的不力.

3.2 分位值曲面

不同历时、洪峰与洪量组合下的洪水事件有可能会造成相同的效应，即不同的E(D，Q，V)可以具有相同的安全率或危险率^[14].对于E^∨，给定一个p(0＜p＜1)值，存在不同的(d，q，v)组合使P_safe＝p成立，即在三维的实数空间里，具有相同效应的(d，q，v)点集构成了一个等曲面，即P_safe＝p条件下的分位值曲面^[15]：S_p^∨＝{(d，q，v)∈R³：P_safe＝C(u_d，u_q，u_v)＝p}；同样地，对于E^∧，在P_safe＝p条件下具有相同效应的(d，q，v)点集构成的等曲面为：S_p^∧＝{(d，q，v)∈R³：P_safe＝1－$\hat{C}$(1－u_d，1－u_q，1－u_v)＝p}.若将等曲面S_p^∨或S_p^∧当作一个临界面，则可以将三维的实数空间划分成3部分：(1)次临界域$\mathfrak{R}$_p^＜＝{(d，q，v)∈R³：P_safe＜p}；(2)临界面S_p^∨或S_p^∧；(3)超临界域$\mathfrak{R}$_p^＞＝{(d，q，v)∈R³：P_safe＞p}.任意一个E(D，Q，V)的空间点必然会落在这3部分其中一个之内，若以等曲面作为洪水风险的临界面，任何落在次临界域$\mathfrak{R}$_p^＜之内的E(D，Q，V)都可视为临界条件下的绝对安全事件，落在超临界域$\mathfrak{R}$_p^＞之内的E(D，Q，V)都可视为临界条件下的危险事件，落在临界面上的E(D，Q，V)则为警戒事件或相对安全事件.因此，依据具有相同效应的历时、洪峰与洪量组合构成的等曲面划分的次临界域、临界面和超临界域可以分别定义为洪水风险临界条件(P_safe＝p)下的绝对安全域、警界面和危险域.

3.3 二次重现期

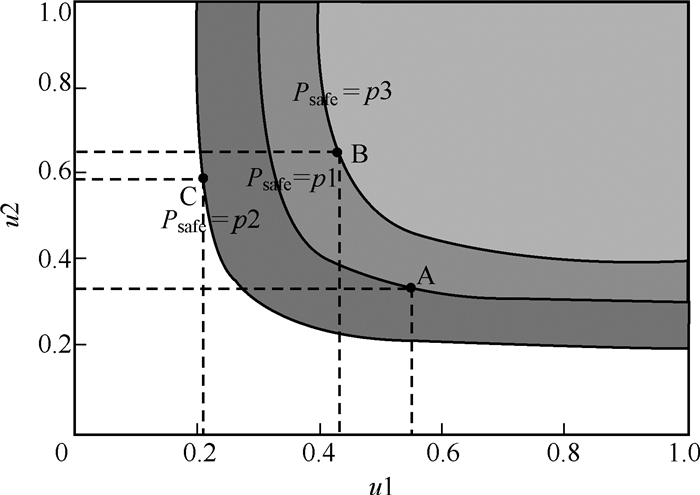
基于“或”重现期和“且”重现期对安全与危险域识别的局限性，若将空间点落在$\mathfrak{R}$_p^＞内的事件视为危险事件，空间点落在$\mathfrak{R}$_p^＞外的事件视为安全事件，则临界条件下的安全与危险域如图 4所示.由图 4可见，临界面上的任意一点都具有相同的安全与危险域，p值越大，危险域越小(p2＜p1＜p3)；p值较小的危险域必定会覆盖p值较大的危险域($\mathfrak{R}$_p2^＞∈$\mathfrak{R}$_p1^＞∈$\mathfrak{R}$_p3^＞).显然，这样的安全与危险域定义对于洪水风险管理来说是非常合理的，并且避免了对安全事件与危险事件的错误判定.将C(u_d，u_q，u_v)＝p作为临界条件，则E(D，Q，V)落在$\mathfrak{R}$_p^＞内的概率即危险率为P[C(u_d，u_q，u_v)＞p]，因此C(u_d，u_q，u_v)＝p条件下的重现期即可定义为：

$ {{T}_{\text{K}}}=\frac{1}{P[\mathit{C}\text{(}{{\mathit{u}}_{d}}\text{, }{{\mathit{u}}_{q}}\text{, }{{\mathit{u}}_{v}}\text{)}>\mathit{p}]}=\frac{1}{1-{{K}_{\text{C}}}(\mathit{p})} $

(9)

T_K称为二次重现期(Secondary return period)或Kendall重现期，K_C为Kendall分布函数^[16]：

$ {{K}_{\text{C}}}(\mathit{p})=p+\sum\limits_{i=1}^{k-1}{\frac{{{(-1)}^{k}}}{i!}{{[\varphi (\mathit{p})]}^{k}}{{h}_{i}}(p)} $

(10)

$ {h_i}({p}) = \left\{ \begin{array}{l} \frac{{\partial p}}{{\partial \varphi (p)}},i = 1\\ {h_1}(p)\frac{{\partial {h_{i - 1}}({p})}}{{\partial p}},i \ge 2 \end{array} \right. $

(11)

对于三维Gumbel-Hougaard copula，Kendall分布函数可以表达为：

$ {{K}_{\text{C}}}(p)=p-\frac{p(3\theta-\text{ln}\mathit{p}\text{-1})\text{ln}\mathit{p}}{2{{\theta }^{2}}} $

(12)

由公式(7)、(8)和(9)以及C的非递减性可知，单变量重现期、“或”重现期、“且”重现期和二次重现期四者的关系^{[14, 17]}为：T^∨ ≤T≤T_K≤T^∧，当且仅当u_j＝0时，等号成立.

3.4 多变量设计值

在单变量频率分析中，给定一个重现期，通过概率分布的反函数即可估算出对应的设计分位值.而对于多变量的情形，同一个重现期可以有不同的分位值组合与之对应，并且这些分位值组合不能通过概率分布的反函数直接估算.具有相同二次重现期T_p(C(u_d，u_q，u_v)＝p)的历时、洪峰与洪量分位值组合构成了一个三维点集，即等曲面S_p^∨.在这些不同的分位值组合中，必然存在一个组合(d_ml，q_ml，v_ml)使联合概率密度f(d，q，v)达到最大值，即在T_p条件下所有的分位值组合中，该组合出现的可能性最大.由于在洪水风险管理与工程的设计中，常常要追求经济上的节约，在成本较低的情况下可以承受较大的风险，因此在设定的防洪重现期下，出现可能性最大的历时、洪峰与洪量组合便成为防洪工程设计参考标准的一种上佳选择.

$ ({{d}_{ml}}, {{q}_{ml}}, {{v}_{ml}})=\underset{(d, q, v)\in \mathit{S}_{p}^{\vee }}{\mathop{\text{arg}\ \text{max}\mathit{f}\text{(}\mathit{d, q, v}\text{)}}}\, $

(13)

$ f(d, q, v)=\mathit{c}\text{(}{{\mathit{u}}_{d}}, {{u}_{q}}, {{u}_{v}}\text{)}{{\mathit{f}}_{d}}\text{(}\mathit{d}\text{)}{{\mathit{f}}_{q}}\text{(}\mathit{q}\text{)}{{\mathit{f}}_{v}}\text{(}\mathit{v}\text{)} $

(14)

式中，c为三维Gumbel-Hougaard copula的概率密度函数，f_d(d)、f_q(q)和f_v(v)则分别为历时、洪峰和洪量的概率密度函数.

综上所述，二次重现期条件下的洪水多变量分位值估算步骤可以总结为：

(1) 设定一个二次重现期T_p，通过公式(9)和(12)推求出p＝K_C^[－1](1－1/T_p)；

(2) 利用式(4)，计算所有使C(u_d，u_q，u_v)＝p成立的概率组合(u_d，u_q，u_v)；

(3) 由式(15)计算出使f(d，q，v)达到最大值的一组(u_d，u_q，u_v)；

(4) 最后分别再根据边缘分布的反函数推求出历时、洪峰和洪量的分位值(d_ml，q_ml，v_ml)，d_ml＝F^－1(u_d)、q_ml＝F^－1(u_q)、v_ml＝F^－1(u_v).

4 案例研究

博罗站位于东江下游，是东江流域重要的水文控制站点之一.本文选用博罗站1953 2010年的日流量观测数据作为研究资料，依据年最大极值理论，首先提取每年的最大日流量作为该年极端洪水事件的洪峰流量，以洪峰流量为基准，再按流量过程线提取并计算出该场洪水的历时与洪量，总共提取了58场洪水作为博罗站点多变量洪水频率分析的样本序列.历时与洪峰、洪量样本两两间的Kendall秩相关系数表明洪水特征属性间存在较强的相关性，其中，洪峰与洪量的相关性最大(0.665)，历时与洪量次之(0.623)，历时与洪峰则相对较小(0.355).

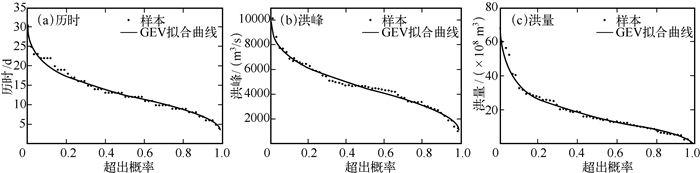
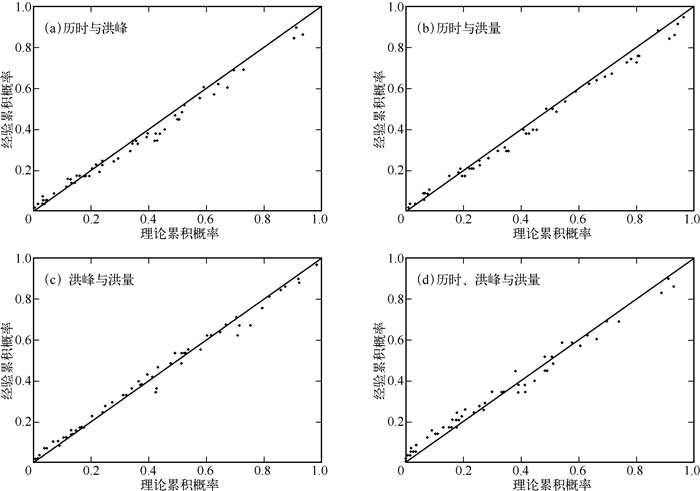
为了检验GEV和Gumbel-Hougaard copula构造洪水事件联合分布的合理性，选用水文分析中常用的对数正态分布(GNO)、广义逻辑斯特分布(GLO)和皮尔逊三型分布(PE3)，Clayton和Frank copula^[12]分别对历时、洪峰和洪量样本进行拟合优度检验，并与GEV和Gumbel-Hougaard copula进行对比.选用的分布参数均采用极大似然法进行估计，拟合优度检验则依据Akaike信息准则(AIC)^[7]，AIC值越小，代表拟合优度越高.选用的备选分布都通过了K-S检验，表明选用的分布都可用于样本的拟合.各种分布的拟合优度AIC值如表 1所示，虽然拟合优度检验的结果并没有显示GEV和Gumbel-Hougaard copula对所有历时、洪峰和洪量样本以及它们间组合的拟合都是最优的(GEV对历时和Gumbel-Hougaard copula对历时与洪量组合的拟合为次优)，但从总体角度和出于极值分布的考虑，我们选用GEV和Gumbel-Hougaard copula分别作为边缘分布和多变量分布来构造洪水特征属性间的联合分布.图 5和图 6所示的GEV和Gumbel-Hougaard copula对历时、洪峰和洪量样本的拟合效果亦表明两者用于构造洪水联合分布是合理的.

历时、洪峰和洪量保证率分别为96 %、98 %、99 %和99.5 %时的单变量重现期、“或”重现期、“且”重现期和二次重现期计算值如表 2所示，在同一保证率水平下(保证率不为0)，二次重现期与“且”重现期相差较小，与“或”重现期则相差较大；保证率越小，二次重现期与“或”重现期和“且”重现期之间的差值则越小，随着保证率的增大，三者的差值逐渐增大.根据3.4所述步骤计算的25、50、100和200年重现期历时、洪峰和洪量的多变量设计值以及单独推算的单变量设计值如表 3所示，单独推算的历时与洪量设计值均比多变量推算的大，而多变量洪峰设计值则要大于单变量设计值，并且随着重现期的增大，两者的差值逐渐减小.一场洪水造成的效应并不是由单个特征属性决定的，而是多个特征属性共同作用的结果，如高洪峰伴随大洪量的洪水造成的影响和破坏要比高洪峰伴随小洪量的洪水大，长历时高洪峰的洪水造成的影响和破坏要比短历时高洪峰的洪水大.再者，历时、洪峰与洪量之间的组合以及出现的概率又取决于它们间的相关结构和联合分布.因此，相比于单变量设计值，考虑了洪水多个属性联合特征的多变量设计值为防洪工程设计提供了更加全面和可靠的参考信息.

5 结论

1) 传统的“或”和“且”多变量重现期对安全与危险域的识别具有局限性，重现期与危险域范围大小的矛盾会造成对安全事件与危险事件的错误识别.

2) 根据C(u_d，u_q，u_v)＝p临界条件并利用Kendall函数定义的二次重现期，具有同一临界水平下任意历时、洪峰与洪量组合对安全与危险域识别的一致性，重现期越大，对应的危险域则越小，避免了对安全事件与危险事件的错误识别，更有利于指导洪水风险的管理.

3) 给定二次重现期条件下的洪水事件可以具有不同的历时、洪峰与洪量组合，在工程设计中，与每个特征属性同时取较大值相比，依据出现概率最大的原则推算的设计值组合可以满足以较低成本承受较大风险的追求.相比于单变量设计值，考虑了洪水多个属性联合特征的多变量设计值为防洪工程设计提供了更加全面和可靠的参考信息.