(2: 北京大学城市人居环境科学与技术实验室,深圳 518055)
(3: 珠江水资源保护科学研究所,广州 510611)
(2: Key Laboratory for Urban Habitat Environment Science and Technology, School of Environment and Energy, Peking University, Shenzhen 518055, P.R.China)
(3: Research Institute of Pearl River Water Resources Protection, Guangzhou 510611, P.R.China)
东江是珠江3大支流之一,流域内人口约占广东全省总人口的50 %,GDP占全省总量的70 %,在全省政治、经济和社会中占有重要地位[1].东江是珠江三角洲东部的主要水源,其中,香港特别行政区80 %的淡水引自东江[2].作为基础性和战略性资源,东江水资源的丰枯状况直接影响流域内经济社会发展与稳定.然而,全球气候变化导致极端水文事件频发,增加了水资源的不确定性[3].在此背景下,通过水库等水利工程调节和管理水资源显得尤为重要.
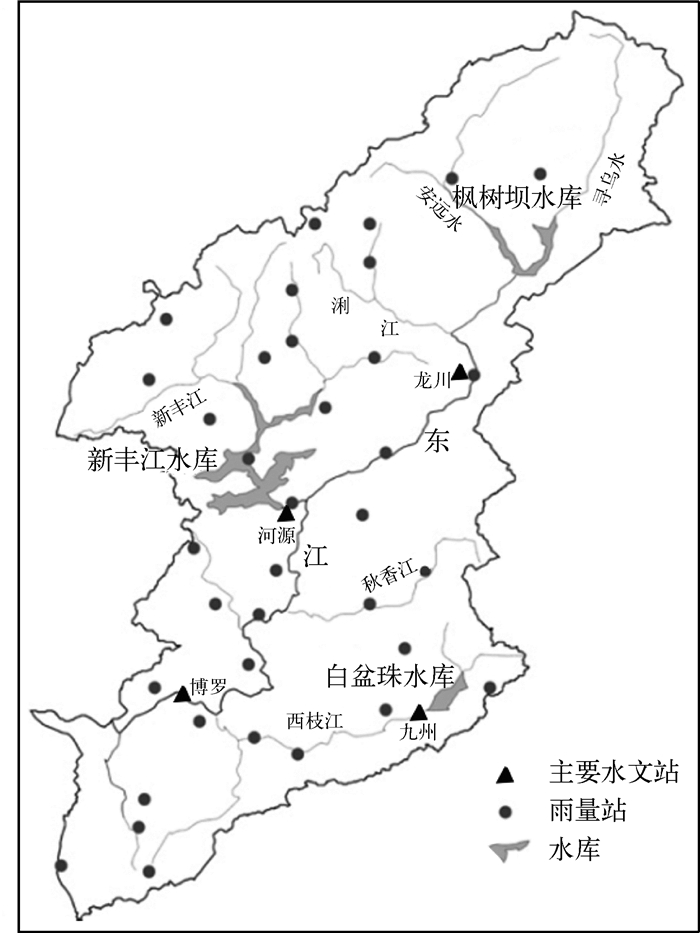
东江流域3大水库自上游而下依次为枫树坝水库、新丰江水库和白盆珠水库(图 1),3者分别位列广东省大型水库第2、1、5位,库容合计占东江流域大中水库总库容的92 %,对流域内水量、水质和水生态调控具有重要作用[4-5].近年来,随着各流域大批水库电站的建成和投入使用,水库群联合调度成为“节能发电”、“洪水资源化”时代背景下的新要求[6].2008年,广东省政府颁布《广东省东江流域水资源分配方案》,要求3大水库实行防洪、供水、发电等多目标联合优化调度.水库来水特征是水库群联合调度设计的基础.面对新要求,研究3大水库入库流量的丰枯遭遇特性及丰枯补偿的可能性对水库群的优化调度具有重要意义.
|
图 1 东江流域3大水库位置 Fig.1 Location of the three biggest reservoirs in Dongjiang River basin |
不同水文区的丰枯遭遇本质上属于多变量联合概率和条件概率的问题.目前,多变量水文分析方法主要有多元正态分布法[7]、特定边缘分布构成的联合分布法[8]、非参数方法[9]、多维转一维方法[10]、经验频率法[11]等,但各方法均存在自身的局限与不足[12].Copula函数克服了传统方法的不足,将联合分布分为边缘分布和相关性结构分别处理,具有很大的灵活性和适应性,在暴雨、洪水、干旱等水文事件分析中日益受到重视[13-17].本文利用Copula函数,构建新丰江水库、枫树坝水库和白盆珠水库入库流量的联合分布,分析3大水库的丰枯遭遇和补偿特性,以期为水库群的联合调度提供理论参考和决策支持.
1 方法与数据 1.1 Copula函数[18]n-维Copula函数是具有以下性质的函数C:In→I
1) C的定义域In∈[0, 1]n;
2)
3)
如果F1,F2,…,Fn是连续的一维分布函数,令ui=Fi,则C(u1,u2,…,un)是一个边缘分布服从均匀[0, 1]的多元分布函数.
Copula函数将联合分布分为变量的边缘分布和变量间的相关性结构分别处理,不要求变量同分布,可连接任意边缘分布构造联合分布,且转换过程中不产生信息失真,具有独特的优越性.Copula函数大体上分为椭圆型、Archimedean型和二次型.本文主要采用在水文领域广泛应用的Archimedean Copula.该函数族构造相对简单,适应性强,可分为对称型和非对称型两种.其中,对称型的构造形式为:
| $ C({u_1}, {u_2}, \cdots, {u_n}) = {\varphi ^{- 1}}[\varphi ({u_1}) + \varphi ({u_2}) + \cdots + \varphi ({u_n})] $ | (1) |
式中,
Gumbel-Hougaard (GH) Copula生成元ϕ(t)=(-lnt)θ,适用于变量间正相关的情形.
| $ {C_\theta }\left( {u, v} \right) = {\rm{exp}}(- {[{(-{\rm{ln}}u)^\theta } + {(-{\rm{ln}}v)^\theta }]^{1/\theta }}), \theta \in \left[{1, {\rm{ }}\infty } \right) $ | (2) |
Clayton Copula生成元ϕ(t)=t-θ-1,Clayton Copula仅能描述正相关的随机变量.
| $ C\left( {u, v} \right) = {({u^{-\theta }} + {v^{-\theta }}-1)^{ - 1/\theta }}, \theta \in \left( {0, {\rm{ }}\infty } \right) $ | (3) |
Ali-Mikhail-Haq (AMH) Copula生成元ϕ(t)=
| $ C(u, v) = uv/(1- \theta (1- u)(1- v)), \theta \in [-1, 1) $ | (4) |
Frank Copula生成元为ϕ(t)=
| $ C\left( {u, v} \right) = \frac{1}{\theta }{\rm{ln}}\left( {1 + \frac{{({{\rm{e}}^{-\theta u}}-1)({{\rm{e}}^{-\theta v}} - 1)}}{{{{\rm{e}}^{ - \theta }} - 1}}} \right), \theta \in R\backslash \left\{ 0 \right\} $ | (5) |
式中,u、v为边缘分布函数,θ为Copula函数的参数,下同.
由以上二维对称型Copula可推演得到相应的三维对称型Copula函数,但后者要求变量两两间的相关性结构相同或相似,限制了其应用.此处采用对应的三维非对称型Archimedean Copula,其表达式为:
Gumbel-Hougaard (GH) Copula:
| $ C({u_1},{u_2},{u_3}) = {\rm{exp}}\{ - {({[{( - {\rm{ln}}{u_1})^{{\theta _2}}} + {( - {\rm{ln}}{u_2})^{{\theta _2}}}]^{{\theta _1}/{\theta _2}}} + {( - {\rm{ln}}{u_3})^{{\theta _1}}})^{1/{\theta _1}}}\} ,{\theta _2} \ge {\theta _1} \in \left[ {1{\rm{ }}, + \infty } \right) $ | (6) |
Clayton Copula:
| $ C({u_1},{u_2},{u_3}) = {[{(u_1^{ - {\theta _2}} + u_2^{ - {\theta _2}} - 1)^{{\theta _1}/{\theta _2}}} + u_3^{{\theta _1}} - 1]^{ - 1/{\theta _1}}},{\theta _2} \ge {\theta _1} \in \left[ {0, + \infty } \right) $ | (7) |
Ali-Mikhail-Haq (AMH) Copula:
| $ C({u_1}, {u_2}, {u_3}) = \frac{{{u_1}{u_2}{u_3}}}{{[1-{\theta _1}(1-{u_3})][1-{\theta _2}(1-{u_2})(1-{u_1})] + {\theta _1}{u_1}{u_2}(1 - {u_3})}}, {\theta _2} \ge {\theta _1} \in \left[{-1, {\rm{ }}1} \right) $ | (8) |
Frank Copula:
| $ C({u_1},{u_2},{u_3}) = - {\theta ^{ - 1}}{\rm{ln}}[1 - {(1 - {{\rm{e}}^{ - \theta }})^{ - 2}}(1 - {{\rm{e}}^{ - \theta {u_1}}})(1 - {{\rm{e}}^{ - \theta {u_2}}})(1 - {{\rm{e}}^{ - \theta {u_3}}})],\theta \in (0{\rm{ }} + \infty ) $ | (9) |
式中,u1、u2、u3为边缘分布函数,θ1和θ2为参数.
1.2 边缘分布用适宜的边缘分布描述各单个变量是应用Copula函数的第一步.不同地域的不同水文变量可能服从不同的分布.针对东江流域3大水库的入库流量,本文采用Pearson-Ⅲ分布(P-Ⅲ)、极值分布(GEV)、指数分布(EXP)和对数正态分布(LOGN)对各变量进行拟合,利用稳健性较好的线性矩法[19]进行参数估计,采用Kolmogorov-Smirnov(K-S)方法[20]检验边缘分布的可行性,并用均方根误差法(RMSE)、概率点据相关系数法(PPCC)[21]和AIC信息准则法[22]评价确定最优的边缘分布.其中,AIC包括模型的偏差和模型参数导致的不稳定性,计算方法为:
| $ {\rm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({{\mathit{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }}_i}-{\mathit{x}_i})}^2}} $ | (10) |
| $ {\rm{AIC}} = n{\rm{ln}}({\rm{MSE}}) + 2m $ | (11) |
式中,m为分布函数参数的个数.AIC值越小,说明分布函数的拟合效果越好.
1.3 Copula函数的参数估计、拟合检验与优选对于4种二维Copula,采用相关性指标法[23]估算参数.该方法如下:
1) 根据式(12)估算样本的Kendall相关系数:
| $ \tau = {\rm{ }}\frac{2}{{n\left( {n- 1} \right)}}{\rm{ }}\sum\limits_{1 \le i < j \le n} {sign} [({x_i}-{x_j})({y_i} < {y_j})] $ | (12) |
式中,{(x1,y1),(x2,y2),…,(xn,yn)}为随机样本,sign为符号函数.
2) 根据Copula函数的参数θ与Kendall相关系数的关系计算θ,具体关系见文献[23].
对于4种三维Copula,相关性指标法不再适用,采用极大似然法估计其参数.
在此基础上,采用K-S检验联合分布的合理性,采用AIC信息准则和RMSE进行拟合评价与函数优选.
1.4 丰枯遭遇本文把丰枯指标分为丰、平、枯3级,取丰、枯水划分的累积概率分别为pf=62.5 %和pk=37.5 % [11],即丰水:Xi>Xpf,枯水:Xi<Xpk,平水:Xpk<Xi<Xpf.其中,Xi是第i年入库流量,Xpk和Xpk即为丰水或枯水分界值.
入库流量的丰枯遭遇本质上是特定条件下的联合概率问题.设两个水库的入库流量分别为X、Y,则两者同丰的概率为P(X>Xpf,Y>Ypf)=1-upf-vpf+C(upf,vpf),X丰Y枯的概率为P(X>Xpf,Y<Ypk)=vpk-C(upf,vpk);X平Y丰的概率为:P(Xpk<X<Xpf,Y<Ypt)=upf-vpk-C(upf,vpf)+C(upk,vpf).式中,upf、vpf、vpk和upk分别为Xpf、Ypf、Ypk和Xpk的边缘分布函数值.其它丰枯遭遇情形可依此类推进行计算.
1.5 数据本文收集了3大水库1986 2008年的月入库流量资料,将每年的4至9月定为汛期,10月至次年3月定为非汛期,整理获得3大水库的汛期、非汛期和全年的入库流量序列,据此利用Copula函数进行丰枯遭遇分析.
2 结果与分析 2.1 入库流量边缘分布的确定采用P-Ⅲ、GEV、EXP和LOGN对3大水库汛期、非汛期和全年入库流量进行拟合,并进行拟合检验与评价,确定最优边缘分布,拟合检验结果见表 1.以新丰江汛期为例,4种分布的K-S检验值均小于临界值0.3608,说明它们在一定程度上均能代表样本的总体分布.其中,对数正态分布的AIC和RMSE值最小,PPCC值最大,故选其为最优边缘分布.类似地,确定其它水库不同时期的最优边缘分布.
| 表 1 3大水库不同时期入库流量边缘分布拟合检验结果 Tab.1 The fit test results of the marginal distributions of inflow of the three biggest reservoirs |
采用二维Copula构造3大水库两两间的联合分布.根据式(12)计算两库间的Kendall相关系数τ,进而计算得到3大水库不同时段入库流量二维Copula联合分布的参数(表 2).在汛期、非汛期和全年尺度上,新丰江与枫树坝水库入库流量的Kendall相关系数均最高,表明两者关系紧密,大小一致性相对较好;白盆珠与其它两个水库间的Kendall相关系数均较小,表明其与另外两个水库在入库流量上的一致性相对较差.利用K-S检验、AIC信息准则和均方根误差最小法确定最优的二维Copula函数.结果发现,除了汛期新丰江与枫树坝两库间的最优二维Copula为Clayton Copula外,其它情景下的最优二维Copula均为GH Copula.
| 表 2 3大水库二维联合分布参数估计结果 Tab.2 Parameter estimations of 2-dimensional joint distributions of any two of the three biggest reservoirs |
采用三维Copula构造3大水库的联合分布.利用极大似然法进行参数估计,然后进行拟合检验与评价,结果见表 3.类似地,选出不同时期的最优三维Copula函数.其中,汛期和全年的最优Copula为GH Copula,非汛期为Frank Copula.
| 表 3 3大水库三维联合分布拟合检验结果* Tab.3 The fit test results of the joint distribution of inflow of the three biggest reservoirs |
根据3大水库入库流量两两间的Copula函数,可以得到相应的二维联合分布,并据此计算特定条件下的联合概率.对全年入库流量,3大水库两两间的二维联合概率P(X<x,Y<y)分布如图 2所示.据此可得两个水库入库流量同时小于任意特定值的概率,以及特定概率下两个水库入库流量的可能组合,尤其用于分析两库同枯的不利情景.比如,新丰江水库和枫树坝水库全年入库流量均小于20×108 m3的概率为0.5 %,新丰江水库全年入库流量小于40×108 m3且白盆珠水库全年入库流量小于10×108 m3的概率为10 %.再如,枫树坝水库和白盆珠水库的联合概率为0.5 %时,两者全年入库流量的组合可能为:枫树坝水库小于30×108 m3且白盆珠水库小于5.3×108 m3,枫树坝水库小于20×108 m3且白盆珠水库小于6.5×108 m3,或枫树坝水库小于15×108 m3且白盆珠水库小于9.0×108 m3.

|
图 2 3大水库两两间入库流量(全年)联合分布及联合概率P(X<x,Y<y)等值线图 Fig.2 The joint distributions and joint probability of annual inflow of any two reservoirs(P(X < x, Y < y)) |
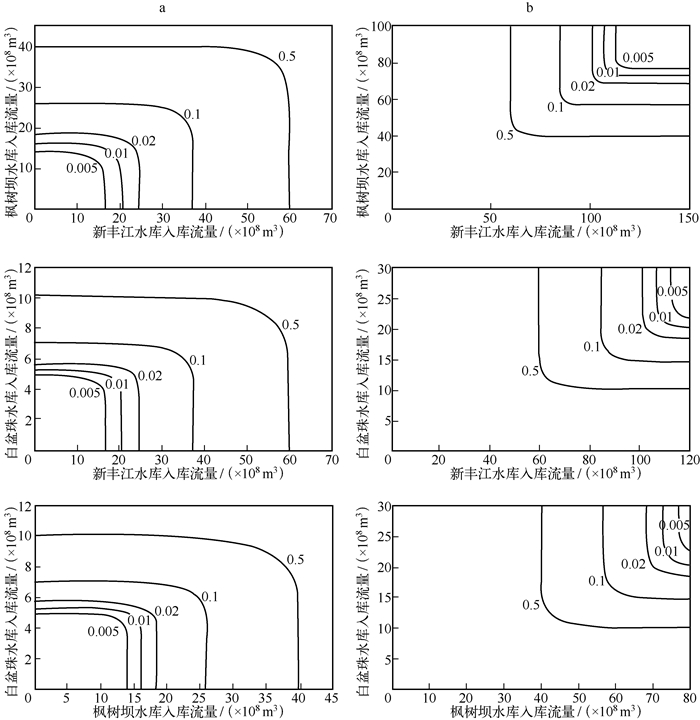
两个水库至少有一个的入库流量小于特定值的概率P(X<x或Y<y)见图 3a,该情景主要用于枯水预防.比如,新丰江水库全年入库流量小于35×108 m3或枫树坝全年入库流量小于25×108 m3的概率是10 %,即平均来看每10年两库中至少有一库发生小于等于该量级的枯水.两个水库至少有一个的入库流量大于特定值的概率P(X>x或Y>y)见图 3b,据此可分析水库间以多补少的可行性.比如,新丰江水库全年入库流量大于82×108 m3或白盆珠水库全年入库流量小于15×108 m3的概率是10 %,表明两库以多补少的概率不低于10 %.
|
图 3 3大水库两两间入库流量(全年)联合概率等值线图(a:P(X<x或Y<y);b:P(X>x或Y>y)) Fig.3 The contour maps of joint probability of annual inflow of any two reservoirs (a:P(X < x or Y < y); b:P(X > x or Y > y)) |
两个水库入库流量同时大于特定值的概率P(X>x,Y>y)见图 4,该情景可用于丰水调蓄分析.比如,枫树坝水库年入库流量大于55×108 m3且白盆珠全年入库流量大于12×108 m3的概率是10 %,表明平均来看每10年两库将发生大于或等于上述量级的较丰入库流量,水库可参考制订丰水调蓄预案.受篇幅限制,此处省略了汛期和非汛期3大水库上述4种联合概率的计算成果图.

|
图 4 3大水库两两间入库流量(全年)联合概率P(X>x,Y>y)等值线图 Fig.4 The contour maps of joint probability of annual inflow of any two reservoirs(P(X > x, Y > y)) |
3大水库两两间丰、平、枯划分下的遭遇概率见表 4.总体而言,3大水库两两间丰枯同步的概率大于丰枯异步的概率.其中,非汛期两库间丰枯同步的概率大于汛期,丰枯异步的概率小于汛期.同一时期,新丰江水库与枫树坝水库丰枯同步的概率最大,其中非汛期的丰枯同步概率高达78.00 %,全年丰枯同步的概率为69.18 %.新丰江水库与白盆珠水库,及枫树坝水库与白盆珠水库丰枯同步、丰枯异步的概率差异不显著,两者均位于50 %左右,以丰枯同步的概率稍高.这是由于新丰江水库与枫树坝水库入库流量的一致性较好,而白盆珠与其它两个水库间的一致性相对较差所致,这为新丰江、枫树坝两库与白盆珠水库相互补偿提供了可能.
| 表 4 3大水库两两间不同时期典型丰枯遭遇概率(%) Tab.4 The wetness-dryness encountering probabilities of any two reservoirs' inflow of different periods |
在丰枯同步情景中,两库同丰与两库同枯的概率相近,均位于20 % ~33 %之间;两库同平的概率最小,位于7 % ~15 %之间.在丰枯异步情景中,同一时期两库一平一枯的概率最大,一丰一平的概率居中,一丰一枯的概率最小(汛期新丰江水库与枫树坝水库例外).
2.4 3大水库丰枯遭遇分析利用三维Copula函数构建的3大水库联合分布,计算得到3大水库的丰枯遭遇概率(表 5).3大水库丰枯同步的概率在全年、汛期和非汛期均较大,依次为42.29 %、41.74 %和51.99 %.这是由于3大水库地理位置相近,水文气候性质相似,导致丰枯一致性相对较高.非汛期的丰枯同步概率明显高于汛期.这是因为径流在非汛期主要受地下水补给,而在汛期径流同时受地下水和降雨补给,后者的空间分布差异[24]降低了3大水库的丰枯一致性.在丰枯同步情景中,同丰和同枯的概率远大于同平的概率.如对全年而言,同丰和同枯的概率分别为20.80 %和17.82 %,而同平的概率仅为3.67 %.
| 表 5 3大水库不同时期典型丰枯遭遇概率(%) Tab.5 The wetness-dryness encountering probabilities of the three biggest reservoirs in different periods |
东江自上游而下依次为枫树坝、新丰江和白盆珠水库.当上游水库来水充沛而下游水库来水偏少时,则前者可在一定程度上补偿后者.具体而言,当枫树坝水库是丰水,而新丰江与白盆珠水库至少有一个是平水或枯水时,枫树坝水库对下游具有良好的补偿能力,这种丰枯遭遇的概率合计为16.70 %;当枫树坝是平水,而新丰江与白盆珠水库至少有一个是枯水时,枫树坝水库对下游具有一定的补偿能力,这种丰枯遭遇的概率合计为13.11 %;故枫树坝水库对下游具有补偿能力的概率合计为29.81 %.当新丰江水库为丰水,白盆珠水库为枯水或平水时,新丰江水库对下游具有良好的补偿能力,概率为13.76 %;当新丰江水库为平水,白盆珠水库为枯水时,新丰江水库对下游具有一定的补偿能力,概率为9.27 %;故新丰江水库对下游具有补偿能力的概率合计为23.03 %.当枫树坝水库为枯水,新丰江与白盆珠水库至少有一个也为枯水,或当新丰江和白盆珠水库均为枯水时,枫树坝与新丰江水库对下游均无补偿能力,这种丰枯遭遇的概率分别为32.75 %和22.32 %.
3 结论利用Copula函数,构建了东江流域新丰江、枫树坝和白盆珠3大水库入库流量的二维和三维联合分布,对其丰枯遭遇进行分析,主要结论如下:
1) 通过构建3大水库的联合分布,可以获得水库间不同入库流量条件下的概率,以及特定概率下不同水库入库流量的可能组合,对3大水库的联合优化调度具有重要的理论与实践价值.
2) 3大水库两两间丰枯同步的概率大于丰枯异步的概率,非汛期两库丰枯同步的概率大于汛期.新丰江与枫树坝水库入库流量的一致性较好,同一时期两者丰枯同步的概率最大;白盆珠与新丰江、枫树坝入库流量的一致性相对较差,丰枯异步的概率相对较大,这为其它两个水库与白盆珠水库丰枯互补提供了可能.
3) 对3大水库三维联合分布研究显示,3大水库丰枯同步的概率在全年、汛期和非汛期均较大,依次为42.29 %、41.74 %和51.99 %,其中同丰和同枯的概率远大于同平的概率.枫树坝与新丰江水库对下游具有补偿能力的概率分别为29.81 %和23.03 %,不具有补偿能力的概率分别为32.75 %和22.32 %.
| [1] |
严彬. 东江流域降水特性分析. 广东水利水电, 2011, 8: 57-60. |
| [2] |
Chen YD, Zhang Q, Lu X et al. Precipitation variability (1956-2002) in the Dongjiang River (Zhujiang River basin, China) and associated large-scale circulation. Quaternary International, 2011, 244(2): 130-137. DOI:10.1016/j.quaint.2010.08.013 |
| [3] |
IPCC. Summary for policymakers. Climate Change 2007: The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 2007.
|
| [4] |
黄国如, 李春. 东江干流突发性重金属污染的水库调度效应研究. 水电能源科学, 2013, 31(6): 82-85. |
| [5] |
胡培, 陈晓宏. 东江三大水库联合调度下惠州河段水温变化响应研究. 水文, 2013, 33(1): 38-43. |
| [6] |
郭生练, 陈炯宏, 刘攀等. 水库群联合优化调度研究进展与展望. 水科学进展, 2010, 21(4): 496-503. |
| [7] |
Yue S. Joint probability distribution of annual maximum storm peaks and amounts as represented by daily rainfalls. Hydrological Science Journal, 2000, 45(2): 315-326. DOI:10.1080/02626660009492327 |
| [8] |
Kotz S, Balakrishnan N, Johnson NL. Continuous multivariate distributions. New York: Wiley, 2000.
|
| [9] |
Kim T, Valdés JB, Yoo C. Nonparametric approach for bivariate drought characterization using Palmer drought index. Journal of Hydrologic Engineering, 2006, 11(2): 134-143. DOI:10.1061/(ASCE)1084-0699(2006)11:2(134) |
| [10] |
费永法. 多元随机变量的条件概率计算方法及其在水文中的应用. 水利学报, 1995(8): 60-66. |
| [11] |
郑红星, 刘昌明. 南水北调东中两线不同水文区降水丰枯遭遇性分析. 地理学报, 2000, 55(5): 523-532. DOI:10.11821/xb200005002 |
| [12] |
郭生练, 闫宝伟, 肖义等. Copula函数在多变量水文分析计算中的应用及研究进展. 水文, 2008(3): 1-7. |
| [13] |
Genest C, MacKay J. The joy of copulas: Bivariate distributions with uniform marginals. American Statistician, 1986(40): 280-283. |
| [14] |
Shiau JT. Fitting drought and severity with two-dimensional copulas. Water Resources Management, 2006, 20(5): 795-815. DOI:10.1007/s11269-005-9008-9 |
| [15] |
Favre A, El Adlouni S, Perreault L et al. Multivariate hydrological frequency analysis using copulas. Water Resources Research, 2004, 40: W01101. |
| [16] |
Salvadori G, de Michele C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resources Research, 2004, 40(12): W12511. |
| [17] |
Zhang L, Singh VP. Bivariate rainfall frequency distributions using Archimedean copulas. Journal of Hydrology, 2007, 332: 93-109. DOI:10.1016/j.jhydrol.2006.06.033 |
| [18] |
NelsonRB. An introduction to Copulas. New York: Springer, 1999.
|
| [19] |
Hosking JRM, Wallis JR. Regional frequency analysis: An approach based on L-moments. UK: Cambridge University, 1997.
|
| [20] |
Massey Jr FJ. The Kolmogorov-Smirnov test for goodness of fit. Journal of the American statistical Association, 1951, 46(253): 68-78. DOI:10.1080/01621459.1951.10500769 |
| [21] |
Filliben JJ. The probability plot correlation coefficient test for normality. Technometrics, 1975, 17(1): 111-117. DOI:10.1080/00401706.1975.10489279 |
| [22] |
Bozdogan H. Model selection and Akaike's information criterion (AIC): The general theory and its analytical extensions. Psychometrika, 1987, 52(3): 345-370. DOI:10.1007/BF02294361 |
| [23] |
Genest C, Rivest LP. Statistical inference procedures for bivariate Archimedean Copulas. American Statistical Association, 1993, 88(423): 1034-1043. DOI:10.1080/01621459.1993.10476372 |
| [24] |
刘德地, 陈晓宏. 东江流域降水场时空分布特征分析. 水文, 2008, 28(2): 82-86. |
 2015, Vol. 27
2015, Vol. 27 

