(2: 中山大学水资源与环境系,广州 510275)
(3: 中山大学华南地区水循环与水安全广东省普通高校重点实验室,广州 510275)
(4: 江西师范大学鄱阳湖湿地与流域研究教育部重点实验室,南昌 330022)
(2: Department of Water Resources and Environment, Sun Yat-sen University, Guangzhou 510275, P.R.China)
(3: Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong High Education Institute, Sun Yat-sen University, Guangzhou 510275, P.R.China)
(4: Key Laboratory of Poyang Lake Wetland and Watershed Research, Ministry of Education, Jiangxi Normal University, Nanchang 330022, P.R.China)
鄱阳湖是我国目前最大的淡水湖泊、同时也是长江干流重要的调蓄性湖泊,在长江流域发挥着巨大的调蓄洪水和保护生物多样性等特殊生态与防洪功能.鄱阳湖是我国十大生态功能保护区之一,也是世界自然基金会划定的全球重要生态区之一[1-2].自1990s以来,鄱阳湖流域洪水和干旱事件发生的频率不断增加,特别是极端干旱和洪水事件发生频率增加[3-5],21世纪以来,流域的干旱程度不断加剧,2003、2006和2007年的持续枯水事件和2011年的旱涝急转事件,导致鄱阳湖几近枯竭,严重威胁着湖区上千万居民的用水安全,并引起人们的高度关注.
国内外学者对鄱阳湖流域的水文特征[6-7]和洪、枯水特征[1, 8-9]进行大量研究,同时对于鄱阳湖流域干旱的气候特征进行研究,揭示气候变化对流域内干旱变化的影响[10-12].尽管对于鄱阳湖流域的干旱研究较多,但是大部分研究区域集中于鄱阳湖区或者仅从气象干旱角度研究鄱阳湖流域的干旱特征.干旱主要分为气象干旱、水文干旱、农业干旱和社会经济干旱四类[13],对于鄱阳湖流域水文干旱研究甚少,且运用多个干旱指标,特别是将水文干旱和气象干旱相结合的干旱研究尚未深入开展.基于此,本文建立基于气象干旱与水文干旱指标相结合的二维干旱状态变量,运用马尔科夫链模型,从干旱灾害形成、演变和持续方面对鄱阳湖流域干旱灾害进行研究,同时预测未来6个月非水文干旱到水文干旱的概率,该项研究对鄱阳湖流域的抗旱具有重要的科学与现实意义.
1 数据来源本文所用数据为鄱阳湖流域主要水文控制站(外洲、李家渡、梅港、渡峰坑和万家埠)1956-2005年长序列月径流量资料,资料来源于江西省水文局;水文控制站上游相近的主要气象站1956-2005年长序列月降雨量,资料来源于国家气象中心(图 1).本数据具有一定的代表性,径流量缺失的数据,取缺失数据的前后3 d的平均值,缺失的降雨量通过建立线性回归方程进行计算.
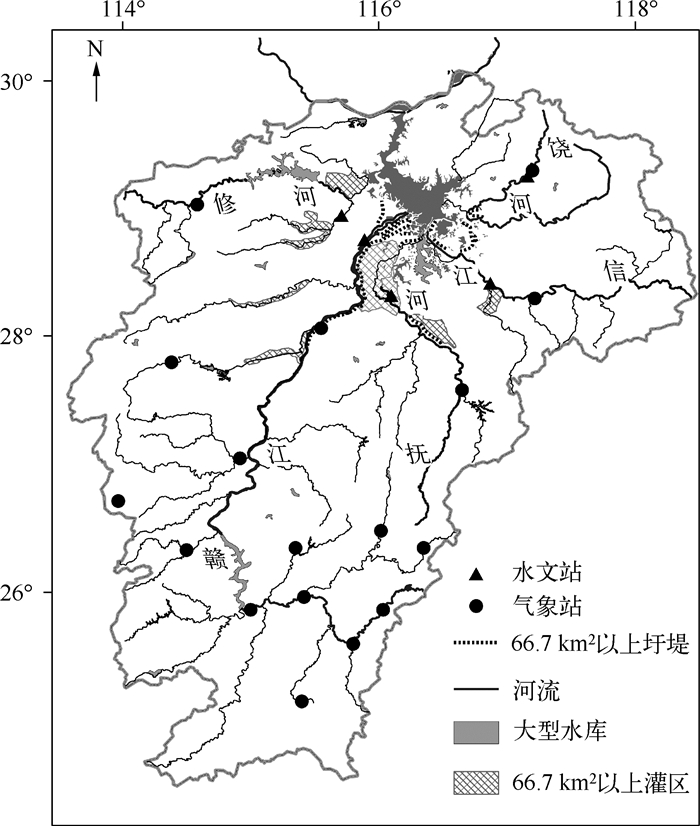
|
图 1 鄱阳湖流域水文站点、气象站点以及水库地理位置示意 Fig.1 Location of hydrological stations, meteorological stations, water reservoirs in the Lake Poyang Basin |
标准化径流指数(standardized runoff index,SRI)是以McKee提出的标准化降雨指数(standardized precipitation index,SPI)为理论依据的[14].本文中径流量是用月径流量中值计算,与月平均径流量相比较,月径流量的中值不受枯水季节的某时段连续降水的影响,能很好地代表枯水季节的径流量. SPI的原理就是McKee等提出[15]用伽马(Г)分布概率密度函数计算某一时间尺度的降水量累积概率.为消除样本的自相关性,将时间序列中不同月份的SPI值先分别计算,再合起来得到整个时间序列的SPI值.假定计算时间尺度为m个月的标准降水指标(通常m取3、6、12、24等),依次对连续m个月的月降水资料求和,得到m个月累积降水序列.在累积降水序列中,选取所有年份中某个月份的值,形成另一个序列(例如选取1956-2005年7月份的值),采用Gamma分布对其配线,配线完成后,计算累积降水的累积概率,再通过标准正态分布反函数转换为标准正态分布,所得结果即是该月份的标准降水指标值,具体计算公式及步骤参考文献[15-16].短时间尺度(1、3、6月等)的SRI和SPI值可以反映农作物在生长期的水分供给情况[16].由于鄱阳湖流域以季节性干旱为主,鄱阳湖流域短时期的干旱对于农业生产威胁最大[11],因此本文计算SPI的尺度采用3个月.
本文建立一个新的二维变量的干旱状态——SPI-SRI对鄱阳湖流域干旱进行研究. SPI和SRI都服从均值和方差相同的正态分布,SPI和SRI的相关系数是双正态分布散点图(图 2),根据Eyton对二维变量的相关系数分级方法[17],利用双正太分布特性和等概率椭圆划分无旱状态.根据Guttman定义SPI的无旱值是[-0.5,0.5],本文定义SRI无旱值的范围也是[-0.5,0.5],因此无旱等级点必须满足SPI和SRI介于-0.5和0.5之间,同时无旱等级点也必须满足距原点(0,0)的马氏距离小于0.5.马氏距离表示数据的协方差距离,它是一种有效的计算2个未知样本集相似度的方法.与欧氏距离不同的是,它考虑到各种特性之间的联系,还可以排除变量之间相关性的干扰.这些小于0.5马氏距离的SPI-SRI二维变量点形成一个等概率的椭圆,椭圆内的点划分为正常状态,椭圆外的SPI-SRI二维变量点划分等级依据SPI和SRI值与0之间的关系,本文将SPI-SRI二维变量划分为5个等级,具体见表 1.
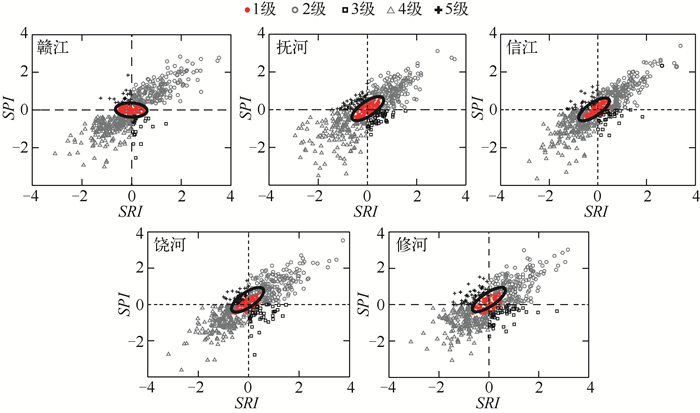
|
图 2 鄱阳湖流域水文站和气象站对应综合干旱指数的相关关系 Fig.2 The SRI and SPI correlation plots for the coupled hydrological stations and meteorological stations in Lake Poyang Basin |
| 表 1 SPI-SRI二维联合干旱指标的状态划分 Tab.1 SPI-SRI categories |
设马尔科夫链有S个状态,记转移状态为1,2,…,m,某一转移时刻的状态为S个状态之一,转移概率pij[18]为:
| $ {p_{ij}}(n, k) = P({X_{n + k}} = j\left| {{X_n} = i} \right.)(i, j = 1, 2, \ldots, m;n, k{\rm{为正整数}}) $ | (1) |
| $ {p_{ij}} = {n_{ij}}/\sum\limits_{i = 1}^S {{n_{ij}}} $ | (2) |
式中,pij(n,k)为过程从时刻n状态j经k步转移到状态j的概率.一般而言pij(n,k)与i,j,k和n有关.当pij(n,k)与i,j,k和n无关(与初始状态无关)时,则称为齐次马尔科夫链.通过转移概率pij分别计算X0到Xm的连续m个月的状态均是i的期望滞留时间和状态i到状态j的平均首达时间[19].
一阶马尔科夫模型并不一定能很好地分析时间序列过程,本文运用AIC模型[20]对一阶马尔科夫模型和二阶马尔科夫模型进行评估,AIC值越低,表明模型越适合鄱阳湖流域.
| $ AIC(r) =-2{L_r} + {S^r}(S-1) $ | (3) |
其中,L1和L2分别为:
| $ {L_1} = \sum\limits_{i = 1}^S {\sum\limits_{j = 0}^S {{n_{ij}} \cdot \ln ({p_{ij}})} } $ | (4) |
| $ {L_2} = \sum\limits_{h = 0}^S {\sum\limits_{i = 0}^S {\sum\limits_{j = 0}^S {{n_{hij}} \cdot \ln ({p_{hij}})} } } $ | (5) |
式中,L1、L2分别表示一阶和二阶马尔科夫链模型的对数似然值.
在计算马尔科夫链模型之前必须检验随机过程是否满足马氏性,本文运用χ2检验法检验马尔科夫链的马氏性[20].当样本容量足够大时,统计量:
| $ {\chi ^2} = \sum\limits_{i = 1}^S {\sum\limits_{j = 0}^S {\frac{{{{({n_{ij}}-{e_{ij}})}^2}}}{{{e_{ij}}}}} } $ | (6) |
| $ {e_{ij}} = \frac{{\sum\limits_{j = 0}^S {{n_{hij}}} \cdot \sum\limits_{i = 0}^S {{n_{hij}}} }}{n} $ | (7) |
式中,n为样本总量.
3 结果与分析 3.1 综合干旱指标分析鄱阳湖流域赣江、抚河、信江、饶河和修水的SPI-SRI综合干旱指数相关系数见图 2,根据表 2的分级标准,将SPI-SRI综合干旱指数划分为5个状态,椭圆内的点代表状态1,根据干旱形成过程,状态3代表干旱的初始阶段——气象干旱,由于连续无降水引起地表水资源量的减少,形成了水文干旱(状态4);然后降水事件发生,气象干旱得以恢复到正常或者湿润状态,但是不足以立刻恢复水文干旱到正常或者湿润状态,因此状态5代表气象不干旱、水文干旱的状态.如果降水足以恢复水文干旱到正常或者湿润状态的时候,这时就有状态5转向状态1或者状态2.根据公式(3)~(5),鄱阳湖流域各站点数据均满足马氏性.通过AIC模型对一阶、二阶马尔科夫链模型进行评估,发现赣江、抚河、信江、饶河和修河的一阶马尔科夫链模型AIC值(1062、1310、1260、1262和1399)远低于二阶马尔科夫链模型AIC值(2134、2591、2454、2467和2757),因此本文选择一阶马尔科夫链模型作为预测SPI-SRI综合干旱指数的模型. 图 3显示鄱阳湖流域SPI-SRI变化趋势基本一致,在1950s-1960s和1980s,鄱阳湖流域以干旱为主;进入1990s以后,鄱阳湖流域以洪涝为主,但是2000年之后流域有干旱趋势,其他时间段旱涝交替发生.
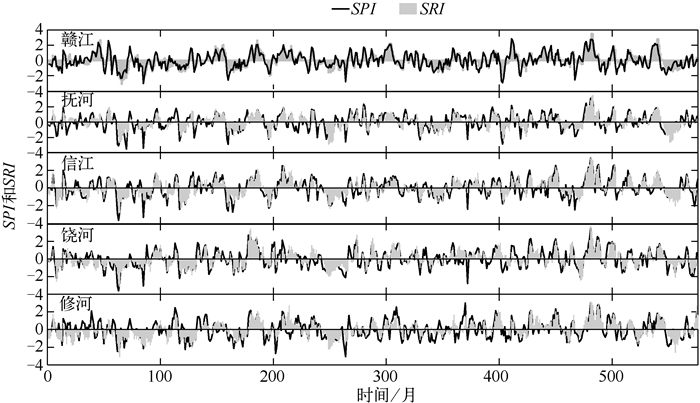
|
图 3 鄱阳湖流域SRI和SPI示意 Fig.3 The time series of SRI and SPI values in Lake Poyang Basin |
| 表 2 鄱阳湖流域各状态的一步转移概率* Tab.2 One-step transition probability matrix in Lake Poyang Basin |
从整体上来说,赣江流域状态1的发生频率最大(0.563),其次是状态4和状态2;其他“四河”状态2和状态4发生的频率高,平均发生频率达0.283和0.297.赣江流域的状态3和状态5发生频率低于其他“四河”,但是鄱阳湖流域“五河”的状态3和状态5发生的概率远低于其他状态,这表明鄱阳湖流域单独的气象干旱或者水文干旱发生频率低,而气象干旱和水文干旱同旱或者同涝的频率高.从年内分布来开,鄱阳湖流域的不同月份干旱状态1、状态2和状态4占的频率最大,赣江流域各月状态1发生频率最高,1-4月和7月状态4发生频率大于状态2,表明该时段的干旱发生频率大;抚河流域、信江流域、饶河流域和修河流域各月主要以状态2和状态4为主,其中抚河流域1-3、5-6和11月状态4发生频率高,信江流域在1-2、5-9月和12月状态4发生频率高,饶河流域状态4发生高的月份集中在1-2、5-8和10-12月.而修河流域在4-10月状态4发生概率高,其易发生干旱的月份大于其他流域,赣江和抚河月平均发生状态4的概率低于信江、饶河和修河(图 4).
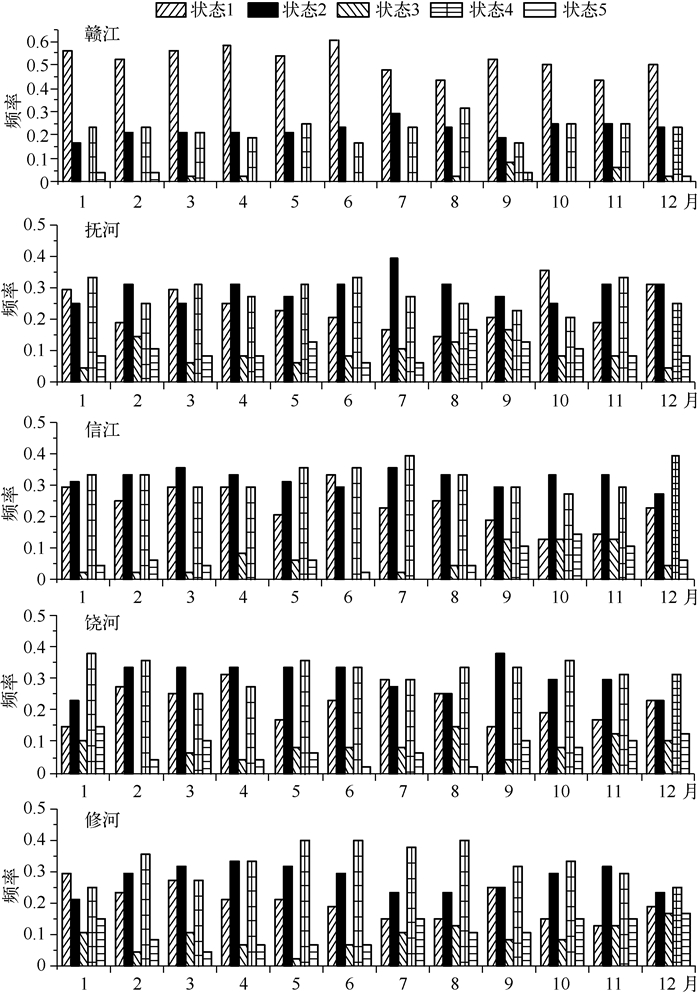
|
图 4 鄱阳湖流域不同月份5种状态出现的频率 Fig.4 Frequency of five states in different months in Lake Poyang Basin |
鄱阳湖流域“五河”的各等级之间的转移概率(表 2)可以看出,鄱阳湖流域状态2之间的一步转移概率(连续湿润)和状态4之间的一步转移概率(连续干旱)是各个流域中概率最高的,分别达到0.67和0.65,表明鄱阳湖流域连续湿润或者干旱的概率最大.赣江流域的状态1连续发生的概率(0.66)高于其他流域,而状态2、状态3和状态5发生的概率低于其他流域.饶河流域状态4之间一步转移概率(0.72)高于其他流域.抚河流域状态4转到状态5的概率(0.17)大于其他流域,鄱阳湖流域状态5转到状态2或者状态4的概率基本一致,这反映了状态5后趋向干旱或者湿润的概率相同.鄱阳湖流域中状态2和状态4、状态2和状态5、状态3和状态5之间的相互转移概率均小于0.1(赣江流域概率是0),远远低于其他状态之间的转移概率,这反映了湿润状态(状态2)与水文干旱(状态4、状态5)的相互转移概率低,湿润状态必须经历气象干旱才能发生水文干旱,水文干旱必须经历气象不干旱才能达到湿润状态.赣江流域其他状态一步转移到状态3和状态5的概率远小于其他地区,特别是状态2和状态4的一步转移概率远低于其他流域,状态3一步转移到状态4的概率高于其他流域.
3.3 综合干旱指标的重现期和历时由有限序列计算所得的转移概率是一个与初始阶段各状态分布有密切联系的条件概率.但是马尔科夫链概型的理论研究已经证明,随着过程的发展,初始阶段的影响逐渐消失,因而当n趋向于无穷大时,体系在时间n处于状态j的概率不依赖于在时刻0的初始状态,绝对概率分布收敛于一个独立于初始转移矩阵的极限分布.不同流域各等级的重现期可知,鄱阳湖流域和状态4的重现期最小(3.5个月),其发生的频率最高,其次是状态2的重现期(3.9个月)(图 5a).状态5的重现期最大(26.7个月),发生频率最低,其次是状态3,且状态3和状态5重现期远大于其他状态,这进一步表明鄱阳湖流域单独气象干旱或者水文干旱发生的频率低.从流域来看,赣江流域各状态重现期差别最大,赣江流域状态3和状态5的重现期最大,而信江流域各状态重现期差别最大,其次是饶河流域,信江流域状态3和状态5重现期长达17.4和18.0个月,状态2和状态4的重现期则分别是3.1和3.0个月,抚河流域和修河流域的重现期变化与信江流域基本一致.
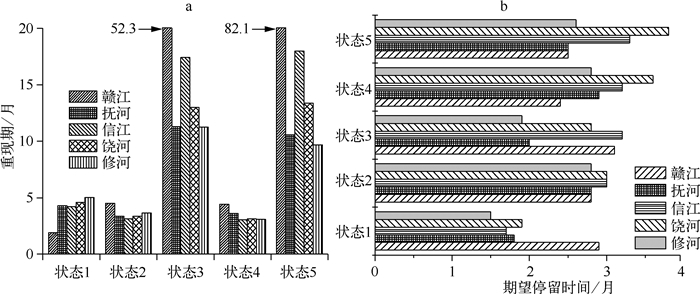
|
图 5 鄱阳湖流域各站点SRI-SPI分级的重现期(a)和期望停留时间(b) Fig.5 The return period(a) and expected residence time(b) of a given SRI-SPI class developed for individual locations in Lake Poyang Basin |
鄱阳湖流域各状态的期望停留时间,即各状态的历时见图 5b.鄱阳湖流域状态1的历时最小(2.0个月),状态2和状态4的历时最大(2.9个月),饶河流域状态5的历时最大(3.8个月).饶河流域各状态平均历时最大(3.0个月),抚河流域的平均历时最小(2.4个月).饶河和信江状态2的历时最大(3.0个月),状态4和状态5的饶河流域的历时也高于其他流域,这说明饶河流域和信江流域湿润状态或者干旱状态持续时间长.赣江流域的状态4和状态5的历时是流域中最小的,状态1的历时远大于其他流域,这表明赣江流域干旱持续时间短,状态1历时最长.
3.4 干旱灾害特征分析利用计算各等级的平均首达时间演绎干旱灾害形成、演化和持续性(图 6A),干旱灾害历时是指从一个状态到另一个状态经历的时间(以月为单位).干旱灾害分为干旱灾害形成、干旱灾害演变和干旱灾害持续3个阶段,干旱灾害形成历时主要从湿润状态或正常状态到气象干旱、水文干旱经历的时间;干旱灾害演变历时主要包括气象干旱、水文不干旱状态到水文干旱状态的历时(状态3到状态4)和气象、水文干旱到气象不干旱、水文干旱状态的历时(状态4到状态5);干旱灾害持续历时主要包括水文干旱状态到正常状态、湿润状态的历时(状态4或状态5到状态1或状态2). 图 6A中点越趋向于圆心处,平均首达时间越大,表明干旱形成缓慢,但是到达湿润状态的周期短,点离圆心越远,平均首达时间越小,表明干旱形成较快,但是到达湿润状态的周期长,干旱灾害的危害性越大.然而干旱持续时间首达时间越大,到达湿润状态的周期越长,干旱灾害越严重,为了保持与干旱灾害形成、干旱灾害演变的危险方向的一致性,将干旱灾害持续以反向显示. 图 6A箭头指示方向,表示干旱灾害的危险性由小到大的趋势.
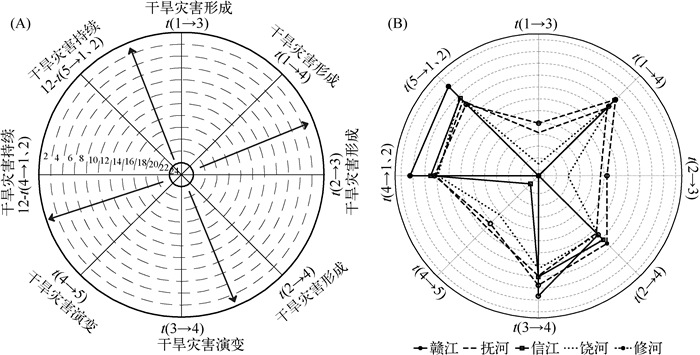
|
图 6 鄱阳湖流域各站点平均首达时间演绎干旱灾害形成、演化和持续性 Fig.6 The interpretation of the developed first passage of times in terms of hazard of drought formation, evolution and persistence and drought hazard developed in Lake Poyang Basin |
图 6B是鄱阳湖流域干旱灾害演变雷达图,修河流域是鄱阳湖流域各河流状态1、状态2到状态3、状态4的平均首达时间是最小的,这表明修河流域在干旱灾害形成中危害最大,抚河流域在干旱演变的过程中(状态4到状态5)的平均首达时间最小(11.7个月),其干旱危害最大.赣江流域在干旱灾害形成和干旱灾害演变(状态4到状态5)的过程中干旱危害最小,但是在干旱灾害持续(状态5到状态1)的平均首达时间最小(2.7个月),干旱危险最大.饶河流域与赣江类似,在干旱灾害形成中危害小,但是在干旱灾害持续中(状态4到状态1)干旱危险最大.
3.5 干旱灾害预测图 7是预测了初始状态是非水文干旱状态(状态1、状态2、状态3)到水文干旱状态(状态4、状态5)的未来6个月的发生概率.随着预测时间的增加,非水文干旱转移到水文干旱的概率增加,但是赣江流域部分状态转移随着时间的增加而降低.从非水文干旱转移到状态4的概率(0.25)远大于非水文干旱转移到状态5的概率(0.06),这表明鄱阳湖流域在非水文干旱状态下易发生水文气象干旱.修河流域大部分从非水文干旱转移到水文干旱的概率远高于其他流域,其中状态1转移到状态4的概率低于信江流域和饶河流域(图 7B~F).信江流域在非水文干旱状态转移到状态5的概率是全流域最低的,然而信江流域非水文干旱状态转移到水文气象干旱状态的概率较高,表明信江流域非水文干旱状态很难发生状态5,但是易发生水文气象干旱.赣江流域从非水文干旱转移到水文干旱的概率是最低的(图 7A~C、7F),这表明赣江流域在正常或者湿润状态下很难发生水文干旱,赣江流域在状态3的情况下前3个月极易发生水文气象干旱,但是随后发生水文气象干旱概率降到全流域最低(图 7E).
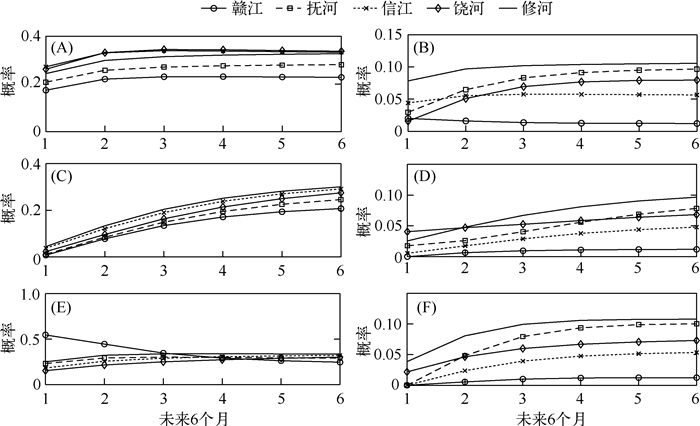
|
图 7 预测状态1-状态3综合干旱指数在未来6个月的水文干旱(状态4-状态5)发生概率(A:表示状态1—状态4;B:表示状态1—状态5;C:状态2-状态4;D:状态2-状态5;E:状态3-状态4;F:状态3-状态5) Fig.7 Probability to arrive at hydrological dry conditions (class 4 and 5) in 1, 2 and 3-moths time horizon starting from: (A-B):normal hydrological conditions (class 1), (C-D) wet conditions (class 2) and (E-F) wet hydrological and dry meteorological conditions (class 3) |
运用基于降水和水资源短缺的SPI和SRI干旱指数,建立了包含气象干旱指标和水文干旱指标的二维变量的干旱状态,通过一阶马尔科夫链模型对二维变量干旱指数的等级进行概率、重现期和历时分析,同时预测未来6个月非水文干旱到水文干旱的概率,得到以下结论:
1) 建立的水文气象干旱指数,从干旱灾害形成、演变和持续3方面对干旱灾害进行研究,修河流域在干旱形成中危害大,抚河流域在干旱演变中危害大,赣江流域和饶河流域在干旱持续中危害大,赣江流域在干旱灾害形成和干旱灾害演变的过程中干旱危害最小.鄱阳湖流域以水文气象干旱为主,单独的气象干旱或者水文干旱发生频率低.赣江流域在鄱阳湖“五河”流域中面积最大,流域森林覆盖率高和水库及其库容量也最大[7],赣江流域抵御干旱的能力就远大于其他流域,因此赣江流域干旱灾害在发展和演变过程中的危害远低于其他流域,流域面积大的赣江在干旱持续过程中回到正常或者湿润状态历时大于其他流域,其干旱灾害过程中危害最大.
2) 赣江流域在状态1和状态3历时最长,抚河流域和修河流域在状态2和状态4历时最长,信江流域和饶河流域在状态4和状态5历时最长.鄱阳湖流域连续湿润或者干旱的概率最大,湿润状态(状态2)与水文干旱(状态4、状态5)的相互转移概率低,赣江流域状态2、状态3和状态5发生的概率低于其他流域.赣江流域面积大,干旱发生频率低[11],鄱阳湖流域西北部的信江和饶河干旱发生频率最高且强度较大[11],流域面积和干旱频率、强度的时空分布不均引起了状态转移频率分布的差异性.
3) 在长期干旱预测中,鄱阳湖流域从状态2到状态4或者状态5的概率最低,状态1或者状态3到达状态4的概率最大.修河流域从非水文干旱易发生水文干旱,赣江流域在正常或者湿润状态下很难发生水文气象干旱,但是赣江流域在状态3的情况下前3个月极易发生水文气象干旱,随后发生水文气象干旱的概率降到全流域最低.
| [1] |
Zhang Q, Sun P, Chen XH et al. Hydrological extremes in the Lake Poyang Basin, China: changing properties, causes and impacts. Hydrological Processes, 2011, 25: 3121-3130. DOI:10.1002/hyp.v25.20 |
| [2] |
张强, 孙鹏, 江涛. 鄱阳湖流域水文极值演变特征、成因与影响. 湖泊科学, 2011, 23(3): 445-453. |
| [3] |
叶许春, 张奇, 刘健等. 鄱阳湖流域天然径流变化特征与水旱灾害. 自然灾害学报, 2012, 21(1): 140-147. |
| [4] |
闵骞. 20世纪90年代鄱阳湖洪水特征的分析. 湖泊科学, 2002, 14(4): 323-330. DOI:10.18307/2002.0405 |
| [5] |
孙鹏, 张强, 陈晓宏. 基于Copula函数的鄱阳湖流域极值流量遭遇频率及灾害风险. 湖泊科学, 2011, 23(2): 183-190. DOI:10.18307/2011.0204 |
| [6] |
刘健, 张奇, 左海军等. 鄱阳湖流域径流模型. 湖泊科学, 2009, 21(4): 570-578. |
| [7] |
孙鹏, 张强, 陈晓宏等. 鄱阳湖流域水沙时空演变特征及其机理. 地理学报, 2010, 65(7): 828-840. DOI:10.11821/xb201007007 |
| [8] |
闵骞, 占腊生. 1952-2011年鄱阳湖枯水变化分析. 湖泊科学, 2012, 24(5): 675-678. DOI:10.18307/2012.0505 |
| [9] |
孙鹏, 张强, 陈晓宏. 鄱阳湖流域枯水径流演变特征、成因与影响. 地理研究, 2011, 30(9): 1702-1712. |
| [10] |
闵屾, 刘健. 鄱阳湖区域极端降水异常的特征及成因. 湖泊科学, 2011, 23(3): 435-444. |
| [11] |
闵屾, 严蜜, 刘健. 鄱阳湖流域干旱气候特征研究. 湖泊科学, 2013, 25(1): 65-72. DOI:10.18307/2013.0109 |
| [12] |
胡振鹏, 林玉茹. 气候变化对鄱阳湖流域干旱灾害影响及其对策. 长江流域资源与环境, 2012, 21(7): 897-904. |
| [13] |
Mishra AK, Singh VP. A review of drought concepts. Journal of Hydrology, 2010, 391(1): 202-216. |
| [14] |
Shukla S, Wood AW. Use of a standardized runoff index for characterizing hydrologic drought. Geophysical Research Letters, 2008, 35(2): 41-46. |
| [15] |
McKee TB, Doesken NJ, Kleist J. The relationship of drought frequency and duration to time scales. Eighth Conference on Applied Climatology. Anaheim, CA. Am. Meteor. Soc., Boston, 1993, 179-184. |
| [16] |
李剑锋, 张强, 陈晓宏等. 基于标准降水指标的新疆干旱特征演变. 应用气象学报, 2012, 23(3): 322-330. |
| [17] |
Eyton JR. Complementary-color, two-variable maps. Annals of the Association of American Geographers, 1984, 74(3): 447-190. |
| [18] |
王文圣, 丁晶, 金菊良. 随机水文学. 北京:中国水利水电出版社, 2008, 20-23. |
| [19] |
施仁杰. 马尔科夫链基础及其应用. 西安:西安电子科技大学出版社, 1992, 40-45. |
| [20] |
Wilks DS. Statistical methods in the atmospheric sciences. Access Online via Elsevier, 2011. |
| [21] |
王怀清, 赵冠男, 彭静等. 近50年鄱阳湖五大流域降水变化特征研究. 长江流域资源与环境, 2009, 18(7): 615-619. |
 2015, Vol. 27
2015, Vol. 27 

