(2: 中国科学院南京地理与湖泊研究所湖泊与环境国家重点实验室, 南京 210008)
(3: 江苏省水文水资源勘测局无锡分局, 无锡 214031)
(4: 河海大学水文水资源学院, 南京 210098)
(2: State Key Laboratory of Lake Science and Environment, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008, P. R. China)
(3: Wuxi Branch of Jiangsu Province Hydrology and Water Resource Investigation Bureau, Wuxi 214031, P. R. China)
(4: College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China)
在浅水湖泊中,水动力扰动引起的底泥悬浮不仅导致水体透明度下降,还可造成赋存在沉积物中的营养盐向上覆水层释放,增加浅水湖泊富营养化的风险.平均水深1.9m的太湖是典型的浅水富营养化湖泊[1].该湖泊水面开阔,水底地形平坦,多数岸线暴露在长风区条件下,有利于风浪的生成和发展.研究已经证明,太湖底泥悬浮的主要能量来自波浪[2 — 3],湖流的作用几乎可以忽略[4 — 5].因此,解析太湖波浪特征对研究其水动力过程及其生态环境效应具有重要意义.
由于风浪对太湖生态环境具有重要意义,近年来也有不少学者对风浪开展了研究.李一平等[6]在太湖实际波浪观测的基础上,对太湖波浪进行数值模拟,研究了太湖波浪的主要影响因素.刘兴平[7]研究了太湖波浪的生消动态过程并结合湖流三维模型,寻求太湖湖流对波浪的影响.同时,学者们也积极探讨太湖波浪对生态环境的影响,如波浪和湖流共同作用下太湖水体悬浮物输运过程[8],太湖波浪与湖流对沉积物再悬浮的影响[9 — 11],太湖白帽覆盖率的变化与特征[11].这些研究对探求太湖波浪数值模拟成果有一定意义,但都是在假想的定常风或较短时间内的实际风场作用下对太湖波浪的数值模拟.而利用基于动谱平衡方程开发的SWAN模型,就实际风场周年变化条件下太湖波浪时空分布的特征研究还鲜有报道.
本文基于太湖实测风场和波浪数据,通过第3代浅水波浪模型SWAN,分析2013年自然风场条件下太湖不同湖区风浪时空分布特征,并从较大的时空尺度上讨论风浪的生态环境效应,本研究可为太湖生态环境问题的动力学成因研究提供帮助.
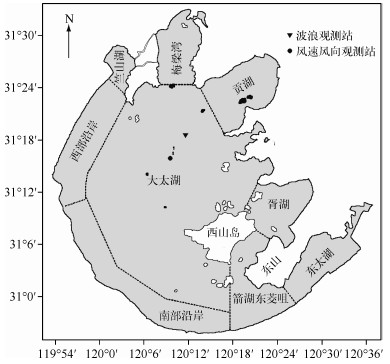
1 数据与方法 1.1 太湖概况太湖(30°55′40″~31°32′58″ N, 119°52′32″~120°36′10″ E)是长江三角洲的一个大型浅水湖泊(图 1).太湖水域面积2338km2,南北长68.5km,东西平均宽34km,最宽处56km.太湖平均水深1.9m,最大水深不超过3m,其最深处位于湖心偏西、平台山以北的区域.太湖湖面开阔,水下地形平坦,平均坡度只有19.7″.按照岸线、水质和水下地形等因素,太湖可分为大太湖、梅梁湾、贡湖、竺山湖、胥湖、西部沿岸、南部沿岸、东太湖和箭湖东茭咀9个湖区[12](图 1).太湖流域夏季受海陆气温差异影响,盛行东南风;冬季受来自西伯利亚的寒流影响,盛行西北风.由于全球气候变暖、城镇化等原因,太湖的年平均风速和最大风速均呈逐年下降的趋势.
|
图 1 观测站及太湖分区示意 Fig.1 Sketch of observation stations and nine regions in Lake Taihu |
SWAN模型建立在波浪能量平衡方程基础上,考虑了波浪作用过程中的波浪折射、反射、浅化、破碎、白帽、底摩擦及波-波相互作用,其中未考虑湖流的作用和波浪绕射的影响.SWAN模型能够很好地运用于海岸、湖泊、河口等浅水区域,为波浪的传播以及带来的影响提供充分的依据.
1.2.1 动谱平衡方程SWAN模型不是以二维能谱密度而是以二维动谱密度表示随机波,因在流场中,动谱密度守恒,而能谱密度不守恒,动谱密度与能谱密度和相对频率的关系为:N(σ, θ)= E(σ, θ)/σ,N(σ, θ)随时间、空间而变化.在笛卡尔直角坐标系下,动谱平衡方程可表示为[13]:
| $ \frac{\partial }{\partial t}N+\frac{\partial }{\partial x}{{C}_{x}}N+\frac{\partial }{\partial y}{{C}_{y}}N+\frac{\partial }{\partial \sigma }{{C}_{\sigma }}N+\frac{\partial }{\partial \theta }{{C}_{\theta }}N=\frac{S}{\sigma } $ | (1) |
式中,方程左边第1项为N随时间的变化率;第2、3项分别表示N在地理空间坐标x、y方向上的传播(Cx和Cy分别为x和y方向的传播速率);第4项表示流场和水深所引起的N在相对频率σ空间的变化;第5项为N在谱分布方向θ空间(谱方向分布范围)的传播;S为以谱密度表示的源汇项,包括风能输入、波与波之间非线性相互作用和由于底摩擦、白浪、破碎等引起的能量损耗;Cx、Cy、Cσ和Cθ分别代表在x、y、σ和θ空间的波浪传播速度.
1.2.2 波浪能量输入和损耗项风能输入使用共振机制[14]和反馈机制[15]来描述,相应的源函数可表示为线性增长和指数增长两部分之和.波浪能量的耗散项主要是白浪、底部摩檫和由水深引起的波破碎.白浪主要由波陡度控制,根据Hasselmann等提出的脉动平均模型进行计算[13];底摩擦采用Collins拖曳理论模型;水深引起的波破碎基于Miche准则,Battjes等[16]根据大量试验数据及现场资料,认为在浅水域,对于不同类型的地貌,随机波的最大破碎波高Hm与水深d的关系可表示为:Hm=γ·d.
1.2.3 波与波之间非线性相互作用在深水域,四相波与波非线性相互作用占主导地位,谱能由谱峰处向低频转移(使得峰频变小)和高频转移(高频处能量由于白浪而耗散掉).在浅水域,三相波与波之间非线性相互作用是主要影响因素,能量由低频向高频处转移.在SWAN模型中,四相波-波相互作用采用Hasselmann等[13]提出的离散相互作用近似法(DIA)计算,在三相波相互作用的计算中,每个谱方向上均采用Eldeberky的集合三相近似模型(LTA)[17],它由Eldeberky等的离散三相近似模型[18]改进而得.
1.2.4 SWAN参数设置SWAN模型物理过程考虑底摩擦效应、白浪损耗和非线性波-波之间相互作用等耗散机制.底摩擦引起的消耗采用Collins模型,底摩擦系数取0.025;破碎系数取均值0.73.沿逆时针方向的谱分布方向θ空间(即谱方向分布范围)的谱方向步长取为10°,谱频率σ计算范围为0.04~1.00Hz,网格数为15.以JONSWAP谱和4阶余弦函数表示二维谱.因入湖河道对太湖波浪的影响较小,可忽略不计,作陆地边界处理.以X10、Y10风场作为模型风输入.计算网格为矩形网格,计算步长1km,由此可将太湖划分为69×69个网格,x、y方向上计算域长度均为69km.同时,模型验证的计算时间域为2014年8月14日6:10至8月17日5:40,计算时间步长设置为10min,模型计算结果输出的时间间隔为30min.模型模拟的计算时间域为2013年1月1日0:00至12月31日23:30,计算时间步长设置为30min,模型计算结果输出的时间间隔为6h.
1.3 数据采集与处理风速、风向观测站位于太湖湖心(31°16′40″N,120°9′16″E),于2013年1月1日0:00至2013年12月31日23:30及2014年8月14日6:10至8月17日5:40逐时记录水面以上10m高度处的10min平均风速,采样时间间隔30min,全湖采用同一风场数据作为输入,将此风场分解至笛卡尔坐标系的x轴和y轴,表现形式为X10、Y10:
| $ {X_{10}} = - {\rm{cos}}\left( {WD \cdot {\rm{\pi }}{\rm{/180}}} \right) \cdot WS $ | (2) |
| $ {Y_{10}} = - \sin \left( {WD \cdot {\rm{\pi }}{\rm{/180}}} \right) \cdot WS $ | (3) |
式中,WD代表站点处的风向,WS代表站点处的风速.
波浪观测使用英国Valeport有限公司生产的采样频率为8Hz的高精度Valeport,观测站位于太湖湖心(31°18′33″N,120°12′22″E),于2014年8月14日6:10至8月17日05:40进行观测,采样时间间隔30min,得到有效波高(Hs)及谱峰周期(Tp)等.
数据统计分析使用Excel和SPSS 20.0软件,作图使用Origin 8.1和Surfer 8软件.采用Pearson相关分析法表示相关性,P<0.01表示两者呈极显著相关,P<0.05表示两者呈显著相关.使用确定性系数表示模拟值与实测值之间的拟合程度:
| $ DC=1-\frac{\sum\limits_{i=1}^{n}{{{\left[{{y}_{\rm{c}}}\left( i \right)-{{y}_{0}}\left( i \right) \right]}^{2}}}}{\sum\limits_{i=1}^{n}{{{\left[{{y}_{\rm{0}}}\left( i \right)-\overline{{{y}_{0}}} \right]}^{2}}}} $ | (4) |
式中,DC为确定性系数,y0(i)为实测值,yc(i)为预报值,y0为实测值的均值,n为资料序列长度.
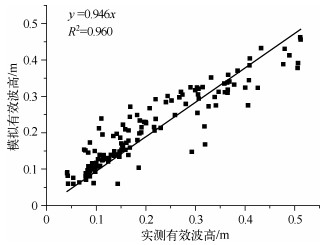
2 结果与讨论 2.1 模型验证通过建立2014年8月14日6:10至8月17日5:40间模拟与实测有效波高值之间的线性关系(图 2),表明模拟与实测有效波高值能够紧密分布在直线y=0.946x两侧,判定系数R2=0.960(样本数n=288);相对误差范围为0.03 % ~28.7 %,均值为10.7 %;实测值与模拟值呈极显著正相关(r=0.83,P<0.01),确定性系数为0.84.可见有效波高的模拟值能够较好地反映太湖波浪的实际情况,SWAN模型能够较好地表现太湖的风浪特征.
|
图 2 模拟与实测有效波高的线性关系 Fig.2 Linear relationship between calculated and measured values of significant wave height |
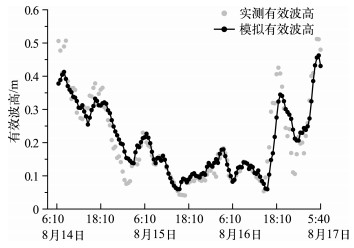
验证结果表明,模拟的有效波高与实测波高变化趋势基本一致(图 3),但两者之间存在一定的误差.在模拟初期,实测值与模拟值误差较大,随着模拟时间的推移,风浪场逐渐形成,模拟值与实测值越来越接近.误差来源[19]可能是:(1)由于全湖采用的是空间均匀的逐时风场,与实际风场有一定的误差;(2)在阻挡物较多的狭长水域以及湖湾内,以此空间均匀风场带来的误差影响就会大些;(3)未考虑波流相互作用;(4)尽管风浪是太湖波浪的主要能量来源,但是实测波浪还包括船行波和潮汐等.
|
图 3 2014年8月14日6:10至17日5:40湖心观测站有效波高实测值与计算值的比较 Fig.3 Comparison of measured and calculated values of significant wave height in the center of Lake Taihu from August 14th 6:10 to 17th 5:40 of 2014 |
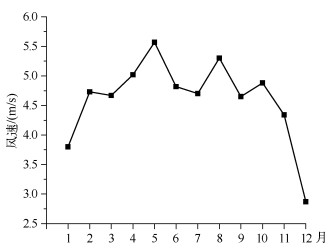
对太湖湖心观测站(图 1)记录的2013年风速、风向开展统计分析.2013年太湖月均风速(图 4)在3.0~6.0m/s之间,其中春季(3-5月)、夏季(6-8月)和秋季(9-11月)风速相对较高,平均约4.9m/s;冬季(2013年1、2和12月)风速低,为3.8m/s.2013年太湖四季风向分布情况见表 1,春季和夏季以东南风为主,秋季以东北风为主,冬季以西北风为主.依据蒲福风级分类标准,2013年太湖风场序列统计情况见表 2.2013年太湖流域主要以轻风、微风、和风为主,风速介于1.6~7.9m/s.其中尤以微风发生频率最高,占全年的31.87 %.全年观测到的最大风速为15.0m/s,达到疾风标准.
|
图 4 太湖湖心气象观测站记录的2013年各月月平均风速变化过程 Fig.4 Changes of monthly average wind speed in 2013 recorded by meteorological station in center of Lake Taihu |
| 表 1 2013年太湖湖心气象站记录的风向统计结果 Tab.1 Analysis of wind direction in 2013 recorded by meteorological station in center of Lake Taihu |
| 表 2 2013年太湖湖心气象站记录的风速等级统计结果 Tab.2 Analysis of wind level in 2013 recorded by meteorological station in center of Lake Taihu |
基于2013年实测风场,利用SWAN模型对太湖2013年1月1日0:00至12月31日23:30的风浪进行模拟,统计分析太湖风浪的时空分布特征.
2013年9个湖区12个月的有效波高的最大值见表 3.2013年太湖的有效波高最大值在0.217~ 0.652m之间.大太湖的风浪总是最强,其有效波高均值为0.523m;而东太湖风浪最小,有效波高均值为0.305m.有文献报道[6, 20],风浪的大小与风速、风时、风区长度有着密切的关系;另外,风浪的影响因子还包括水深、地形、岸线形状、沉水植物覆盖度等.大太湖平均水深2.3m,水面开阔;东太湖平均水深仅为1.05m,水域呈狭长型;这两个湖区的特征有着本质区别,东太湖的水力条件为沉水植物的生长创造了有利的环境.事实上,通过多年的野外观测发现大太湖水底几乎无水草,而东太湖水草生长茂盛.Jackson等[21]和Hamilton等[22]研究认为水生植物能够阻碍波浪的形成,并降低水流速度.因此,水生植物能阻碍波浪的发展,起到消浪的作用;进而可以降低底泥再悬浮[23]和内源释放[24]的可能性.这又恰恰说明草型湖泊(胥湖和东太湖)的透明度和水质优于藻型湖泊(梅梁湾、贡湖和竺山湖)[25 — 26].太湖北部3个湖湾有效波高值大小顺序为:梅梁湾>贡湖>竺山湖.竺山湖水域面积最小,风吹程短,不利于风浪的生长,这是该湖湾有效波高小的主要原因之一.在盛行东南风的夏季,西部沿岸区的有效波高值均比南部沿岸区高,这与西部沿岸区风区长度、岸线形状规则有着密切的关系.
| 表 3 2013年不同湖区各月有效波高最大值(m) Tab.3 Monthly maximum significant wave height in 2013 in different regions of Lake Taihu |
受控于风速、风向的季节波动,太湖春、夏季有效波高均值大于秋、冬季.SWAN模拟结果表明:2013年全太湖春、夏、秋和冬季有效波高平均值分别为0.433、0.444、0.418和0.343m.各湖区有效波高季节分布与此相似,例如:大太湖春、夏、秋、冬季有效波高分别为0.565、0.543、0.546和0.435m;东太湖春、夏、秋、冬季有效波高分别为:0.424、0.419、0.416和0.329m.风速是导致太湖风浪这种季节变化的主要因素.统计分析结果显示,太湖有效波高与风速呈极显著正相关(r=0.47,P<0.01), 即有效波高与风速的季节变化一致,风速越大,有效波高越大.此外,湖流[27]、水位[28]、行船[29]及水生植物等季节变化也可能对风浪季节动态产生影响.
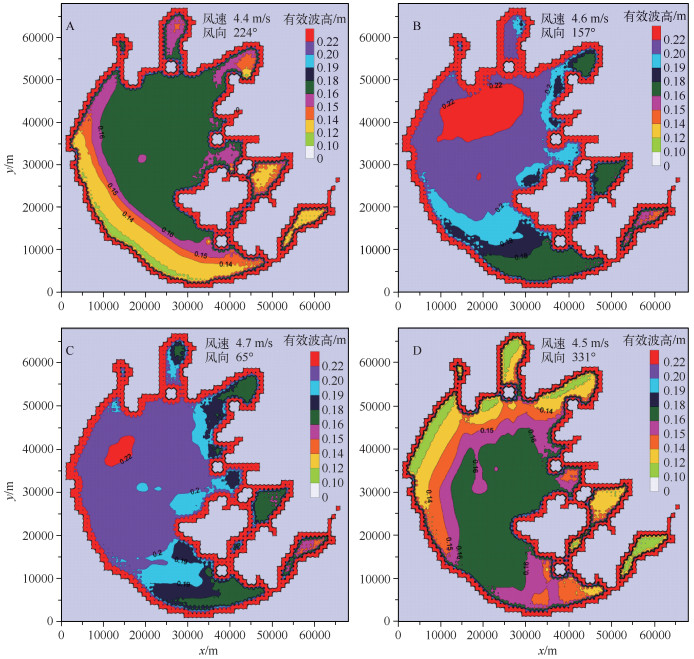
2.3 典型风向下微风引起的波浪季节分布特征由于2013年太湖盛行微风,因此借助所建SWAN模型分析微风风速条件下西南、东南、东北和西北风在太湖形成的风浪空间分布.在西南风作用下,波高由西南沿岸向湖心逐渐变大,绕过西山岛,在梅梁湾和贡湖口达到最大(图 5A).在夏季盛行的东南风作用下,波高由箭湖东茭咀-南部沿岸-湖心逐渐变大,在梅梁湖口以西的湖心区域达到最大(图 5B).在东北风作用下,波高最大值在西部沿岸附近的湖心区域,其次为大太湖和西部沿岸,各湖湾的有效波高基本在0.15~0.18m(图 5C).而西北风引起的风浪的有效波高值则由西北沿岸区向湖心逐渐增大,西山岛附近达到最大;在西山岛的阻碍作用下,胥湖和东太湖的波高明显减小(图 5D).
|
图 5 2013年典型风向下微风引起的太湖有效波高的季节分布 Fig.5 Seasonal distribution of significant wave height in Lake Taihu under different wind directions in 2013 |
风向可以通过改变风区长度来影响风浪生消.不过,不论何种风向下,大太湖的有效波高始终最大,在0.16~0.22m之间.而该湖区也是太湖水动力扰动最为频繁和剧烈的区域.沈吉等[30]观测到湖心大部分湖底露出黄褐色硬质黄土层,局部地区有小于3cm的上覆浮泥,这可能与该区域始终频繁遭受强风浪扰动有关.东太湖和胥湖的有效波高都是最小的,在0.10~0.16m之间(图 5).这两块水域相对封闭,风区长度较小,不利于风浪的成长和发展.这样的水动力条件大大降低了沉水植物的机械损伤,为沉水植物的生长提供了良好的环境;同时,而沉水植物繁盛又可以起到消浪的作用,两者间存在着正反馈机制.
3 结论1) 通过2014年8月14日6:10至8月17日5:40实测有效波高与模拟有效波高比较发现,其变化趋势基本一致,能够紧密分布在直线y=0.946x两侧,判定系数R2=0.960(样本数n=288);相对误差范围为0.03 % ~28.7 %,均值为10.7 %;实测值与模拟值呈极显著正相关(r=0.83,P<0.01),确定性系数为0.84.可见SWAN模型能够较好地体现太湖风浪特征.
2) 受岸线、地形和岛屿等地理因素影响,2013年大太湖的风浪总是最强的,其有效波高均值为0.523m;而东太湖风浪最小,有效波高均值为0.305m.受盛行风场季节变化影响,太湖春、夏季有效波高均值明显大于秋、冬季.太湖波浪的能量主要来源于风场,其有效波高随风速增大,两者呈极显著正相关(r=0.47,P<0.01).
3) 风向可以通过改变风区长度来影响风浪生消.在偏东风作用下,太湖湖西区的风浪大于东部湖区;而受盛行于冬季的偏北风影响,太湖南部水域风浪要大于北部.同时,太湖风浪的时空分布特征是造成太湖水质参数、沉积物和水生植物空间分布差异的重要原因之一.
| [1] |
孙顺才, 黄漪平. 太湖. 北京: 海洋出版社, 1993.
|
| [2] |
秦伯强, 胡维平, 高光等. 太湖沉积物悬浮的动力机制及内源释放的概念性模式. 科学通报, 2003, 48(17): 1822-1831. DOI:10.3321/j.issn:0023-074X.2003.17.002 |
| [3] |
Wu TF, Qin BQ, Zhu GW et al. Modeling of turbidity dynamics caused by wind-induced waves and current in the Taihu Lake. International Journal of Sediment Research, 2013, 28(2): 139-148. DOI:10.1016/S1001-6279(13)60026-8 |
| [4] |
Jin KR, Ji ZG. Calibration and verification of a spectral wind-wave model for Lake Okeechobee. Ocean Engineering, 2001, 28(5): 571-584. DOI:10.1016/S0029-8018(00)00009-3 |
| [5] |
Bailey MC, Hamilton DP. Wind induced sediment resuspension:a lake-wide model. Ecological Modeling, 1997, 99(2): 217-228. |
| [6] |
李一平, 逄勇, 刘兴平等. 太湖波浪数值模拟. 湖泊科学, 2008, 20(1): 117-122. DOI:10.18307/2008.0118 |
| [7] |
刘兴平. 太湖波浪过程的数值模拟. 江苏大学学报:自然科学版, 2009, 30(1): 80-85. |
| [8] |
李一平, 逄勇, 罗潋葱. 波流作用下太湖水体悬浮物输运实验及模拟. 水科学进展, 2009, 20(5): 701-706. |
| [9] |
罗潋葱, 秦伯强. 太湖波浪与湖流对沉积物再悬浮不同影响的研究. 水文, 2003, 23(3): 1-4. |
| [10] |
汤露露, 王鹏, 姚琪. 太湖湖流、波浪、沉积物的三维数值模拟. 水资源保护, 2011, 27(2): 1-5. |
| [11] |
陶蓉茵. 不同风场条件下太湖波浪数值模拟的研究及其应用[学位论文]. 南京: 南京信息工程大学, 2012.
|
| [12] |
刘聚涛, 高俊峰, 姜加虎等. 基于突变理论的太湖蓝藻水华危险性分区评价. 湖泊科学, 2010, 22(4): 488-494. |
| [13] |
Hasselmann S, Hasselmann K, Allender JH et al. Computation and parameterizations of the nonlinear energy transfer in a gravity wave spectrum. Part Ⅱ:Parameterizations of the nonlinear energy transfer for application in wave models.. Journal of Physical Oceangraphy, 1985, 15(11): 1378-1391. DOI:10.1175/1520-0485(1985)015<1378:CAPOTN>2.0.CO;2 |
| [14] |
Phillips OM. On the generation of waves by turbulent wind. Journal of Fluid Mechanics, 1957, 2(5): 417-445. DOI:10.1017/S0022112057000233 |
| [15] |
Miles JW. Hamiltonian formulations for surface waves. Applied Scientific Research, 1981, 37(1/2): 103-110. |
| [16] |
Battjes JA, Stive MJF. Calibration and verification of a dissipation model for random breaking waves. Journal of Geophysical Research, 1985, 90(C5): 9159-9167. DOI:10.1029/JC090iC05p09159 |
| [17] |
Eldeberky Y. Nonlinear transformation of wave spectra in the nearshore zone[Dissertation]. Netherlands:Delft University of Technology, 1996.
|
| [18] |
Eldeberky Y, Battjes JA. Parameterization of triad interactions in wave energy models. Gdansk, Poland:Proceeding Coastal Dynamics Conference, 1995, 140-148. |
| [19] |
许遐祯, 陶蓉茵, 赵巧华等. 大型浅水湖泊太湖波浪特征及其对风场的敏感性分析. 湖泊科学, 2013, 25(1): 55-64. DOI:10.18307/2013.0108 |
| [20] |
曹勇, 孙从军, 高阳俊等. 淀山湖水域风浪要素计算研究. 长江流域资源与环境, 2011, 20(Z1): 39-43. |
| [21] |
Jackson HO, Starrett WC. Turbidity and sedimentation at Lake Chautauqua, lllinois. Journal of Wildlife Management, 1959, 23: 157-168. DOI:10.2307/3797636 |
| [22] |
Hamilton DP, Mitchell SF. An empirical model for sediment resuspension in shallow lakes. Hydrobiologia, 1996, 317(3): 209-220. DOI:10.1007/BF00036471 |
| [23] |
李一平, 逄勇, 李勇. 水动力作用下太湖底泥的再悬浮通量. 水利学报, 2007, 38(5): 558-564. |
| [24] |
逄勇, 李一平, 颜润润等. 内外源共同作用对太湖营养盐贡献量研究. 水利学报, 2008, 39(9): 1051-1059. |
| [25] |
王震, 邹华, 杨桂军等. 太湖叶绿素a的时空分布特征及其与环境因子的相关关系. 湖泊科学, 2014, 26(4): 567-575. DOI:10.18307/2014.0411 |
| [26] |
李英杰, 胡小贞, 胡社荣等. 草、藻型湖泊水体生态及理化特性的实验对比. 生态环境学报, 2009, 18(5): 1649-1654. |
| [27] |
李一平, 逄勇, 刘兴平. 太湖湖流对波浪的影响机制研究. 水利学报, 2007, 38(S1): 303-308. |
| [28] |
Lind OT, Davaloslind LO, Chrzanowski TH et al. Inorganic turbidity and the failure of fishery models. Internationale Revue der Gesamten Hydrobiologie, 1994, 79(1): 7-16. DOI:10.1002/(ISSN)1522-2632 |
| [29] |
Hofmann H, Lorke A, Peeters F. The relative importance of wind and ship waves in the littoral zone of a large lake. Limnology and Oceanography, 2008, 53(1): 368-380. DOI:10.4319/lo.2008.53.1.0368 |
| [30] |
沈吉, 袁和忠, 刘恩峰等. 太湖表层沉积物的空间分布与层序特征分析. 科学通报, 2010, 55(36): 3516-3524. |
 2016, Vol. 28
2016, Vol. 28 

