(2: 江苏省地理信息资源开发与利用协同创新中心, 南京 210023)
(2: Jiangsu Center for Collaboration Innovation in Geographical Information Resource Development and Application, Nanjing 210023, P. R. China)
太湖是我国第三大淡水湖,不仅是国内外享有盛名的旅游胜地,而且是上海、无锡、苏州等地的主要水源,兼有渔业、灌溉、航运等多种功能.自1980s起,太湖的富营养化程度越来越严重,目前全湖处于富营养到重富营养状态,湖泊水质则属于劣Ⅴ类[1].太湖的富营养化导致蓝藻水华现象不断暴发,而且水华面积有逐年扩大、持续时间越来越长的趋势[2].太湖蓝藻水华不仅破坏水体景观和生态系统平衡,蓝藻在生长过程中会释放毒素,消耗水中溶解氧,引起水生生物大量死亡,湖泊水质恶化,严重威胁了湖泊周围地区的饮水安全[3].众多的研究表明太湖藻类数量与水温有很好的相关关系[4-8],由于太湖富营养化为蓝藻生长提供了充足的营养盐,水温成了影响太湖藻类生长的重要环境因子之一,全面有效地监测太湖水温对蓝藻水华的预警预报具有一定的作用.而卫星热红外遥感技术为太湖水温监测提供了一种高效快捷的手段,目前NOAA、TERRA、AQUA、NPP、METOP、FY等系列卫星都能获得相应的热红外遥感数据,其时间分辨率高,但空间分辨率低,难以满足内陆湖泊水温遥感监测;而Landsat系列卫星的TM/ETM+/TIRS数据、TERRA卫星的ASTER数据具有较好的空间分辨率,比较适合内陆湖泊水温遥感监测,但卫星观测周期为16 d,不利于水温动态监测.我国2008年9月6日发射的环境减灾卫星HJ-1B上搭载了一台红外多光谱相机IRS,具有2个近红外通道、1个中红外通道和1个热红外通道,空间分辨率分别为150、150和300 m,对地观测周期为4 d,能够为太湖水温动态遥感监测提供很好的资料.目前,国内学者针对HJ-1B/IRS单通道的热红外资料在遥感算法改进、地表温度和水表面温度反演方面进行了一些研究[9-13],由于像HJ-1B/IRS这种只带一个热红外通道的卫星传感器仍有不少,如Nimbus-7/CZCS、Landsat-7/ETM+、CERBS/IRMSS、FY-3/MERSI,因此很有必要开展基于单通道热红外数据的遥感算法研究.本文将针对HJ-1B/IRS单通道的热红外数据,分别采用普适性单通道算法(generalized single-channel method,GSCM)[14]、辐射传输模型法(radiative transfer code method,RTM)和单窗算法(mono-window algorithm,MWA)[15]反演太湖水温,比较3种反演方法的精度,以期为HJ-1B/IRS资料在太湖水温遥感监测中的业务化应用提供理论依据.
1 数据与方法 1.1 数据2008年11月10-21日和2009年4月16-27日在太湖开展了水体光学实验,测定水质参数、水体光谱、水面气象参数等,其中水表面温度用水温表测量,精度为0.2 K.实验期间获得太湖地区有效的HJ-1B/IRS遥感影像6景,日期为2008年11月10日和14日,2009年4月17日、21日、22日和25日,影像质量好、无云彩,数据为LEVEL 2级产品,下载于中国资源卫星应用中心.在HJ-1B卫星过境时同步实测7个样点的水温(表 1和图 1),两者观测时间相差不到30 min,可以用于IRS热红外数据反演水温的精度验证. 表 1中HJ-1B过境时间和观测天顶角从IRS影像的数据文件中获得,卫星过境时的能见度是由位于太湖的东山气象站(58358)在格林尼治时间(GMT)0:00时和6:00时的观测值内插得到,水汽量是来自全球气溶胶Aeronet网太湖站实测值,大气平均作用温度Ta是由太湖周边气象站—上海站(58362)、南京站(58238)和杭州站(58457)在0:00时(GMT)的探空资料计算的平均值.为了进一步说明IRS热红外数据反演水温的精度,引入了TERRA/MODIS温度产品进行对比,同期的TERRA卫星过境时间如表 1所示,数据从NASA官网http://reverb.echo.nasa.gov/reverb/下载得到.
| 表 1 HJ-1B卫星过境太湖时卫星、气象和水温的信息 Tab.1 Parameters of satellite, meteorology and water surface temperature when HJ-1B passing over Lake Taihu |
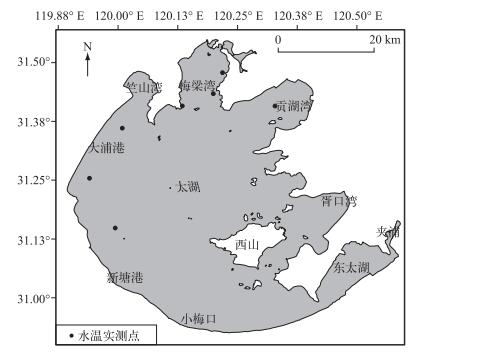
|
图 1 太湖水温实测点的位置 Fig.1 Location of measured water surface temperature (WST) sites in Lake Taihu |
(1) 遥感影像的辐射校正:由于从中国资源卫星中心下载的HJ-1B/IRS影像资料已经做过几何校正,满足研究的需要.这里只对HJ-1B/IRS热红外通道(第4通道)进行辐射校正,将原始的数字信号DN值转化为图像辐亮度.根据IRS影像自述文件中提供的辐射定标系数b和g,按式(1)进行辐射校正:
| $ L = \frac{{DN-b}}{g} $ | (1) |
式中,g=59.421 DN /(W/(m2·sr·µm)),b=-25.441.利用遥感图像处理软件ENVI进行辐射校正,从而计算出辐亮度值L.
(2) 遥感影像亮度温度的计算:根据普朗克定律计算亮度温度TB:
| $ {T_{\rm{B}}}{\rm{ = }}\frac{{{C_2}}}{{\lambda \cdot \ln \left( {1 + \frac{{{C_1}}}{{{\lambda ^5} \cdot L}}} \right)}} $ | (2) |
式中,C1=2πh·c2=1.19104356×108 Wμm4/(m2·sr),C2=h·c/k=1.4387685×104 μmK;h为普朗克常数,取6.626×10-34J·s;c为真空中的光速,取2.998 ×108 m/s;k为波耳茨曼常数,取1.38 ×10-23 J/K;λ为HJ-1B/IRS热红外通道的中心波长,λ=11.576 μm,L是辐亮度值,经式(2)计算便可得到遥感影像的亮度温度.
1.3 研究方法根据热辐射传输原理,当热红外传感器观测湖面时,入瞳辐亮度Lt有3个来源[16]:①水面的热红外辐射Lw,这部分的能量取决于水面温度、水的发射率ε以及水面和传感器之间的大气传输路径中的透过率τ;②大气自身发射的下行热辐射La↓,到达水面后,经水面反射并穿过大气层,被传感器所接收的辐射;③大气自身发射的上行热辐射La↑,直接进入传感器的辐射.研究表明,大气自身发射的热辐射与大气中吸收气体的含量和物理状态有关,主要的影响因素为大气温度和水汽量[14-15].因此,传感器接收到的总入瞳辐亮度Lt可表示为:
| $ {L_{\rm{t}}} = \varepsilon \cdot \tau \cdot {L_{\rm{w}}} + \left( {1-\varepsilon } \right)\tau \cdot L_{\rm{a}}^ \downarrow + L_{\rm{a}}^ \uparrow $ | (3) |
由于水的发射率高,近似为黑体,水面反射率1-ε接近为0,因此经水面反射的大气下行热辐射(1-e)tLa↓部分可忽略,式(3)则简化为:
| $ {L_{\rm{t}}} = \varepsilon \cdot \tau \cdot {L_{\rm{w}}} + L_{\rm{a}}^ \uparrow $ | (4) |
式中,Lt是遥感传感器接收的总热辐射;ε是湖水的发射率,由于太湖是淡水湖泊,而相同温度下发射率主要取决于物质的自身组成,根据ASTER光谱库(http://speclib.jpl.nasa.gov/)中水实测的光谱数据,结合IRS热红外通道的光谱响应函数进行卷积,得到IRS热红外通道水的发射率为0.9871;τ是水面和传感器之间大气传输路径中的透过率,主要受卫星观测几何和大气成分的影响,一般可用辐射传输模型模拟[17]或经验公式[18-19]计算得到;Lw是在一定温度下水面当作黑体时发射的热辐射,是温度遥感反演中待求解的物理量;在温度遥感反演算法中,大气自身发射的上行热辐射La↑一般通过对普朗克函数运用泰勒展开式进行线性近似,最终转化为大气平均作用温度或水汽量的函数[14-15].因此,根据式(4)本文将采用普适性单通道算法、辐射传输模型法和单窗算法从IRS热红外数据中反演太湖水温,并对反演算法进行精度比较.
1.3.1 辐射传输模型法由式(4)可见,要从卫星热红外遥感图像中提取水面发射的热辐射Lw,首先要确定大气透过率τ和大气自身发射的上行热辐射La↑.因此,可利用辐射传输模型MODTRAN 4.0模拟IRS热红外通道的大气透过率和大气上行热辐射, 模拟时的大气模型2008年11月为中纬冬季、2009年4月为中纬夏季,气溶胶模型为城市型,所需的观测天顶角和气象参数见表 1.模拟结果与IRS光谱响应函数进行卷积运算,得到IRS热红外通道的大气透过率和大气上行热辐射(表 2).从IRS热红外图像中可计算出水面发射的热辐射Lw,再根据普朗克函数由Lw计算出太湖水温.
| 表 2 辐射传输模型MODTRAN模拟的HJ/IRS大气参数 Tab.2 Atmospheric parameters simulated by radiative transfer code MODTRAN |
覃志豪等针对Landsat/TM6数据构建了反演地表温度的单窗算法[15],由于本研究是针对水体,在忽略水面反射的大气下行热辐射后,需对原算法进行重新推导,得到反演水温Tw的单窗算法:
| $ {T_{\rm{w}}} = \left\{ {a \cdot \tau \left( {1- \varepsilon } \right) + \left[{1-\left( {1-b} \right)\left( {1-\varepsilon } \right)\tau } \right]{T_{\rm{b}}} -\left( {1 -\tau } \right){T_{\rm{a}}}} \right\}/\left( {\varepsilon \cdot \tau } \right) $ | (5) |
式中,a和b是单窗算法中定义的温度参数
Jiménez-Muñoz等建立了从遥感数据中反演地表温度的普适性单通道算法[14],对于海表面温度SST的反演,算法简化为:
| $ {T_{{\rm{SST}}}} \approx \gamma \left( {\lambda, {T_0}} \right)\left[{\psi _1^{SST}\left( {\lambda, \mathit{w}} \right)L_\lambda ^{{\rm{at-sensor}}} + \psi _2^{\mathit{SST}}\left( {\lambda, \mathit{w}} \right) + \delta \left( {\lambda, {\mathit{T}_0}} \right)} \right] $ | (6) |
式中,L是大气顶层传感器接收的热辐射亮度;γ和δ是热辐射亮度与温度之间按照泰勒线性近似展开的函数,
| $ \alpha \left( {\lambda, {T_0}} \right) \equiv B\left( {\lambda, {T_0}} \right)\left[{1-\left( {\frac{{{c_2}}}{{{T_0}}}\left( {\frac{{{\lambda ^4}}}{{{c_1}}}B\left( {\lambda, {T_0}} \right)} \right) + \frac{1}{\lambda }} \right)} \right] $ | (7) |
| $ \beta \left( {\lambda, {T_0}} \right) \equiv \frac{{{c_2}B\left( {\lambda, {T_0}} \right)}}{{T_0^2}}\left[{\frac{{{\lambda ^4}}}{{{c_1}}}B\left( {\lambda, {T_0}} \right) + \frac{1}{\lambda }} \right] $ | (8) |
式中,T0可看作是卫星传感器的亮度温度;B为普朗克函数;ψ1和ψ2为大气参数,在热红外波段范围可用大气水汽量w来表示.对于IRS热红外通道,ψ1和ψ2的计算表达式为:
| $ {\psi _1} = 0.024764{w^3}-0.031750{w^2} + 0.186992w + 0.993281 $ | (9) |
| $ {\psi _2} =-0.230743{w^3} + 0.255181{w^2}-1.283163w + 0.211181 $ | (10) |
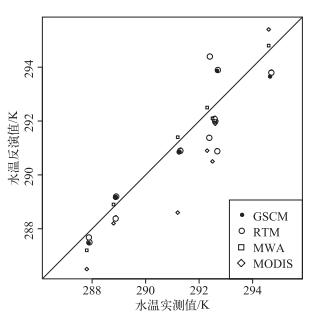
根据前述的3种反演算法,分别从6景IRS热红外遥感图像中反演太湖水温.根据水温实测点的经纬度坐标,从反演结果中提取相应的水温值,并与实测水温进行对比,绘制两者的散点图(图 2)并计算3种反演算法的误差(表 3).为了更好地说明IRS热红外数据反演水温的精度,将同期的TERRA卫星MODIS温度产品与实测水温值进行对比.从图 2可见,3种算法反演的水温值与实测值非常接近,两者的样点都在1 : 1直线附近,与实测水温的相关系数都在0.9以上,以单窗算法的相关性最高,相关系数为0.989,辐射传输模型法其次,相关系数为0.977,普适性单通道算法的相关性最低,为0.917.相比之下,MODIS温度产品的样点偏离1 : 1直线的较多,与实测水温的相关系数为0.935.从散点图可以看出,3种算法从IRS热红外数据中反演的水温值与实测值有很好的吻合度.
|
图 2 水温反演值与实测值的对比散点图 Fig.2 Scatter plot between retrieved WST and measured one |
| 表 3 水温反演算法的误差统计 Tab.3 Statistical errors of WST retrieval algorithms |
表 3给出了IRS热红外数据反演水温的误差指标,平均偏差是各样点反演值与实测值之差的平均值,平均偏差越接近为0说明反演的系统误差越小,大于0则说明反演值比实测值整体偏高,否则相反;而均方根误差和平均相对误差反映了各样点反演值与实测值之间的相对差异,其数值越低说明反演的误差越小、精度越高.与MODIS温度产品相比,3种算法从IRS热红外数据中反演水温的各项误差都明显低于MODIS数据,说明HJ-1B卫星获取的IRS数据质量是可靠的,IRS热红外数据在湖泊水温遥感监测具有一定优势.对于反演水温的3种算法,单窗算法和辐射传输模型法得到的平均偏差为负值,说明这两种方法反演水温时总体上会偏低,而普适性单通道算法的平均偏差为正值,反演水温时会偏高,3种算法中以单窗算法的平均偏差最接近0,说明该方法反演水温的系统误差最小.普适性单通道算法的均方根误差为1.001 K,其他两种算法的均方根误差都小于1.001 K;而3种算法的平均相对误差都在0.3 %以下,总体而言以单窗算法的误差最小,辐射传输模型法其次,普适性单通道算法的误差最大.
分析3种算法产生的误差原因:单窗算法反演水温时需要确定的参数有水的发射率、大气透过率和大气平均作用温度,辐射传输模型法的参数为发射率、大气透过率和大气上行热辐射亮度,而普适性单通道算法的参数仅为大气水汽量.通过对比ASTER光谱数据库中自来水、蒸馏水和海水的光谱发现,水的发射率很稳定,3种水的发射光谱几乎是一致的.由此可见,水的发射率对单窗算法和辐射传输模型法造成的误差可以忽略.大气透过率和大气上行热辐射亮度由辐射传输模型MODTRAN模拟得到,尽管LOWTRAN和MODTRAN在海表温度和地表温度算法开发中被广泛应用,但它们在大气窗口3.4~4.1和8~13 μm内模拟的误差为0.5 % ~2.0 %;另外,由于不同大气模型的差异,热红外波段大气透过率在大气窗口内的误差达6 %,而在大气窗口边缘甚至超过30 % [20-21].因此大气透过率和大气上行热辐射亮度由MODTRAN模拟时带来了不同程度的误差,而在单窗算法中大气平均作用温度Ta根据探空资料由地面到高空200 pha之间每一层的大气温度与水汽量加权平均计算得到[22],相对于模拟的大气上行热辐射亮度,大气平均作用温度能更准确地反映大气自身热辐射情况,因此单窗算法的反演精度比辐射传输模型法更高.普适性单通道算法在反演水温时直接将水体看作黑体,而IRS热红外通道实际计算的水发射率为0.9871,高估的发射率给水温反演带来了误差,因为赵利民等在分析HJ-1B/IRS热红外数据反演地表温度误差时发现,在典型情况地表发射率估算误差为0.01时就能导致0.5 K以上的反演误差[23];另外,普适性单通道算法在温度反演时将大气透过率和大气自身的热辐射都表示为水汽量的函数,龚绍琦等研究表明,除了水汽量外,观测天顶角、能见度、气溶胶类型都会影响热红外波段大气透过率[19];大气自身的热辐射亮度还与大气温度有关.普适性单通道算法中的参数估计给反演结果带来了较大误差,因此该算法水温反演的精度相对较低.
2.2 太湖水温反演结果的统计分析为了进一步探讨3种算法反演太湖水温的整体效果,以2009年4月21日的数据为例进行说明,分别对3种算法反演的太湖水温以及MODIS产品的太湖水温做直方图(图 3),统计其特征参数:水温的最小值、最大值、平均值、标准差、偏度和峰度(表 4).为了剔除图像的异常值,这里的水温最小值和最大值不是图像上的极值,而是直方图左右两侧拐点位置的值,以此对比分析不同算法对IRS热红外数据反演太湖水温的整体效果.
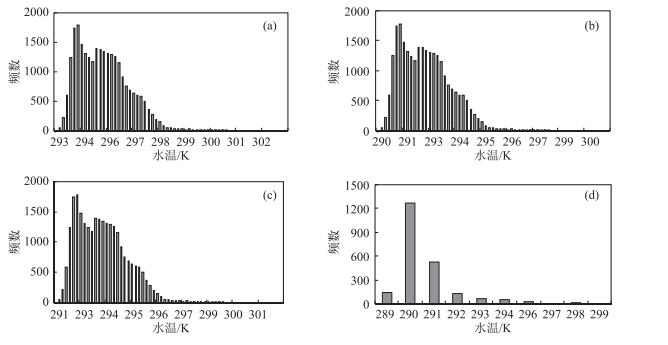
|
图 3 2009年4月21日不同算法反演太湖水温的统计直方图(a~c分别为普适性单通道算法、辐射传输模型法和单窗算法,d为MODIS温度产品) Fig.3 Histogram of WST in Lake Taihu retrieved by different algorithms on April 21, 2009(a-c stand for GSCM, RTM and MWA, d stands for MODIS temperature product) |
| 表 4 2009年4月21日不同算法反演太湖水温的统计结果 Tab.4 Statistical results of WST in Lake Taihu retrieved by different algorithms on April 21, 2009 |
由图 3和表 4可见,尽管3种算法得到太湖水温直方图形态相似,但统计特征值均不同.最小值、最高值和平均值可以反映遥感图像水温值的动态范围和整体状况,普适性单通道算法得到的水温最小值、最高值和平均值最高,其次是单窗算法,再次是辐射传输模型法,MODIS产品的温度最低.这与前面分析的结果是一致的,普适性单通道算法反演的结果要高于实测值,而其它算法都低于实测值.标准差整体反映了遥感图像上各像元的水温值相对于平均值的离散程度,相对于MODIS产品,3种算法反演水温得到的标准差都比较小,其值在1.175~1.231之间,说明水温反演值的离散程度较低.偏度(skewness)和峰度(kurtosis)分别反映图像直方图分布的扁平程度和形状大小.偏度α是用于衡量直方图分布的不对称程度或偏斜程度的指标.当α=0时为正态分布;当α >0时为正偏态,即位于均值右边的数据比左边的少,直观表现为右边的尾部要比左边的尾部长;否则相反. 3种算法反演的水温偏度都在0.981以上,说明图像直方图呈正偏态,图像上低于均值的像元数较多、而高于均值的像元相对要少,3种算法反演的水温正偏态势依次是单窗算法、普适性单通道算法和辐射传输模型法.峰度β是用于衡量图像直方图分布的集中程度或分布曲线的尖峭程度的指标,当峰度β=0时为正态分布;β>0时,表示分布比正态分布更集中在平均值周围,分布呈尖峰状态;β < 0时,表示分布比正态分布更分散,分布呈低峰态. 3种算法反演的水温峰度都在2以上,说明图像各像元的水温值更集中在平均值周围,而这种密集程度依次为:单窗算法、普适性单通道算法和和辐射传输模型法.由于MODIS数据的空间分辨率低,太湖MODIS水温产品的像元数少,温度值的离散程度高,直方图分布呈正偏态、尖峰状态更强.
2.3 太湖水温反演结果的空间特征分析为了更直观地了解3种算法从IRS热红外数据中反演的太湖水温状况,以2009年4月21日的数据为例,分别绘制出太湖水温的空间分布图(图 4),并对水温空间分布图在288~300 K范围内按等间隔分级,划出288~ 291、291~294、294~297和297~300 K 4级,统计每种算法在每个温度等级内所占的面积(表 5).由IRS热红外图像统计的太湖水域总面积约为2350.00 km2,而MODIS图像统计的水域面积为2240.00 km2,MODIS图像统计的水域面积偏低主要是由于其空间分辨率低,较小的水域未能划分出来.从表 5可见,普适性单通道算法反演的水温主要分布在294~297 K之间,其水域面积为1934.19 km2,占太湖总面积的82.3 %,而水温在291~294和297~300 K的区域面积分别为190.89和224.91 km2,占总面积的8.1 %和9.6 %.辐射传输模型法反演的水温主要分布在291~294 K之间,其水域面积为1875.06 km2,占总面积的79.8 %,而水温在288~291、294~297和297~300 K的区域面积分别为190.89、271.80和12.24 km2,占总面积的8.1 %、11.6 %和0.5 %.单窗算法反演的水温主要分布在291~294 K之间,其水域面积为1461.42 km2,占总面积的62.2 %,其次是294~297 K之间,水域面积为862.92 km2,占总面积的36.7 %,而水温在297~300 K之间的水域面积则有25.65 km2,占总面积的1.1 %.而MODIS温度产品的水温分布在288~291 K之间,水域面积为1942.00 km2,占总面积的86.7 %,水温大于291 K的区域仅为298.00 km2,占总面积的13.3 %.由此可见,不同算法反演的水温在空间上存在明显的差异性;普适性单通道算法反演的水温仍然最高,其次是单窗算法,再次是辐射传输模型法,而MODIS温度产品最低,这与前面分析的结果是一致的.但无论是3种算法从IRS热红外数据反演的水温,还是MODIS产品的水温,由于受陆地温度的影响,都是太湖水陆交界位置的水温较高.另外,太湖南部水温要比北部水温高,南部水域如胥口湾、东太湖、夹浦、小梅口、新塘港,特别是西山岛西部区域的水温较高,而北部水域如贡湖湾、梅梁湾、竺山湾、大浦港的水温相对较低,这是因为每年11月至翌年4月正值太湖枯水季,太湖南部地区气温比北部地区高,而水体吸热快、散热慢,气温影响着水温的变化.这一现象正好与陈绍良等[24]对太湖水体温度时空变化规律的研究结果相吻合.由此可见,利用3种算法从HJ-1B卫星IRS热红外数据反演的水温能真实地反映太湖水温的空间分布特征,而MODIS产品的水温相对较低.
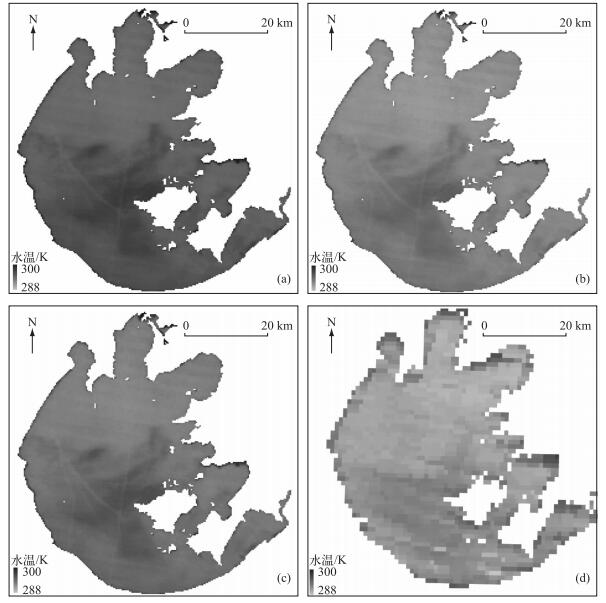
|
图 4 2009年4月21日不同算法反演太湖水温的空间分布(a~c分别为普适性单通道算法、辐射传输模型法和单窗算法,d为MODIS温度产品) Fig.4 Spatial distribution of WST in Lake Taihu retrieved by different algorithms on April 21, 2009(a-c stand for GSCM, RTM and MWA, d stands for MODIS temperature product) |
| 表 5 2009年4月21日不同算法反演太湖不同水温区域面积(km2)统计 Tab.5 Zonal statistics for each WST in Lake Taihu class by different algorithms on April 21, 2009 |
利用6景过境太湖的HJ-1B/IRS热红外影像,分别采用普适性单通道算法、辐射传输模型法和单窗算法反演了太湖水温,并与实测水温和同期的TERRA/MODIS温度产品进行对比,结果表明:
1) 利用3种算法从IRS热红外数据中反演太湖水温的均方根误差在1.001 K以内,而MODIS温度产品的误差为1.507 K,说明HJ-1B卫星IRS热红外数据在湖泊水温遥感监测中具有更好的性能优势和反演精度.
2) 从平均偏差来看,普适性单通道算法反演太湖水温时会偏高,而辐射传输模型法和单窗算法则会偏低. 3种算法以单窗算法的反演精度最高,辐射传输模型法其次,再次为普适性单通道算法,这是算法中不同参数估算误差导致的.
3) 对太湖水温反演图像的直方图统计表明,3种算法反演的水温图像上低于平均值的像元数较多、高于均值的像元相对较少,而且图像各像元的水温值更集中在平均值周围.水温图像的空间特征分析表明,IRS热红外数据反演的水温能真实地反映太湖水温的分布状况.
| [1] |
秦伯强, 王小冬, 汤祥明等. 太湖富营养化与蓝藻水华引起的饮用水危机—原因与对策. 地球科学进展, 2007, 22(9): 897-907. |
| [2] |
马荣华, 孔繁翔, 段洪涛等. 基于卫星遥感的太湖蓝藻水华时空分布规律认识. 湖泊科学, 2008, 20(6): 687-694. DOI:10.18307/2008.0605 |
| [3] |
段洪涛, 张寿选, 张渊智. 太湖蓝藻水华遥感监测方法. 湖泊科学, 2008, 20(2): 145-152. DOI:10.18307/2008.0202 |
| [4] |
王得玉, 冯学智, 周立国等. 太湖蓝藻爆发与水温的关系的MODIS遥感. 湖泊科学, 2008, 20(2): 173-178. DOI:10.18307/2008.0206 |
| [5] |
姜晟, 张咏, 蒋建军等. 基于MODIS数据的太湖蓝藻变化与水温关系研究. 环境科技, 2009, 22(6): 28-31. |
| [6] |
任健, 何浪, 秦铭荣等. 太湖蓝藻生长发育与水温的关系. 中国农业气象, 2009, 30(增1): 126-129. |
| [7] |
陈宇炜, 秦伯强, 高锡云. 太湖梅梁湾藻类及相关环境因子逐步回归统计和蓝藻水华的初步预测. 湖泊科学, 2001, 13(1): 63-71. DOI:10.18307/20010110 |
| [8] |
袁琳娜, 杨常亮, 李晓铭等. 高原深水湖泊水温日成层对溶解氧、酸碱度、总磷浓度和藻类密度的影响:以云南阳宗海为例. 湖泊科学, 2014, 26(1): 161-168. DOI:10.18307/2014.0120 |
| [9] |
段四波, 阎广建, 钱永刚等. 利用HJ-1B模拟数据反演地表温度的两种单通道算法. 自然科学进展, 2008, 18(9): 1001-1008. |
| [10] |
Zhou J, Zhan WF, Hu DY et al. Improvement of mono-window algorithm for retrieving land surface temperature from HJ-1B satellite data chin. Chinese Geographical Science, 2010, 20(2): 123-131. DOI:10.1007/s11769-010-0123-z |
| [11] |
赵少华, 秦其明, 张峰等. 基于环境减灾小卫星(HJ-1B)的地表温度单窗反演研究. 光谱学与光谱分析, 2011, 31(6): 1552-1556. |
| [12] |
Ouyang XY, Li J, Pan YQ et al. Retrieval of land surface temperature over the Heihe River basin using HJ-1B thermal infrared data. Remote Sensing, 2015, 7: 300-318. |
| [13] |
Hu K, Chen F, Liang SW. Application of HJ-1B data in monitoring water surface temperature. Procedia Environmental Sciences, 2011(10): 2042-2049. |
| [14] |
Jiménez-Muñoz JC, Sobrino JA. A generalized single-channel method for retrieving land surface temperature from remote sensing data. Journal of Geophysical Research Oceans, 2003, 108(D22): 4688-4696. DOI:10.1029/2003JD003480 |
| [15] |
覃志豪, Zhang MH, Karnieli A等. 用陆地卫星TM6数据演算地表温度的单窗算法. 地理学报, 2001, 56(4): 456-466. DOI:10.11821/xb200104009 |
| [16] |
张勇, 李元, 戎志国等. 利用大洋浮标数据和NECP再分析资料对FY-2C红外分裂窗通道的绝对辐射定标. 红外与毫米波学报, 2009, 28(3): 188-194. |
| [17] |
孟凡斌, 郑丽. 基于LOWTRAN 7的红外大气透过率计算方法. 光电技术应用, 2009, 24(3): 29-33. |
| [18] |
覃志豪, Li WJ, Zhang MH等. 单窗算法的大气参数估计方法. 国土资源遥感, 2003, 2: 37-43. |
| [19] |
龚绍琦, 孙海波, 王少峰等. 热红外遥感中大气透过率的研究(一):大气透过率模型的构建. 红外与激光工程, 2015, 44(6): 1692-1698. |
| [20] |
Wan ZM, Dozier J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(4): 892-905. DOI:10.1109/36.508406 |
| [21] |
Wan ZM, Dozier J. Effects of temperature-dependent molecular absorption coefficients on the thermal infrared remote sensing of the earth surface. Proc. IGARSS'92, 1992, 1242-1245. |
| [22] |
Sobrino J, Coll C, Caselles V. Atmospheric correction for land surface temperature using NOAA-11 AVHRR channels 4 and 5. Remote Sensing of Environment, 1991, 38: 19-34. DOI:10.1016/0034-4257(91)90069-I |
| [23] |
赵利民, 余涛, 田庆久等. HJ-1B热红外遥感数据陆表温度反演误差分析. 光谱学与光谱分析, 2010, 30(12): 3359-3362. DOI:10.3964/j.issn.1000-0593(2010)12-3359-04 |
| [24] |
陈绍良, 陆建伟, 沈建强. 太湖水体温度时空变化规律的初步研究. 江苏水利, 2009, 3: 38-39. |
 2016, Vol. 28
2016, Vol. 28 
