(2: 中国科学院南京地理与湖泊研究所, 湖泊与环境国家重点实验室, 南京 210008)
(3: 中国科学院大学, 北京 100049)
(2: State Key Laboratory of Lake Science and Environment, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008, P. R. China)
(3: University of Chinese Academy of Sciences, Beijing 100049, P. R. China)
水下光场计算模型主要通过计算不同水深和太阳天顶角、方位角等条件下的辐照度、辐亮度、漫衰减系数等辐射量与表观光学量来反映水下光场的分布.精确模拟水下光场对研究海洋初级生产力、生物地球化学模型以及全球循环模型中的热量收支平衡有重要意义.
水体辐射传输方程描述了电磁波在水中传播时,受介质的吸收、散射等作用的影响发生衰减的过程.水体光学模型的核心就是求解水体辐射传输方程,由于方程本身的复杂性及边界条件的限制,只能利用数值分析的方法得到数值解.求辐射传输方程数值解的方法有Monte Carlo光线追踪法[1-6]、不变嵌入法[7]、离散坐标法[8]和矩阵算法[9-12]等.
Monte Carlo光线追踪法直观地表达辐射传输过程中光束被水中粒子(水分子、悬浮颗粒物等)吸收和散射过程,物理结构清晰.它可以对任意入射光线、散射相函数和固有光学属性分布情况下的水下光场进行三维模拟,可以解决一维模型所不能解决的问题,更加符合客观世界的实际情况.它具有较强的灵活性,可以模拟野外测量难以达到的极限条件[13].在水体光学研究领域,Kattawar[1-2]、Gordon[3]、Kirk[4]、Morel[5]、Mobley[6]等很多学者已经用Monte Carlo方法解决了不同的水体光学问题.国内,曹文熙等运用Monte Carlo方法模拟了浮标浮体阴影及安装仪器自阴影对水下光辐射测量的影响[14].唐军武等[15]和凌在盈[13]利用Monte Carlo方法模拟了水下光场,但没有考虑大气和水底边界状况.
Monte Carlo最大的缺点是计算速度慢,即便有提高计算速度的方法(如方差缩减技术[2, 16]、BMC[3]等),但这些方法也只在一定程度上提高了光子的利用效率. Monte Carlo方法具有计算数据相对独立、串行数据处理少等优良的并行化特性,这种特性很适合用GPU加速运算,基于GPU加速Monte Carlo方法可以几倍、几十倍甚至上百倍地提高计算速度[17-20],在图形渲染、真实感场景模拟等应用领域中应用广泛.
本文主要研究GPU加速的三维水体辐射传输Monte Carlo模拟模型,描述了水体辐射传输Monte Carlo模拟模型的建立过程,并实现了GPU加速.比较分析了两种计算环境下不同海洋光学标准问题及复杂水下光场的加速性能.
1 水体辐射传输Monte Carlo模拟模型水体辐射传输Monte Carlo模拟模型,主要包含大气部分、水气界面、层化水体和水底边界4大模块,其中大气部分包括大气模型和入射光场分布模型(图 1).输入参数包括光子数、入射角度、固有光学量、水深、风速、大气参数、底边界等.输出结果包括辐亮度(L)、辐照度(E)、遥感反射率(Rrs)、遥感反射比(R)、平均余弦(μ)、漫衰减系数(K)等辐射量与表观光学量.该模型实现了模拟任意太阳角度(天顶角和方位角)、不同水体固有光学属性(吸收系数、散射系数和散射相函数)、任意深度条件下,考虑大气、粗糙水面、层化水体和水底边界的水下光场,可以得到辐亮度、辐照度等辐射量的空间分布.该模型暂不考虑Raman散射、偏振和内部光源的影响.

|
图 1 水体辐射传输Monte Carlo模拟模型框图 Fig.1 The flow chart of Monte Carlo simulation model of water |
本文采用的大气模型为RADTRAN-X模型CanKaoWenXian_22.该模型需要的大气参数包括:太阳角度、大气压强、大气类型、相对湿度、降雨量、风速、能见度、臭氧含量、气溶胶参数等,得到特定条件下的漫射天空光辐照度(Esky)、太阳直射光辐照度(Edir)和水面之上总入射辐照度(Etot=Esky+Edir).
光子到达水-气界面之前,与大气中粒子发生相互作用,传播方向发生变化.实际情况下,很难得到天空漫射光的空间分布,需要假设入射光场分布.入射光场分布模型有理想模型和半分析模型,其中常用的理想模型有各向同性模型和心型分布模型[22].本文使用由Harrison等提出的辐亮度分布半分析模型[23],得到上半球空间的入射辐亮度分布.为了方便统计、记录光子信息,把2π立体角上半球空间分为天顶角间隔10°、方位角间隔15°的格网[7],入射光的初始方向为格网的中心对应的天顶角和方位角.
1.2 粗糙水面光子到达水-气界面会发生折射、反射.平静水面情况下,根据Snell定律和菲涅尔反射定律得到折射角和反射率.然而,实际的海面受风浪、波动等影响,几乎不可能是水平的,需要考虑粗糙水面的情况.
粗糙水面的模拟使用Cox等[24]提出的小波面斜率正态分布模型,不考虑重力波.在模拟过程中,考虑小波面的斜率的概率分布计算、相互遮挡问题以及多次反射等问题.此处,存在两个坐标系统:系统坐标系和小波面坐标系,需要进行坐标系转换.系统坐标系以水平面垂直向下为Z轴的正方向,X-Y平面是水平面.小波面坐标系是以小波面的法线作为Z轴,X-Y平面在小波面所在的平面内.
θn是小波面的法线与水平面的法线的夹角,代表小波面的倾斜角度,θn=0时,小波面水平. θn的方差为σ2=0.003+0.00512U,U为风速.
1.3 水体内光子与粒子的相互作用光子与水中粒子发生相互作用时,一部分被吸收,为了减小Monte Carlo统计噪声,本文采用变权重的光子跟踪技术,即每次光子的权重乘以单次散射反照率(ω0)作为被吸收后光子的权重.其中ω0的值越接近于1表示水体散射能力越强,越接近于0表示水体吸收能力越强.
相函数是光子与粒子相互作用后散射方向的概率密度函数.实际模拟中,需要根据水体的类型和水体中组分的含量选择合适的散射相函数.水中粒子的散射主要分为纯水的散射和悬浮颗粒物的散射.纯水的散射相函数采用近似瑞利散射相函数,悬浮颗粒物的散射相函数可使用Petzold在1972年测量的不同水体的体散射函数的平均值,或者使用其它相函数公式(如:Henyey-Greenstein相函数、Fournier-Forand相函数)[25]等.
针对垂向不均一的水体,把野外实际测量的IOP随深度的廓线或者水体层化模型[26]输入水体辐射传输Monte Carlo模拟模型,可以得到垂向异质水体的水下光场分布.
1.4 水底边界光子到达水底边界部分被水底物质吸收,部分被反射,反射的方向和反射率与水底状况有关,一般用二向反射函数(BRDF)定量描述入射光线与出射光线的关系.由于水底BRDF测量存在一定的困难,在研究中通常忽略水底边界的二向性,假设水底表面是反射率固定的朗伯体,反射方向为各向同性.
2 GPU加速的水体辐射传输Monte Carlo模拟最初,GPU(Graphic Processing Unit,图形处理器)是一个高度并行的用于图形渲染任务的计算设备,现在已经发展成为常用的计算处理器.在数据并行运算方面,GPU已经得到了广泛的应用,也变得越来越高效.
水体辐射传输Monte Carlo(MC)模拟模型基于概率统计的方法,模拟光线在水体中与水中粒子相互作用的过程,获取水体的表观光学量.要模拟得到精确的水下光场,需要初始设置大量光子(107),传统利用CPU计算时需要依次计算每个光子在水体中的传播过程,耗时较长,运行效率低.然而,根据MC模拟过程的可并行计算的特点,引入GPU计算可以同时并行计算大量光子,大幅提高计算效率.在基于CPU的水体辐射传输Monte Carlo模型的基础上,按照并行计算的要求,把可以并行计算的部分放到GPU上运行,条件判断、边界确定、结果保存等不具备并行特性的部分在CPU上计算.
对CPU-MC程序进行改写可实现MC模拟模型的GPU并行运算. 表 1列出了两种计算环境的CPU、GPU配置及对应的软件环境.
| 表 1 计算环境描述 Tab.1 Properties of two computer environments |
Mobley等提出了海洋光学的7个标准问题[26],包括理想的简单问题、基本问题、层化水体问题、大气效应问题、粗糙水面问题、水底边界问题和拉曼散射问题.他们用7种辐射传输模型(Hydrolight、离散坐标法和Monte Carlo方法),得到特定条件下的辐射量(辐亮度和辐照度)的平均值,经常被国内外学者作为检验海洋辐射传输模型精度的标准[9, 15].
海洋光学7个标准问题中的基本问题假设为:(1)水体表面水平;(2)水体水平与垂向均一且无限水深;(3)不考虑天空光;(4)太阳光为点光源,天顶角为60°;(5)太阳光在其垂直表面上的辐照度为1 W/(m2·nm);(6)水体内部无Raman散射及内部光源存在;(7)假设水体为高散射(ω0=0.9)或者高吸收(ω0=0.2)水体两种情况;(8)水体散射包括水分子和颗粒物散射两部分. 表 2是对问题1~6的简单描述,参照文献[26]中的表 3,本文没有考虑问题7(Raman散射).
| 表 3 本文模拟结果与Mobley等[26]研究结果的平均值及平均相对误差(入射光子数为107) Tab.3 Ed, Eou and Lu values in this paper and relative error (δ) with average value of Mobley et al[26] (total initial photons are 107) |
利用GPU加速的水体辐射传输Monte Carlo模拟模型,对表 2的6个问题分别进行水下光场模拟.表 3是入射光子数为107,不同标准问题、光学深度、ω0下的模拟结果(下行辐照度(Ed)、上行辐照度(Eou)和向上辐亮度(Lu))与Mobley等[26]的相应模拟结果的平均值(Ed_aver、Eou_aver和Lu_aver),以及它们之间的平均相对误差(δ)(式1),x分别为Ed、Eou和Lu.
| $ \delta = \frac{{\left| {x-{x_-}aver} \right|}}{{{x_-}aver}} \times 100\% $ | (1) |
从对6个标准问题验证的结果(表 3)可以得出,水体辐射传输模拟模型的精度基本达到了Mobley等的研究[26]中多个数值计算模型计算得到的平均值的精度范围. Ed、Eou比Lu的相对误差低,是因为Lu是由落入某个角度范围内少数光子计算得到的,受光子数目影响,稳定性差,而Eou与整个半球空间中的光子数有关,结果相对稳定.在光学深度较大或强吸收水体存在误差较大的情况下(问题3,在60 m处模拟结果误差达到20 %以上),是由于Monte Carlo方法本身存在噪声,复杂水体条件下假设的随机数较多,同样光子数的情况下,在强吸收水体噪声较大.因此,欲得到较好的结果,在强吸收水体需要增加模拟的光子数以保证模拟精度.
3.2 不同模拟条件的GPU加速性能分析对海洋光学基本问题及其组合边界条件下的CPU计算时间、GPU加速的运行时间和加速比进行统计,总光子数为106.
通过GPU加速,在问题1和问题3中加速比为300~500,而问题2和问题6达到了1000多(表 4),这表明GPU加速可以明显提高Monte Carlo算法的运行效率.问题2(ω0=0.9)CPU计算需要2 d(173604 s/3600 s= 48.22 h),而GPU加速之后只需要加入大气模型及天空光之后,GPU加速没有明显提高运算速度,2~3 min(142 s).从CPU的每个光子依次计算,到GPU的许多光子同时在GPU中计算,节省了时间,大幅提高了运行效率.与文献[26]中的表 4中5个MC模型对问题3的计算时间进行比较,运行速度平均提高了236倍.
| 表 4 两种计算环境下不同问题的CPU和GPU计算加速比 Tab.4 Speedup ratio of different problems under two computer environments |
加入大气模型及天空光之后,GPU加速没有明显提高运算速度,反而在一些情况下,计算效率降低.问题4仅能达到几倍到十几倍的加速比,在考虑各种边界条件的复杂水下光场(问题3、4、5、6)模拟时,GPU运算反而降低了运行效率.原因是在大气入射的上半球空间里,总入射光子数根据天空光的分布分配到每个quad(9*24)里,而在非直射方向quad里的光子数量较少,应用GPU加速反而降低了运行时间.
3.3 不同水体散射特性下的加速性能从以上分析可以看出,在同一个标准问题中,ω0=0.2和ω0=0.9的运行时间相差很大.因此,针对不同散射特性条件(ω0=0.1~0.9)下的Monte Carlo模拟的运行时间和效率进行了比较.结果(图 2)表明,两种计算环境下,CPU运行时间相差不大,而计算环境1的GPU运行时间大约为计算环境2的2倍,也就是计算环境2的加速比是计算环境1的2倍.在同一计算环境下,水体从高吸收到高散射的过程中,CPU和GPU的运行时间呈指数增加.在不同散射程度的水体,光子的寿命不同,在高吸收水体,光子存活时间较短.因此,在总入射光子数一定的情况下,高吸收水体的运行时间会短,光子的利用率下降,导致模拟结果的噪声大于高散射水体.
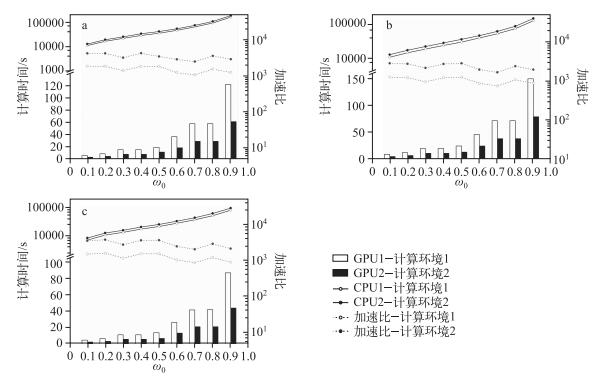
|
图 2 问题2 (a)、5 (b)和6 (c)在两种计算机环境下的CPU和GPU运行时间及加速比(总光子数为106)随ω0的变化 Fig.2 Computing time and speedup ratio vary with ω0 under two computer environments of problem 2 (a), problem 5 (b) and problem 6 (c) |
根据辐射传输理论,利用Monte Carlo模拟方法,开发了包括大气、水-气界面、层化水体、水底边界4大模块的水下光场模拟模型.并利用Mobley等发表的海洋光学标准问题中的问题1~6对模型的精度进行验证.引入GPU加速计算技术,使得水下光场Monte Carlo模拟的加速比得到大幅提高,一些简单问题的加速比可以达到几百到上千.对于不同散射特性的水体,因为光子利用效率不同,需要加大模拟光子数来保证运行结果的准确性.但是,对于包含大气模型和入射光场的水下光场Monte Carlo模拟方面,因为模型需要预先判断每个quad里的光子数,导致大量光子一起运算的并行特性被削弱,GPU并行加速的优势没有得到很好的体现.以后研究中,将进一步解决大气入射光场耦合水下光场的Monte Carlo模拟模型的GPU加速问题.
致谢: 感谢中国科学院南京地理与湖泊研究所马荣华研究员提供的建议和帮助,以及可以应用GPU加速的工作站作为本文的计算环境2.感谢美国University of Massachusetts Boston的Zhongping Lee教授对本研究的建议与帮助.| [1] |
Plass GN, Kattawar GW. Monte Carlo calculations of light scattering from clouds. Applied Optics, 1968, 7(3): 415-419. DOI:10.1364/AO.7.000415 |
| [2] |
Plass GN, Kattawar GW. Radiative transfer in an atmosphere-ocean system. Applied Optics, 1969, 8(2): 455-466. DOI:10.1364/AO.8.000455 |
| [3] |
Gordon HR. Ship perturbation of irradiance measurements at sea. 1:Monte Carlo simulations. Applied Optics, 1985, 24(23): 4172-4182. DOI:10.1364/AO.24.004172 |
| [4] |
Kirk JTO. Monte Carlo study of the nature of the underwater light field in, and the relationships between optical properties of, turbid yellow waters. Marine and Freshwater Research, 1981, 32(4): 517-532. DOI:10.1071/MF9810517 |
| [5] |
Morel A, Gentili B. Diffuse reflectance of oceanic waters:its dependence on Sun angle as influenced by the molecular scattering contribution. Applied Optics, 1991, 30(30): 4427-4438. DOI:10.1364/AO.30.004427 |
| [6] |
Mobley CD, Sundman LK. Effects of optically shallow bottoms on upwelling radiances:Inhomogeneous and sloping bottoms. Limnology and Oceanography, 2003, 48(1): 329-336. |
| [7] |
Mobley CD. Light and water:Radiative transfer in natural waters. New York: Academic Press, 1994.
|
| [8] |
Jin Z, Stamnes K. Radiative transfer in nonuniformly refracting layered media:atmosphere-ocean system. Applied Optics, 1994, 33(3): 431-442. DOI:10.1364/AO.33.000431 |
| [9] |
何贤强, 潘德炉, 白雁等. 基于矩阵算法的海洋-大气耦合矢量辐射传输数值计算模型. 中国科学:D辑:地球科学, 2006(9): 860-870. |
| [10] |
张鉴, 何晓雄, 赵凤生. 利用大气-海洋系统辐射传输模拟水色遥感信息量的变化特性. 量子电子学报, 2003(5): 623-628. |
| [11] |
何贤强, 潘德炉, 白雁等. 基于辐射传输数值模型PCOART的大气漫射透过率精确计算. 红外与毫米波学报, 2008(4): 303-307. |
| [12] |
何贤强, 潘德炉, 白雁等. 海洋-大气耦合矢量辐射传输粗糙海面模型. 光学学报, 2010(3): 618-624. |
| [13] |
凌在盈. 基于Monte Carlo方法的水体二向反射分布函数(BRDF)模拟[学位论文]. 杭州: 浙江大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10335-2010166338.htm
|
| [14] |
曹文熙, 吴廷芳, 杨跃忠等. 光学浮标阴影效应的蒙特卡洛模拟. 高技术通讯, 2003(3): 80-84. |
| [15] |
唐军武, 田国良, 陈清莲. 离水辐射非朗伯特性的Monte Carlo模拟及分析. 海洋学报:中文版, 2000(2): 48-57. |
| [16] |
Plass GN, Kattawar GW, Guinn JJA. Radiative transfer in the earth's atmosphere and ocean:influence of ocean waves. Applied Optics, 1975, 14(8): 1924-1936. DOI:10.1364/AO.14.001924 |
| [17] |
Fang Q, Boas DA. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Optics Express, 2009, 17(22): 20178-20190. DOI:10.1364/OE.17.020178 |
| [18] |
Preis T, Virnau P, Paul W et al. GPU accelerated Monte Carlo simulation of the 2D and 3D Ising model. Journal of Computational Physics, 2009, 228(12): 4468-4477. DOI:10.1016/j.jcp.2009.03.018 |
| [19] |
Ren N, Liang J, Qu X et al. GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues. Optics Express, 2010, 18(7): 6811-6823. DOI:10.1364/OE.18.006811 |
| [20] |
Wang Y, Li P, Jiang C et al. GPU accelerated electric field Monte Carlo simulation of light propagation in turbid media using a finite-size beam model. Optics Express, 2012, 20(15): 16618-16630. DOI:10.1364/OE.20.016618 |
| [21] |
Gregg WW, Carder KL. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnology and Oceanography, 1990, 35(8): 1657-1675. DOI:10.4319/lo.1990.35.8.1657 |
| [22] |
Mobley CD, Sundman LK. HydroLight 5-EcoLight 5 Technical Documentation. Sequoia Scientific, Inc, 2008. |
| [23] |
Harrison AW, Coombes CA. An opaque cloud cover model of sky short wavelength radiance. Solar Energy, 1988, 41(4): 387-392. DOI:10.1016/0038-092X(88)90035-7 |
| [24] |
Cox C, Munk W. Measurement of the roughness of the sea surface from photographs of the Suns Glitter. Journal of the Optical Society of America, 1954, 44(11): 838-850. DOI:10.1364/JOSA.44.000838 |
| [25] |
Mobley CD, Sundman LK, Boss E. Phase function effects on oceanic light fields. Applied Optics, 2002, 41(6): 1035-1050. DOI:10.1364/AO.41.001035 |
| [26] |
Mobley CD, Gentili B, Gordon HR et al. Comparison of numerical models for computing underwater light fields. Applied Optics, 1993, 32(36): 7484-7504. DOI:10.1364/AO.32.007484 |
 2016, Vol. 28
2016, Vol. 28 