(2: 南京信息工程大学, 水文气象学院, 南京 210044)
(2: College of Hydrometeorology, Nanjing University of Information Science & Technology, Nanjing 210044, P. R. China)
湖泊底泥在波浪作用下的运动过程产生了内源污染,是湖泊水体中营养盐来源的重要方面,从而加剧了湖泊的富营养化.前人对水流泥沙运动规律进行了大量的试验和分析,有着丰富的研究成果. 1960s Jonsson就对波浪作用下的泥沙起动进行了大量的研究,建立了边界层等理论[1],窦国仁院士对于波浪作用下泥沙的起动规律进行了深入的研究,得出了泥沙起动公式[2].黄建维对新港浮泥作了专题研究[3],严恺等在港口波浪潮流泥沙运动规律的研究中形成了一整套完整的理论[4].王军等对淤积固结条件下粘性细泥沙起动冲刷研究进行了综述[5],在冲刷水槽试验中环形水槽各种侵蚀冲刷水槽均被广泛使用.曹叔尤等利用环形水槽试验建立了淤积物的冲刷率公式[6]等等.研究表明,波浪作用下的细颗粒泥沙与粗颗粒泥沙的起动机理存在着较大的差异,粗颗粒泥沙的起动以形成沙波运动为主要特征;淤泥质泥沙的起动以泥沙的卷起、悬扬为主要特征;细颗粒泥沙的起动则介于粗颗粒与淤泥质泥沙之间,以底泥的卷起、悬扬为主,同时又有部分底质的输移,其运动特征与泥沙颗粒粒径和颗粒级配有密切关系.因此一些学者对细颗粒泥沙的卷起特性作了一些研究,由于细颗粒泥沙相对于粗颗粒泥沙的表面面积较大,颗粒间的相互摩擦、吸附将形成一个框架结构,往往比粗颗粒泥沙有更多的空隙,其达到密实稳定的历时相对较长,重度变化也较大,故对起动流速的影响也颇大.因此,在研究细颗粒泥沙的起动时,除应考虑波浪要素对起动流速的影响外,还应考虑细颗粒泥沙的特性及其在密实过程中重度对起动流速的影响[7].国内外学者对于粗颗粒泥沙在波浪作用下的起动、输移的研究较多,也较为成熟.而对于淤泥质泥沙的研究则相对薄弱.
同时,对于泥沙运动规律的研究主要集中在对于海岸[8]、河口[9]、河流[10]、闸下[11]泥沙起动及沉降方面,对于波浪作用下泥沙起动后的输沙研究主要局限于利用数值模拟计算的方法,对于河床的输沙研究也是局限于有建筑物作用下的河床、海床的冲刷变化,对于湖泊底泥输沙研究则相对缺乏.而在河口湖泊地区,当淤积粘性细泥沙吸附部分污染物时,这些污染物的迁徙扩散又与粘性细颗粒泥沙的起动输沙过程紧密联系,因此研究波浪作用下粘性细颗粒泥沙起动输沙问题具有重要实际意义[12].太湖位于江苏省南部、浙江省北部,是中国第二大淡水湖;龙感湖位于湖北省和安徽省交界处,也是一个淡水湖泊;巢湖位于江淮之间,地处合肥、巢湖二市和肥东、肥西、庐江三县境内,是中国著名的五大淡水湖之一.虽然3个湖泊从地理位置来看相距较远,但底泥的泥沙特性相似,均属于细颗粒泥沙范畴[13].本文通过波浪水槽试验,研究3个湖泊底泥起动以后的输沙规律,可以预测一定风浪条件下湖泊底泥的输沙量,使我们认识到在大风条件下湖泊水体含沙浓度的时空变化,可以进一步预测底泥营养盐的释放,为研究湖泊水质波动成因分析以及风浪作用下水环境变化的预测分析提供参考依据.
1 底泥特性太湖的底泥样品采自于太湖的梅梁湾,龙感湖的底泥样品采自于龙感湖的湖心部位,巢湖的底泥样品采自于两个位置:巢湖(J)靠近湖岸;巢湖(Y)靠近湖中心位置.样品采集时间是2004年夏季,当时太湖梅梁湾水质属于重度富营养状态[14];巢湖西半湖水质属于重度富营养状态,东半湖水质相对好于西半湖[15];龙感湖自1974年以来,流域大范围化学肥料的使用增加了入湖可溶性营养盐的排放量,从而导致水质逐渐恶化,总体而言水质好于太湖和巢湖[16]. 3个湖泊均属于大型浅水湖泊,对于研究内源污染问题具有共性.样品采集使用彼得森抓泥器,采集湖底表层20 cm以内的底泥.
从淤泥外观颜色来看,太湖底泥呈暗灰色,龙感湖和巢湖底泥呈土黄色. 3个湖泊内底泥样品的粒度分析结果见表 1,根据中值粒径大小,3个湖泊的底泥样品均属于粘性细颗粒泥沙范畴.
| 表 1 淤泥粒径 Tab.1 Diameter of sediment |
试验装置如图 1,试验水槽全长25 m,高0.8 m,宽0.5 m,水槽进口设有平推式造波设备,以产生规则波,水槽尾端设有消浪网,中间的铺沙段装有间距为5 m的两个采集波高的波高仪.整个系统采用计算机自动控制.铺沙段长度为6 m,铺设泥层厚度为10 cm.试验前底泥在水槽中经搅拌均匀后自然沉降,2天后测定底泥容重,然后开始试验.在天然湖泊中,底泥容重的垂直分布规律是随着深度增加容重逐渐增大.铺沙段底泥样品经自然沉降2 d后表层底泥容重达到1.30 g/cm3左右,接近天然湖泊底泥的表层密实状态,因此可以用来研究湖泊表层底泥的起动和冲刷.试验时波高先从小波开始,然后逐渐增大,直至底泥处于起动状态下测定其波高.在淤泥起动试验中,观察和测定了不同水深不同波周期下淤泥起动的波高Hc.在此试验的基础上,重点研究3个湖泊4种泥样波浪作用下的输沙,在一种泥样一种容重下,试验水深为30 cm,波周期为1.0 s试验条件下,共进行了12组试验.考虑实测太湖在大风天8 m/s的风速持续1 h以后的水体含沙浓度最大可以达到2.58 kg/m3[14],在输沙试验开始时通过测定垂线含沙浓度,1 h后垂线平均含沙浓度与天然湖泊相当,由此确定输沙试验的最大的波高H5,在起动波高与最大波高之间划分4个不同波高等级H1~H4,并使H1>H2>H3>H4>H5>Hc,从而研究输沙率与波高的变化规律.

|
图 1 波浪水槽示意图(单位:m) Fig.1 Layout of wave flume |
通过测定水体的含沙浓度来计算不同波高下的输沙率.以太湖底泥为研究重点,研究5组不同波高下的输沙变化过程,对于龙感湖和巢湖底泥分别实测2组波高下的输沙变化过程,输沙试验的波浪水文条件见表 2,试验结果按如下公式计算:
| 表 2 试验波浪水文条件* Tab.2 Wave conditions of experiment |
| $ E = \frac{{\rho \cdot V}}{{s \cdot t}} $ | (1) |
| $ \rho = \frac{{\left( {{\rho _1} + {\rho _2}} \right){V_1} + \left( {{\rho _2} + {\rho _3}} \right){V_2} + \left( {{\rho _3} + {\rho _4}} \right){V_3} + \ldots }}{{2\sum\limits_{i = 1}^n {{V_i}} }} $ | (2) |
式中,E为输沙率,ρ为水体平均含沙浓度,V为水体总体积,s为淤泥床面面积,t为掀沙时间,ρ1、ρ2、ρ3为垂线含沙浓度分布,V1、V2、V3为分层水体体积.
3 结果与分析波浪水槽试验先从小波开始,随着波高的逐渐加大,在临底水流切应力的作用下,床面上的一些轻质絮状物首先开始前后滚动,随着波浪动力的加大,床面泥沙由少量动到普遍运动,但泥沙颗粒做往复振动,基本不悬浮,此时判定为泥沙起动[1].对粘性细颗粒泥沙,粘结力和静水压力远超过重力,起动后再加大波浪动力,因突然失去粘结力和附加静水压力而悬浮,床面泥沙开始悬起,瞬时含沙量随波浪底部水质点速度的变化而变化,短时间内底层含沙量明显高于上层,底部形成高含沙层.当波浪作用时间延长后,泥沙开始向上层水体扩散.当波浪作用停止后,悬起的泥沙迅速沉降,高含沙层随即消失.上述现象表明,波浪作用下底泥的输移不同于较粗泥沙的底部推移质输沙,也不同于水流作用下淤泥的全断面悬浮输移,其输移主要以临底高含沙层泥沙沿波浪底部水质点运动方向往复运动.试验中发现,开始时,高含沙层水体的厚度和平均含沙量均随波浪动力的增大而增大,但当厚度达到一定值后,即使再加大波浪动力,其厚度也基本不变,而此时,高含沙层平均含沙量迅速增大.由于波浪非对称性引起的传质速度较小,尽管波浪兴起的含沙量较大,但在一个周期内,其净输沙也非常小.同时,在波高较小的条件下,泥沙的悬扬和扩散往往达不到水体上部,而只限于临底一定高度内,泥沙扩散高度随波高的增大而增大,3个湖泊4种泥样在波浪作用下的输沙过程规律基本相似.
泥沙起动后,加大波浪动力,泥沙自床面悬浮,向上层水体扩散.含沙量沿水深分布自泥沙床面向上逐渐减小.通过实测垂线含沙量分布,根据公式计算波浪输沙率.太湖底泥的输沙率变化过程为:当波高小于12 cm时,波浪的输沙率比较小;当波高大于12 cm时,波浪的输沙率明显增大(图 2a).试验中最大的波高为13.59 cm,当波浪达到最大波高时,起始输沙率比较大,冲刷5 min后输沙率下降明显,10 min后输沙率呈缓慢递减态势.龙感湖底泥的输沙率变化过程为:当波高小于10 cm时,波浪的输沙率比较小;当波高大于10 cm时,波浪的输沙率明显增大(图 2b).试验中最大的波高为11.90 cm时,当波浪达到最大波高时,起始输沙率比较大,输沙试验在30 min以内输沙率下降明显,在90 min的试验过程中输沙率呈缓慢递减态势.巢湖底泥的输沙率变化过程为:当波高小于10 cm时,波浪的输沙率比较小;当波高大于10 cm时,波浪的输沙率明显增大(图 2c、2d).试验中最大的波高为13.11 cm,当波浪达到最大波高时,起始输沙率比较大,输沙试验在20 min以内输沙率下降明显,在60 min以后输沙率基本趋于稳定.

|
图 2 太湖(a)、龙感湖(b)、巢湖(J)(c)和巢湖(Y)(d)的底泥输沙率变化过程 Fig.2 Scour rates of sediments from Lakes Taihu (a), Longgan (b), Chaohu (J)(c) and Chaohu (Y)(d) |
从图 2可以看出,波高越大输沙率越大,同样波高下,输沙率随着时间呈递减的趋势.波浪作用下,泥沙自床面起始悬浮强度大,随着波浪作用时间的延长,水体含沙量逐渐增大,水流夹带泥沙的能力也有所降低,输沙强度逐渐减小,波浪冲刷60 min以后,输沙率基本近似稳定.
4 公式的建立前人波浪泥沙研究结果表明[17-18],Shields参数是研究波浪泥沙输移的良好指标,波浪的挟沙能力应与其底部波浪Shields参数呈正比.按Madsen等的方法[19],波浪Shields参数可写为:
| $ {\psi _{\rm{m}}} = \frac{{{\tau _{\rm{m}}}}}{{\left( {{\rho _{\rm{s}}}-\rho } \right) \cdot {\rm{g}} \cdot \mathit{d}}} $ | (3) |
式中,ρs和ρ分别为泥沙颗粒和水的比重:g为重力加速度;d为泥沙颗粒粒径;τm为床面剪切应力的最大瞬时值,定义为:
| $ {\tau _{\rm{m}}} = \frac{1}{2}{f_{\rm{w}}} \cdot \rho \cdot u_{\rm{b}}^2 $ | (4) |
式中,ub为波浪水质点近底水平速度的最大值,由微幅波理论确定;fw为Jonsson波浪摩擦系数,可按下式计算,即:
| $ {f_{\rm{w}}} = \exp \left[{5.213{{\left( {\frac{{{a_{\rm{b}}}}}{\gamma }} \right)}^{-0.194}}-5.977} \right] $ | (5) |
当日αb/γ≤1.59时,取fw=0.30.其中,γ为床面糙率,对于平底床面通常取泥沙中值粒径值,由于波浪作用下湖底泥面的沙纹尺度非常小,在此次计算中均取泥沙中值粒径值D50;ab为近底水质点运动的有效振幅.用上述公式对本次试验资料进行计算,3个湖泊4种底泥波浪作用下的起动切应力起动切应力在0.27~ 0.32 N/m2之间,平均值为0.30 N/m2,4种泥样差别不大(表 3),可以看出湖泊底泥的特性具有相同的特征和起动的相似性.不同波高下淤泥冲刷时切应力计算结果如表 4所示,可以看出,在相同的水深和波周期条件下,当底泥起动后,随着波高的增大,水体中含沙量亦逐渐增大,通过计算结果也可以看出水流对底泥冲刷的切应力亦逐渐增大.
| 表 3 波浪作用下淤泥起动切应力 Tab.3 Incipient shear stress of sediment under wave |
| 表 4 波浪作用下淤泥冲刷时的切应力 Tab.4 Scour shear stress of sediment under wave |
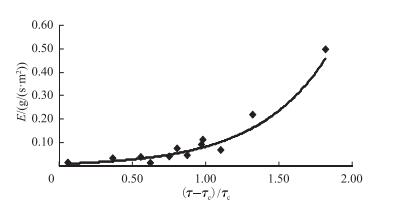
由于输沙率随着波浪作用时间呈递减变化,根据公式
|
图 3 输沙率曲线 Fig.3 Curve of scour rate |
| $ E = 0.0107\exp \left[{2.0676\left( {\frac{{\tau-{\tau _{\rm{c}}}}}{{{\tau _{\rm{c}}}}}} \right)} \right] $ | (6) |
其中指数相关求得随沉积物结构而变的系数E0 =0.0107、α=2.0676.通过天然的水深和波要素可以计算冲刷时切应力,进而计算天然情况下的底泥输沙率(表 5).
| 表 5 波浪作用下底泥的输沙率 Tab.5 Scour rate of sediment under wave |
1) 3个湖泊4个泥样的中值粒径基本在0.01 mm以下,属于黏性细颗粒泥沙范畴.在泥沙特征以及起动、输沙的过程方面具有相似性.
2) 在30 cm水深、波周期为1.0 s条件下,3个湖泊底泥的起动波高介于5.5~7.2 cm之间,平均值为6.5 cm;起动切应力介于0.27~0.32 N/m2之间,平均值为0.30 N/m2.
3) 泥沙起动后,波高越大,泥沙悬浮越强,输沙率越大,水体含沙量沿水深分布自泥沙床面向上逐渐减小.
4) 同样波高作用下,输沙率随着波浪作用时间的延长呈递减的趋势.随着水体含沙量逐渐增大,水流夹带泥沙的能力也有所降低,其强度逐渐减小,然后输沙率达到近似稳定.在已知水深和波要素的条件下可以计算波浪作用下的冲刷切应力,进而根据公式计算输沙率,从而得到大风天时波浪对湖泊床面的侵蚀程度.
| [1] |
Jonsson IG, Wave boundary layer and friction factors. In:Proc. 10th Int Conf Coastal Eng. ASCE, Tokyo, 1966:127-148.
|
| [2] |
窦国仁. 窦国仁论文集. 北京: 中国水利水电出版社, 2003.
|
| [3] |
黄建维. 连云港泥沙静水沉降试验及粘性泥沙沉降特性的探讨. 南京水利科学研究院报告, 1980. |
| [4] |
严恺, 梁其荀. 海洋工程. 北京: 海洋出版社, 2002.
|
| [5] |
王军, 谈光鸣, 舒彩文. 淤积固结条件下粘性细泥沙起动冲刷研究综述. 泥沙研究, 2008(3): 75-80. |
| [6] |
曹叔尤, 杜国翰. 粘性土冲淤的试验研究. 泥沙研究, 1986(4): 73-82. |
| [7] |
罗肇森, 罗勇. 浮泥挟沙力和输沙规律的研究和应用. 南京:南京水利科学研究院报告, 1998. |
| [8] |
张玮, 濮勋, 廖迎娣. 淤泥质海岸近海风电塔基局部冲刷计算研究. 海岸工程, 2010, 28(2): 105-109. |
| [9] |
孙志林, 张翀超, 黄赛花等. 黏性非均匀沙的冲刷. 泥沙研究, 2011(3): 44-48. |
| [10] |
王万杰, 韩龙喜, 孙玉龙等. 京杭运河底泥起动和冲刷率试验研究. 中国农村水利水电, 2007(9): 30-35. |
| [11] |
田小平, 王斌, 陈剑. 乌牛新闸下游冲刷模型试验及经验公式适用性. 水利水电科技进展, 2017, 34(4): 75-78. |
| [12] |
秦伯强. 太湖水环境面临的主要问题、研究动态与初步进展. 湖泊科学, 1998, 10(4): 1-9. DOI:10.18307/1998.0401 |
| [13] |
钱宁, 万兆惠. 泥沙运动力学. 北京: 科学出版杜, 1983.
|
| [14] |
陈润, 王跃奎, 高怡等. 2004~2008年太湖水质变化原因及治理对策. 水电能源科学, 2010, 28(11): 35-37. DOI:10.3969/j.issn.1000-7709.2010.11.012 |
| [15] |
刘伟. 巢湖蓝藻重度发生时的水质特征分析. 中国环境监测, 2007, 23(4): 101-102. |
| [16] |
陈诗越, 吴爱琴, 于兴修. 长江中下游湖泊富营养化过程探析——以龙感湖为例. 临沂师范学院学报, 2004, 26(6): 58-61. |
| [17] |
Sato S, Horikawa K. Sand ripple geometry and sand transport mechanism due to irregular oscillatory flow.Proc. 21st Coastal Eng. Conf., ASCE, 1988, 1748-1762. |
| [18] |
Zhou YR, Chen YP, Ma QN. Threshold of sediment movement in different wave boundary layers. China Ocean Engineering, 2001, 15(4): 50-520. |
| [19] |
Madsen OS, Grant WD. Quantitative description of sediment transport by waves.Proc. 15th Coastal Eng.Conf. ASCE, 1976, 1093-1112. |
 2016, Vol. 28
2016, Vol. 28 
