(2: 天津市水文水资源勘测管理中心, 天津 300060)
(2: Tianjin Municipal Administrative Center of Hydrology and Water Resources, Tianjin 300060, P. R. China)
数字水文学和数字水文模型技术的发展得益于DEM/DTM技术的提出和遥感以及计算机等技术的发展[1].通过DEM地形数据可以便捷地提取出流域边界以及流域内的河网水系.利用遥感地貌数据则能分析出流域土壤植被的空间分布情况.以单元水文理论为基础, 流域空间数据作为支撑的基于DEM的水文模型是当前水文模型发展的方向, 也是水文模拟技术研究的热点[2].基于DEM的水文模型既能反映水文循环的时空变化, 也能模拟自然条件变化以及人类活动对水文循环过程的影响.
国内基于DEM的水文模型研究很多[3-7].栅格新安江模型是基于DEM水文模型的一种[8].栅格新安江模型以栅格为计算单元, 以三水源新安江模型为理论基础, 以地形数据、植被覆盖和土壤类型作为参数空间分析依据.该模型在湿润地区有着理想的应用效果[9-11].本文选取天津于桥水库流域上游的水平口流域作为研究对象.选取流域1978-2012年内的洪水做模拟预报研究, 对模型结构参数率定以及洪水要素的空间变化进行讨论, 探究模型在半湿润地区的适用性.
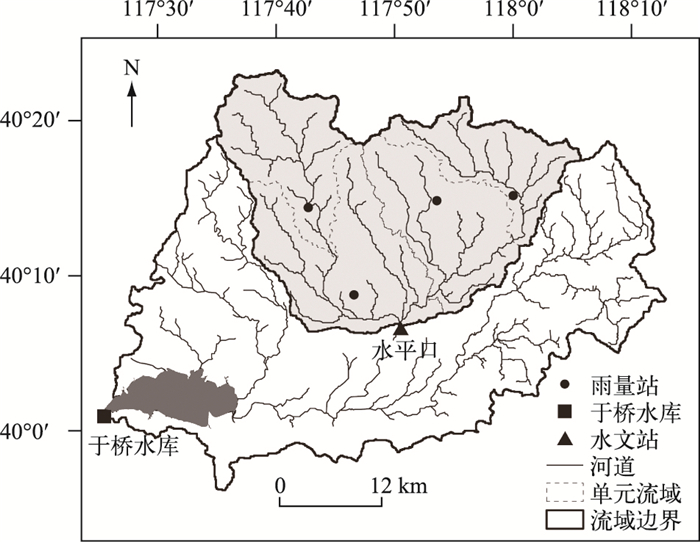
1 流域概况 1.1 自然地理水平口流域(图 1)面积799 km2, 主河道长69.5 km, 平均坡度13.9%.沙河是流域内干流, 呈扇状.河流呈现季节性特征, 上半支在汛期外基本呈干枯断流状态, 下半支常年有水.流域内大部分地处山区、半山区, 流域内海拔高度由北向南递减.现有的森林植被都是天然次生林和人工林, 主要分布在山地丘陵地区.土壤主要是潮褐土.
|
图 1 水平口流域内水系及站点分布 Fig.1 Distribution of rivers and stations in Shuipingkou Basin |
水平口属于暖温带半湿润大陆性季风气候.流域内的雨量集中, 雨热同季.降水年内分布不均, 夏季多达67%~76%.流域内的降水由北向南递减, 多年平均降水为700~750 mm.
1.3 数据资料雨量资料为1978-2012年间遵化等站的逐日降水量和降水量摘录; 蒸发资料为水平口水文站1978-2012年间逐日水面蒸发; 实测日流量资料来自水平口水文站1978-2012年间逐日平均流量和年洪水水文要素摘录.水平口流域上游有大河局、般若院和上关3座水库, 选取这些水库1978-2012年间的放水资料, 模型计算中作为入流处理.
本文使用由美国太空总署(NASA)和国防部国家测绘局(NIMA)提供的90 m×90 m DEM数据, 由美国马里兰大学(UMD)提供的全球1 km精度的植被覆盖数据和由联合国粮农组织(FAO)和维也纳国际应用系统研究所(IIASA)构建的世界土壤数据库(HWSD)提供的1 km精度的土壤类型数据.
2 栅格新安江模型 2.1 原理概念性新安江模型是根据湿润地区的产汇流规律总结提炼出来的流域水文模型.该模型在我国的湿润和半湿润地区广泛应用并取得成功在于其张力水蓄水容量以及自由水蓄水容量频率分布曲线的提出.但是这两条曲线没法直接反演到空间相关位置.因此, 将概念性新安江模型栅格化处理的关键是将概念性模型的频率分布曲线对应到空间栅格点.研究表明, 流域的某些特征要素(如地形曲率等)具有空间频率分布.这为两条频率分布曲线的空间反演提供了基础.
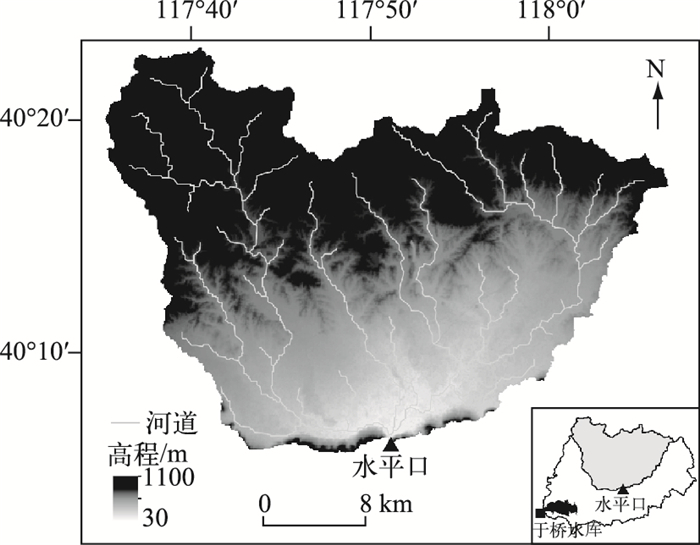
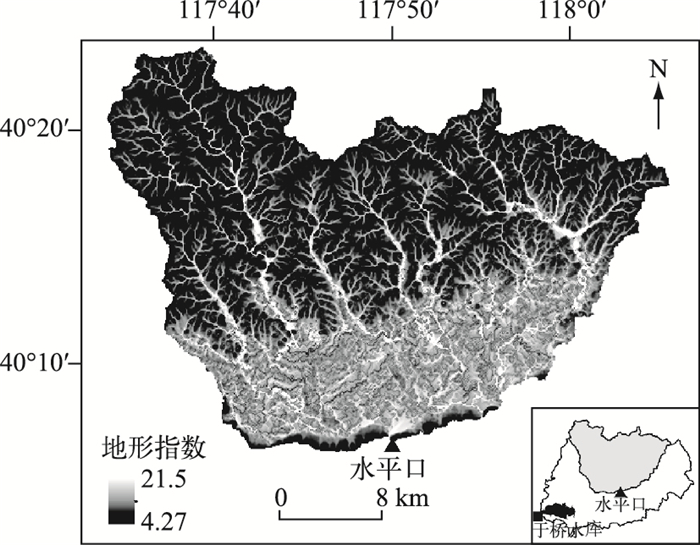
栅格新安江模型选择地形指数来描述两种蓄水容量曲线的分布.地形指数被普遍地用来描述地形和土壤水空间分布的规律以及计算饱和汇流面积[12].对比图 2和图 3, 可以直观地看到河道附近地区的地形指数大多较大, 这些区域的地下水埋深一般较浅, 即缺水量较少; 而在流域的上游以及距离河道较远的山坡地区, 地形指数的值比较小, 一般缺水量较大.这进一步说明了建立地形指数与相关土壤水含水层厚度函数关系式的可行性.
|
图 2 水平口流域的高程 Fig.2 DEM of Shuipingkou Basin |
|
图 3 水平口流域的地形指数空间分布 Fig.3 Distribution of topographic index in Shuipingkou Basin |
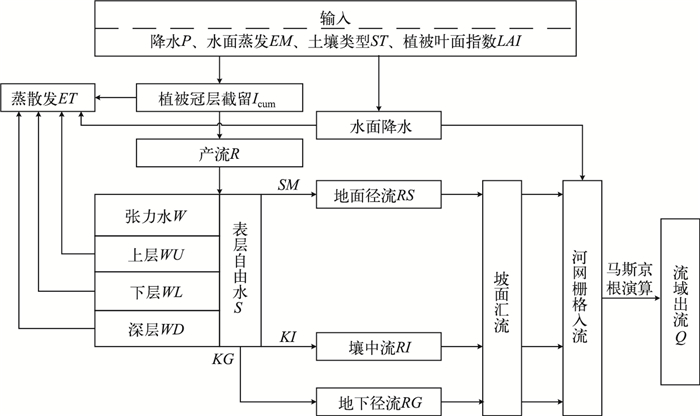
模型的计算是以栅格作为基本计算单元, 并假设栅格内的水文特性以及地形地貌特征是一致的.模型的计算结构如图 4所示, 主要分为截留蒸散发计算、产流分水源计算以及汇流演算3个部分.
|
图 4 模型计算结构 Fig.4 Structure of the model |
模型中的产汇流参数WM、SM、KI和KG是需要获得空间分布的参数.
WM和SM反映的是栅格单元土壤张力水和自由水的蓄水能力[13].依据模型原理中的分析以及土壤水的相关定义建立WM和SM的函数表达式:
| $ WM = \left( {{\theta _{{\rm{fc}}}} - {\theta _{{\rm{wp}}}}} \right) \cdot {L_{\rm{a}}} \cdot TWI $ | (1) |
| $ SM = \left( {{\theta _{\rm{s}}} - {\theta _{{\rm{fc}}}}} \right) \cdot {L_{\rm{h}}} \cdot TWI $ | (2) |
式中, TWI, 即Topographic Wetness Index, 地形指数.θfc、θwp和θs是由栅格内土壤类型确定的土壤特征参数[14], 它们的空间分布是固定的. La和Lh分别表示缺水土壤层的厚度和腐殖质层的厚度, 它们是通过地形指数计算出来的.
KG反映的是基岩和土壤的渗透性, KI反映的是表层土的渗透性[13], 均与栅格内的土壤类型有关, 可以借助土壤的空间分布关系来表示KG和KI的空间分布[15]. KG和KI是并联参数[13], 满足式(3), 其中KG+KI代表出流的快慢, KG/KI代表地下径流和壤中流的比.模型率定计算过程中需要满足结构性约束KG+KI=0.7.符合实际意义, 在每次率定计算后, 都取所有栅格单元的KG+KI均值与0.7做比较, 再调整, 使流域平均KG+KI满足结构性约束.
| $ \left\{ \begin{array}{l} KG + KI = {\left( {\frac{{{\theta _{\rm{s}}}}}{{{\theta _{{\rm{fc}}}}}}} \right)^{OC}}\\ \frac{{KI}}{{KG}} = \frac{{1 + 2\left( {1 - {\theta _{{\rm{wp}}}}} \right)}}{{ROC}} \end{array} \right. $ | (3) |
式中, OC为自由水出水综合影响因子, ROC为自由水出流校正系数.
而模型中汇流参数主要是集总参数.汇流计算中, 日模计算采用线性水库和滞后演算法, 对应单元流域出口栅格t时刻出流为:
| $ {Q^{t + Lag}} = {Q^{t + Lag}} \cdot {C_{{\rm{sch}}}}{\rm{ + }}\left( {\sum\limits_{j = 1}^k {Q_{s, j}^t} + \sum\limits_{j = 1}^k {Q_{i, j}^t} + \sum\limits_{j = 1}^k {Q_{g, j}^t} } \right)\left( {1 - {C_{{\rm{sch}}}}} \right) $ | (4) |
式中, Qs, jt、Qit, j、Qgt, j分别为单元流域内j栅格t时刻的地表、壤中和地下径流; Csch为河网消退系数; Lag为河网汇流滞时.
Csch为线性水库与滞后演算法汇流参数[13], 反映全流域河网的调蓄能力. Csch控制着洪水的坦化程度.
次洪模型采用基于栅格的马斯京根法将3种产流和河道水流演算到流域出口.以地表径流为例, 对应栅格的t时刻出流为:
| $ Q_{i + 1}^{t + 1} = \sum\limits_k {{{\left( {{C_0} \cdot Q_i^t + {C_1} \cdot Q_i^{t + 1} + {C_2} \cdot Q_{i + 1}^t} \right)}_k} + Q_{s, i + 1}^{t + 1}\left( {1 - {f_{{\rm{ch}}}}} \right)} $ | (5) |
式中, fch为栅格地表径流汇入河道的比例.
km和xm是马斯京根法的汇流参数[13].模型中按照径流成分差异分为4组参数. km反映的是栅格间的汇流时间, 根据文献[16], 从河道、地表、壤中到地下, 其取值大小依次减小. xm、kmi、kmg相对不敏感, 主要调试kmch和kms.
3 结果与分析 3.1 参数率定从模型预处理求算出的水平口流域WM和SM空间分布可以很直观地看出来, 越靠近河道的地方, 颜色越深, 表示特征蓄水容量越小(图 5、6).

|
图 5 水平口流域张力水蓄水容量空间分布 Fig.5 Distribution of calculated tension water storage capacity in Shuipingkou Basin |
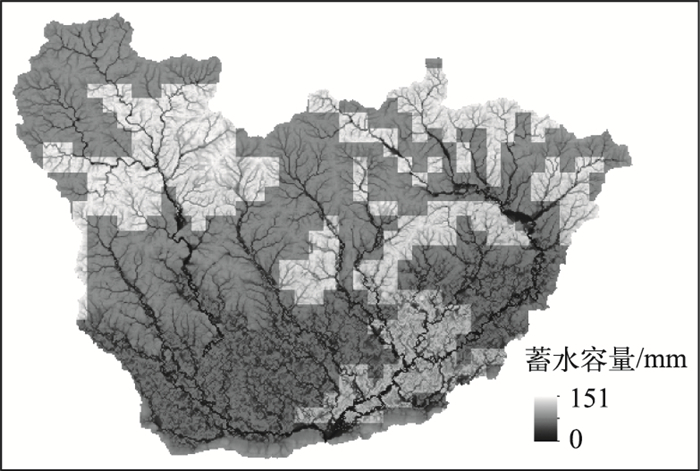
|
图 6 水平口流域自由水蓄水容量空间分布 Fig.6 Distribution of calculated free water storage capacity in Shuipingkou Basin |
率定的模型参数如表 1所示.
| 表 1 模型参数 Tab.1 The model parameters |
选取19782012年间的9场典型洪水进行次洪模型模拟与预报, 其中选定前8场洪水用来模拟率定次洪模型参数, 最后1场用来检验, 结果如表 2所示.
| 表 2 次洪洪水模拟成果统计 Tab.2 The simulation results |
根据GB/T 224822008《水文情报预报规范》可知:模型模拟结果中, 水平口流域的8场洪水, 径流深合格率为87.5%, 洪峰合格率为100%.预报检验的1场洪水径流深和洪峰都合格. 9场次洪无论是径流深误差还是径流量误差都达到了乙等精度要求.总的来说模型对峰大量大的洪水模拟效果要好于峰量偏小的洪水过程.
从检验期20121073013号洪水模拟结果来看, 仍有一定的误差, 初步分析如下:模型流域的下垫面条件如土壤、植被覆盖等随时间的变化没能显式地体现出来.调研发现:随着该地区水资源形势的日益严峻, 区域内的水利工程数量逐年增加.同时, 当地居民修建了大量的水窖和小型拦设施.这些人类活动使得流域的产流量减小, 汇流时间变长, 进而导致次洪模拟预报的洪峰峰值和洪量都偏小.
3.3 产流面积变化分析受流域下垫面的影响, 随着降雨的时空变化, 流域的产流面积不断变化.对流域产流面积变化规律进行研究和定量描述, 对确定流域产流量有重要的意义.传统的概念性新安江模型为分散性结构, 受其根据经验总结提出的蓄水容量分布曲线的局限性只能得出流域出口断面的流量过程, 无法对流域面上具体点或区域的水文过程进行反演和研究.栅格新安江模型在概念性新安江模型的基础上, 显式地构建了栅格单元上蓄水容量与土壤类型、植被覆盖以及地形坡度等下垫面特征的关系, 结合降水过程, 能反映水文过程在时空尺度上的变化.
选取1978080808次洪水过程为例进行分析, 本次洪水的降水空间分布基本均匀. 图 7表示的是这场次洪不同时刻空间各个栅格的蓄水状态, 栅格值越接近1表示栅格越接近蓄满的状态.在降雨初期(图 7a), 流域南部的地势较低的区域以及河道附近随着降雨过程的进行逐渐呈现蓄满的状态.说明这片地区发生洪水灾害的可能性较大, 应该加强巡视.随着降水过程的进行(图 7b), 降水强度的增加, 产流区域面积也在逐渐变大, 最后达到全流域最大的蓄满状态(图 7c), 此时流域的东南大部分地区以及西北的部分地区达到蓄满状态, 发生洪灾的可能性较大.通过图 7可以直观地看出空间栅格不同时刻土壤的蓄水状态, 这对流域内的防洪减灾有一定的参考价值.
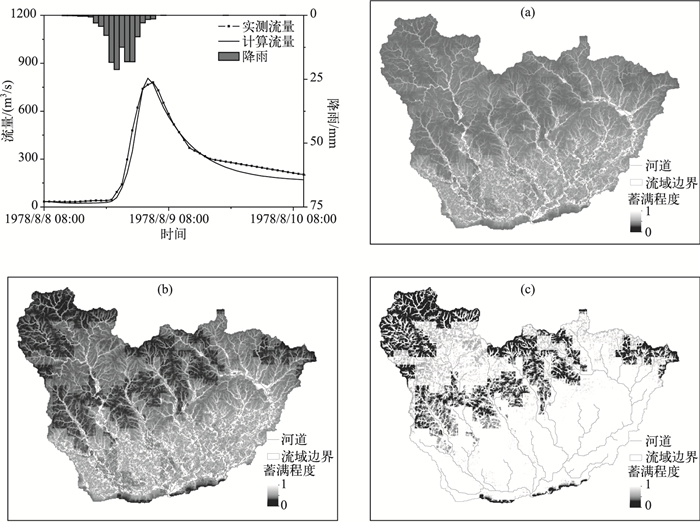
|
图 7 1978080808号洪水降水径流模拟过程和不同时刻栅格蓄水状态空间分布 Fig.7 The result and soil state distribution of No. 1978080808 Flood (a~c表示随着降水的进行, 流域逐渐蓄满的变化过程) |
本文使用栅格新安江模型在于桥水库流域的水平口地区进行应用, 模型较好地反映了产流面积的时空变化, 达到理想的计算精度.初步验证了该模型在半湿润地区的适用性.模型的结构和参数仍然需要进一步的研究和调整来提高模型的适用性、体现流域内人类生活生产活动的影响.总的来说, 栅格新安江模型是水文模型精细化发展的一种趋势, 是传统水文模型理论与地理信息技术结合的产物, 模型除对自身结构参数进行研究调整外, 还需与山坡水文学和地理信息技术研究的最新进展进行跟进.
致谢: 感谢黄鹏年、钟栗、孙如飞师兄对本研究提供的帮助和宝贵建议.| [1] |
Li Zhilin, Zhu Qing. Digital elevation model. Wuhan: Wuhan University Press, 2001. [李志林, 朱庆. 数字高程模型. 武汉: 武汉大学出版社, 2001.]
|
| [2] |
Wang Zhonggen, Liu Changming, Zuo Qiting et al. Constructing distributed hydrological model based on DEM. Progress in Geography, 2002, 21(5): 430-439. [王中根, 刘昌明, 左其亭等. 基于DEM的分布式水文模型构建方法. 地理科学进展, 2002, 21(5): 430-439. DOI:10.11820/dlkxjz.2002.05.004] |
| [3] |
Huang Ping, Zhao Jiguo. Study on watershed distributed hydrological model and its application prospect. Journal of China Hydrology, 1997(5): 5-9. [黄平, 赵吉国. 流域分布型水文数学模型的研究及应用前景展望. 水文, 1997(5): 5-9.] |
| [4] |
Hao Zhenchun, Su fengge. Study on distributed monthly hydrological model and its application in Huaihe River basin. Advances in Water Science, 2000, 11(1): 36-43. [郝振纯, 苏凤阁. 分布式月水文模型研究及其在淮河流域的应用. 水科学进展, 2000, 11(1): 36-43.] |
| [5] |
Liu Zhiyu, Xie Zhenghui. Improvement of the TOPKAPI model and its application in the Huaihe River basin flood simulation study. Journal of China Hydrology, 2003, 23(6): 1-7. [刘志雨, 谢正辉. TOPKAPI模型的改进及其在淮河流域洪水模拟中的应用研究. 水文, 2003, 23(6): 1-7.] |
| [6] |
Xiong Lihua, Guo Shenglian, Tian Xiangrong. Distributed hydrological model based on DEM and its application. Advances in Water Science, 2004, 15(4): 517-520. [熊立华, 郭生练, 田向荣. 基于DEM的分布式流域水文模型及应用. 水科学进展, 2004, 15(4): 517-520.] |
| [7] |
Li ZJ, Zhang K. Comparison of three GIS-based hydrological models. Journal of Hydrologic Engineering, 2008, 13(5): 364-370. DOI:10.1061/(ASCE)1084-0699(2008)13:5(364) |
| [8] |
Yao Cheng.Development and application of grid-based distributed Xinanjiang Model[Dissertation].Nanjing:Hohai University, 2007(in Chinese with English abstract). [姚成. 基于栅格的分布式新安江模型构建与分析[学位论文]. 南京: 河海大学, 2007. ]
|
| [9] |
Yao C, Li Z, Bao H et al. Application of a developed Grid-Xinanjiang model to Chinese watersheds for flood forecasting purpose. Journal of Hydrologic Engineering, 2009, 14(9): 923-934. DOI:10.1061/(ASCE)HE.1943-5584.0000067 |
| [10] |
Yao Cheng, Ji Yiqiu, Li Zhijia et al. Parameter estimation and application of grid-based Xin'anjiang model. Journal of Hohai University (Natural Sciences), 2012, 40(1): 42-47. [姚成, 纪益秋, 李致家等. 栅格型新安江模型的参数估计及应用. 河海大学学报:自然科学版, 2012, 40(1): 42-47.] |
| [11] |
Yao Cheng, Zhang Yuxia, Li Zhijia. Application and comparison of cell-to-cell diffusion wave and Muskingum routing methods. Journal of Hohai University (Natural Sciences), 2013(1): 6-10. [姚成, 章玉霞, 李致家. 扩散波与马斯京根法在栅格汇流演算中的应用比较. 河海大学学报:自然科学版, 2013(1): 6-10.] |
| [12] |
Beven KJ, Kirkby MJ. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d'appel variable de l'hydrologie du bassin versant. Hydrological Sciences Journal, 1979, 24(1): 43-69. DOI:10.1080/02626667909491834 |
| [13] |
Zhao Renjun, Wang Peilan. Study on parameters of Xinanjiang model. Journal of China Hydrology, 1988, 8(6): 2-9. [赵人俊, 王佩兰. 新安江模型参数的分析. 水文, 1988, 8(6): 2-9.] |
| [14] |
Rui Xiaofang. Principles of hydrology. Beijing: China Water&Power Press, 2004. [芮孝芳. 水文学原理. 北京: 中国水利水电出版社, 2004.]
|
| [15] |
Koren VI, Smith M, Wang D et al.Use of soil property data in the derivation of conceptual rainfall-runoff model parameters//15th Conference on Hydrology, Long Beach, American Meteorological Society, Paper.2000.
|
| [16] |
Wu Xianfeng.Research on distributed watershed hydrological model:a case study of Lushi basin in the Yellow River[Dissertation].Beijing:Beijing Normal University, 2003(in Chinese with English abstract). [吴险峰. 分布式流域水文模型研究——黄河小花间卢氏以上流域案例研究[学位论文]. 北京: 北京师范大学, 2003. ]
|
 2016, Vol. 28
2016, Vol. 28 
