(2: 中国科学院水库水环境重点实验室 重庆 400714)
(3: 中国科学院重庆绿色智能技术研究院 重庆 400714)
(4: 中国长江三峡集团公司 北京 100038)
(2: Key Laboratory of Reservoir Water Environment, Chinese Academy of Sciences, Chongqing 400714, P.R.China)
(3: Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing 400714, P.R.China)
(4: China Three Gorges Corporation, Beijing 100038, P.R.China)
目前,水-气界面温室气体通量的监测方法通常有:模型估算法、箱法、微气象法和遥感反演法等[1].而模型估算法作为国际水电协会(IHA)推荐使用的温室气体监测方法之一,因其简单、灵活、易操作等特点在野外现场监测中最为常用,所得成果也不胜枚举,比如Demarty等[2]、Atilla等[3]、Roland等[4]、范成新等[5]分别对加拿大Eastmain水库及湖泊、美国Superior湖、巴西5个水库和我国太湖的温室气体进行监测.
模型估算法的原理是根据空气和水体内气体成分的浓度梯度并运用Fick定律来估算通量[6].想要得到较准确的监测结果,气体在这两种介质中的浓度测定和传质系数的确定就成了最关键的核心.但是浓度和传质系数会严重地受到监测时环境因素如pH值、水温、风速的影响.本文将以三峡库区支流澎溪河水-气界面的温室气体通量(以CO2为例)的实际采样数据为基础,尝试分析模型估算法的可靠性和3个环境参数(pH值、水温和风速)对温室气体扩散通量(以CO2为例)的敏感性.
1 材料与方法 1.1 研究区域与样品采集澎溪河流域(31°00′~31°42′N,107°56′~108°54′E)位于四川盆地东部边缘,流域面积5173 km2,干流全长182.4 km,是三峡库区北岸中段流域面积最大的支流(图 1).该水域在夏季低水位阶段平均水深不足10 m,冬季高水位阶段平均水深将超过40 m,水域物理边界呈现显著的季节性交替特征,澎溪河流域包含了峡谷、消落区以及湖库等各种特征的水域,其在三峡水库中具有代表性.为开展对水-气界面温室气体通量(以CO2为例)的计算,本研究选择澎溪河流域内的温泉、开县、白家溪、养鹿、渠马、高阳、黄石、双江8个研究点位.于2011年1-12月一个完整的丰、枯水期运行阶段开展逐月跟踪观测.采集位置选取在澎溪河中心河面,采样水深为0.5 m,采样时间控制在每月10日的9:30-16:30之间.
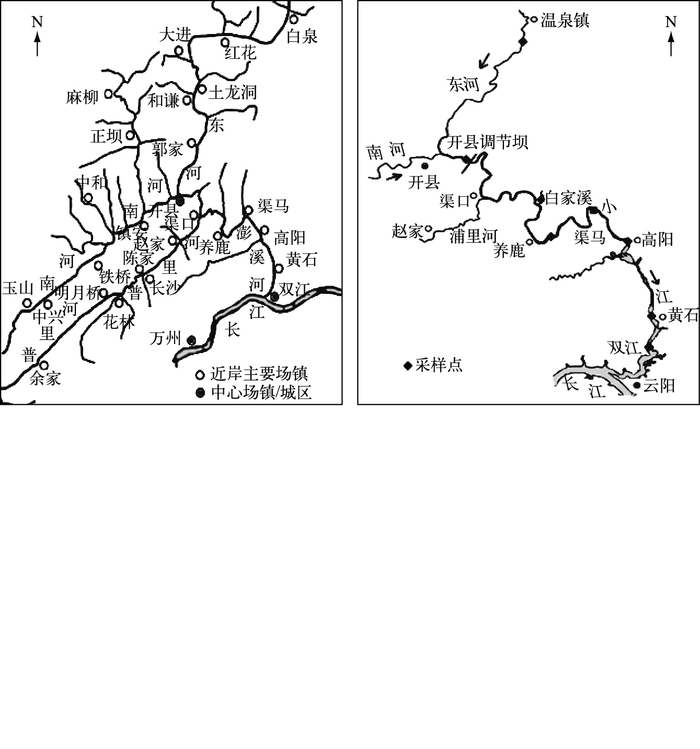
|
图 1 澎溪河流域水系及采样点示意图 Fig.1 Sketch of backwater area and sampling sites in the Pengxi River |
所有数据均录入Excel或Origin软件进行统计分析,采用变异系数CV值表征数据变化幅度.采用YSI®ProODO溶解氧仪现场测定水温(精度0.1℃);采用SMAR®AR-836风速仪现场测量水面上方2 m处的瞬时风速(U2)(精确度0.1 m/s),并通过公式(5)换算成水面上方10 m风速(U10,m/s);采用YSI®63现场测定水体pH值(精度0.01);采用HACH®微量滴定器(精度为1.25 μl)及标准硫酸溶液现场滴定碱度;水体中的二氧化碳分压(pCO2)跟据pH值、碱度及亨利常数计算而得;采用手持式数字大气压计现场测定气温和大气压.
2 水-气界面温室气体模型估算法 2.1 模型估算法的通量计算原理根据Fick定律,对于淡水水体,水-气界面CO2交换通量(正为释放、负为吸收)可由公式(1)计算得出[7]:
| ${F_{{\rm{C}}{{\rm{O}}_2}}} = {k_x}({C_{{\rm{water}}}} - {C_{{\rm{air}}}})$ | (1) |
式中,FCO2为水-气界面CO2扩散通量(mmol/(m2·h));kx为CO2传质系数(cm/h);Cwater为CO2在水中的浓度(mmol/L);Cair为现场温度及压力下CO2气体在水中的饱和浓度(mmol/L).
对于传质系数kx的估算,目前通用的2种模型分别是薄边界层模型(TBL)和表面更新模型(SRM). TBL模型是假定气体转移是由水表面的薄边界层控制的水-气界面的浓度与大气中气体浓度形成溶解平衡;而SRM模型是假定水面漩涡可取代水表面薄层,且取代速度决定于水的被搅动程度.针对湖泊、水库生态系统的研究,目前世界范围内对kx系数的确定绝大多数采用的是1989年Jähne等[8]和1998年Cole等建立的经验公式[9-11]:
| ${k_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = {k_{600}}{\left( {\frac{{600}}{{Sc}}} \right)^{0.67}}$ | (2) |
| ${k_{600}} = 2.07 + 0.215U_{10}^{1.7}$ | (3) |
| $Sc\left( {{\rm{C}}{{\rm{O}}_2}} \right) = 1911.1 - 118.11t + 3.4527{t^2} - 0.04132{t^3}$ | (4) |
| ${U_{10}} = {U_z}\left[ {1 + \frac{{{{\left( {{C_{{\rm{d}}10}}} \right)}^{1/2}}}}{\kappa }{\rm{ln}}\left( {\frac{{10}}{z}} \right)} \right]$ | (5) |
式中,k600为六氟化硫(SF6)气体的交换系数(cm/h);Sc为t℃下CO2的Schmidt常数;U10为水面上方10 m处风速(m/s);t为温度(℃);z为测量风速时的高度(m);Uz为高度z时的风速大小(m/s);Cd10为10 m时的阻力系数,取0.0013;κ为Von Karman常数,取0.41.
对水中CO2浓度的确定采用水化学平衡法,即通过测定水样中溶解性无机碳(DIC)浓度或碱度、pH值及水温求得水中CO2浓度[12].水体中DIC由CO2、H2CO3、HCO3-和CO32-组成,平衡时各组份在水溶液中的浓度主要与pH值、水温和水中离子强度(I)有关.假设淡水系统中离子强度I=1,根据CO2在水溶液中的碳酸平衡原理:
| ${\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_{\rm{2}}}{\rm{O}} \leftrightarrow {{\rm{H}}_{\rm{2}}}{\rm{CO}}_3^* \leftrightarrow {{\rm{H}}^{\rm{ + }}}{\rm{ + HCO}}_3^ - \leftrightarrow 2{{\rm{H}}^ + } + {\rm{CO}}_3^{2 - }$ | (6) |
计算水溶液中CO2浓度:
| $c{\left( {{\rm{C}}{{\rm{O}}_2}} \right)_{{\rm{water}}}} = \frac{{c\left( {{{\rm{H}}^ + }} \right) \cdot c\left( {{\rm{HCO}}_3^ - } \right)}}{{{K_1}}}$ | (7) |
| $c{\left( {{\rm{C}}{{\rm{O}}_2}} \right)_{{\rm{water}}}} = \frac{{{\rm{DIC}}}}{{1 + \frac{{{K_1}}}{{c\left( {{{\rm{H}}^ + }} \right)}} + \frac{{{K_1} \cdot {K_2}}}{{c{{\left( {{{\rm{H}}^ + }} \right)}^2}}}}}$ | (8) |
式中,c(CO2)water为水中CO2浓度(mmol/L);K1、K2为平衡常数;c(H+)和c(HCO3-)分别为水中H+和HCO3-浓度(mmol/L);DIC为水中溶解性无机碳浓度(mmol/L).
通常K1、K2计算公式[13]为:
| $p{K_1} = - 6320.813/{T_K} - 19.569224{\rm{ln}}{T_K} + 126.34048$ | (9) |
| $p{K_2} = - 5143.692/{T_K} - 14.613358{\rm{ln}}{T_K} + 90.18333$ | (10) |
式中,T为采样时的水温(℃).
2.2 技术路线图模型估算法的实施技术路线如图 2所示.
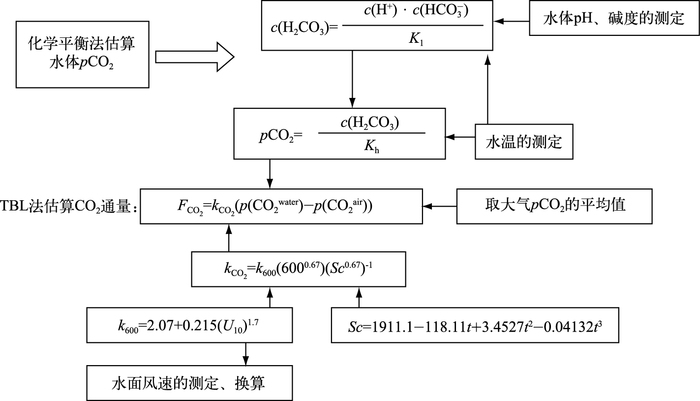
|
图 2 模型估算法(水化学平衡)计算示意 Fig.2 Process of model calculated method (water chemical equilibrium) |
Morris筛选法为目前应用较广的一种局部灵敏度分析方法[14]. Morris筛选法选取模型其中一变量xi,其余参数值固定不变,在变量阈值范围内随机改变xi,运行模型得到目标函数y(x)=y(x1、x2、x3、…、xn)的值,用影响值ei判断参数变化对输出值的影响程度[15],公式为:
| ${e_i} = \left( {{y^*} - y} \right)/{\Delta _i}$ | (11) |
式中,y*为参数变化后的输出值;y为参数变化前的输出值;Δi为参数i的变幅.
修正的Morris筛选法采用自变量以固定步长变化,灵敏度判别因子取Morris多个平均值[16],公式为:
| ${S_i} = \sum\limits_{i = 0}^{n - 1} {\frac{{\left( {{Y_{i + 1}} - {Y_i}} \right)/{Y_0}}}{{({P_{i + 1}} - {P_i})/100}}} /\left( {n - 1} \right)$ | (12) |
式中,Si为灵敏度判别因子;Yi为模型第i次运行输出值;Yi+1为模型第i+1次运行输出值;Y0为参数率定后计算结果初始值;Pi为第i次模型运算参数值相对于率定参数后参数值变化的百分率;Pi+1为第i+1次模型运算参数值相对于率定后初始参数值的变化百分率;n为模型运行次数.
3.2 参数敏感度分级参照已有文献[17]对参数局部灵敏度的分级,进行灵敏度分析说明(表 1).
| 表 1 参数敏感度分级[17] Tab.1 Sensitivity classes |
在模型估算法的基础上,对澎溪河流域从上游到下游8个点位(温泉、高阳、双江等)的水-气界面CO2扩散通量进行计算,结果见表 2.
| 表 2 研究期间澎溪河流域的水-气界面CO2扩散通量 Tab.2 CO2 diffusion flux of water-air interface in Pengxi River during the study period |
由于CO2扩散通量、pH、水温、风速的量纲不同,所以用CV来表征全年数据组的离散程度.由表 2可知,澎溪河上、中、下游8个监测点位3组现场指标中pH的CV最小,CV均呈现出pH<水温<风速的趋势,pH值的变化对CO2扩散通量变化影响最大.
纵向比较各个点位的全年监测结果(表 2)发现,位于上游的温泉点位CO2扩散通量、pH和水温的CV值均最小;位于下游的双江点位CO2扩散通量和pH的CV值均最大. pH值的变化与CO2扩散通量的变化保持一致.在白家溪点位,水温和风速的CV值同时达到最大,而该点位CO2与pH的CV值处于较大值位置,说明pH值、水温和风速都对CO2扩散通量变化产生了影响,但当水温和风速的变化幅度最大时,CO2扩散通量变化未达到最大值,CO2扩散通量的CV值未达到最大.
这表明在澎溪河流域内,pH、水温、风速均能对CO2扩散通量产生较大影响,并且pH值对CO2扩散通量影响最大. pH值是高灵敏参数,风速和水温是灵敏参数.
澎溪河上游温泉-开县段分别布设了温泉和开县两个点位.两个点位全年的水-气界面CO2通量释放量大于吸收量.温泉点位全年CO2通量呈现释放态,而开县点位也仅在10月份时呈现吸收态,吸收值为0.654 mmol/(m2·h).其余月份均呈现释放态.温泉点位全年CO2释放通量均值为6.226 mmol/(m2·h);最大值出现在3月,为11.733 mmol/(m2·h);最小值出现在2月,为0.837 mmol/(m2·h).而开县点位的释放通量最大值出现在2月,为19.057 mmol/(m2·h).纵观全年,上游点位CO2释放通量枯水期大于丰水期,在冬季高水位时期(枯水期),CO2释放维持在一个较高的水平(图 3).

|
图 3 研究期间澎溪河流域水-气界面CO2扩散通量的变化趋势 Fig.3 Trend of CO2 diffusion flux of water-air interface in Pengxi River during the study period |
在澎溪河流域中游的白家溪-养鹿区段分别布设了白家溪、养鹿、渠马点位.冬季高水位时期3个点位的CO2释放量较大,养鹿和白家溪点位在12月CO2释放量达到最大值,分别为21.548和14.954 mmol/(m2·h).渠马点位的全年CO2释放通量范围为-1.741~7.178 mmol/(m2·h).这3个点位在3、4、5、8、10月的CO2释放通量呈现吸收态,其余月份均为释放态,且全年的水-气界面CO2释放通量均大于吸收通量. 3-5月时,CO2释放/吸收通量一直维持在一个较低水平;进入夏季以后,6-10月CO2释放量起伏较大,由吸收态逐渐变为释放态,并呈折线上升状态;进入冬季以后,CO2释放量上升较快,一直到达全年最高释放量(图 3).
在澎溪河下游的高阳-双江区段布设了高阳、黄石、双江3个监测点位.全年的水-气界面CO2通量呈现释放态,但释放通量小于中上游监测点位. 3个点位的全年变化趋势较为一致.在春季,CO2释放通量逐渐降低,变为吸收态;在3-8月之间,CO2释放/吸收通量呈现出折线上升的状态;进入冬季以后,CO2释放通量逐渐增大,并保持在一个较高的水平(图 3).
综上所述,在研究区域内,从上游到下游8个点位的水-气界面CO2扩散通量全年变化趋势基本一致,均呈现出3-5月CO2释放/吸收通量较低,6-10月呈现较大波动,折线上升状态. 11-12月的CO2释放通量直线上升,呈现高释放通量状态.全年的CO2的释放量大于吸收量.
4.2 模型估算法的敏感性分析本研究选取水温、风速和pH值作为模型估算法的局部敏感性分析变量.依据本次实验监测的计算结果和多年积累的三峡库区支流澎溪河历年环境指标,确定相关参数及其取值范围(表 3).
| 表 3 模型估算法(水化学平衡)主要参数、取值范围及其初始值 Tab.3 Major parameters and their initial values |
采用修正的Morris筛选法对三峡库区支流澎溪河某次采样时CO2扩散通量的局部敏感性分析结果进行定量表达,以5%为固定步长对水温值和风速值进行扰动.因为pH<7.5时无法使用此方法计算,因此pH以1%为固定步长进行扰动.分别取其值的-20%(-4%)、-15%(-3%)、-10%(-2%)、-5%(-1%)、5%(1%)、10%(2%)、15%(3%)和20%(4%),而其他参数值固定不变,观测CO2扩散通量对这些环境参数的敏感度.结果表明,水温与CO2扩散通量呈正相关,且在靠近0点时出现较大的拐点(图 4a);风速与CO2扩散通量呈正相关(图 4b);pH值与CO2扩散通量呈负相关,该参数系数越大,CO2扩散通量越小,且变化量逐渐减小(图 4c).
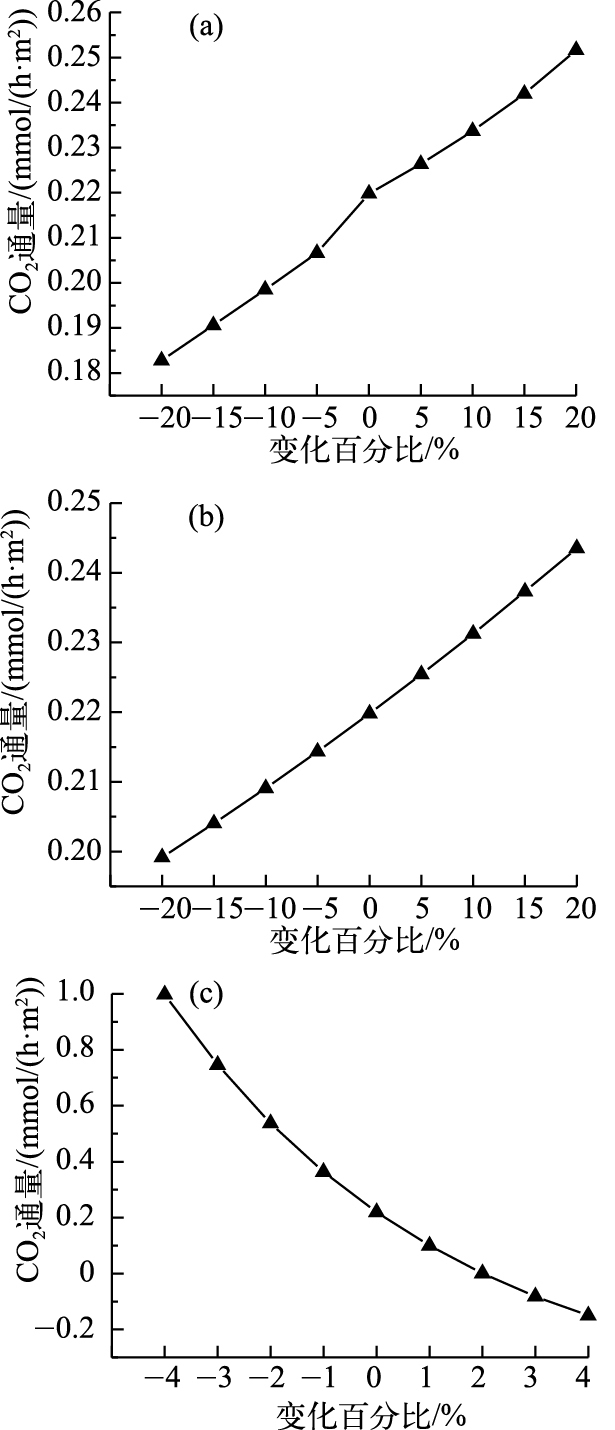
|
图 4 水温(a)、风速(b)和pH值(c)对结果的影响 Fig.4 Effect of results: water temperature (a), wind velocity (b) and pH (c) |
经过修正的Morris筛选法计算得出水温、风速和pH值的CO2扩散通量灵敏度分别为0.783、0.504和-20.614,并且绘制了不同参数组合的灵敏度分布三角图(图 5). 3个参数中pH值是最敏感的参数,其|Si|=20.614≥1为高灵敏参数;水温和风速敏感因子分别为0.783和0.504,均落在了0.2≤|Si|<1区间内,属于灵敏参数.这说明水温、风速和pH值均会对CO2扩散通量的结果产生较大的影响,这对现场水温、风速和pH值的监测提出了更为精确的要求.
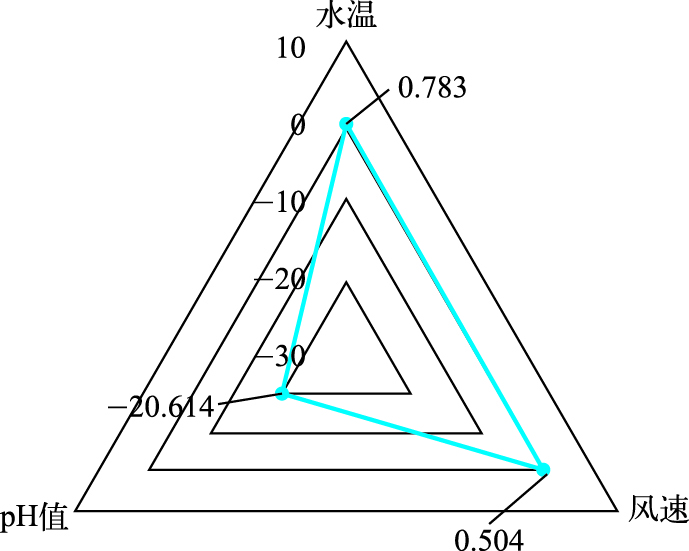
|
图 5 灵敏度参数分布 Fig.5 Sensitivity analysis of the parameters |
上述敏感性分析结果是将模型估算法计算水-气界面CO2扩散通量的过程认作一个整体,但是根据其计算原理也可以将模型估算法计算水-气界面CO2扩散通量划分为两个相对独立的计算模型:一个是根据水中的DIC计算其分压pCO2,它主要受到pH和水温这两个环境参数的影响;另一个模型则是根据前者所计算得到的pCO2来推算CO2扩散通量情况,它主要受到水温和10 m风速的影响.分别对这两个模型进行环境参数敏感性的分析,以此来验证两种方法的结果是否一致.
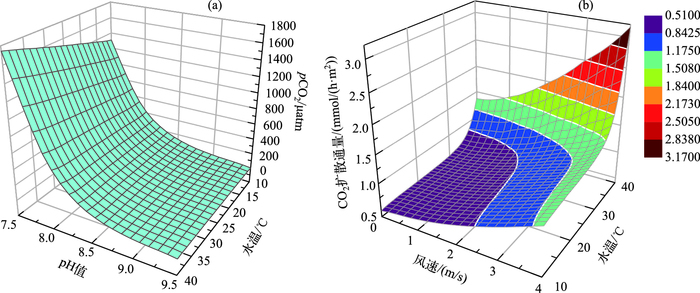
假设水体离子强度为1,参考本次水-气界面CO2扩散通量监测的研究结果和澎溪河历年环境参数的变化范围,取pH值的变化范围为7.5~9.5,水温的变化范围为10~40℃,根据第1部分模型估算通量法的公式(6)~(10)进行计算.结果表明,pH值对计算结果的影响是曲线,而水温的影响则是直线,pH值变化对pCO2的影响要大于水温(图 6a).可见利用模型估算法(水化学平衡法)来计算水中pCO2时,pH对计算结果的敏感性最大,其次为水温.因此,水体pH的监测准确度是直接导致pCO2计算误差的主要原因.为了最大限度避免测量pH产生的误差,除了需要现场测量外,每次采样前都应该对pH仪器进行校正.
|
图 6 不同环境参数下水体pCO2(a)和CO2扩散通量(b)的变化情况 Fig.6 Changes of pCO2 (a) and CO2 diffusion flux(b) in different environment parameters |
在对第2个模型进行敏感性分析时,非环境参数水体中pCO2取全年平均值1061 μatm,大气中pCO2由于常年变化较小,根据联合国政府间气候变化专门委员会(IPCC)的研究,取IPCC参考值379 μatm;环境参数水温的变化范围为10~40℃,10 m风速的变化范围为0~4 m/s.根据第1部分模型估算通量法的公式(1)~(5)进行计算.结果表明,当水温<30℃,表层水体与大气中CO2的分压差保持一定时,风速对水-气界面CO2扩散通量的影响要大于水温,10 m风速每提高1 m/s,其CO2的扩散通量便呈指数增长;而当水温超过30℃时,温度对扩散通量的影响作用逐渐增大,其拐点大约在35~36℃之间.当达到40℃时,由于气体溶解度的急剧下降,水温代替风速成为影响CO2扩散通量的主要因素(图 6b).
在实际监测过程中,由于三峡库区澎溪河全年水温的变化幅度不大,且在监测过程不易被干扰,因此水温的精确性容易得到保证.但是在现场监测风速时,由于风速的易变性和不确定性,就增加了CO2扩散通量监测的难度和不确定性.对于pH值的监测,由于其敏感因子比水温和风速高出30~40倍,因此其精确性要求更高.根据多年累积资料可得,三峡澎溪河地区全年pH平均值为8.06±0.36,为了保证CO2扩散通量计算的准确性,pH值的测量误差应当保证在±0.08以下,这样才会使得最后的计算结果误差不会超过0.1 mmol/(h·m2).因此,除了现场测量外,每次采样前都应该对pH仪器进行校正.而当水体pH<7.5时,就不适合用模型估算法(水化学平衡法)来进行CO2扩散通量的计算了.
| [1] |
Zhao Yan, Zeng Yuan, Wu Bingfang et al. Review of methods for measuring greenhouse gas flux from the air-water interface of reservoirs. Advances in Water Science, 2011, 22(1): 135-146. [赵炎, 曾源, 吴炳方等. 水库水气界面温室气体通量监测方法综述. 水科学进展, 2011, 22(1): 135-146.] |
| [2] |
Demarty M, Bastien J, Tremblay A. Annual follow-up of gross diffusive carbon dioxide and methane emissions from a boreal reservoir and two nearby lakes in Québec, Canada. Biogeosciences, 2011, 8: 41-53. DOI:10.5194/bg-8-41-2011 |
| [3] |
Atilla N, McKinley G, Bennington V et al. Observed variability of Lake Superior pCO2. Limnology and Oceanography, 2011, 56(3): 775-786. DOI:10.4319/lo.2011.56.3.0775 |
| [4] |
Roland F, Vidal L, Pacheco F et al. Variability of carbon dioxide flux from tropical (Cerrado) hydroelectric reservoirs. Aquatic Sciences, 2010, 72: 283-293. DOI:10.1007/s00027-010-0140-0 |
| [5] |
Fan Chengxin, Hu Weiping, Phillip W et al. Carbon dioxide partial pressure and carbon fluxes of air-water interface in Taihu Lake, China. Chinese Journal of Oceanology and Limnology, 2005, 23(1): 29-38. DOI:10.1007/BF02845140 |
| [6] |
Gelbrecht J, Fait M, Dittrich M et al. Use of GC and equilibrium calculations of CO2 saturation index to indicate whether freshwater bodier in north-eastern Germany are net sources or sinks for atmospheric CO2. Fresenius' Journal of Analytical Chemistry, 1998, 361: 47-53. DOI:10.1007/s002160050832 |
| [7] |
Trfmbly A, Varflvy I, Rochm C et al. Greenhouse gas emissions fluxes and processes hydroelectric reservoirs and natural environments. New York: Springer, 2005, 725-732.
|
| [8] |
Jähne B, Libner P, Fischer R et al. Investigating the transfer processes across the free aqueous viscous boundary layer by the controlled flux method. Tellus B, 1989, 41B: 177-195. DOI:10.1111/teb.1989.41B.issue-2 |
| [9] |
Cole JJ, Caraco NF. Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by addition of SF6. Limnology and Oceanography, 1998, 43: 647-656. DOI:10.4319/lo.1998.43.4.0647 |
| [10] |
Roehm CL, Prairie YT, Giorgio PA. The pCO2 dynamics in lakes in the boreal region of northern Québec, Canada. Global Biogeochem Cycles, 2009, 23: GB3013. |
| [11] |
Sibgh S, Bhatti TS, Kothari DP. Wind power estimation using artificial neural network. J Energy Eng, 2007, 133: 46-52. DOI:10.1061/(ASCE)0733-9402(2007)133:1(46) |
| [12] |
Worrall F, Lancaster A. The release of CO2 from riverwaters-the contribution of excess CO2 from groundwater. Biogeochemistry, 2005, 76: 299-317. DOI:10.1007/s10533-005-6449-4 |
| [13] |
Sobek S, Tranvik LJ, Cole JJ. Temperature independence of carbon dioxide supersaturation in global lakes. Global Biogeochem Cycles, 2005, 19: GB2003. |
| [14] |
Francos A. Sensitivity analysis of distributed environmental simulation models: Understanding the model behavior in hydrological studies at the catchment scale. Reliability Engineering and System Safty, 2003, 79(2): 205-218. DOI:10.1016/S0951-8320(02)00231-4 |
| [15] |
Zador J, Zsely IG, Turanyi T. Local and global uncertainty analysis of complex chemical kinetic systems. Reliability Engineering System Safety, 2006, 91: 1232-1240. DOI:10.1016/j.ress.2005.11.020 |
| [16] |
Hao Fanghua, Ren Xiyan, Zhang Xuesong et al. Uncertain affecting factor of the non-point source pollution load. China Environmental Science, 2004, 24(3): 270-274. [郝芳华, 任希岩, 张雪松等. 洛河流域非点源污染负荷不确定性的影响因素. 中国环境科学, 2004, 24(3): 270-274.] |
| [17] |
Lenhart L, Eckhardt K, Fohrer N et al. Comparison of two different approaches of sensitivity analysis. Physics and Chemistry of the Earth, 2002, 27: 645-654. DOI:10.1016/S1474-7065(02)00049-9 |
 2017, Vol. 29
2017, Vol. 29 

