(2: 河海大学水安全与水科学协同创新中心 南京 210098)
(2: National Cooperative Innovation Center for Water Safety & Hydro-Science of Hohai Universtiy, Nanjing 210098, P.R.China)
在我国,山区中小河流数量众多,沿岸水土条件好、耕地多、人口密集,且绝大多数山区中小河流都位于无资料地区,未得到系统的治理,防洪能力普遍偏低.每到汛期,便会出现洪涝灾害,严重威胁人民群众的生命和财产安全.兴建防洪设施不是一朝一夕的工程,所以提高山区中小河流预报精度是当务之急.其中,准确地预测流域洪峰滞时更具有实用意义,可为防洪时疏散群众、转移财产提供重要参考.
目前国内外关于洪峰滞时的研究较多,Talei等把洪峰滞时作为选择降雨径流模型特定洪水事件的依据[1-2]. Banasik等指出洪峰滞时对确定瞬时单位线中的峰现时间和峰值有重要意义[3]. Leopold、Hood、Kang等对比不同的城市化程度,分析了洪峰滞时的变化[4-6].周敏敏等比较了土地利用变化前后流域平均滞时的变化,并分析了滞时与净流深和洪峰流量的相关关系[7].
然而,无资料地区缺少可靠的实测数据,无法直接算出每场洪水的洪峰滞时.近年来,得益于GIS技术与计算机能力快速发展,利用数字高程模型(DEM)进行流域数字化和提取流域地貌特征的方法已得到广泛研究[8-9].加强分析地貌特征,有助于明确流域水文过程中各类参数的物理意义,对无资料地区进行水文参数移植及开展水文模拟和预报具有一定的借鉴意义[10].而流域地貌特征对流域水文过程影响的研究主要集中在产汇流[11]、降雨径流关系[12]、产沙特性[13-15]、产污特性和水质[15]等方面,但流域地貌特征对滞时的影响研究却并不多见. Jeong等[16]研究了韩国锦江流域的洪峰滞时与流域特征的相关关系,并给出了一个多元线性回归方程.这是国际上较早的定量分析滞时与流域特征的研究.但其仅选取流域面积、流域长度、流域坡度等8个流域特征进行多元线性回归分析,考虑并不周到.
鉴此,本文选取皖南山区和大别山区27个中小流域,基于DEM从流域系统和土地覆被两个方面定量描述流域地貌格局特征,运用相关、回归、通径分析等方法,分析地貌格局对流域平均洪峰滞时的影响.尝试将此定量关系移用至无资料地区,间接得出目标流域的平均洪峰滞时.
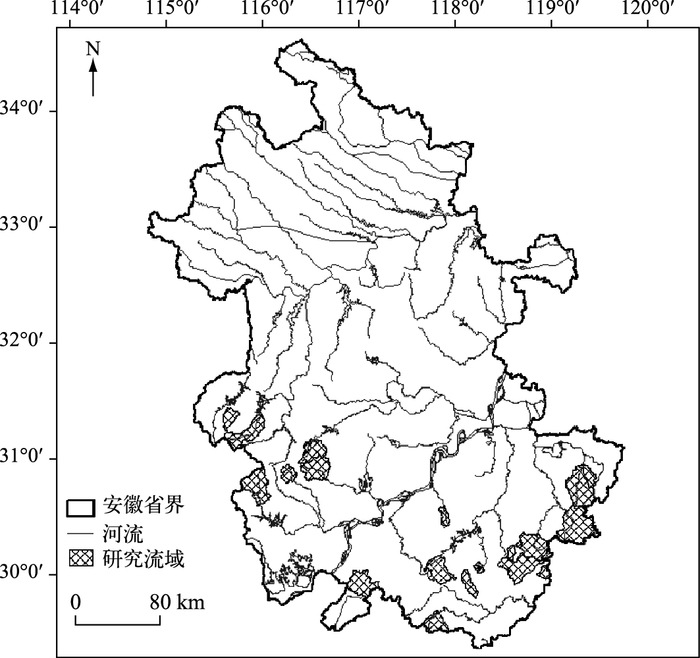
1 研究概况 1.1 研究区域概况本研究区域(29.5°~31.5°N,115.6°~119.5°E)包括皖南山区及大别山区(图 1).其中皖南山区地形以山地丘陵为主,主要地区属于长江流域;大别山区为江淮分水带,主要属于淮河流域.在两块山区中共选取黄尾河、呈村等27个独立的中小流域进行研究,各流域均位于河流上游山区,属自然闭合流域,没有受到水库等水工建筑影响.
|
图 1 研究区27个流域分布 Fig.1 Distribution of 27 basins in study area |
皖南山区属于亚热带湿润地区,年平均气温16℃左右,一年中日平均气温≥10℃的积温为4800~5200℃,气候温暖湿润,进入雨季后,由于地形抬升对降雨影响较明显,山区降水量在1200 mm以上,为安徽省的多雨地区.该区气候随季节变化大,水资源分布不均匀,多暴雨,常发生洪涝灾害、干旱和地温冻害.
大别山区地处亚热带, 年平均气温14~16℃,一年中日平均气温≥0℃的积温为5200℃,日平均气温≥10℃的积温为4700~4900℃,无霜期210~240 d,降雨量在1200 mm以上,山区降水一般随高度增加而增加,大别山区是全省的降雨中心,降雨量的季节和年际变化较大,常有洪涝干旱灾害发生.
1.2 地形地貌因子和地表覆盖类型提取本文在Coffman等[17]研究成果的基础上,将流域地貌指标分为两组(表 1).一组与流域系统相关,包括形状特征及结构特征两类;另一组与土地覆被相关,以各类土地利用类型所占比例表示.
| 表 1 流域地貌格局分类体系 Tab.1 Classification system for watershed topography |
提取地形地貌因子的DEM数据(来源于中国科学院计算机网络信息中心国际科学数据镜像网站)精度为90 m×90 m,数据采集时间为2000年;LandCover数据(来源于国家基础地理信息中心)精度为30 m×30 m,数据采集时间为2010年.应用ArcGIS10.1软件提取各项指标[18],其中整个流域下垫面信息提取基于Arc HydroTools来实现,处理步骤包括数据格式转换、提取水系河网、划分子流域边界等.河网分级采用Horton-Strahler分级系统[19].流域的部分主要参数见表 2.
| 表 2 各流域主要地貌参数 Tab.2 Primary topography parameters of 27 basins |
定义洪峰滞时为流域内最大实测降雨到出口断面洪峰之间的时间间隔[20].它反映了流域洪水响应过程的快慢,与流域地貌格局密切相关.考虑到系列的连续性、代表性和时间序列的统一性,本文在研究区域内选取黄尾河等27个流域1967-2010年的实测流量、雨量资料,均处理成Δt = 1 h的时段数据.采用泰森多边形法计算流域面平均雨量;流量资料为各水文站的实测资料.计算各流域多场单峰洪水的洪峰滞时,取其算术平均,从而得到各流域平均洪峰滞时(Tp),计算结果如表 3所示.
| 表 3 流域平均洪峰滞时计算结果 Tab.3 The average peak lag time of 27 basins |
回归分析是确定两种或两种以上变量间相互依赖定量关系的一种统计分析方法.它基于观测数据建立变量间适当的依赖关系,以分析数据内在规律,并可用于预报、控制等问题.回归模型一般形式为:
| $Y = {\beta _0} + {\beta _1} \cdot {X_1} + {\beta _2} \cdot {X_2} + \cdots + {\beta _m} \cdot {X_m} + u$ | (1) |
应变量Y可以近似地表示为自变量X1、X2、…、Xm的线性函数. β0为常数项,β1、β2、…、βm为偏回归系数,表示在其他自变量保持不变时,Xj增加或减少一个单位时Y的平均变化量,u为随机误差(残差)[22].
基于前人建立经验公式的合理性[23],本文在回归模型一般形式的基础上稍作改动:
| ${\rm{ln}}Y = {\rm{ln}}{\beta _0} + {\beta _1} \cdot {\rm{ln}}{X_1} + {\beta _2} \cdot {\rm{ln}}{X_2} + \cdots + {\beta _m} \cdot {\rm{ln}}{X_m} + u$ | (2) |
变形后为:
| $Y = {{\rm{e}}^{{\beta _0}}} \cdot X_1^{{\beta _1}} \cdot X_1^{{\beta _2}} \cdots X_m^{{\beta _m}} \cdot u\prime $ | (3) |
式中,应变量Y可以近似地表示为自变量X1、X2、…、Xm幂次乘积形式.所以本文在进行多元回归分析之前,对所有数据进行对数化处理.
2.1.1 相关分析先对27个流域的流域系统各格局因子与平均洪峰滞时进行相关分析.结果表明,流域长度、面积、周长3个形状特征以及河网密度、细度比两个结构特征与平均洪峰滞时的正相关性显著;河道维持常数、流域平均坡度、流域相对高差、地形粗糙度、结构比与平均洪峰滞时的负相关性显著;而伸长比、粗糙数等常用水文参数与平均洪峰滞时的相关性并不显著(表 4).因此,可将流域长度、面积、周长、圆度比等形状特征因子和河道维持常数、流域平均坡度、细度比、河网密度等结构特征因子与平均洪峰滞时做回归分析.考虑到流域的土地覆被情况也作用于流域洪水响应过程,对洪峰滞时造成一定影响, 进一步加入森林、草地、耕地、水体、城市用地等土地利用因子做回归分析.
| 表 4 流域系统形态结构特征指标与平均洪峰滞时的相关性 Tab.4 Correlation coefficients between average peak lag time and pattern factors in watershed system |
为便于做多元线性回归分析,将自变量、因变量数值均取ln值以满足公式(2).从而令变量之间具有线性关系,这是进行线性回归分析的前提.除了线性关系,进行多元线性回归分析还需要其他3个假设:
1) 独立性:自变量不能有多重共线性;
2) 正态性:自变量任意线性组合,残差服从正态分布;
3) 方差齐性:自变量任意线性组合,因变量方差不变,残差齐性.
为了满足独立性要求,本文采用的变量筛选方法为逐步回归.逐步回归的基本思想是将变量逐个引入模型,每引入一个解释变量后都要进行F检验,并对已经选入的解释变量逐个进行t检验,当原来引入的解释变量由于后面解释变量的引入变得不再显著时,将其删除.这是一个反复的过程,直到既没有显著的解释变量选入回归方程,也没用不显著的解释变量从回归方程中剔除为止.依据上述思想,可利用逐步回归筛选并剔除引起多重共线性的变量.关于正态性和方差齐性的假设,则在回归分析之后进行检验.
运用逐步回归法(Alpha=0.05,n=27)在满足模型独立性条件下,最终确定影响平均洪峰滞时的主导因子,并计算出多元线性回归方程各因子的系数.
决定系数(R2)代表回归方程对因变量的解释程度.该模型R2=0.734,表明该回归模型能解释因变量接近75%的变差.
标准系数可以反映自变量对因变量的影响程度. 表 5中同时给出了自变量多重共线性的检验,其中VIF是方差膨胀因子,刻画了相比多重共线性不存在时方差增大数值,一般VIF>10,即认为存在多重共线性.从表 5可见,各自变量VIF<10,故认为该回归模型不存在多重共线性的问题.此外,容差是VIF的倒数.
| 表 5 系数 Tab.5 Coefficient |
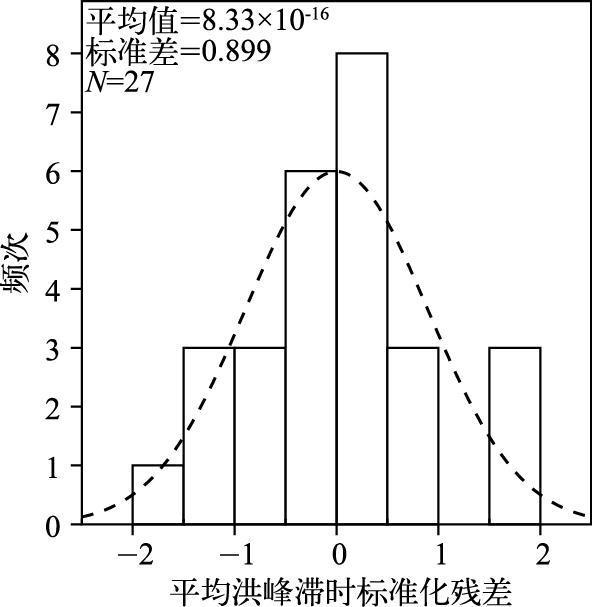
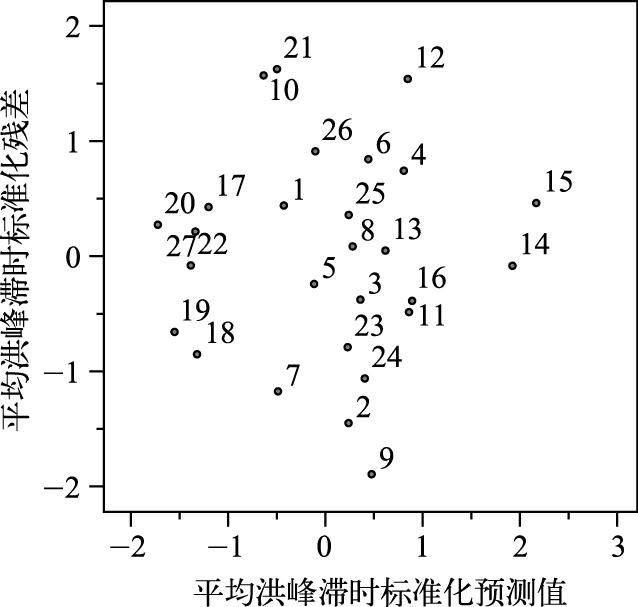
残差基本服从正态分布(图 2),标准化残差基本在[-1, 1]之间波动(图 3),与自变量无关,满足方差齐性假设.
|
图 2 标准化残差正态曲线直方图 Fig.2 Normal curve histogram of residual |
|
图 3 标准化预计值和残差散点图 Fig.3 Scatter plot of normalized expected value and residual |
综上,圆度比、形状系数、流域相对高差、河道分支频率、森林覆盖率是影响滞时的主要指标,将模拟所得系数代入公式(3),可得洪峰滞时的回归分析方程为:
| ${T_{\rm{p}}} = 160.77 \times \frac{{R_{\rm{c}}^{0.798} \cdot C_{\rm{f}}^{1.481} \cdot F_{\rm{c}}^{0.412}}}{{R_{\rm{f}}^{0.287} \cdot R_{\rm{p}}^{0.804}}}$ | (4) |
式中,Tp为平均洪峰滞时(h),Rc为圆度比,Cf为河道分支频率,Fc为森林覆盖率,Rf为形状系数,Rp为流域相对高差(m).
从公式(4)可以看出,流域相对高差、形状系数与平均洪峰滞时均呈负相关关系,表明在景观阻力和流域系统水力传导能力一定的条件下,随着流域相对高差、形状系数增大,流域单元的平均水流势能也会增加,因而水流速度更大,洪水响应过程更快,从而洪峰滞时更短.而圆度比、河道分支频率以及森林覆盖率与平均洪峰滞时呈正相关关系,表明在降雨强度和流域系统水力传导能力一定的条件下,越接近圆形、河道分支越多、森林覆盖越广的流域,其洪水响应过程越慢,洪峰滞时越长.
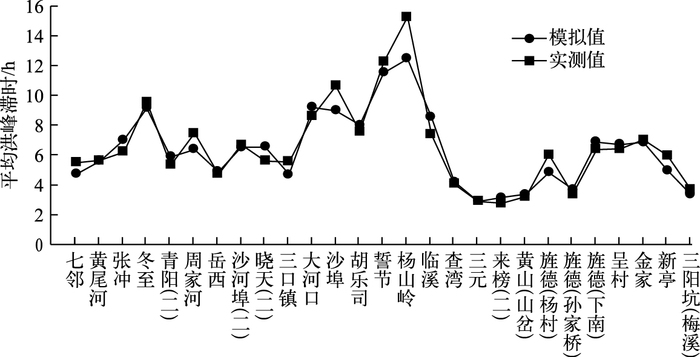
模拟的平均洪峰滞时与实测资料计算所得的平均洪峰滞时大致相当,说明模型模拟效果较好(图 4).
|
图 4 平均洪峰滞时实测值与模拟值对比 Fig.4 Comparison between observation and simulation values of average peak time lag |
通过上述逐步回归分析,得到具有统计学意义的回归方程,若要从洪水响应的物理过程上佐证公式(4)的合理性,则需要更深入地挖掘地貌格局因子对平均洪峰滞时的影响机理.因此本文在逐步回归分析的基础上采用通径分析进一步探讨.
通过对自变量与应变量之间表面直接相关性的分解,将相关系数分解为直接通径系数(某一自变量对因变量的直接作用)和间接通径系数(该自变量通过其他自变量对因变量的间接作用)[23].通径分析的理论已证明,任一自变量与因变量y之间的简单相关系数=与y的直接通径系数+所有与y的间接通径系数,任一自变量与因变量y的间接通径系数=相关系数×通径系数.在通径分析过程中,一般认为最难计算的就是通径系数.事实上,通过软件进行线性回归计算,计算结果给出的线性回归方程的标准系数(standardized coefficients)即为我们需要的通径系数.通径分析结果如表 6、7所示.
| 表 6 平均洪峰滞时与地貌参数的简单相关系数 Tab.6 The simple correlation coefficients between average peak time lag and geomorphic parameters |
| 表 7 通径分析计算结果 Tab.7 The results of path analysis |
由通径分析计算结构可知,流域相对高差对平均洪峰滞时的直接影响最大,表现为负相关,说明流域相对高差越大,平均洪峰滞时越小,与实际相符.圆度比通过流域相对高差间接对平均洪峰滞时产生影响,形状系数和森林覆盖率对平均洪峰滞时的直接影响较小.一般来说,植被覆盖对流域汇流过程有阻滞作用,会导致平均洪峰滞时增大,森林覆盖率本身对平均洪峰滞时的直接影响为正方向;但本研究区域主要为山区,森林覆盖率高的土地一般在上游,面积坡度大,流域汇流过程更快,反而导致平均洪峰滞时减小,森林覆盖率对平均洪峰滞时的最终影响为负方向.这也解释了森林覆盖率对平均洪峰滞时的直接通径系数为负,而简单相关系数为正(表 6).
综上,可以从物理成因的角度进一步解释公式(4)中各系数的合理性,公式(4)所构建的回归模型除了具有统计学上的意义,同时符合实际情况.
3 模型验证为讨论上文构建模型的外延性,选取皖南山区黄山(山岔)流域进行验证.该流域位于长江支流青弋江上游,属自然闭合流域,未受水工建筑等影响,且气候以及地形条件均符合皖南山区上游典型的中小流域特征.故选取该流域1978-2010年水文站完整序列实测资料,从中选取31场汛期典型单峰洪水,计算流域平均洪峰滞时,并提取该流域的地貌参数,所得结果如表 8所示.
| 表 8 黄山(山岔)验证模型所需的参数 Tab.8 Parameters of Huangshan(Shancha) Basin for testing model |
将表 8中各参数代入公式(4),得到流域平均洪峰滞时为2.97 h.根据实测资料所得的平均洪峰滞时与公式(4)计算得到的平均洪峰滞时的绝对误差为13.2 min,模拟效果较好,说明模型具有较好的外延性.由此,认为该模型能够定量分析地貌格局对流域平均洪峰滞时的影响,若将此定量关系移用至皖南山区无资料地区,可间接得出目标流域的平均洪峰滞时,揭示影响流域水文过程的重要因子,为发展水文相似理论提供基础分析,具有一定的实用意义.
4 结论与展望本文为解决无资料地区的洪峰滞时研究提出了新思路,即通过数学分析方法定量揭示地形地貌因子及地表覆盖类型对平均洪峰滞时的影响机制,同时建立平均洪峰滞时与地貌因子之间的数学公式.对于特定流域,建立水文过程与地貌特征的定量关系,发展流域水文相似理论,提高无资料地区的水文预测水平.
为消除多元线性回归中多重共线性的影响,采用了逐步回归的变量筛选方式.回归模型各项指标良好,回归效果显著,具有统计学意义.方程式模拟效果较好,可以合理表达70%以上的研究流域.进一步采用通径分析方法定量研究各地貌因子对平均洪峰滞时的物理影响机制.基于回归分析得到的简单相关系数矩阵和回归系数矩阵,计算各自变量对平均洪峰滞时的直接通径系数和间接通径系数.通径分析结果揭示了流域相对高差对平均洪峰滞时的直接影响最大,同时通过其他因子(圆度比等)对平均洪峰滞时存在明显间接影响.
模型的验证结果表明模型具有较好的外延性,在站网密度较低的皖南山区,由于实际降雨和流量过程的缺测,如何模拟出较为精确的洪水响应过程,一直是水文研究的难点.本文根据地形地貌因子,基于数学方法得出流域平均洪峰滞时,可为皖南无资料地区的洪水预报提供佐证.
此类从地貌参数的角度推求流域平均洪峰滞时的方法,在无资料地区具有显著的实际应用效果,更加方便快捷.但是,本研究仅初步揭示了地貌特征与洪水响应特征的密切联系,而流域的洪水响应特征还受到其他诸多因素的影响,本文对于地貌参数的选取尚未做到足够精确合理,以后的研究中可先对地貌参数做主成分分析,提高计算精度.且本文仅是从统计学上的角度进行回归分析,故所得方程式只能应用于下垫面条件相似的流域,因此流域相似性的研究也是后续研究的另一重点及难点.
| [1] |
Talei A, Chua LHC, Quek C. A novel application of a neuro-fuzzy computational technique in event-based rainfall-runoff modeling. Expert Systems with Applications, 2010, 37(12): 7456-7468. DOI:10.1016/j.eswa.2010.04.015 |
| [2] |
Talei A, Chua LHC. Influence of lag time on event-based rainfall-runoff modeling using the data driven approach. Journal of Hydrology2012, 2012, 438(1): 223-233. DOI:10.1016/j.jhydrol.2012.03.027 |
| [3] |
Banasik K, Hejduk A. Ratio of basin lag times for runoff and sediment yield processes recorded in various environments. Sediment Dynamics from the Summit to the Sea, 2014, 367: 163-169. |
| [4] |
Leopold LB. Lag time for small drainage basins. Catena, 1991, 18(2): 157-171. DOI:10.1016/0341-8162(91)90014-O |
| [5] |
Hood MJ, Clausen JC, Warner GS. Comparison of stormwater lag times for low impact and traditional residential development. Journal of the American Water Resources Association, 2007, 43(4): 1036-1046. DOI:10.1111/j.1752-1688.2007.00085.x |
| [6] |
Kang IS, Park JI, Singh VP. Effect of urbanization on runoff characteristics of the On-Cheon Stream watershed in Pusan, Korea. Hydrological Processes, 1998, 12(2): 351-363. DOI:10.1002/(ISSN)1099-1085 |
| [7] |
Zhou Minmin, Qu Simin, Shi Peng et al. Response of basin lag time to land use change in Dapoling Basin in upper Huaihe River. Journal of Hohai University(Natural Sciences), 2015, 43(2): 100-106. [周敏敏, 瞿思敏, 石朋等. 淮河上游大坡岭流域土地利用方式变化引起的流域滞时变化. 河海大学学报, 2015, 43(2): 100-106.] |
| [8] |
Mackay DS, Band LE. Extraction and representation of nested catchment areas from digital elevation models in lake-dominated topography. Water Resour Res, 1998, 34(4): 897-901. DOI:10.1029/98WR00094 |
| [9] |
Liang CJ, Mackay DS. A general model of watershed extraction and representation using globally optimal flow paths anf up-slope contributing areas. Int J Geogr Inf Sci, 2000, 14(4): 337-358. DOI:10.1080/13658810050024278 |
| [10] |
Cai Feng, Fan Juan, Li Zhijia. Analysis and applications of relationship between concentration parameters of Xin'anjiang model and topographic attributes. Water Resources and Power, 2011, 29(5): 19-21. [蔡峰, 范娟, 李致家. 新安江模型汇流参数与地貌特征规律分析及应用. 水电能源科学, 2011, 29(5): 19-21.] |
| [11] |
Liang Ke, Li Zhijia, Kan Guangyuan. Novel flow concentration method and its application in ungauged area. Yellow River, 2016, 38(3): 15-21. [梁珂, 李致家, 阚光远. 新型汇流计算方法及其在缺资料地区的应用. 人民黄河, 2016, 38(3): 15-21.] |
| [12] |
Liu Jintao, Wang Aihua, Wei Yu et al. Analyzing the influence of geomorphologic structure factors on runoff characteristics of catchments. Advances in Water Science, 2015, 26(5): 631-638. [刘金涛, 王爱花, 韦玉等. 流域地貌结构因子对径流特征的影响分析. 水科学进展, 2015, 26(5): 631-638.] |
| [13] |
Liao Yishan, Cai Qiangguo, Qin Fen et al. Geomorphological feature and scale effect on sediment yield and soil erosion in hilly loess areas, North China. Journal of Soil and Water Conservation, 2008, 37(1): 1-6. [廖义善, 蔡强国, 秦奋等. 基于DEM的黄土丘陵沟壑区流域地貌特征及侵蚀产沙尺度研究. 水土保持学报, 2008, 37(1): 1-6.] |
| [14] |
Salim AHA. Geomorphological analysis of the morphometric characteristics that determine the volume of sediment yield of Wadi Al-Arja, South Jordan. Journal of Geographical Sciences, 2014, 24(3): 457-474. DOI:10.1007/s11442-014-1100-8 |
| [15] |
Tang Lihua. Geomorphology-based water-sediment-pollutant model and its application [Dissertation]. Beijing: Tsinghua University, 2009. [唐莉华. 基于地貌特征的流域水-沙-污染物耦合模型及其应用[学位论文]. 北京: 清华大学, 2009. ] ]
|
| [16] |
Jeong SM, Park SC, Kim HS et al. Lag times and peak coefficients for watersheds in the Kum River Basin. Bridging the Gap, 2001, 3: 1-10. DOI:10.1061/40569(2001)456 |
| [17] |
Coffman DM, Turner AK, Melhorn WN. The water system: Computer programs for stream network analysis. Lafayette, Indiana: Purdue University Water Resources Research Center, 1971.
|
| [18] |
Tang Guoan, Yang Xin et al. ArcGIS geographic information systems spatial analysis experimental course. Second Edition. Beijing: Science Press, 2012, 478-509. [汤国安, 杨昕等. ArcGIS地理信息系统空间分析实验教程. 第二版. 北京: 科学出版社, 2012, 478-509.]
|
| [19] |
Rui Xiaofang. Principles of hydrology. Beijing: China Water & Power Press, 2004, 21. [芮孝芳. 水文学原理. 北京: 中国水利水电出版社, 2004, 21.]
|
| [20] |
Li Qi, Wen Kang. Power factor flow rate calculation in the general equation of the geomorphologic unit hydrograph. Haihe Water Resources, 1989(1): 6-12. [李琪, 文康. 地貌单位线通用公式中动力因子--流速计算的研究. 海河水利, 1989(1): 6-12.] |
| [21] |
Shi Liwen. SPSS 19.0 statistical analysis-from entry to the master. Beijing: Tsinghua University Press, 2012. [时立文. SPSS 19.0统计分析--从入门到精通. 北京: 清华大学出版社, 2012.]
|
| [22] |
Song Xiaoyuan, Zhu Zhongyuan, Liu Yanwei et al. Application of path analysis in stepwise linear regression SPSS. Arid Zone Research, 2016, 33(1): 108-113. [宋小园, 朱仲元, 刘艳伟等. 通径分析在SPSS逐步线性回归中的实现. 干旱区研究, 2016, 33(1): 108-113. DOI:10.13866/j.azr.2016.01.13] |
 2017, Vol. 29
2017, Vol. 29 
