(2: 华南地区水循环和水安全广东普通高校重点实验室, 广州 510275)
(2: Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong Higher Education Institutes, Sun Yat-sen University, Guangzhou 510275, P.R.China)
我国大多数水文监测站点的洪水观测数据时间序列较短,观测系列通常只有几十年[1],同时洪水灾害风险具有随机、模糊、灰色等诸多的不确定性[2].在现有条件下洪水灾害的风险是估不准的,传统概率计算方法(如概率论、数理统计等理论与方法)建立在大量连续时间序列统计资料基础上,而实际中会常遇到“小样本”的不完备信息问题,存在不精确和不确定的理论瓶颈[3-4].因此,为了提高洪水灾害的风险分析结果的可靠性和准确性,从有限的实测资料中挖掘更多洪水信息的研究显得尤为重要.
近年来,许多研究者都通过POT抽样法扩大了洪水样本,在此基础上进行洪水次数、量级、风险等研究,弥补改善了传统AMS抽样样本较少的这一缺陷[5-9].与传统年最大值(Annual Maximum Series, AMS)抽样相比,超定量(Peak-over-Threshold, POT)抽样扩大了样本容量,不仅反映洪水量级,还能反映洪水发生过程,相比较而言,更具物理相关性,能更有效利用实测资料描述洪水特征,能更充分利用洪水信息[10-12].
自从黄崇福等[13-16]系统提出信息扩散、内集-外集模型(IOSM)等多种模糊风险评价方法用于洪水灾害风险分析、地震灾害风险分析等领域后,邹强[17]、Liu等[18]、Feng等[19]将IOSM模型应用于洪水灾害、火灾、台风灾害等领域,在有限的观测样本中进行了较为完备、可靠地灾害风险分析.使用基于信息分配原理建立的内集-外集模型,可以针对信息不足而导致风险值估不准的缺陷,将样本进行模糊处理来充分利用样本的模糊过渡信息,使具有单值观测值的样本点转化为具有模糊集值的样本集,从而尽可能地填补小样本信息存在的不完备空隙,通过有限的知识来试图挖掘信息的内在联系和发生规律.通过这个途径,将所有样本的单值信息扩散到设定好的控制域中所有点上,得到较为丰富的信息资料[20],可在保证期望值合理可靠的前提下体现风险估计的不精确性、不完备性,为快速而合理的风险判断、及时而有效的风险规避提供科学依据[13-15].
在模糊处理技术领域的信息分配中,存在一个瓶颈问题——控制点的选取.传统内集-外集模型控制点的选取通常采用Otness等[21]提出的控制点选择公式,但是该公式的前提是正态总体和样本量较大时,因此在选取内集-外集模型的控制点时,直接引用会出现一些问题,特别是信息较为集中且存在特大值的时候,部分控制区间会没有样本点.因而本文将对其进行改进,根据皮尔逊Ⅲ型曲线的频率分析结果确定控制区间,将原来的等步长IOSM模型改进为根据皮尔逊Ⅲ型曲线的频率分析结果确定控制区间的不等步长P-IOSM模型.
综上所述,本研究在POT抽样基础上,以南方湿润区武江流域为例,将基于信息分配原理改进的不等步长P-IOSM模型应用到洪灾风险分析中,从有限的实测资料中挖掘尽可能多的洪水信息,在现有信息不完备条件下得到了可能性概率风险值,可为决策者提供多层次、多值化的洪水风险信息.
1 研究区与数据来源研究区域为武江流域(24°50′~25°31′N,112°50′~113°35′E),面积7097 km2, 干流全长260 km, 为珠江流域北江水系的一级支流,发源于湖南省临武县三峰岭,于韶关市汇入北江.
洪水超定量序列和年最大值序列的提取采用武江下游重要控制站犁市(二)水文站1956-2009年的日流量资料(其中“2006·07”洪水作特大洪水处理)[6].
2 研究方法 2.1 POT样本提取POT样本提取有两个关键,即洪峰样本独立性判别和超定量序列门限值的确定[12].
2.1.1 洪峰样本独立性判别标准进行洪水超定量频率分析的前提是超定量洪峰样本具有独立性.本文结合美国水资源协会(USWRC)提出的判别标准与王善序等提出的超定量抽样原则[6-7],进行洪峰独立性判别.
同时选取两个连续洪峰的条件为[12]:
| $\begin{split} θ>5+\text{ln}(A)且X_{\text{min}}<0.75 \text{min}[Q_{1},Q_{2}] \end{split}$ | (1) |
式中,θ为两个峰间的间隔时间(d);A为流域面积(km2);Qi为第i场洪水的最大日流量.
不满足上述条件的连续洪峰中,只取其中最大一次洪峰[1].
2.1.2 超定量序列门限值确定超定量序列门限值S是确定超定量序列样本的重要参数.目前普遍认为,门限值S的选择并不唯一,关键在于使提取的超定量样本服从某些标准.门限值应根据超定量系列发生次数分布、超定量洪水频率分布以及独立同分布假设共同确定[12].
(1)超定量样本均值法:Davison等[22]认为门限值应在以下范围内选取:超定量样本超过部分的均值(
(2)分散指数法:Ashkar等[23]认为门限值的选择应使样本分散指数在一个置信区间内,以确保超定量发生次数服从Poisson分布.
| $\begin{split} I=\text{var}(m)/\text{mean}\left(m\right) \end{split}$ | (2) |
| $\begin{split} h=\frac{∑\limits^{NY}_{i=1}[m\left(i\right)-\bar m]^2}{\bar m}=I\left(NY-1\right) \end{split}$ | (3) |
式中,m为年超定量发生次数序列,m(i)为第i年的超定量发生次数;NY为实测资料的年数;I为超定量序列发生次数的分散指数;h服从自由度为(NY-1)的卡方分布.
泊松过程的分散指数为1,取置信区间为[5%, 95%],则若χ2(5%)/(NY-1)<I<χ2(95%)/(NY-1),超定量次数服从泊松分布;其中χ2(5%)的自由度为(NY-1).
(3)年均超定量发生次数n法:n>1.65时采用指数分布做POT模型能取得较好的效果[24],n过大易影响样本独立性;国内关于洪水超定量频率分析多控制在2~3次[5].
本文在满足条件(1)和(2)的门限值范围内,选择满足n>2的较大门限值.
2.2 P-Ⅲ型频率曲线我国一般采用P-Ⅲ型频率曲线来计算设计洪水[25],分布参数采用适线法估计,具体计算公式参考相关文献[26-27].
2.3 改进的内集-外集模型(P-IOSM) 2.3.1 内集-外集模型(IOSM)设洪水的观测样本为:
| $\begin{split} X=\left\{{x}_{1},{x}_{2},…,x_{n}\right\} \end{split}$ | (4) |
设U是样本X的论域,
| $\begin{split} U=\{{u}_{1},{u}_{2},…{u}_{m}\} \end{split}$ | (5) |
IOSM用来计算不利事件发生在区间
| $\begin{split} {I}_{j}=[{u}_{j}-\frac{\text{Δ}}{2},{u}_{j}+\frac{\text{Δ}}{2}],j=1、2、…、m \end{split}$ | (6) |
显然控制点
根据样本点分布的具体情况和IOSM的计算要求,区间总数m的确定方法为[21]:
| $\begin{split} m=1.87(n-1)^{0.4} \end{split}$ | (7) |
当样本点
为了方便地计算,首先给出样本集合X关于区间
(1)内集
(2)外集
(1)内指标集
(2)外指标集
如果
| $\begin{split} {q}_{ij}=\left\{\begin{array}{l}1-\frac{\left|{x}_{i}-{u}_{j}\right|}{\text{Δ}},|{x}_{i}-{u}_{j}|≤\text{Δ}\\ 0,|{x}_{i}-{u}_{j}|≥\text{Δ}\end{array}\right.\ \ \ {x}_{i}∈X,{u}_{j}∈U \end{split}$ | (8) |
样本点
| $\begin{split} q^-_{ij}=\left\{\begin{array}{c}1-{q}_{ij},{x}_{i}∈{X}_{\text{in}-j}\\ 0,{x}_{i}∈{X}_{\text{out}-j}\end{array}\right. \end{split}$ | (9) |
| $\begin{split} q^+_{ij}=\left\{\begin{array}{c}{q}_{ij},{x}_{i}∈{X}_{\text{out}-j}\\ 0,{x}_{i}∈{X}_{\text{in}-j}\end{array}\right. \end{split}$ | (10) |
显然,对于
| $\begin{split} {π}_{{I_j}}\left(p\right)=\left\{\begin{array}{c}{∧}_{s∈S}{q^-_{sj}},p={p}_{0}\\ ……\\ {∨}_{{S}_{1},{S}_{2},{S}_{3}∈S,{S}_{1}≠{S}_{2}≠{S}_{3}}(q^-_{{s}_{1}j}∧q^-_{{s}_{2}j}∧q^-_{{s}_{3}j}),p={p}_{{n}_{j}-3}\\ {∨}_{{S}_{1},{S}_{2}∈S,{S}_{1}≠{S}_{2}}(q^-_{{s}_{1}j}∧q^-_{{s}_{2}j}),p={p}_{{n}_{j}-2}\\ {∨}_{s∈S}q^-_{sj},p={p}_{{n}_{j}-1}\\ 1,p={p}_{{n}_{j}}\\ {∨}_{t∈T}q^+_{tj},p={p}_{{n}_{j}+1}\\ {∨}_{{t}_{1},{t}_{2}∈T,{t}_{1}≠{t}_{2}}(q^+_{{t}_{1}j}∧q^+_{{t}_{2}j}),p={p}_{{n}_{j}+2}\\ {∨}_{{t}_{1},{t}_{2},{t}_{3}∈T,{t}_{1}≠{t}_{2}≠{t}_{3}}(q^+_{{t}_{1}j}∧q^+_{{t}_{2}j}∧q^+_{{t}_{3}j}),p={p}_{{n}_{j}+3}\\ ……\\ {∧}_{t∈T}q^-_{tj},p={p}_{n}\end{array}\right. \end{split}$ | (11) |
式中,
根据给点的样本集合X,可以得到在
| $\begin{split} ∏={\left({π}_{{I_j}}\left({p}_{i}\right)\right)}_{m\left(n+1\right)}=\left( \begin{array}{c} {π}_{{I}_{1}}\left({p}_{0}\right)&{π}_{{I}_{1}}\left({p}_{1}\right)&…&{π}_{{I}_{1}}\left({p}_{n}\right)\\ {π}_{{I}_{2}}\left({p}_{0}\right)&{π}_{{I}_{2}}\left({p}_{1}\right)&…&{π}_{{I}_{2}}\left({p}_{n}\right)\\ …&…&…&…\\ {π}_{{I}_{m}}\left({p}_{0}\right)&{π}_{{I}_{m}}\left({p}_{1}\right)&…&{π}_{{I}_{m}}\left({p}_{n}\right) \end{array}\right) \end{split}$ | (12) |
当采用式(7)确定控制区间,存在特大值的时候会出现部分区间可能性概率为0,导致流量较小区间可能性估计值小于流量较大区间的异常现象.因而对其进行改进,基于皮尔逊Ⅲ型能较好拟合我国大多数河流的洪水系列,因而将原来的等步长IOSM模型改进为根据皮尔逊Ⅲ型曲线的频率分析结果确定控制区间的不等步长P-IOSM模型.
设
| $\begin{split} {I}_{j}=[{I}_{jP\text{min}},{I}_{jP\text{max}}],j=1、2、…、m \end{split}$ | (13) |
| $\begin{split} {\text{Δ}}_{j}={I}_{jP\text{max}}-{I}_{jP\text{min}},j=1、2、…、m \end{split}$ | (14) |
同时,式(8)改为:
| $\begin{split} {q}_{ij}=\left\{\begin{array}{l}1-2\frac{{x}_{i}-{u}_{j}}{{\text{Δ}}_{j}+{\text{Δ}}_{j+1}},0≤{x}_{i}-{u}_{j}≤{\text{Δ}}_{j}/2+{\text{Δ}}_{j+1}/2\\ 1-2\frac{{u}_{j}-{x}_{i}}{{\text{Δ}}_{j-1}+{\text{Δ}}_{j}},0≤{u}_{j}-{x}_{i}≤{\text{Δ}}_{j-1}/2+{\text{Δ}}_{j}/2\\ 0,{x}_{i}-{u}_{j}≥{\text{Δ}}_{j}/2+{\text{Δ}}_{j+1}/2或{u}_{j}-{x}_{i}≥{\text{Δ}}_{j-1}/2+{\text{Δ}}_{j}/2\end{array}\right. {x}_{i}∈X,{u}_{j}∈U \end{split}$ | (15) |
由式(8)可知,在一个概率-可能性分布里,区间数量为m,可能性数量为n+1.可以这样认为,任意一个区间
| $\begin{split} E[{u}_{j}]=∑\limits^{n}_{i=0}{ω}_{i}·{p}_{i} \end{split}$ | (16) |
式中,
| $\begin{split} {ω}_{0}=\frac{1}{2}\left({μ}_{0}+{\text{max}}_{0≤r≤n}{μ}_{r}-{\text{max}}_{0<r≤n}{μ}_{r}\right) \end{split}$ | (17) |
| $\begin{split} {ω}_{i}=\frac{1}{2}({\text{max}}_{0≤r≤i}{μ}_{r}-{\text{max}}_{0≤r<i}{μ}_{r}+{\text{max}}_{i≤r≤n}{μ}_{r}-{\text{max}}_{i<r≤n}{μ}_{r}),1≤i≤n-1 \end{split}$ | (18) |
| $\begin{split} {ω}_{n}=\frac{1}{2}\left({\text{max}}_{0≤r≤n}{μ}_{r}-{\text{max}}_{0≤r<n}{μ}_{r}+{μ}_{n}\right) \end{split}$ | (19) |
式中,μr=πIj(pr),r=0、1、…、n.显然,ωi≥0且
这样,根据式(16)就得到了各个区间的期望值.在此基础上,计算得到不利事件发生在区间
| $\begin{split} p({u}_{j})=E[{u}_{j}]/∑\limits^{m}_{j=1}E[{u}_{j}],j=1、2、…、m \end{split}$ | (20) |
那么风险估计值即为可能性估计值的累积:
| $\begin{split} P\left({u}_{j}\right)=p\left(u≥{u}_{j}\right)=∑\limits^{n}_{k=j}p\left({u}_{k}\right) \end{split}$ | (21) |
根据公式(1),符合独立性判别标准的洪峰之间的时间间隔约为14天.对犁市(二)站54年日流量资料进行洪峰独立性判别,提取独立洪峰超定量样本.在提取过程中,部分洪峰虽然流量较大,但因洪峰之间时间间隔小于14天或者洪峰之间最小流量过大,不满足独立性判别标准而未入选.
根据所选独立洪峰,综合考虑超定量样本均值法、分散指数法和年均超定量发生次数,通过试算,确定最大门限值取S=1079 m3/s,年均超定量发生次数为2.4,样本数目为130个.
具体确定过程如下:
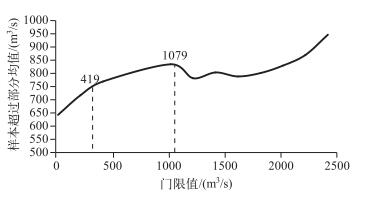
a.对门限值进行试算,由图 1超定量样本超过部分均值
|
图 1 超定量样本超过部分均值与门限值的关系曲线 Fig.1 The relation curve between the values that average of the peak over threshold minus the corresponding threshold and the corresponding thresholds |
b.计算超定量序列发生次数的分散指数,绘制分散指数图,由且图 2可知S>324 m3/s时分散指数位于[5%,95%]的置信区间内,即年超定量个数服从泊松分布.

|
图 2 分散指数图 Fig.2 Figure of dispersion index |
c.根据a和b可知在324~1079 m3/s范围内选择满足n>2的门限值,选择最大门限值以加强样本独立性,取S=1079 m3/s,n=2.4.由此提取130个洪峰构成POT样本.
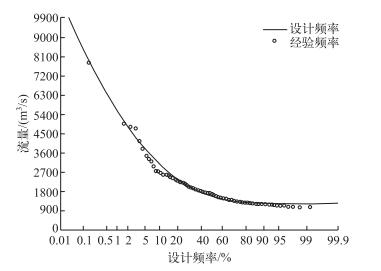
3.2 P-Ⅲ型频率分析根据POT取样获取130个独立洪峰样本, 其中2006年7月洪水作特大洪水处理, 对POT序列进行P-Ⅲ型频率分析, 拟合效果优良,相关系数达到0.98(图 3).
|
图 3 犁市(二)站POT洪水频率曲线 Fig.3 POT flood frequency curve of Lishi(2) station |
各设计频率洪峰流量见表 1.
| 表 1 犁市(二)站不同设计频率对应洪峰流量 Tab.1 Corresponding peak discharge of different design frequencies in Lishi(2) station |
如果采用式(7)确定控制区间,则区间数目为14,根据IOSM模型计算[7500, 8000]区间最大可能性概率为0.008,而区间[7000, 7500]、[6500, 7000]、[6000, 6500]、[5500, 6000]可能性概率都为0,这与现实不符,原因是观测样本有限,观测样本并未能覆盖所有区间,因而导致了部分区间可能性概率都为0的情况.因而皮尔逊Ⅲ型曲线的频率分析结果确定控制区间,根据不同设计频率洪峰流量划分控制区间, 得到控制区间与相应控制中心值(表 2).
| 表 2 控制区间与相应控制中心值(m3/s) Tab.2 The intervals and the corresponding discrete domains |
根据一维线性信息分配函数即公式(8)计算扩散信息矩阵qij,然后根据公式(9)和公式(10)分别计算得到游离信息矩阵
| 表 3 基于P-IOSM的可能性-概率分布 Tab.3 Probability-possibility distribution based on P-IOSM |
|
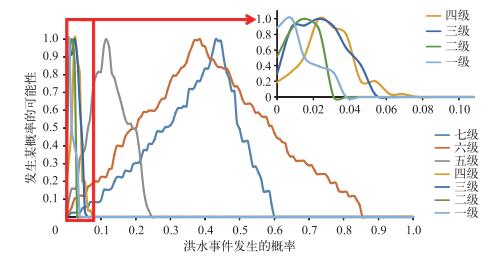
图 4 基于P-IOSM的可能性-概率分布 Fig.4 Figure of probability-possibility distribution based on P-IOSM |
由表 3和图 4可以看出灾害等级越高的洪水,其最大可能性(可能性为1)对应的概率值越小,与灾害等级越高的洪水发生的概率越小这一现实相符.
根据公式(16)~(21)来计算得到不同等级灾害概率估计值p(uj)、风险估计值P(uj), 从PPD可知,从不利事件样本X出发,不能确定不利事件发生的概率值,而是一个模糊集,即一个不利灾害事件对应着几个概率值,只是可能程度不同而已.它充分体现了在现有条件下自然灾害风险估不准这一特性,与实际情况更加接近.
例如对控制点u4而言,虽然洪峰流量落在以u4=3440为控制中心的区间3073<x < 3807内以p=0.023的可能性最大(为1),但是也不能忽视其他概率发生的可能性,即便是对于从不发生的p=0,仍然也有0.191的可能性.
不同级别灾害的可能性-概率分布具有相似的规律,只是其最大可能性对应的概率不同.
如果用传统直方图计算频率,用以代替概率,可计算出七级、六级、五级、四级、三级、二级、一级的概率依次为0.431、0.385、0.115、0.023、0.023、0.015和0.008,与基于P-IOSM计算的各等级灾害最大可能性一致,但若仅使用传统直方图计算灾害发生概率,则会出现三级灾害和四级灾害出现概率相等的结论,实际上三级灾害出现概率应小于四级灾害,这在PPD中有所体现,三级灾害发生概率为0.015有0.914可能性,四级灾害发生概率为0.015只有0.518可能性,说明三级灾害比四级灾害更大可能性概率为0.015,即三级灾害比四级灾害发生概率小的可能性更大,同时从表 4可知三级灾害出现概率为0.023,小于四级灾害的出现概率0.028,与现实相符.
| 表 4 基于P-ISOM的风险评估值结果 Tab.4 Risk value estimation based on P-IOSM |
可能性-概率分布本身保留了许多不确定信息,这些附加信息更贴近事实,能为决策者提供更多的依据,从而使决策结果更加可靠实用.
4 结论与展望基于武江流域犁市(二)水文站1956-2009年实测日流量数据提取了POT样本, 在考证历史洪水进行特大值处理的基础上,构建基于P-Ⅲ模型确定控制点而改进的非等步长内集-外集模型(P-IOSM)进行洪水模糊风险分析.主要结论如下:
1)与年最大值模型相比,采用POT模型进行洪水样本选取,能充分利用实测洪水信息,增大样本容量,降低抽样误差,从有限的观测数据中获取更多洪水样本信息.
2)基于P-Ⅲ模型确定控制点,能够使洪水信息更为合理地在研究区域上分配,解决了洪水信息集中且存在较大值时,无法合理分配区间的问题.
3)结合POT与P-IOSM的洪水风险分析得到的可能性-概率分布,挖掘了更多的不确定信息,这些附加信息更贴近事实,能为决策者提供更多的依据,从而使决策结果更加可靠实用.
在将来的研究中,如果能获取流域内更多站点数据资料时,将可以制定出整个流域的洪水风险图,从而为决策者提供更直观更强有力的支持,具有良好的工程应用情景.
| [1] |
Wang Shanxu. The flood frequency analysis based on POT flood series. Yangtze River, 1999, 30(8): 23-25. [王善序. 洪水超定量系列频率分析. 人民长江, 1999, 30(8): 23-25.] |
| [2] |
Huang Chongfu. Fuzzy risk assessment of urban natural hazards. Fuzzy Sets & Systems, 1996, 83(2): 271-282. |
| [3] |
Zou Qiang. Study on the theory and method of comprehensive analysis and intelligent assessment of flood disaster risk[Dissertation]. Wuhan: Huazhong University of Science & Technology, 2013. [邹强. 洪灾风险综合分析与智能评价的理论与方法[学位论文]. 武汉: 华中科技大学, 2013. ]
|
| [4] |
Huang Qiang, Chen Zishen. Multivariate flood risk assessment based on the secondary return period. J Lake Sci, 2015, 27(2): 352-360. [黄强, 陈子燊. 基于二次重现期的多变量洪水风险评估. 湖泊科学, 2015, 27(2): 352-360. DOI:10.18307/2015.0221] |
| [5] |
Fang Bin, Guo Shenglian, Cai Xiaoling et al. Flood frequency analysis based on FPOT method. Water Power, 2005, 31(2): 9-12. [方彬, 郭生练, 柴晓玲等. FPOT方法在洪水频率分析中的应用研究. 水力发电, 2005, 31(2): 9-12.] |
| [6] |
Zhang Lijuan, Chen Xiaohong, Ye Changqing et al. POT flood frequency analysis with historical floods in Wujiang River. Journal of Hydraulic Engineering, 2013(3): 268-275. [张丽娟, 陈晓宏, 叶长青等. 考虑历史洪水的武江超定量洪水频率分析. 水利学报, 2013(3): 268-275.] |
| [7] |
Ye Changqing, Chen Xiaohong, Zhang Lijuan et al. Changing rule and influence of threshold for peak-over-threshold flood series under the changing environment in Wujiang, China. Advances in Water Science, 2013(3): 392-401. [叶长青, 陈晓宏, 张丽娟等. 变化环境下武江超定量洪水门限值响应规律及影响. 水科学进展, 2013(3): 392-401.] |
| [8] |
Martins ES, Stedinger JR. Generalized Maximum likelihood pareto—Poisson estimators for partial duration series. Water Resources Research, 2001, 37(10): 2551-2557. DOI:10.1029/2001WR000367 |
| [9] |
Parent E, Bernier J. Bayesian POT modeling for historical data. Journal of Hydrology, 2003, 274(1/2/3/4): 95-108. |
| [10] |
Dai Changjun, Liang Zhongmin, Luan Chengmei et al. Advance in flood frequency analysis for partial duration series. Advances in Water Science, 2006, 17(1): 136-140. [戴昌军, 梁忠民, 栾承梅等. 洪水频率分析中PDS模型研究进展. 水科学进展, 2006, 17(1): 136-140.] |
| [11] |
Beguería S. Uncertainties in partial duration series modelling of extremes related to the choice of the threshold value. Journal of Hydrology, 2005, 303(1/2/3/4): 215-230. |
| [12] |
Lang M, Ouarda TBMJ, Bobée B. Towards operational guidelines for over-threshold modeling. Journal of Hydrology, 1999, 225(3/4): 103-117. |
| [13] |
Huang Chongfu ed. The natural disaster risk assessment: Theory and practice. Beijing: Science Press, 2006. [黄崇福. 自然灾害风险评价:理论与实践. 北京: 科学出版社, 2006.]
|
| [14] |
Huang Chongfu. An application of calculated fuzzy risk. Information Sciences—Informatics & Computer Science an International Journal, 2002, 142(142): 37-56. |
| [15] |
Huang Chongfu, Moraga C, Yuan X eds. Calculation vs. Subjective Assessment with Respect to Fuzzy Probability//Computational Intelligence. Theory and Applications. Berlin Heidelberg:Springer, 2001: 392-411.
|
| [16] |
Huang Chongfu ed. The natural disaster risk analysis and management. Beijing: Science Press, 2012. [黄崇福. 自然灾害风险分析与管理. 北京: 科学出版社, 2012.]
|
| [17] |
Zou Qiang, Zhou Jianzhong, Zhou Chao et al. Flood disaster risk analysis based on variable fuzzy sets theory. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(5): 126-132. [邹强, 周建中, 周超等. 基于可变模糊集理论的洪水灾害风险分析. 农业工程学报, 2012, 28(5): 126-132.] |
| [18] |
Liu X, Zhang J, Cai W et al. Information diffusion-based spatio-temporal risk analysis of grassland fire disaster in northern China. Knowledge-Based Systems, 2010, 23(1): 53-60. DOI:10.1016/j.knosys.2009.07.002 |
| [19] |
Feng LH, Luo GY. Analysis on fuzzy risk of landfall typhoon in Zhejiang province of China. Mathematics & Computers in Simulation,, 2009, 79(11): 3258-3266. |
| [20] |
Zou Q, Zhou J, Zhou C et al. The practical research on flood risk analysis based on IIOSM and fuzzy α-cut technique. Applied Mathematical Modelling, 2012, 3271-3282.
|
| [21] |
Otnes RK, Enochson L eds. Digital time series analysis. Taylor & Francis: Wiley, 1972.
|
| [22] |
Davison AC, Smith RL. Models for exceedances over high thresholds. Journal Royalty Statistical Society B, 1990, 52(3): 393-442. |
| [23] |
Ashkar F, Ouarda TBMJ. On some methods of fitting the generalized Pareto distribution. Journal of Hydrology, 1996, 177: 117-141. DOI:10.1016/0022-1694(95)02793-9 |
| [24] |
Cunnane C. A note on the poisson assumption in partial duration series models. Water Resource Research, 1979, 15: 489-494. DOI:10.1029/WR015i002p00489 |
| [25] |
Jin Sheng, Lei Xiaoyun, Li Hui et al. Hydrological P-Ⅲ frequency curve calculation software development research. South-to-North Water Transfers and Water Science & Technology, 2009, 7(5): 70-72. [靳晟, 雷晓云, 李慧. 水文P-Ⅲ频率曲线计算软件开发研究. 南水北调与水利科技, 2009, 7(5): 70-72.] |
| [26] |
Liu Guangwen. The parameter estimation of Pearson Ⅲ distribution. Journal of China Hydrology, 1990(4): 1-15. [刘光文. 皮尔逊Ⅲ型分布参数估计. 水文, 1990(4): 1-15.] |
| [27] |
Song Dedun, Ding Jing. The application of probability weighted moments to estimating the parameters for Pearson type-Ⅲ distribution. Journal of Hydrology, 1988, 101(101): 47-61. |
| [28] |
Shen Q, Zhao R. Risk assessment of serious crime with fuzzy random theory. Information Sciences, 2010, 180(22): 4401-4411. DOI:10.1016/j.ins.2010.07.027 |
 2017, Vol. 29
2017, Vol. 29 

