(2: Desert Research Institute, Las Vegas Nevada 89119, USA)
(3: 浙江省水文局, 杭州 310009)
(2: Desert Research Institute, Las Vegas Nevada 89119, USA)
(3: Zhejiang Provincial Hydrology Bureau, Hangzhou 310009, P.R.China)
马斯京根河道水流演算方法自1938年提出以来[1],进行了大量的相关研究,获得了一系列理论和应用成果,是迄今为止应用最广泛、获得理论研究成果最多的河道水流演算方法[2-4].马斯京根法的理论研究主要有模型检验研究、模型结构的物理基础分析论证研究、模型结构改进研究、模型参数率定与时变关系研究四类.
模型结构检验研究主要是对实际河道上下断面洪水期的流量观测资料,用马斯京根法模型据上断面流量计算下断面流量,通过与实测下断面流量的比较,分析误差大小和误差特征,进而评判模型结构的合理性与模拟实际洪水的效果[5-9].
模型结构的物理基础分析论证主要是对蓄泄关系的物理基础和马斯京根法演算方程与简化圣维南方程组的差分模型间的关系,分析模型结构的物理基础,间接证明模型的物理性[10-13].模型结构改进研究主要是对线性蓄泄关系进行非线性化的改进和结构的进一步简化关系研究,以考虑河段蓄量与出流流量间的非线性关系[14-15].模型参数率定与时变关系研究主要是参数率定方法研究和考虑流量比重系数X和传播时间K的时间变化影响因素,建立参数随水力特征因素变化的函数关系,应用于模型模拟洪水的计算中[16-18].
所有的马斯京根法研究和应用成果都限制在有稳定水位流量关系线的河段,对于流量关系线不稳定或不存在水位流量关系的潮汐河段,马斯京根流量演算法模拟实际洪水效果就不好或根本无法使用[19-22].
本文根据河段蓄量与过水断面和流量蓄泄关系,与水流连续关系,构成过水断面积与流量双变量耦合演算模型,以解决流量关系线不稳定或不存在水位流量关系的潮汐河段洪水演算问题.
1 双变量耦合演算模型结构河道一维水流,假设没有旁侧入流,由过水断面面积(A)和流量(Q)表达的连续方程:
| $\begin{split} \frac{\text{∂}A}{\text{∂}t}+\frac{\text{∂}Q}{\text{∂}x}=0 \end{split}$ | (1) |
为了使方程闭合,还需要一个描述过水断面面积和流量两者关系的方程,水动力学中以力的平衡为基础构建了两者关系.但由于其中摩阻力与实际差异很大,常导致使用效果不好[23-26].水文学中提出蓄泄关系,构成马斯京根河道水流演算方法[1], 但方法只适用于有稳定水位流量关系线的河段[19-22].本文通过分别建立河段蓄水量与断面面积、河段蓄水量与流量的关系,获得断面面积与流量的关系,构造完备的双变量耦合演算模型(以下简称双变量模型).
对于以体积单位表达的河段蓄量(W),可表示为河段长(L)和河段平均过水断面面积(
| $\begin{split} W=L·\bar A \end{split}$ | (2) |
公式(2)中L又可以表达为河段内水流运动平均速度(
| $\begin{split} L=K·\bar u \end{split}$ | (3) |
由公式(2) 和(3),蓄量又可以表达为水流传播时间与平均流量(
| $\begin{split} W=K·\bar Q \end{split}$ | (4) |
比较公式(2)和(4),得:
| $\begin{split} L\bar A=K·\bar Q \end{split}$ | (5) |
公式(5) 建立了
| $\begin{split} \bar A=α·A_j+\left(1-α\right)A_{j+1} \end{split}$ | (6) |
| $\begin{split} \bar Q=χ·Q_j+\left(1-χ\right)Q_{j+1} \end{split}$ | (7) |
式中,
则公式(5)、式(6) 和式(7) 组成的断面面积与流量关系结构:
| $\begin{split} L·α·A_j+L\left(1-α\right)A_{j+1}=K·χ·Q_j+K\left(1-χ\right)Q_{j+1} \end{split}$ | (8) |
天然河道的断面过水断面形状比较复杂且沿程变化[27],可以假设平均断面面积等于上、下断面面积的加权平均,公式(7)代入(4)就是马斯京根法的蓄泄关系,其结构的合理性已有大量证明[1-18].所以公式(5)、(6)和(7)组成的面积与流量关系结构是具有合理性的.
公式(1)采用Pressimann四点隐式差分格式,有:
| $\begin{split} \frac{θ}{\text{Δ}x}\text{Δ}Q_{j+1}+\frac{1}{2\text{Δ}t}\text{Δ}A_{j+1}=\frac{θ}{\text{Δ}x}\text{Δ}Q_j-\frac{1}{2\text{Δ}t}\text{Δ}A_j+\frac{1}{\text{Δ}x}\left(Q^i_j-Q^i_{j+1}\right) \end{split}$ | (9) |
公式(8)考虑前后时间相减得:
| $\begin{split} -K\left(1-χ\right)\text{Δ}Q_{j+1}+L\left(1-α\right)\text{Δ}A_{j+1}=K·χ·\text{Δ}Q_j-L·α·\text{Δ}A_j \end{split}$ | (10) |
式中,
| $\begin{split} \left| \begin{array}{c} \frac{θ}{\text{Δ}x}&\frac{1}{2\text{Δ}t}\\-K\left(1-χ\right)&L\left(1-α\right) \end{array} \right|=\frac{θ}{\text{Δ}x}L\left(1-α\right)+\frac{K\left(1-χ\right)}{2\text{Δ}t}>0 \end{split}$ | (11) |
公式(11)对于任意在(0, 1) 范围内变化的权系数
为了检验模型结构的合理性、应用于实际河段模拟的有效性,选择河段考虑旁侧入流比例小和河段距离短两个条件,主要考虑如下3方面因素:
(1)两个河段距离短些.因为连续方程差分以河段长为步长,这步长值越大,差分误差就大;
(2)区间面积不大,旁侧入流比例小.因为连续方程式(1)忽略了旁侧入流项,旁侧入流比例大,将导致这忽略带来的误差就大;
(3)不同水力和河道断面特征的河段.使得模型对不同河道和水力特征具有广泛的代表性.
根据这3条原则,本次研究选择了全国涉及长江、黄河、珠江、辽河、松花江五大水系,还选择了塔里木河等内陆河流和入海河流,具有各种水力、各种河道断面特征的代表性,其河段特征与资料年份见表 1.选择的洪水是每年汛期的洪水过程,为了考虑检验的充分性,选择洪水历时尽可能长,一般短则10 d,长的1个月,最长的连续3个月;洪水选择也考虑大、中、小各种洪水的代表性;年份选择主要考虑前后相连;计算时段间隔采用半小时.
| 表 1 河段资料统计 Tab.1 Statistics of the river data used in the study |
为了充分检验模型的效果,同时把马斯京根法模型参数和双变量模型参数进行率定,马斯京根模型把3个汇流参数进行率定(考虑区间来水,3系数之和不为1),这样参数个数与双变量模型相同.马斯京根汇流演算模型为:
| $\begin{split} Q·C_{t+1}=C_0·I_{t+1}+C_1·I_t+C_2·Q·C_t \end{split}$ | (12) |
双变量模型,为了与马斯京根法比较,将式(9)代入(10),消去
| $\begin{split} &ΔQ_{j+1}=B_{1}·ΔQ_{j}+B_{2}·ΔA_{j}+B_{3}(Q^{i}_{j}-Q^{i}_{j+1})\\ &B_{1}=(2θ·L(1-α)Δt-K·χ·Δx)/(2θ·L(1-α)Δt+K(1-χ)·Δx)\\ &B_{2}=L(2α-1)Δx/(2θ·L(1-α)Δt+K(1-χ)·Δx)\\ &B_{3}=L(1-α)2Δt/(2θ·L(1-α)Δt+K(1-χ)·Δx) \end{split}$ | (13) |
与马斯京根法类似,以I表达上断面流量,以A表达上断面面积,则可得双变量模型的流量演算式为:
| $\begin{split} &Q·C_{t+1}=Q·C_{t}+B_{1}(I_{t+1}-I_{t})+B_{2}(A_{t+1}-A_{t})+B_{3}(I_{t}-Q·C_{t}) \end{split}$ | (14) |
也可类似地将式(9)代入(10),消去
模型检验,除辽河外的河段选择最后一年的洪水资料为模型检验,其余年份为参数率定.检验期洪水演算模型模拟的效果统计见表 2. DC(Ma)和DC(New)分别为马斯京根和双变量模型率定期确定性系数,VDC(Ma)和VDC(New)分别表示马斯京根和双变量模型检验期确定性系数计算结果.
| 表 2 河段率定期和检验期效果统计表 Tab.2 Simulation results of calibration and validation periods |
从率定期和检验期结果看,16个河段中有15个河段双变量模型效果好,河段平均确定性系数也是双变量模型高些;从各河段稳定性看,马斯京根法的确定性系数变幅很大,双变量模型更稳定.
为进一步分析比较模型模拟实际洪水的情况,将资料系列最长的辽河铁岭-马虎山河段检验结果进行详细分析.铁岭-马虎山河段采用的洪水资料为1955-1994年间选择了18年汛期的所有大洪水和几次代表性的中小洪水,其中前期10年的资料用于模型参数率定,后期8年11场洪水用于模型检验. 表 3列出了辽河铁岭-马虎山河段检验期11场洪水的检验结果,QCp(Ma)和QCp(New)分别表示马斯京根模型和双变量模型计算的洪峰;DC(Ma)和DC(New)分别表示马斯京根模型和双变量模型计算的确定性系数.
| 表 3 辽河铁岭-马虎山河段检验结果 Tab.3 Simulation results of Tieling-Mahushan river channel in Liao River |
从表 3检验期各场洪水确定性系数看,双变量模型的平均确定性系数为0.753,略高于马斯京根的0.734,各场洪水变幅也比马斯京根法更小,与16个河段结论一致.
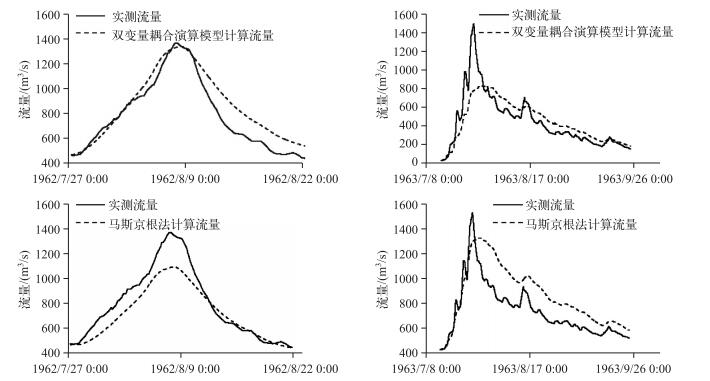
7号是马斯京根模型模拟最差的洪水,8号是双变量模型模拟最差的洪水.对比马斯京根法计算流量与实测流量过程,比较8号洪水(图 1b,1d),8号洪水降雨时空分布不均匀,洪水的区间降雨主要出现在洪峰附近,造成洪峰附近流量叠加使得实测流量大于双变量模型计算流量,双变量模型受区间来水影响;比较7号洪水(图 1a,1c),马斯京根模型受误差累计影响. “马斯京根模型受误差累计影响”主要体现在储蓄结构中,因为当储蓄关系与实际有出入时,其计算蓄量偏差需要连续几个时段的累积才能弥补其影响.马斯京根法计算的7号洪水,初始计算蓄量偏小,计算出流也偏小,使得涨水段计算流量连续偏小,其误差通过涨水段的累计直到峰后才近似抵消.所以双变量模型改进需要更细地考虑区间来水模拟结构,而马斯京根模型需要改进模型结构,即更细地考虑河段断面面积变化对蓄量的影响结构.
|
图 1 双变量耦合模型7、8号(a,b)以及马斯京根法7、8号(c,d)洪水计算结果 Fig.1 Simulation results of flood NO.7, NO.8 by coupling routing model(a, b), and Muskingum routing model(c, d) |
本研究根据河段蓄水量等于平均过水断面面积与河段长乘积和蓄水量等于河段平均流量与传播时间的乘积两个物理计算公式,提出了过水断面面积与流量的关系:
| $\begin{split} L·α·A_j+L\left(1-α\right)A_{j+1}=K·χ·Q_j+K\left(1-χ\right)Q_{j+1} \end{split}$ | (15) |
与水流连续方程构成了双变量耦合演算模型:
| $\begin{split} \left\{\begin{array}{l}\frac{θ}{\text{Δ}x}\text{Δ}Q_{j+1}+\frac{1}{2\text{Δ}t}\text{Δ}A_{j+1}=\frac{θ}{\text{Δ}x}\text{Δ}Q_j-\frac{1}{2\text{Δ}t}\text{Δ}A_j+\frac{1}{\text{Δ}x}\left(Q^i_j-Q^i_{j+1}\right)\\ -K\left(1-χ\right)\text{Δ}Q_{j+1}+L\left(1-α\right)\text{Δ}A_{j+1}=K·χ·\text{Δ}Q_j-L·α·\text{Δ}A_j\end{array}\right. \end{split}$ | (16) |
通过四大水系(包括内陆河流和入海河流)的16个河段汛期洪水资料的模拟检验,将双变量耦合通用演算模型与传统的马斯京根法进行了效果比较,结果表明双变量耦合演算模型的模拟精度高于马斯京根法,而且模拟效果更加稳定.
本研究提出的模型在结构合理性方面与现有的马斯京根流量演算模型相近,效果比马斯京根法稍好一些,适用于区间来水影响较小的河段.主要优点是具有通用性,模型结构简单,使用资料要求低,实用性强.与马斯京根模型类似,双变量耦合模型可与新安江模型等结合进行洪水预报,成果具有进一步研究和推广应用价值.
| [1] |
Wang Zhesun, Jin Juliang, Wei Yiming et al. Application of accelerating genetic algorithm to parameter estimation of Muskingum Flood Routing Model. Scientia Geographica Sinica, 2010(6): 916-920. [汪哲荪, 金菊良, 魏一鸣等. 加速遗传算法在马斯京根洪水演算模型参数估计中的应用. 地理科学, 2010(6): 916-920.] |
| [2] |
Koussis AD. Assessment and review of the hydraulics of storage flood routing 70 years after the presentation of the Muskingum method. Hydrological Sciences Journal, 2009, 54(1): 43-61. DOI:10.1623/hysj.54.1.43 |
| [3] |
Perumal M. Discussion of "Assessment and review of the hydraulics of storage flood routing 70 years after the presentation of the Muskingum method". Hydrological Sciences Journal, 2010, 55(8): 1427-1430. DOI:10.1080/02626667.2010.491260 |
| [4] |
Fread DL. Flood routing: A synopsis of past, present, and future capability. Proceeding of the Int. Symp. On Rainfall-runoff modeling, Mississippi, 1981, 521-542. |
| [5] |
Jing Liyang, Zhang Xingnan, Wang Jun et al. Application of GIS in simulation of river basin hydrology in Three Gorges Project reservoir. Journal of Hydraulic Engineering, 2004(4): 15-20. [井立阳, 张行南, 王俊等. GIS在三峡流域水文模拟中的应用. 水利学报, 2004(4): 15-20.] |
| [6] |
Zhang Jun, Guo Shenglian, Li Chaoqun et al. Comparative study on conceptual hydrological models. Engineering Journal of Wuhan University, 2007(2): 1-6. [张俊, 郭生练, 李超群等. 概念性流域水文模型的比较. 武汉大学学报(工学版), 2007(2): 1-6.] |
| [7] |
Danáčová MM, Szolgay J. On the use of the Muskingum method for the simulation of flood wave movements. Slovak Journal of Civil Engineering, 2010, XVIII((3): 14-20. |
| [8] |
Singh VP, McCann RC. Some notes on Muskingum method of flood routing. Journal of Hydrology, 1980, 48(3): 343-361. |
| [9] |
Bao Hongjun, Li Zhijia, Wang Lili. Study of flood forecasting for upper reaches of the River above Lutaizi. Journal of Hydraulic Engineering, 2007(S1): 440-448. [包红军, 李致家, 王莉莉. 淮河鲁台子以上流域洪水预报模型研究. 水利学报, 2007(S1): 440-448.] |
| [10] |
Wang GT, Yao Chunmei, Cairo Okoren et al. 4-point FDF of Muskingum method based on the complete St Venant equations. Journal of Hydrology, 2005, 324(1): 339-349. |
| [11] |
Shao Nianhua, Shen Bing. Application of chaotic particle swarm optimization to parameter estimation in Mustingum Model. Journal of Water Resources & Water Engineering, 2009(6): 30-33. [邵年华, 沈冰. 混沌粒子群优化算法在马斯京根模型参数优化中的应用. 水资源与水工程学报, 2009(6): 30-33.] |
| [12] |
Cunge JA. On the subject of a flood propagation computation method(Muskingum Method). Journal of Hydraulic Research, 1969, 7(2): 205-230. DOI:10.1080/00221686909500264 |
| [13] |
Cheng Liang, Wang Zongzhi, Hu Siyi et al. Flood routing model incorporating intensive streambed infiltration. Science China: Earth Sciences, 2015(2): 207-215. [程亮, 王宗志, 胡四一等. 强烈下渗条件下天然河道洪水演进模拟方法. 中国科学:地球科学, 2015(2): 207-215.] |
| [14] |
Xie Ping, Xia Jun. Theory on the role of conceptual elements in the process of transition. Journal of Hydraulic Engineering, 1995, 10: 65-68. [谢平, 夏军. 论概念性元素的推移和坦化作用. 水利学报, 1995, 10: 65-68. DOI:10.3321/j.issn:0559-9350.1995.10.011] |
| [15] |
Yuan Xiaohui, Zhang Shuangquan, Zhang Yongchuan et al. Parameter estimation of nonlinear Muskingum Model using mixed genetic algorithm. Journal of Hydraulic Engineering, 2001(5): 77-81. [袁晓辉, 张双全, 张勇传等. 非线性马斯京根模型参数率定的新方法. 水利学报, 2001(5): 77-81.] |
| [16] |
Perumal Muthiah, Ranga Raju KG. Field applications of a variable-parameter Muskingum Method. Journal of Hydrologic Engineering, 2001, 6(3): 196-207. DOI:10.1061/(ASCE)1084-0699(2001)6:3(196) |
| [17] |
Lu Fan, Jiang Yunzhong, Wang Hao et al. Application of multi-agent genetic algorithm to parameter estimation of Muskingum Model. Journal of Hydraulic Engineering, 2007(3): 289-294. [鲁帆, 蒋云钟, 王浩等. 多智能体遗传算法用于马斯京根模型参数估计. 水利学报, 2007(3): 289-294.] |
| [18] |
He Hui, Zhang Jianyun. A new mathematical algorithm for estimating the parameters of the Muskingum River Flow Routing Model. Journal of China Hydrology, 1998(5): 15-18. [何惠, 张建云. 马斯京根法参数的一种数学估计方法. 水文, 1998(5): 15-18.] |
| [19] |
Bao Weimin, Zhao Chao, Wang Hao et al. Application of a bi-directional stage routing model in a tidal reach. IAHS Publ, 2007, 311: 45-52. |
| [20] |
Bao Weimin, Zhang Xiaoqin, Qu Simin. Dynamic correction of roughness in the Hydrodynamic Model. Journal of Hydrodynamics, 2009, 21(2): 255-263. DOI:10.1016/S1001-6058(08)60143-2 |
| [21] |
Bao Weimin, Zhang Xiaoqin, Yu Zhongbo et al. Real-time equivalent conversion correction on river stage forecasting with manning's formula. Journal of Hydrologic Engineering, 2011, 16(1): 1-10. DOI:10.1061/(ASCE)HE.1943-5584.0000279 |
| [22] |
Qu Simin, Bao Weimin, Shi Peng et al. Water-stage forecasting in a multitributary tidal river using a bidirectional muskingum method. Journal of Hydrologic Engineering, 2009, 14(12): 1299-1308. DOI:10.1061/(ASCE)HE.1943-5584.0000120 |
| [23] |
Zhang Xiaoqin, Bao Weimin, Yu Zhongbo et al. Real-time correction on the river stage forecasting with an equivalent stage approach. IAHS Publication, 2009, 331: 275-283. |
| [24] |
Zhang Xiaoqin, Bao Weimin. Modified saint-venant equations for flow imulation in Tidal River. Water Science and Engineering, 2012, 5(1): 34-45. |
| [25] |
Zhang Xiaoqin, Bao Weimin. A river stage correction approach using Fourier series. Hydrology Research, 2013, 44(4): 658-672. DOI:10.2166/nh.2012.149 |
| [26] |
Zhang Xiaoqin, Bao Weimin. Hydrodynamic simulation in Tidal Rivers using fourier series. Journal of Hydrologic Engineering, 2013, 18(11): 1408-1415. DOI:10.1061/(ASCE)HE.1943-5584.0000526 |
| [27] |
Pan Xiaochun. Iterative algorithm of water surface profile along natural river. Electric Power Survey & Design, 2002(3): 54-58. [潘晓春. 天然河道水面曲线的迭代算法. 电力勘测设计, 2002(3): 54-58.] |
 2017, Vol. 29
2017, Vol. 29 

