(2: 南京信息工程大学江苏省大气环境与装备技术协同创新中心, 南京 210044)
(3: 中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室, 北京 100101)
(2: Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET), Nanjing University of Information Science and Technology, Nanjing 210044, P.R.China)
(3: Key Laboratory of Ecosystem Network Observation and Modeling, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, P.R.China)
湖泊蒸发量是湖泊水循环的关键过程,大型湖泊通过蒸发向大气贡献水汽,对区域气候有重要的影响[1].准确量化湖泊蒸发量不仅对湖泊水文循环研究有重要的意义,而且对于研究湖泊对当地大气的水汽贡献、开发区域气候数值模型和治理湖泊生态环境等都有重要的科学意义.
湖泊蒸发量的估算包括直接观测、蒸发模型和间接反算等多种方法.首先,传统的直接观测的方法是用蒸发皿(池)观测值代表湖泊蒸发值[2],随着观测技术的进步,目前观测精度比较高的直接观测方法包括涡度相关法[3-6]和通量梯度法[7]等,优点是观测数据精度高,缺点是需要精密的仪器做定点的长期连续监测,安装和维护的成本和难度都较高.
其次,蒸发模型可以分为5类[6],包括基于能量平衡闭合理论和通量梯度理论的综合模型[8-10]、基于全球太阳辐射和气温经验公式的太阳辐射-气温模型[11]、基于温度和日照时数经验公式的模型[12]、基于湖面与参考高度比湿之差的Dalton模型[13]和基于温度的经验模型[14].通过对比19个湖泊蒸发模型,Wang等[6]发现综合模型(特别是Priestley-Taylor模型,以下简称PT模型)的模拟结果与观测值最为接近,但是该类模型需要辐射收支和能量平衡的观测数据作为输入量,数据较难获取.
最后,间接反算法包括水量平衡方程[15]、同位素质量守恒方程[16]和卫星数据反演方法[17]等.其中卫星数据反演方法是结合地面气象资料和卫星观测的地表温度计算水热通量.水量平衡法是通过观测湖泊的水量收支计算湖泊蒸发量,优点是通过水文数据即可计算湖泊蒸发量,缺点是入湖水量和出湖水量的估算误差会导致蒸发量计算结果的误差.同位素水量平衡法是在水量平衡法的基础上增加同位素的约束条件,能弥补水量平衡法计算误差大的缺点,提高计算精度,而水量收支各项的同位素组分相对而言比较容易获取,目前该方法得到了较为广泛的应用,如地中海[18](面积215.6×104 km2,平均水深1491 m,最大水深5093 m)、南美洲的Lake Titicaca[19](面积4.2 km2,最大水深100 m)、日本的Lake Biwa[20](面积674 km2,最大水深103 m)、非洲的Lake Edward[21](面积2325 km2,最大水深117 m)、加拿大的Lake Okanagan[22](面积344 km2,最大水深242 m)、北美洲的Laurentian Great Lakes[23](面积245000 km2,最大水深405 m)等水体.在我国,章新平等[24]利用这种方法计算了青海湖(面积4456 km2,最大水深32 m)的蒸发量.可以看出,该方法主要被用于高纬度和较深水体蒸发的计算,对于低纬度地区大型浅水湖泊的应用则很少.
太湖是典型的大型浅水湖泊,面积约为2400 km2,平均水深为1.9 m.而且与太湖相连的河道数量有100多条,部分河道的水流方向有季节变化,水量收支情况复杂,因此,太湖为我们提供了良好的实验场地,检验稳定同位素质量守恒模型对于低纬度大型浅水湖泊的适用性.以往研究者们采用各种方法研究太湖的蒸发量:毛锐[25]
采用蒸发池观测了水面蒸发,并采用气候指数模型、池湖蒸发差值模型和修正彭曼法蒸发模型等计算了太湖蒸发量[26];沈行毅[27]采用Penman公式计算了太湖蒸发量;Qin等[15]采用水量平衡法计算太湖蒸发量;Lee等[5]建立了太湖中尺度涡度通量网,连续监测太湖与大气之间的物质和能量交换;Xiao等[7]建立了通量梯度观测系统,同步观测湖泊与大气之间的CO2、H2O和水汽通量;Hu等[28]通过对比涡度相关观测、湖泊陆面过程模型和蒸发皿蒸发量等研究了1979-2013年太湖蒸发量的变化趋势.但是迄今为止,还没有人采用同位素质量守恒方法计算太湖的蒸发量.
本文的目的是基于太湖湖水、出/入湖河水、大气水汽的同位素组分的观测数据,计算太湖蒸发量,并且以PT模型的计算结果为参考,评价同位素质量守恒方程的准确性,以期为水文学、气象学和生态学的相关研究提供科学参考.
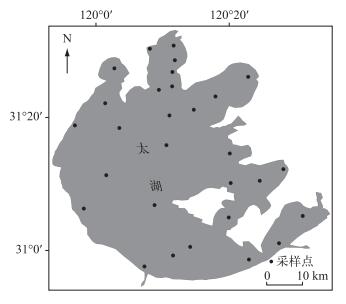
1 材料与方法 1.1 试验站点和观测方法本研究以太湖为研究对象(图 1).简单来讲,每个季度采集湖水和河水样本,并测量水样的
|
图 1 太湖采样点分布 Fig.1 Distribution of sampling sites in Lake Taihu |
自2013年5月开始,在环太湖51条河道采集水样,测量水样的δ18O.根据太湖流域管理局发布的《水情月报》(http://www.tba.gov.cn/),将环太湖分区为武澄锡虞区、湖西区、浙西区、杭嘉湖区和阳澄淀泖区,望亭水利枢纽、太浦闸和梅梁湖泵站的水量单独计算.各分区采样河道为:武澄锡虞区(梁溪河、直湖港、武进港、蠡河和壬子港),湖西区(太滆运河、漕桥河、殷村港、沙塘港、烧香港、茭渎港、新渎港、社渎港、官渎港、洪巷港、陈东港、大浦港、朱渎港、黄渎港、庙渎港、双桥港、八房港、定化港、乌溪港和大港口),浙西区(长丰港、夹浦港、合溪新港、长兴港和杨家浦港),杭嘉湖区(小梅港、长兜港、大钱港、罗溇、幻溇、濮溇、汤溇、吴溇和庙港),阳澄淀泖区(戗港、大浦河、三船路河、外苏州河、瓜泾口、胥江、吕浦港、浒光运河和金墅港).
本文采用水量权重法计算入湖和出湖河水的δ18O,主要分为以下2个步骤:(1) 根据2009年环太湖入湖和出湖河流的水量[30],先对每一个分区根据河道水量计算出该分区的水量权重δ18O值;(2) 再根据《水情月报》中每个分区的入出湖水量,计算入湖河水和出湖河水的水量权重δ18O值.
1.3 水量平衡方程和同位素质量守恒方法根据水量平衡方程,湖水蓄水量的变化取决于入湖和出湖水量的差异:
| $\begin{split} \frac{\text{d}·V}{\text{d}t}=I+P-E-Q \end{split}$ | (1) |
式中,dV/dt是太湖蓄水量的变化,t为时间,I为入湖河水流量,P为降水量,E为蒸发量,Q为出湖河水流量.
若将公式(1) 中各项都乘以对应的同位素含量,则构成同位素质量守恒方程,即:
| $\begin{split} \frac{\text{d}(V\text{·δ}_\text{L})}{\text{d}t}=I·\text{δ}_\text{I}+P·\text{δ}_\text{P}-E·\text{δ}_\text{E}-Q·\text{δ}_\text{Q} \end{split}$ | (2) |
式中,δL、δI、δP、δE和δQ分别是湖水、入湖河水、降水、湖泊蒸发水汽和出湖河水的同位素含量.
为了计算湖面蒸发,并维持水量平衡,可以联合公式(1) 和(2),消去Q,得到:
| $\begin{split} E=\frac{V\frac{\text{d}\text{δ}_\text{L}}{\text{d}t}+(\text{δ}_\text{L}-\text{δ}_\text{Q})\frac{\text{d}V}{\text{d}t}+I(\text{δ}_\text{Q}-\text{δ}_\text{I})+P(\text{δ}_\text{Q}-\text{δ}_\text{P})}{\text{δ}_\text{Q}-\text{δ}_\text{E}} \end{split}$ | (3) |
本文中,太湖入湖河水流量、蓄水量及其变化来源于水利部太湖流域管理局的《水情月报》(http://www.tba.gov.cn/),降水量来源于太湖周边无锡、湖州和东山气象站的气象资料,湖水和河水同位素组成来源于湖水和河水采样分析结果(详见1.1和1.2部分). δP用在常熟生态试验站获得的回归公式计算[31];而δE采用Craig-Gordon模型[32]计算得到:
| $\begin{split} \text{δ}_\text{E}=\frac{α^{-\text{1}}_{\text{eq}}·\text{δ}_\text{L}-h·\text{δ}_\text{V}-ε_{\text{eq}}-(1-h)ε_\text{k}}{1-h+{10^{-3}}(1-h)ε_\text{k}} \end{split}$ | (4) |
式中, h为大气水汽压相对于水面温度下饱和水汽压的相对湿度;δV为大气水汽的δ18O,通过观测值与大气水汽混合比建立的回归关系获得;εk为动力学分馏系数,根据Merlivat等[33]的模型推导出与风速的函数关系.
对于
| $\begin{split} ε_{\text{k}}=0.00058u^{4}-0.018u^{3}+0.21u^{2}-1.1u+8.9 \end{split}$ | (5) |
式中,u为3.5 m高度处的风速.
而αeq和εeq是平衡分馏系数(εeq = (1 -1/αeq) × 103, ‰),通过水面温度计算得到,计算公式为[34]:
对于
| $\begin{split} α_{eq}=1.137×10^{3}/T^{2}-0.4156/T-2.0667×10^{-3} \end{split}$ | (6) |
PT模型[8]基于可利用能量(即净辐射与水体热储量之差)计算湖泊蒸发量:
| $\begin{split} λ·E=1.26\frac{s}{s+γ}(R_\text{n}-\text{Δ}Q) \end{split}$ | (7) |
式中,λ为蒸发潜热,E为湖泊蒸发量,Rn为净辐射,ΔQ为水体热储量的变化,s为饱和水汽密度曲线斜率,γ为干湿球温度计常数.
根据湖面温度、湖水温度(20、50、100和150 cm深度处)和底泥温度的观测数据,计算每个月月初和月末的各层温度的日平均值.然后采用下面的公式计算深度权重平均水温,即:
| $\begin{split} \overline{T_\text{w}}=\frac{1}{z}∑\limits^n_{i=1}T_{\text{w}i}·\text{Δ}z_i \end{split}$ | (8) |
式中,z为水体深度,Δzi为第i层的深度,Twi为第i层水体的平均水温,n为水体分层,当水深小于150 cm时,n=4,即分层为0~20、20~50、50~100、100 cm至底泥;当水深大于150 cm时,n=5,即分层为0~20、20~50、50~100、100~150、150 cm~底泥.
接着,利用月初和月末的深度权重平均水温的变化计算水体热储量变化,即:
| $\begin{split} ΔQ=ρ_\text{w}·c_{\text{pw}}\frac{\text{Δ}\overline{T_\text{w}}}{\text{Δ}t} z \end{split}$ | (9) |
式中, ρw为水密度,cpw为比热容,Δt为时间间隔,本研究的时间步长为1个月.
| $\begin{split} s=\frac{1000×4098(0.6108\text{exp}\left(\frac{17.27T_\text{a}}{T_\text{a}+237.3}\right)}{(T_\text{a}+237.3)^2} \end{split}$ | (10) |
| $\begin{split} γ=\frac{1013P_\text{a}}{0.622×{10}^6λ} \end{split}$ | (11) |
式中, Pa为大气压(Pa).
2 结果与分析 2.1 PT模型计算的太湖蒸发量以往太湖的研究结果表明,PT模型计算的湖泊蒸发量与涡度相关的观测结果吻合度很高[5-6],由于涡度相关系统受供电情况、仪器支架和周边地物的影响较大,获得连续的数据较为困难,因此,本文采用PT模型的计算结果作为参考值.
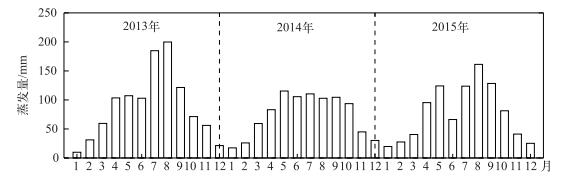
采用PT模型计算的2013-2015年太湖蒸发量有明显的季节变化:5-9月蒸发量较大,冬季蒸发量较小(图 2). 2013-2015年各年5-9月蒸发量之和分别占当年总蒸发量的67%、60%和65%. 2013-2015年的月蒸发量最高值分别出现在8、7和8月,分别为200、110和161 mm;最低值均出现在1月,分别为10、17和20 mm.其次,太湖年蒸发量有明显的年际变化,2013-2015年各年总蒸发量分别为1069、894和935 mm.最后,夏季各月份月蒸发量的年际差异较大,2013年7和8月的蒸发量明显高于其他年的相同月份,2个月份蒸发量之和为385 mm,而2014和2015年对应的蒸发量分别为213和285 mm.另外,2015年6月份的蒸发量明显低于其他年的相同月份,仅为66 mm.
|
图 2 Priestley-Taylor模型计算的太湖月蒸发量 Fig.2 Monthly evaporation of Lake Taihu calculated using Priestley-Taylor model |
太湖2013-2015年水量的收入和支出以河流输送为主,降水量和湖泊蒸发量的水量相对较小.入湖河水流量的平均值为8.3×108 m3/月,降水量的平均值为2.6×108 m3/月;出湖河水流量的平均值为8.4×108 m3/月,蒸发量的平均值为2.8×108 m3/月;湖泊蓄水量3年平均值为0.1×108 m3/月,即多年尺度上太湖水容量基本不变(图 3).

|
图 3 太湖水量收支各项的时间序列图(其中蒸发量为水量平衡方程的计算结果) Fig.3 Time series of water budgets of Lake Taihu(Evaporation in this figure was calculated using the water mass balance method) |
其次,太湖水量收支有明显的年际变化.就年总量而言,2013-2015年入湖河水流量的各年总量分别为89.0×108、101.6×108和107.0×108 m3,出湖水量分别为90.1×108、104.1×108和108.3×108 m3. 2013-2015年每月入湖水量的变化范围分别为(3.8~10.6)×108、(4.9~14.6)×108和(3.3~21.1)×108 m3;月出湖水量的变化范围为(4.7~11.7)×108、(4.2~12.7)×108和(3.8~20.8)×108 m3.
最后,2015年6和7月收支水量明显高于其他月份,太湖蓄水量也明显高于其他时段. 6和7月入湖河水流量都高于其他月份,分别为21.1×108和18.0×108 m3;7月份出湖河水流量较高,为20.8×108 m3;而6月降水量较大,为8.2×108 m3.通过分析《水情月报》发现,该时段并未开启“引江济太”工程,入湖水量主要来自于湖西区的河流.
另外,值得注意的是用水量平衡法计算蒸发量对入湖和出湖水量的数据准确性非常敏感.在研究时段内,由于2013年2月、2014年4月和2015年3月缺少《水情月报》资料,如果入出湖水量和蓄水量变化是采用《太湖流域片水情年报》的年总量反算,那么计算的月蒸发量就是负值.为了计算年总蒸发量,以下的分析会直接采用PT模型的计算结果插补这几个月的蒸发量.
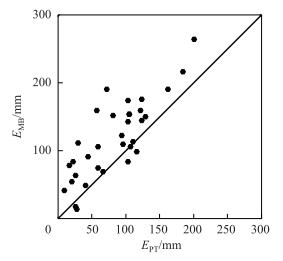
通过水量平衡方法计算的月蒸发量与PT模型计算的结果对比,发现水量平衡法计算的月蒸发量明显偏高,平均误差为36 mm(图 4).对于年总蒸发量,水量平衡方法估算的2013-2015年各年蒸发量分别为38.1×108、30.6×108和29.0×108 m3,而PT模型的计算结果分别为25.9×108、21.2×108和22.4×108 m3.
|
图 4 Priestley-Taylor公式和水量平衡方法计算的太湖月蒸发量对比 Fig.4 Comparison of monthly evaporation over Lake Taihu calculated using the Priestley-Taylor equation and the water mass balance method |
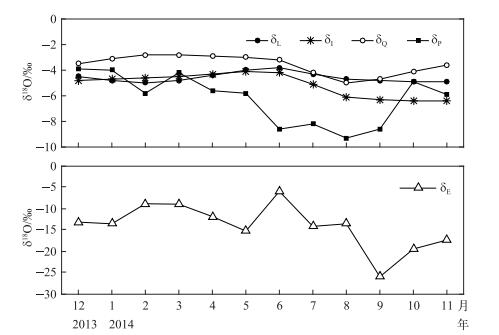
2013年12月至2014年11月太湖水量收支各项的δ18O的时间序列如图 5所示.湖泊蒸发的δ18O最低,降水同位素富集程度略高,湖水和河水的δ18O值较高(图 5).入湖河水的δ18O值最低,湖水δ18O值居中,而出湖河水的δ18O值最高.产生这种现象的原因是水从进入到流出太湖经历了蒸发过程,湖水中的18O同位素不断富集[29, 35].
|
图 5 2013年12月至2014年11月太湖各个水量收支项δ18O月均值的时间序列 Fig.5 Time series of monthly δ18O of each water budget item from December 2013 to November 2014 |
为了保证计算结果的稳定性,通常在年尺度上应用同位素质量守恒模型. 2013年12月至2014年11月期间,同位素质量守恒模型各项数值如表 1所示,其中年平均蓄水量为51.6×108 m3,蓄水量的年变化为3.3×108 m3,全年降水量为33.5×108 m3,入湖水量为99.6×108 m3,以上各项的不确定性取值为观测值的10%,蓄水量年变化的不确定性加倍,取值为年变化值的20%.湖水、降水、入湖河水和出湖河水的δ18O的全年水量权重平均值分别为-4.6‰、-7.2‰、-5.2‰和-3.7‰,这些同位素组分观测的不确定性是液态水同位素分析仪的观测精度,为0.1‰;湖水δ18O的年变化为-0.4‰,不确定性取值为0.2‰.蒸发水汽δ18O通过Craig-Gordon模型计算得到,为-14.6‰,不确定性取值为1.46‰.基于以上数据和公式(3),采用蒙特卡洛方法模拟太湖蒸发量,结果为(21.0±2.7)×108 m3,即893±114 mm.
| 表 1 同位素水量平衡方程各项数值* Tab.1 Values for each item in the isotopic mass balance equation |
太湖月蒸发量与气象和环境因子之间的相关系数如表 2所示.首先,水面温度、气温和日照时数均与月蒸发量存在显著的正相关关系,气压与月蒸发量呈显著负相关.这一点不难理解,夏季温度高、日照时数长、气压低,湖泊蒸发量大.其次,风速和降水量与蒸发量之间不存在相关关系.再次,空气比湿、水面温度下的饱和比湿、以及二者之差均与蒸发量呈显著正相关.需要说明的是,虽然某些环境和气象因子与湖泊蒸发量存在相关关系,但也只能说明它们存在相同的季节变化,并不能说明它们是控制湖泊蒸发的因子.
| 表 2 太湖月蒸发量与气象和环境因子的相关系数 Tab.2 Correlation between monthly evaporation and meteorological and environmental variables |
研究湖泊蒸发量的控制因子,需要基于蒸发的理论进行分析.根据水气界面物质传输理论,风速、水面温度下的饱和比湿(qs)与空气比湿(qa)之差(qs-qa)对湖泊蒸发有控制作用.在小时尺度上,风速的变化会影响湖面蒸发量,但是在月尺度上,各个季节月平均风速变化幅度不大,如2013年1月至2015年12月期间,风速的变化范围为2.1~3.1 m/s,因此对于月蒸发量而言,风速的变化几乎没有影响.而qs-qa与月蒸发量之间存在显著相关关系,说明在月尺度上,qs-qa是控制湖泊蒸发量的因子.另外,根据PT公式的理论,湖泊接收到的可利用能量(即净辐射与水体热储量之差)是控制湖泊蒸发的因子.太湖月蒸发量与净辐射Rn和可利用能量Rn-ΔQ存在显著正相关关系,与ΔQ之间不存在相关关系.
在年尺度上,太湖年总蒸发量仅与大气比湿的年均值存在显著相关关系(r=0.999, P<0.05),与其他因子无显著相关性.
3.2 几种模型计算结果的对比本文以PT模型计算结果为参考值,对比分析水量平衡法和同位素质量守恒方法的准确性.通过对比太湖5个涡度相关通量站观测的湖泊蒸发量和PT模型的计算结果,Lee等[5]和Wang等[6]发现二者一致性很好,即PT模型的计算结果可以表征太湖蒸发量的真值.以2013年12月至2014年11月为研究时段,PT模型计算的湖泊蒸发量为885 mm;水量平衡法的计算结果为1247 mm,相对误差为41%;而同位素质量守恒方程的结果与PT模型结果较为接近,为893 mm.由此可见,水量平衡法的误差较大,同位素质量守恒方法计算的湖泊蒸发量结果较为可靠.
3种估算蒸发的方法都各有优缺点.首先,PT模型的准确度较高,但对观测的要求高,需要连续观测净辐射、准确观测水温廓线.其次,水量平衡法所需的水量收支数据是常规的水文和气象观测项目,数据容易获取,但是由于蒸发量是太湖水量收支中的小项,计算误差较大.如前所述,2013-2015年太湖入湖和出湖河水流量的月均值分别为8.3×108和8.4×108 m3/月,而蒸发量的月均值均为2.8×108 m3/月,蒸发量仅占入湖/出湖水量的1/3左右.假设入湖或出湖水量估算的相对误差为10%,即0.8×108 m3/月,水量平衡法计算出的蒸发量的误差就有0.8×108 m3/月,相对误差达到29%,由此可见,入湖水量和出湖水量估算中的微小误差,就会引起蒸发量估算结果的较大误差.另外,《水情月报》中的入湖和出湖水量可能忽略了一些小支流的流量,也忽略了湖泊与地下水的交换.因此通过水量平衡方法计算的蒸发量存在较大的不确定性.最后,稳定同位素质量守恒方法是在水量平衡方程的基础上加入了稳定同位素组成的限制项,提高了年蒸发量估算的准确度,而且数据相对容易获取.但这种方法只能用于计算年蒸发量,不适合在月尺度上使用,这是因为:(1)月尺度的时间过短,同位素富集信号可能不够强;(2)月尺度上的水量收支项估算的相对误差比较大,而年尺度上的相对误差就小得多,例如假设入湖和出湖水量估算的绝对误差是0.8×108 m3,那么对于月平均水量而言相对误差约为10%,但是相对于年总入湖/出湖水量而言,相对误差仅为0.8%,因此,在年尺度上采用稳定同位素质量守恒计算蒸发量,误差就比较小;(3)月尺度上太湖蓄水量变化幅度较大,有时甚至高于入湖/出湖水量,公式(3) 右边分子第2项的权重加大,不确定性也增大,而在年尺度上太湖蓄水量基本不变,公式(3) 中第2项基本对计算结果没有影响.
3.3 太湖蒸发量的研究结果对比对于太湖蒸发量,研究者们通过不同的方法得到了一些研究结果.沈行毅等[27]采用修正Penman公式计算1959-1978年多年平均太湖水面年蒸发量为1109.9 mm. Qin等[15]通过调查115条河流的水量和湖泊蓄水量的变化,用水量平衡方程算得2001年5月-2002年4月太湖蒸发量为17.71×108 m3,约为760 mm. Wang等[6]基于涡度相关方法得到的2011年9月-2012年8月太湖北部和西部的蒸发量分别为1061和1109 mm. Hu等[28]采用CLM4-LISSS离线湖泊模型和修正后蒸发皿资料,得到1979-2013年期间太湖平均年蒸发量分别为977和1007 mm.本文的研究表明太湖蒸发量存在明显的年际变化,PT模型的计算结果表明2013、2014和2015年的年蒸发量分别为1069、894和935 mm.由此可见,太湖蒸发量存在明显的年际变化,不同方法得到的结果也不尽相同.
4 结论通过对比分析PT模型、水量平衡方程和同位素质量守恒模型对太湖蒸发量的模拟结果,评价同位素质量守恒模型在太湖的适用性,结果发现:
1) 太湖蒸发量存在明显的季节变化和年际变化,5-9月的蒸发量占全年总蒸发量的60%以上,2013-2015年的年总蒸发量分别为1069、894和935 mm;对于降雨量偏多、日照时数偏少的月份,蒸发量较往年同期明显偏少.
2) 对于2013年12月-2014年11月,PT模型计算的蒸发量为885 mm,水量平衡法的结果明显偏高,而同位素质量守恒模型的计算结果为893 mm,较为合理.
3) 影响太湖蒸发量季节变化的因子是净辐射和水面温度下的饱和比湿与空气比湿之差.
综上所述,为了准确估算湖泊蒸发量,有必要综合对比多种研究方法的计算结果.而同位素质量守恒模型以其采样简单、精度较高的优势,值得推广,但是需要积累更多的同位素观测资料,进一步检验该方法的长期适用性.
| [1] |
Bryan AM, Steiner AL, Posselt DJ. Regional modeling of surface-atmosphere interactions and their impact on Great Lakes hydroclimate. Journal of Geophysical Research: Atmospheres, 2015, 120(3): 1044-1064. DOI:10.1002/2014JD022316 |
| [2] |
Xie Airu, Zhang Jincan. Discussion on the representative sites of water level and evaporation over Lake Taihu. Hydrology, 1993(4): 33-35, 32. [谢皑如, 张锦灿. 太湖湖区水位和蒸发代表站的探讨. 水文, 1993(4): 33-35.] |
| [3] |
Blanken PD, Spence C, Hedstrom N et al. Evaporation from Lake Superior: 1: Physical controls and processes. Journal of Great Lakes Research, 2011, 37: 707-716. DOI:10.1016/j.jglr.2011.08.009 |
| [4] |
Spence C, Blanken PD, Hedstrom N et al. Evaporation from Lake Superior: 2: Spatial distribution and variability. Journal of Great Lakes Research, 2011, 37: 717-724. DOI:10.1016/j.jglr.2011.08.013 |
| [5] |
Lee X, Liu S, Xiao W et al. The Taihu eddy flux network: An observational program on energy, water, and greenhouse gas fluxes of a large freshwater lake. Bulletin of the American Meteorological Society, 2014, 95(10): 1583-1594. DOI:10.1175/BAMS-D-13-00136.1 |
| [6] |
Wang W, Xiao W, Cao C et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. Journal of Hydrology, 2014, 511: 811-824. DOI:10.1016/j.jhydrol.2014.02.012 |
| [7] |
Xiao W, Liu S, Li H et al. A flux-gradient system for simultaneous measurement of the CH4, CO2 and H2O fluxes at a lake-air interface. Environmental Science and Technology, 2014, 48: 14490-14498. DOI:10.1021/es5033713 |
| [8] |
Priestley CHB, Taylor RJ. On the assessment of surface heat flux and evaporation using large-scale parameters. Monthly Weather Review, 1972, 100(2): 81-92. DOI:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 |
| [9] |
Elsawwaf M, Willems P, Feyen J. Assessment of the sensitivity and prediction uncertainty of evaporation models applied to Nasser Lake, Egypt. Journal of Hydrology, 2010, 395: 10-22. DOI:10.1016/j.jhydrol.2010.10.002 |
| [10] |
Rosenberry DO, Winter TC, Buso DC et al. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. Journal of Hydrology, 340, 149-166. DOI:10.1016/j.jhydrol.2007.03.018 |
| [11] |
McMahon TA, Peel MC, Lowe L et al. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrology and Earth System Sciences, 2013, 17: 1331-1363. DOI:10.5194/hess-17-1331-2013 |
| [12] |
Blaney HF, Criddle, WD. Determining consumptive use and irrigation water requirements. Technical Bulletin No.1275, Agricultural Research Service, U.S. Department of Agriculture in cooperation with the office of Utah State Engineer. U.S. Government Printing Office, Wathington D.C., 1962.
|
| [13] |
Garratt JR ed. The atmospheric boundary layer. New York: Cambridge University Press, 1992, 101-104. |
| [14] |
Palmer WC, Havens AV. A graphical technique for determining evapotranspiration by the Thornthwaite method. Monthly Weather Review, 1958, 86: 123-128. DOI:10.1175/1520-0493(1958)086<0123:AGTFDE>2.0.CO;2 |
| [15] |
Qin B, Xu P, Wu Q et al. Environmental issues of Lake Taihu, China. Hydrobiologia, 2007, 581: 3-14. DOI:10.1007/s10750-006-0521-5 |
| [16] |
Dincer T. The use of oxygen 18 and deuterium concentrations in the water balance of lakes. Water Resources Research, 1968, 4(6): 1289-1306. DOI:10.1029/WR004i006p01289 |
| [17] |
Lofgren BM, Zhu YC. Surface energy fluxes on the Great Lakes based on satellite-observed surface temperatures 1992 to 1995. Journal of Great Lakes Research, 2000, 26: 305-314. DOI:10.1016/S0380-1330(00)70694-0 |
| [18] |
Gat JR, Shemesh A, Tziperman E et al. The stable isotope composition of waters of the eastern Mediterranean Sea. Journal of Geophysical Research, 1996, 101: 6441-6451. DOI:10.1029/95JC02829 |
| [19] |
Zuber A. On the environmental isotope method for determining the water balance of some lakes. Journal of Hydrology, 1983, 61: 409-427. DOI:10.1016/0022-1694(83)90004-5 |
| [20] |
Taniguchi M, Nakayama T, Tase N et al. Stable isotope studies of precipitation and river water in the Lake Biwa basin, Japan. Hydrological Processes, 2000, 14: 539-556. DOI:10.1002/(SICI)1099-1085(20000228)14:3<539::AID-HYP953>3.0.CO;2-L |
| [21] |
Russell JM, Johnson TC. The water balance and stable isotope hydrology of Lake Edward, Uganda-Congo. Journal of Great Lakes Research, 2006, 32: 77-90. DOI:10.3394/0380-1330(2006)32[77:TWBASI]2.0.CO;2 |
| [22] |
Wassenaar LI, Athanasopoulos P, Hendry MJ. Isotope hydrology of precipitation, surface and ground waters in the Okanagan Valley, British Columbia, Canada. Journal of Hydrology, 2011, 411: 37-48. DOI:10.1016/j.jhydrol.2011.09.032 |
| [23] |
Jasechko S, Gibson JJ, Edwards TWD. Stable isotope mass balance of the Laurentian Great Lakes. Journal of Great Lakes Research, 2014, 40: 336-346. DOI:10.1016/j.jglr.2014.02.020 |
| [24] |
Zhang Xinping, Yao Tandong. Estimation of lake evaporation by stable isotopic ratio. Journal of Glaciology and Geocryology, 1997, 19(2): 161-166. [章新平, 姚檀栋. 利用稳定同位素比率估计湖泊的蒸发. 冰川冻土, 1997, 19(2): 161-166.] |
| [25] |
Mao Rui. Preliminary experimental study of evaporation from water surface of Lake Tai and Lake Tuangui, Jiangsu Province. Oceanologia et Limnologia Sinica, 1978, 9(1): 26-35. [毛锐. 太湖、团氿湖水面蒸发的初步研究. 海洋与湖沼, 1978, 9(1): 26-35.] |
| [26] |
Mao Rui. Forecasting model of evaporation from Taihu Lake and its application. J Lake Sci, 1992, 4(4): 8-14. [毛锐. 太湖水面蒸发量预报模型及其应用. 湖泊科学, 1992, 4(4): 8-14. DOI:10.18307/1992.0402] |
| [27] |
Shen Xingyi. Climatological calculation on the evaporation over Lake Taihu. Hydrology, 1984, 4: 12-18. [沈行毅. 太湖水面蒸发量的气候学计算. 水文, 1984, 4: 12-18.] |
| [28] |
Hu C, Wang Y, Wang W et al. Trends in evaporation of a large subtropical lake. Theoretical and Applied Climatology, 2016 (online published). DOI: 10.1007/s00704-016-1768-z.
|
| [29] |
Xu Jingzheng, Xiao Wei, Xiao Qitao et al. Temporal dynamics of stable isotopic composition in Lake Taihu and controlling factors. Environmental Science, 2016, 37(7): 2470-2477. [徐敬争, 肖薇, 肖启涛等. 湖水氢氧同位素组分的时间变化特征及影响因子分析. 环境科学, 2016, 37(7): 2470-2477. DOI:10.13227/j.hjkx.2016.07.008] |
| [30] |
Yan Shuwen, Yu Hui, Zhang Lulu et al. Water quantity and pollutant fluxes of inflow and outflow rivers of Lake Taihu, 2009. J Lake Sci, 2011, 23(6): 855-862. [燕姝雯, 余辉, 张璐璐等. 2009年环太湖入出湖河流水量及污染负荷通量. 湖泊科学, 2011, 23(6): 855-862. DOI:10.18307/2011.0605] |
| [31] |
Liu J, Song X, Yuan G et al. Stable isotopic compositions of precipitation in China. Tellus B, 2014, 66: 22567. DOI:10.3402/tellusb.v66.22567 |
| [32] |
Craig H, Gordon LI. Deuterium and oxygen 18 variations in the ocean and the marine atmosphere. In: Tongiorgi E ed. Stable isotopes in oceanographic studies and paleotemperatures. Laboratorio di Geologia Nucleare, Pisa, Italy, 1965, 9-130. |
| [33] |
Merlivat L, Jouzel J. Global climatic interpretation of the deuterium-oxygen 18 relationship for precipitation. Journal of Geophysical Research, 1979, 84(C8): 5029-5033. DOI:10.1029/JC084iC08p05029 |
| [34] |
Majoube M. Oxygen-18 and deuterium fractionation between water and steam. Journal de Chimie Physique et de Physico-Chimie Biologique, 1971, 68(10): 1423-1436. |
| [35] |
Xiao W, Wen X, Wang W et al. Spatial distribution and temporal variability of stable water isotopes in a large and shallow lake. Isotopes in Environmental & Health Studies, 2016, 52(4/5): 443-454. DOI:10.1080/10256016.2016.1147442 |
 2017, Vol. 29
2017, Vol. 29 
