(2: 南京水利科学研究院生态环境研究中心, 南京 210029)
(3: 中国科学院生态环境研究中心, 北京 100085)
(2: Center for Eco-Environmental Research, Nanjing Hydraulic Research Institute, Nanjing 210029, P. R. China)
(3: Research Center for Eco-Environment Sciences, Chinese Academy of Sciences, Beijing 100085, P. R. China)
水是人类社会重要的基础性自然资源,而湖泊是世界上重要的淡水资源库之一.然而,随着社会经济的快速发展,湖泊水环境已遭受严重的污染,众多湖泊呈现出严重的富营养化问题,降低了湖泊功能,加剧了水资源短缺.无论是经济发达还是发展中国家与地区,都面临着不同程度的湖泊富营养化问题[1].加拿大的温尼伯湖,受集水区域内大量农业生产的影响,每年有高达5900 t的总磷和56300 t的总氮净输入该湖泊[2],导致沉积物中氮、磷浓度迅速增加,并在夏季出现越来越严重的蓝藻水华.非洲最大的内陆渔业基地维多利亚湖,受沿岸生活污水、工业废水排放等影响,在1990s鱼类能够生长繁殖的区域面积减少了70%,蓝藻水华暴发时,水中蓝藻浓度可达34000 cells/ml,水体透明度下降到1 m左右[3].欧洲湖泊同样面临严重的富营养化问题:如匈牙利的巴拉顿湖[4]、位于瑞士和德国交界的Constance湖[5]等都出现过严重的富营养化现象.我国由于近几十年经济高速发展,湖泊资源的不合理开发利用,使湖泊富营养化进程大大加快,如滇池、太湖、巢湖等都已处于富营养化状态.
湖泊富营养化和藻类水华严重威胁着生态安全和饮用水安全,在湖泊生态系统未根本性恢复到健康状态之前,及时准确进行湖泊水华预测对湖泊水环境管理具有重要作用.富营养化数学模型是进行湖泊水环境预测、治理和管理的重要工具.从1970s至今,富营养化模型有了很大的发展,经历了由单一元素向多种元素、局部过程向系统过程、时空均质性向时空异质性的发展[6],大致可分为4类:单一营养物质负荷模型[7]、浮游植物与营养盐相关模型[8]、生态水动力模型[9-13]以及人工智能模型[14-18].由于对富营养化及水华暴发的机理尚未完全清楚,导致模型过程概化、参数率定、边界条件设定等存在误差,从而降低模型的精度.随着观测技术的快速发展,高质量的监测数据量迅速增加,如何有效利用不断增长的监测数据和持续改进的数值模型,是当前研究的热点.
数据同化是将观测数据与数值模型计算结果相融合,对模型状态进行最优估计,实现模型状态和参数的不断更新,从而提高模型的模拟精度.国内外学者在数据同化方面开展了大量研究,已成功应用于数值天气预报[19]、海洋科学[20]、水文预报[21]以及陆面过程[22]等多个领域. 1990s后,数据同化发展为连续数据同化和顺序数据同化两大类.连续数据同化算法定义一个同化的时间窗口T,利用该同化窗口内的所有观测数据和模型状态值进行最优估计,通过迭代以不断调整模型初始场,最终将模型轨迹拟合到同化窗口周期内获取的所有观测上,如三维变分和四维变分算法等[23].三维变分进行的是三维空间的全局分析,避免了分析不是全局最优的问题;但三维变分无法利用后面时刻的资料来订正前面的结果,同化的解在时间上不连续.四维变分是三维变分的推广,考虑了时间维,成为目前最常用的变分方法,在很多数值天气预报业务系统(如欧洲中期天气预报中心、美国国家大气研究中心等)中使用.四维变分可同化多时刻的资料,也可在代价函数中加上其他的弱约束项.但对于复杂模式而言,由正模型的离散形式直接得到伴随方程的离散形式,仍然是一个比较艰巨的任务,因此,在计算方面,四维变分比三维变分代价大得多.近年来,以卡尔曼滤波为代表的顺序数据同化方法得到了广泛应用[24],其独特优势在于:①与传统最优插值算法相比,它使得预报误差随模型动态发展,而最优插值中的预报误差是给定的,脱离了模型状态的动态变化;②与变分相比,卡尔曼滤波提供了状态量的均值及其相应的误差协方差,而变分无法提供状态量的协方差矩阵;③卡尔曼滤波无需编写模型的伴随模式,更容易实现.由于卡尔曼滤波需要分析和存储随时间变化的协方差,因此计算量大,在状态线性变化和高斯分布假设条件下能获得最优解;但是在数据同化中状态变量通常都是非线性变化的,且高斯分布条件也很难满足,从而导致其使用受到极大的制约.基于集合论和统计理论的集合卡尔曼滤波(EnKF)[25]具有程序设计相对简单、不需要伴随或切线性算子、可应用于非线性系统、易于实现并行运算等优点,弥补了传统卡尔曼滤波的不足.
本研究选择成熟的Delft3D-BLOOM作为富营养化模型,以太湖为研究对象,建立了基于EnKF的蓝藻浓度数值模型与数据同化系统,通过分析确定了初始场扰动、观测场扰动、集合数等同化系统的关键参数,提高了太湖蓝藻水华预测精度,为集合卡尔曼滤波在湖库富营养化模型数据同化中的应用提供了参考.
1 材料与方法 1.1 研究区域及采样点分布太湖(30°55′40″~31°32′58″N,119°52′32″~120°36′10″E)是我国第二大淡水湖,是典型的浅水湖泊,湖面面积2338.11 km2,南北长68.5 km,东西平均宽34 km,最大水深2.6 m,平均水深1.89 m,湖盆形态呈浅碟形[26].太湖自1990s中期大部分区域已达到中营养到富营养状态,尤其是梅梁湾处于重度富营养水平[27].针对太湖水体富营养化现象,国家采取了一些相应措施改善水质,虽然取得一定成效,但未能从根本上解决太湖富营养化问题[28]. 1980s太湖水体中藻类以绿藻、硅藻、蓝藻为总体优势群,分别占40%、28%和20%.而1990s以来,太湖蓝藻不仅呈全湖性分布,而且出现时间长,几乎全年出现,蓝藻门最高时约占总量的91.6%[29]. 2003年以来,蓝藻水华开始向湖心扩散,严重时几乎覆盖整个太湖的非水生植被区[30]. 2007年暴发了大面积蓝藻水华,无锡贡湖水源地受到严重污染,引发供水危机. 2008年太湖藻类平均密度为1.488×107 cells/L,其中蓝藻密度为1.199×107 cells/L[29].从2009—2011年太湖水质特性(表 1)可见,蓝藻门生物量远大于其他门类.因此,本研究选择太湖为对象,开展蓝藻浓度数值模型的数据同化分析.
| 表 1 2009—2011年太湖水质特性 Tab.1 Water quality attributes of Lake Taihu during 2009-2011 |
本研究收集了太湖2009—2011年的水文、水动力、水质和藻类生物量数据.其中水文、水动力数据来自太湖流域管理局,包括18条主要出入湖河流水位及流量数据,监测频率为每月1次;太湖5个水位监测站的水位数据,监测频率为每天1次.其余数据除光照来自中国气象科学数据共享网(http://data.cma.cn/site/index.html)外,全湖29个站点(图 1)的水温(T)、光照、溶解氧(DO)、氨氮(NH3-N)、硝酸盐氮(NO3--N)、总氮(TN)、总磷(TP)、磷酸盐(PO43-)、叶绿素a、蓝藻生物量、绿藻生物量和硅藻生物量数据依托太湖流域管理局采样与分析设备自测获得,监测频率为每月1次,水温、溶解氧现场测定,具体的水质特性见表 1.

|
图 1 太湖监测点位分布(1:三号标、2:拖山、3:直湖港、4:小湾里、5:竺山湖、6:龙头、7:大贡山、8:沙墩港、9:渔业村、10:贡湖、11:东太湖、12:庙港、13:戗港外、14:乌龟山、15:平台山、16:焦山、17:14号灯标、18:湖心南、19:横山、20:大浦口、21:伏东、22:夹浦、23:新塘、24:小梅口、25:大钱闸、26:西山、27:胥口、28:漫山、29:胥湖) Fig.1 Distribution of monitoring sites in Lake Taihu |
Delft3D-BLOOM模型是广泛应用于计算初级生产力、叶绿素a浓度、浮游植物功能群结构的二维水生态模型,由荷兰WL | Delft Hydraulics开发,现已得到广泛应用.它可以模拟包括蓝藻、绿藻和硅藻在内多达15类浮游植物的生消. Los等[31]对荷兰North Sea的叶绿素a浓度进行了模拟;Chen等[32]利用Delft3D模拟了淀山湖不同季节水动力水质条件下藻类的生长情况;Kuang等[33]在香港大鹏湾应用Delft3D模型研究其水体干湿两季的水文环境和水华的运移规律;Lee等[34]在珠江入海口基于Delft3D建立了三维模型来研究赤潮对流.为了模拟藻类在不同环境条件下的适应性,通常将藻类分为光能限制型(E-型)、氮限制型(N-型)和磷限制型(P-型)3种类型.模型主要包括营养物质输移和初级生产力等主要过程.在计算过程中与水动力模块Delft3D-FLOW耦合,由于太湖水动力以风生流为主,模拟时风场条件设置参考许旭峰等[26]的研究成果.
对于浅水湖泊,水体中物质的输移采用包括源汇项及反应项的二维对流扩散方程:
| $ \frac{{\partial C}}{{\partial t}} = {D_x}\frac{{{\partial ^2}C}}{{\partial {x^2}}}-{v_x}\frac{{\partial C}}{{\partial x}} + {D_y}\frac{{{\partial ^2}C}}{{\partial {y^2}}}-{u_y}\frac{{\partial C}}{{\partial y}} + S-fR\left( {C, t} \right) $ | (1) |
式中,C为浓度(kg/m3);Dx和Dy分别为x和y方向上的扩散系数(m2/s);S为源项;t为时间(s);vx和vy分别为x和y方向上的涡流粘度(m2/s);fR(C, t)为反应项,考虑了氮的硝化、反硝化、藻类吸收和矿化过程,磷的吸附、解吸、藻类吸收和矿化过程,溶解氧的耗氧、大气复氧、藻类光合作用泌氧和呼吸作用耗氧等过程,具体参考Delft3D-WAQ技术手册[35].
BLOOM中初级生产力主要取决于温度修正的特定生长速率、死亡速率和维持性呼吸速率,其函数为:
| $ kg{p_i} = \mathit{ProAlg}_i^0 \cdot \mathit{TcPAlg}_i^T $ | (2) |
| $ kmr{t_i} = \mathit{MorAlg}_i^0 \cdot \mathit{TcMAlg}_i^T $ | (3) |
| $ krs{p_i} = \mathit{ResAlg}_i^0 \cdot \mathit{TcRAlg}_i^T $ | (4) |
式中,kgpi为藻类的生长速率(d-1),ProAlgi0为藻类在0℃时的生长速率(d-1),TcPAlgiT为生长速率温度系数,kmrti为藻类死亡速率(d-1),MorAlgi0为藻类在0℃时的死亡速率(d-1),TcMAlgiT为死亡速率温度系数,krspi为藻类维持性呼吸速率(d-1),ResAlgi0为藻类在0℃时的维持性呼吸速率(d-1),TcRAlgiT为维持性呼吸速率温度系数.各参数率定后的取值见表 2[36].
| 表 2 类3种限制类型相关参数率定后的取值[36] Tab.2 Values of E-limited, N-limited and P-limited parameters of tliree algal function groups after calilDration[36] |
EnKF的计算过程包括预报和分析两部分,其主要计算步骤为:
1) 预报阶段:在预报阶段,根据公式(5)来预测集合中每个成员在T+ΔT时刻的状态变量.
| $ C_{T + \Delta T}^i = f\left( {C_T^i, u_{T + \Delta T}^i, \theta _T^i} \right) + \xi _{T + \Delta T}^i, i = 1、\cdots 、n $ | (5) |
| $ u_{T + \Delta T}^i = {u_{T + \Delta T}}\left( {1 + {\eta ^i}} \right), {\eta ^i} \sim N\left( {0, \eta } \right) $ | (6) |
| $ \theta _0^i = {\theta _0}\left( {1 + {\sigma ^i}} \right), \sigma \sim N\left( {0, \sigma } \right) $ | (7) |
| $ \xi _{T + \Delta T}^i \sim N\left( {0, \xi } \right) $ | (8) |
式中,f为模型算子;CT+ΔTi为T+ΔT时刻的状态变量预测值;uT+ΔTi为驱动数据,通过对初始数据增加均值为0、方差为σ的高斯白噪声生成;本研究的驱动数据主要包括太阳辐射和水温;θ0i为待同化的参数,是在初始值θ0的基础上增加均值为0、方差为σ的高斯白噪声生成;ξT+ΔTi代表由模型结构不确定性引起的误差,该噪声的方差为模拟状态变量的10%.
2) 分析阶段:在分析阶段,根据公式(9)对参数进行更新,然后通过公式(12)求得更新后的参数集合估计最优值.
| $ \theta _{T + \Delta T}^{i + } = \theta _T^{i + } + K_{T + \Delta T}^\theta \left( {C_{T + \Delta T}^i-\hat C_{T + \Delta T}^i} \right) $ | (9) |
| $ \hat C_{T + \Delta T}^{i + } = \hat C_{T + \Delta T}^i + \omega _{T + \Delta T}^i, \omega _{T + \Delta T}^i \sim N\left( {0, \omega } \right) $ | (10) |
| $ K_{T + \Delta T}^\theta {\rm{ = }}\beta _{T + \Delta T}^{\theta \hat C}{\left( {\beta _{T + \Delta T}^{CC} + \beta _{T + \Delta T}^{\hat C\hat C}} \right)^{-1}} $ | (11) |
| $ {\theta _{T + \Delta T}}{\rm{ = }}E\left[{\theta _{T + \Delta T}^{i + }} \right]{\rm{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {\theta _{T + \Delta T}^{i + }} $ | (12) |
式中,θT+ΔTi+为状态分析值;θTi+为T时刻状态预测值;KT+ΔTθ为更新参数的卡尔曼增益矩阵;
状态变量根据公式(13)进行更新,通过公式(15)求得更新后状态变量集合的平均值作为最优的状态估计.
| $ C_{T + \Delta T}^{i + } = C_{T + \Delta T}^i + K_{T + \Delta T}^C\left( {C_{T + \Delta T}^i-\hat C_{T + \Delta T}^i} \right) $ | (13) |
| $ K_{T + \Delta T}^C = \beta _{T + \Delta T}^{C\hat C}{\left( {\beta _{T + \Delta T}^{CC} + \beta _{T + \Delta T}^{\hat C\hat C}} \right)^{-1}} $ | (14) |
| $ {C_{T + \Delta T}}{\rm{ = }}E\left[{C_{T + \Delta T}^{i + }} \right] = \frac{1}{n}\sum\limits_{i = 1}^n {C_{T + \Delta T}^{i + }} $ | (15) |
式中,E表示取平均值;n为集合个数;KT+ΔTC为更新状态变量的卡尔曼增益矩阵;
采用EnKF方法对实际观测数据进行同化之前,需要进行数值实验,以确定合理的同化方案.首先恰当的参数设置有利于EnKF方法获得更令人满意的结果[37]. EnKF是利用各成员在集合平均值上的离散度来统计出预报误差协方差和分析误差协方差.要准确估计一个概率密度,需要一定的集合数,如果集合数太少,模型的误差协方差可能会估计错误;如果集合数过多,则会不可避免地带来巨大的计算量,并且当集合数超过一定数量后,同化结果将趋于稳定,而不再有大幅度的改进[38].在参考前人研究的基础上,为有效地平衡同化精度和计算量,本研究对不同的集合数取值对同化结果的影响进行了研究.
其次,虽然理论上将观测数据与预报模型结合,通过数据同化方法能够实现模型模拟结果和观测数据的最佳融合,但这种“最佳”与模型的模拟误差协方差和观测误差协方差的精度密切相关.预测误差协方差和观测误差协方差的估计准确与否,是决定EnKF方法同化精度的关键.然而,实际应用中很难精确得到这些统计量信息[39],因此对模拟误差协方差和观测误差协方差进行优化估计是EnKF方法应用过程中的必要步骤.不同的应用实际其同化方案不同,数据同化方案的设计应兼顾同化精度和计算负荷.因此,在具体应用之前,应进行数值实验以确定合理的同化方案.
1.6 模型性能分析分别采用均方根误差(root mean square error, RMSE)和一致性指数(Index of Agreement, IOA)来定量衡量模型的模拟值与观测值的一致程度.
| $ RMSE = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{C_i}-{{\hat C}_i}} \right)}^2}/n} } $ | (16) |
式中,Ci为模拟值,
| $ IOA = 1-\frac{{\sum {{{\left( {{y_{\rm{o}}}-{y_{\rm{s}}}} \right)}^2}} }}{{{{\sum {\left( {\left| {{y_{\rm{s}}}-{{\bar y}_{\rm{o}}}} \right| + \left| {{y_{\rm{o}}} - {{\bar y}_{\rm{o}}}} \right|} \right)} }^2}}} $ | (17) |
式中,yo为蓝藻生物量观测值,ys为蓝藻生物量模型模拟值.
2 结果选择蓝藻生物量作为状态变量,选择敏感性最高的E-型蓝藻最大生长速率温度系数作为待同化参数[40],以太湖29个站点每月1次的蓝藻生物量实测值作为观测值,对模型的状态变量和参数进行同化.首先将模型计算1年(2009-01-01—2009-12-31),使模型达到稳定后,在2010-01-01—2011-12-31时段开展数据同化.
2.1 数据同化方案确定研究设置了6种集合数(30、50、70、100、200和500),并用RMSE来表征不同集合数下同化后的状态变量与观测值的一致程度.从图 2可以看出随着集合数的增大,RMSE逐渐减小,当集合数达到100后,RMSE减小速度大幅降低,同化结果趋于稳定.
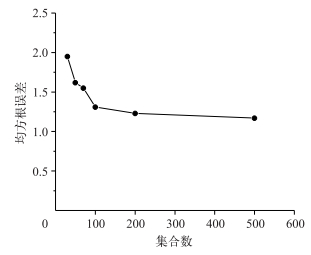
|
图 2 不同集合数下的均方根误差 Fig.2 Root mean square error (RMSE) of different ensemble sizes |
本研究将观测误差和模拟误差均分别设置了1%、10%、20%、30% 4种情况. 表 3列出了16种不同的观测误差和模拟误差组合下同化结果的RMSE.从表中可以看出,当观测误差为1%、模拟误差为10%和20%时,同化结果的RMSE均较小,且差别不大.
| 表 3 不同观测误差和模拟误差下的均方根误差 Tab.3 RMSE under different error variance settings for observation and simulation |
根据以上分析,确定适合本研究实例和富营养化模型的集合卡尔曼滤波数据同化设置:集合数为100,模拟误差为10%,观测误差为1%.
2.2 数据同化分析 2.2.1 只同化状态变量采用直接插值法对蓝藻生物量进行更新,即参数值保持不变,不对观测值和状态变量进行扰动,直接以观测值作为状态变量的最优估计.将太湖29个观测站蓝藻生物量的观测值插值到整个研究区域,在模型按设置的时间步长(dt)进行计算的过程中,在有观测值的时刻,将插值后得到的观测场作为下一时刻蓝藻生物量的初始场对模型继续进行计算.考虑到监测站点众多,计算结果无法一一列出,故从8个湖区各取1个代表性站点进行结果展示.从图 3可以看出,在每次遇到观测值时刻之后,数据同化模型结果比Delft3D-BLOOM直接模拟结果更为接近观测值,然后又趋近于Delft3D-BLOOM模拟值.当采用状态变量同化模式时,大部分站点模拟结果的IOA值较Delft3D-BLOOM直接模拟结果的IOA值有所上升(图 4),说明状态变量同化对提高模型的预测精度有一定效果.
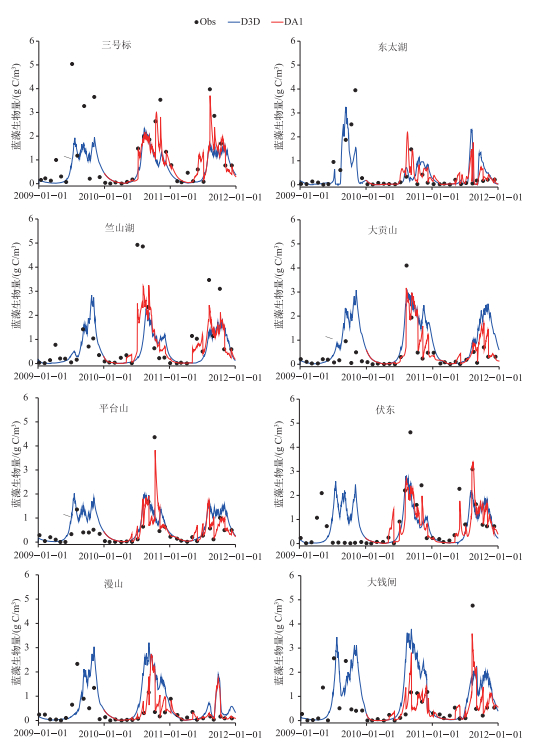
|
图 3 蓝藻生物量观测值(Obs)、Delft3D-BLOOM直接模拟值(D3D)以及只同化状态变量时的模拟值(DA1) Fig.3 Observations (Obs), simulation results of Delft3D-BLOOM (D3D) and state variables assimilated model (DA1) of blue-green alga biomass |
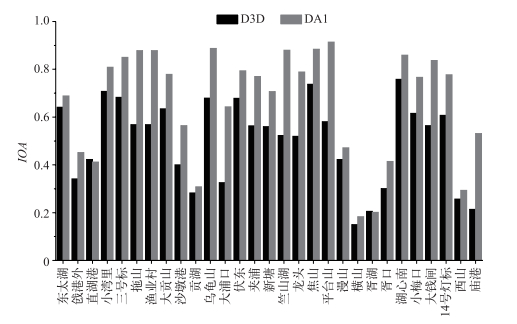
|
图 4 Delft3D-BLOOM直接模拟结果和只同化状态变量时模拟结果的IOA值 Fig.4 IOA values of Delft3D-BLOOM model and state variables assimilated model |
采用太湖29个观测站点实测的蓝藻生物量数据,对Delft3D-BLOOM模型的状态变量和参数同时进行同化.结果显示经过EnKF方法对模型参数和状态同时进行更新后,模型的预测精度有了明显的提高(图 5).模拟结果不仅可以很好地反映蓝藻生物量的变化趋势,而且对蓝藻生物量峰值的模拟结果有显著改善.采用EnKF方法进行数据同化后,模拟结果的IOA值有显著提高,绝大部分达到0.9以上(图 6),说明同时对状态变量和参数进行同化对提高模型的预测精度有明显效果.
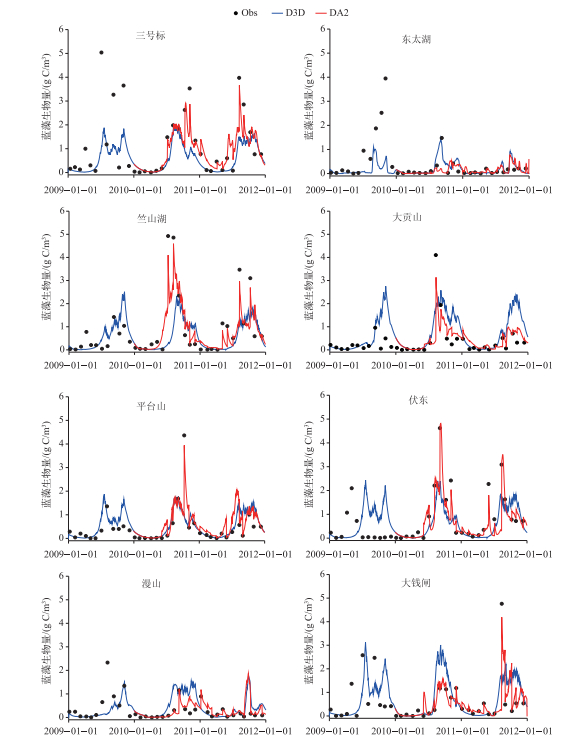
|
图 5 蓝藻生物量观测值、Delft3D-BLOOM直接模拟值以及同时同化状态变量和参数时的模拟值(DA2) Fig.5 Observations, simulation results of Delft3D-BLOOM, simulation results state variables and parameter assimilated model (DA2) of blue-green alga biomass |
|
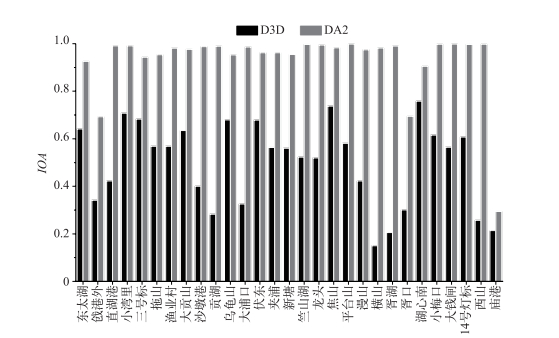
图 6 Delft3D-BLOOM直接模拟结果以及同时同化状态变量和参数时模拟结果的IOA值 Fig.6 IOA values of Delft3D-BLOOM model, state variables and parameter assimilated model |
通过对比Delft3D-BLOOM模型本身模拟结果的IOA值、只同化状态变量、同时同化状态变量和参数时的IOA值大小发现,采用只同化状态变量的模式时,模拟结果的IOA值较BLOOM模型本身模拟结果的IOA值略有上升;采用同时同化状态变量和参数的模式时,模拟结果的IOA值较BLOOM模拟结果有了明显的提高(图 7).这说明同时同化状态变量和参数的同化模式较只同化状态变量的同化模式更优.
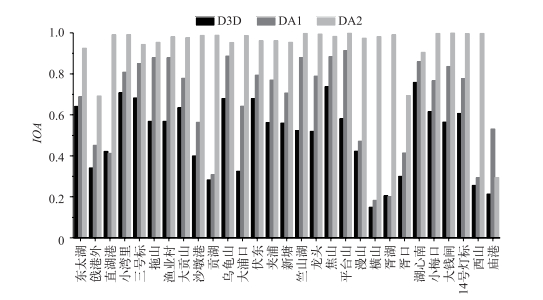
|
图 7 Delft3D-BLOOM直接模拟结果、只同化状态变量时模拟结果以及同时同化状态变量和参数时模拟结果的IOA值 Fig.7 IOA values of Delft3D-BLOOM, state variables assimilated model and state variables and parameter assimilated model |
本研究通过数据同化方法,利用监测数据,持续动态地提升了太湖蓝藻浓度模拟模型计算精度. Evensen等[41]和Houtekamer等[42]的研究结果表明当集合数为100左右时即可获得令人满意的结果.本文数值实验表明当集合数<100时,模型的RMSE随集合数的增大而快速减小,集合数的大小对RMSE影响较大;当集合数>100时,集合数对RMSE的影响不明显, 主要原因是EnKF统计误差相关场存在虚假的相关,而集合数的增加会减少虚假的相关.因此,集合数设置为100既能达到较理想的模拟精度,又能兼顾同化系统的计算效率.
系统噪声是数据同化的一个关键要素,对同化性能有重要影响[43].当设置的观测误差较小时,认为观测值的精度较高,同化结果就会更接近观测值;同理,当设置的模拟误差较小时,认为模型模拟值的精度较高,则同化结果会较为接近模拟值.一般情况下,我们认为观测值的误差较小,相较模拟值,观测值更接近真实值. Rens[43]研究了状态变量系统噪声对模型输出叶绿素a浓度的影响,发现当模拟误差为1%、5%、10%、15%、20%和25%时,叶绿素a浓度的误差均稳定在3%左右.师春香等[44]进行单点陆面土壤湿度同化试验时,根据经验选取模拟误差3%,观测误差分别取1%和3%,同化后进行对比得到当观测误差取1%时结果更优.从本研究进行的16种不同观测误差和模拟误差组合下同化结果的RMSE来看,当模拟误差一定时,RMSE随观测误差的增大而增大;当观测误差一定时,RMSE随模拟误差的增大而增大的趋势并不明显.所以,观测误差对同化精度的影响较模拟误差大,李渊等[24]在太湖叶绿素a模型分析中也得到了相似的结论.对本研究而言,最合适的观测误差为1%,模拟误差为10%.
从图 4和图 6的IOA值可以看出两种同化模式都不同程度提高了模型的模拟精度,但是在个别时刻数据同化后的结果比未同化的结果差,可能此时模型误差被低估,以至于模型状态更新的时候忽略了数据同化的预报集合.当只同化状态变量时,在有观测值的时刻数据同化模拟结果接近观测值,这是因为采用直接插值法对状态变量进行同化时,遇到观测值的时刻对初始场重新赋值,使得模拟结果瞬间重合观测值;但由于初始场对模型计算结果的影响随着时间步长的增加逐渐消失,模型的计算结果逐渐趋近Delft3D-BLOOM直接模拟的结果.当同时同化状态变量和参数时,模型的预测精度有了很大的提高,模拟结果不仅可以很好地模拟蓝藻生物量的变化趋势,还使蓝藻生物量峰值的模拟效果有了很大的提升.同时对状态变量和参数进行同化时,一方面对状态变量进行同化为下一时段的模型计算提供了更精确的初始场;另一方面,根据站点实测值同化后得到的参数更适合当前时段的系统,这两方面共同改善了模型的模拟精度[45].因此,采用监测数据动态更新状态变量和模型参数可有效提升复杂的湖泊富营养化数值模型的模拟精度.
4 结论1) 同化方案的设置对模型效率和计算成本具有显著影响.在本研究中,当集合数为100时,模型数据同化的计算效率和模拟精度均可得到令人满意的结果;当模拟误差设置为10%、观测误差设置为1%时,同化后的模拟精度最高;观测误差较模拟误差对系统的影响更大.
2) 采用EnKF方法进行数据同化后,模型的模拟结果IOA值均得到提高.只同化状态变量时,大部分站点的IOA值略有上升;同时同化状态变量和参数时,绝大部分站点的IOA值有显著提高,且达到0.9以上.
3) 同化状态变量对提高模型预测精度有一定效果,但是效果维持的时间很短;同时同化状态变量和参数比只同化状态变量时的结果更优,其模拟结果不仅能很好地反映蓝藻生物量的变化趋势,还显著提高了蓝藻生物量峰值的模拟精度,有助于提升对蓝藻水华的预测能力.
| [1] |
Qin Boqiang, Xu Hai, Dong Baili. Eutrophication of lakes governance theory and practice. Beijing: Higher Education Press, 2011, 161-162. [秦伯强, 许海, 董百丽. 富营养化湖泊治理的理论与实践. 北京: 高等教育出版社, 2011, 161-162.]
|
| [2] |
Board LWS. Reducing nutrient loading to Lake Winnipeg and its watershed: Our collective responsibility and commitment to action. Lake Winnipeg Stewardship Board, 2006: 30.
|
| [3] |
Ochumba PBO, Kibaara DI. Observations on blue-green algal blooms in the open waters of Lake Victoria, Kenya. African Journal of Ecology, 1989, 27(1): 23-34. DOI:10.1111/j.1365-2028.1989.tb00925.x |
| [4] |
Wang Debin, Nie Ming, Geng Kaiyou. Comparative study on pollution control between dianchi lake and balaton lake. Journal of Kunming University, 2013, 35(6): 51-53. [王德斌, 聂铭, 耿开友. 滇池与巴拉顿湖污染治理的比较研究. 昆明学院学报, 2013, 35(6): 51-53.] |
| [5] |
Straile D, Geller W. Crustacean zooplankton in Lake Constance from 1920 to 1995: Response to eutrophication and re-oligotrophication. Advances in Limnology, 1998, 53: 255-274. |
| [6] |
Liu Yuanbo, Chen Weimin. Review on simulation study on algal dynamics. J Lake Sci, 2000, 12(2): 171-177. [刘元波, 陈伟民. 湖泊藻类动态模拟. 湖泊科学, 2000, 12(2): 171-177. DOI:10.18307/2000.0212] |
| [7] |
Vollenweider RA. Input-Output models with special reference to the phosphorus loading concept in limnology. Schweizerische Zeitschrift für Hydrologie, 1975, 37(1): 53-84. |
| [8] |
Han Fei, Chen Yongcan, Liu Zhaowei. Advance in the eutrophication models for lakes and reservoirs. Advances in Water Science, 2003, 14(6): 785-791. [韩菲, 陈永灿, 刘昭伟. 湖泊及水库富营养化模型研究综述. 水科学进展, 2003, 14(6): 785-791.] |
| [9] |
Jørgensen SE, Mejer H, Friis M. Examination of a lake model. Ecological Modelling, 1978, 4(2): 253-278. |
| [10] |
Liang Li, Deng Yun, Zheng Meifang et al. Predicting of eutrophication in the LongChuan River based on CE-QUAL-W2 model. Resources and Environment in the Yangtze Basin, 2014(s1): 103-111. [梁俐, 邓云, 郑美芳等. 基于CE-QUAL-W2模型的龙川江支库富营养化预测. 长江流域资源与环境, 2014(s1): 103-111.] |
| [11] |
Chen Faxing. Numercial simulation of water quality in Minghu reservoir based on EFDC and water quality prediction. Yellow River, 2016, 38(1): 85-87. [陈法兴. 基于EFDC模型的明湖水库水质数值模拟及预测. 人民黄河, 2016, 38(1): 85-87.] |
| [12] |
Zhong Xiaohang, Wang Feier, Yu Jie et al. Application of WASP model and gini coefficient in the total amount control of water pollutant: A case study in Tiaoxi estuary of south Taihu Lake. Journal of Zhejiang University: Science Edition, 2015, 42(2): 181-188. [钟晓航, 王飞儿, 俞洁等. 基于WASP水质模型与基尼系数的水污染物总量分配——以南太湖苕溪入湖口区域为例. 浙江大学学报:理学版, 2015, 42(2): 181-188.] |
| [13] |
Wei Xingyao, Wang Chao, Wang Peifang. AQUATOX model for study of eutrophication of tributaries. Water Resources and Power, 2016(3): 44-48. [魏星瑶, 王超, 王沛芳. 基于AQUATOX模型的入湖河道富营养化模拟研究. 水电能源科学, 2016(3): 44-48.] |
| [14] |
Whigham PA, Recknagel F. Predicting chlorophyll-a in freshwater lakes by hybridising process-based models and genetic algorithms. Ecological Modelling, 2001, 146(1): 243-251. |
| [15] |
Zhang Chengcheng, Shen Aichun, Zhang Xiaoqing et al. Application of support vector machine to evaluate the eutrophication status of Taihu Lake. Acta Ecologica Sinica, 2013, 33(23): 7563-7569. [张成成, 沈爱春, 张晓晴等. 应用支持向量机评价太湖富营养化状态. 生态学报, 2013, 33(23): 7563-7569.] |
| [16] |
Wang Xuelian, Song Yuzhi, Kong Fanfan et al. Estimation of chlorophyll-a concentration in Taihu Lake by using Back Propagation (BP) neural network forecast model. Chinese Journal of Agrometeorology, 2016, 37(4): 408-414. [王雪莲, 宋玉芝, 孔繁璠等. 利用BP神经网络模型对太湖水体叶绿素a含量的估算. 中国农业气象, 2016, 37(4): 408-414.] |
| [17] |
Xiang Xianquan, Tao Jianhua. Eutrophication model of Bohai bay based on GA-SVM. Journal of Tianjin University, 2011, 44(3): 215-220. [向先全, 陶建华. 基于GA-SVM的渤海湾富营养化模型. 天津大学学报, 2011, 44(3): 215-220.] |
| [18] |
Xu Xiaoyi, Han Lianghua, Luo Guyuan et al. Prediction of chlorophyll-a by Genetic BP neural network. China Water and Wastewater, 2012, 28(1): 68-71. [许晓毅, 韩亮华, 罗固源等. 遗传-BP神经网络法预测叶绿素a浓度变化. 中国给水排水, 2012, 28(1): 68-71.] |
| [19] |
Panofsky R. Objective weather-map analysis. Journal of Meteorology, 1949, 6(6): 386-392. DOI:10.1175/1520-0469(1949)006<0386:OWMA>2.0.CO;2 |
| [20] |
Pham DT, Verron J, Roubaud MC. A singular evolutive extended Kalman filter for data assimilation in oceanography. Journal of Marine Systems, 1998, 16(3): 323-340. |
| [21] |
Weerts AH, El Serafy GY. Particle filtering and ensemble Kalman filtering for state updating with hydrological conceptual rainfall-runoff models. Water Resources Research, 2006, 42(9): 123-154. |
| [22] |
Galantowicz JF, Entekhabi D, Njoku EG. Tests of sequential data assimilation for retrieving profile soil moisture and temperature from observed L-band radiobrightness. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(4): 1860-1870. DOI:10.1109/36.774699 |
| [23] |
Ma Jianwen, Qing Sixian. Recent advances and development of data assimilation algorithms. Advances in Earth Science, 2012, 27(7): 747-757. [马建文, 秦思娴. 数据同化算法研究现状综述. 地球科学进展, 2012, 27(7): 747-757.] |
| [24] |
Li Yuan, Li Yunmei, Lü Heng et al. Sensitivity analysis on Lake Taihu data assimilation scheme of chlorophyll-a concentration. J Lake Sci, 2015, 27(1): 163-174. [李渊, 李云梅, 吕恒等. 太湖叶绿素a同化系统敏感性分析. 湖泊科学, 2015, 27(1): 163-174. DOI:10.18307/2015.0119] |
| [25] |
Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research Atmospheres, 1994, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
| [26] |
Xu Xufeng, Liu Qingquan. Numerical study on the characteristics of wind-induced current in Taihu lake. Chinese Journal of Hydrodynamics, 2009, 24(4): 512-518. [许旭峰, 刘青泉. 太湖风生流特征的数值模拟研究. 水动力学研究与进展, 2009, 24(4): 512-518.] |
| [27] |
Guo Jing, Chen Qiuwen, Li Weifeng. Application of lake model SALMO to the Meiliang Bay of Taihu lake. Acta Scientiae Circumstantiae, 2012, 32(12): 3119-3127. [郭静, 陈求稳, 李伟峰. 湖泊水质模型SALMO在太湖梅梁湾的应用. 环境科学学报, 2012, 32(12): 3119-3127.] |
| [28] |
Qin Boqiang, Wang Xiaodong, Tang Xiangming et al. Drinking water crisis caused by eutrophication and cyanobacterial bloom in lake Taihu: Cause and measurement. Advances in Earth Science, 2007, 22(9): 896-906. [秦伯强, 王小冬, 汤祥明等. 太湖富营养化与蓝藻水华引起的饮用水危机——原因与对策. 地球科学进展, 2007, 22(9): 896-906.] |
| [29] |
Gu Suli, Chen Fang, Sun Jiangling. Analysis of cyanobacteria monitoring and algal blooms in Taihu Lake. Water Resources Protection, 2011, 27(3): 28-32. [顾苏莉, 陈方, 孙将陵. 太湖蓝藻监测及暴发情况分析. 水资源保护, 2011, 27(3): 28-32.] |
| [30] |
Wang Changyou, Yu Yang, Sun Yunkun et al. The discussion of the early forecasting of cyanobacteria bloom in the Lake Taihu based on ELCOM-CAEDYM model. China Environmental Science, 2013, 33(3): 491-502. [王长友, 于洋, 孙运坤等. 基于ELCOM-CAEDYM模型的太湖蓝藻水华早期预测探讨. 中国环境科学, 2013, 33(3): 491-502.] |
| [31] |
Los FJ, Villars MT, Tol MWMVD. A 3-dimensional primary production model (BLOOM/GEM) and its applications to the (southern) North Sea (coupled physical-chemical-ecological model). Journal of Marine Systems, 2008, 74(1/2): 259-294. |
| [32] |
Chen Y, Lin W, Zhu J et al. Numerical simulation of an algal bloom in Dianshan Lake. Chinese Journal of Oceanology and Limnology, 2016, 34(1): 231-244. DOI:10.1007/s00343-015-4298-0 |
| [33] |
Kuang C, Lee JHW. Physical hydrography and algal bloom transport in Hong Kong waters. China Ocean Engineering, 2005, 19(4): 539-556. |
| [34] |
Lee JHW, Qu B. Hydrodynamic tracking of the massive spring 1998 red tide in Hong Kong. Journal of Environmental Engineering, 2004, 130(5): 535-550. DOI:10.1061/(ASCE)0733-9372(2004)130:5(535) |
| [35] |
WL | Delft hydraulics. Delft3D-WAQ technical reference manual. Delft, The Netherlands, 2009. http://www.delftsoftware.com.
|
| [36] |
Li Z, Chen Q, Xu Q. Modeling algae dynamics in Meiliang Bay of Taihu Lake and parameter sensitivity analysis. Journal of Hydro-environment Research, 2014, 9(2): 216-225. |
| [37] |
Eknes M, Evensen G. An Ensemble Kalman filter with a 1-D marine ecosystem model. Journal of Marine Systems, 2002, 36(1): 75-100. |
| [38] |
Huang Chunlin, Li Xin. Sensitivity analysis on land data assimilation scheme of soil moisture. Advances in Water Science, 2006, 17(4): 457-465. [黄春林, 李新. 土壤水分同化系统的敏感性试验研究. 水科学进展, 2006, 17(4): 457-465.] |
| [39] |
Simon E, Bertino L. Application of the Gaussian anamorphosis to assimilation in a 3-D coupled physical-ecosystem model of the North Atlantic with the EnKF: a twin experiment. Ocean Science, 2009, 5(4): 495-510. DOI:10.5194/os-5-495-2009 |
| [40] |
Huang J, Gao J, Hörmann G. Hydrodynamic-phytoplankton model for short-term forecasts of phytoplankton in Lake Taihu, China. Limnologica-Ecology and Management of Inland Waters, 2012, 42(1): 7-18. DOI:10.1016/j.limno.2011.06.003 |
| [41] |
Evensen G, Van LPJ. Assimilation of Geosat altimeter data for the Agulhas current using the ensemble Kalman filter with a quasigeostrophic model. Monthly Weather Review, 1996, 124(1): 85-96. DOI:10.1175/1520-0493(1996)124<0085:AOGADF>2.0.CO;2 |
| [42] |
Houtekamer PL, Mitchell HL. A sequential ensemble Kalman filter for atmospheric data assimilation. Monthly Weather Review, 2001, 129(1): 123-137. DOI:10.1175/1520-0493(2001)129<0123:ASEKFF>2.0.CO;2 |
| [43] |
Rens EG. Improving the algal bloom prediction in the North Sea by Ensemble Kalman Filtering in the GEM/BLOOM Model[Dissertation]. Delft: Delft University of Technology, 2013. http://repository.tudelft.nl/view/ir/uuid:ba51915d-048e-42a5-a004-8022f82ca83a
|
| [44] |
Shi Chunxiang, Xie Zhenghui, Qian Hui et al. Based on satellite remote sensing data of China's regional soil moisture EnKF data assimilation. Science China Earth Science, 2011, 41(3): 375-385. [师春香, 谢正辉, 钱辉等. 基于卫星遥感资料的中国区域土壤湿度EnKF数据同化. 中国科学:地球科学, 2011, 41(3): 375-385.] |
| [45] |
Mao J, Lee JH, Choi K. The extended Kalman filter for forecast of algal bloom dynamics. Water Research, 2009, 43(17): 4214-4224. DOI:10.1016/j.watres.2009.06.012 |
 2017, Vol. 29
2017, Vol. 29 


