(2: 中国科学院大学, 北京 100049)
(2: University of Chinese Academy of Sciences, Beijing 100049, P. R. China)
太阳光进入水体后,受到水体中的悬浮颗粒物、浮游植物和有色可溶性有机物(CDOM)等水体组分吸收和散射作用的影响,下行辐照度随深度呈接近指数式的衰减.表征下行辐照度在水体中衰减的参数称为下行漫衰减系数(Downwelling diffuse attenuation coefficient, Kd)(下文简称漫衰减系数).漫衰减系数是表观光学量,由水体各组分吸收和后向散射、入射光场环境和水深等因素共同决定[1-2];但由于环境光场影响通常较小,主要由水体吸收和散射等固有光学特性决定,因此,漫衰减系数也常被作为“准固有光学量”[3].实际上,深度z处的光场强度受水体表面至深度z处光辐射传输的综合影响而不仅是深度z处的光束衰减,因此通常使用的漫衰减系数是一定水层内的垂直平均值[4].漫衰减系数对指示水生态系统中生态过程和生物地球化学循环功能的潜在变化具有重要作用[5],在水体浑浊度[6]、输沙和底泥再悬浮[7-8]、上层水体热量传输[9-10]、浮游植物光合作用[11-12]和自然水体初级净生产力[13-14]等研究中发挥着重要作用.
相较于常规测量方法,卫星遥感是大范围获取漫衰减系数最为省时、有效和快速的方法;实际上490 nm处下行漫衰减系数Kd(490)是最为常用的水色遥感标准产品之一[15].目前,对水体漫衰减系数遥感估算算法已有大量研究,主要集中在大洋水体,可以归纳为3类:(1)类型Ⅰ:构建漫衰减系数与叶绿素a浓度的经验关系[16],这是因为大洋Ⅰ类水体漫衰减系数主要受浮游植物的影响;(2)类型Ⅱ:以辐射传输理论为核心的半分析算法,构建Kd(490)与水体固有光学特性、边界条件(如太阳高度角和水面状况等)之间的关系[4, 17-20];(3)类型Ⅲ:构建Kd(490)与离水辐亮度Lw、遥感反射率(Remote Sensing Reflectance,Rrs)等表观光学量的统计关系[15, 21-23].但在中国近岸海域及内陆湖泊水体,Kd(490)经常在10 m-1以上[24-26],叶绿素a、无机悬浮物、CDOM在不同水域不同季节对光衰减的贡献差别很大,而且在这些水域大气校正也存在较大的不确定性.通过大洋一类水体建立的类型Ⅰ和类型Ⅱ应用到这些水域时会产生较大误差;而类型Ⅲ简单易于构建,是目前在浑浊水体中应用较多的Kd(490)遥感估算方法[27].
事实上,针对近海和内陆Ⅱ类水体光学特性,国内外学者基于统计关系对Kd(490)遥感估算进行了大量研究.王晓梅等[28]针对黄东海Ⅱ类水体光学特性,利用Rrs(555)+Rrs(670)并结合Rrs(490)/Rrs(555)的反演模式建立了Kd(490)估算算法;崔廷伟等[22]利用渤海近岸水体生物光学数据集建立了Kd(490)估算经验算法,并以ENVISAT MERIS数据为例进行了模型的示范应用;乐成峰等[24]以Rrs(550)、Rrs(675)、Rrs(731)作为自变量建立了秋季太湖水体的Kd(490)估算的多元回归模型;Zhang等[25]利用MODIS数据的859 nm和745 nm通道分别构建了太湖水体Kd(PAR)遥感估算的单波段模型.但由于经验模型具有很大的空间和季节局限性,且针对不同的卫星波段选择差异较大,目前缺少一种适用于不同卫星传感器数据、具有较强普适性的Kd(490)估算模式.
目前MODIS/EOS(2000年至今)是全球海洋和大型内陆水体水色遥感主要传感器之一,空间分辨率为250~1000 m,白天之内过境2次,数据获取较为容易,具有较长的时间跨度,可以为大型湖泊水色长时间序列观测提供数据基础. GOCI/CMOS为世界首次发射的静止海洋水色传感器,具有可见光到近红外8个波段,空间分辨率为500 m,时间分辨率较高,可提供8:00—15:00每小时的遥感影像,是研究大型湖泊水体水质参数动态变化的一个很好的选择. MSI/Sentinel-2(2015年12月至今)在可见光到近红外之间有13个光谱波段(443~2190 nm),具有较高的空间分辨率(10、20、60 m),可以满足内陆水体的遥感探测需求,具有很好的漫衰减系数遥感反演的潜力. OLCI/Sentinel-3(2016年10月至今)作为延续MERIS/ENVISAT进行全球海洋水色观测的传感器,拥有更多的光谱波段(21个,400~1020 nm)和更强的稳定性,是未来水色遥感的重要数据源.这些卫星数据各有特点,能否针对这些卫星传感器构建一个具有相对普适性的Kd(490)遥感算法?
本文结合2008—2013年太湖4次实测数据,参考已有的算法研究成果,尝试构建一种相对普适的、可以适用于多种卫星传感器的高精度Kd(490)遥感估算模型,为将来从不同时间和空间尺度分析太湖水体Kd(490)动态变化规律,揭示太湖水体光生态环境特征服务,具有重要的科学研究意义和实用价值.
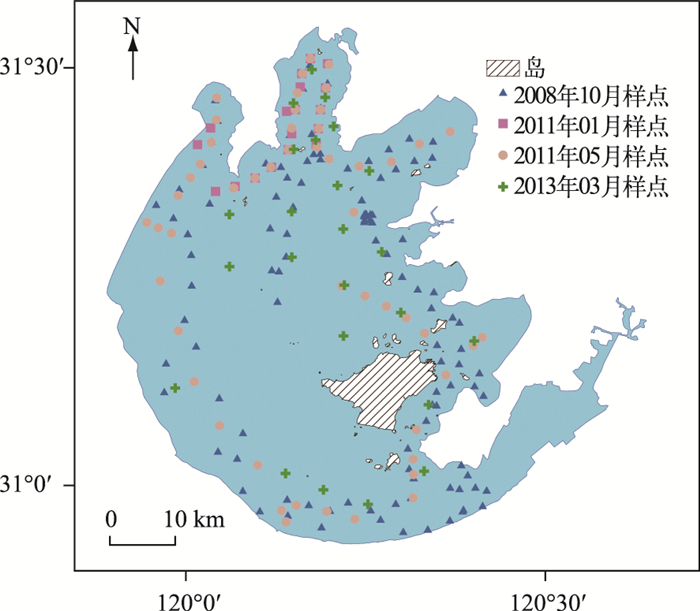
1 材料与方法 1.1 研究区概况太湖(30°56′~31°34′N,119°54′~120°36′E,图 1),面积约2338 km2,平均水深约1.9 m,是中国第三大淡水湖[29].近年来随着太湖地区经济高速发展,太湖水体水质逐渐恶化,富营养化严重,蓝藻水华频繁暴发[30].太湖是典型的内陆Ⅱ类水体,光学特性复杂,水体漫衰减系数存在着较大的时空差异[31-33].
|
图 1 太湖水体实测采样点分布 Fig.1 Spatial distribution of sampling sites in Lake Taihu |
2008年10月、2011年1月、2011年5月和2013年3月对太湖进行了4次野外巡测(图 1和表 1),采样时间通常为9:00~16:30之间,测量时天气晴朗,平均风速2.5 m/s左右,现场测量遥感反射率、水下辐照度和辐亮度、后向散射系数等;并利用棕色瓶采集表层至30 cm处的水样用于室内化学分析.采集得到198组有效样点数据,其中43个样点没有测量水下辐照度和辐亮度.
| 表 1 太湖主要水色参数浓度与水体光学特性统计* Tab.1 Bio-optical properties of water and concentrations of water parameter collected from 4 cruise surveys in Lake Taihu |
水体遥感反射率使用ASD公司生产的FieldSpec Pro FR便携式分光辐射光谱仪(波段为350~1050 nm),采用“水表面以上测量法”进行水面光谱测量,测量时遵守NASA测量规范[34-35].水面以下光谱数据用德国Trios水下光谱仪采集,该仪器具有3个探头,位于同一深度,可同时测量上行辐亮度Lu(λ, z)、上行辐照度Eu(λ, z)和下行辐照度Ed(λ, z),波段测量范围为318~950 nm,光谱分辨率3.3 nm,测量深度取0.3、0.6、0.9、1.2、1.5 m.为了尽量减少船体阴影带来的测量误差,测量时用撑杆将仪器伸出船沿1.5 m左右,并选择在船向阳一侧采集数据.总颗粒物的光谱吸收系数ap(λ)、非色素颗粒物的吸收系数ad(λ)和色素颗粒物的吸收系数aph(λ)、有色可溶性有机物(CDOM)吸收系数ag(λ)等采用岛津UV 2600测量[34].颗粒物的后向散射系数bbp(λ)采用美国Hobilabs公司6通道(420、442、470、510、590、700 nm)后向散射系数测量仪HS-6P现场测量得到,在进行Sigma光路补偿后,以510 nm为参考波长,通过幂函数拟合得到400~700 nm处颗粒物的后向散射系数[34].叶绿素a(Chl.a)浓度使用丙酮萃取法和分光光度计法测定[30].总悬浮物(SPM)浓度、无机悬浮物(SPIM)浓度和有机悬浮物(SPOM)浓度采用称重法测定[30].
1.2.2 漫衰减系数的计算水下辐照度在光学性质均一的水体中遵从指数规律衰减[5],通过对不同深度处的下行辐照度进行指数回归得到[4, 17]:
| $ {\mathit{K}_{\rm{d}}}\left( \mathit{\lambda } \right){\rm{ = - }}\left[{{\rm{ln}}\;{\mathit{E}_{\rm{d}}}\left( {\mathit{\lambda }{\rm{, }}\mathit{z}} \right){\rm{-ln}}\;{\mathit{E}_{\rm{d}}}{\rm{(}}\mathit{\lambda }{\rm{, }}{\mathit{z}_{\rm{c}}}{\rm{)}}} \right]{\rm{/(}}\mathit{z}{\rm{ - }}{\mathit{z}_{\rm{c}}}{\rm{)}} $ | (1) |
式中,Kd(λ)为水深zc~z处的光谱下行平面辐照度平均光谱漫衰减系数(m-1),zc为参考水深,z为水深(m),Ed(λ, z)和Ed(λ, zc)分别为z和zc处的光谱下行平面辐照度(W/(m2·nm).本文中zc选择0.3 m,并且只有当回归方程决定系数R2≥0.97时认为测量有效,否则认为测量无效[34].
1.2.3 卫星波段遥感反射率重采样为构建和评价适用于不同卫星传感器的Kd(490)反演算法,本文基于MODIS/EOS、OLCI/Sentinel-3、GOCI/COMS和MSI/Sentinel-2等传感器波段设置,结合实测遥感反射率(Rrs)和卫星光谱响应函数(Spectral response function,SRF)模拟各卫星波段遥感反射率[36]:
| $ {\mathit{R}_{{\rm{rs, satellite}}}}\left( \mathit{\lambda } \right){\rm{ = }}\frac{{\int_{{\mathit{\lambda }_1}}^{{\mathit{\lambda }_{\rm{2}}}} {{\mathit{R}_{{\rm{rs}}}}\left( \mathit{\lambda } \right){\rm{\cdot}}\mathit{SR}{\mathit{F}_{{\rm{satellite}}}}\left( \mathit{\lambda } \right){\rm{d}}\mathit{\lambda }} }}{{\int_{{\mathit{\lambda }_1}}^{{\mathit{\lambda }_{\rm{2}}}} {\mathit{SR}{\mathit{F}_{{\rm{satellite}}}}\left( \mathit{\lambda } \right){\rm{d}}\mathit{\lambda }} }} $ | (2) |
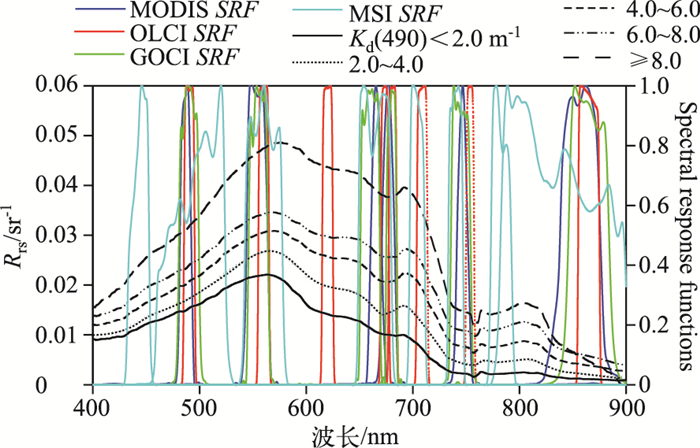
式中,Rrs, satellite(λ)为以中心波长表示的模拟的卫星波段遥感反射率,Rrs(λ)为波长λ处实测光谱遥感反射率,SRFsatellite(λ)为波长λ处卫星光谱响应函数值(图 2).
|
图 2 不同Kd(490)值下水体遥感反射率平均光谱及MODIS、OLCI、GOCI、MSI卫星光谱响应函数 Fig.2 Average remote sensing reflectance spectrum in different ranges of Kd(490) and the SRF of MODIS, OLCI, GOCI and MSI |
在对模型估算值和实测值进行验证和比较时,采用3个指标评价模型性能,主要包括模型拟合决定系数R2、平均绝对误差百分比(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE).其中:
| $ \mathit{MAPE}{\rm{ = }}\frac{1}{\mathit{N}}\sum\nolimits_{\mathit{i} = 1}^\mathit{N} {\frac{{\left| {{\mathit{K}_{\rm{d}}}{{\left( {{\rm{490}}} \right)}_{{\rm{m, }}\mathit{i}}}{\rm{ - }}{\mathit{K}_{\rm{d}}}{{\left( {{\rm{490}}} \right)}_{{\rm{e, }}\mathit{i}}}} \right|}}{{{\mathit{K}_{\rm{d}}}{{\left( {{\rm{490}}} \right)}_{{\rm{m, }}\mathit{i}}}}}} $ | (3) |
| $ \mathit{RMSE}{\rm{ = }}\sqrt {\frac{1}{\mathit{N}}\sum\nolimits_{\mathit{i} = 1}^\mathit{N} {{{\left( {{\mathit{K}_{\rm{d}}}{{\left( {{\rm{490}}} \right)}_{{\rm{m, }}\mathit{i}}}{\rm{ - }}{\mathit{K}_{\rm{d}}}{{\left( {{\rm{490}}} \right)}_{{\rm{e, }}\mathit{i}}}} \right)}^2}} } $ | (4) |
式中,N为样点数,Kd(490)m为实测Kd(490)值,Kd(490)e为估算Kd(490)值.
2 结果与分析 2.1 太湖水体漫衰减系数特性分析 2.1.1 太湖水体Kd(λ)光谱特征太湖水体漫衰减系数光谱Kd(λ)呈现出明显的Ⅱ类水体光谱特征,从蓝光波段到红光波段数值逐渐减小,700 nm波段后数值增加,750 nm左右最高,随后下降,810 nm出现低值,之后再次增加(图 3a).在蓝光波段440 nm处,水体Kd(λ)范围在1.13~9.68 m-1之间,平均值为5.83±2.08 m-1;在绿光波段555 nm处,水体Kd(λ)范围在0.53~5.82 m-1之间,平均值为3.07±1.28 m-1;在红光波段675 nm处,水体Kd(λ)范围在0.90~5.31 m-1之间,平均值为3.09±1.02 m-1. 400~550 nm波段,由于受颗粒物吸收系数控制,Kd(λ)随波长增加呈现指数式衰减;但其中部分样点在440 nm处由于受浮游植物色素吸收的影响形成一个峰值(图 3b);之后直到700 nm左右水体Kd(λ)变化不大,只是在675 nm附近受浮游植物色素的吸收影响形成一个较小的峰值(图 3b).在700~900 nm范围内,由于水体各组分吸收系数和后向散射系数都远小于纯水的吸收系数,水体光束衰减主要由纯水吸收导致,水体Kd(λ)呈现与纯水吸收系数相似的光谱特征[24].

|
图 3 太湖水体漫衰减系数光谱曲线(a), 太湖水体不同组分吸收系数和后向散射系数均值光谱曲线(b) Fig.3 Spectral curves of diffuse attenuation coefficient in Lake Taihu(a); The mean curves of absorption coefficients and backscattering coefficients for different components(b) |
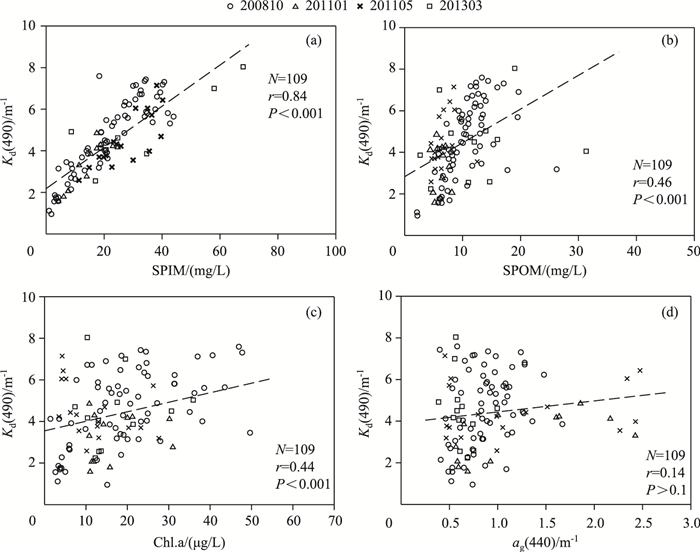
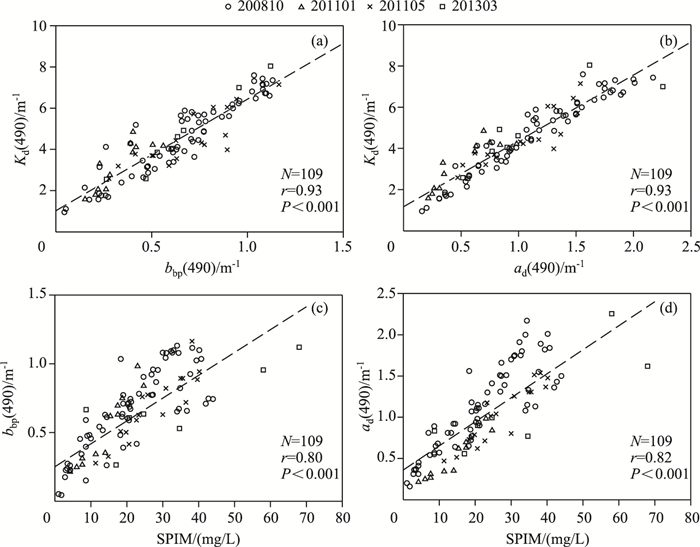
漫衰减系数大小主要由纯水、水中颗粒物和溶解物质浓度共同决定,其中纯水影响水体漫衰减系数的本底值,而其变化主要来源于SPIM、SPOM、Chl.a和CDOM等的影响[37].分析Kd(490)与主要水色参数相关关系(图 4),结果显示除了黄色物质ag(440)之外(P>0.1),均存在显著的统计相关性(P<0.001);需要注意的是,Kd(490)与SPIM相关系数在四者中最高(r=0.84),这表明太湖水体Kd(490)主要由无机悬浮物控制,这是由于太湖水体悬浮物以无机悬浮物为主,对光的衰减占主导地位;Kd(490)与SPOM的相关系数(r=0.46)略高于其与Chl.a的相关系数(r=0.44),这表明有机悬浮物与浮游植物色素不是影响水下光照衰减和分布的首要因子,但有机悬浮物对水下光照衰减的影响略大于浮游植物色素的影响,这是因为一方面有机悬浮物本身就包括浮游植物及其色素,另一方面Chl.a对光的衰减主要集中在其吸收峰光谱波段而在490 nm处对光衰减影响较小.进一步分析发现(图 5),Kd(490)与ad(490)和bbp(490)同样存在显著的统计相关性(r均为0.93,P<0.001),而ad(490)和bbp(490)主要受SPIM影响(r分别为0.82、0.80,P<0.001),这表明无机悬浮物的吸收和散射是Kd(490)的主要影响因子.综上所述,自然光在太湖水体中的衰减主要是水体无机悬浮物的吸收和散射所致,其次是有机悬浮物、浮游植物色素的影响,CDOM的影响较小.
|
图 4 Kd(490)与SPIM(a)、SPOM(b)、Chl.a(c)和CDOM(d)关系的散点图 Fig.4 The relationships between Kd(490) and four bio-optical parameters of the water: SPIM(a), SPOM(b), Chl.a(c) and CDOM(d) |
|
图 5 Kd(490)与bbp(490)(a)、ad(490)(b)关系;SPIM与bbp(490)(c)、ad(490)(d)关系 Fig.5 The relationships between Kd(490) and bbp(490)(a) or ad(490)(b); The relationships between SPIM and bbp(490)(c) or ad(490)(d) |
2008—2013年期间4次野外巡测共采集得到198组样点数据,其中43个样点没有测量水下辐照度和辐亮度,剔除Kd测量无效样点后(R2<0.97),剩余109个样点可以用于漫衰减系数模型分析.将这些数据随机分为两组,其中2/3样点(N=72)用于模型建立,其余1/3(N=37)用于模型验证.
结合实测光谱数据,参考现有的常用Kd(490)估算算法,综合考虑MODIS/EOS、OLCI/Sentinel-3、GOCI/COMS和MSI/Sentinel-2等传感器波段设置,利用72组测试数据率定了12个Kd(490)估算算法模型系数并对反演结果进行了比较(9个经验算法、3个半分析算法,表 2),用于确定适用于太湖水体Kd(490)的遥感估算算法.
| 表 2 不同Kd(490)估算模型和应用到太湖数据的结果* Tab.2 Different Kd(490) algorithms and their results when applied to field data in Lake Taihu |
经验算法包括单波段、波段比值和波段组合模型.由于太湖水体Kd(490)受无机悬浮物影响较大,而随着波长向红光、近红外波段的增加Rrs更能突出悬浮物特征信息[38].单波段模型(模型1~2)利用近红外波段(745、859 nm波段)Rrs分别构建Kd(490)遥感估算模型[25],结果2个单波段模型精度都较低(R2<0.6,RMSE>1.1 m-1,MAPE>27 %).波段比值模型(模型3~5)[20, 23]将大洋一类水体常用蓝绿波段比值模型扩展到蓝红(490 nm/620 nm)、红蓝(674 nm/490 nm)、红绿(674 nm/555 nm)等波段比值,红蓝、红绿波段比值相比单波段模型效果有明显提升,特别是红绿波段比值(R2=0.72,RMSE=0.89 m-1,MAPE=21.58 %),这是因为无机悬浮物是太湖水体漫衰减系数的主要影响因素,555、674 nm波段Rrs足以反映水体总悬浮信息[39-40],并且,比值形式可以减小水体中非悬浮物(主要为CDOM)的影响.波段组合模型(模型6~9)[22, 24, 28, 41]中,模型6主要是将与Kd(490)相关性较好的波段(745、555、674 nm)作为自变量建立Kd(490)的遥感估算模型;模型7~9在大洋一类水体常用蓝绿波段比值基础上引入了能够反映浑浊水体信号变化信息的波段和、比值、差等波段组合形式;最终结果模型6和8估算精度较高(R2>0.70,RMSE<0.90 m-1,MAPE<23.0 %).
半分析算法是在数值求解辐射传输模型的基础上,通过求解a和bb,建立漫衰减系数的半分析模型[4, 17-20].模型10利用准分析算法(multiband quasi-analytical algorithm,QAA)反演水体吸收和后向散射系数,结合半分析模型得到Kd(490);模型11在模型10的基础上进行简化,利用bb(490)和709 nm处辐照度比R(709)良好的线性关系得到490 nm处总吸收系数和总后向散射系数;模型12以bb(490)和670 nm处辐照度比R(670)的线性关系为基础反演了490 nm处的吸收和后向散射系数.结果表明3个半分析模型精度都不高(R2<0.65,RMSE>1.1 m-1,MAPE>25.0 %),这主要是由于这些算法中的经验步骤不适用于光学特性复杂的内陆Ⅱ类水体,使得固有光学量的反演出现了较大的误差(a(490)估算R2<0.6,RMSE>0.6 m-1,MAPE>25.0 %;bb(490)估算R2<0.7,RMSE>0.2 m-1,MAPE>25.0 %),该误差最终传递给要反演的Kd(490),导致估算结果精度低于经验模型.
综上所述,红绿波段比值(模型5)、波段组合模型6、8等3种模型均适用于太湖水体Kd(490)遥感估算.考虑卫星实际应用时,波段组合模型形式较为复杂,而且模型8中引入了内陆水体大气校正精度存在较大的不确定性的蓝光波段(490 nm),因此,不推荐用于内陆湖泊水体Kd(490)卫星遥感估算.红绿波段比值(674 nm/555 nm)模型相对输入波段更少,模型复杂度更低,简单易行,因此,推荐红绿波段比值(674 nm/555 nm)模型作为太湖水体Kd(490)的遥感估算模型.此外,波段比值形式在一定程度上可以消除环境因素的干扰[34, 42-43],还可以减少大气校正的影响[44].
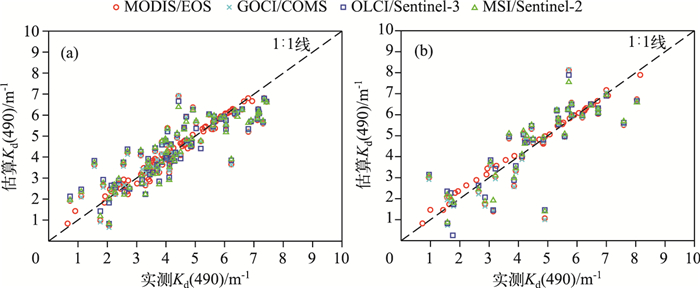
2.3 卫星传感器的估算模型系数率定与算法验证基于实测光谱的模型探究结果表明,红绿波段比值(674 nm/555 nm)对于太湖水体的Kd(490)估算精度较高且简单易行,因此被采用作为卫星估算的基础.但是,由于波段设置和光谱响应函数的差异,不同传感器在红绿波段处的遥感反射率有所差异;因此,需要针对不同传感器波段设置选择Kd(490)估算模型建模波段,并重新率定模型系数.在建模波段选择时,综合考虑模型波段需求与传感器波段设置,分别选择MODIS/EOS中心波长678、551 nm波段,GOCI/COMS中心波长680、555 nm波段,OLCI/ Sentinel-3中心波长673.75、560 nm波段,以及MSI/Sentinel-2中心波长665、560波段作为Kd(490)估算模型建模波段,基于模拟的各卫星波段遥感反射率Rrs, satellite重新率定了模型系数(表 3).可以看出,不同卫星传感器Kd(490)遥感估算模型精度均较高(图 6a,N=72,R2>0.7,RMSE<0.9 m-1,MAPE<22.0 %),并且验证结果较好(图 6b,N=37,R2>0.7,RMSE<0.9 m-1,MAPE<22.0 %).模型估算值与实测值基本都分布在1 :1线附近(图 6),整体都没有明显的高估或者低估现象,结果表明该模型可以用于多种卫星传感器数据的太湖水体Kd(490)遥感估算.
| 表 3 不同传感器Kd(490)遥感估算建模波段与模型系数 Tab.3 Parameters of algorithm to estimate Kd(490) for different satellite sensors |
|
图 6 Kd(490)反演结果与验证:建模数据集(a);验证数据集(b) Fig.6 Red-green ratio algorithm for estimating Kd(490) using simulated satellite sensors using in-situ Rrs in Lake Taihu: calibration(a); validation(b) |
以太湖实测数据为基础,通过分析发现太湖水体漫衰减系数光谱Kd(λ)受纯水、水中颗粒物和溶解物质浓度影响呈现出明显的二类水体光谱特征,并且太湖水体水下光照衰减和分布主要受无机悬浮物的吸收和散射控制,其次是有机悬浮物、浮游植物色素的影响,CDOM的影响较小.基于实测光谱的Kd(490)估算算法探究发现红绿波段的波段比值精度较高,适用性强,且其在一定程度上可以减少大气校正的影响和环境因素的干扰;因此,推荐红绿波段比值模型作为Kd(490)遥感估算模型(具体参数见表 3):
| $ {\mathit{K}_{\rm{d}}}\left( {{\rm{490}}} \right){\rm{ = }}\mathit{a}\left[{{\mathit{R}_{{\rm{rs}}}}{\rm{(Red)/}}{\mathit{R}_{{\rm{rs}}}}{\rm{(Green)}}} \right]{\rm{ + }}\mathit{b} $ | (5) |
该模型反演精度较高,验证结果表明模型适用性较强,可应用到水色卫星上实现太湖水体Kd(490)的卫星遥感监测与研究,为太湖水体水质评价与生态修复提供基础资料.另外,未来工作将Kd(490)估算模型实际应用到水色卫星数据上(MODIS/EOS、GOCI/COMS、OLCI/Sentinel 3和MSI/Sentinel 2等),并揭示其时空分布.
致谢: 感谢国家科技基础条件平台——国家地球系统科学数据共享平台——湖泊—流域科学数据中心(http://lake.geodata.cn)提供数据支撑;感谢王点、梁其椿、张壹萱、房旭等在野外数据采集中的辛勤工作.| [1] |
Gordon HR, Brown OB, Jacobs MM. Computed relationships between the inherent and apparent optical properties of a flat homogeneous ocean. Applied Optics, 1975, 14(2): 417-427. DOI:10.1364/AO.14.000417 |
| [2] |
Gordon HR. Dependence of the diffuse reflectance of natural waters on the sun angle. Limnology and Oceanography, 1989, 34(8): 1484-1489. DOI:10.4319/lo.1989.34.8.1484 |
| [3] |
Baker KS, Smith RC. Quasi-inherent characteristics of the diffuse attenuation coefficient for irradiance. Proceedings of SPIE, 1980, 2: 60-63. DOI:10.1117/12.958264 |
| [4] |
Lee ZP, Du KP, Arnone R. A model for the diffuse attenuation coefficient of downwelling irradiance. Journal of Geophysical Research:Oceans, 2005, 110(C2): 93-106. DOI:10.1029/2004JC002275 |
| [5] |
Mobely CD. Light and water:radiative transfer in natural waters. New York: Academic Press, 1994.
|
| [6] |
Kirk J. Monte Carlo study of the nature of the underwater light field in, and the relationships between optical properties of, turbid yellow waters. Marine and Freshwater Research, 1981, 32(4): 517-532. DOI:10.1071/MF9810517 |
| [7] |
Majozi NP, Salama MS, Bernard S et al. Remote sensing of euphotic depth in shallow tropical inland waters of Lake Naivasha using MERIS data. Remote Sensing of Environment, 2014, 148(148): 178-189. DOI:10.1016/j.rse.2014.03.025 |
| [8] |
Ma R, Tang J, Dai J et al. Absorption and scattering properties of water body in Taihu Lake, China:absorption. International Journal of Remote Sensing, 2006, 27(19): 4277-4304. DOI:10.1080/01431160600851835 |
| [9] |
Stramska M, Zuzewicz A. Influence of the parametrization of water optical properties on the modelled sea surface temperature in the Baltic Sea. Oceanologia, 2013, 55(1): 53-76. DOI:10.5697/oc.55-1.053 |
| [10] |
Wu Y, Tang CC, Sathyendranath S et al. The impact of bio-optical heating on the properties of the upper ocean:A sensitivity study using a 3-D circulation model for the Labrador Sea. Deep Sea Research Part Ⅱ:Topical Studies in Oceanography, 2007, 54(23): 2630-2642. DOI:10.1016/j.dsr2.2007.08.019 |
| [11] |
Loiselle SA, Bracchini L, Cózar A et al. Variability in photobleaching yields and their related impacts on optical conditions in subtropical lakes. Journal of Photochemistry and Photobiology B:Biology, 2009, 95(2): 129-137. DOI:10.1016/j.jphotobiol.2009.02.002 |
| [12] |
Mcclain CR, Arrigo K, Tai KS et al. Observations and simulations of physical and biological processes at ocean weather station P, 1951-1980. Journal of Geophysical Research:Oceans, 1996, 101(C2): 3697-3713. DOI:10.1029/95JC03052 |
| [13] |
Bergamino N, Horion S, Stenuite S et al. Spatio-temporal dynamics of phytoplankton and primary production in Lake Tanganyika using a MODIS based bio-optical time series. Remote Sensing of Environment, 2010, 114(4): 772-780. DOI:10.1016/j.rse.2009.11.013 |
| [14] |
Lee Z, Lance VP, Shang S et al. An assessment of optical properties and primary production derived from remote sensing in the Southern Ocean (SO GasEx). Journal of Geophysical Research:Oceans, 2011, 116(C4): 111-121. DOI:10.1029/2010JC006747 |
| [15] |
Austin R, Petzold TJ. The determination of the diffuse attenuation coefficient of sea water using the Coastal Zone Color Scanner//Oceanography from space. Boston:Springer, 1981, 239-256. DOI:10.1007/978-1-4613-3315-9_29 |
| [16] |
Morel A, Huot Y, Gentili B et al. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sensing of Environment, 2007, 111(1): 69-88. DOI:10.1016/j.rse.2007.03.012 |
| [17] |
Lee ZP, Darecki M, Carder KL et al. Diffuse attenuation coefficient of downwelling irradiance:An evaluation of remote sensing methods. Journal of Geophysical Research:Oceans, 2005, 110(C2): 93-106. DOI:10.1029/2004JC002573 |
| [18] |
Lee Z, Hu C, Shang S et al. Penetration of UV-visible solar radiation in the global oceans:Insights from ocean color remote sensing. Journal of Geophysical Research:Oceans, 2013, 118(9): 4241-4255. DOI:10.1002/jgrc.20308 |
| [19] |
Doron M, Babin M, Mangin A et al. Estimation of light penetration, and horizontal and vertical visibility in oceanic and coastal waters from surface reflectance. Journal of Geophysical Research:Oceans, 2007, 112(C6): 137-154. DOI:10.1029/2006JC004007 |
| [20] |
Wang M, Son S, Hardinf LW. Retrieval of diffuse attenuation coefficient in the Chesapeake Bay and turbid ocean regions for satellite ocean color applications. Journal of Geophysical Research:Oceans, 2009, 114(C10): 244-254. DOI:10.1029/2009JC005286 |
| [21] |
Mueller JL. SeaWiFS algorithm for the diffuse attenuation coefficient, K(490), using water-leaving radiances at 490 and 555 nm, Chapter 3 of SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3. NASA TM-2000-206892, Vol. 11. Greenbelt M D:NASA GSFC, 24-27.
|
| [22] |
Cui Tingwei, Zhang Jie, Ma Yi et al. Remote sensing retrieval model for the diffuse attenuation coefficient Kd(490) of Bohai Sea. Journal of Remote Sensing, 2009, 13(3): 411-422. [崔廷伟, 张杰, 马毅等. 渤海近岸水体漫衰减系数Kd(490)遥感反演模型. 遥感学报, 2009, 13(3): 411-422.] |
| [23] |
Krater S, Brockmann C, Moore G. Using MERIS full resolution data to monitor coastal waters-A case study from Himmerfjärden, a fjord-like bay in the northwestern Baltic Sea. Remote Sensing of Environment, 2008, 112(5): 2284-2300. DOI:10.1016/j.rse.2007.10.006 |
| [24] |
Le Chengfeng, Lee Yunmei, Zha Yong et al. Optical properties and rem ote sensing retrieval model of diffuse attenuation coefficient of Taihu Lake water body. Chinese Journal of Applied Ecology, 2009, 20(2): 337-343. [乐成峰, 李云梅, 查勇等. 太湖水体漫射衰减系数的光学特性及其遥感反演模型. 应用生态学报, 2009, 20(2): 337-343.] |
| [25] |
Zhang Y, Liu X, Yin Y et al. A simple optical model to estimate diffuse attenuation coefficient of photosynthetically active radiation in an extremely turbid lake from surface reflectance. Optics Express, 2012, 20(18): 20482-20493. DOI:10.1364/OE.20.020482 |
| [26] |
Qiu Z, Wu T, Su Y. Retrieval of diffuse attenuation coefficient in the China seas from surface reflectance. Optics Express, 2013, 21(13): 15287-15297. DOI:10.1364/OE.21.015287 |
| [27] |
Xi H, Zhang Y. Total suspended matter observation in the Pearl River estuary from in situ and MERIS data. Environmental Monitoring & Assessment, 2011, 177(1-4): 563-574. DOI:10.1007/s10661-010-1657-3 |
| [28] |
Wang Xiaomei, Tang Junwu, Ding Jing et al. The retrieval algorithms of diffuse attenuation and transparency for the Case-Ⅱ waters of the Huanghai Sea and the East China Sea. Acta Oceanologica Sinica, 2005, 27(5): 38-45. [王晓梅, 唐军武, 丁静等. 黄海, 东海二类水体漫衰减系数与透明度反演模式研究. 海洋学报, 2005, 27(5): 38-45.] |
| [29] |
Wang Sumin, Dou Hongshen. Chinese lakes. Beijing: Science Press, 1998. [王苏民, 窦鸿身. 中国湖泊志. 北京: 科学出版社, 1998.]
|
| [30] |
Duan H, Feng L, Ma R et al. Variability of particulate organic carbon in inland waters observed from MODIS Aqua imagery. Environmental Research Letters, 2014, 9(8): 084011. DOI:10.1088/1748-9326/9/8/084011 |
| [31] |
Ma R, Jiang G, Duan H et al. Effective upwelling irradiance depths in turbid waters:A spectral analysis of origins and fate. Optics Express, 2011, 19(8): 7127-7138. DOI:10.1364/OE.19.007127 |
| [32] |
Ma R, Duan H, Lv C et al. Unusual links between inherent and apparent optical properties in shallow lakes, the case of Taihu Lake. Hydrobiologia, 2011, 667(1): 149-158. DOI:10.1007/s10750-011-0646-z |
| [33] |
Shi K, Zhang Y, Liu X et al. Remote sensing of diffuse attenuation coefficient of photosynthetically active radiation in Lake Taihu using MERIS data. Remote Sensing of Environment, 2014, 140(44): 365-377. DOI:10.1016/j.rse.2013.09.013 |
| [34] |
Ma Ronghua, Duan Hongtao, Tang Junwu et al. Remote sensing of lake environment. Beijing: Science Press, 2010. [马荣华, 段洪涛, 唐军武等. 湖泊水环境遥感. 北京: 科学出版, 2010.]
|
| [35] |
Tang Junwu, Tian Guoliang, Wang Xiaoyong et al. The methods of water spectra measurement and analysis Ⅰ:Above-Water Method. Journal of Remote Sensing, 2004, 8(1): 37-44. [唐军武, 田国良, 汪小勇等. 水体光谱测量与分析Ⅰ:水面以上测量法. 遥感学报, 2004, 8(1): 37-44. DOI:10.11834/jrs.20040106] |
| [36] |
Xue K, Zhang Y, Duan H et al. A remote sensing approach to estimate vertical profile classes of phytoplankton in a eutrophic lake. Remote Sensing, 2015, 7(11): 14403-14427. DOI:10.3390/rs71114403 |
| [37] |
Zhang Yunlin, Qin Boqiang, Chen Minwei et al. Regression analysis of beam attenuation coefficient under water in Lake Taihu. Oceanologia et Limnologia Sinica, 2004, 35(3): 209-213. [张运林, 秦伯强, 陈伟民等. 太湖水体光学衰减系数的特征及参数化. 海洋与湖沼, 2004, 35(3): 209-213.] |
| [38] |
Sun Deyong, Lee Yunmei, Wang Qiao et al. Study on remote sensing estimation of suspended matter concentration based on in situ hyperspectral data in Lake Tai waters. Journal of Infrared and Millimeter Waves, 2009, 28(2): 124-128. [孙德勇, 李云梅, 王桥等. 基于实测高光谱的太湖水体悬浮物浓度遥感估算研究. 红外与毫米波学报, 2009, 28(2): 124-128.] |
| [39] |
Tang Junwu, Ding Jing, Tian Jiwei et al. Neural network models for the retrieval of chlorophyll, total suspended matter, and gelbstoff concentrations of case-Ⅱ waters in Yellow Sea and East China Sea. Chinese High Technology Letters, 2005, 15(3): 83-88. [唐军武, 丁静, 田纪伟等. 黄东海二类水体三要素浓度反演的神经网络模型. 高技术通讯, 2005, 15(3): 83-88.] |
| [40] |
Cao Zhigang, Duan Hongtao, Cui Haishan et al. Remote estimation of suspended matters concentrations using ⅦRS in Lake Hongze, China. Infrared and Millimeter Waves, 2016, 35(4): 462-469. [曹志刚, 段洪涛, 崔海山等. 基于ⅦRS数据洪泽湖悬浮物浓度估算算法研究. 红外与毫米波学报, 2016, 35(4): 462-469. DOI:10.11972/j.issn.1001-9014.2016.04.014] |
| [41] |
Hu Lianbo, Zhang Tinglu. A method to derive the diffuse attenuation coefficient Kd(490) in the East China Sea. Ocean Technology, 2012, 31(4): 60-63. [胡连波, 张亭禄. 一种东中国海水体漫衰减系数Kd(490)的反演方法. 海洋技术, 2012, 31(4): 60-63.] |
| [42] |
Lee Suju, Wu Qian, Wang Xuejun et al. Correlations between reflectance spectra and contents of chlorophyll-a in Chaohu Lake. J Lake Sci, 2002, 14(3): 228-234. [李素菊, 吴倩, 王学军等. 巢湖浮游植物叶绿素含量与反射光谱特征的关系. 湖泊科学, 2002, 14(3): 228-234. DOI:10.18307/2002.0306] |
| [43] |
Koponen S, Pulliainen J, Kallio K et al. Lake water quality classification with airborne hyperspectral spectrometer and simulated MERIS data. Remote Sensing of Environment, 2002, 79(1): 51-59. DOI:10.1016/S0034-4257(01)00238-3 |
| [44] |
Stramska M, Stramski D. Variability of particulate organic carbon concentration in the north polar Atlantic based on ocean color observations with Sea-viewing Wide Field-of-view Sensor (SeaWiFS). Journal of Geophysical Research:Oceans, 2005, 110(C10): 423-436. DOI:10.1029/2004JC002762 |
 2017, Vol. 29
2017, Vol. 29 


