流域水文模拟技术自1950s以来发展迅速,它对流域各种水文过程进行模拟[1],并依靠水文模型来实现.概念性水文模型是具有明确物理意义的确定性模型,由于水文过程复杂多样,人们对于水文现象的认识不足且观测能力有限,对同一水文过程会产生不同的概化和假设,因此概念性水文模型数量繁多[2].国内外学者对不同的水文模型做过许多对比研究,赵人俊[3]在中国湿润地区7个流域分别对三水源新安江模型、萨克拉门托(SAC)模型和水箱模型的参数进行研究,发现不同参数取值能够产生相同的精度,在进行水文模型研究时,不能只重视精度而忽视水文规律;Petheram等[4]在澳大利亚北部地区对概念性水文模型进行研究,发现不同模型在率定过程中模拟结果有好有坏,但在无资料地区预报时所有模型表现相似;Fenicia等[5]在卢森堡选择3个下垫面特征不同的流域,应用12种模型进行研究,发现在渗透性较强的砂岩区域,并联水库结构模型比串联水库结构模型表现好,而在渗透性较差的页岩和泥灰岩地区,串联水库结构模型模拟结果较好.
集合预报思想起源于气象领域[6],它将不同模型的结果进行综合并得出更加稳定可靠的预报结果.在过去的几十年里,集合预报方法越来越受到水文学家的关注和欢迎,常用的有简单平均法、加权平均法和贝叶斯模型平均法(BMA)等.许多研究表明单一模型预报结果具有较大的不确定性[7-8],Ajami等[9]发现多模型组合后的预报结果优于单一模型结果;Hsu等[10]对多种集合预报方法对比分析,发现连续贝叶斯模型集合法(SBC)和连续最大后验概率模型选择(SMAP)集合方法比固定权重的简单平均法和加权平均法表现更好;Duan等[11]使用多模型在3个流域进行模拟,并用BMA方法将各模型结果集合.研究表明不同模型在反映真实水文过程的不同方面各有特长,变权重的BMA集合预报方法可以综合各模型优点,提供更好的概率预报结果.
本文选用新安江模型、TOPMODEL、萨克拉门托(SAC)模型、超渗产流模型、增加超渗产流的新安江模型、先超后蓄模型和新安江—海河模型共7种概念性水文模型,在3个半湿润流域进行模拟比较,讨论各模型在半湿润地区的适用性,探究针对流域特点对传统模型进行改进后能否提高模拟精度;根据模型模拟结果好坏,选择不同数量的模型,应用BMA集合预报方法进行多组集合,探究集合后结果与参与集合模型数量之间的关系.
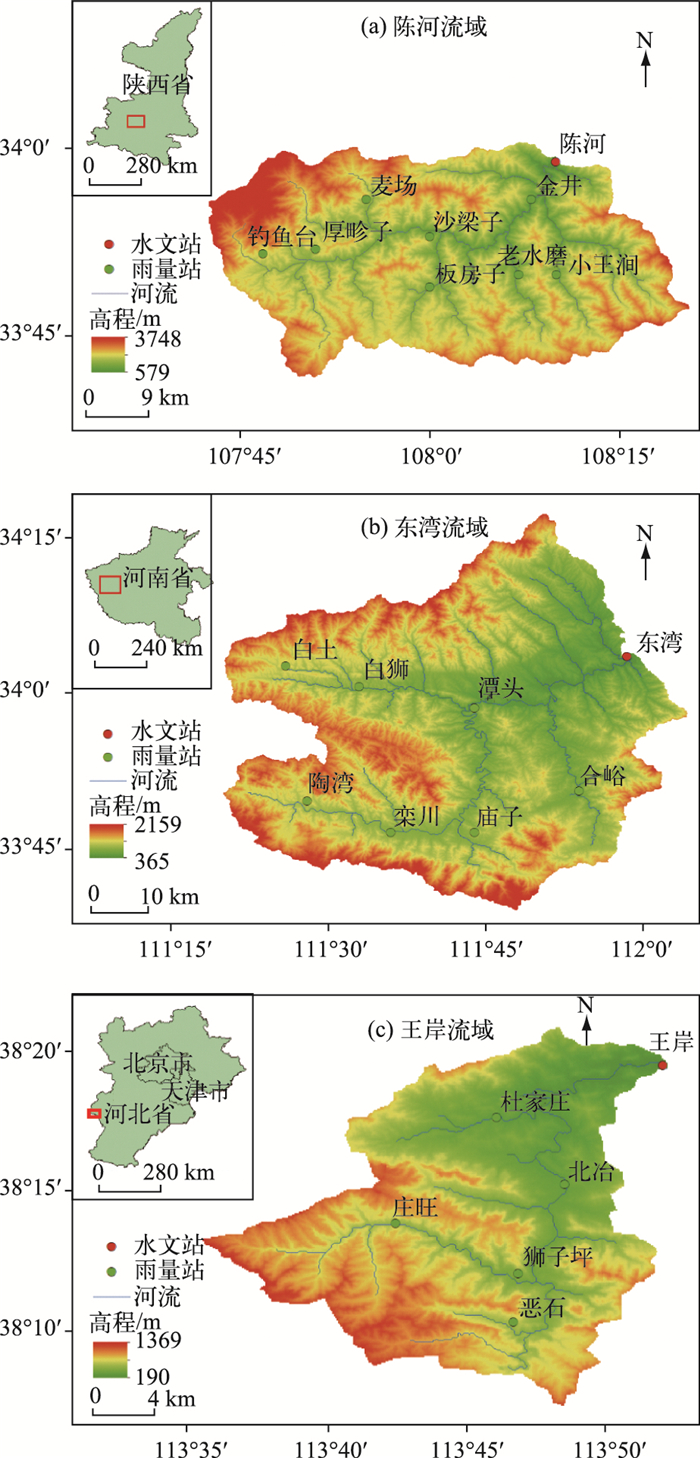
1 流域选取、模型选择与参数率定选取陕西省黑河陈河水文站以上流域(简称陈河流域)、河南省伊河东湾水文站以上流域(简称东湾流域)和河北省险溢河王岸水文站以上流域(简称王岸流域)作为研究流域,3个流域(图 1)均位于半湿润地区.陈河流域面积1350 km2,多年平均降水量800 mm,河流水量主要系雨水补给,洪水主要由局部暴雨引起.东湾流域面积2623 km2,多年平均降水量804 mm,流域内水系呈扇形分布,汇流条件好,容易产生较大洪水.王岸流域面积416 km2,多年平均降水量613 mm,流域内多为深山峡谷,河道比降大,汇流速度快.本研究用到的数据包括各水文站日流量、时段流量,各雨量站日雨量、时段雨量以及蒸发数据,这些资料全部来自于当地水文局.
|
图 1 流域地理位置 Fig.1 Location of three basins |
本文选择7个模型进行模拟研究.新安江模型、TOPMODEL及SAC模型为经典的概念性模型;新安江—海河模型[12]是针对海河流域产汇流特点,在新安江模型的基础上提出的.由于海河流域下垫面条件复杂,水利工程较多,地下水开采严重,因此在新安江模型分水源模块中加入表层与地下水拦蓄模块.考虑到河流前期河道较干,河道内采沙现象较多,因此增加河道初损计算.王岸流域为海河流域的子流域,仅使用该模型在王岸流域应用,另2个流域只应用其它6种模型.超渗产流模型、增加超渗产流的新安江模型及先超后蓄模型为灵活架构模型[13].超渗产流模型采用Green-Ampt下渗公式,认为产流量大小由降雨强度和地面下渗能力两者共同决定,超渗产流只发生在地表,不考虑地下径流.增加超渗产流的新安江模型在新安江模型的基础上加入了超渗产流计算,在流域内未蓄满面积上采用Green-Ampt公式计算超渗地面径流,而不考虑壤中流与地下径流.先超后蓄模型把径流分为地表径流和地下径流两种水源,当雨强大于下渗强度时产生地表径流,土壤含水量达到田间持水量时产生地下径流.
本研究在模型参数率定过程中将人工优选法和SCE-UA自动优选法相结合,使率定结果更为准确可靠. SCE-UA算法是由Duan等[14-15]提出来的一种全局优化算法,该算法稳定性好,收敛速度快,尤其在计算高维问题时优势明显[16].由于模型参数较多,存在异参同效现象,单纯使用自动优选法会使参数优化取值不唯一,或陷入局部最优解.而人工优选法又存在优选速度慢,参数精度低的问题.同时使用人工优选法和SCE-UA自动优选法可有效克服两种方法各自的缺点.以新安江模型为例,新安江模型的参数都有明确的物理意义,对于不太敏感的参数,根据其物理意义和经验取初始值,手动调参.而对于河网水流消退系数CS,自由水蓄水容量SM和壤中流消退系数CI这些比较敏感且独立性强的参数,使用SCE-UA算法自动优选参数. 表 1为7个模型中部分主要参数介绍.
| 表 1 模型的主要参数与物理意义 Tab.1 Parameters and their physical meaning of 7 models |
通过对3个流域各场洪水过程线分析可知,流域中既有历时较长,洪量较大的洪水,又有洪峰流量大,涨洪过程迅速的洪水,因此,选择洪量相对误差、洪峰相对误差和确定性系数作为模型模拟评判标准,洪量相对误差和洪峰相对误差在20%以内为合格[17].
2.1 陈河流域模拟结果比较选择陈河水文站2003—2012年共20场洪水计算,其中前12场洪水用来率定,后8场洪水用来验证,各模型模拟结果见表 2.
| 表 2 陈河流域不同模型洪水模拟结果对比 Tab.2 Flood simulation results of different models in Chenhe Basin |
各模型模拟结果在洪量合格率和洪峰合格率方面率定期基本均高于验证期,而确定性系数验证期比率定期高(表 2).分析各场洪水过程线,发现验证期有7场洪水涨洪前和退水阶段过程线平稳,因此模拟过程线整体上与实测过程线拟合较好,确定性系数较高,而验证期洪水洪峰误差普遍大于率定期.由于陈河流域面积较小,洪水汇流时间短,暴雨过后河道内涨洪迅速,洪峰流量大,对于洪峰的准确预报是最重要的.在比较两场洪水预报结果好坏时,应先比较其洪峰相对误差,在洪峰误差接近时再比较洪量误差和确定性系数.
新安江模型在陈河流域模拟结果最好,验证期洪量合格率为75%,洪峰合格率为75%,确定性系数均值为0.86,在6个模型中均为最高,说明陈河流域产流以蓄满产流为主,与新安江模型产流模式相似(表 2).增加超渗产流的新安江模型在洪量合格率和洪峰合格率方面与新安江模型相同,但验证期确定性系数均值为0.61,比新安江模型差,增加了超渗部分计算并没有提高模拟精度.增加超渗产流的新安江模型在流域未蓄满面积上只考虑超渗地面径流,这种假设与陈河流域实际情况并不相符,在未蓄满面积上仍会产生壤中流与地下径流. TOPMODEL模拟结果不好,尤其是对洪峰的模拟较差,验证期洪峰合格率仅有38%.由于TOPMODEL是以地形为基础的半分布式水文模型,当地下水位抬升至地表时才会产生地表径流.陈河流域地下水位较深,强度大的降雨在短时间内并不会造成地下水位明显的变化,使模型计算的地表径流量偏小.因此,对于雨强大、历时短的降雨引起的陡涨陡落型洪水,TOPMODEL模拟的洪峰流量比实际偏小.
2.2 东湾流域模拟结果比较选取东湾水文站1962—2011年共36场洪水,21场用来率定,15场用来验证,各模型模拟结果见表 4.
| 表 3 陈河流域各模型主要参数率定值 Tab.3 Calibration value of 6 models parameters in Chenhe Basin |
| 表 4 东湾流域不同模型洪水模拟结果对比 Tab.4 Flood simulation results of different models in Dongwan Basin |
增加超渗产流的新安江模型在东湾流域模拟结果最好,验证期洪量合格率为73%,洪峰合格率为67%,均略高于新安江模型(表 4).说明在东湾流域,超渗产流计算部分发挥了作用,在流域未蓄满面积上以超渗地面径流为主,壤中流和地下径流所占比重较少.超渗产流模型模拟结果最差,验证期洪量合格率与洪峰合格率均仅有33%.由于超渗产流模型只考虑超渗的地表径流,不考虑壤中流和地下径流,这与东湾流域产流方式不相符.东湾流域为半湿润流域,以蓄满产流为主,在全流域上只计算超渗产流必定会产生较大误差.先超后蓄模型模拟结果不如新安江模型,该模型汇流模块采用与新安江模型相同的线性水库法,产流模块将径流分为地表径流和地下径流,并未考虑壤中流.在流域内坡度较大的坡面上,即使雨强小于土壤下渗强度,仍会形成较大比例的壤中流,这是造成洪量模拟误差的主要原因.
2.3 王岸流域模拟结果比较选择王岸水文站1988—2008年共20场洪水计算,13场用来率定,7场用来验证.王岸流域下垫面条件复杂,河道洪水多受水利工程拦蓄影响,且流域内地下水开采量较大,地下水位下降严重.在这些人为因素影响下,王岸流域洪水过程与自然状态下洪水过程差异较大,模拟结果确定性系数均极低,在评判模型好坏时意义不大,只选择洪量相对误差和洪峰相对误差作为评价指标.各模型模拟结果见表 5.
| 表 5 王岸流域不同模型洪水模拟结果对比 Tab.5 Flood simulation results of different models in Wang'an Basin |
大部分模型在王岸流域模拟结果不佳,洪量合格率和洪峰合格率均较低(表 5).而新安江—海河模型验证期洪量合格率最高,达到71%,相比新安江模型洪量合格率提高了一倍以上,说明在新安江模型基础上加入的表层与地下水拦蓄模块发挥了作用,该模块有效模拟出王岸流域水利工程和地下水开采对河道洪量造成的影响.虽然洪峰合格率没有提高,但考虑到王岸流域大部分场次洪水洪峰流量偏低,且洪峰受水利工程调蓄影响大,较难模拟,因此将洪量合格率视为评价模型最重要的指标,认为新安江—海河模型模拟结果在所有模型中最优.
2.4 各模型综合比较对比各模型在3个半湿润流域的模拟结果可以看出,新安江模型在陈河流域和东湾流域模拟结果较好,虽然在王岸流域效果不佳,但由于王岸流域下垫面条件特殊,各模型合格率普遍较低.因此认为新安江模型在半湿润流域水文模拟方面具有较好的适用性与稳定性,半湿润流域产流以蓄满产流为主,与新安江模型产流计算方式一致.增加超渗产流的新安江模型在陈河流域模拟结果不如新安江模型,但在东湾流域模拟结果优于新安江模型.说明这两个流域产流模式略有不同,陈河流域产流方式主要为蓄满产流,而东湾流域超渗产流占有一定比例.增加超渗产流的新安江模型更适用于雨强较大,地表坡度大,容易产生超渗地面径流的半湿润流域.专门针对海河流域特点设计出的新安江—海河模型在王岸流域模拟效果好于其它模型.针对不同流域各自的特点,对模型做出适当的调整与改进,可能会使改进后的模型更适合于某一特定流域.超渗产流模型在3个流域模拟结果均较差,该模型并不适合半湿润流域,模型产流机理与实际不相符. TOPMODEL、SAC模型和先超后蓄模型在3个流域模拟结果一般,尤其在陈河流域和东湾流域,各项评价指标均不如新安江模型.
3 BMA集合预报方法应用研究使用BMA方法对所有模型结果集合,分析比较集合后的结果与单一模型模拟结果的区别.进一步选择不同的模型进行多种集合,比较不同集合方法的效果与差别.
3.1 BMA集合预报方法简介BMA是一种基于贝叶斯理论的统计分析方法[18].该方法考虑到模型本身的不确定性,以单个模型为最优的后验概率作为权重,对各模型预报结果的后验分布进行加权,得出综合预报结果[19].
根据BMA理论,综合预报量y的后验分布为:
| $ p\left( {y|{D_{{\rm{obs}}}}} \right) = \sum\limits_{i = 1}^k {P\left( {{M_i}|{D_{\rm{obs}}}} \right)} p\left( {y|{M_i}{D_{{\rm{obs}}}}} \right) $ | (1) |
式中, Dobs={y1, y2,…,yT}为用来率定模型的实测资料,M={M1, M2, …,Mk}为所有模型组成的模型空间.根据贝叶斯理论,在实测资料Dobs给定的情况下模型Mi为最优模型的后验概率P(Mi|Dobs)的形式为:
| $ P\left( {{M_i}|{D_{obs}}} \right) = \frac{{p\left( {{D_{{\rm{obs}}}}{\rm{|}}{M_i}} \right)P\left( {{M_i}} \right)}}{{\sum\limits_{i = 1}^k {P\left( {{D_{\rm{obs}}}|{M_i}} \right)} P\left( {{M_j}} \right)}} $ | (2) |
式中, P(Mi)是模型Mi为最优模型的先验概率; P(Mi|Dobs)即为各模型权重值,随时间变化而不断变化和进步.
3.2 BMA集合预报方法应用比较采用BMA方法对3个半湿润流域各模型验证期的洪水进行集合,并与各单一模型做比较,所得结果见表 6.根据前面分析的各评价指标在不同流域的适用性,在陈河和东湾流域选择洪峰合格率与确定性系数作为模型评判标准,在王岸流域选择洪量合格率与洪峰合格率作为模型评判标准.
| 表 6 BMA集合预报法与单一模型模拟结果对比 Tab.6 Simulation results comparison among BAM scheme and 7 single models |
在陈河流域,BMA集合预报方法洪峰合格率达到88%,相比其它6个单一模型有所提高,确定性系数均值为0.86,与6个单一模型中确定性系数最高的新安江模型相当;在东湾流域,BMA方法洪峰合格率为40%,不如多数单一模型模拟结果,而确定性系数均值为0.73,高于单一模型中模拟结果最好的新安江模型;在王岸流域,BMA方法在洪峰合格率方面没有提高,但洪量合格率达到86%,高于所有单一模型(表 6).通过分析各场洪水过程线可以看出,陈河流域BMA方法在洪峰和涨落段模拟效果都比较好. 图 2为陈河流域2010072101号洪水BMA方法与模拟结果最好的2个单一模型的对比,该场洪水经BMA方法集合后洪峰相对误差为-3.34%,确定性系数为0.88,均好于6个单一模型.在东湾流域和王岸流域,BMA方法模拟的洪峰较实测普遍偏低,但涨落洪过程拟合较好,洪量合格率和确定性系数比单一模型高.尤其在王岸流域,评价模型的指标以洪量合格率为主,经BMA方法集合后洪量合格率比新安江—海河模型高出15%.

|
图 2 陈河流域2010072101号洪水模拟结果对比 Fig.2 Simulated hydrograph comparison of different methods for the flood 2010072101 in Chenhe Basin |
因此认为,BMA集合预报方法在陈河流域和王岸流域模拟结果比单一模型好,在东湾流域洪峰合格率较低,不如单一模型.但BMA方法具有单一模型不具备的优势:它能够降低模拟结果的不确定性,避免过分依赖于某一单一模型造成的误差,而且除了确定性结果外,BMA集合预报法能够提供某一置信区间内的概率预报结果,更好地为防洪决策提供依据.
3.3 不同集合方法对比选择陈河流域验证期的8场洪水进行研究,分别用BMA方法对不同模型集合.由于超渗产流模型和TOPMODEL在陈河流域模拟结果较差,做集合预报时去掉这两个模型,用BMA方法对其他4个模型进行集合(记为BMA4);新安江模型和增加超渗产流的新安江模型洪峰合格率和洪量合格率最高,单独对这两个模型进行集合(记为BMA2),并将BMA2和BMA4的结果与6个模型集合(记为BMA6)结果进行比较.
由于BMA集合预报法既可以给出确定的均值预报,又能给出某一置信区间内的不确定预报,因此在比较3种BMA方法时使用确定性结果评价指标和概率预报结果评价指标分别进行评价.确定性结果评价指标采用洪峰相对误差和确定性系数.在许多研究中概率结果评价常采用离散度(ES)和排名概率评分(RPS)[20-21]等指标,但这些指标不适用于比较模型数量不同的集合预报结果.本研究选用覆盖率(CR)、平均相对带宽(BR)[22]和洪峰相对带宽(BP)来评价概率预报结果. CR是由熊立华等[23]提出的表征置信区间(本研究取90%置信度)覆盖实测值比例的指标,CR值等于落在置信区间内的实测值数量与实测值总数的比值,同一置信度下,CR值越高,说明概率预报结果越可靠.
BR计算公式为:
| $ {B_{\rm{R}}} = \frac{1}{K}\sum\limits_{i = 1}^k {\frac{{{q_{{\rm{u}}i}}-{q_{{\rm{l}}i}}}}{{{Q_i}}}} $ | (3) |
式中,K为总时段数,qui、qli分别为i时刻预报置信上限和置信下限值(m3/s),Qi为i时刻实测流量(m3/s).
BP计算公式为:
| $ {B_{\rm{P}}} = \frac{{{q_{{\rm{up}}}}-{q_{{\rm{lp}}}}}}{{{Q_{\rm{p}}}}} $ | (4) |
式中, qup、qlp分别为洪峰时刻预报置信上限和置信下限值(m3/s);Qp为实测洪峰流量(m3/s). BR和BP分别评价整场洪水过程和洪峰时刻概率预报结果好坏,在同一置信度下,相对带宽值越小,说明概率预报结果越精确.
(1)确定性结果对比. 3种BMA方法确定性结果统计如表 7所示,其中洪峰相对误差平均值为各洪水洪峰相对误差绝对值的平均值.
| 表 7 陈河流域3种BMA方法确定性结果评价指标对比 Tab.7 Certainty forecasting results comparison among three BMA schemes in Chenhe Basin |
BMA6方法洪峰相对误差平均值为13.82%,确定性系数均值为0.86,在3种方法中均为最好,BMA4方法和BMA2方法洪峰相对误差均值和确定性系数均值比较接近(表 7).
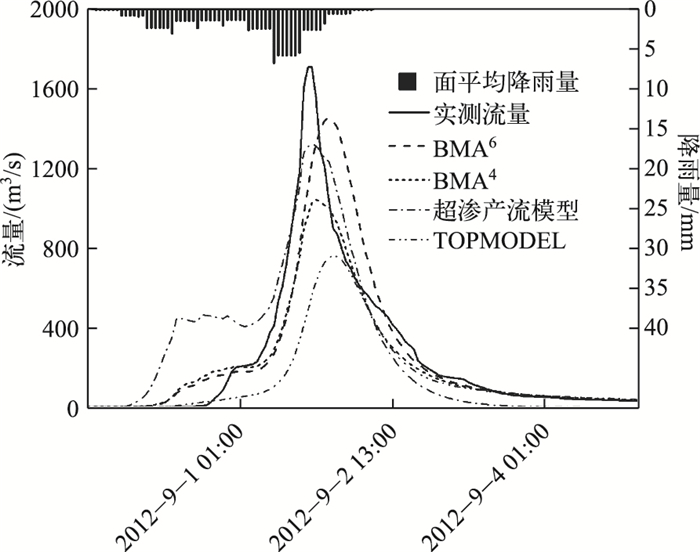
相比于BMA6方法,BMA4方法在集合多模型时去掉了洪峰合格率最低的TOPMODEL以及洪量合格率和确定性系数最低的超渗产流模型,但集合结果却不如BMA6方法.分析各场洪水过程线可以看出,超渗产流模型模拟的洪峰普遍偏大,而TOPMODEL模拟的洪峰偏小. BMA集合预报方法的优点是各模型所占权重会实时改变,模拟结果越好的模型被赋予的权重越大,当所有单一模型模拟洪峰都小于实测值时,洪峰相对较大的超渗产流模型模拟结果更接近实测,其权重值也最大;相反,当各单一模型模拟洪峰普遍偏大时,洪峰相对较小的TOPMODEL就会被赋予较大的权重. 图 3为陈河流域2012083013号洪水模拟结果,该场洪水实测洪峰流量1710 m3/s,超渗产流模型模拟洪峰流量为1322 m3/s,在6个单一模型中洪峰最高,TOPMODEL模拟洪峰流量763 m3/s,为6个单一模型中最低.使用BMA6方法做集合时,超渗产流模型所占权重较大,因此集合预报结果的洪峰流量也较大,而TOPMODEL模拟效果不好,权重值极小,对最终集合结果几乎没有影响.当使用BMA4方法做集合时,由于缺少了洪峰流量更接近实测的超渗产流模型,使最终集合结果洪峰流量小于BMA6方法,洪峰相对误差更大.从图 3中还可看出,该场洪水BMA6方法模拟结果的峰现时间误差较BMA4方法更大.由计算数据可知,BMA6方法模拟结果峰现时间误差为-4 h,BMA4方法为-1 h,超渗产流模型为0 h,TOPMODEL为-5 h.在洪峰出现时间上BMA6方法模拟结果受到了TOPMODEL结果的影响,误差稍大.
|
图 3 陈河流域2012083013号洪水2种BMA方法结果对比 Fig.3 Simulated hydrograph comparison of 2 BMA schemes for the flood 2012083013 in Chenhe Basin |
BMA2方法将模拟结果最好的新安江模型和增加超渗产流的新安江模型进行集合,但效果并不如BMA6方法. BMA2方法模型样本数较小,并且2个单一模型模拟结果比较接近,当2个模型都模拟不佳时,集合后结果也较差.因此BMA2方法稳定性不好,不能适用于各种类型的洪水.
(2) 概率预报结果对比. 3种BMA方法概率预报结果如表 8所示,选择90%置信度计算得到置信区间.
| 表 8 陈河流域3种BMA方法概率预报结果评价指标对比 Tab.8 Probabilistic forecasting results comparison among 3 BMA schemes in Chenhe Basin |
3种BMA方法平均覆盖率都在90%以上,BMA6方法与BMA4方法平均覆盖率比较接近,稍高于BMA2方法(表 8).在平均相对带宽和洪峰相对带宽方面,BMA6方法比另外2种集合方法更优,BMA4方法平均相对带宽值低于BMA2方法,而洪峰相对带宽值高于BMA2方法.整体来看,BMA6方法对于整场洪水过程和洪峰部位的概率预报精度最高,BMA4方法整场洪水过程的概率预报结果好于BMA2方法,洪峰部位概率预报结果不如BMA2方法. 图 4为BMA6方法对陈河流域2010年8月18日洪水的预报结果.

|
图 4 陈河流域2010081820号洪水BMA6方法预报结果 Fig.4 Forecasting results of BMA6 scheme for the flood 2010081820 in Chenhe Basin |
综合确定性结果和概率预报结果,BMA6方法集合效果最好,BMA4方法和BMA2方法不相上下.由此可以看出,BMA集合预报方法能放大各模型的优点,忽视其缺点,即使总体模拟效果不好的模型,如果在各别场次洪水中模拟结果较好,也能为集合预报结果起到促进作用.
4 结论选用新安江模型、TOPMODEL、SAC模型、超渗产流模型、增加超渗产流的新安江模型、先超后蓄模型和新安江—海河模型共7种概念性水文模型,在3个半湿润流域进行模拟比较,并使用BMA集合预报方法对不同水文模型模拟结果集合,对比分析各种集合方法的应用效果.
研究结果表明,新安江模型和增加超渗产流的新安江模型在半湿润流域应用效果好于其它模型,超渗产流模型在半湿润流域模拟结果最差.半湿润流域产流方式以蓄满产流为主,在流域部分面积上会形成超渗地面径流,不同流域超渗产流所占比例不同.针对每个流域各自特点,比如产流方式不同、下垫面情况不同,人为因素影响等,对传统模型做出改进可以提高模拟精度.
BMA集合预报方法能够综合各单一模型的优点,避免过分依赖于某一单一模型造成误差,降低预报结果的不确定性,集合后的结果在洪量合格率和确定性系数方面有显著提高.而且BMA方法还能提供某一置信区间内的概率预报结果,定量评价模型不确定性的影响.通过对比不同模型集合结果,发现当BMA方法中模型数量较少时,集合结果稳定性差,不能适应各种类型的洪水,适当增加集合模型数量后,BMA方法能更有效地综合各模型优势,提高确定性预报结果和概率预报结果的精度.
致谢: 感谢刘开磊博士对本研究提供的帮助和宝贵建议.| [1] |
Zhao Renjun. Hydrological modeling of watershed. Beijing: Water Resources and Electric Power Press, 1984, 1-10. [赵人俊. 流域水文模拟. 北京: 水利电力出版社, 1984, 1-10.]
|
| [2] |
Li Zhijia, Jiang Tingting, Huang Pengnian et al. Impact and analysis of watershed precipitation and topography characteristics on model simulation results. Advances in Water Science, 2015, 26(4): 473-480. [李致家, 姜婷婷, 黄鹏年等. 降雨和地形地貌对水文模型模拟结果的影响分析. 水科学进展, 2015, 26(4): 473-480.] |
| [3] |
Zhao Renjun. Study on comparison and analysis of watershed hydrologic models. Journal of China Hydrology, 1989(6): 1-5. [赵人俊. 流域水文模型的比较分析研究. 水文, 1989(6): 1-5.] |
| [4] |
Petheram C, Rustomji P, Chiew FHS et al. Rainfall-runoff modeling in northern Australia:A guide to modeling strategies in the tropics. Journal of Hydrology, 2012, 462/463: 28-41. DOI:10.1016/j.jhydrol.2011.12.046 |
| [5] |
Fenicia F, Kavetski D, Savenjie HHG et al. Catchment properties, function, and conceptual model representation:Is there a correspondence?. Hydrological Processes, 2014, 28(4): 2451-2467. DOI:10.1002/hyp.9726 |
| [6] |
Day GN. Extended streamflow forecasting using NWSRFS. Journal of Water Resources Planning and Management, 1985, 111(2): 157-170. DOI:10.1061/(ASCE)0733-9496(1985)111:2(157) |
| [7] |
Barnston AG, Mason SJ, Goddard L et al. Multimodel ensembling in seasonal climate forecasting at IRI. Bulletin of the American Meteorological Society, 2003, 84(12): 1783-1796. DOI:10.1175/BAMS-84-12-1783 |
| [8] |
Krishnamurti TN, Kishtawal CM, LaRow TE et al. Improved weather and seasonal climate forecasts from multimodelsuperensemble. Science, 1999, 285(5433): 1548-1550. DOI:10.1126/science.285.5433.1548 |
| [9] |
Ajami NK, Duan QY, Sorooshian S. An integrated hydrologic Bayesian multimodel combination framework:Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resources Research, 2007, 43(1): W01403. |
| [10] |
Hsu K, Moradkhani H, Sorooshian S. A sequential Bayesian approach for hydrologic model selection and prediction. Water Resources Research, 2009, 45: W00B12. |
| [11] |
Duan QY, Ajami NK, Gao XG et al. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Advances in Water Resources, 2007, 30(5): 1371-1386. DOI:10.1016/j.advwatres.2006.11.014 |
| [12] |
Li Zhijia, Yao Yumei, Dai Jiannan et al. Study on impact of basin cushion changes on river floods by hydrological modeling. Journal of Hydroelectric Engineering, 2012, 31(3): 5-10. [李致家, 姚玉梅, 戴健男等. 利用水文模型研究下垫面变化对洪水的影响. 水力发电学报, 2012, 31(3): 5-10.] |
| [13] |
Li Zhijia, Huang Pengnian, Yao Cheng et al. Application of flexible-structure hydrological models in different runoff generation regions. Advances in Water Science, 2014, 25(1): 28-35. [李致家, 黄鹏年, 姚成等. 灵活架构水文模型在不同产流区的应用. 水科学进展, 2014, 25(1): 28-35.] |
| [14] |
Duan QY, Gupta VK, Sorooshian S. Shuffled complex evolution approach for effective and efficient global minimization. Journal of Optimization Theory and Application, 1993, 76(3): 501-521. DOI:10.1007/BF00939380 |
| [15] |
Sorooshian S, Duan QY, Gupta VK. Optimal use of the SCE-UA global optimization method for calibrating watershed models. Journal of Hydrology, 1994, 158(3/4): 265-284. |
| [16] |
Song Xingyuan, Shu Quanying, Wang Haibo et al. Comparison and application of SCE-UA, genetic algorithm and simplex method. Engineering Journal of Wuhan University, 2009, 42(1): 6-15. [宋星原, 舒全英, 王海波等. SCE-UA、遗传算法和单纯形优化算法的应用. 武汉大学学报(工学版), 2009, 42(1): 6-15.] |
| [17] |
Ministry of Water Resources Hydrology Bureau. GB/T 22482-2008 Standard for hydrological information and hydrological forecasting. Beijing: China Standard Press, 2008, 5-6. [水利部水文局. GB/T 22482-2008水文情报预报规范. 北京: 中国标准出版社, 2008, 5-6.]
|
| [18] |
Hoeting JA, Madigan D, Raftery AE et al. Bayesian model averaging:Atutorial. Statistical Science, 1999, 14(4): 382-401. DOI:10.1214/ss/1009212519 |
| [19] |
Dai Rong. Study on applications of Bayesian model averaging in the combination of hydrological models[Dissertation]. Nanjing:Hohai University, 2008. [戴荣. 贝叶斯模型平均法在水文模型综合中的应用研究[学位论文]. 南京: 河海大学, 2008. http://d.wanfangdata.com.cn/Thesis/Y1268183 ]
|
| [20] |
Bradley AA, Hashino T, Schwartz SS. Distributions-oriented verification of probability forecasts for small data samples. Weather and Forecasting, 2003, 18(5): 903-917. DOI:10.1175/1520-0434(2003)018<0903:DVOPFF>2.0.CO;2 |
| [21] |
Franz KJ, Hartmann HC, Sorooshian S et al. Verification of national weather service ensemble streamflow predictions for water supply forecasting in the Colorado River basin. Journal of Hydrometeorology, 2003, 4(6): 1105-1118. DOI:10.1175/1525-7541(2003)004<1105:VONWSE>2.0.CO;2 |
| [22] |
Liang Zhongmin, Jiang Xiaolei, Cao Yanxu et al. Probabilistic flood forecasting considering rainfall uncertainty. Journal of Hohai University:Natural Sciences, 2016, 44(1): 8-12. [梁忠民, 蒋晓蕾, 曹炎煦等. 考虑降雨不确定性的洪水概率预报方法. 河海大学学报:自然科学版, 2016, 44(1): 8-12.] |
| [23] |
Xiong LH, Shamseldin AY, O'Connor KM. A non_linear combination of the forecasts of rainfall-runoff models by the first-order Takagi-Sugeno fuzzy system. Journal of Hydrology, 2001, 245(1-4): 196-217. DOI:10.1016/S0022-1694(01)00349-3 |
 2017, Vol. 29
2017, Vol. 29 

