(2: 中国电建集团中南勘测设计研究院有限公司, 长沙 410014)
(3: Desert Research Institute, Las Vegas Nevada USA, 89119)
(2: Power China Zhongnan Engineering Corporation Limited, Changsha 410014, P. R. China)
(3: Desert Research Institute, Las Vegas Nevada USA, 89119)
在水文模拟和水文预报中,土壤含水量作为洪水预报模型的一个状态量,对预报结果有着不可忽视的影响,尤其是流域内前期土湿对洪水预报精度有很大的影响[1].现有水文预报模型系统大多是基于气象资料经模型计算得出土壤含水量情况,缺乏土壤含水量模拟检验,更缺乏对基于土壤墒情实时监测的水文预报模型应用研究.然而经模型计算得到的土壤含水量毕竟与实际土壤含水量存在偏差,而且可能会出现随着时间的推移误差不断积累的现象,直接影响净雨计算的准确性,给水文预报结果带来误差,从而影响洪水预报的整体预报精度[2].因此,利用实时监测的土壤墒情资料,改进传统的模型结构,减少土壤含水量的模拟误差对洪水预报结果产生的不良影响成为洪水预报重要的研究课题.
Jackson等[3]在改进水文模拟时最早采用同化土壤含水量的方法,他采用直接插入的同化方法,将实际观测的土壤含水量代替由水文模型模拟出的土壤含水量,以此提高模型计算精度. Pauwels等[4]利用统计校正法与牛顿松弛法两种同化方法将ERS卫星微波遥感所获得的土壤含水量与基于TOPMODEL的TOPLATS模型的数据进行同化,通过比较发现集总式与分布式两个版本的TOPMODEL模型在同化了遥感反演的土壤含水量数据之后,均可以提高水文预报的精度. Parajka等[5]通过对奥地利320个流域进行径流试验研究,表明卫星微波遥感25 km分辨率土壤含水量数据对流域水文预报有一定的作用.数据同化的主要工作是把各种来源不同、误差时间信息不同或者空间分辨率不同的观测资料融入一个数值动力模型中利用数学方法进行计算,从而在实际观测值与模型解之间找到一个最优解.但数据同化技术对土壤含水量的修正并不能直接用于水文模型,因为遥感技术观测的土壤含水量数据与水文模型中的土壤含水量并不是同一个概念,例如,新安江模型中土壤含水量是指蓄水深度(mm),且目前还没有能够将遥感观测的土壤水数据转换成洪水预报模型中的值的有效手段[2].
此外,由于现有观测技术尚不成熟、观测设备不够先进,导致实测土壤墒情数据存在较大的粗差,若不经过抗差处理,无法用于水文模型计算.本文采用抗差技术对观测资料进行处理,利用抗差技术所具有的误差抗御性,减少观测粗差对预报系统的影响,并采用系统响应反演修正方法修正初始土壤含水量,以提高模型的预报精度.
1 方法介绍 1.1 土壤墒情资料抗差技术抗差模型的建立主要涉及土壤含水率的分布关系,本研究中抗差模型结构采用多元回归模型:
| $ \theta {C_{i, t}} = {\alpha _1} \cdot {\theta _{1, t}} + {\alpha _2} \cdot {\theta _{2, t}} + \cdots + {\alpha _{i-1}} \cdot {\theta _{i-1, t}} + {\alpha _{i + 1}} \cdot {\theta _{i{\rm{ + }}1, t}}{\rm{ + }} \cdots {\rm{ + }}{\alpha _m} \cdot {\theta _{m, t}} $ | (1) |
式中, θCi, t为待估计的土壤含水率,i为估计变量序号,θk, t(k=1、2、…、i-1、i+1、…、m)为观测的土壤含水率,αk(k=1、2、…、i-1、i+1、…、m)为待估计的常系数,m为回归变量个数.
考虑到流域内土壤含水率所有测站、垂线上所有测点之间都存在相关性,所以变量个数m最大值是所有测站垂线测点的总和.但由于测站垂线测点的相关性存在差异,贡献度也不同,所以回归建模采用逐步回归方法建模,使得所选择的每个变量都是具有重要贡献度,贡献度小的变量被剔除.这样,对序号为i的估计变量θCi,t,通过逐步回归建模,其变量的个数也是随i变化的m(i).逐步回归建模,就可获得一系列变量个数不同的回归模型[6-8].
本研究采用Hampel估计,其抗差权函数[9]为:
| $ \omega \left( u \right) = \left\{ \begin{array}{l} \;\;\;\;\;\;\;1, \;\;\;\;\;\;\;\;\;\;\left| u \right| \le a\\ \;\;\;\;a/\left| u \right|, \;\;\;a < \left| u \right| \le b\\ \frac{{a\left( {c-\left| u \right|} \right)}}{{\left( {c-b} \right)\left| u \right|}}, \;\;b < \left| u \right| \le c\\ \;\;\;\;\;0, \;\;\;\;\;\;\;\;\;\;\;\;\left| u \right| > c \end{array} \right. $ | (2) |
式中, u为观测值残差,a、b和c为3个参数,即:当观测值残差绝对值|u|不大于a时,等价权取原观测权;|u|在a与b之间时,采用绝对和极小法(也是稳健估计);|u|在b与c之间时,等价权随着残差的增大而减小,从而限制这部分观测值对参数的影响;|u|大于c时,观测值不予采用[10].这些常参数要预先通过实际资料进行分析确定,而且在选取时要考虑抗差性和风险的平衡,对于不同的观测变量θCi, t,其相应的误差分布不同,参数值也随之变化.所以,严格意义上说,这是3个变参数.
1.2 土壤含水量系统响应反演方法如图 1所示,将新安江模型作为一个系统,通过给初始土壤含水量W0一个单位的变化量,使得模型的产流系列R发生变化,进一步使得计算的流量系列Qc在原始计算结果上产生的变化就称为系统响应,而变化后的流量系列与原始计算流量系列之差则称为初始土壤含水量的系统响应曲线[2].

|
图 1 系统示意图 Fig.1 Schematic diagram of the system |
在模型的输入变量和状态变量中只考虑土壤含水量对预报的影响,将上述系统归纳如下:
| $ Q\left( t \right) = Q\left( {W, \lambda, t} \right) $ | (3) |
式中,Q为流域出口断面流量,W为土壤含水量,λ为模型参数,t为时间.
由于新安江模型考虑了降雨和下垫面分布不均的特性,将计算流域划分为多个单元流域,对应于每个单元有其相应的初始土壤含水量,因此,对各单元的初始土壤含水量进行分单元修正.
对式(3)进行微分处理,如下:
| $ {\rm{d}}Q\left( {W, \lambda, t} \right) = \frac{{{\rm{d}}Q}}{{dW}}{|_{W = {W_0}}}{\rm{d}}W $ | (4) |
将样本长度为L的Q(t)=[Q1, Q2, …, QL]T,W=[W1,W2, …, Wm]T及W0=[W1,0, W2,0, …, Wm,0]T的分量计算代入式(4)中,可得:
| $ \left\{ \begin{array}{l} Q\left( {W, \lambda, 1} \right) = Q\left( {{W_0}, \lambda, 1} \right) + \frac{{\partial Q\left( {W, \lambda, 1} \right)}}{{\partial {W_1}}}\left| {_{W = {W_0}}} \right.\Delta {W_1} + \frac{{\partial Q\left( {W, \lambda, 1} \right)}}{{\partial {2_1}}}\left| {_{W = {W_0}}\Delta {W_2}{\rm{ + }} \cdots {\rm{ + }}} \right.\\ \;\;\;\;\;\;\;\;\;\frac{{\partial Q\left( {W, \lambda, 1} \right)}}{{\partial {W_m}}}\left| {_{W = {W_0}}\Delta {W_m} + {e_1}} \right.\\ Q\left( {W, \lambda, 2} \right) = Q\left( {{W_0}, \lambda, 2} \right) + \frac{{\partial Q\left( {W, \lambda, 2} \right)}}{{\partial {W_1}}}\left| {_{W = {W_0}}} \right.\Delta {W_1} + \frac{{\partial Q\left( {W, \lambda, 2} \right)}}{{\partial {W_2}}}\left| {_{W = {W_0}}\Delta {W_2} + } \right. \cdots {\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\frac{{\partial Q\left( {W, \lambda, 2} \right)}}{{\partial {W_m}}}\left| {_{W = {W_0}}\Delta {W_m} + {e_2}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ Q\left( {W, \lambda, L} \right) = Q\left( {{W_0}, \lambda, L} \right) + \frac{{\partial Q\left( {W, \lambda, L} \right)}}{{\partial {W_1}}}\left| {_{W = {W_0}}} \right.\Delta {W_1} + \frac{{\partial Q\left( {W, \lambda, L} \right)}}{{\partial {W_2}}}\left| {_{W = {W_0}}\Delta {W_2} + } \right. \cdots {\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\frac{{\partial Q\left( {W, \lambda, L} \right)}}{{\partial {W_m}}}\left| {_{W = {W_0}}\Delta {W_m} + {e_L}} \right. \end{array} \right. $ | (5) |
式(5)可写成如下矩阵形式:
| $ Q\left( {W, \lambda, t} \right){\rm{ = }}Q\left( {{W_0}, \lambda, t} \right) + U \cdot \Delta W + E $ | (6) |
式中, Q(W, λ, t)表示实测出口断面流量过程,简写为Q0;Q(W0, λ, t)表示模型计算流量过程,即Qc;系统响应矩阵
U矩阵中的每一项可以通过差分近似微分求解:
| $ \begin{array}{l} \frac{{\partial Q\left( {W, \lambda, t} \right)}}{{\partial {W_i}}}{|_{W = {W_0}}} = \\ \frac{{Q\left( {\left( {{W_{1, 0}}, \cdots, {W_{i, 0}} + \Delta {W_i}, \cdots, {W_{m, 0}}} \right), \lambda, t} \right)-Q\left( {\left( {{W_{1, 0}}, \cdots, {W_{i, 0}}, \cdots, {W_{m, 0}}} \right), \lambda, t} \right)}}{{\Delta {W_i}}} \end{array} $ | (7) |
式中, t=1, 2, …, L为时间尺度;i=1, 2, …, m为空间尺度.
U矩阵的具体计算过程为:在保持其他单元值不变的情况下分别给每个单元的初始土壤含水量增加一个单位量,用改变后的初始值作为新安江模型的输入进行计算,模拟得到的新流量系列与原始模型计算流量系列的差值为该单元初始土壤含水量的系统响应曲线,作为系统响应矩阵U中对应于该单元初始土壤含水量的一列参与计算[11-15].
初始土壤含水量的修正量ΔW可根据最小二乘估计求得:
| $ \Delta W = {\left( {{U^T}U} \right)^{-1}}{U^T}\left( {Q\left( {W, \lambda, t} \right)-Q\left( {{W_0}, \lambda, t} \right)} \right) $ | (8) |
由此可得修正后的初始土壤含水量(W′0)为:
| $ {W'_0} = {W_0} + \Delta W $ | (9) |
则修正流量系列(Q′c)为:
| $ {{Q'}_c} = Q\left( {{{W'}_0}, \lambda, t} \right) $ | (10) |
本研究以典型的概念性水文模型——三水源新安江模型为基础,设计基于土壤含水量的降雨径流预报模型.三水源新安江模型蒸散发计算采用三层蒸发模型;产流计算采用蓄满产流模型;径流划分采用自由水蓄水库结构将总径流划分为地表径流、壤中流和地下径流3种;流域汇流采用线性水库;河道汇流采用马斯京根分段连续演算法[16].具体的建模步骤如下:
1) 采用观测的同步土壤墒情、雨量、径流资料分析径流、降雨与实测土壤墒情的关系.由于实测土壤墒情资料存在较大的观测误差,采用抗差分析方法,对观测误差进行抗差估计,以减小观测误差对土壤含水量估计的影响.
2) 采用流域实测土壤墒情及雨洪资料进行模型分析计算,确定模型参数[17-20].根据建立的模型计算出每场洪水的逐小时土壤含水量.
3) 建立抗差后的实测土壤含水率θ与模型计算土壤含水量W之间的函数关系;并根据该函数关系,用实测土壤含水率推算模型土壤含水量,作为新安江模型的输入进行洪水模拟.
4) 采用土壤含水量系统响应反演修正方法,改进洪水初始时刻的土壤含水量,以提高预报模型的模拟精度.
3 模型应用与检验 3.1 实验流域概况本文实验流域为宝盖洞流域,位于浏阳市古港镇宝盖洞村,为洞庭湖水系湘江支流浏阳河一级支流宝盖河的宝盖水文站以上流域,水文站以上河长约6.8 km,流域控制集水面积22.1 km2,流域高程在200~1200 m.流域内基本属自然生态,典型山地,植被茂密,坡陡沟深,河流短促,有2级小拦河坝及微小型引水式水力发电站,无水库.宝盖河流域地处亚热带季风气候区,具有湿热多雨、夏热冬寒的特点,暴雨频繁,洪水由暴雨产生,具有陡涨陡落的特点.宝盖洞水文站测验河流属山溪性小河,水位随洪水暴涨暴落. 1954年7月25日,日雨量达412.5 mm,23—25日3 d雨量达618.8 mm.测验河道高,水流速大,可达7 m/s以上,洪水时砾石滚动并有漂浮物.流域内受人类活动影响较少,植被保护较好,河流含沙量小.
流域内共布设有7个雨量站(寒婆坳、白果树、白屋场、芦前、双冲、印心台、宝盖洞),6个土壤墒情自动监测站(寒婆坳、白果树、白屋场、芦前、双冲、印心台)和1个水文控制站(宝盖洞水文站; 28°22′N, 113°44′E)(图 2),站网密度足够且分布合理.为了保证系统设备的协调工作和减小系统误差,所有的土壤墒情测站均统一采用ZNY.HDJ-1墒/旱情自动化系统设备,各测点(测点深度分别为20、40、60 cm)均采用相同的传感器探头.流域水系及站点布设见图 2.

|
图 2 宝盖洞流域水系及站点分布 Fig.2 The drainage and station distribution of Baogaidong Basin |
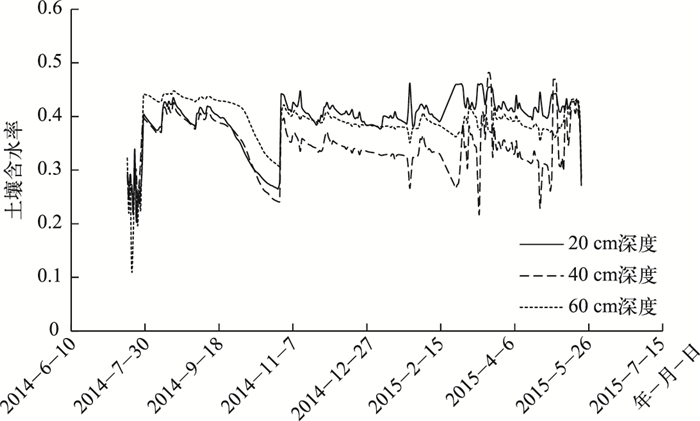
本研究旨在利用观测的土壤墒情数据,改进传统的模型结构,设计基于实测土壤墒情资料的降雨径流预报模型.而实测资料总是存在误差的,因此,在将观测资料用于模型构建和模型参数率定前,首先要对观测资料进行合理性和可靠性分析,了解观测资料存在的问题.资料分析主要从观测资料时间变化特征、土壤含水率资料与降雨资料的相关性以及土壤含水率资料与蒸发资料的相关性三个方面展开.本流域无蒸发资料,故借用附近流域双江口站(28°20′11.6″N, 112°40′20.8″E)的蒸发观测资料.不同深度各测点土壤含水率观测值逐日变化情况如图 3所示(以芦前站为例),芦前站逐日土壤含水率在时间序列上波动剧烈,其他5个站情况均与该站类似.各站逐日土壤含水率与降雨和蒸发之间的相关系数分别见表 1和表 2.由表 1和表 2可以看出,土壤含水率资料与降雨资料呈正相关关系,与蒸发资料呈负相关关系,但土壤含水率资料与降雨和蒸发资料相关系数的绝对值都很小,即土壤含水率资料与降雨和蒸发资料之间的相关性很差,不能直接用于模型计算,必须经过抗差技术处理,才可以加以利用.
|
图 3 芦前站垂向各测点土壤含水率观测值逐日变化情况 Fig.3 Variation of daily measured soil moisture in vertical of Luqian station |
| 表 1 逐日土壤含水率与降雨相关系数 Tab.1 The correlation coefficient between daily soil moisture and rainfall |
| 表 2 逐日土壤含水率与蒸发的相关系数 Tab.2 The correlation coefficient between daily soil moisture and evaporation |
本研究首先将实测土壤墒情资料转换为土壤含水率,再研究实测土壤含水率与模型计算土壤含水量之间的关系.实测土壤含水率与模型计算土壤含水量之间,物理成因上讲是存在线性关系的.由于实验流域观测的土壤墒情资料存在诸多误差因素,导致由土壤墒情资料转换而来的土壤含水率与模型计算土壤含水量之间的相关性很差.本研究采用全流域平均土壤含水率与新安江模型计算土壤含水量直接建立函数关系,其关系式为:
| $ W{\rm{ = 522}}{\rm{.92}}\left( {\theta-0.30} \right) + 60 $ | (11) |
式中, W为模型计算土壤含水量(mm),θ为实测土壤含水率.全流域平均土壤含水率与新安江模型计算土壤含水量的关系见图 4.

|
图 4 实测土壤含水率(θ-0.30)与土壤含水量(W-60)的关系 Fig.4 The relationship between measured soil moisture(θ-0.30) and soil water content(W-60) calculated by model |
本研究选取宝盖洞流域2014—2015年26场洪水作为模型检验资料.用式(11)由实测土壤含水率计算的土壤含水量,用新安江模型模拟的洪水结果见表 3(R0是次洪实测径流深, er是计算径流深相对误差,Qp是实测洪峰流量,eq是计算洪峰流量相对误差).
| 表 3 实测土壤含水率直接用于模型计算的洪水模拟结果 Tab.3 The flood simulation results which are calculated by measured soil moisture |
利用1.1节介绍的土壤墒情资料抗差技术,对由式(11)计算得到的土壤含水量W进行抗差计算,得到抗差后的土壤含水量Wr.将26场洪水初始时刻的抗差计算土壤含水量Wr与新安江模型计算得到的土壤含水量Wmod比较,建立抗差土壤含水量Wr与模型计算土壤含水量Wmod之间的关系,具体关系见图 5.用经过抗差计算后的土壤含水量Wr代入新安江模型计算的洪水结果见表 4.

|
图 5 抗差含水率与模型计算的土壤含水量关系 Fig.5 The relationship between robust soil moisture and soil water content calculated by model |
| 表 4 抗差土壤含水量用于模型计算的洪水模拟结果 Tab.4 The flood simulation results which are calculated by robust soil water content |
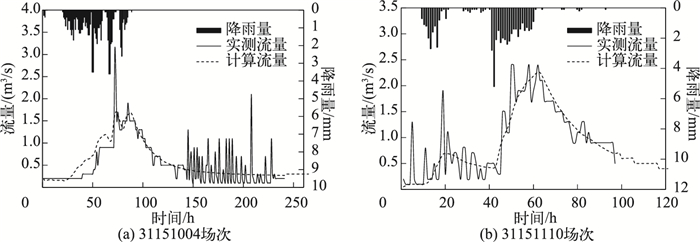
在抗差计算的基础上,采用2.2节介绍的土壤含水量系统响应反演修正方法,改进洪水初始土壤含水量.改进的洪水初始土壤含水量修正结果见表 5. 表 5中WU为上层土壤含水量,WL为下层土壤含水量,WD为深层土壤含水量.加入土壤含水量系统响应反演修正方法后的洪水模拟结果见表 6.加入抗差技术和系统响应反演修正方法后,洪水合格率达到92.3 %,仅有31151004和31151108两场洪水模拟不合格(表 6),图 6是其中2场洪水(不合格和合格各1场,洪号分别为31151004和31151110)的模型计算结果图.
|
图 6 典型洪水的模型计算结果图 Fig.6 The model simulation results of two typical floods |
| 表 5 土壤含水量系统响应反演修正结果 Tab.5 The results of system response correction for soil water content |
| 表 6 土壤含水量系统响应反演修正的洪水模拟结果 Tab.6 The flood simulation results using soil water content corrected by system response curve |
1) 对实测土壤含水率资料和雨洪资料分析发现,实测土壤含水率资料在时间序列上波动剧烈,土壤含水率资料与降雨和蒸发资料的相关性很差.鉴于此,土壤含水率测量探针的埋设方式以及数据采集处理方式还有待进一步验证和探讨.
2) 实测土壤含水率与模型计算土壤含水量之间,物理成因上讲是存在线性关系的.但由图 4和表 3结果可以看出,实测土壤含水率与模型计算土壤含水量之间相关性很差,无明显的函数关系.使用计算的土壤含水量用新安江模型计算的26场洪水结果,效果很不理想,其合格率低于20 %.说明实测土壤含水率资料观测误差很大,不能直接用于模型计算.实时土壤含水率数据与模型使用的土壤含水量之间的对应关系还需要大量实测数据的分析和研究.
3) 比较表 4和表 3可得,采用抗差估计对观测资料进行处理后,用抗差土壤含水量代入新安江模型计算的洪水模拟结果比较抗差前,洪水模拟精度有明显提高,合格率由19.2 %提高到了61.5 %,说明抗差估计能有效降低观测误差对土壤含水量估计的影响.但总体精度还是很低,模型模拟精度还低于乙等方案.
4) 比较表 6和表 4可得,采用土壤含水量系统响应反演修正方法,改进洪水初始土壤含水量,洪水模拟结果整体上有很大提高,洪水合格率达到了92.3 %,整体方案达到并超过了甲级.相对来说次洪径流深提高的幅度比洪峰大,这是合理的,因为初始土壤含水量的改进,最直接的改进结果是次洪计算径流深,通过改进径流深再影响洪峰.而土壤含水量系统响应误差修正的目标信息是洪量,所以洪量的提高幅度比洪峰大.
5) 计算结果可知,31151004场次洪水计算洪峰流量偏小,导致洪水模拟不合格(表 6),但31151004场次洪水的实测洪峰明显存在观测粗差,实际的洪峰应该与计算洪峰相近(图 6a),而另一场模拟不合格的洪水情况与此类似.而31151110场次洪水实测流量过程波动很大,应该是由于观测误差引起的(图 6b).总体来说,改进后的模型的洪水模拟结果较好.
4 结论本文提出了一种基于实测土壤墒情的水文预报方法,将实时监测到的土壤墒情转化为流域水文模型可以直接使用的土壤含水量,论证了将土壤墒情资料用于实时预报的可行性.建立了基于实测土壤墒情的降雨径流预报模型,并加入土壤含水率误差抗差估计技术和土壤含水量系统响应修正方法,提高了将土壤墒情应用于模型计算的模拟精度和系统的稳定性.将该模型应用于实验流域——宝盖洞流域进行验证,洪水模拟合格率达到了92.3 %,整体模拟效果达到甲级.这表明将土壤含水量实时监测数据用于水文模型预报是可行的,利用实测土壤墒情资料改进的三水源新安江模型可以在湿润半湿润地区实时洪水预报中进行推广应用.
| [1] |
Mi Sujuan, Tang Jiakui, Zhang Xianfeng et al. Soil moisture assimilation based on Variable Infiltration Capacity and Ensemble Kalman Filter. Geography and Geo-Information Science, 2013, 29(1): 91-95. [米素娟, 唐家奎, 张显峰等. 基于VIC模型与集合卡尔曼滤波的土壤水分同化研究. 地理与地理信息科学, 2013, 29(1): 91-95.] |
| [2] |
Shu Huilian. The soil moisture error correction method based on system response curve of flood forecasting model[Dissertation]. Nanjing:Hohai University, 2016. [束慧连. 模型土壤含水量的系统响应曲线修正方法[学位论文]. 南京: 河海大学, 2016. ]
|
| [3] |
Jackson TJ, Schmugge TJ, Nicke AD et al. Soil moisture updating and microwave remote sensing for hydrological simulation. Hydrological Sciences Journal, 1981, 26(3): 305-319. DOI:10.1080/02626668109490889 |
| [4] |
Pauwels VRN, Hoeben R, Verhoestn EC et al. The importance of the spatial patterns of remotely sensed soil moisture in the improvement of discharge predictions for small scale basins through data assimilation. Journal of Hydrology, 2001, 251: 88-102. DOI:10.1016/S0022-1694(01)00440-1 |
| [5] |
Parajka J, Naemi V, Bloschl G et al. Assimilating scatterometer soil moisture data into conceptual hydrologic models at coarse scales. Hydrology and Earth System Sciences, 2006, 10: 353-368. DOI:10.5194/hess-10-353-2006 |
| [6] |
Bao Weimin, Wang Hao, Zhao Chao et al. Robust estimation of AR model parameters. Journal of Hohai University:Natural Sciences, 2006, 34(3): 258-261. [包为民, 王浩, 赵超等. AR模型参数的抗差估计研究. 河海大学学报:自然科学版, 2006, 34(3): 258-261.] |
| [7] |
Bao Weimin, Ji Haiyang, Hu Qimei et al. Robust estimation theory and its application to hydrology. Advances in Water Science, 2003, 14(4): 528-532. [包为民, 嵇海祥, 胡其美等. 抗差理论及在水文学中的应用. 水科学进展, 2003, 14(4): 528-532.] |
| [8] |
Shen Dandan, Bao Weimin, Liu Kexin et al. Study on parameter robust estimation for Muskingum Model. China Rural Water and Hydropower, 2016(7): 72-74. [沈丹丹, 包为民, 刘可新等. 马斯京根汇流参数抗差估计研究. 中国农村水利水电, 2016(7): 72-74.] |
| [9] |
Zhao Chao. Robust real-time flood forecasting system[Dissertation]. Nanjing:Hohai University, 2006. [赵超. 流域实时洪水抗差预报系统研究[学位论文]. 南京: 河海大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10294-2006077442.htm ]
|
| [10] |
Tuo Liwen, Wu Youping. Weighting function selection of a new robust estimation method. Geomatics and Spatial Information Technology, 2008, 31(1): 181-182, 185. [脱立文, 吴友平. 一种新的稳健估计方法的权函数选取. 测绘与空间地理信息, 2008, 31(1): 181-182, 185.] |
| [11] |
Si Wei, Bao Weimin, Gupta HV. Updating real-time flooding forecasts via the dynamic system response curve method. Water Resources Research, 2015, 51: 1-17. DOI:10.1002/2014WR015707 |
| [12] |
Bao Weimin, Asce M, Si Wei et al. Flow updating in real-time flood forecasting based on runoff correction by a dynamic system response curve. Journal of Hydrologic Engineering, 2014, 19(4): 747-756. DOI:10.1061/(ASCE)HE.1943-5584.0000848 |
| [13] |
Si Wei, Bao Weimin, Qu Simin. Runoff error correction in real-time flood forecasting based on dynamic system response curve. Advances in Water Science, 2013, 24(4): 497-503. [司伟, 包为民, 瞿思敏. 洪水预报产流误差的动态系统响应曲线修正方法. 水科学进展, 2013, 24(4): 497-503.] |
| [14] |
Bao Weimin, Liu Kexin, Zhang Xiaoqin et al. Runoff error proportionality coefficient correction method based on system response. Advances in Water Science, 2014, 10: 476-482. [包为民, 刘可新, 张小琴等. 产流误差比例系数的系统响应修正方法. 水科学进展, 2014, 10: 476-482.] |
| [15] |
Liu Kexin, Bao Weimin, Zhang Xiaoqin et al. A system response correction method with runoff error smooth matrix. Journal of Hydraulic Engineering, 2015, 46(8): 960-966. [刘可新, 包为民, 张小琴等. 产流误差平稳矩阵的系统响应修正方法. 水利学报, 2015, 46(8): 960-966.] |
| [16] |
Bao Weimin. Hydrological forecasting. Beijing: China Water and Power Press, 2011, 143-163. [包为民. 水文预报. 北京: 中国水利水电出版社, 2011, 143-163.]
|
| [17] |
Bao Weimin, Zhang Xiaoqin, Zhao Liping. Parameter estimation method based on parameter function surface. Technological Sciences, 2013, 56(6): 1485-1498. DOI:10.1007/s11431-013-5224-3 |
| [18] |
Si Wei, Bao Weimin, Qu Simin. Problem of objective function of error square sum in parameter calibration. Water Resources and Power, 2013, 31(8): 19-21. [司伟, 包为民, 瞿思敏. 误差平方和目标函数在参数率定过程中遇到的问题. 水电能源科学, 2013, 31(8): 19-21.] |
| [19] |
Zhang Kun, Bao Weimin, Zhao Liping et al. Optimization algorithm of HBV Model based on linearized parameter calibration and its application. Water Resources and Power, 2013, 31(9): 8-11. [张坤, 包为民, 赵丽平等. 基于参数线性化率定法的HBV模型的优化算法及应用. 水电能源科学, 2013, 31(9): 8-11.] |
| [20] |
Bao Weimin, Zhang Kun, Wang Hongyan et al. Application of the linearized parameter calibration method for HBV-IWS model. Journal of Hydraulic Engineering, 2013, 44(10): 1210-1216. [包为民, 张坤, 王红艳等. 参数线性化率定方法在HBV-IWS模型中的应用. 水利学报, 2013, 44(10): 1210-1216.] |
 2017, Vol. 29
2017, Vol. 29 
