(2: 沂沭泗水利管理局水文局(信息中心), 徐州 221000)
(2: Water Conservancy Administration of the Yi-Shu-Si River Basin, Xuzhou 221000, P. R. China)
随着水文学理论方法发展和计算机技术的进步,洪水演进模型已经成为水情业务部门开展河道洪水预报的重要技术手段[1-2].但是受河道洪水汇流过程复杂性以及模型自身结构特点的影响,不同模型在各场次洪水的预报实践中,往往表现出明显差异.在洪水预报中,如何降低模型选择带来的不确定性,以及如何在保证预报精度与结果可靠性的同时,为防汛调度提供更为丰富的水情信息,成为洪水预报领域亟待解决的问题.
目前国内外常采用动力波以及扩散波理论描述河道一维非恒定水流运动.在动力波理论中,一般以圣维南方程组描述洪水波传播过程,其数值解法常被称为水力学方法[3];在扩散波理论中,圣维南方程组中的惯性项被忽略,摩阻比降只考虑水面比降,其方法常被称为水文学方法[4].两种方法各自优缺点明显,水力学方法精度较高,但受限于断面尺寸、糙率等资料获取困难;水文学方法运算简便,但在平原河网以及人类活动剧烈的河道,采用扩散波理论近似描述洪水状态变化剧烈的洪水运动情况并不合理.除以上两类方法之外,基于数据驱动的黑箱子模型也较多地应用于描述上游、支流入流—下游出流的多输入—单输出关系.此类方法多以回归分析、神经网络、支持向量机等理论作为基本算法[5],应用简单,但是其本身对洪水传播过程模拟不严谨,只能以统计分析的形式反映水文规律,且往往面临过拟合、易陷入局部鞍点等问题.
在了解洪水演进模型的优点与局限的基础上,取长补短进行多模型综合,已被证明是降低洪水预报中模型选择不确定性的有效措施.近些年发展起来的贝叶斯平均法(Bayesian Model Averaging,BMA)在大气和水文等模型的综合中得到了广泛关注和应用.基于BMA的模型综合方法实质上是将实测与不同模型得出的模拟结果作为先验信息,通过亚高斯模型或蒙特卡罗方式进行参数估计,计算各模型相对最优的权重等参数值,获取对预报变量后验概率分布的描述. Duan等[6]应用BMA法进行水文模型的综合,结果表明,BMA法可提高模型模拟精度,推求的预报量后验概率分布可分析模拟结果的不确定性.相对于传统GLUE等方法[7],其优势在于能够综合多模型预报结果,有助于提高概率预报结果的鲁棒性能的同时,提供更多可靠的洪水预报信息;同时,BMA能够通过权重等参数去量化评价各模型相对最优的概率,在贝叶斯理论框架下,提供模型选择不确定性的量化评价指标.然而,BMA在水文领域的研究,往往停留于应用层面,对BMA模型参数的讨论较为少见;本研究立足于淮河流域洪水预报工作,拟通过研究BMA的权重参数与单一预报模型相对优劣之间的相关关系,揭示BMA模型权重的统计现象所反映的物理规律,以认识BMA的性能与优势,提高洪水预报技术水平.
1 方法描述 1.1 洪水预报方法本研究采用3种基本的河道洪水演进模型,分别为BPNN方法、马斯京根流量演算法(以下简称“马法”)、一维水动力学模型(以下简称“水力学法”).在进行河道洪水演进模拟中,除干流上游断面来水外,还需要考虑支流与干流之间水量交换,因此在BPNN方法的输入层节点包括干流及所有支流流量(图 1),而马法、水力学方法则以干流来水作为上边界条件,以支流流量作为外部边界条件.

|
图 1 基于BPNN的河道洪水演进模拟示意 Fig.1 Diagrammatic sketch for BPNN based flood routing |
由于试验流域中各行蓄洪区、闸门的实际调度记录严重不足,且本研究并不关注各单一预报模型自身的精度问题,因此所用的3种方法均不考虑行蓄洪调度.
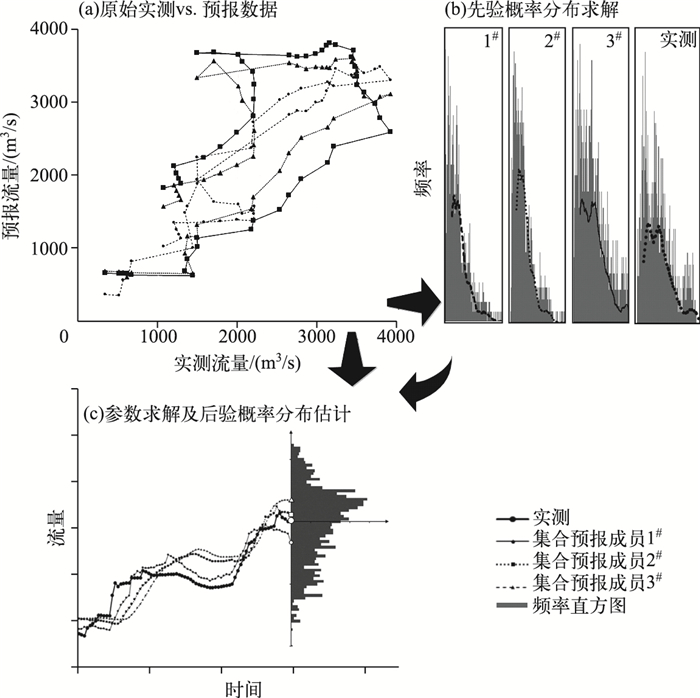
1.2 BMA模型简述BMA模型是以集合预报各成员为相对最优的概率为权重,综合实测、模拟序列先验信息,对各集合预报成员的概率分布加权平均获取预报变量后验概率分布.参照Liang等[8]所提供的方法,BMA运算流程如下.采用对数正态分布函数描述实测、多模型预报流量序列的概率分布特征.在此基础上,将原始数据经正态分位数变换至正态空间.在正态空间下,采用最大似然估计方法推求BMA模型的参数.基于蒙特卡罗原理,大量抽样获取预报变量在正态空间下的近似后验分布情况;进而转换至原始空间,获得预报变量的后验概率分布(图 2).算法细节信息见参考文献[8-9].
|
图 2 BMA集合预报模型原理示意 Fig.2 Flow of the BMA ensemble forecasting method |
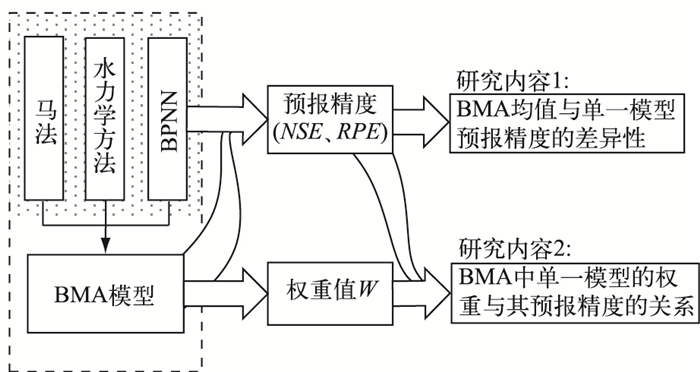
结合洪水预报的实际需求,本研究拟从以下两个方面开展讨论(图 3).
|
图 3 研究路线图 Fig.3 The methodology of this study |
1) 在实时洪水预报方案相差较大的设定试验条件下,比较传统单一模型以及集合预报方法所提供的洪水过程与洪峰预报结果的精度差异,以检验以往相关研究中关于两类方法预报结果的相关结论.
2) 统计各集合预报成员(即单一模型)模拟精度在不同场次洪水中变化趋势以及BMA模型中的权重值,以分析单一模型精度与BMA模型中表示模型相对优劣程度的参数权重之间的联系.
2 试验流域与数据介绍淮河流域地处长江、黄河之间,降水量年内分布不均,每年6—9月份的降雨量占年降水量的55%~80%,汛期暴雨频繁且集中,易发生大范围的流域性大洪水.尤其对于淮河中游来讲,大量水利工程设施的调控,导致河道水流运动严重偏离自然状态,洪水预报难度大.淮河流域暴雨洪水的频繁特性与洪水状态的复杂性之间的矛盾凸显,使得本流域洪水预报工作显得尤为重要,水文情报部门需要提供足够多有效的信息以供防汛调度决策.本研究选择淮河鲁台子—吴家渡区间作为试验流域,以吴家渡站流量过程为分析对象,研究基于BMA多模型集合预报方法的应用效果.试验流域位置及流域概化图见图 4.

|
图 4 试验流域概化图 Fig.4 Location of the studied align="right"iver reaches |
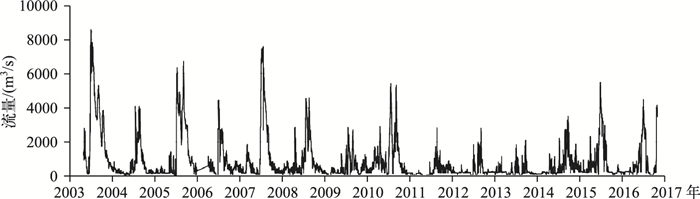
淮河吴家渡站2003—2016年流量过程见图 5.根据水文资料代表性的要求,从现有资料中筛选出包含大、中、小洪水的共19场洪水,其中2008、2009、2010、2012、2013、2014年各2场;2006年0场;其余年份各1场.
|
图 5 吴家渡站历史洪水过程示意 Fig.5 Observed flood discharge of the Wujiadu Station |
依照试验流域河道洪水演进过程构建BPNN的模型结构.考虑到本研究以上游鲁台子站作为河道入流,旁侧有来自上桥闸、蒙城闸的支流来水,因此构建BPNN模型对下游吴家渡站进行流量过程预报时,模型输入节点数设定为3,分别对应鲁台子、上桥闸、蒙城闸流量;输出节点数设定为1,对应吴家渡站流量.
考虑到本研究中所有洪水演进模型均仅用于数值模拟试验,需要选择相对可靠的训练样本进行参数训练,因此在BPNN运算执行之前可以采用本场洪水的上游、支流、下游流量数据训练BPNN参数.同理,BMA参数也采用本场洪水资料进行训练. BMA后验采样数目设定为1×104;集合预报成员数目为3,与洪水演进模型数目一致.
2.3 评价指标介绍采用的确定性预报结果的评价指标包括NSE[10](Nash-Sutcliffe Efficiency coefficient)、RPE[11](Relative Peak Error),NSE越高、RPE越低,表明预报结果与实测的相符程度越大,预报精度越高.另外采用相关系数指标,讨论单一模型精度与BMA的权重值之间关系.相关系数是由Karl Pearson提出,用于描述两变量之间线性相关程度的指标,又称作Pearson Product-moment Correlation Coefficient[12](PPCC).有如下规定:0<|PPCC|≤0.3,弱相关;0.3<|PPCC|≤0.5,实相关.受限于文章篇幅,此处不再对各指标计算公式进行阐述.
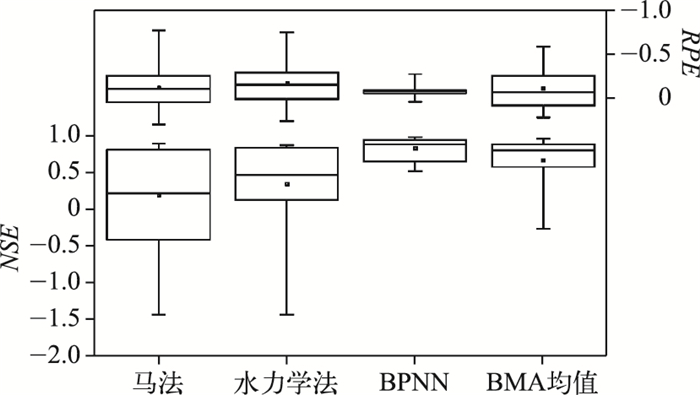
3 模拟结果统计分析 3.1 结果统计统计以上19场洪水中,马法、水力学法和BPNN法3种单一模型及BMA均值预报结果,采用箱型图的形式展示. 图 6中箱体中间横线表示中位数,小方框代表均值,上下两端横线表示系列的最大、最小值. NSE指标对应箱体上下边界代表四分位数,上下两端横线表示系列的最大、最小值;RPE指标所对应箱体的各部位所指代统计指标与之相反.
|
图 6 确定性洪水预报结果对比 Fig.6 Box-plot of the RPE or NSE values for the deterministic forecasts |
从NSE指标变化可以看出, BPNN方法的上下四分位数、中位数、均值与最大、最小值均高于马法及水力学方法,表明该方法对洪水过程模拟精度比另外2种方法要更好. 3种方法的RPE均值、中位数相差不大,表明3种方法对于洪峰流量的计算精度大体相当;而BPNN的上、下四分位数及最大、最小值指标均明显低于另外2种方法,表明在本试验中BPNN对洪峰流量的模拟精度较为稳定,相对马法与水力学方法所提供洪峰计算结果更可靠.另外,需要注意的是,由于本研究未考虑实际的行蓄洪区及闸门调度,因此所模拟结果可能出现系统误差,导致3个模型的RPE指标的均值都大于0.
将BMA均值与3个单一模型计算结果进行统计比较,可知:BMA运算结果NSE值的各项分布特征指标均介于BPNN与马法、水力学方法的相应指标之间,表明BMA预报与实际洪水过程重合度较高,对洪水过程模拟的性能低于BPNN方法,但高于马法、水力学方法;从RPE统计值的分布特征进行比较,发现除四分位数之外,BMA的RPE统计指标中的均值、中位数与最大、最小值介于BPNN与另外两种方法的相应指标之间,表明BMA对洪峰流量的模拟能力不高于其集合预报成员中较高者,但是也不低于其中较低者.
以上对确定性模拟结果的分析,进一步印证以往相关研究[8-9, 13]中所强调的,基于BMA的多模型集合预报能够避免最终模拟结果较差的可能性,与此同时模拟精度一般介于其集合预报成员中精度较高、较低者之间.然而,在实际洪水预报中,尤其当没有足够资料率定所采用的模型,或不确定哪一个模型适用于当前场次洪水预报时,采用BMA模型对多个备选的预报结果进行综合,是相对稳妥的解决方案.
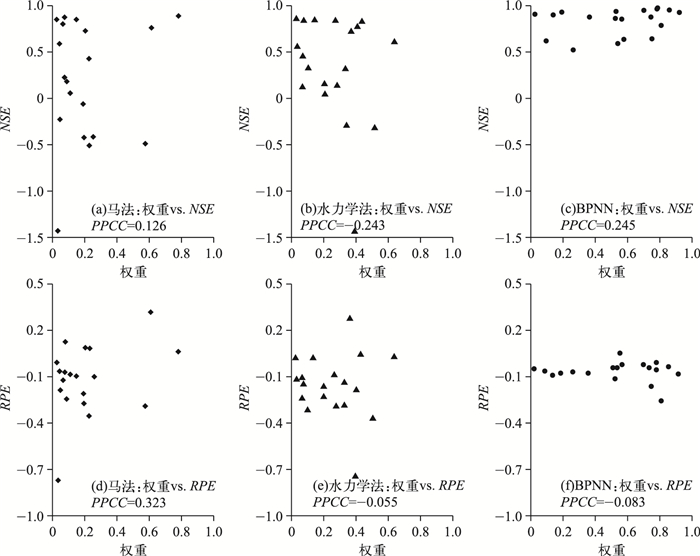
3.2 结果分析根据马法、水力学法和BPNN法3个单一模型的NSE、RPE值以及各方法在每场洪水中的BMA权重值,尝试绘制3个模型的NSE或RPE指标与权重的相关图,并计算得到相关系数值(图 7).
|
图 7 模型预报精度与权重相关性示意 Fig.7 Correlation analysis on statistics of the forecasts and the BMA weight values for each model |
图 7各图中,点据分布较为散乱,表明3个模型的NSE、RPE指标均不与权重值呈显著相关关系.其中,马法的RPE指标与相应权重值相关系数为0.323,略高于“实相关”关系的阈值;除此之外的的5种情形下,模型预报精度指标(NSE、RPE)与权重的相关系数均在0~0.3之间,仅呈弱相关关系.以上可见,单场洪水中各单一模型的模拟精度与其在BMA中的权重值不存在显著线性相关,即模型在某一单场洪水中表现的好坏程度,与其在BMA模型中的最优概率值(即权重值)大小并不同步,不能够根据本场洪水资料所得的BMA似然参数评判该模型在本场洪水中的表现.
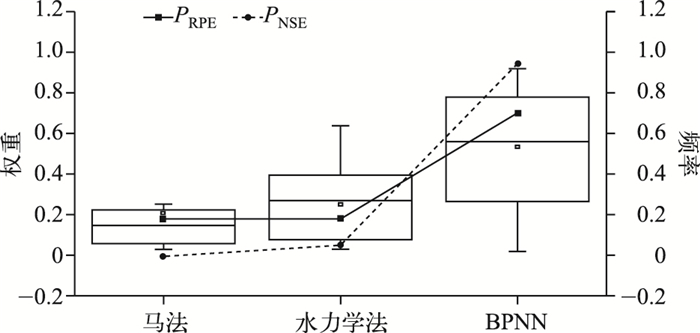
鉴于权重值表征模型相对最优的概率,研究分别以NSE、RPE作为评价模型单场洪水模拟精度的指标,通过统计19场洪水中各模型相对最优的频率与权重值做简单比较,以进一步研究两者之间是否存在联系.例如,在某场洪水中,当以NSE指标评判各模型模拟精度时,出现马法比其余两种方法更好的情况,则记马法相对最优次数加1;依次类推,统计19场洪水中,马法为最优的次数总数与洪水场次数目(19)的比值,得到基于NSE指标的马法为最优的频率值,记作PNSE.MSK.该指标反映着马法在多场次洪水预报中,预报结果相对其余2个模型更优的频率,根据统计理论可知,当采样数目足够大时,频率值近似于模型为最优的概率值,即BMA中权重值W. 图 8中,各模型权重值W绘制于主坐标轴(箱型图),PNSE、PRPE位于次坐标轴(折线图).
|
图 8 试验中模型为最优的频率与模型权重值对比结果 Fig.8 Statistically optimal frequency vs. the BMA weight values for the three models |
3个模型PRPE值与BMA模型中各模型权重值W的均值(或中位数)的数值相差不大,且3个模型的PRPE指标相对大小与权重值的变化趋势一致(图 8).例如,PRPE.MSK、PRPE.HDY、PRPE.BPNN分别为0.158、0.158、0.684,对应的WAVG统计值分别为0.208、0.258、0.534.类似的情况同样发生在以NSE指标统计模型最优频率的模拟试验中.对PRPE、PNSE与WAVG、WMED的相关关系做了对照(图 9).三模型的PRPE指标值视作一个系列,可以计算该系列与其他指标值的系列之间的相关系数,并作统计分析.图中,对角线中表示统计项目,左下方、右上方分别为各项目两两相关关系的示意图与相关系数值.

|
图 9 试验中模型为最优的频率与权重的相关关系 Fig.9 Correlations among PRPE, PNSE and WAVG, WMED |
4个指标之间的两两相关关系非常显著,即使相关性相对较低的PNSE与WMED之间,其相关系数也达到0.968.根据以上统计资料与分析结果,可以大致得出以下结论:模型在单场洪水中表现的好坏程度与其在BMA模型中相对最优概率关联不大;模型在多场洪水中总体表现得好坏程度与其相对最优概率较为相近. WAVG、WMED与PNSE、PRPE之间的相关关系进一步证明了单一模型的平均预报精度水平与其权重之间的统计相关性(图 9).
结合图 8、图 9中分析结果可知,BMA模型中的权重反映的是在大量洪水预报中,模型最优的概率,与单场洪水预报中模型的模拟精度不存在必然联系;只有当统计模型精度也是大量洪水预报中的平均水平时,两者才基本一致.这也进一步佐证了洪水预报中的经验,模型在单场洪水中的表现,并不能代表其平均水平,不能够因模型在少数几场洪水中表现较好或较差就过分依赖或武断的舍弃该模型,以避免因模型不适用而为洪水预报工作带来困扰;在较多场次洪水预报中表现较优的模型,其统计指标较为稳定,在实时洪水预报中可以有更大机会成为较优模型适合于洪水预报应用.
根据以上统计结果,当实测资料序列不够长时,采用一定的策略自动生成大量的水文数据,当做先验信息用于BMA的参数训练,所得到的权重等参数的估算结果对于指导洪水预报有一定的参考价值.对于自动化程度要求较高或数据信息量较大的洪水预报业务,考虑采用BMA模型进行多模型信息融合,可以有效避免人工干预操作,且高效利用现有数据,并可提供较高精度、可靠的洪水预报结果.
4 结论本研究从集合预报结果精度、基于BMA的模型适用性评价两方面展开讨论,目的在于提高对BMA的预报能力与参数特性的正确认识,提高BMA所提供预报信息的有效利用价值,以协助提升现有洪水预报水平.选择淮河鲁台子—吴家渡区间作为试验流域,通过比较吴家渡站流量过程预报精度,进一步验证了集合预报结果精度较高、表现稳定的特点;通过统计分析模型模拟精度与在BMA模型中权重值之间关系,利用统计结果初步证明了的模型平均性能与BMA模型的参数之间同步情况良好,增强了概率预报方法与传统洪水预报技术之间的相互关联.
根据本研究可以得出如下结论用于指导洪水预报.在进行洪水预报时,尤其在多个模型的预报精度区别不大或不存在成熟的预报模型的情形下,采用BMA集合预报能够有效的避免因模型选择带来的误差放大效应,有利于控制预报误差,提高预报结果精度与稳定性;在进行大量洪水预报后,根据统计结果,在备选模型中,各模型为最优的频率与该模型的BMA权重值应当相差不大,否则就要检查所采用的精度评价指标是否合理、先验信息是否完善、模型自身结构上是否存在导致表现异常的因素等;在无资料地区水文模型比较研究中,采用插补、同化等技术手段扩充不完备的先验信息,进而应用BMA模型提供模型相对最优的指标,是辅助进行模型适用性评价、增强评价可靠性程度的可行手段.
以上工作对于推广BMA模型法在水文预报中的应用具有积极作用,但是受限制于本研究所采用的单一预报模型比较少,今后将考虑增强对多模型或多组参数的集合预报研究,进一步考察研究中讨论成果.
| [1] |
Todini E. A model conditional processor to assess predictive uncertainty in flood forecasting. International Journal of River Basin Management, 2008, 6(2): 123-137. DOI:10.1080/15715124.2008.9635342 |
| [2] |
Chang Lu, Liu Kailei, Yao Cheng et al. Real-time flood forecasting and dispatching system in complicated river basin:Example for the section between Wangjiaba to Xiaoliuxiang Stations in Huaihe River. J Lake Sci, 2013, 25(3): 422-427. [常露, 刘开磊, 姚成等. 复杂河道洪水预报系统研究——以淮河王家坝至小柳巷区间流域为例. 湖泊科学, 2013, 25(3): 422-427. DOI:10.18307/2013.0317] |
| [3] |
WMO Manual on Flood Forecasting and Warning (Vols. WMO-No. 1072). Geneva, CH:World Meteorological Organization, 2011.
|
| [4] |
Cunge JA. On the subject of a flood propagation computation method (Muskingum method). Journal of Hydraulic Research, 1969, 7(2): 205-230. DOI:10.1080/00221686909500264 |
| [5] |
Chang FJ, Chen PA, Lu YR et al. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. Journal of Hydrology, 2014, 517: 836-846. DOI:10.1016/j.jhydrol.2014.06.013 |
| [6] |
Duan Q, Ajami NK, Gao X et al. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Advances in Water Resources, 2007, 30(5): 1371-1386. DOI:10.1016/j.advwatres.2006.11.014 |
| [7] |
Mantovan P, Todini E. Hydrological forecasting uncertainty assessment:Incoherence of the GLUE methodology. Journal of Hydrology, 2006, 330(1): 368-381. |
| [8] |
Liang Z, Wang D, Guo Y, Zhang Y et al. Application of Bayesian model averaging approach to multimodel ensemble hydrologic forecasting. J Hydrol Eng, 2011, 18(11): 1426-1436. |
| [9] |
Raftery AE, Madigan D, Hoeting JA. Bayesian model averaging for linear regression models. Journal of the American Statistical Association, 1997, 92(437): 179-191. DOI:10.1080/01621459.1997.10473615 |
| [10] |
Nash JE, Sutcliffe JV. River flow forecasting through conceptual models part I-A discussion of principles. Journal of Hydrology, 1970, 10(3): 282-290. DOI:10.1016/0022-1694(70)90255-6 |
| [11] |
Brath A, Montanari A, Toth E. Analysis of the effects of different scenarios of historical data availability on the calibration of a spatially-distributed hydrological model. Journal of Hydrology, 2004, 291(3): 232-253. |
| [12] |
Yue S, Ouarda T, Bobée B. A review of bivariate gamma distributions for hydrological application. Journal of Hydrology, 2001, 246(1): 1-18. |
| [13] |
Cloke HL, Pappenberger F. Ensemble flood forecasting:A review. Journal of Hydrology, 2009, 375(3): 613-626. |
 2017, Vol. 29
2017, Vol. 29 
