(2: Desert Research Institute, Las Vegas, NV, 89119)
(3: 辽宁省柴河水库管理局, 铁岭 112000)
(4: 陕西省水文水资源勘测局, 西安 710068)
(5: 上海市浦东新区水文水资源管理署, 上海 200129)
(2: Desert Research Institute, Las Vegas, NV, 89119)
(3: Liaoning Provincial Chaihe Reservoir Administration, Tieling 112000, P. R. China)
(4: Shanxi Provincial Hydrology and Water Resources Survey, Xi'an 710068, P. R. China)
(5: Shanghai Pudong New Area Hydrology and Water Resource Administration, Shanghai 200129, P. R. China)
流域水文模型通过对实际水文系统进行简化和近似,实现流域水文过程的分析和预测,成为了水文规律研究和解决实际问题的重要手段[1].由于流域水文系统的不确定性,预报模型自身不完备,输入信息受到噪声污染等因素影响,流域水文模型直接模拟计算的结果精度往往难以达到要求[2].因此利用实时的水文观测数据,对模型状态进行校正是十分重要的.国内外学者将卡尔曼滤波与水文模型、水动力模型相结合,取得了不错的效果.葛守西等[3]将圣维南方程进行离散化,建立了基于标准卡尔曼滤波的水动力学校正模型.吴晓玲等[4]结合马斯京根矩阵解法,将标准卡尔曼滤波应用于河道旁侧入流反演,取得了较好的效果.对于水文模型这类非线性系统,线性离散卡尔曼滤波的效果有限.对于非线性系统,扩展卡尔曼滤波(Extended Kalman Filter, EKF)得到了广泛的应用. Lü等[5]将扩展卡尔曼滤波应用到土壤含水量估计中,取得了较好的效果.对于强非线性的系统,扩展卡尔曼滤波对非线性函数的直接线性化往往引入较大的误差.当系统具有强非线性时, EKF估计精度下降,甚至发散[6]. Evensen[7]于1994年提出了集合卡尔曼滤波(Ensemble Kalman Filter, EnKF),EnKF通过集合来近似相关统计量. Moradkhani等[8]将集合卡尔曼滤波应用于同时估计概念性降雨径流模型的模型参数和模型状态.由于EnKF易于应用并且具有鲁棒性,因而在水文数据同化领域得到了广泛的应用[9-10].由于集合卡尔曼滤波使用采样方法来近似传播均值和协方差,因而样本数直接决定了估计效果.样本数越大,效果越好,计算负担越大[11]. Wan等[12]于2000年提出了基于无迹变换的卡尔曼滤波方法,无迹卡尔曼滤波(Unscented Kalman Filter, UKF)通过选取采样点来完成均值和协方差的捕捉和传递,与EKF的对照试验表明,UKF的效果更好[13]并且计算量与EKF基本相当.
UKF在水文模型实时校正上的应用,国内外尚属空白.本文首次将UKF方法引入集总式新安江模型,建立了基于无迹滤波校正的实时流域洪水预报模型,并将其应用到实际流域的洪水预报当中,对方法的准确性和实用性进行验证.
1 无迹卡尔曼滤波基本原理 1.1 非线性系统滤波对于线性系统,状态后验均值和协方差可以通过线性函数传递直接得到.而对于非线性系统而言,后验均值和协方差均不能通过非线性函数传播准确得到.对于非线性系统而言,最重要的是精确的得到状态的后验概率密度.但系统后验状态概率密度函数的求解往往极为复杂,难以获得精确的最优滤波.因而实际应用中,需要能够稳定寻找贝叶斯滤波的近似解[14]. EKF、EnKF和UKF及其改进算法都属于此类. 3种方法的主要区别在于通过非线性系统传播均值和协方差的方法不同. EKF的主要思想是对非线性函数进行线性化[15],而EnKF和UKF的主要思想类似,通过采样点(集合)进行近似,本文主要研究UKF.
1.2 无迹卡尔曼滤波UKF的基本思想是选取一定数量的采样点(Sigma Points)来捕捉均值和协方差信息,直接通过非线性函数进行传递,通过传递后的点集来估计状态后验均值和协方差[16].对于任意非线性状态后验分布,无迹变换所获得的均值和方差能保证至少二阶以上逼近精度,对于高斯分布,至少能够保证三阶以上精度[17]. Sigma点的采样策略主要有单形采样和对称采样等[17]. Julier[18]提出了一种可用于任意采样策略的修正框架:比例无迹变换.本研究使用了比例对称采样策略来完成采样.
考虑如下加性白噪声条件下的非线性高斯系统:
| $ {X_k} = f\left( {{X_{k - 1}}} \right) + {W_{k - 1}} $ | (1) |
| $ {Z_k} = h\left( {{X_k}} \right) + {V_k} $ | (2) |
式中, Xk是系统的状态向量;Wk-1是系统过程噪声;Zk是量测向量;Vk是量测噪声;f(·)和h(·)分别为非线性系统状态转移函数和量测函数;k表示时间.
采样策略使用比例对称采样策略,考虑加性白噪声的UKF的递推算法如下[12]:
(1) 根据选定的采样策略确定一组Sigma点:
| $ \chi _{k - 1\left| {k - 1} \right.}^i = \left\{ \begin{array}{l} {{\hat X}_{k - 1\left| {k - 1} \right.}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {i = 0} \right)\\ {{\hat X}_{k - 1\left| {k - 1} \right.}} + {\left( {\sqrt {\left( {L + \lambda } \right)P\left( {k - 1\left| {k - 1} \right.} \right)} } \right)_i}\;\;\;\;\;\;\;\left( {i = 1,2, \cdots ,L} \right)\\ {{\hat X}_{k - 1\left| {k - 1} \right.}} - {\left( {\sqrt {\left( {L + \lambda } \right)P\left( {k - 1\left| {k - 1} \right.} \right)} } \right)_{i - L}}\;\;\;\left( {i = L + 1,L + 2, \cdots ,2L} \right) \end{array} \right. $ | (3) |
式中,
对应权重:
| $ W_0^{\left( m \right)} = \lambda /\left( {L + \lambda } \right) $ | (4) |
| $ W_0^{\left( c \right)} = \lambda /\left( {L + \lambda } \right) + \left( {1 - {\alpha ^2} + \beta } \right) $ | (5) |
| $ W_i^{\left( c \right)} = W_i^{\left( m \right)} = 1/\left[ {2\left( {L + \lambda } \right)} \right]\left( {i = 1,2, \cdots ,2L} \right) $ | (6) |
其中:
| $ \lambda = {\alpha ^2}\left( {L + \kappa } \right) - L $ | (7) |
式中, L是状态变量维数;λ, α, κ和β均为比例对称变换的参数.
(2) 时间更新:
| $ {\chi _{k\left| {k - 1} \right.}} = f\left( {{\chi _{k - 1\left| {k - 1} \right.}}} \right) $ | (8) |
式中, χk|k-1是式(3)生成的Sigma点通过非线性函数f(·)传播后的结果.
| $ {{\hat X}_{k\left| {k - 1} \right.}}{\rm{ = }}\sum\limits_{i = 0}^{2L} {W_i^{\left( m \right)}\chi _{k\left| {k - 1} \right.}^i} $ | (9) |
式中,
| $ {P_{k\left| {k - 1} \right.}} = \sum\limits_{i = 0}^{2L} {W_i^{\left( c \right)}\left[ {\chi _{k\left| {k - 1} \right.}^i - {{\hat X}_{k\left| {k - 1} \right.}}} \right]{{\left[ {\chi _{k\left| {k - 1} \right.}^i - {{\hat X}_{k\left| {k - 1} \right.}}} \right]}^T}} + Q $ | (10) |
式中, Q是系统过程噪声方差阵;Pk|k-1是一步预测误差协方差阵.
(3) 量测更新:
| $ {\gamma _{k\left| {k - 1} \right.}} = h\left( {{\chi _{k\left| {k - 1} \right.}}} \right) $ | (11) |
式中, h(·)是非线性系统量测函数.式(11)中的Sigma点集χk|k-1是利用
| $ {{\hat Y}_{k\left| {k - 1} \right.}} = \sum\limits_{i = 0}^{2L} {W_i^{\left( m \right)}\gamma _{k\left| {k - 1} \right.}^i} $ | (12) |
式中,
| $ {P_{{{\hat Y}_k}\left| {{{\hat Y}_k}} \right.}} = \sum\limits_{i = 0}^{2L} {W_i^{\left( c \right)}\left[ {\gamma _{k\left| {k - 1} \right.}^i - {{\hat Y}_{k\left| {k - 1} \right.}}} \right]{{\left[ {\gamma _{k\left| {k - 1} \right.}^i - {{\hat Y}_{k\left| {k - 1} \right.}}} \right]}^T}} + R $ | (13) |
| $ {P_{{{\hat X}_k}\left| {{{\hat Y}_k}} \right.}} = \sum\limits_{i = 0}^{2L} {W_i^{\left( c \right)}\left[ {\chi _{k\left| {k - 1} \right.}^i - {{\hat X}_{k\left| {k - 1} \right.}}} \right]{{\left[ {\gamma _{k\left| {k - 1} \right.}^i - {{\hat Y}_{k\left| {k - 1} \right.}}} \right]}^T}} $ | (14) |
| $ K = {P_{{{\hat X}_k}\left| {{{\hat Y}_k}} \right.}}P_{{{\hat Y}_k}\left| {{{\hat Y}_k}} \right.}^{ - 1} $ | (15) |
式中, K是增益矩阵;R是量测噪声方差.
| $ {{\hat X}_k} = {{\hat X}_{k\left| {k - 1} \right.}} + K\left( {{Y_k} - {{\hat Y}_{k\left| {k - 1} \right.}}} \right) $ | (16) |
式中, Yk是量测值;
| $ {P_k} = {P_{k\left| {k - 1} \right.}} - K \cdot {P_{{{\hat Y}_k}\left| {{{\hat Y}_k}} \right.}} \cdot {K^T} $ | (17) |
滤波状态变量选取,直接决定实时校正模型是否合理,并将影响到校正结果.系统状态变量的选取必须要遵循系统状态的定义和要求,系统状态是指:系统的一组变量,结合这组变量的当前取值,输入和描述系统动态特性的方程,就能完全预测系统未来的状态和输出响应.用来表示动态系统状态的状态变量个数应该尽可能少,并且一般有多组状态变量可供选择[20].对于一个使用滤波校正的流域水文模型而言,在模型输入确定的情况下,根据选择的水文模型状态变量的当前取值,就能完全确定流域出口断面的流量(模型输出).以新安江模型中的蓄满产流为例,假定蓄满产流模型使用三层蒸散发模型,产流子模型的输入为降水和蒸散发能力,输出为产流.葛守西[21]建立了使用三层水帐模式和抛物线型流域蓄水容量曲线的蓄满产流模型卡尔曼滤波算法,将WU(上层土壤含水量)、WL(下层土壤含水量)、WD(深层土壤含水量)作为状态变量进行校正.实际上,对于产流子模型,理论上可以选择的状态变量为WU、WL、WD和W(土壤含水量)中任意3个的组合.如果全部选择,则会冗余,并且可能会造成校正结果与水文模型本身逻辑结构相悖(3层土壤含水量之和不等于土壤含水量).
状态变量维数过高会引起卡尔曼滤波计算量增大,并且可能出现滤波不稳定情况[21].为了避免状态变量维数过大,本研究中水文模型采用集总式新安江模型.模型的输入是研究流域的面平均雨量和蒸发能力,输出是流域出口流量和蒸发.蓄满产流使用三层蒸散发模型,分水源使用自由水蓄水库[22],坡面汇流使用线性水库.坡面汇流的总径流作为输入进入河网汇流,河网汇流部分使用滞后演算法[23].
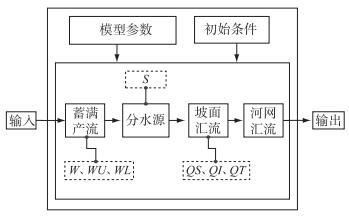
综合以上关于状态变量选取的分析和新安江模型的结构,本研究使用的模型结构和状态变量如图 1所示.虚线框内是本研究选择的对应子模型的状态变量.
|
图 1 新安江模型结构和状态变量(W表示土壤含水量,WU表示上层土壤含水量,WL表示下层土壤含水量,S表示自由水蓄量,QS表示地表径流,QI表示壤中流,QT表示总径流) Fig.1 Structure and state variables of the XAJ model |
根据考虑加性白噪声的UKF递推算法和2.1节的分析,基于无迹卡尔曼滤波的新安江实时校正模型的计算流程如下:
(1) 根据选定的比例对称采样策略和对应参数,结合上一时段的误差协方差矩阵,对前一时段的状态变量进行采样,生成Sigma点.
(2) 计算Sigma点通过新安江模型方程的传播结果.
(3) 根据权重和传播后的Sigma点推求传递后的均值(得到状态变量预测和输出预测)和协方差.
(4) 计算增益矩阵,根据实测流量和输出预测更新模型状态量,更新误差协方差矩阵,转入步骤(1).
3 模型应用 3.1 资料情况及新安江模型参数本文选取闽江流域西北部的邵武流域进行计算分析,流域控制面积2745 km2.流域内植被情况良好,主要受亚热带季风影响.气候温暖湿润,雨量充沛,属于典型的南方湿润地区.使用1988-1998年共11 a的逐日资料作为日模型资料,日模型资料主要用来率定产流模型参数,并为次洪模拟提供状态量初值,流量资料来自流域控制站邵武站.次洪资料是从上述时段内选取的17场洪水资料,结合次洪资料,使用人工试错法率定新安江模型参数.本文使用的新安江模型参数见表 1.为了方便研究滤波校正效果,新安江模型的计算结果将在3.3中与滤波校正结果一并给出.
| 表 1 新安江模型参数 Tab.1 Parameters for XAJ model |
无迹卡尔曼滤波器的参数包括无迹变换参数、量测噪声方差和过程噪声方差.
3.2.1 无迹变换参数α是正值的比例系数,可以设置为一个非常小的正值以减小高阶项的影响[12]. β用来吸收状态量的先验分布信息,对于高斯分布,β=2是最优的. κ是二次缩放因子,一般令κ=0.当β=0并且α=1时,比例对称采样策略退化为一般对称采样策略[12].
当λ < 0时,可能会协方差在递推的过程中失去半正定性[24].即一般要求:
| $ \lambda = {\alpha ^2}\left( {L + \kappa } \right) - L \ge 0 $ | (18) |
由式(18)可知,当α取值过小时,必有λ < 0. α不应过小,该参数取值过小时将导致式(3)中的Cholesky分解无法进行,进而导致递推无法进行.基于以上原则,结合试算,本次研究取α=0.95、β=2、κ=0.
3.2.2 量测噪声方差和过程噪声方差流域水文模型仅仅是对实际情况的近似,模型与实际情况有一定的差距,因而一般来说,实测流量要比模拟流量更加可靠.鉴于此,量测噪声方差取值不宜过大.过程噪声协方差阵取Q=aI的形式, a通过试算确定.在试算过程发现中,当a取值偏大时,同样会使协方差矩阵失去半正定性.另外在a不变时,适当增大R的取值能够帮助保持协方差矩阵的半正定性.基于以上原则,经过试算,取a=0.4.在a确定之后,调整R的取值,本研究取R=50.
3.3 应用结果及分析 3.3.1 评价指标为了全面地比较新安江模型和滤波校正的效果,本文采用了5个评价指标:均方根误差(Root Mean Square Error, RMSE)、平均偏差(Mean Bias Error, MBE)、纳须系数(Nash-Sutcliffe efficiency value, NSE)洪峰相对误差(PeakRE)和峰现时差(PeakLag, h)[25].
| $ RMSE = {\left( {\frac{{\sum\limits_{t = 1}^N {{{\left[ {{Q_{{\rm{sim}}}}\left( t \right) - {Q_{{\rm{obs}}}}\left( t \right)} \right]}^2}} }}{N}} \right)^{1/2}} $ | (19) |
式中, N表示模拟序列(实测序列)总历时(长度),Qsim(t)表示时间t的模型输出值,Qobs(t)表示时间t的对应观测值.
| $ MBE = \frac{1}{N}\sum\limits_{t = 1}^N {\left[ {{Q_{{\rm{sim}}}}\left( t \right) - {Q_{{\rm{obs}}}}\left( t \right)} \right]} $ | (20) |
| $ NSE = 1 - \frac{{\sum\limits_{t = 1}^N {{{\left[ {{Q_{{\rm{sim}}}}\left( t \right) - {Q_{{\rm{obs}}}}\left( t \right)} \right]}^2}} }}{{\sum\limits_{t = 1}^N {{{\left[ {{Q_{{\rm{obs}}}}\left( t \right) - \overline {{Q_{{\rm{obs}}}}} } \right]}^2}} }} $ | (21) |
式中,
| $ PeakRE = \frac{{Pea{k_{{\rm{sim}}}} - Pea{k_{{\rm{obs}}}}}}{{Pea{k_{{\rm{obs}}}}}} $ | (22) |
式中, Peaksim表示模拟洪峰,Peakobs表示实测洪峰.
| $ PeakLag = PeakTim{e_{{\rm{sim}}}} - PeakTim{e_{{\rm{obs}}}} $ | (23) |
式中, PeakTimesim表示模拟洪峰峰现时间,PeakTimeobs表示实测洪峰峰现时间.
NSE被广泛应用于评价水文模型模拟效果,其将实测值的平均值(
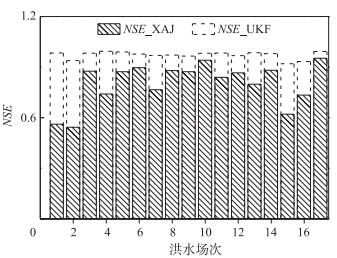
在前述模型结构、模型参数、滤波器参数前提下,以试验流域出口断面的流量序列作为观测资料更新模型状态,分别使用5个指标对原始模型结果和无迹卡尔曼滤波校正模型结果进行评价. 图 2给出了原始模型和无迹卡尔曼滤波校正模型的NSE模拟结果.
|
图 2 XAJ模型和UKF校正模型的NSE结果 Fig.2 NSE values of XAJ model and modified model using UKF |
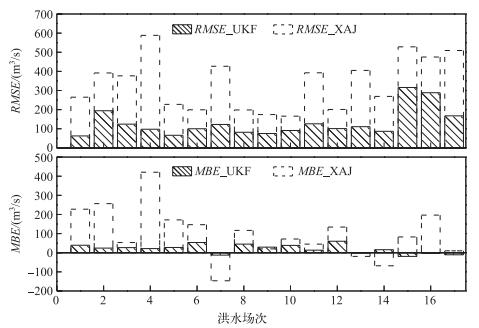
相比XAJ原始模拟结果,经过滤波校正后的模拟效果显著提升(图 2).平均NSE由0.80上升到0.97.值得注意的是,有3场洪水的NSE明显低于平均值,分别是第2、15、16场,这3场洪水将在后面进行分析.为了更加全面地评价2种方法的效果,图 3给出了2种方法的RMSE和MBE计算结果.
|
图 3 XAJ模型和UKF校正模型的RMSE和MBE计算结果 Fig.3 Results of RMSE and MBE obtained by XAJ model and modified model using UKF |
经过滤波校正后,RMSE的均值由347.8 m3/s减小到129.9 m3/s.校正后的每场洪水MBE的绝对值稳定减小. 2个指标的评价效果与NSE的评价效果基本一致,这说明UKF能够显著且稳定地提高XAJ模型模拟精度.全部17场洪水的NSE、RMSE和MBE结果见表 2.
| 表 2 原始模型和滤波校正的NSE、RMSE和MBE 3种指标结果统计 Tab.2 Results of NSE, RMSE and MBE for XAJ model and modified model using UKF |
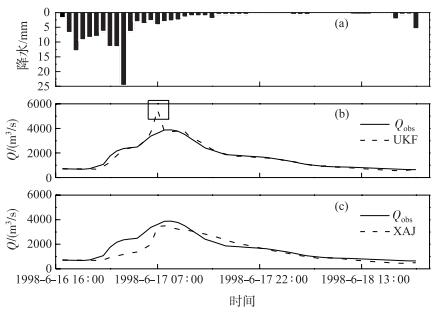
下面将以第16场洪水为例,分析3场效果较差洪水,图 4给出了第16场洪水原始模型结果和UKF校正后的结果比较.
|
图 4 典型洪水原始模型结果和UKF校正结果比较 Fig.4 Comparison of results of the typical flood event obtained by XAJ model and modified model using UKF |
与原始模型模拟结果相比,滤波校正后的涨水段和退水段总体上都与实测系列更加接近.但是由中间的图可以看出,UKF校正后的洪峰(黑色框中的点,5500 m3/s)要明显高于实测洪峰(3880 m3/s)和新安江模型模拟洪峰(3520 m3/s),这是引起该场次洪水校正效果相对较差的主要原因.在认为原始XAJ模型建模基本合理的假设下,导致这个突变点的可能原因可以分为2类:第一类是资料误差,主要指降水资料和出口断面流量资料误差;第二类是校正误差.从洪峰出现前的涨水段较高的拟合程度来看,滤波校正后的模型状态应该更加接近真实状态,因而校正导致误差的可能性比较低. 1998-6-17 02 :00的降水量达到25 mm,远远高于时段平均水平(图 4a).滤波校正后的流量过程对于这一异常输入反应明显,而实测流量过程线洪峰附近流量变化平缓,没有受到这一异常降水的影响,这是不合理的,因此考虑可能的原因为洪峰漏测.另外2场洪水情况类似,经过校正后的流量过程均为涨水段和退水段拟合较好,洪峰偏高.洪峰全部17场洪水(原始模型,滤波校正)的洪峰相对误差和峰现时差见表 3.
| 表 3 原始模型和滤波校正洪峰结果统计 Tab.3 Results of peak information obtained by XAJ model and modified model using UKF |
经过滤波校正后的洪峰相对误差和峰现时差都明显降低,校正后的洪峰大多与实测洪峰拟合较好(表 3).洪峰相对误差绝对值的平均值由14.8 %减小到10.4 %,峰现时差绝对值的平均值由1.9 h下降到1.0 h.结合表 2可知,相比于原始模型的模拟结果,NSE较低的3场洪水(“MJSW19920616”、“MJSW19980613”和“MJSW19980616”)的整体模拟效果较好,但洪峰模拟效果较差.
4 结论无迹卡尔曼滤波是一种非线性滤波器,通过引入无迹变换来解决均值和协方差估计的非线性变换问题.本文讨论了滤波状态变量的选取方法与影响,并将讨论结果应用到新安江模型的实时校正中,结合无迹卡尔曼滤波,提出了基于无迹卡尔曼滤波的新安江实时校正模型.滤波结合实测值对选定的新安江模型状态变量进行校正,不仅直接校正了模型状态变量,同时可以校正流域出口断面计算值,也为未来时刻模型预报提供更加准确的状态变量,从而提高预报精度.
本文以闽江邵武流域的实际洪水过程为例,初步研究了无迹卡尔曼滤波在流域洪水预报中的应用,研究表明,无迹卡尔曼滤波能够使模型状态趋近于真实状态,有效提高原始模型计算精度,可用于实际流域的实时校正.结合水情自动化监测系统,根据实测系列对模型状态进行实时校正,进而提高预报精度,为防洪调度决策提供技术支撑.
流域前期土壤含水量对预报精度往往具有较大影响,为了充分利用现有的遥感数据和遥测数据,在未来的研究中可以考虑使用无迹卡尔曼滤波技术将土壤水分遥测估算结果同化到分布式新安江模型中,同化流域水文模型的通量数据(降水为主)以提高预报精度.另外,构建合理的过程噪声方差和量测噪声方差的理论选取方法,还需要深入的后续研究.
| [1] |
Bao WM. Hydrological forecasting:3rd edition. Beijing: China Water & Power Press, 2006. [包为民. 水文预报:第3版. 北京: 中国水利水电出版社, 2006.]
|
| [2] |
Madsen H, Skotner C. Adaptive state updating in real-time river flow forecasting-A combined filtering and error forecasting procedure. Journal of Hydrology, 2005, 308(1): 302-312. |
| [3] |
Ge SX, Cheng HY, Li YR. Real time updating of hydrodynamic model by using Kalman filter. Journal of Hydraulic Engineering, 2005(6): 687-693. [葛守西, 程海云, 李玉荣. 水动力学模型卡尔曼滤波实时校正技术. 水利学报, 2005(6): 687-693.] |
| [4] |
Wu XL, Wang CH, Xiang XH. Inverse analysis of lateral inflow in real-time correction. Advances in Water Sciences, 2009(1): 52-57. [吴晓玲, 王船海, 向小华. 实时校正中的旁侧入流反演方法. 水科学进展, 2009(1): 52-57.] |
| [5] |
Lü H, Yu Z, Zhu Y et al. Dual state-parameter estimation of root zone soil moisture by optimal parameter estimation and extended Kalman filter data assimilation. Advances in Water Resources, 2011, 34(3): 395-406. DOI:10.1016/j.advwatres.2010.12.005 |
| [6] |
Liu Y, Weerts AH, Clark M et al. Advancing data assimilation in operational hydrologic forecasting:progresses, challenges, and emerging opportunities. Hydrology & Earth System Sciences, 2012, 16(10): 3863-3887. |
| [7] |
Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research:Oceans, 1994, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
| [8] |
Moradkhani H, Sorooshian S, Gupta HV et al. Dual state-parameter estimation of hydrological models using ensemble Kalman filter. Advances in Water Resources, 2005, 28(2): 135-147. DOI:10.1016/j.advwatres.2004.09.002 |
| [9] |
Lü H, Hou T, Horton R et al. The streamflow estimation using the Xinanjiang rainfall runoff model and dual state-parameter estimation method. Journal of Hydrology, 2013, 480: 102-114. DOI:10.1016/j.jhydrol.2012.12.011 |
| [10] |
Yu F, Li HT, Zhang CM et al. Data assimilation on soil moisture content based on multi-source remote sensing and hydrologic model. Journal of Infrared and Millimeter Waves, 2014, 33(6): 602-607. [余凡, 李海涛, 张承明等. 多源遥感数据与水文过程模型的土壤水分同化方法研究. 红外与毫米波学报, 2014, 33(6): 602-607.] |
| [11] |
Wang W, Kou XH. Methods for hydrological data assimilation and advances of assimilating remotely sensed data into rainfall-runoff models. Journal of Hohai University:Natural Sciences, 2009(5): 556-562. [王文, 寇小华. 水文数据同化方法及遥感数据在水文数据同化中的应用进展. 河海大学学报:自然科学版, 2009(5): 556-562.] |
| [12] |
Wan EA, Van Der Merwe R. The unscented Kalman filter for nonlinear estimation//Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000. AS-SPCC. IEEE, 2000, (1): 153-158.
|
| [13] |
Van Der Merwe R, Wan EA. The square-root unscented Kalman filter for state and parameter-estimation//Acoustics, Speech, and Signal Processing, 2001. Proceedings(ICASSP'01). 2001 IEEE International Conference on. IEEE, 2001, (6): 3461-3464.
|
| [14] |
Zhao L, Wang XX, Li Liang et al. Nonlinear system filtering theory. Beijing: National Defend Industry Press, 2012. [赵琳, 王小旭, 李亮等. 非线性系统滤波理论. 北京: 国防工业出版社, 2012.]
|
| [15] |
Han XJ, Li X. Review of the nonlinear filters in the land data assimilation. Advance in Earth Science, 2008, 23(8): 813-820. [韩旭军, 李新. 非线性滤波方法与陆面数据同化. 地球科学进展, 2008, 23(8): 813-820.] |
| [16] |
Julier SJ, Uhlmann JK, Durrant-Whyte HF. A new approach for filtering nonlinear systems//American Control Conference, Proceedings of the 1995. IEEE, 1995, (3): 1628-1632. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=529783
|
| [17] |
Julier SJ, Uhlmann JK. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations//American Control Conference, 2002. Proceedings of the 2002. IEEE, 2002, (2): 887-892. http://www.researchgate.net/publication/3961258_Reduced_sigma_point_filters_for_propagation_of_means_and_covariances_through_nonlinear_transformations
|
| [18] |
Julier SJ. The scaled unscented transformation//American Control Conference, 2002. Proceedings of the 2002. IEEE, 2002, (6): 4555-4559.
|
| [19] |
Haykin S. Kalman filtering and neural networks. New York: Wiley, 2001.
|
| [20] |
Dorf RC, Bishop RH. Modern control systems. New Jersey: Pearson, 2011.
|
| [21] |
Ge SX. Modern Techniques In Flood Forecasting. Beijing: China Water & Power Press, 1999. [葛守西. 现代洪水预报技术. 北京: 中国水利水电出版社, 1999.]
|
| [22] |
Zhao RJ. The Xinanjiang model applied in China. Journal of Hydrology, 1992, 135(1): 371-381. |
| [23] |
Zhao RJ. Flow concentration model based on Time-varying Linear System. Hydrology, 1991(4): 22-24. [赵人俊. 时变线性系统流域汇流模型. 水文, 1991(4): 22-24.] |
| [24] |
Julier S, Uhlmann J, Durrant-Whyte HF. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482. DOI:10.1109/9.847726 |
| [25] |
Nash JE, Sutcliffe JV. River flow forecasting through conceptual models part Ⅰ-A discussion of principles. Journal of Hydrology, 1970, 10(3): 282-290. DOI:10.1016/0022-1694(70)90255-6 |
| [26] |
Schaefli B, Gupta HV. Do nash values have value?. Hydrological Processes, 2007, 21(15): 2075-2080. DOI:10.1002/(ISSN)1099-1085 |
 2018, Vol. 30
2018, Vol. 30 

