(2: 广东省华南地区水安全调控工程技术研究中心, 广州 510275)
(2: Center of Water Security Engineering and Technology in Southern China of Guangdong, Guangzhou 510275, P. R. China)
水文干旱事件通常基于设定的河川径流阈值,采用游程方法提取[1-2].一次干旱事件一般包含历时、强度和峰值等特性指标,因此水文干旱事件是多个变量(两变量或三变量)随机过程,且变量之间存在相依性. Copula是基于变量相依性的多变量边缘分布连接函数,已经广泛应用于水文干旱多变量联合分布模拟[3-6].
Copula函数及边缘分布确定后,传统联合重现期分析在判断安全或危险事件上有可能存在误判. Kendall联合重现期概念的提出和应用,改进了多变量联合设计的可靠性[7-8].某一特定联合重现期是由无穷多个变量组合值构成,如两变量的等值线和三变量的等值面.如何在特定联合重现期的等值线或等值面上,选取一组设计值的联合分布设计研究逐渐受到关注.传统设计方法是基于同频思路选取多变量设计组合值[9-10],但这种方法过于主观,没有考虑边缘和联合分布的特性. Salvadori等[7]定义了最大可能权函数(Most-likely weight function),基于边缘及联合分布密度选取最大可能发生的多变量组合.
随着区域经济快速发展和流域水资源开发利用,人类活动特别是大型水库的建设运行,显著改变了河川径流过程,从而影响水文干旱特征.目前,定量评估水库径流调节作用对水文干旱的影响研究较少,尹正杰等[11]定量刻画了水库径流调节对水文干旱单一指标的影响,但没有考虑对水文干旱联合分布的影响.
因此,本文以东江流域为例,以满足当地需水要求的河道内最小流量管理目标为阈值,基于水库入库和出库流量还原河川天然径流过程,采用游程理论分别提取实测和天然径流过程的水文干旱事件,构建水文干旱指标多变量联合分布Copula模型,基于Kendall联合重现期并采用最大可能权函数设计多变量组合值,通过对比实测和天然径流过程的水文干旱联合分布特征,定量评估水库径流调节作用对水文干旱多变量联合特征的影响程度,为水文干旱多变量模拟和设计提供了一种新方法,并为当地抗旱减灾的水资源多维风险评估和管理提供科学依据.
1 方法和数据 1.1 干旱指标联合分布与边缘分布模拟根据Sklar定理,多变量联合分布可定义为:
| $ F\left( {{x_1}, \cdots ,{x_d}} \right) = C\left[ {F\left( {{x_1}} \right), \cdots ,F\left( {{x_d}} \right)} \right] = C\left( {{u_1}, \cdots ,{u_d}} \right) $ | (1) |
式中, C(u1, …, ud)为边缘分布在[0, 1]区间的Copula联结函数,u1=F(x1), …, ud=F(xd)为各单变量的边缘分布,即累积频率. d为联合分布的维数,即变量个数.当模拟水文干旱指标三变量联合分布,d=3,x1、x2和x3分别为干旱特征的3个指标:历时、强度和峰值; 当模拟干旱指标两变量联合分布时,则d=2,x1和x2为干旱指标中任意2个.
Copula函数构造多样,其中Meta-Elliptic Copulas的Meta-Gaussian Copula模型,在水文干旱多变量联合分布模拟中具有良好效果[12]. d维Meta-Gaussian Copula的分布函数C(u1, …, ud)和密度函数c(u1, …, ud)分别为:
| $ C\left( {{u_1}, \cdots ,{u_d}} \right) = \int_{ - \infty }^{{b_1}} \cdots \int_{ - \infty }^{{b_d}} {g\left( {{\omega _1}, \cdots ,{\omega _d}} \right)d{\omega _1} \cdots d{\omega _d}} $ | (2) |
| $ c\left( {{u_1}, \cdots ,{u_d}} \right) = {\left| \Sigma \right|^{ - 1/2}}\exp \left( { - {\zeta ^T}{\Sigma ^{ - 1}}\zeta /2 + {\zeta ^T}\zeta /2} \right) $ | (3) |
其中:
| $ g\left( {{\omega _1}, \cdots ,{\omega _d}} \right) = {\left( {2\pi } \right)^{ - d/2}}{\left| \Sigma \right|^{ - 1/2}}\exp \left( { - {\omega ^T}{\Sigma ^{ - 1}}\omega /2} \right) $ | (4) |
式中, b1=Φ-1(u1), …, bd=Φ-1(ud),其中Φ-1(·)为标准正态分布的逆函数;Σ为相关系数矩阵是模型参数,ω为被积函数变量矩阵ω=[ω1, …, ωd]T,ζ=[b1, …, bd]T.
变量间相关性采用Kendall τ、Spearman秩相关系数ρ和Pearson古典相关系数γ,联合分布模型拟合检验采用基于Rosenblatt变换的Kolmogorov-Smirnov(K-S)法[13].边缘分布考虑三参数的广义极值分布(GEV)、皮尔逊Ⅲ型(P-Ⅲ)、广义帕累托分布(GP)和两参数的韦布尔分布(WBL)、对数正态分布(LOGN)、伽马分布(GAMA)共6种常用模型,通过K-S法和Anderson-Darling(A-D)法进行拟合检验,并综合考虑均方根误差(RMSE)、赤池信息准则(AIC)和检验统计量概率P值进行优选[14-15].联合分布及边缘分布模型参数均采用最大似然法估计.
1.2 超越概率、重现期与设计值就水文干旱特征研究来说,通常关注干旱指标大于设定阈值的概率或重现期,即:
| $ \hat P = 1 - F\left( x \right) = 1 - u = \hat u $ | (5) |
| $ \hat T = 1/\left( {{N_E} \cdot \hat P} \right) = 1/\left( {{N_E} \cdot \hat u} \right) $ | (6) |
式中, F(x)或u为历时、强度或峰值的累积频率,
干旱指标两变量联合超越概率
| $ \hat C = 1 - \left( {{u_1} + {u_2}} \right) + C\left( {{u_1},{u_2}} \right) $ | (7) |
式中, (u1, u2)为历时、强度和峰值其中任意两变量组合.
干旱指标三变量联合超越概率
| $ \hat C = 1 - \left( {{u_1} + {u_2} + {u_3}} \right) + C\left( {{u_1},{u_2}} \right) + C\left( {{u_1},{u_3}} \right) + C\left( {{u_2},{u_3}} \right) - C\left( {{u_1},{u_2},{u_3}} \right) $ | (8) |
式中, (u1, u2, u3)为历时、强度和峰值的三变量组合.
Kendall联合重现期是以联合概率相等的一系列事件为临界曲线,来识别危险事件或安全事件[7-8].因此,干旱指标的Kendall联合重现期,其对应的联合超越概率可用Kendall分布函数
| $ {K_{\hat C}} = P\left( {\hat C \le q} \right) $ | (9) |
式中, q∈(0, 1),
由于
| $ {K_{\hat C}} = \frac{1}{n}\sum\limits_{i = 1}^n {1\left( {\hat C \le q} \right)} $ | (10) |
式中, n为Monte Carlo模拟组合的数目,通常可取104或更大.
由此可以进一步计算干旱指标两变量或三变量的Kendall联合超越重现期
| $ {{\hat T}_K} = 1/\left( {{N_E} \cdot {K_{\hat C}}} \right) $ | (11) |
单变量的重现期和设计值是一一对应的.但是对于多变量来说,任一给定的联合重现期理论上是有无数种组合值.但在水文水资源工程与管理实践中,有时需要明确给出一种设计组合.为此,可定义最大可能权函数[7],即:
| $ \left( {{u_{1,m}}, \cdots ,{u_{d,m}}} \right)\left| {_{{{\hat T}_k}}} \right. = \arg~ \max f\left( {{x_1}, \cdots ,{x_d}} \right) $ | (12) |
| $ f\left( {{x_1}, \cdots ,{x_d}} \right) = c\left( {{u_1}, \cdots ,{u_d}} \right)f\left( {{x_1}} \right), \cdots ,f\left( {{x_d}} \right) $ | (13) |
式中, (u1, m, …, ud, m)为该方法选取的累积频率组合,反映了给定联合重现期
具体设计步骤如下:1)基于干旱指标样本值确定的边缘及联合分布模型和参数,然后采用Monte Carlo法模拟m次n组(u1, u2)或(u1, u2, u3),m和n均取104或更大;2)根据式(5)~(11)可反算出m组任一给定联合重现期
| $ {x_1} = {F^{ - 1}}\left( {{u_{1,m}}} \right),{x_2} = {F^{ - 1}}\left( {{u_{2,m}}} \right),{x_3} = {F^{ - 1}}\left( {{u_{3,m}}} \right) $ | (14) |
为了定量评估水库径流调节对水文干旱的影响,可定义相对变化Rv:
| $ {R_v} = 100 \cdot \left( {{D_1} - {D_2}} \right)/{D_2} $ | (15) |
式中, Rv为实测径流的水文干旱特征指标相对于天然径流的变化(%),即水库径流调节对水文干旱特征变化的影响程度;D1和D2分别为实测径流和天然径流的水文干旱特征指标或设计值.
1.4 流域概况及数据东江流域属于中国珠江水系(图 1),流域控制站博罗以上集水面积分别为25325 km2.东江流域水资源开发程度较高,新丰江水库、枫树坝水库和白盆珠水库三大水库分别运行于1961、1974和1986年,均为多年调节型水库,对流域河川径流过程影响显著[16-17].随着区域经济的快速发展,东江流域近些年的水资源供需矛盾日益突显,特别是2004-2005年的冬、春季极端干旱,严重威胁到了东江流域下游及珠江三角洲部分地区的供水安全.为此,《广东省东江流域水资源分配方案》规定了东江干流重要断面的最小流量管理目标,其中博罗站流量为320 m3/s.
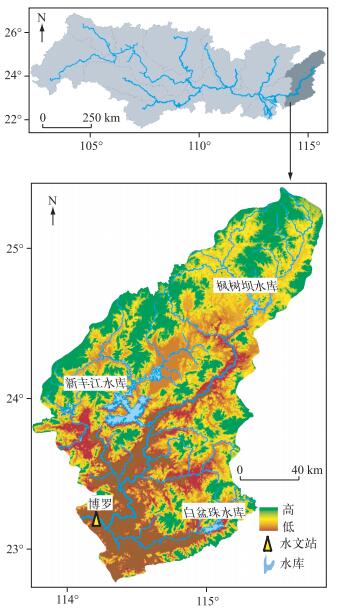
|
图 1 东江流域地理位置、水文站点及三大水库分布 Fig.1 Location of Dongjiang Basin, the hydrological gauging station and distribution of three reservoirs |
本文基于博罗站1954年4月-2009年3月共55 a(水文年)的实测月径流过程,根据三大水库入库和出库的月平均流量,计算水库调节的月径流量(出库-入库).实测月径流过程扣除水库调节的月径流量,形成了博罗站天然径流系列.自新丰江水库运行起至今的实测径流系列(1961年4月-2009年3月),实际上反映了东江水文干旱受到流域水库的径流调节影响.以最小管理流量320 m3/s为阈值,根据游程方法分别截取实测系列和天然系列的水文干旱事件,每一次干旱事件的干旱指标包括历时、强度和峰值,分别反映干旱持续时间、干旱期间的总缺水量和最大的月缺水量.
2 结果与讨论 2.1 水文干旱特征图 2为东江流域博罗站的月径流过程(纵坐标采用了对数刻度),低于阈值的部分即为发生的水文干旱事件. 1954-2009年期间,还原的天然径流水文干旱事件次数为58次,年均约1.05次.经过水库径流调节作用的1961-2009年期间,干旱事件实际发生30次,年均约0.63次,减少了约40.7 %.
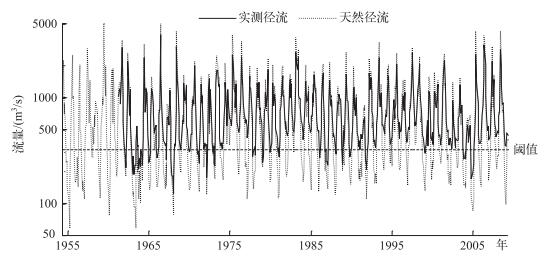
|
图 2 月径流过程及水文干旱事件 Fig.2 Streamflow processes and hydrological drought events |
干旱指标统计特征见表 1.天然径流的干旱事件最长历时为8个月,分别出现在1962年11月-1963年6月和1963年8月-1964年3月,历时达到7个月分别出现在1954年10月-1955年4月、1955年10月-1956年4月、1990年10月-1991年4月、1998年10月-1999年4月和2001年11月-2002年5月.在水库径流调节作用下,干旱事件最长历时为6个月,分别发生在1962年12月-1963年5月和2004年10月-2005年3月.
| 表 1 干旱指标统计特征 Tab.1 Statistical characteristics of drought properties |
干旱最大强度的总缺水量约为35.12亿m3,出现在1962年11月-1963年6月.最大峰值的月缺水量约为6.80亿m3,出现在1955年3月和1963年5月,博罗站流量约为57.7 m3/s.经过水库径流调节作用,最大强度的总缺水量约为17.82亿m3,发生在1967年10月-1968年2月.最大峰值的月缺水量约为5.06亿m3,发生在1968年1月,博罗站流量约为124.6 m3/s.
水库径流调节作用通常会缩短干旱历时,并降低干旱强度.历时、强度和峰值的均值分别由4.07月、12.63亿m3和4.15亿m3,降低到2.37月、3.91亿m3和1.81亿m3,分别减少了41.8 %、69.0 %和56.5 %;中位值分别由4.00月、12.19亿m3和4.41亿m3,降低到2.00月、2.11亿m3和1.56亿m3,分别减少了50.0 %、82.7 %和64.7 %.最小1个月的干旱强度由0.46亿m3降低到0.03亿m3,减少了93.3 % (表 1).
2.2 干旱指标边缘分布特征及设计值干旱指标边缘分布拟合检验结果显示,历时只接受WBL模型,强度和峰值能接受除了GP模型之外的其他备选模型.综合考虑RMSE、AIC和检验统计量概率P值的计算结果,实测和天然径流的干旱指标边缘分布均采用WBL模型,其P值均大于显著性检验水平0.05,见表 2.经验和理论的累积频率Q-Q关系图显示(图 3),频率关系点据基本上在等值线附近,强度和峰值呈现出更好的拟合效果. WBL模型的累积频率分布F(x)和密度函数f(x)分别为:
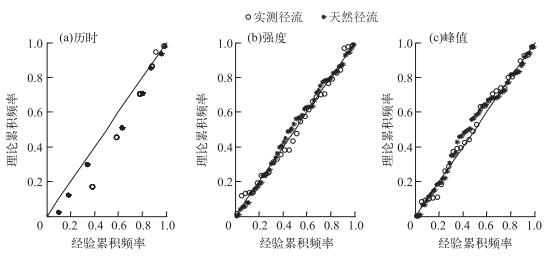
|
图 3 干旱指标边缘分布经验与理论累积频率Q-Q关系 Fig.3 Q-Q of empirical and theoretical cumulative frequencies of marginal distribution of drought properties |
| $ F\left( x \right) = 1 - {{\rm{e}}^{ - {{\left( {x/\lambda } \right)}^k}}} $ | (16) |
| $ f\left( x \right) = \left( {k/\lambda } \right){\left( {x/\lambda } \right)^{k - 1}}{{\rm{e}}^{ - {{\left( {x/\lambda } \right)}^k}}} $ | (17) |
式中,k和λ为模型参数.
由于水库径流调节作用改变了东江水文干旱特征,尽管对于同一个干旱指标来说,实测径流和天然径流的最优分布模型相同,但二者之间的参数差别明显(表 2).
| 表 2 干旱指标边缘分布 Tab.2 Marginal distribution of drought properties |
根据干旱指标边缘理论分布和参数,各单变量重现期设计值变化如图 4(横坐标采用对数坐标).与天然径流相比较,实测径流的设计值变化曲线向下移动,这表明在水库径流调节作用下,干旱指标单变量设计值明显变小.重现期介于2~100 a之间,历时、强度和峰值分别下降了约2.48~2.96月、11.08~17.83亿m3和1.92~3.54亿m3.随着重现期增大,水库的影响程度(相对变化的绝对值)逐渐减少.历时、强度和峰值2 a一遇设计值的下降幅度分别约为72.7 %、94.2 %和83.7 %,100 a一遇设计值则分别降低到约为28.7 %、49.5 %和26.4 %.主要原因是水库径流调节作用增加了下游干旱期间的径流量,且对低重现期的干旱指标影响程度更大.
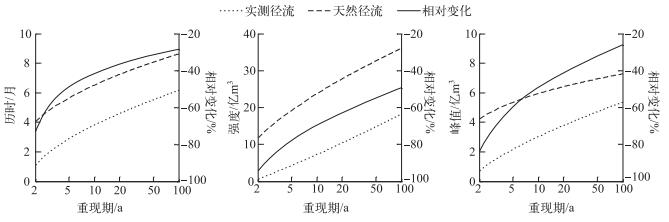
|
图 4 干旱指标单变量重现期设计值 Fig.4 Change of design value of the univariate return period for drought properties |
经过水库径流调节作用,历时-强度的相关系数略有下降,而历时—峰值和强度—峰值的相关系数均有所上升.干旱指标之间的Kendall、Spearman和Pearson相关系数均大于0.5,表明东江水文干旱指标之间具有较高的正相关性(表 3).
| 表 3 干旱指标相依性 Tab.3 Dependence of drought properties |
联合分布经验和理论的累积频率Q-Q关系显示(图 5),频率关系点据基本上在等值线附近.但与历时有关联合分布拟合图中(图 5a、5b和5d),低值部分点据向下偏离等值线,即理论频率明显大于经验频率,其主要原因是干旱历时在低值部分的重复值较多.拟合检验结果显示,检验统计量的概率P值均明显大于显著性检验水平0.05(表 4),表明Meta-Gaussian Copula能够很好地模拟东江流域水文干旱指标两变量和三变量联合分布.干旱指标两变量联合分布参数见表 4,而三变量联合分布参数是由两两分布参数构成的矩阵.
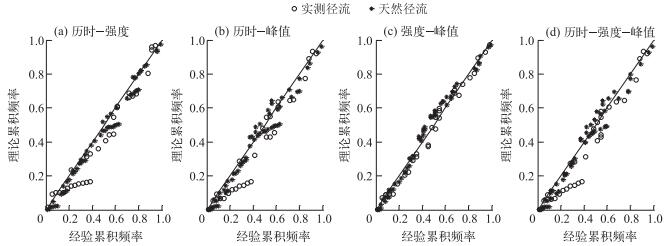
|
图 5 干旱指标联合分布经验与理论累积频率Q-Q关系 Fig.5 Q-Q of empirical and theoretical cumulative frequencies of joint distribution of drought properties |
| 表 4 干旱指标联合分布 Tab.4 Joint distribution of drought properties |
基于干旱指标联合分布模型和参数,干旱指标两变量联合超越重现期为2、5、10、20、50和100 a的等值散点线如图 6(双坐标轴均采用海森坐标).与天然径流相比较,实测径流的干旱指标联合超越重现期等值散点线向坐标原点内移,表明任意一对干旱指标,其两变量联合超越重现期在流域水库径流调节作用后明显变大.基于最大权函数设计的两变量累积频率组合如图 6中的空心点位置,结果显示干旱指标的一对组合值基本位于同频位置(图 6中的对角线)附近,即u1, m≈u2, m.
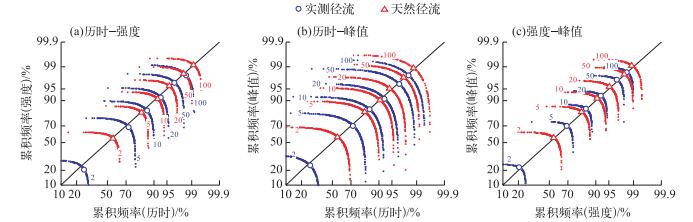
|
图 6 干旱指标两变量联合超越重现期 Fig.6 Bivariate exceeding joint return period of drought properties |
干旱指标三变量联合超越重现期等值散点面如图 7,变化特征与两变量类似.与天然径流相比较,实测径流的干旱指标联合超越重现期等值散点面向坐标原点内移,表明同一组干旱指标,其三变量联合超越重现期在流域水库径流调节作用后明显变大.尽管三变量联合超越重现期等值散点面在二维平面投影的两变量组合点比较分散(图 8),但最大可能权函数设计的干旱指标三变量组合,也基本上处于同频位置(图 7和图 8中的对角线)附近,即u1, m≈u2, m≈u3, m.

|
图 7 干旱指标三变量联合超越重现期 Fig.7 Trivariate exceeding joint return period of drought properties |
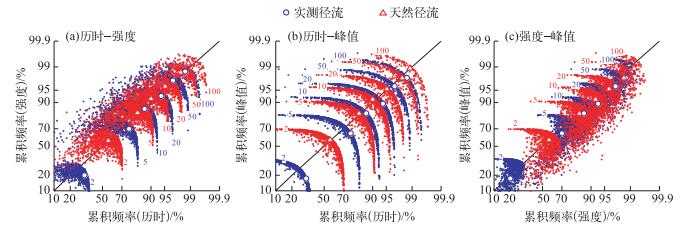
|
图 8 干旱指标三变量联合超越重现期的二维投影 Fig.8 Two-dimensional projection of trivariate exceeding joint return period of drought properties |
干旱指标联合超越重现期的设计组合值结果见表 5.不管是任意两个变量的联合设计,还是三变量联合设计,单个干旱指标设计值差别较小.以联合超越重现期10 a一遇为例,天然径流的设计干旱历时、强度和峰值分别约为7.07~7.34月、23.92~24.77亿m3和5.94~6.04亿m3,实测径流的则分别降低到约为3.89~4.04月、7.20~7.97亿m3和2.99~3.12亿m3.
| 表 5 干旱指标联合设计值 Tab.5 Joint design values of drought properties |
很显然,实测径流的各干旱指标设计值均明显小于天然径流,表明东江流域的水库径流调节作用对于缓解当地水文干旱效果明显.联合超越重现期越小,水库径流调节对干旱指标设计值的影响程度(设计值相对变化的绝对值)越大.如100 a一遇的联合超越重现期,其干旱历时、强度和峰值设计值的相对变化绝对值,分别约为26.3 % ~28.6 %、48.2 % ~52.7 %和26.1 % ~30.2 %;联合重现期2 a一遇,历时、强度和峰值的相对变化程度(绝对值)分别上升为64.0 % ~68.8 %、94.3 % ~94.6 %和81.6 % ~86.1 % (表 6).影响程度从大到小依次为强度、峰值和历时.
| 表 6 干旱指标设计值的相对变化(%) Tab.6 Change in joint design values of drought properties |
东江流域水文干旱历时、强度和峰值的统计最优分布均为WBL分布.在水库径流调节作用下,干旱指标单变量设计值明显变小.随着重现期增大,水库影响程度逐渐减少.历时、强度和峰值2 a一遇设计值的下降幅度分别约为72.7 %、94.2 %和83.7 %,100 a一遇则分别降低到约为28.7 %、49.5 %和26.4 %.
水文干旱指标之间具有较高的正相关性,Meta-Gaussian Copula能够很好地模拟水文干旱指标两变量和三变量联合分布.同一组干旱指标,其两变量和三变量联合超越重现期在水库影响下明显变大.基于最大可能权函数设计结果显示,水文干旱指标的两变量和三变量设计组合值基本均位于同频位置附近.基于任意两个变量的联合设计和三变量联合设计,单个干旱指标设计值差别较小.联合超越重现期越小,水库对联合设计值的影响程度越大.
在水库影响下,联合超越重现期100 a一遇的历时、强度和峰值设计值分别下降了约26.3 % ~28.6 %、48.2 % ~52.7 %和26.1 % ~30.2 %;2 a一遇的分别下降了约64.0 % ~68.8 %、94.3 % ~94.6 %和81.6 % ~86.1 %.受影响程度从大到小依次为强度、峰值和历时.
值得注意的是,根据目前水库运行模式,若要满足河道内最小管理流量目标,联合超越重现期10 a一遇的历时、强度和峰值依然达到了约3.89~4.04月、7.20~7.97亿m3和2.99~3.12亿m3.
| [1] |
Zelenhasić E, Salvai A. A method of streamflow drought analysis. Water Resources Research, 1987, 23(1): 156-168. DOI:10.1029/WR023i001p00156 |
| [2] |
Tallaksen LM, Massen H, Clausen B. On the definition and modelling of streamflow drought duration and deficit volume. Hydrological Science Journal, 1997, 42(1): 15-33. DOI:10.1080/02626669709492003 |
| [3] |
Dong QJ, Xie P. Advances in hydrological drought research. Journal of China Hydrology, 2014, 34(4): 1-7. [董前进, 谢平. 水文干旱研究进展. 水文, 2014, 34(4): 1-7.] |
| [4] |
Cheng L, Jin JL, Li JQ et al. Advances in the study of drought frequency analysis. Advances in Water Science, 2013, 24(2): 296-302. [程亮, 金菊良, 郦建强等. 干旱频率分析研究进展. 水科学进展, 2013, 24(2): 296-302.] |
| [5] |
Xiao MZ, Zhang Q, Chen YQ et al. Hydrological drought frequency analysis of east river basin based on trivariate Copulas function. Journal of Natural Disasters, 2013, 22(2): 99-108. [肖名忠, 张强, 陈永勤等. 基于三变量Copula函数的东江流域水文干旱频率分析. 自然灾害学报, 2013, 22(2): 99-108.] |
| [6] |
Chen YD, Zhang Q, Xiao M et al. Evaluation of risk of hydrological droughts by the trivariate Plackett copula in the East River basin (China). Natural Hazards, 2013, 68(2): 529-547. DOI:10.1007/s11069-013-0628-8 |
| [7] |
Salvadori G, Michele CD, Durante F. On the return period and design in a multivariate framework. Hydrology and Earth System Science, 2011, 15(11): 3293-3305. DOI:10.5194/hess-15-3293-2011 |
| [8] |
Huang Q, Chen ZS. Multivariate flood risk assessment based on the secondary return period. J Lake Sci, 2015, 27(2): 352-360. [黄强, 陈子燊. 基于二次重现期的多变量洪水风险评估. 湖泊科学, 2015, 27(2): 352-360. DOI:10.18307/2015.0221] |
| [9] |
Li TY, Guo SL, Yan BW et al. Derivative design flood hydrograph based on trivariate joint distribution. Journal of Hydroelectric Engineering, 2013, 32(3): 10-14, 38. [李天元, 郭生练, 闫宝伟等. 基于多变量联合分布推求设计洪水过程线的新方法. 水力发电学报, 2013, 32(3): 10-14, 38.] |
| [10] |
Tu XJ, Chen XH, Zhao Y et al. Responses of hydrological drought properties and water shortage under changing environments in Dongjiang River basin. Advances in Water Science, 2016, 27(6): 810-821. [涂新军, 陈晓宏, 赵勇等. 变化环境下东江流域水文干旱特征及缺水响应. 水科学进展, 2016, 27(6): 810-821.] |
| [11] |
Yin ZJ, Huang W, Chen J. Impacts of reservoir flow regulation on hydrological drought. Journal of China Hydrology, 2009, 29(2): 41-44. [尹正杰, 黄薇, 陈进. 水库径流调节对水文干旱的影响分析. 水文, 2009, 29(2): 41-44.] |
| [12] |
Ma M, Song S, Ren L et al. Multivariate drought characteristics using trivariate Gaussian and Student t copulas. Hydrological Processes, 27(8): 1175-1190. DOI:10.1002/hyp.8432 |
| [13] |
Dobrić J, Schmid F. A goodness of fit test for copulas based on Rosenblatt's transformation. Computation Statistics and Data Analysis, 2007, 51(9): 4633-4642. DOI:10.1016/j.csda.2006.08.012 |
| [14] |
Tu X, Singh VP, Chen X et al. Uncertainty and variability in bivariate modeling of hydrological droughts. Stochastic Environmental Research and Risk Assessment, 2016, 30(5): 1317-1334. DOI:10.1007/s00477-015-1185-3 |
| [15] |
Tu XJ, Du YL, Chen XH et al. Modeling and design on joint distribution of precipitation and tide in the coastal city. Advances in Water Science, 2017, 28(1): 49-58. [涂新军, 杜奕良, 陈晓宏等. 滨海城市雨潮遭遇联合分布模拟与设计. 水科学进展, 2017, 28(1): 49-58.] |
| [16] |
Tu XJ, Chen XH. Characteristics variability study of regional river runoff time series based on change point recognition. Journal of Natural Resources, 2010, 25(11): 1930-1937. [涂新军, 陈晓宏. 基于变点识别的区域河川径流量特征值变异研究. 自然资源学报, 2010, 25(11): 1930-1937. DOI:10.11849/zrzyxb.2010.11.012] |
| [17] |
Tu XJ, Chen XH, Zhang Q et al. Streamflow annual distribution and its influencing factors in Dongjiang River, South China. Advances in Water Science, 2012, 23(4): 493-501. [涂新军, 陈晓宏, 张强等. 东江径流年内分配特征及影响因素贡献分解. 水科学进展, 2012, 23(4): 493-501.] |
 2018, Vol. 30
2018, Vol. 30 

