(2: 合肥工业大学土木与水利工程学院, 合肥 230009)
(3: 合肥工业大学水资源与环境系统工程研究所, 合肥 230009)
(2: School of Civil Engineering, Hefei University of Technology, Hefei 230009, P. R. China)
(3: Institute of Water Resources and Environmental Systems Engineering, Hefei University of Technology, Hefei 230009, P. R. China)
水资源短缺和水土环境恶化已成为制约中国乃至全球农业和经济可持续发展的瓶颈[1-2].如何合理配置和高效利用有限的水资源,使其既保障基本生活与生态环境供水,又能满足工农业生产需求,实现区域经济、社会和环境的可持续发展,一直是水科学重点研究和解决的关键科学问题[2-5]. 1950s以来,国内外学者以系统分析与协调理论为基础[6-8],通过改进或应用不同优化算法求解优化配置模型[8-11],建立了许多区域水资源配置模型,取得了丰硕的研究成果[8-11].现有研究成果中的配置水源多为可控的地表水和地下水,很少包含大气有效降水和土壤水等非常规水源[8, 12],而对于灌区水资源供需平衡而言,大气有效降水和土壤水的作用不可忽视.为此,广义水资源配置的理念、方法体系及配置模型被提出,取得了突破性成果[12-14].广义水资源配置理念较为超前,然而目前水资源配置工作大多基于水资源评价成果而开展,对于在现有评价体系之外的大气降水、土壤水等非常规水源缺乏相应的基础数据积累,在实际使用中存在较大困难[12].为此,本文以巢湖流域大官塘坝水库灌区为例[15],依托灌溉试验站田间降水-作物耗水-土壤水相互转化的长序列试验成果,建立灌区田间尺度水量蓄-耗-灌-排全过程的模拟模块,制定不同类型塘坝和骨干水库的水量分配仿真规则,构建库塘联合灌区水量分配仿真模拟模型,模拟灌区降水、土壤水、塘坝和水库的引、提灌溉水量及相互转化关系,提出了基于正交试验的库塘联合灌溉系统水资源优化调控技术体系,为库塘联合灌区水量分配方案、水库和塘坝调度规则及作物灌溉制度等地制定提供理论依据.
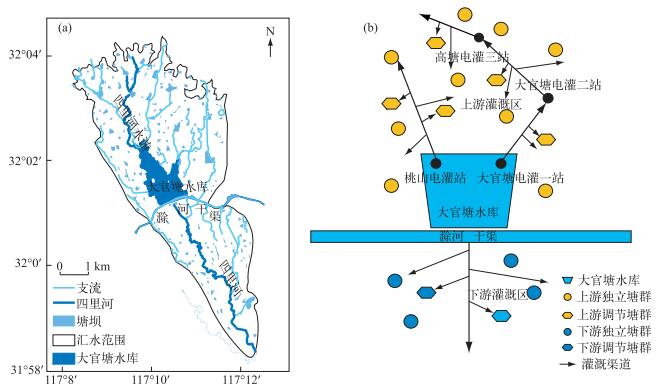
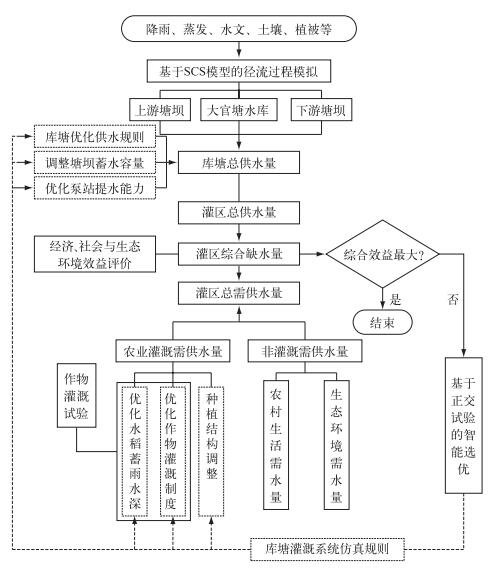
1 研究区概况大官塘水库(31.96°~32.07°N, 117.13°~117.20°E)位于巢湖流域南淝河支流四里河上游,总库容1208万m3,死库容8万m3,兴利库容656万m3,流域内有大官塘雨量站1处,逐日水库水位和下泄流量观测站1处,是一座以灌溉为主,结合防洪、农村生活供水和水产养殖等的反调节中型水库[15],水库左右岸各建有提水泵站1座,综合设计提水能力2.7 m3/s,但由于泵站原建工程标准偏低,加之年久失修,现状泵站提水能力仅为1.3 m3/s.大官塘水库灌区国土面积30.8 km2,其中水库上游集水面积21 km2,总耕地面积20.7 km2,水田15.7 km2,具体多年平均作物种植结构见表 1.据水利普查数据,该区上游共有塘坝148处,其中塘容大于5万m3共8处,1~5万m3共58处,1万m3以下82处,总塘容220万m3;下游共有塘坝65处,其中塘容大于5万m3共1处,1~5万m3共18处,1万m3以下46处,总塘容67万m3.该区地质构造多为第三纪红砂岩、砂质页岩,无良好含水层发育,土壤密实板结,地下水储存平均仅为2~3万m3/km2,埋藏在50~60 m左右,且分布零散,只能满足部分区域农村人畜供水.因此,该区灌溉水源主要依托骨干大官塘水库及上下游塘坝拦蓄地表径流,是巢湖流域典型库塘灌溉系统,流域水系和水资源系统结构见图 1.本文以此为研究区,开展基于模拟优化与正交试验的水资源优化配置研究,具体技术路线图见图 2.
| 表 1 大官塘水库灌区多年平均作物种植结构调查 Tab.1 Multi-year average crop planting structure in reservoir irrigation area of Daguantang Reservoir |
|
图 1 大官塘水库流域水系(a)和水资源系统结构概化图(b) Fig.1 Watershed water map(a) and water resources system structure generalization(b) of Daguantang Reservoir watershed |
|
图 2 库塘联合灌溉系统水资源优化调控技术框图 Fig.2 Water resources optimal control technology road map of reservoirs and ponds combined irrigation system |
SCS模型是美国农业部水土保持局(Soil Conservation Service, SCS)于1950s研制的小流域设计洪水模型,其能反映不同土壤类型、不同土地利用方式及前期土壤含水量对降雨径流的影响,是基于流域的实际入渗量与实际径流量之比等于流域该场降雨前的最大可能入渗量(或潜在入渗量S)与最大可能径流之比的假定基础上建立的,基本降雨径流关系为[16-17]:
| $ R = \left\{ {\begin{array}{*{20}{c}} {\frac{{{{\left( {P - \lambda \cdot S} \right)}^2}}}{{P + \left( {1 - \lambda } \right)S}}}&{\left( {P \ge \lambda \cdot S} \right)}\\ 0&{\left( {P < \lambda \cdot S} \right)} \end{array}} \right. $ | (1) |
式中,R为径流量(mm);P为降雨量(mm);S为当时最大可能入渗量(mm);λ为初损率.在美国的试验农业小流域一般取λ=0.2,在运用该模型的时候,λ的具体取值根据流域水文资料加以率定,或移用水文相似区的取值,本文将利用大官塘水库降雨及入库径流资料率定λ.
由于S值的变化范围很大,不便于取值,因此引入无因次参数CN(Curve Number),其取值范围为[0, 100],定义经验关系如下[16-17]:
| $ S = 254\left( {100/CN - 1} \right) $ | (2) |
式中,CN是一个无量纲参数,其反映流域前期土壤湿润度(Antecedent Moisture Condition, AMC)、植被、坡度、土壤类型及土地利用现状的综合特性,能反映下垫面条件对产汇流的影响.
SCS模型根据该次降雨前5 d降雨量把前期土壤湿润程度分为3级,分别代表干燥(AMCⅠ)、中等湿润(AMCⅡ)和湿润(AMCⅢ)3种状态,且不同湿润状况的CN值有如下相互转换关系[18]:
| $ C{N_1} = C{N_2} - \frac{{20\left( {100 - C{N_2}} \right)}}{{100 - C{N_2} + \exp \left[ {2.533 - 0.0636\left( {100 - C{N_2}} \right)} \right]}} $ | (3) |
| $ C{N_3} = C{N_2} \cdot \exp \left[ {0.00673\left( {100 - C{N_2}} \right)} \right] $ | (4) |
大官塘水库灌区土壤分布主要以黄褐土与黄棕壤为主,其演化而来的耕作土壤为马肝土,该土质地黏重,土壤多为黏壤至黏土,按SCS土壤定义分类属于C类土壤. SCS模型根据前期降雨指数(前5日降雨量之和)的大小将土壤前期水分划分为干燥(AMCⅠ)、中等湿润(AMCⅡ)、湿润(AMCⅢ)3个等级,根据研究区灌溉试验观测资料与实践经验,划分前期土壤湿润程度等级标准如表 2所示.
| 表 2 大官塘水库灌区前期土壤湿润程度等级划分标准 Tab.2 Antecedent soil moisture level grading standards of Daguantang Reservoir |
统计大官塘水库灌区不同土地利用类型的面积与比例,结合水文土壤组特征及前期湿润程度条件,查CN值表[16-18],确定AMCⅡ条件下的CN2值,其余CN1和CN3分别由式(3)和式(4)求取,CN计算值为:CN1=75.8、CN2=88.7、CN3=95.7.
为率定SCS模型的参数,选取大官塘水库灌区1991-2014年7场典型降雨过程,以前4场降雨过程来建模率定参数,用后3场降雨过程进行模型验证.运用遗传算法[19-20]优化率定日尺度下的模型参数λ,其中目标函数为:
| $ f = \min {\left( {\sum\limits_{i = 1}^n {{M_{i,j}}} - \sum\limits_{i = 1}^n {{Q_{i,j}}} } \right)^2} $ | (5) |
式中,Mi,j为第j次降雨过程的第i天的模拟入库径流量,Qi,j为第j次降雨过程的第i天的实测入库径流量.
SCS模型参数的优化结果为λ=0.069.具体各场次降雨过程的拟合及验证结果如表 3所示.
| 表 3 大官塘水库典型降雨径流过程模拟的率定及验证结果* Tab.3 Calibration and verification results of typical rainfall runoff process simulation in Daguantang Reservoir |
基于SCS模型的降雨径流模拟模型在率定期内4场典型降雨过程的模拟与实测入库径流量的绝对误差在0.23 % ~17.80 %之间,Nash-Sutcliffe效率系数为0.977;验证期3场典型降雨过程的模拟与实测入库径流量的绝对误差在0.72 % ~11.48 %之间,Nash-Sutcliffe效率系数为0.969;可见,在建模率定和模型验证时的误差较小、精度较高,表明该模型用于大官塘水库灌区的降雨径流模拟是合适的(表 3).
3 基于仿真规则的库塘联合灌溉系统水量分配模拟模型 3.1 库塘联合灌溉系统水资源结构概化与描述如何在兼顾和权衡水文资料与水资源系统结构的真实程度的基础上,实现对复杂水资源系统结构的概化,是构建水量分配模拟模型的关键问题之一[20-21].本文借鉴虚拟水库的概念,将上下游分布面广而量大的塘坝进行虚拟概化:1)将上游(滁河干渠以北)所有与灌溉渠道连通具有调节功能的塘坝合并成一个“虚拟水库”,称为“上游调节塘群”,相应的入流和排水都进行合并处理;2)将上游所有不与灌溉渠道连通的独立塘坝合并成一个“虚拟水库”,称为“上游独立塘群”,相应的入流和排水都进行合并处理;3)将下游(滁河干渠以南)所有与引水渠连通具有调节功能的塘坝合并成一个“虚拟水库”,称为“下游调节塘群”,相应的入流和排水都进行合并处理;4)将下游所有不与引水渠连通的独立塘坝合并成一个“虚拟水库”,称为“下游独立塘群”,相应的入流和排水都进行合并处理.通过上述概化处理后,大官塘水库灌溉系统的水资源结构分别为:大官塘水库、“上游调节塘群”、“上游独立塘群”、“下游调节塘群”和“下游独立塘群”5部分.
3.2 各计算单元中基本元件的水量平衡方程 3.2.1 田间水量平衡方程田间水量平衡方程式如下:
| $ {W_{i,j}} = {W_{i,j - 1}} + {P_j} + {M_{i,j}} + {G_{i,j}} - K{c_{i,j}} \cdot E{T_{0j}} - {S_{i,j}} - {X_{i,j}} $ | (6) |
式中,Wi, j、Wi,j-1分别为第i种作物第j时段末和时段初的田间贮水量(mm);Pj为第j时段的降雨量(mm);Mi,j为第i种作物第j时段的入田灌溉水量(mm);Gi,j为第i种作物第j时段对地下水的直接利用量(mm),本文中大官塘水库灌区地下水一般埋深50~60 m左右,作物对地下水的直接利用量可忽略,均取值0;Kci,j为第i种作物第j时段的作物系数;ET0j为第j时段的参考作物蒸腾量(mm);Si,j为第i种作物第j时段的田间渗漏量(mm);Xi,j为第i种作物第j时段的田间弃水量(mm).
田间贮水量Wi,j的计算公式为:
| $ {W_{i,j}} = h{c_{i,j}} + \gamma \cdot {H_{i,j}} \cdot {\theta _{i,j}} $ | (7) |
式中,hci,j为第i种作物第j时段的田间水层深度(mm),如果是旱作物则取值为0;Hi,j为第i种作物第j时段的计算土层深度(mm);γ为计算土层深度的土壤干容重(g/cm3);θi,j为第i种作物第j时段的土壤含水率(占干土重的比例).
入田灌溉水量Mi,j的计算公式为:
| $ {M_{i,j}} = \frac{{\alpha \cdot M{Q_{i,j}}}}{{S{Q_{i,j}}}} \times {10^{ - 7}} $ | (8) |
式中,MQi,j为第i种作物第j时段的从供水源取水量(m3);α为农田灌溉水有效利用系数;SQi,j为第i种作物第j时段的灌溉面积(hm2).
| $ E{T_{{\rm{c}}i,j}} = E{T_{0j}} \cdot K{c_{i,j}} $ | (9) |
式中,ET0j为第j时段的参考作物蒸腾量(mm);Kci,j为第i种作物第j时段的作物系数. ET0采用彭曼—蒙蒂斯(Penman-Monteith)公式[22-23]:
| $ E{Y_0} = \frac{{0.408\mathit{\Delta} \left( {{R_{\rm{n}}} - G} \right) + \gamma \frac{{900}}{{T + 273}}{U_2}\left( {{e_{\rm{a}}} - {e_{\rm{d}}}} \right)}}{{\mathit{\Delta} + \gamma \left( {1 + 0.34{U_2}} \right)}} $ | (10) |
式中,ET0为参考作物蒸腾量(mm/d);Δ为温度-饱和水汽压曲线在T处的切线斜率(kPa/℃);Rn为净辐射(MJ/(m2 ·d));G为土壤热通量(MJ/(m2 ·d));γ为湿度表常数(kPa/℃);T为平均气温(℃);U2为2 m高处风速(m/s);ea为饱和水汽压(kPa);ed为实际水汽压(kPa).
依据安徽省主要作物需水量等值线图研究成果,参照联合国粮农组织(FAO)推荐的84种作物的标准作物系数和修正公式[23],结合淠史杭和八斗灌溉试验站历年灌溉试验成果,来综合确定各作物不同生育阶段的作物系数Kc.
3.2.2 水库水量平衡方程大官塘水库水量平衡方程式如下:
| $ V{k_j} = V{k_{j - 1}} + {P_j} \cdot SSk \times {10^{ - 1}} + W{k_j} - MQ{k_j} - M{l_j} - M{e_j} - S{k_j} - X{k_j} $ | (11) |
式中,Vkj、Vkj-1为大官塘水库第j时段末、时段初的库容(万m3);Pj为第j时段的降雨量(mm);SSk为水库的水面面积(km2);Wkj为第j时段入库水量(万m3);MQkj为水库第j时段农业灌溉供水量(万m3);Mlj为水库第j时段农村生活供水量(万m3);Mej为水库第j时段生态环境供水量(万m3);Skj为水库第j时段的蒸发渗漏损失水量(万m3);Xkj为水库第j时段的弃水量(万m3).
3.2.3 塘坝水量平衡方程塘坝水量平衡方程式如下:
| $ V{t_{k,j}} = V{k_{k,j - 1}} + {P_j} \cdot SS{t_k} \times {10^{ - 1}} + W{t_{k,j}} - MQ{t_{k,j}} - S{t_{k,j}} - X{t_{k,j}} $ | (12) |
式中,Vtk,j、Vtk,j-1为第k处塘坝第j时段末、时段初的蓄水量(万m3);Pj为第j时段的降雨量(mm);SStk为第k处塘坝的水面面积(km2);Wtk,j为第k处塘坝第j时段的来水量(万m3);MQtk,j为第k处塘坝第j时段灌溉供水量(万m3);Stk,j为第k处塘坝第j时段的蒸发渗漏损失量(万m3);Xtk,j为第k处塘坝第j时段的弃水量(万m3).
3.3 库塘联合灌溉系统水量分配模拟模型运行规则制订经多次实地调研和专家咨询讨论,在对大官塘水库灌区水资源特点和开发利用现状充分理解基础上,将实践经验用数学思维定量化后,确定了如下水量分配原则:1)大官塘水库在保障农村生活用水和生态环境用水安全的前提下,合理分配其他水库蓄水量;2)各类型塘坝的蓄水量在任何情况下均可全部合理分配供给农业灌溉,当塘坝蓄水量为0时,才根据具体作物生长与灌溉制度从水库中合理地引、提水灌溉.根据上述原则,确定了大官塘水库灌区供水与取水的优先顺序:
1) 水源供水的先后顺序为:弃水(塘坝、水库)→塘坝放水→水库放水.具体地,对于大官塘水库上游集水区,如是塘坝控制区来水优先充蓄塘坝,蓄满后则产生塘坝弃水,此时优先用塘坝弃水,不足水量由塘坝供给,最后不足水量从水库提水,同时从水库提水还可以充蓄上游调节塘坝,剩余塘坝弃水和非塘坝控制的来水充蓄水库,蓄满后则产生水库弃水进入下游区.对于下游区,上游水库弃水优先充蓄下游调节塘坝,蓄满则产生塘坝弃水,非塘坝控制来水直接形成弃水,塘坝控制区来水优先充蓄塘坝,蓄满后则产生塘坝弃水,此时优先用塘坝弃水,不足水量由塘坝供给,最后不足水量从水库引水,同时从水库引水也可充蓄下游调节塘坝. 2)用水户取水的优先顺序为:基本需水(农村生活与生态环境需水之和)→生产需水(农业灌溉).具体地,优先满足基本用水需求,然后再进行农业灌溉供水.
依据库塘灌溉系统水量分配原则及灌区内水源供水与用水户取水的顺序,制订了库塘灌溉系统水量分配模拟模型的具体规则,具体如下:
3.3.1 上游区水量分配仿真规则规则1:对于上游非塘坝控制来水,直接形成弃水进入水库;对于上游塘坝控制来水,优先充蓄上游塘坝,蓄满后产生弃水进入水库;对于水库来水优先充蓄水库,蓄满后形成弃水进入下游区;结束程序.
规则2:用上游初始缺水量减去上游弃水量,如果大于零运行规则3,否则,上游弃水减去上游初始缺水量作为水库来水充蓄水库,蓄满后形成弃水进入下游区,结束程序.
规则3:计算上游区塘坝可供水量,用由规则2计算后的缺水量减去上游区塘坝可供水量,如果大于零则运行规则4,否则结束程序.
规则4:计算上游区从水库提水能力和水库可供水量的最小值,并以此作为上游区水库可供水量,用由规则3计算后的缺水量减去上游区水库可供水量,如果大于零则为上游区最终缺水量,否则结束程序.
依据公式(6)和灌区灌溉制度计算上游区作物需灌水量,如果需灌水量等于零,则运行规则1,否则以需灌溉水量作为系统的初始缺水量,首先判断上游区是否有弃水,若有弃水则运行规则2,否则运行规则3.
3.3.2 下游区水量分配仿真规则规则5:对于下游非塘坝控制来水,直接形成弃水排出境外;对于下游调节塘坝控制来水和上游水库弃水,优先充蓄调节塘坝,蓄满后产生弃水排出境外;对于下游独立塘坝控制来水,优先充蓄独立塘坝,蓄满后产生弃水排出境外;结束程序.
规则6:用下游初始缺水量减去下游弃水量,如果大于零则运行规则7,否则,下游区弃水减去下游初始缺水量为弃水排出境外,结束程序.
规则7:计算下游区塘坝可供水量,用由规则6计算后的缺水量减去下游区塘坝可供水量,如果大于零则运行规则8,否则结束程序.
规则8:计算下游区从水库引水能力和水库可供水量的最小值,并以此作为下游区水库可供水量,用由规则7计算后的缺水量减去上游区水库可供水量,如果大于零则为下游区最终缺水量,否则结束程序.
依据式(6)和灌区灌溉制度计算下游区作物需灌水量,如果需灌水量等于零,则运行规则5,否则以需灌溉水量作为下游区初始缺水量,首先判断下游区是否有弃水,若有弃水则运行规则6,否则运行规则7.
3.4 库塘联合灌溉系统水量分配模拟模型的参数率定库塘联合灌溉系统水量分配仿真规则制订后,按照水流在实际水资源系统中的流动方向与供给关系,将各计算单位及其基本连接起来,编写描述水量分配仿真规则的计算程序,实现对库塘联合灌溉系统水量分配的仿真模拟.该模拟模型存在作物的灌溉制度、作物非充分灌溉条件下的耗水经验公式或折算系数、土壤基本特征参数、上下游灌溉水有效利用系数等参数.这些参数的合理确定决定了模拟模型的实用性.
本文采取经验与智能优化相结合的方式来率定模型参数,其率定过程如下:
1) 据调查,目前大官塘灌区习惯种植水稻,灌溉主要针对水稻基本采取常规大水漫灌,而旱作物灌溉基本采取保苗补充性灌溉的方式.量化确定该区现状灌溉模式为:①水稻采用常规灌溉方式,当稻田没有水层(即hc=0 mm)时,对水稻进行灌溉,灌水至稻田水层水深50 mm;②当旱作物受旱胁迫(即0~40 cm的平均土壤含水率低于土壤田间持水含水率的50 %)持续5天后,进行补充性保苗灌溉,灌水至0~40 cm的平均土壤含水率达到土壤田间持水含水率的90 %;③水稻田间蓄雨水深跟灌溉水深上限一致Hm=50 mm.
2) 依托淠史杭、肥东及八斗等灌溉试验站长序列灌溉试验资料推求水稻和旱作物在非充分灌溉条件下的耗水经验公式或折算系数.水稻不同生育期不同断水天数的ea值计算经验公式如下:
| $ {e_{\rm{a}}} = \left\{ {\begin{array}{*{20}{c}} {E{T_{\rm{c}}}\left( {1.70 \times {{10}^{ - 5}}{T^3} - 9.24 \times {{10}^{ - 4}}{T^2} + 1.23 \times {{10}^{ - 3}}T + 0.998} \right)}&{分蘖期}\\ {E{T_{\rm{c}}}\left( {2.80 \times {{10}^{ - 5}}{T^3} - 2.98 \times {{10}^{ - 4}}{T^2} - 2.41 \times {{10}^{ - 2}}T + 1.005} \right)}&{拔节期}\\ {E{T_{\rm{c}}}\left( { - 2.00 \times {{10}^{ - 4}}{T^3} + 5.80 \times {{10}^{ - 3}}{T^2} - 7.52 \times {{10}^{ - 2}}T + 1.0} \right)}&{抽穗开花期}\\ {E{T_{\rm{c}}}\left( { - 1.80 \times {{10}^{ - 5}}{T^3} + 1.41 \times {{10}^{ - 3}}{T^2} - 4.14 \times {{10}^{ - 2}}T + 1.004} \right)}&{成熟期} \end{array}} \right. $ | (13) |
对于旱作物,当土壤含水率0.5θt < θ < 0.75θt时,作物蒸腾平均折算系数φ1=0.8,则eai=0.8×ETci;当土壤含水率0.35θt < θ < 0.5θt时,作物蒸腾平均折算系数φ2=0.4,则eai=0.4×ETci.
3) 依托淠史杭、肥东及八斗等灌溉试验站长序列灌溉试验站资料,结合安徽土壤普查数据来综合确定土壤的基本特征参数,具体为:土壤0~40 cm饱和含水率θb=0.35、田间持水含水率θt=0.29、凋萎含水率θt=0.16,旱作物土壤计算土层深度H1=400 mm,水稻土壤计算土层深度H2=300 mm,计算土层深度的土壤干容重γ=1.42 g/cm3.
4) 以某一典型年(2001年)实际逐日用水过程作为模拟模型的需水目标,以上下游塘坝及水库取水灌溉量的模拟值与实际调查值之差的平方和最小为优化目标,运用遗传算法[19-20]求解优化模型,优化率定上下游的灌溉水有效利用系数等参数,具体为上游灌溉水有效利用系数α1=0.59,下游灌溉水有效利用系数α2=0.57,上下游灌溉水有效利用系数与该区实际调查值0.6左右相符,可见上述库塘系统水量分配模拟模型用于大官塘水库灌区的灌溉过程仿真模拟是适宜的.
4 基于正交试验的库塘联合灌溉系统水资源优化调控模型 4.1 库塘联合灌溉系统水资源优化调控模型的构建 4.1.1 目标函数本文中库塘联合灌溉系统水资源优化调控的目的是在保障基本需水供水安全的前提下,通过水资源优化调控实现经济效益最大,具体目标函数为:
| $ F = \max \left\{ {\sum\limits_{i = 1}^m {\sum\limits_j^n {{\delta _{ij}}{B_{ij}}{Y_{ij}}} } - \sum\limits_j^n {bk{d_j}} - \sum\limits_j^n {Int{s_j}} - \sum\limits_j^n {Int{x_j}} - \sum\limits_j^n {In{b_j}} } \right\} $ | (14) |
式中,δij为第i种作物第j年的价格(元/kg);Bij为第i种作物第j年的播种面积(hm2);Yij为第i种作物第j年的产量(由具体不同作物灌溉供水量用作物水模型来计算求取)(kg);bkdj为泵站第j年的提水电费投入(元);Intsj为上游区塘坝清淤扩容工程投资平均折算至第j年的投入(由具体泵站提水灌溉水量来求取)(元);Intxj为下游区塘坝清淤扩容工程投资平均折算至第j年的投入(元);Inbj是水库提水泵站恢复和提升供水能力的工程投资平均折算至第j年的投入(元).
4.1.2 调控变量由前述分析可知,大官塘水库灌区现况存在如下问题:1)上、下游塘坝蓄水能力偏小,尤其下游调节塘坝的蓄水容量明显不足,导致库塘供水系统弃水偏多,无法充分拦蓄利用地表水资源;2)上、下游区种植结构不协调,现行灌溉制度不合理,特别是上游水稻播种面积明显偏大,加之现行水稻灌溉以常规大水漫灌为主,水稻蓄雨水深也较浅,导致缺水现象突出.
为此,本文选取调控变量如下:1)上游作物种植结构,Bsij;2)下游作物种植结构,Bxij;3)水稻浅湿灌溉间歇天数,T;4)水稻田间蓄雨水深,Hm;5)上游独立塘坝容量,Vtdsmax;6)上游调节塘坝容量,Vtfsmax;7)下游独立塘坝容量,Vtdxmax;8)下游调节塘坝容量,Vtfxmax;9)水库泵站提水能力,Qtg.
4.1.3 约束条件1) 田间水量平衡约束详见式(6);2)大官塘水库水量平衡约束详见式(11);3)塘坝水量平衡约束详见式(12),上述约束均为等式约束. 4)水库泵站提水能力约束:上游区塘坝供水不能满足灌水需求时,需从水库提水灌溉,因此要考虑水库泵站提水能力的限制. 5)其他约束:如灌溉保证率约束、设计参数的非负性约束、灌溉供水渠道最大输水流量限制等.
4.2 库塘联合灌溉系统水资源优化调控模型的求解运用正交试验原理,设置调控变量A上下游塘坝容量、B水库泵站提水能力、C水稻间歇灌溉的间歇天数、D水稻田间蓄雨水深为3水平4影响因素的正交试验表[24-25].结合前述构建的降雨径流模拟模型和水量分配仿真模拟模型,通过正交试验极差分析得出最优组合后,再以此最优组合为输入,以逐年作物种植结构为优化变量,用遗传算法[19-20]求解在最优组合下的最优作物种植结构与作物收益,从而实现对库塘联合灌溉系统水资源优化调控模型的求解.
4.2.1 调控变量变化范围的确定① 上下游塘坝容量.据调查,现状塘坝蓄水深度都在0.8~1.5 m之间,蓄水少、占地多.为此,通过对塘坝的清淤整治,提高蓄水至2.5~3.5 m,则可扩大塘容至现状的2~3倍.在清淤整治的基础上,再新建塘坝以增加塘坝蓄水容量,则由于占地的投入,导致塘坝扩容投入会明显增加.为此,本文选择的三水平分别为:1)局部塘坝清淤整治;2)全部能清淤的塘坝均清淤整治;3)在塘坝清淤的基础上,进行塘坝新建,以增大上下游塘坝蓄水容量.具体A影响因素的3水平取值见表 4.
| 表 4 因素A的水平处理 Tab.4 Standard grade level of Factor A |
② 水库泵站提水能力.据调查,大官塘水库现状提水能力仅为1.3 m3/s,可通过泵站维修改造提高泵站提水能力,也可通过新建泵站以进一步增加泵站的提水能力,但新建泵站由于占地与土建工程的投入,导致泵站提水能力提升的投入明显增大.本研究选择因素B的3个水平分别为:1)局部维修改造现有泵站;2)维修改造现有泵站,恢复至设计提水能力;3)在泵站现有提水能力恢复至设计能力的基础上,进行泵站的新建,以增大水库一级泵站提水能力.具体因素B的3水平B1、B2和B3分别为2.1、2.7和3.3 m3/s.
③ 水稻间歇灌溉的间歇天数.水稻间歇灌溉在巢湖流域的灌溉试验与大田推广中取得良好的效果,但大官塘水库灌区水稻灌溉仍以常规灌溉为主,只有局部采取水稻间歇灌溉方式.根据淠史杭、肥东及八斗等灌溉试验站长序列水稻节水灌溉试验成果确定因素C的3个水平,具体见表 5.
| 表 5 因素C的水平处理 Tab.5 Standard grade level of Factor C |
④ 水稻田间蓄雨水深.水稻田间蓄雨水深是影响水稻对降雨直接利用的重要因素,依据水稻节水灌溉试验成果与实践经验来选取因素D的3个水平,具体见表 6.
| 表 6 因素D的水平处理 Tab.6 Standard grade level of Factor D |
由前述分析,本文正交试验选优设置为3水平4因素,根据正交试验原理[24-25],设计正交表L9(34).运用正交试验分析原理与方法,经极差分析求取系统最优控制组合参数,见表 7.由表 7极差分析结果可知,各因素对系统综合指标的影响大小依次为:Rx2>Rx4>Rx3>Rx1,且最优因素组合为A2B1C3D3.
| 表 7 大官塘水库灌区水资源调控正交试验的极差分析 Tab.7 Range analysis of orthogonal experiment of water resources regulation in Daguantang Reservoir irrigation district |
大官塘灌区作物种植结构,小麦与油菜、玉米与大豆的生长期、作物需水量与需水规律基本一致,可分别归类为午季旱作物和秋季旱作物;水稻种植为一季中稻,为秋季水稻(表 1).因此,作物种植可简化为水稻(秋季旱作物)-午季旱作物轮作,作物灌溉需水量主要取决于水稻播种面积.此外,该区下游农田灌溉水源条件好,引水渠设计引水能力满足下游5.87 km2水稻灌溉需求,在水资源优化配置时,优先满足下游5.87 km2水稻的灌溉.基于此,作物种植的调控变量为上游逐年水稻的播种面积Bss.
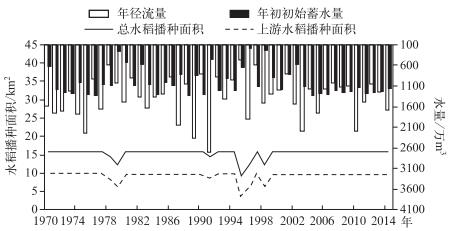
将前述正交试验最优组合A2B1C3D3的具体参数作为模型输入,以大官塘灌区上游不同来水频率不同初始蓄水量下的水稻播种面积为调控变量,以公式(14)为目标函数,运用遗传算法[19-20]求解水资源优化调控模型,得出逐年适宜的水稻播种面积(图 3).大官塘水库灌区上游不同降雨频率不同初始蓄水量下适宜的水稻种植比例见表 8.
|
图 3 大官塘水库灌区优化调控模式下逐年适宜的水稻播种面积 Fig.3 Yearly suitable rice sown of water resources optimization and control mode in Daguantang Reservoir irrigation area |
| 表 8 大官塘水库灌区上游不同降雨频率不同初始蓄水量下适宜的水稻种植比例 Tab.8 Appropriate rice planting ratio under different rainfall frequencies and initial water storage capacities in upstream of Daguantang Reservoir irrigation area |
在考虑工程措施与非工程措施综合作用下,对库塘联合灌溉系统进行水资源优化调控后,灌区灌溉过程得以明显改善,除1978-1979、1994-1998年连续干旱作用下,适宜水稻播种面积出现一定的下降外,其余年份基本能保障在上游区种植最大适宜水稻种植比例(耕地的70 %)、下游区种植最大适宜水稻种植比例(耕地的90 %)(图 3).可见,通过库塘灌溉系统水资源优化调控,可实现水量跨年甚至多年间合理调配,提高灌区抗旱减灾能力,保障农村经济可持续发展.
4.2.4 库塘联合灌溉系统水资源优化调控结果分析以图 1中逐年水稻播种面积代入前述构建的库塘联合水资源优化调控模型体系,求取模拟年份内逐年水量调配过程与作物收益,并分析了不同来水频率平均作物收益及与现状的对比分析结果.
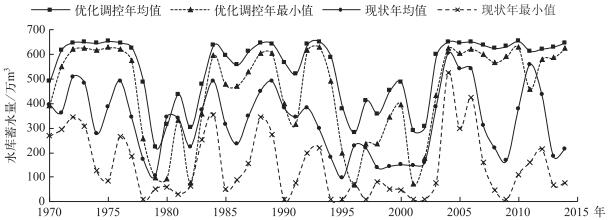
由图 3~图 5及表 9可知,大官塘水库灌区在库塘联合灌溉系统水资源优化调控下,可显著改善灌区农业灌溉供需合理性,具体结果如下:
|
图 4 库塘联合灌溉系统水资源优化调控及现状灌溉模式下水库年均及年最小蓄水量 Fig.4 The annual average and annual minimum storage capacity of water resources regulation and current irrigation mode about reservoirs and ponds combined irrigation system |
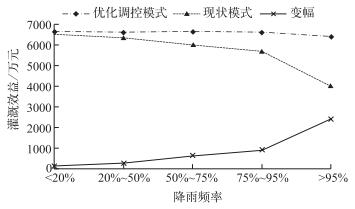
|
图 5 库塘联合灌溉系统水资源优化调控与现状灌溉模式下不同降雨频率的年均作物收益 Fig.5 Annual crop yields for different rainfall frequencies of water resources regulation and current irrigation mode about reservoirs and ponds combined irrigation system |
| 表 9 库塘联合灌溉系统水资源优化调控与现状灌溉模式下的水量供需及作物收益对比分析 Tab.9 Comparative analysis of water supply and demand and crop yields of water resources regulation and current irrigation mode about reservoirs and ponds combined irrigation system |
1) 在模拟计算的45 a中,多年平均水稻种植面积由14.93 km2提高至15.33 km2,同时还显著降低了年均总需灌溉需水量及缺水量,多年平均总需灌溉需水量降低了426.8万m3,降幅达37.6 %;多年平均总灌溉缺水量减少了196.7万m3,多年平均缺水率由18.0 %降低至1.0 %.
2) 在模拟计算的45 a中,虽塘坝多年平均供水量与现状基本持平,但塘坝供水的合理性得到显著提升,枯水年(75 % < P < 95 %)年均供水量高达764.1万m3,增幅达44.9 %;干旱年(P>95 %)年均供水量达到596.5万m3,增幅达20.8 %,增强了塘坝的年际供水能力,提升了塘坝枯水期的供水能力.
3) 在模拟计算的45 a中,多年平均从水库取水量降低了239.3万m3,降幅达73.7 %,显著降低了从水库灌溉取水量;水库多年平均蓄水量由449.5万m3提高至543.9万m3,增幅达21.0 %,多年平均最低蓄水量由146.1万m3提高至323.7万m3,提高了1.21倍,年最低蓄水量低于80万m3农业灌溉控制线的年份由21 a降至3 a,显著提高了水库多年平均蓄水量,明显降低了水库蓄水量在年际及年间的变化幅度.有力保障大官塘水库在灌区水资源多年调控作用的发挥,显著增强了该区抗旱减灾能力,为大官塘水库渔业与旅游业地发展提供了强力保障.
4) 在模拟计算的45 a中,水资源优化调控模式较现状模式的作物收益增加值随降雨频率的增加而显著增加,由P < 20 %时的140.1万元增加至P>95 %时的2398.5万元,多年平均作物收益增加了542.7万元,多年平均增收9.0 %.可见,本文提出的水资源优化调控可显著增加灌区作物收益,且增加收益随着降雨频率的增加(趋于干旱)而增加,可明显提高灌区干旱期的作物收益,显著增强抗旱减灾能力.
5 结论1) 通过工程措施(上下游塘坝蓄水能力和水库泵站提水能力)与非工程措施(库塘系统供水规则、作物种植结构、水稻灌溉间歇天数、水稻田间蓄雨水深及灌溉制度)的综合作用,以保障灌区基本需水(包括农村生活需水与生态环境需水)供水安全前提下的经济效益最大化为目标,依托灌溉试验站田间降水-作物耗水-土壤水相互转化的长序列试验成果,综合运用系统仿真与正交试验原理,提出了基于仿真模拟与正交试验的库塘联合灌溉系统水资源优化调控技术体系,并以大官塘水库灌区为例开展应用研究.
2) 应用该水资源优化调控技术体系优选了大官塘水库灌区适宜的水利工程规模与布局(上游塘坝容量500万m3,下游塘坝容量190万m3,上游水库提水泵站能力恢复至2.1 m3/s),确定了适宜的节水灌溉技术模式与灌溉制度,制定了库塘灌溉系统科学的水量调度规则,提出了具有可操作性的作物种植结构调整规则.通过与现状灌溉模式下农业灌溉水量供需过程及作物收益的对比分析,结果表明:1)在保障农村生活和生态环境供水需求下,多年平均总灌溉缺水量减少了196.7万m3,多年平均缺水率由18.0 %降低至1.0 %. 2)改善了塘坝供水的合理性,提升了塘坝的年际供水能力,增强了塘坝枯水期的供水能力. 3)提高了水库多年平均蓄水量,明显降低了水库蓄水量在年际及年间的变化幅度,有力保障骨干水库在灌区水资源多年调控作用的发挥,为大官塘水库渔业与旅游业地发展提供了强力保障. 4)灌区作物收益随降雨频率的增加而增加,明显提高了灌区干旱期的作物收益,显著增强了抗旱减灾能力.
| [1] |
Su XL, Kang SZ. Research advances and key topics on optimal allocation of water resources based on ecosystem in the arid areas. Transactions of the CSAE, 2005, 21(1): 167-172. [粟晓玲, 康绍忠. 干旱区面向生态的水资源合理配置研究进展与关键问题. 农业工程学报, 2005, 21(1): 167-172.] |
| [2] |
Su XL, Kang SZ. Multi-objectives allocation model of water resources and its application in the Shiyang River basin. Transactions of the CSAE, 2009, 25(11): 128-132. [粟晓玲, 康绍忠. 石羊河流域多目标水资源配置模型及其应用. 农业工程学报, 2009, 25(11): 128-132. DOI:10.3969/j.issn.1002-6819.2009.11.023] |
| [3] |
Loucks DP. Sustainable water resources management. Water International, 2000, 25(1): 3-10. DOI:10.1080/02508060008686793 |
| [4] |
Yan HY, Jia SF. Water balance and water resources allocation of Qinghai Lake. J Lake Sci, 2003, 15(1): 35-40. [燕华云, 贾绍风. 青海湖水量平衡分析与水资源优化配置研究. 湖泊科学, 2003, 15(1): 35-40. DOI:10.18307/2003.0105] |
| [5] |
Qi XB, Huang ZD, Qiao DM et al. Research advances on the reasonable water resources allocation in irrigation district. Advances in Water Science, 2015, 26(2): 287-295. [齐学斌, 黄仲冬, 乔冬梅等. 灌区水资源合理配置研究进展. 水科学进展, 2015, 26(2): 287-295.] |
| [6] |
Zhao D, Shao DG, Liu BJ. Method of disposition on water resources of irrigation district and its applications. Transactions of the CSAE, 2004, 20(4): 69-73. [赵丹, 邵东国, 刘丙军. 灌区水资源优化配置方法及应用. 农业工程学报, 2004, 20(4): 69-73.] |
| [7] |
Parsinejad M, Yazdi AB, Araghinejad S et al. Optimal water allocation in irrigation networks based on real time climatic data. Agricultural Water Management, 2013, 117(1): 1-8. |
| [8] |
Chen XN, Duan CQ, Qiu L et al. Application of large scale system model based on particle swarm optimization to optimal allocation of water resources in irrigation areas. Transactions of the CSAE, 2008, 24(3): 103-106. [陈晓楠, 段春青, 邱林等. 基于粒子群的大系统优化模型在灌区水资源优化配置中的应用. 农业工程学报, 2008, 24(3): 103-106.] |
| [9] |
Chen WB, Dong ZC, Zhang YF. Optimization the allocation of irrigated areas water resources based on memory gradient hybrid genetic algorithm. Transactions of the CSAE, 2008, 24(6): 10-13. [陈卫宾, 董增川, 张运凤. 基于记忆梯度混合遗传算法的灌区水资源优化配置. 农业工程学报, 2008, 24(6): 10-13.] |
| [10] |
Maqsood I, Huang GH, Huang YF et al. ITOM:an interval-parameter two-stage optimization model for stochastic planning of water resources systems. Stochastic Environmental Research and Risk Assess, 2005, 19(2): 125-133. DOI:10.1007/s00477-004-0220-6 |
| [11] |
Liu JY, Zhang Q, Deng XY et al. Quantitative analysis the influences of climate change and human activities on hydrological processes in Poyang Basin. J Lake Sci, 2016, 28(2): 432-443. [刘剑宇, 张强, 邓晓宇等. 气候变化和人类活动对鄱阳湖流域径流过程影响的定量分析. 湖泊科学, 2016, 28(2): 432-443. DOI:10.18307/2016.0224] |
| [12] |
Zhao Y, Lu CY, Xiao WH. Study on rational deployment of generalized water resources Ⅱ. Model. Journal of Hydraulic Engineering, 2007, 38(2): 163-170. [赵勇, 陆垂裕, 肖伟华. 广义水资源合理配置研究(Ⅱ)——模型. 水利学报, 2007, 38(2): 163-170.] |
| [13] |
Han YP, Lei HJ, Pan HW et al. Evaluation on water resources sustainable utilization based on virtual water and generalized water resources theory. Journal of Hydraulic Engineering, 2011, 42(6): 729-736. [韩宇平, 雷宏军, 潘红卫等. 基于虚拟水和广义水资源的区域水资源可持续利用评价. 水利学报, 2011, 42(6): 729-736.] |
| [14] |
Zhao Y, Lu CY, Qin CH et al. Study on rational deployment of generalized water resources Ⅲ. Application. Journal of Hydraulic Engineering, 2007, 38(3): 274-281. [赵勇, 陆垂裕, 秦长海等. 广义水资源合理配置研究(Ⅲ)——应用实例. 水利学报, 2007, 38(3): 274-281.] |
| [15] |
Zhang LB, Zhang ZY, Jin JL et al. Study on simulation model for reservoir-pool water resources system in reservoir irrigation district. Journal of Irrigation and Drainage, 2014, 33(4/5): 385-389. [张礼兵, 张展羽, 金菊良等. 水库灌区库塘水资源系统模拟模型研究. 灌溉排水学报, 2014, 33(4/5): 385-389.] |
| [16] |
Mishra SK, Singh VP. Long-term hydrological simulation based on the soil conservation service curve number. Hydrol Processes, 2004, 18(7): 1291-1313. DOI:10.1002/(ISSN)1099-1085 |
| [17] |
Jiang SM, Jin JL, Xu H et al. Computational model of pond re-storage times in Jianghuai hilly area based on SCS model. Transactions of the CSAE, 2013, 29(18): 117-124. [蒋尚明, 金菊良, 许浒等. 基于径流曲线模型的江淮丘陵区塘坝复蓄次数计算模型. 农业工程学报, 2013, 29(18): 117-124. DOI:10.3969/j.issn.1002-6819.2013.18.015] |
| [18] |
Mishra SK, Singh VP, Sansalone JJ et al. A modified SCS-CN method:characterization and testing. Water Resources Management, 2003, 17(1): 37-68. DOI:10.1023/A:1023099005944 |
| [19] |
Jin JL, Yang XH, Ding J. An improved simple genetic algorithm-accelerating genetic algorithm. System Engineering Theory and Practice, 2001, 21(4): 8-12. [金菊良, 杨晓华, 丁晶. 标准遗传算法的改进方案——加速遗传算法. 系统工程理论与实践, 2001, 21(4): 8-12.] |
| [20] |
Wang ZZ, Wang YT, Chen YW et al. Multi-objective reservoir regulation model based on simulation rules and intelligent optimization and its application. Journal of Hydraulic Engineering, 2012, 43(5): 564-579. [王宗志, 王银堂, 陈艺伟等. 基于仿真规则与智能优化的水库多目标调控模型及其应用. 水利学报, 2012, 43(5): 564-579.] |
| [21] |
Wang ZZ, Hu SY, Wang YT. Water quantity and water quality control based on initial water rights allocation in river basins. Beijing: Science Press, 2011. [王宗志, 胡四一, 王银堂. 流域初始水权分配及水量水质调控. 北京: 科学出版社, 2011.]
|
| [22] |
Jin JL, Yuan CY, Jiang SM et al. Assessment of drought resistance ability for pond and retaining dam irrigated area of Jianghuai hilly area based on water supply and demand balance analysis. Journal of Hydraulic Engineering, 2013, 44(5): 534-541. [金菊良, 原晨阳, 蒋尚明等. 基于水量供需平衡分析的江淮丘陵区塘坝灌区抗旱能力评价. 水利学报, 2013, 44(5): 534-541.] |
| [23] |
Pereira A, Green S, Nova NA. Penman-Monteith reference evapotranspiration adapted to estimate irrigated tree transpiration. Agricultural Water Management, 2006, 83(1/2): 153-161. |
| [24] |
Cheng JL, Sun XH. Simulation technology, orthogonal design, analytic hierarchy process and irrigation area optimization rules. Journal of Hydraulic Engineering, 1990, 12(9): 36-40. [程吉林, 孙学华. 模拟技术、正交设计、层次分析与灌区优化规则. 水利学报, 1990, 12(9): 36-40.] |
| [25] |
Cheng JL, Guo YY, Jin ZS. The optimal method and its application of large system mathematical programming experiment. Science in China:Series E, 1998, 28(3): 254-258. [程吉林, 郭元裕, 金兆森等. 大系统数学规划试验选优方法及其应用. 中国科学:E辑, 1998, 28(3): 254-258.] |
 2018, Vol. 30
2018, Vol. 30 


