揭示流域水文过程的复杂变化规律、掌握未来水文演变情势，是研究解决实际水文水资源问题的基本依据和必要前提.由于受许多复杂因素(包括随机因素)的共同作用和影响^[1-3]，水循环过程复杂多变，欲对其准确认识十分困难^[4].特别是近几十年受全球变化影响的日益加剧，水循环过程更加复杂多变^[5-7].我国许多流域(地区)水循环过程发生明显变异^[8]，水资源时空分布更加趋于不均匀化，加剧了水资源匮乏的局面，水安全形势十分严峻；另一方面，极端水文事件发生的频率和强度不断提高，诱发了许多更加严重的自然灾害，对水利工程运行调度、工农业生产和经济社会发展带来了巨大威胁.未来全球变化将极有可能对我国水资源区域分布产生更为显著的影响，并对供水安全、粮食安全、南水北调工程、水利现代化建设等国家重大工程和战略规划的预期效果产生不利影响^[9-11].

中长期(月尺度及以上)水文模拟预报是理解和认识未来水文情势的重要途径^[12].由于采用的技术手段不同，目前用于水文模拟预报的模型主要分为两类：水文物理模型与基于水文时间序列分析的数学模型^[13].前者主要利用一系列数理方程描述具有物理成因联系的水文变量间的复杂互馈关系，因此需要大量的数据与计算工作量以满足模型参数率定与模型验证的需要^[14].然而，目前对产汇流物理机制和水文过程的认识仍不完全清楚，且受到许多随机因素的干扰和影响，水文预报结果具有不确定性^[15-17]；此外，各种水文物理模型都有一定的局限性和适用条件，无法完全满足实际需求.因此，准确掌握未来水文演变情势一直是水文学研究的难题.

相比水文物理模型，基于水文时间序列分析的数学模型(本文将其称为水文时间序列模型)是认识未来水文演变情势的另一重要技术手段.这类模型以水文时间序列的组成和变化特性为基础，主要利用数学方法描述水文变量之间的相互关系，具有对数据量需求小和计算简单等特点，尤其在中长期水文模拟预测方面有明显优势^[18-20].本文主要对目前常用的水文时间序列预报方法进行综述，重点讨论这类方法用于预报时存在的问题以及解决办法，并尝试提出一个水文时间序列概率预报方法的通用架构，为相关研究提供借鉴和参考.

关于水文时间序列预报已有大量研究^[21-22]，且早期研究主要分为两类：一类是基于水文要素本身的演变规律进行预报(单变量法)，如周期均值叠加法、序列相关性分析方法等，这类方法大多基于水文序列平稳性的基本假设；另一类是基于水文气象物理因子与水文变量之间的关系进行预报(多变量法)，如成因分析方法、历史演变法等，这类方法引入水文要素变化响应机理分析，具有更长的预见期，且为变化环境下非一致性水文序列的预报提供了可行的思路.随着对水文现象认识的不断深入，以及新技术方法的发展与应用，新的水文序列预报方法也陆续应用于水文模拟预报^[23]，包括模糊预测方法^[24]、人工神经网络^[18]、灰色系统分析^[25]、混沌动力学方法^[26]、小波分析^[27-28]、支持向量机^[29]等新的人工智能模型与方法^[30-31].基于水文时间序列特性进行模拟预报的方法要求精细分析和描述水文资料，如果对水文资料的认识不足甚至有误，将严重影响水文序列模拟预报结果的可靠性.下面分别对各类常用方法的基本原理和局限性进行综述.

成因分析方法是较早应用于水文序列模拟预报的一类方法，其基本思路是根据水文气象物理因子与水文变量之间的关系进行模拟预报^[32]，主要利用数理统计方法构建物理因子和水文变量之间的关系，其中多元回归分析方法是最重要和最成熟的方法之一.为了达到客观分析、浓缩信息、简化计算等目的，回归分析经常与主成分分析、聚类分析、典型相关分析等方法结合运用.影响水文模拟预报的物理因子以大气环流、海洋以及天文地球物理因子等为主.该方法由于存在以下局限，使得应用效果受到限制：(1)结果精度偏低.虽然该方法引入水文要素变化响应机理分析，具有一定的物理基础，但受水文变量与物理因子间的复杂互馈关系认知所限，只能对少数物理因子进行分析，导致应用逐步回归分析、聚类分析等数学方法进行定量预报时精度偏低^[32]；(2)物理因子选择困难.应用成因分析方法时物理因子的选取是首要问题，综合分析目前研究成果认为，物理因子应该满足物理意义明确、统计贡献显著两个基本要求，但同样由于对水文变量与物理因子间的关系认知有限，难以选择合理的物理因子；(3)实用性较差.成因分析方法建立在大量数据资料的基础上，但常常难以获取满足要求的水文气象资料，导致预报结果的精度和可靠性较差^{[15, 17]}；(4)方法改进受到限制.由于目前对大气环流变化及降水的形成机制并不十分清楚，且还涉及到时空尺度转换、物理过程复杂庞大等许多技术难题未能得到有效解决，使得该类方法在应用中受限.

序列相关性分析是基于水文要素自身演变规律进行模拟预报的方法.水文时间序列一般由确定成分(趋势、周期、突变等)和随机成分组成，首先对这些成分进行识别和分离^[2]，然后基于随机成分的时域相依性选择合适的模型进行描述.常见的方法主要包括自回归滑动平均(auto-regressive moving average，ARMA)模型及其衍生类型、均生函数模型、最邻近抽样回归、马尔科夫链等^[33].随着模型应用领域越来越广，一些具有处理非线性能力的模型(threshold auto-regressive模型、双线性模型、指数回归模型等)也逐步应用于水文模拟预报^[34].应用序列相关性分析方法进行预报时，主要存在以下问题：(1)水文序列变化特性复杂，但常用的ARMA类模型仅从时间域上描述水文序列的变化特性，不利于揭示和认识复杂的水文现象；(2)水文序列往往具有非线性和多时间尺度特性，使用线性模型得到的水文序列预报结果往往较差^[35]，且部分非线性模型也无法满足实际需求；(3)序列相关性分析方法是基于水文序列平稳性假设，但受环境变化影响水文序列非平稳特性逐渐显现，使得该方法应用受到限制；(4)所用水文气象数据的质量情况会直接影响序列相关性分析的结果，而实际研究中往往难以获得大量可靠的水文气象数据资料.

人工神经网络(artificial neural network，ANN)是一种模仿人类大脑结构和功能进行分布式并行计算的非参数化信息处理系统. 1990s以来，随着计算机性能的改进和提高以及网络类型多样化和结构完善，该方法在水文和气象等领域逐渐得到应用.研究结果表明：采用适当的3层ANN模型可以描述任意复杂的水文非线性系统，是解决水文领域复杂非线性问题的一个有效工具.相比传统时间序列分析方法，ANN模型对水文时间序列预报的能力有很大提高，在径流预报、短期需水量预报、降雨-径流过程预报^[36]等方面均有体现. ANN模型可以解决复杂的水文非线性问题^[37]，但也存在一些不足之处：(1)由于人工神经网络模型应用于水文分析与计算的物理基础尚不完善，且建模过程中需要一定的技巧和经验，限制了人工神经网络的应用和推广；(2)人工神经网络模型并行处理的信息分布储存机制不清楚，可能会造成网络具有冗余性，从而影响预报结果的精度和可靠性^[38]；(3)人工神经网络模型有时模拟精度较高，而预测精度较差，这主要与模型拟合精度的选取有关.

针对目前水文序列预报方法精度偏低问题，除了各方法自身存在缺陷和局限性之外，更主要的原因是：未能根据待分析水文序列的具体成分构成和变化特性选择合理的模型，导致预报过程存在一定盲目性.水文系统是一个复杂的巨系统，水文序列主要由确定成分和随机成分组成^[2]，表现出随机性、非线性、非平稳性和多时间尺度变化等复杂特性.尤其是水文过程在不同时间尺度上的变化特性存在明显差异，且长期演变规律还具有一定的随机性.因此，在水文模拟预报时需要区分水文序列的不同成分和变化特性，有针对性地选择合理的模型.例如，若水文序列的随机性较明显时，应选用序列相关性分析方法或数理统计分析方法为宜；若序列的确定成分呈现较明显的线性趋势，选用线性回归模型即可得到较优的结果；反之，若序列确定成分表现出复杂的非线性和非平稳性，则需要根据具体情况选择相应的模型才能得到准确的结果.

通过对目前常用的水文序列预报方法及研究成果进行对比分析，得到以下认识：

1) 序列预报前应进行序列分解.由大量研究结果得到一个重要认识：如果直接对实测水文序列进行预报，往往无法得到准确的结果^[17].经分析认为主要是由于水文序列在不同时间尺度上的变化特性存在明显差异，而并非单个时间尺度上的简单波动和变化^[39-41].因此，欲得到可靠的水文序列预报结果，应该首先认识序列的复杂组成和多时间尺度上的复杂特性，为实际预报过程提供依据.此外，由于每种模型只适用于分析水文序列的某些具体特性，为了提高水文序列预报结果的准确性，也需要进行序列分解和变化特性识别.

2) 序列中确定成分和随机成分应分别进行预报.水文序列主要由确定成分和随机成分组成，前者基于一定的物理机制形成，表现为水文序列的趋势和周期等确定性变化规律；后者则是由一系列随机和不确定因素综合作用形成，表现为水文序列的相依性和纯随机变化.由于形成两种成分的物理机制不同，变化特性也存在显著差异.随机成分对序列中的确定成分造成很大干扰，且与水文极值密切相关^[42].大量研究表明：水文序列极值的预报结果往往很差^[17].一方面，水文极值表现出纯随机特性，并不能被确定性水文模型准确预报；另一方面，受诸多因素影响，水循环过程表现出明显的非一致性和不确定性^[43].近年来，许多学者通过模型改进提高水文序列的预报精度，但不少研究^[44-46]表明水文极值预报的可靠性仍然较差.随着极端水文事件日益频发，由此诱发的自然灾害越来越严重，给水利工程设计和运行调度、工农业生产等带来巨大威胁，水文极值问题已成为水文学研究的热点问题.因此，为提高水文序列预报结果的精度和可靠性，应该首先分离水文序列的确定成分和随机成分，然后分别进行预报.

3) 水文序列预报结果需要进行不确定性估计.受自然因素和人为因素的影响，水文序列预报的不确定性普遍存在.模型参数选取、模型结构选择、参数率定和目标函数确定等均存在不确定性，且会制约水文预报的实用性^[47].因此，对预报结果进行不确定性分析是当前水文预报学科研究亟需攻破的关键科学问题之一^[48].为了提高水文序列预报结果的合理性和可靠性，应该在预报过程中定量评估预报结果的不确定性问题.水文序列预报的不确定性分析可从以下两方面着手：一方面加强水文统计特性和物理机制的研究，减少人为因素造成的不确定性；另一方面综合多种不确定性分析方法的优势，建立更合理的不确定性分析方法.

4) 模型集成效果常常优于单个模型效果.水文时间序列表现出多种复杂特性，每种模型都是针对其某些特性进行分析，存在自身的缺陷和局限性，且受水文变量与物理因子之间的复杂互馈关系认知所限，对水文序列的组成和变化特性认识不足，采用单一模型对水文序列进行预报往往无法满足实际需求.因此，集合多种模型建立更优的预报方法，如确定性模型和不确定性方法的有效耦合是未来的发展趋势.大量研究结果证明模型集成的效果常常优于单个模型的预报结果^[49-51]，如小波分析方法、ARIMA模型等与ANN集成对降水径流过程进行预报^[52]，这主要归结于不同模型之间的优势互补^[53].为了克服单个模型和方法的缺陷，很多新技术和新方法也不断引入水文序列预报中，例如信息熵理论、非线性理论和小波理论等，很好地促进了水文序列预报理论与方法的发展.

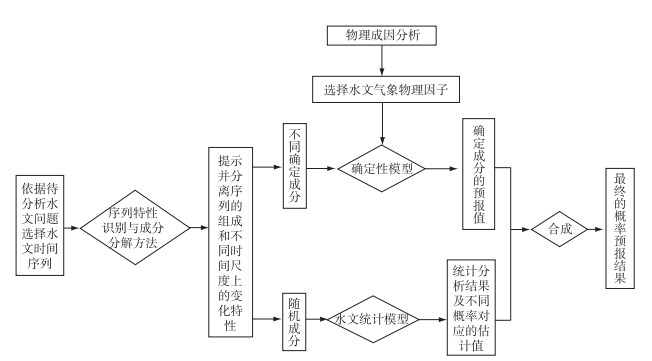
基于目前水文时间序列预报研究中存在的不足和得到的上述认识，此处尝试提出更为合理的水文时间序列概率预报方法，其通用架构如图 1所示.基本思路为：(1)根据待分析水文序列的特点及所要研究的问题，选择合适的序列分解方法，对水文序列的随机成分以及不同时间尺度的确定成分进行准确识别和分离；(2)依据确定成分的特性选择合理的确定性模型；(3)结合物理成因分析，对确定性模型的预报因子进行合理解释，得到确定性预报结果；(4)选用合理的水文统计学方法描述随机成分的统计特性，并经分析得到不同保证率对应的估计值(或区间值)，实现对确定性模拟结果不确定性的定量描述；(5)将两部分预报结果叠加，得到最终的预报结果.

图 1(Fig.1)

图 1 水文时间序列概率预报方法通用架构图 Fig.1 Universal framework for hydrological time series probabilistic forecasting

所提方法既克服了成因分析方法精度偏低、序列相关性分析基于平稳性假设等缺点，还可以避免由于对水文序列的变化特性认识不足，导致简单问题复杂化的发生.尤其在分析气候变化与剧烈人类活动(水利工程、城市化等)导致水文序列一致性遭到破坏等问题时，所提方法由于通过序列分解得到非一致性成分(周期、趋势等)并进行单独处理，因此更能发挥其优势.大量实例研究结果(表 1给出的3个实例)表明^[54]，相比常规预报方法，所提方法主要体现出3个优点：可靠的水文物理基础；在精度、合格率和预见期方面均具有高效性；具有不确定性定量评估能力.

表 1(Tab.1)

表 1 应用不同模型得到3个实测水文序列1步预测结果的评估结果 Tab.1 Evaluation of 1-step ahead forecasting results of three hydrological cases obtained by different models 案例 模型* 模型结构 指标(训练期) 指标(验证期) AARE TS5 TS10 TS20 R2 AARE TS5 TS10 TS20 R2 RS1 M1 6-9-1 0.42 0.08 0.15 0.47 0.75 0.57 0.00 0.00 0.12 0.23 M2 6-9-1 0.33 0.32 0.55 0.73 0.88 0.42 0.16 0.25 0.52 0.78 M3 6-7-1 0.41 0.24 0.38 0.52 0.85 0.49 0.08 0.15 0.32 0.58 M4 3-5-1 0.29 0.38 0.58 0.78 0.91 0.39 0.22 0.33 0.55 0.83 RS2 M1 6-10-1 0.51 0.08 0.17 0.27 0.62 0.54 0.00 0.10 0.20 0.27 M2 6-10-1 0.35 0.32 0.42 0.72 0.82 0.44 0.10 0.30 0.47 0.67 M3 4-6-1 0.46 0.10 0.17 0.58 0.74 0.45 0.10 0.30 0.40 0.40 M4 2-5-1 0.34 0.35 0.57 0.70 0.85 0.41 0.20 0.30 0.50 0.73 RS3 M1 4-5-1 0.61 0.16 0.23 0.30 0.37 0.63 0.00 0.00 0.00 0.19 M2 4-5-1 0.31 0.32 0.57 0.78 0.95 0.34 0.30 0.46 0.67 0.76 M3 7-8-1 0.33 0.35 0.53 0.81 0.93 0.44 0.10 0.23 0.43 0.59 M4 2-3-1 0.30 0.35 0.55 0.81 0.95 0.31 0.50 0.87 1.00 0.91 *: M1为常规BPNN神经网络；M2为序列消噪后建立的BPNN网络；M3为序列分解后建立的BPNN网络；M4为基于通用框架构建的人工神经网络，具体利用小波消噪和小波分解得到序列中的不同确定性成分和随机成分. RS1序列为开都河大山口站实测20 a(1978 1997年)的月径流序列；RS2序列为南京站实测41 a(1961 2001年)的月降雨序列；RS3为徐州韩桥煤矿实测125 d(2003年6月1日10月3日)的矿井总涌水量序列，主要受当地降雨影响. AARE表示平均相对误差绝对值；TS表示不同阈值误差的统计值；R2表示相关系数值.

表 1 应用不同模型得到3个实测水文序列1步预测结果的评估结果 Tab.1 Evaluation of 1-step ahead forecasting results of three hydrological cases obtained by different models

依据上述概率预报方法，实际应用过程中需要对下列问题进行重点分析和讨论：

1) 水文序列不同确定成分及随机成分分解.上述水文时间序列概率预报方法以准确分析序列不同组成和变化特性为基础.水文序列表现出复杂的变化特性，需要对其分解以便得到更准确的认识.对目前较成熟的序列分解方法进行整理^[55]，趋势分析方法大致分为4类：数据拟合法(最小二乘法、最大似然法等)、时域分析法(MK检验、Spearman秩次检验、Sen's斜率估计法等)、频域分析法(滑动平均法、快速傅里叶变换法、方差谱密度分析法等)和时频域分析法(小波分析方法、经验模态分解等)；周期识别方法主要有周期图法、快速傅里叶变换法、最大熵谱分析法、小波分析以及经验模态分解；突变检验方法主要有过程线法、滑动平均法和Hurst系数法等.不同方法具有特定的适用条件和范围，因此为提高水文序列分解结果的可靠性，需要选择合理的方法，探讨不同方法的组合应用.此处推荐使用离散小波能量密度谱方法^[56]进行序列分解.该方法以随机过程的标准能量分布为基础，不仅可以分解序列中的随机成分，而且可以定量判别序列不同时间尺度变化特性的统计显著性，进而得到周期成分与趋势成分，为水文时间序列模拟预测奠定基础.

2) 预报模型选择和改进.预报模型是直接影响水文预报结果精度和可靠性的关键因素.基于水文序列分解结果，应依据确定成分和随机成分的具体变化特性分别选择合理的预报模型.由于不同模型针对水文序列的不同特性，且各方法在理论上有待进一步完善.因此，深入研究常规预报模型和水文统计方法的改进和完善等问题，是未来中长期水文预报需要关注的重要内容.

3) 多种模型联合使用.目前用于水文序列预报的模型很多，各模型都有一定的适应性和局限，且水文时间序列的变化特性和组成复杂，使用单一模型对水文序列进行预报的结果较差，精度往往达不到实际需要.因此，结合其他方法进行水文序列分析，通过挖掘各模型的优势可以得到更优的水文时间序列分析方法，提高水文序列预报结果的精度和可靠性.本文提出的水文序列概率预报方法正是基于此思路的一次尝试.

4) 加强物理成因分析与数理统计分析相结合.数理统计方法是以水文序列本身的组成和变化特性或者水文变量与物理因子间的统计关系为基础，主要利用数学方法描述各变量之间的相互关系，可以很好地揭示水文序列的组成和变化特性，对水文预报具有重要作用，但其结果缺乏可靠的物理过程基础.应该认识到只有引入水文要素变化响应机理分析，同时研究水文序列变化特性及其物理机制，才能从根本上解决水文预报难题，不仅使其具有更长预见期和更高精度，而且还可为变化环境下的非平稳水文过程预报提供一个可行的思路.

研究水文序列中长期预报问题具有重要的理论和实际意义.本文主要对水文序列预报方法进行了综述，指出了各类方法存在的主要问题和局限性.在总结水文序列预报研究得到4个主要认识的基础上，基于序列组成及其不同特性的复杂特性，提出了一个水文序列概率预报方法的通用架构.所提方法已在许多流域得到了具体应用，且取得了良好的应用效果.限于篇幅，本文不再赘述更多应用实例.实际研究具体问题时，可以利用该方法寻求合理的模型和手段加以解决.为进一步完善水文序列预报方法，需对一些问题进行深入研究和探讨.例如，为深入揭示水文序列的组成和复杂变化特性、准确分离序列的确定性成分等，尝试多种方法联合使用.随着对水文问题认识层次的逐渐深入以及相关难题的逐步解决，未来水文预报结果的精度将会得到更大提高.