(2: 河海大学环境学院, 南京 210098)
(3: 苏州科技大学, 苏州 215009)
(4: 环境保护部华南环境科学研究所, 广州 510655)
(5: 环境保护部南京环境科学研究所, 南京 210042)
(6: 中国电建集团华东勘测设计研究院有限公司, 杭州 310014)
(2: College of Environment, Hohai University, Nanjing 210098, P. R. China)
(3: Suzhou University of Science and Technology, Suzhou 215009, P. R. China)
(4: South China Institute of Environmental Science, Guangzhou 510655, P. R. China)
(5: Nanjing Institute of Environmental Science, Ministry of Environmental Protection, Nanjing 210042, P. R. China)
(6: HydroChina Huadong Engineering Corporation, Hangzhou 310014, P. R. China)
湖泊作为一种常见且重要的水体,近年来受到气候变化和人类活动的影响,许多湖泊富营养化问题非常严重,水生态环境也持续恶化.藻类模型作为湖泊环境管理决策的一种有效工具被广泛应用和研究[1],但是由于模型受到各种外界因素的干扰,存在着不可避免的不确定性.为了提高模型的模拟精度,增强模型模拟的科学合理性,需要对水质模型的不确定性来源进行分析.
模型的不确定性来源大致可以分为结构、输入数据、参数以及计算误差4类[2].近年来随着计算机技术的发展,各种水环境模型结构更加完善,但是同时参数也更多,参数的影响变得非常重要,尤其是敏感性参数对于模拟结果不确定性贡献非常大.大量关于湖泊水环境模型敏感性分析的研究表明与生物生长代谢以及死亡速率有关的参数都较敏感[3-7].同时敏感性参数会随着湖泊大小和深度呈现差异,尤其是一些易受风浪和边界条件影响的大型浅水湖泊,在这些水体中水动力以及浮游藻类生长过程非常复杂,光照、温度以及沉降速度等因素对模型的模拟结果影响也较大.例如在威尼斯泻湖模型中,光照强度以及磷半饱和常数较为敏感[8-9].而在滇池模型中,硝化速率以及光削减系数较为敏感[10].但是对于太湖这样面大水浅、水环境复杂的淡水湖泊,藻类模型敏感性研究较少,对于大型富营养化浅水湖泊模型的参数敏感性认识不足.
本研究选取太湖作为典型的大型浅水湖泊进行分析,选取国内外常用的EFDC(environmental fluid dynamic code)模型,结合已有数据资料建立太湖藻类模型并选取叶绿素作为模型输出.本研究利用区域敏感性分析方法(regionalized sensitivity analysis, RSA)和普适似然不确定性分析方法(generalized likelihood uncertainty estimation, GLUE)对参数随机取样并进行敏感性分析,量化参数对模拟结果的影响和每个参数的敏感性,并通过与后验分布得到参数可能的取值范围.研究结果能够帮助对比分析这类湖泊的参数敏感性特点,提高参数调整的效率和模型模拟精度,为选取较优、较符合实际的湖泊藻类模型参数提供参考.
1 研究区域本文以中国第三大浅水湖泊太湖(30°05′~32°08′N,119°08′~122°55′E)为研究对象.太湖总面积2338 km2,平均水深1.9 m,最大水深为2.6 m.太湖流域夏季主导风向是东南风,冬季主导风向是西北风,平均风速3.5~5.0 m/s.太湖底部为坡度为0°0′19.66″的平底地形,周边水系复杂,本研究将环湖河道概化为30条河[11],编号如图 1所示.由于水动力条件较弱,营养盐浓度较高,因此太湖在夏、秋季节常暴发藻类水华,并且存在着较大的空间差异性,其中竺山湾和梅梁湾最为严重,藻类最多,东部沿岸区最少[12].为方便分析,本研究将太湖划分为8个湖区(图 1),其中4个典型湖区(梅梁湾、西南湖区、湖心区和东部湖区)在地理位置上包含了湖心(湖心区)、湖湾(梅梁湾和东部湖区)和湖岸(西南湖区);在水动力情况上包含了以湖流(东部湖区)和波浪(其他湖区)为主的湖区;在水质情况上包含了高营养盐负荷和高藻类浓度的梅梁湾,中营养盐负荷和中藻类浓度的湖心区以及低营养盐负荷和低藻类浓度的东部湖区,因此选取这4个典型湖区进行参数的敏感性分析.

|
图 1 研究区域划分 Fig.1 Division of the study areas |
选取国内外常用的EFDC模型来模拟太湖的水动力和水质过程.采用笛卡尔直角坐标划分网格,共划分4464个网格,每个网格单元边长为750 m,垂直方向采用σ坐标将太湖分为3层[13].为满足流体静力学的连续性和避免产生σ坐标带来的压力梯度错误,通过改变网格密度和插值方式使模型湖底坡度小于0.33[11].模型使用大气条件、表面风力、出入湖的流量和水质作为边界条件.其中边界河道输入条件来自太湖周边的大小出入河流概化成的30条主要河流(图 1);降雨量数据来自太湖附近8个监测站,大气条件和风场采用中国科学院南京地理与湖泊研究所太湖湖泊生态系统国家野外观测研究站的数据.模拟年份为2005年,太湖平均风速为5 m/s,年平均气温为17.7℃,年平均降雨量为1833 mm,平均太阳辐射为245 W/m2,平均云覆盖系数为0.6.模拟初始日期为1月1日,假设初始水位为水平,设置为模拟时段第1 d的平均值,初始流速设为0 m/s[13].模型采用稳定的初始条件和边界条件,计算时间为365 d,时间步长为10 s.模型参数的设置已经使用实测值进行了率定[11, 13-14].
2.2 分析方法采用区域敏感性分析方法RSA和普适似然不确定性分析方法GLUE来分析参数的敏感性. RSA方法是由Hornberger等提出的[15],通过比较每组参数所得到的模拟值与实测值,获得参数组的行为(即拟合度较高)和非行为(即拟合度较低)特征,并计算参数的累计分布. RSA方法具有对最优条件进行弱化并使用一些定量或定性方式来决定参数取舍的特点[16]. GLUE方法是Beven等基于RSA方法提出的用于评价预测结果不确定性的全局方法,是一个Monte Carlo方法[17].这两种方法的基本原理是首先将参数抽样后代入模型运行,计算每个模拟结果与实测值的似然值,设定阈值为0.5,将似然值低于该阈值的参数组筛除,把似然值高于该阈值的重新进行归一化,最后按照似然值的大小排序,求出在某置信度下模型预报的不确定性范围并分析参数的敏感性.由于在实际监测中测量指标大多为叶绿素,为了方便比较,本研究中采用可以表征藻类含量的叶绿素作为目标函数进行分析.具体步骤如下:
1) 确定参数的取值范围和先验分布
根据文献中水质模型的参数设置[18-21],并针对大型浅水湖泊的特点,在选取参数时首先考虑到蓝藻是太湖的优势藻类,因此去除了模型中反映其他藻类(如绿藻、硅藻和其他大型浮游藻类)生长特性的参数,如藻类生长率、藻类基础代谢速率、藻类牧食速率等.在预模拟实验中也发现太湖的内源释放速率对于营养盐模拟影响十分大,但是由于本模型主要研究的是水质模块中与藻类有关的参数,模型的沉积模块并没有开启,水质模块中的内源释放更类似于外部输入条件而不是参数,因此不考虑.另外,参考温度、藻类生长最佳水深和其他通用的参数也被筛除,再根据剩余参数的计算方程,选取了方程的一阶反应项系数、沉降项等.最终选择蓝藻最大生长速率、蓝藻基础代谢速率等40个参数作为水质模型输入参数.假定各个参数符合均匀分布,且参数之间取值相互独立,模型参数、意义及其取值范围见表 1.
| 表 1 模型输入参数抽样取值范围 Tab.1 Parameters used for the Latin hypercube sampling |
2) 模拟计算
对于拉丁超立方抽样(LHS)的次数,本研究对100、200、300、400和500次5种情况进行了鲁棒性检验,发现当抽样次数大于400次时,抽样运行结果保持稳定.故使用LHS方法进行随机抽样,生成500组参数,运行模型,得到500组输出结果.
3) 定义似然判据
选择最常用的Nash-Stucilffe确定性系数作为似然判据[22],表达式为:
| $ L\left( {{\theta _i}/Y} \right) = 1-\alpha _i^2/\alpha _0^2 $ | (1) |
式中,L(θi/Y)表示第i组参数的似然判据,αi2表示模拟序列的误差方差,α02表示实测序列的方差.
| $ l\left( {{\theta _i}/Y} \right) = \frac{{L\left( {{\theta _i}/Y} \right)-{L_{\min }}\left( {{\theta _i}/Y} \right)}}{{{L_{\max }}\left( {{\theta _i}/Y} \right)-{L_{\min }}\left( {{\theta _i}/Y} \right)}} $ | (2) |
式中,l(θi/Y)为归一化后的似然值, Lmin(θi/Y)和Lmax(θi/Y)分别为最小和最大似然值.将归一化后的似然值进行排序,分别选取95 %和5 %作为90 %置信区间的上下边界分位点.计算区间覆盖率、不确定区间宽度和相对不确定宽度等指标评估模型由参数导致的不确定性.
4) 参数敏感性分析
根据在步骤3)中得到的似然值大小将参数组分为10组,每组分别计算其累计似然分布,这些似然值有总和为1的特点.分析似然值最好的10 %,如果在参数分布区间内所得到的累计似然函数是一条直线,表示该参数的可识别性较差.如果累计似然函数偏离较大则表明参数较敏感.
5) 参数敏感性量化
对得到的累计似然函数使用K-S检验[23](Kolmogorov-Smirnov test).使用最大垂向偏离度(Maximum Vertical Distance, MVD)来定义敏感指数并根据敏感指数的大小将参数分为不同的敏感级别.
3 结果与讨论 3.1 参数敏感性针对500组参数组合使用定义的似然判据计算每一组参数组合对应的似然值,将似然值按大小分为10组后得到在参数取值区间上的累计似然函数图,通过各个累计似然函数的最大偏离度计算参数敏感性指数.在40个参数中,敏感参数即MVD>0.11,P < 0.05的参数有7个,在4个湖区的敏感指数如图 2.
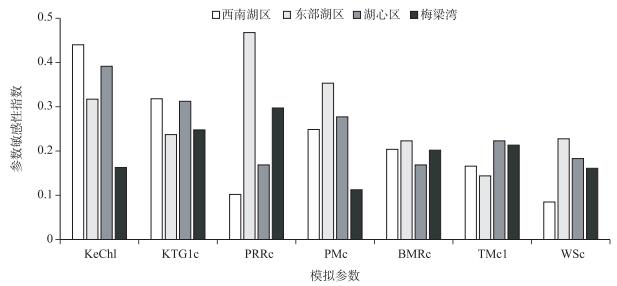
|
图 2 叶绿素模拟参数敏感性指数(KeChl:叶绿素消光系数;KTG1c:低温时对蓝藻影响系数;PRRc:蓝藻牧食速率;PMc:蓝藻最大生长速率;BMRc:蓝藻基础代谢速率;TMc1:蓝藻生长适宜温度最小值;WSc:蓝藻沉降速率) Fig.2 Sensitive indices in the simulation of chlorophyll |
7个敏感参数可以根据模型的控制方程分为藻类生长项(KeChl、KTG1c、PMc和TMc1)、藻类基础代谢项(BMRc)、藻类牧食项(PRRc)和藻类沉降项(WSc).其中藻类生长项的敏感参数最多,这部分的敏感性较高,是影响模拟结果的重要因素.藻类生长参数在其他富营养湖泊如滇池和加里利海中也被发现是至关重要的[24-25].在模型中,藻类生长项过程较为复杂,参数也较多,一般通过限制因子的方式对藻类生长进行描述.大致将影响藻类生产速率的限制性因子分为3种:营养盐、光照和温度. KeChl是光照限制因子中的最敏感参数,主要是由于在太湖这样藻类易暴发的浅水湖泊,水体透明度受藻类的影响非常明显,而对于一些富营养化问题较轻的深水湖泊,背景消光系数则是光照限制因子中的最敏感参数,如华盛顿湖[26]. KTG1c和TMc1被发现是温度限制因子中的最敏感参数,这主要可能是由于太湖冬、夏季温差较大,而对于滇池这样冬、夏季温差较小的大型浅水湖泊模型中[24],类似的参数就并不十分敏感.相比光照和温度等能量因素,营养盐对于模拟的影响较小,主要是由于太湖本身的营养盐水平较高,相对于能量因素限制性较小.
对于部分参数,参数敏感性空间变化较大,如PRRc和KeChl.将敏感参数在不同湖区进行敏感性排序(表 2).对于营养盐浓度较高的梅梁湾,与能量相关的参数(KeChl和KTG1c)较为敏感,而东部湖区营养盐浓度较低,最大生长速率(PMc)和藻类牧食速率(PRRc)最敏感.对于湖心区,敏感性参数较其他的湖区明显得多,这主要可能是湖心区较强的水动力导致的,水体交换和污染物迁移转化以及藻类生长过程受到水动力的影响变得活跃,从而对于参数变化较为敏感.
| 表 2 参数敏感性排序 Tab.2 Sensitivity ranks of parameters |
综合以上考虑,在模拟类似太湖这样的面大、水浅的水动力水质状况复杂的湖泊时,需要重点调整这些敏感参数,并且对于营养盐浓度不同的湖区需要分区考虑,达到更好的模拟湖泊水动力水质的目的.
3.2 模拟结果的不确定性4个湖区的模拟结果对应的置信度为90 %的不确定性区间如图 3所示,4个湖区模拟结果的趋势和实测值的基本一致,区间覆盖率平均为79 %,说明大部分实测值在不确定性区间内,模型基本可信,可以用于太湖水体富营养化模拟.
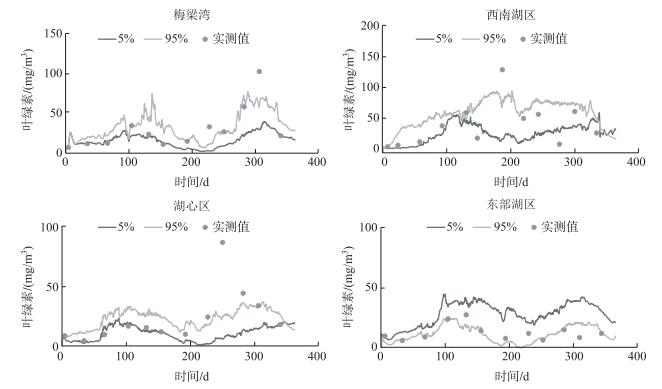
|
图 3 4个湖区叶绿素模拟结果90 %置信区间与实测值 Fig.3 Uncertainty interval and monitoring data of chlorophyll in four subareas |
不确定性在不同湖区差异较大,可能主要是受到水动力和边界条件以及营养盐和藻类浓度的影响.湖心区以及西南湖区相对梅梁湾的水动力条件要更强[13],因此与水动力息息相关的藻类变化过程也更加活跃,受到参数的影响也更强.而梅梁湾等湖湾区由于靠近湖岸,受到外边界输入输出河流的影响较大,实测值存在较大的不确定性,模型的模拟结果对于外边界设置的精确程度较为敏感[11].对于营养盐和藻类浓度较低的东部湖区其区间覆盖率较高(91.67 %),相对不确定性(132.58 %)也最高;而对于较高浓度的梅梁湾则相反,区间覆盖率较低(66.67 %),相对不确定性也较小(74 %)(表 3).这说明对于营养盐和藻类浓度低的湖区,模拟结果的不确定性较大,需要加以关注.
| 表 3 4个湖区不确定性指标 Tab.3 Uncertainty indicators in four subareas |
模拟结果的不确定性也在随时间不断变化,4个湖区模拟前期的不确定性较小,随着时间不断增加,尤其是在100~150 d以后,不确定性显著增加,根据之前的敏感性结果,大部分敏感参数与温度和光照有关,随着温度的升高以及光照的增强,藻类的生长项更加活跃,因此敏感性参数导致的结果不确定性也随之增加.
虽然大部分实测值在不确定区间内,但有部分实测值偏离较远.例如,西南湖区和梅梁湾的部分峰值,模拟结果低估了实际的浓度.这可能是河流、监测数据等存在外部不确定性因素造成的,这些因素也是调整水质模型时不可忽视的重要因素.
3.3 参数取值范围由于本研究先验分布都是均匀分布的,因此可以通过参数似然值的后验分布直观地发现模型参数的适当范围.例如藻类最大生长速率参数(PMc)(图 4),参数取值在2.3~2.6的范围内,似然值的累计密度最大,说明在此区间范围内模型模拟的范围普遍较好.而当取值大于3.8时,累计密度明显减小,模拟结果较差,结合其他湖区的结果得到可能的取值范围为2.0~3.8.最终得到7个敏感参数的取值范围(表 4).
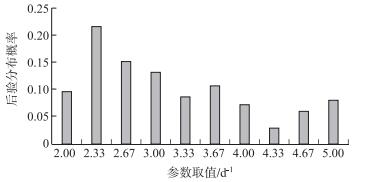
|
图 4 参数最大生长速率的后验分布 Fig.4 Posterior distribution of PMc |
| 表 4 参数可能取值范围 Tab.4 Possible ranges of sensitive parameters |
虽然可以通过调整参数达到优化模型模拟的目的,但是由于广泛存在的其他不确定性因素,仅仅通过参数调整无法达到最优化的目的.并且由于参数之间存在着实际意义上的相互联系,异参同效的现象非常普遍,往往参数的组合比单个参数的取值更有意义,因此给出的敏感参数取值范围并不是准确的取值,仅供参考.
| [1] |
Chen L, Yang Z, Liu H. Assessing the eutrophication risk of the Danjiangkou Reservoir based on the EFDC model. Ecological Engineering, 2016, 96: 117-127. DOI:10.1016/j.ecoleng.2016.02.021 |
| [2] |
Radwan M, Willems P, Berlamont J. Sensitivity and uncertainty analysis of river water quality modelling. Journal of Hydroinformatics, 2002, 6(2): 83-99. |
| [3] |
Omlin M, Brun R, Reichert P. Biogeochemical model of Lake Zürich:sensitivity, identifiability and uncertainty analysis. Ecological Modelling, 2001, 141(1/2/3): 105-123. |
| [4] |
Arhonditsis G, Tsirtsis G, Karydis M. The effects of episodic rainfall events to the dynamics of coastal marine ecosystems:applications to a semi-enclosed gulf in the Meditteranean Sea. Journal of Marine Systems, 2002, 35(3/4): 183-205. |
| [5] |
Li Y, Wang ZM, Zhang LJ et al. Analysis of parameter sensitivity of two-dimensional water quality model. Journal of Water Resources & Water Engineering, 2014, 25(1): 7-12. [李燕, 王自明, 张龙江等. 二维水质模型参数的敏感性分析. 水资源与水工程学报, 2014, 25(1): 7-12.] |
| [6] |
Luo C, Li ZF, Xi Q et al. Sensitivity analysis of hydrological and water quality parameters of HSPF Model. Journal of Agro-Environment Science, 2014, 33(10): 1995-2002. [罗川, 李兆富, 席庆等. HSPF模型水文水质参数敏感性分析. 农业环境科学学报, 2014, 33(10): 1995-2002. DOI:10.11654/jaes.2014.10.017] |
| [7] |
Li Z, Chen Q, Xu Q. Modeling algae dynamics in Meiliang Bay of Taihu Lake and parameter sensitivity analysis. Journal of Hydro-environment Research, 2015, 9(2): 216-225. DOI:10.1016/j.jher.2014.10.001 |
| [8] |
Pastres R, Franco D, Pecenik G et al. Local sensitivity analysis of a distributed parameters water quality model. Reliability Engineering System Safety, 1997, 57(1): 21-30. DOI:10.1016/S0951-8320(97)00014-8 |
| [9] |
Pastres R, Ciavatta S. A comparison between the uncertainties in model parameters and in forcing functions:its application to a 3D water-quality model. Environmental Modelling & Software, 2005, 20(8): 981-989. |
| [10] |
Yi X, Zou R, Guo H. Global sensitivity analysis of a three-dimensional nutrients-algae dynamic model for a large shallow lake. Ecological Modelling, 2016, 327: 74-84. DOI:10.1016/j.ecolmodel.2016.01.005 |
| [11] |
Li YP, Qiu L, Tang CY et al. Uncertainty and sensitivity analysis of input conditions in large shallow lake hydrodynamic model. China Environmental Science, 2014, 34(2): 410-416. [李一平, 邱利, 唐春燕等. 湖泊水动力模型外部输入条件不确定性和敏感性分析. 中国环境科学, 2014, 34(2): 410-416.] |
| [12] |
Ma RH, Kong FX, Duan HT et al. Spatio-temporal distribution of cyanobacteria blooms based on satellite imageries in Lake Taihu, China. J Lake Sci, 2008, 20(6): 687-694. [马荣华, 孔繁翔, 段洪涛等. 基于卫星遥感的太湖蓝藻水华时空分布规律认识. 湖泊科学, 2008, 20(6): 687-694. DOI:10.18307/2008.0605] |
| [13] |
Li YP, Tang CY, Yu ZB et al. Uncertainty and sensitivity analysis of large shallow lake hydrodynamic models. Advances in Water Science, 2012, 23(2): 271-277. [李一平, 唐春燕, 余钟波等. 大型浅水湖泊水动力模型不确定性和敏感性分析. 水科学进展, 2012, 23(2): 271-277.] |
| [14] |
Li Y, Tang C, Zhu J et al. Parametric uncertainty and sensitivity analysis of hydrodynamic processes for a large shallow freshwater lake. International Association of Scientific Hydrology Bulletin, 2015, 60(6): 1078-1095. DOI:10.1080/02626667.2014.948444 |
| [15] |
Hornberger GM, Spear RC, Hornberger GM et al. An approach to the preliminary analysis of environmental systems. Journal of Environmental Management, 1981, 12: 1. |
| [16] |
Li Y, Wang ZM, Zhang LJ et al. Analysis of parameter sensitivity of two-dimensional water quality model. Journal of Water Resources and Water Engineering, 2014, 25(1): 7-12. [李燕, 王自明, 张龙江等. 二维水质模型参数的敏感性分析. 水资源与水工程学报, 2014, 25(1): 7-12.] |
| [17] |
Beven K, Binley A. The future of distributed models-Model calibration and uncertainty prediction. Hydrological Processes, 2010, 6(3): 279-298. |
| [18] |
Analysis EMFL. Eutrophication model for Lake Washington (USA):Part Ⅰ. Model description and sensitivity analysis. Ecological Modelling, 2005, 187(2): 140-178. |
| [19] |
Seo DI, Kim MA. Application of EFDC and WASP7 in series for water quality modeling of the Yongdam Lake, Korea. Journal of Korea Water Resources Association, 2011, 44(6): 439-447. DOI:10.3741/JKWRA.2011.44.6.439 |
| [20] |
Wang Z, Zou R, Zhu X et al. Predicting lake water quality responses to load reduction:a three-dimensional modeling approach for total maximum daily load. International Journal of Environmental Science and Technology, 2014, 11(2): 423-436. DOI:10.1007/s13762-013-0210-7 |
| [21] |
Wang Y, Jiang Y, Liao W et al. 3-D hydro-environmental simulation of Miyun reservoir, Beijin. Journal of Hydro-environment Research, 2014, 8(4): 383-395. DOI:10.1016/j.jher.2013.09.002 |
| [22] |
Freer J, Beven K, Ambroise B. Bayesian estimation of uncertainty in runoff prediction and the value of data:An application of the GLUE approach. Water Resources Research, 1996, 32(7): 2161-2173. DOI:10.1029/95WR03723 |
| [23] |
Kottegoda NT, Rosso R. Statistics, probability, and reliability for civil and environmental engineers. Journal of America Chemistry Society, 1997, 10(2): 501-503. |
| [24] |
Yi X, Zou R, Guo H. Global sensitivity analysis of a three-dimensional nutrients-algae dynamic model for a large shallow lake. Ecological Modelling, 2016, 327: 74-84. DOI:10.1016/j.ecolmodel.2016.01.005 |
| [25] |
Bruce LC, Hamilton D, Imberger J et al. A numerical simulation of the role of zooplankton in C, N and P cycling in Lake Kinneret, Israel. Ecological Modelling, 2006, 193(3/4): 412-436. |
| [26] |
Arhonditsis GB, Brett MT. Eutrophication model for Lake Washington (USA). Ecological Modelling, 2005, 187(2/3): 140-178. |
 2018, Vol. 30
2018, Vol. 30 

