(2: 安徽省水利部淮河水利委员会水利科学研究院, 水利水资源安徽省重点实验室, 蚌埠 233000)
(3: 自然灾害过程与防控研究安徽省省级重点实验室, 芜湖 241002)
(4: 北京师范大学环境演变与自然灾害教育部重点实验室, 北京 100875)
(5: 北京师范大学地表过程与资源生态国家重点实验室, 北京 100875)
(2: Key Laboratory of Water Conservancy and Water Resources of Anhui Province, Water Resources Research Institute of Anhui Province and Huaihe River China, Bengbu 233000, P. R. China)
(3: Anhui Key Laboratory of Natural Disaster Process and Prevention, Wuhu 241002, P. R. China)
(4: Key Laboratory of Environmental Change and Natural Disaster, Ministry of Education, Beijing Normal University, Beijing 100875, P. R. China)
(5: State Key Laboratory of Surface Process and Resource Ecology, Beijing Normal University, Beijing 100875, P. R. China)
近年来,在气候变化和人类活动的综合影响下,极端气象水文事件(如暴雨和洪水等)频发[1],致使河流水文情势发生显著变化.据联合国公布资料显示,洪涝灾害所造成的损失已占全球自然灾害损失的20%,使洪水风险管理受到国际科研和管理机构高度关注[2-5].变化环境下所导致的水文变异使得流域径流序列形成的环境背景“平稳性”已发生显著变异. Milly等[6]认为,变化环境下的“平稳性”假设已不再适合作为水资源风险评估的默认假设,采用现有水文过程分析方法将会面临由变化环境带来的设计频率失真风险.因此,非平稳性水文序列频率的研究近年来受到格外关注. Rigby等[7]提出广义可加模型(简称GAMLSS),该模型可以构建分布函数参数和多个解释变量的线性、非线性、参数和非参数关系,并且扩展了分布函数的选择范围,具有很大的灵活性;Cunderlik等[8]提出非平稳条件下汇流的洪水频率模型,该模型将分位数函数分为本地时间相关分量(包括位置和尺度分布参数)以及在二阶非平稳假设下与时间变化无关的区域分量,主要应用均质区域. Chen等[9]结合非参数离散小波变换(DWT)和综合经验模态分解(EEMD),采用参数加权最小二乘法(WLS),通过评估台湾主要气象站年平均最大日降水量的非平稳性来识别这3种方法的适用性.另外非平稳性研究方法也引起国内学者的广泛关注[10-13].
气候变化和人类活动的共同影响下,淮河流域降水和径流的时空特征发生了显著变化.杜鸿等[14]通过对淮河流域极端径流的时空变化规律分析发现,淮河流域的极端径流事件以1960s和1970s居多,主要来自淮河干流、淮南山区及伏牛山区;魏凤英等[15]采用小波变换和广义极值分布等方法分析了1922—2007年淮河流域夏季降水的年际和年代际震荡特征. 1990s末以来,淮河流域夏季降水准2年振荡特征突出,极端强降水事件的概率显著增加;刘思敏等[16]基于淮河流域内229个气象站点1950—2012年的实测逐小时降水数据研究发现,淮河流域暴雨事件高发区域呈现出从流域部分地区向全流域扩张的趋势.极端降水和气候事件的增加,导致淮河流域洪涝灾害频发,近60年先后出现了17个洪涝年份(发生频率为4年一次),年均受涝面积269.8万hm2,成灾面积140.8万hm2,分别占全流域耕地面积的21%和11%.严重的洪涝灾害不仅影响工农业生产、人民生活和生态环境,给国民经济也造成重了大损失.
因地处南北气候、中低纬度和海陆相三种过渡带的重叠地区,淮河流域天气系统复杂多变,形成了该区上游区域“无降水旱、有降水涝、强降水洪”的典型区域旱涝特征[14].淮河流域水利工程众多,极大地改变了河川的平稳性,河川径流的平稳假设受到挑战.然而目前对淮河流域径流变化的研究主要是基于平稳性条件下开展的,且多集中于降水、气候变化和农业干旱风险评价等方面,对于非平稳性条件下的径流变化特征的研究几乎未涉及.随着极端气候事件的增加,致使极端水文事件增加将近1倍.在变化环境下将径流和其他水文过程做稳定性过程处理可能不再合理,尤其是依据水文过程稳定性假设构建的传统频率分析模型计算的设计标准修建的流域开发利用工程、防洪和抗旱工程等,将面临由变化环境引起的水文变异导致的风险.淮河径流是否具有平稳性,然而对于淮河流域的非平稳性洪水的研究并不多见.因此,本文基于GAMLSS模型与洪水频率分析模型开展淮河流域的非平稳性洪水特征研究.该研究可为提高淮河流域的防洪减灾能力,促进流域经济社会的可持续发展提供有力的支撑.
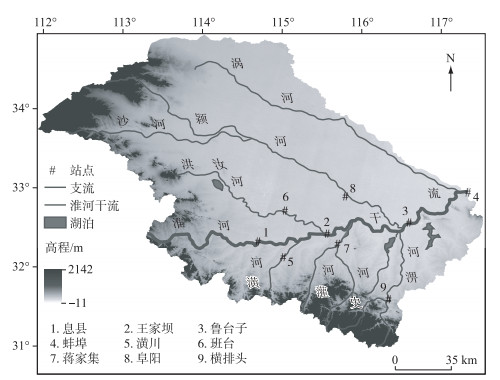
1 研究区域与数据淮河流域(30°55′~36°36′N, 111°55′~121°25′E)(图 1),地跨鲁、皖、苏、豫和鄂五省;介于长江和黄河两流域之间,总面积27万km2,人口约1.8亿,耕地面积1333万hm2,流域以占全国10%的耕地面积生产全国近20%的粮食,平均每年向国家提供商品粮约占全国商品粮的1/4,在我国农业生产中的地位举足轻重.因此,本文选取淮河流域位于干流和主要支流上的9个水文控制站点的年最大日流量数据进行统计分析,数据起止年限为:王家坝站,1964—2016年;潢川站和横排头站,1980—2016年;其余各站点均为1956—2016年.
|
图 1 研究区及水文站点位置 Fig.1 Locations of the study region and hydrological stations |
Pettitt非参数检验法是基于Mann-Whitney的统计函数[17].均值和方差变异是水文变异的两种基本类型,是用于描述时间序列模型的参数变化的单因素变量[18-19].该方法通过检验时间序列要素均值和方差变化进行变异点分析,认为两个样本x1, …, xt和xt+1, …, xn均来自同一整体:
| $ {\mathit{U}_{\mathit{t}{\rm{, }}\mathit{n}}}{\rm{ = }}{\mathit{U}_{\mathit{t}{\rm{ - 1, }}\mathit{n}}}{\rm{ + }}\sum\limits_{\mathit{j}{\rm{ = 1}}}^\mathit{n} {{\rm{sgn}}\left( {{\mathit{x}_\mathit{t}}{\rm{ - }}{\mathit{x}_\mathit{j}}} \right)} $ | (1) |
式中,xt为水文序列中第t个点的值,xj为水文序列中的第j个点的值,t=2、3、…、n.式(1)用于均值突变检测,用Pettitt法检测序列方差变异,需要对水文序列进行处理[17]:
| $ {\mathit{Y}_\mathit{i}}{\rm{ = }}{\left( {{\mathit{x}_\mathit{i}}{\rm{ - }}{\mathit{L}_\mathit{i}}} \right)^{\rm{2}}} $ | (2) |
用式(2)进行突变检测,若存在突变点则为方差突变. x1、x2、…、xn表示实测洪水极值序列;L代表参考函数Loess函数;Y代表残差平方和序列.
2.2 GAMLSS模型将时间序列均值和方差突变及时间趋势纳入广义可加模型(generalized additive models for location scale and shape,GAMLSS模型)的框架中进行突变和时间趋势检测. GAMLSS模型可用于检测时间序列的平稳性和非平稳性,是一种半参数回归模型[20].
在GAMLSS模型中,假设同一时间序列y1, y2, …, yn相互独立并且服从分布函数FY(yi|θi), θi=(θ1, θ2, …, θp)表示p个参数(位置、尺度和形状参数)形成的向量.记gk(·)表示θk与解释变量Xk和随机效应项之间的单调函数关系:
| $ {\mathit{g}_\mathit{k}}\left( {{\mathit{\theta }_\mathit{k}}} \right){\rm{ = }}{\mathit{\eta }_\mathit{k}}{\rm{ = }}{\mathit{X}_\mathit{k}}{\rm{\cdot}}{\mathit{\beta }_\mathit{k}}{\rm{ + }}\sum\limits_{\mathit{j}{\rm{ = 1}}}^{{\mathit{J}_\mathit{k}}} {{\mathit{Z}_{\mathit{jk}}}{\rm{\cdot}}{\mathit{\gamma }_{\mathit{jk}}}} {\rm{}} $ | (3) |
式中, ηk和θk是长度为n的向量,βkT={β1k, β2k, …, βJkk}是长度为Jk的参数向量,Xk是长度为n×Jk的解释变量矩阵,Zjk是已知的n×qjk固定设计矩阵,γjk是正态分布随机变量.如果不考虑随机效应对分布参数的影响时,即令Jk=0,式(3)就变成一个全参数模型:
| $ {\mathit{g}_\mathit{k}}\left( {{\mathit{\theta }_\mathit{k}}} \right){\rm{ = }}{\mathit{\eta }_\mathit{k}}{\rm{ = }}{\mathit{X}_\mathit{k}}{\rm{\cdot}}{\mathit{\beta }_\mathit{k}}{\rm{}} $ | (4) |
当解释变量为时间t时,解释变量矩阵Xk可以表示为:
| $ {\mathit{X}_\mathit{k}}{\rm{ = }}{\left[ {\begin{array}{*{20}{c}} 1&\mathit{t}& \cdots &{{\mathit{t}^{{\mathit{I}_\mathit{k}}{\rm{ - 1}}}}}\\ 1&\mathit{t}& \cdots &{{\mathit{t}^{{\mathit{I}_\mathit{k}}{\rm{ - 1}}}}}\\ 1&\mathit{t}& \cdots &{{\mathit{t}^{{\mathit{I}_\mathit{k}}{\rm{ - 1}}}}}\\ 1&\mathit{t}& \cdots &{{\mathit{t}^{{\mathit{I}_\mathit{k}}{\rm{ - 1}}}}} \end{array}} \right]_{\mathit{n}{\rm{ \times }}{\mathit{I}_\mathit{k}}}}{\rm{}} $ | (5) |
将式(5)代入式(4)可以得到分布参数与解释变量时间t的函数关系:
| $ \left\{ \begin{array}{l} {\mathit{g}_{\rm{1}}}\left( {{\mathit{\theta }_{\rm{1}}}\left( \mathit{t} \right)} \right){\rm{ = }}{\mathit{\beta }_{{\rm{11}}}}{\rm{ + }}{\mathit{\beta }_{{\rm{21}}}}\mathit{t}{\rm{ + }} \cdots {\rm{ + }}{\mathit{\beta }_{{\mathit{I}_{\rm{1}}}{\rm{1}}}}{\rm{\cdot}}{\mathit{t}^{{\mathit{I}_{\rm{1}}}{\rm{ - 1}}}}\\ {\mathit{g}_{\rm{2}}}\left( {{\mathit{\theta }_{\rm{2}}}\left( \mathit{t} \right)} \right){\rm{ = }}{\mathit{\beta }_{{\rm{12}}}}{\rm{ + }}{\mathit{\beta }_{{\rm{21}}}}\mathit{t}{\rm{ + }} \cdots {\rm{ + }}{\mathit{\beta }_{{\mathit{I}_{\rm{2}}}{\rm{2}}}}{\rm{\cdot}}{\mathit{t}^{{\mathit{I}_{\rm{2}}}{\rm{ - 1}}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{M}{\rm{}} \end{array} \right. $ | (6) |
本文主要探讨均值和方差(分别对应位置参数和尺度参数)的平稳性,选择4种最常用的两参极值分布进行分析:Gumbel(GU)、Gamma(GA)、Lognormal(LOGNO)和Weibull(WEI).以时间t作为唯一的解释变量,构造参数θ1(均值)和θ2(方差)与时间t的线性函数,由公式(6)可以得出:
| $ {\mathit{g}_{\rm{1}}}\left( {\mathit{\theta }_1^\mathit{i}} \right){\rm{ = }}{\mathit{t}_\mathit{i}}{\rm{\cdot}}{\mathit{\beta }_{\rm{1}}} $ | (7) |
| $ {\mathit{g}_{\rm{2}}}\left( {\mathit{\theta }_2^\mathit{i}} \right){\rm{ = }}{\mathit{t}_\mathit{i}}{\rm{\cdot}}{\mathit{\beta }_{\rm{2}}} $ | (8) |
本文通过GAMLSS模型,建立时间序列分布矩与时间的函数关系,将趋势和突变统一纳入到非平稳性框架中进行分析.主要用两参数模型分析未发生突变点的站点年最大洪峰流量序列,分为以下4种模型:①平稳性模型,θ1和θ2均为常数;②θ1非平稳,θ1是时间t的线性函数;③θ2非平稳,θ2是时间t的线性函数;④θ1、θ2均非平稳,θ1和θ2均为时间t的线性函数.用赤池信息量准则AIC(Akaike Information Criterion)值选择最优拟合分布模型和函数,用残差诊断图(worm图)分析模型拟合质量.通过这种方式,可以比较不同概率分布、趋势和突变点(均值/方差)的序列在非平稳性框架中的效果.
2.3 非平稳性洪水频率分析模型Vogel提出一个结合两参数对数正态分布函数所构造的非平稳性洪水频率分析模型,本文仅给出模型的基本表达式、洪水放大因子和重现期表达式,模型的具体推导和构建过程见文献[21].
模型基本表达式:
| $ {\mathit{x}_\mathit{p}}\left( \mathit{t} \right){\rm{ = exp}}\left[ {\mathit{\bar y}{\rm{ + }}\mathit{\hat \beta }\left( {\mathit{t}{\rm{ - }}\frac{{{\mathit{t}_{\rm{1}}}{\rm{ + }}{\mathit{t}_\mathit{n}}}}{2}} \right){\rm{ + }}{\mathit{z}_\mathit{p}}{\rm{\cdot}}{\mathit{s}_\mathit{y}}} \right]{\rm{}} $ | (9) |
式中,y为年最大日流量系列对数值的均值,
洪水放大因子:现在设计洪水必须乘以洪水放大系数获得未来跟现在洪水同量级的设计洪水值[21].洪水放大因子大于1,表明未来设计洪水值要高于现在设计值,意味着现有的防洪过程设计标准可能无法满足未来防洪需求;洪水放大因子小于1,则相反.
| $ \mathit{M}{\rm{ = }}\frac{{{\mathit{x}_\mathit{p}}\left( {\mathit{t}{\rm{ + \Delta }}\mathit{t}} \right)}}{{{\mathit{x}_\mathit{p}}\left( \mathit{t} \right)}}{\rm{ = exp(}}\mathit{\hat \beta }{\rm{\cdot\Delta }}\mathit{t}{\rm{)}} $ | (10) |
式中,M为洪水放大因子;Δt为时间间隔;其他变量意义同上.
重现期:现在发生的洪水在间隔t年后,其重现期大小.
| $ {\mathit{T}_{\rm{f}}}{\rm{ = }}\frac{{\rm{1}}}{{{\rm{1 - \Phi }}\left[ {{\mathit{z}_{\mathit{p}{\rm{0}}}}{\rm{ - }}\frac{{\mathit{\hat \beta }{\rm{\cdot\Delta }}\mathit{t}}}{{{\mathit{s}_\mathit{y}}}}{\rm{}}} \right]}} $ | (11) |
式中,Tf为未来重现期;Φ(·)为标准正态分布累积概率分布函数,其他变量意义同上.
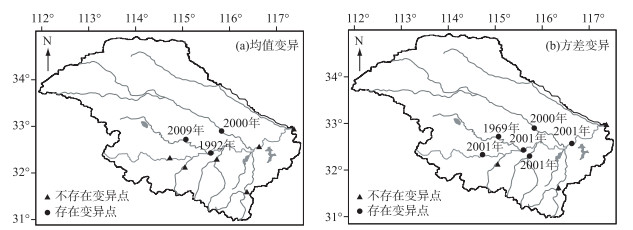
3 结果 3.1 变异点分析淮河流域的王家坝、班台和阜阳站年最大洪峰流量序列发生了均值变异和方差变异,息县、蒋家集和鲁台子年最大洪峰流量仅发生了方差变异,而蚌埠、潢川和横排头年最大洪峰流量的均值和方差均没有发生变异(图 2a、b).淮河流域继2000年发生干旱后,2001年发生了春夏秋冬连续干旱的大旱年,7月份息县站降水较常年同期减少99%,大旱年也导致了淮河干流和史灌河的水文站的方差发生变异.蚌埠、潢川和横排头水文站的年最大洪峰流量未发生变异,与其他站点相比,淮河南岸的潢川和横排头站所在的潢河和淠河的流域面积是最小的,分别为2400和6000 km2.流域面积越小,其径流的变化越大,但是潢河(石山口水库)和淠河(佛子岭水库、响洪甸水库、磨子潭水库和白莲崖水库)上游有大型水库,其调节拦蓄了其流域的大量洪水.虽然淠河属于山区型河道,坡陡水浅水流急,易受洪水侵袭[22],但是其水库防洪库容远较大,因此气候变化和水利工程的调节使得潢河和淠河未发生变异.而蚌埠站未发生变异,主要是因为蚌埠站控制流域面积大,且蚌埠到王家坝之间分布了大量的城东湖、瓦埠湖、高塘湖等天然湖泊和荆山湖等行蓄滞洪区,因此蚌埠年最大洪峰流量在极端降水和暴雨事件增多的前提下,因为水利工程的调节未发生变异.
|
图 2 淮河流域年最大洪峰流量序列变异点分布 Fig.2 The distribution of annual maximum peak flow change points in the Huaihe River Basin |
淮河流域9个水文站点中未出现仅存在均值变异的站点,除了王家坝的均值变异(1992年)、阜阳的均值/方差变异(2000年)和班台的均值/方差变异(2009年/1969年)以外,其他站点的方差变异时间均发生在2001年,这主要是因为近60年来,全流域年平均气温具有升高趋势,尤其是在1990s之后增暖趋势更加明显,并于1990s中后期发生暖化突变[23];淮河流域降水量年际波动较为强烈,1990之前降水量基本呈下降趋势,而2000年后明显上升[24]. 2000年是旱涝急转发生面积最大(48.08%)的年份,其中王家坝南岸和北岸旱涝急转发生频率高达40%左右[25].因而王家坝站在1992年发生均值变异主要是受到旱涝急转的影响,其是在1991年爆发全流域性大洪水而在1992年发生干旱所导致.
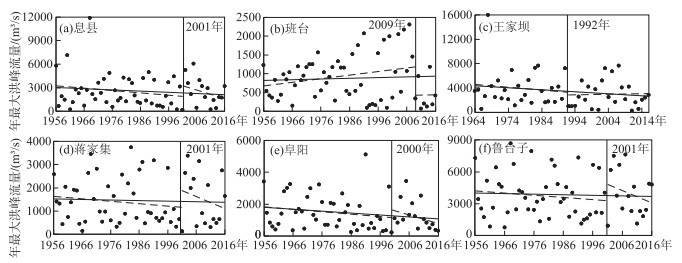
3.2 时间趋势分析表 1中仅为方差变异的水文站年最大洪峰流量在变异后呈减小趋势,但是减小趋势并不显著;方差和均值变异的阜阳水文站变异前的年最大洪峰流量通过了信度95%显著性检验,减小趋势显著,班台站年最大洪峰流量趋势恰好与阜阳站相反,呈增加趋势,且变异前的增加趋势显著;王家坝站与其他5个变异站点不同,变异前年最大洪峰流量呈减小趋势,变异点后呈增加趋势.整体上,淮河流域年最大洪峰流量除了阜阳和潢川下降趋势显著外,其他站点呈不显著性下降趋势,而横排头却呈不显著性上升趋势.通过分析变异点对趋势变化的影响发现(图 3),息县、蒋家集、阜阳和鲁台子站的变异点对趋势变化的影响大体一致,除阜阳站在变异前存在显著时间趋势性外,其余各站点在变异前、后序列均无显著趋势性.班台站整体序列呈微弱上升趋势,受变异点影响,变异前上升趋势较为明显(图 3b).王家坝站(图 3c)整体序列呈下降趋势,受变异点影响,变异前呈下降趋势,变异后呈上升趋势.由此可见,趋势分析时进行变异点识别是至关重要的,如果不考虑变异点的影响,趋势分析结果将会误导对序列统计特征的判断[26].
| 表 1 存在突变点序列变异点前、后子序列趋势检验结果 Tab.1 Trend test results for subseries posterior and prior to the change points |
|
图 3 变异点对趋势分析的影响 Fig.3 The impact of change points on trend test results |
由上述分析可知,突变点和时间趋势可能导致年最大洪峰极值序列具有非平稳性,本文用GAMLSS模型检测洪峰极值序列的变化.主要用两参数模型分析流域的年最大洪峰流量序列,由表 2可知,在没有发生突变的3个站点中,潢川站和蚌埠站年最大洪峰流量的最佳拟合分布函数为两参数的Weibull分布,而Lognormal分布是横排头站的最佳拟合函数.从序列平稳性来分析,潢川站和蚌埠站最优模型为平稳性模型,横排头站选择θ1、θ2均非平稳(表 2).潢川站非平稳性模型与平稳性模型AIC值相差范围在1.73~5.22之间;蚌埠站和横排头站差值分别在1.97~5.54和0.61~2.50之间.而横排头站非平稳模型仅比平稳性模型小0.61.对于发生突变的6个站点(表 2),Weibull分布函数为最佳选择,符合息县、班台和王家坝站年最大洪峰流量的拟合模拟;Gamma分布函数次之,其是蒋家集和班台站的最优拟合函数;Gumbel分布函数则没有适合的站点.从序列平稳性来看,有4个站点最优模型为平稳性模型,而班台站和蒋家集站分别选择θ1非平稳与θ2非平稳模型,无站点选择θ1、θ2均非平稳.从AIC值来看(表 3),发生突变的6个站点中阜阳站平稳性与非平稳性的AIC差值的范围最小,仅在0.90~2.802之间,班台站的θ1非平稳性模型与平稳性模型的AIC值差值最大,达到8.15.
| 表 2 GAMLSS模型分析结果* Tab.2 Analysis results of GAMLSS model |
| 表 3 与表 2相对应的各站点最优概率分布的AIC值 Tab.3 The AIC values of the best probability distribution for the corresponding stations in Tab. 2 |
从整体上来看,淮河中上游的9个站点中,有5个站点的最优拟合分布函数是Weibull函数,其次是Lognormal分布函数;班台、蒋家集和横排头站的选择的最优分布模型为非平稳性模型,其余6个站点选择的最优模型是平稳性模型.未发生突变的3个站点差值范围相对而言较小,其平稳性模型和非平稳性模型区别并不明显,而发生突变的6个站点的平稳性模型与非平稳性模型AIC差值范围普遍较大.因而,GAMLSS模型拟合的结果与突变点、趋势分析的结果相吻合,未发生突变的站点其趋势变化不明显.
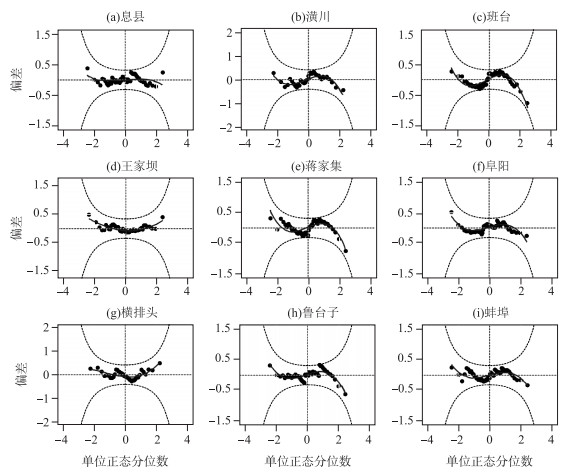
3.4 基于GAMLSS模型残差分析残差图的分布趋势可以帮助判断所拟合的线性模型是否满足有关假设,残差序列的分布状况是评估模型拟合效果的重要依据[27].为检验表 3最终确定的回归模型是否合理,图 4是将各站点年最大洪峰流量序列服从表 3最优分布模型条件下的GAMLSS模型进行残差分析.各站点的样本点沿着红色曲线并且位于两条黑色曲线(95%置信曲线)中间,显示GAMLSS模型所对这9个站点拟合较好(图 4).为了更直观地反映残差的分布情况,绘出残差正态QQ图(图 5). GAMLSS模型拟合的各个站点正态QQ图的残差点沿着理论直线分布,基本保持一致状态,而且概率点据相关系数R也非常接近1,这说明实际残差序列与理论残差序列有非常好的相关关系.因此从残差分布的角度,各站点基于GAMLSS模型选择的最优拟合函数对淮河中上游9个站点具有很好的拟合效果.
|
图 4 各站点GAMLSS拟合的残差检测图 Fig.4 Residual detection of GAMLSS fit at each site |

|
图 5 基于GAMLSS各站点线性回归正态QQ图 Fig.5 Based on GAMLSS site linear regression normal QQ map |
基于GAMLSS模型得到年最大洪峰流量序列的最优拟合结果(图 4、图 5),根据参数的计算结果做出分位图(图 6),然后统计落在每条分位曲线下方实际的频率值(表 4).各站点年最大洪峰流量序列的分位图中,非平稳性站点中横排头站和蒋家集站的分位曲线随时间序列变化呈现波动趋势,班台站的点虽然波动趋势不明显,但其在25%和75%分位线上产生较大偏差,均为6.15%,实际频率分布不是很合理.其余平稳性站点中除阜阳站在25%和潢川站在75%偏差较大外,总体频率分布较为合理,而且落在各条分位曲线下方实际的频率与理论概率小,偏差值仅为0.08%.由于水文序列趋势变化可能为整体趋势,也可能为局部趋势,所以对于水文长序列变化分析仅用平稳性条件下的线性趋势反映整个序列的变化并不合适.本文选用的水文序列较长,如果用平稳性的线性描述较长序列的趋势就可能造成偏差,淮河中上游非平稳性站点序列的实际和理论分位图在局部时段出现了明显的波动偏差(图 6).故而基于GAMLSS模型的两参极值分布可能会使站点频率曲线分布产生偏差,则需要通过GAMLSS模型检验站点的平稳性,然后根据实际与理论曲线的偏差大小,选择是否要引入更多的参数来描述序列非线性趋势变化.
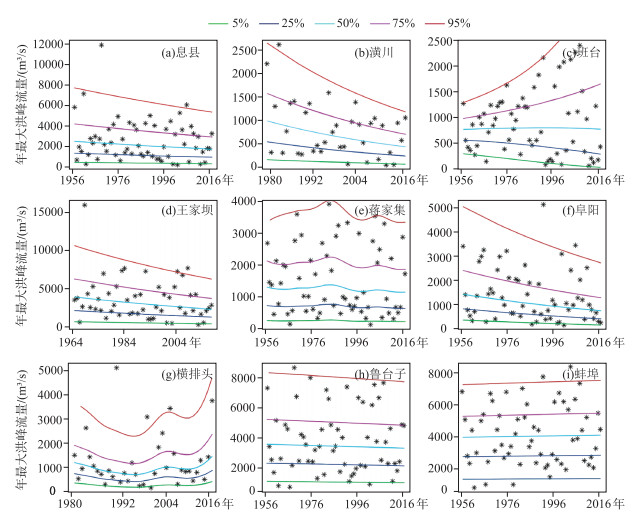
|
图 6 各站点年最大洪峰流量序列分位图 Fig.6 The annual maximum peak flow sequence of each station |
| 表 4 实际频率与理论分位数曲线概率对比 Tab.4 Comparison of actual frequency and theoretical quantile curve probability |
图 7为非平稳性洪水频率分析模型对淮河流域洪水频率分析,结果发现同一站点的年最大洪峰流量在不同的年份其设计流量值是不同的.横排头和蚌埠水文站年不同重现期的设计流量随时间增加而增加,其他站点不同重现期的设计流量则恰好相反. 图 8为各站点年最大洪峰流量累积频率曲线变化图,通过皮尔逊Ⅲ型分布模型计算所得,其是经验频率曲线拟合最优的一种模型[28].因经验点与Cs=2Cv曲线拟合较好,选择此曲线作为皮尔逊Ⅲ型分布累积频率曲线.将皮尔逊Ⅲ型分布模型与非平稳性模型计算所得流量设计值相比较分析显示(图 7、图 8和表 5),淮河流域非平稳设计流量随着时间跨度呈减小趋势.而各站点在10年一遇与20年一遇的非平稳设计流量值与皮尔逊Ⅲ型分布设计流量值相差不大,但随着时间跨度的增加,30年一遇、50年一遇和100年一遇的设计流量相差却越来越大.尽管王家坝、鲁台子、蚌埠和横排头站使用非平稳模型计算的不同重现期的设计流量随着时间变化呈降低趋势,但是其非平稳性模型计算的不同重现期的设计流量远高于平稳性模型,说明目前现有的防洪工程设计标准较低,对于未来洪水抵御能力弱;息县、潢川、班台和蒋家集在2010年之后,非平稳性的重现期10年和20年下的设计流量低于平稳性的.淮河流域应当提高超过30年一遇的的防洪标准,提高淮河流域应对大的洪水事件能力.
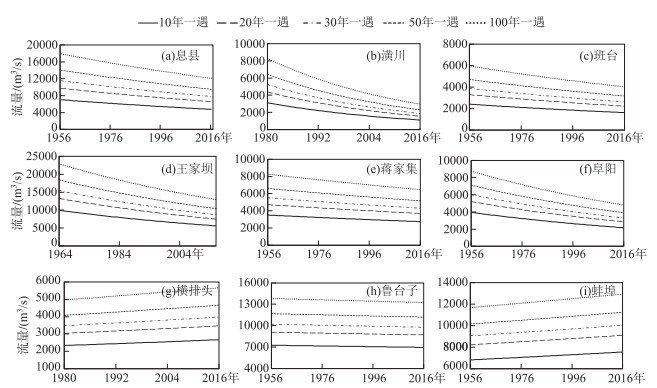
|
图 7 10年、20年、30年、50年一遇和百年一遇设计流量值随时间变化 Fig.7 Design flow value of annual maximum peak flow in different return periods with time |
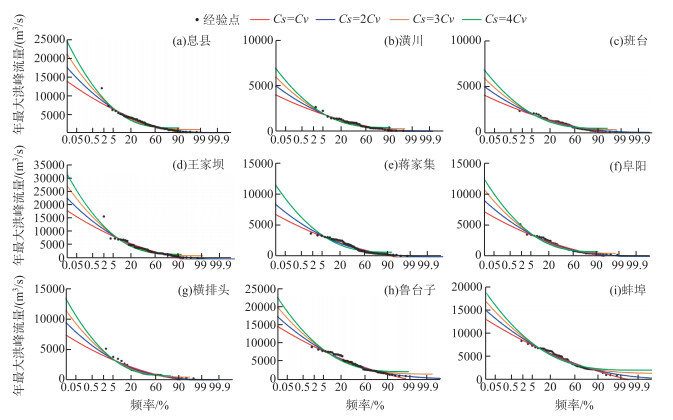
|
图 8 基于皮尔逊Ⅲ各站点年最大洪峰流量累积频率曲线 Fig.8 Cumulative frequency curves of annual maximum peak flow at each station based on Pearson type Ⅲ |
| 表 5 基于皮尔逊Ⅲ不同重现期的年最大洪峰流量(m3/s) Tab.5 Annual maximum peak flow in different return periods based on Pearson type Ⅲ |
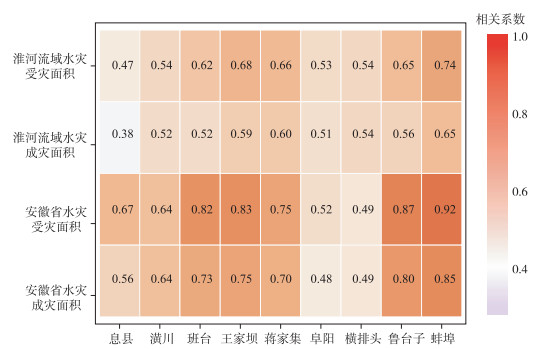
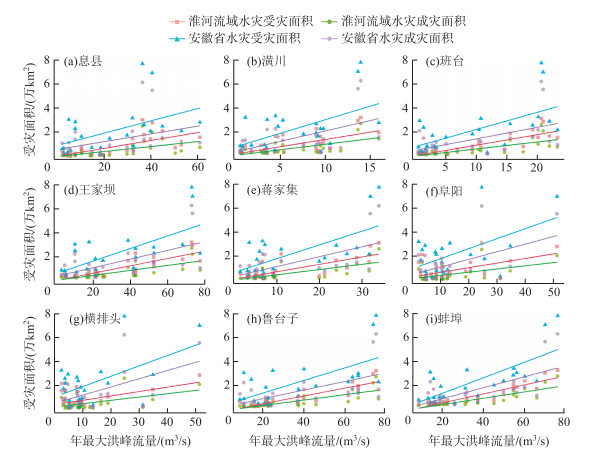
图 9给出了洪水放大因子和年最大洪峰流量百年一遇重现期随时间的变化情况(30年间隔).横排头站和蚌埠站(图 9)经过30年的变化,其洪水放大因子随着时间增加呈上升趋势且大于1,百年一遇重现期不足80年,意味着现有的防洪工程设计标准可能无法满足未来防洪需求.潢川站、王家坝站和阜阳站洪水放大因子均小于1,这些站点经过30年的变化百年一遇重现期将均超过300年,淮河流域的防洪取得了显著的成就.同时洪涝灾害频发对农业生产和社会经济发展起阻碍作用,洪涝灾害的受灾面积及成灾面积综合反应了灾害对粮食产量波动的危害程度.通过对淮河流域9个水文站点与洪涝灾害成灾及受灾面积做相关性分析可知,各站点年最大洪峰流量与淮河流域、安徽省灾害面积相关性基本上都通过了95%的显著性检验,王家坝、蒋家集、鲁台子和蚌埠站与淮河流域和安徽省洪涝灾害的相关性均突破了99%的显著性检验(图 10, 图 11).尤其是蚌埠站的相关系数最大,其位于淮河中游与洪泽湖之间,控制的集水面积高达121330 km2,淮河蚌埠河段河床平缓,易受到洪涝灾害的影响.从区域性差异来看,淮河流域各站点年最大洪峰流量变化对安徽省水灾受灾面积影响较大,这主要是因为淮河流域暴雨洪涝灾害主要集中在流域中上游安徽阜南县蒙洼蓄洪区及周边地势低洼地,使得安徽省成为淮河流域洪涝灾害受灾最严重的省区.安徽皖北地区的耕地面积占全省总耕地面积56.2%,由于耕地抵御洪水灾害能力弱,易受淹农田比例非常高[29].
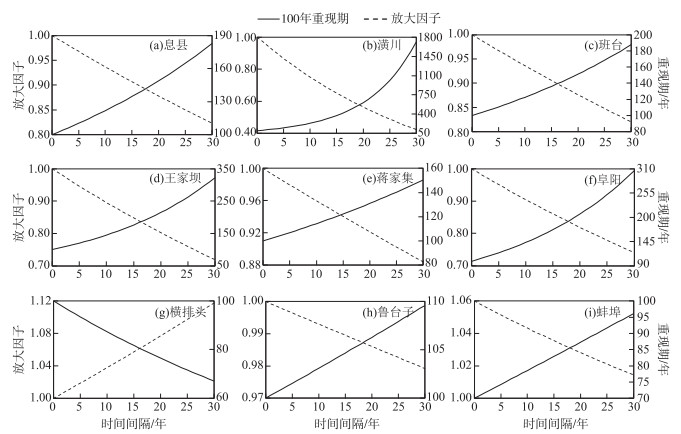
|
图 9 洪水放大因子和百年一遇重现期随时间的变化 Fig.9 The flood magnification factors and 100-year return period changing with time |
|
图 10 各站点年最大洪峰流量与淮河流域、安徽省灾害面积相关性 Fig.10 The correlation between maximum annual peak flow of each station and the disaster area of Huaihe River Basin, Anhui Province |
|
图 11 各站点年最大洪峰流量与淮河流域、安徽省灾害面积散点图 Fig.11 The scatter plot between maximum annual peak flow of each station and the disaster area of Huaihe River Basin and Anhui Province |
总的来说,淮河流域不仅是中国各大流域人口密度最高的地区,也是重要粮食生产基地和能源基地,1983—2014年淮河流域粮食播种面积从16.4×104 km2增加到了19.2×104 km2.大量种植的水稻、小麦等粮食作物是洪涝灾害最重要的承灾体.淮河流域自2000年以来GDP和人口也在不断增加,截至2014年GDP增加了55846.03亿元,人口也增加了1719.99万人.这在一定程度上改变了淮河流域水文情势,以致淮河流域年最大洪峰流量的设计流量在极端事件增加的情况下随着时间跨度呈减小趋势.但值得注意的是,人们在推进社会经济发展的同时,盲目围垦造田、乱砍乱伐等引起河道变更、水土流失也会造成淮河自身抗涝能力减弱.
4 结论通过Pettitt与M-K非参数检验法、GAMLSS模型和非平稳性洪水频率分析模型等方法,对淮河流域9个水文站点年最大洪峰极值序列的非平稳性假设进行了全面分析,得出以下结论:
1) 通过Pettitt法检验淮河中上游9个水文站点时间序列要素的均值和方差变化进行变异点分析发现:潢川、横排头和蚌埠站点的年最大洪峰流量未发生明显变异;共有6个站点的年最大洪峰流量发生均值或方差变异,变异时间主要集中在2000年左右.其中班台、王家坝和阜阳站的年最大洪峰流量发生均值变异,变异时间分别为2009、1992和2000年;班台站、王家坝站、阜阳站的年最大洪峰流量发生方差和均值变异.
2) 淮河中上游9个水文站点中有5个站点的最优拟合分布函数是两参数的Weibull函数,其次是Lognormal分布函数;班台、蒋家集和横排头站的选择的最优分布模型为非平稳性模型,其余6个站点选择的最优模型是平稳性模型.各站点基于GAMLSS模型选择的最优拟合函数对淮河流域站点具有很好的拟合效果.非平稳性站点中横排头站和蒋家集站的分位曲线随时间序列变化呈现波动趋势,班台站在25%和75%分位线上产生较大偏差,实际分布不是很合理.其余平稳性站点中除阜阳站在25%和潢川站在75%偏差较大外,总体频率分布较为合理.
3) 通过比较各站点在皮尔逊Ⅲ型分布模型和非平稳性洪水频率分析模型的设计流量值发现,尽管淮河流域非平稳设计流量随着时间跨度呈减小趋势,各站点在10年一遇与20年一遇的非平稳设计流量值与皮尔逊Ⅲ型分布设计流量值相差不大,但30年一遇、50年一遇和100年一遇的设计流量相差却越来越大,淮河干流的王家坝、鲁台子和蚌埠在非平稳性的设计流量远高于在皮尔逊Ⅲ型的设计流量.
4) 横排头站和蚌埠站经过30年变化,其洪水放大因子随着时间增加呈上升趋势且大于1,百年一遇重现期不足80年,意味着现有的防洪过程设计标准可能无法满足未来防洪需求.潢川站、王家坝站和阜阳站经过30年变化,百年一遇重现期将均超过300年.各站点年最大洪峰流量与淮河流域、安徽省水灾面积相关性基本上都通过了95%的显著性检验,王家坝、蒋家集、鲁台子和蚌埠站与淮河流域和安徽省洪涝灾害的相关性均突破了99%的显著性检验.
| [1] |
Schiermeier Q. Increased flood risk linked to global warming. Nature, 2011, 470(7334): 316. DOI:10.1038/470316a |
| [2] |
Reinsurance M. Topics geo: natural catastrophes 2014. Munich Re, 2015: 26-27.
|
| [3] |
European Commission. Directive 2007/60/EC of the European parliament and of the council of 23 October 2007 on the assessment and management of flood risk. Official Journal of the European Union, 2007, 288: 27-34. |
| [4] |
Schelfaut K, Panneman B, Craats IVD et al. Bringing flood resilience into practice:The FREEMAN Project. Environmental Science & Policy, 2011, 14(7): 825-833. |
| [5] |
Priest SJ, Suykens C, Rijswick HFMWV et al. The European Union approach to flood risk management and improving societal resilience:Lessons from the implementation of the floods directive in six European countries. Ecology and Society, 2016, 21(4): 4-8. DOI:10.5751/ES-08685-210404 |
| [6] |
Milly PCD, Betancourt J, Falkenmark M et al. On critiques of "Stationarity is Dead:Whither Water Management?". Water Resources Research, 2015, 51: 7785-7789. DOI:10.1002/2015WR017408 |
| [7] |
Rigby RA, Stasinopoulos DM. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society, 2010, 54(3): 507-554. |
| [8] |
Cunderlik JM, Burn DH. Non-stationary pooled flood frequency analysis. Journal of Hydrology, 2003, 276(14): 210-223. |
| [9] |
Chen PC, Wang YH, You JY et al. Comparison of methods for non-stationary hydrologic frequency analysis:Case study using annual maximum daily precipitation in Taiwan. Journal of Hydrology, 2016, 545: 197-211. |
| [10] |
Ren LL, Shen HR, Yuan F et al. Hydrological drought characteristics in the Weihe catchment in a changing environment. Advances in Water Science, 2016, 27(4): 492-500. [任立良, 沈鸿仁, 袁飞等. 变化环境下渭河流域水文干旱演变特征剖析. 水科学进展, 2016, 27(4): 492-500.] |
| [11] |
Lu F, Xiao WH, Yan DH et al. Progresses on statistical modeling of non-stationary extreme sequences and its application in climate and hydrological change. Journal of Hydraulic Engineering, 2017, 48(4): 379-389. [鲁帆, 肖伟华, 严登华等. 非平稳时间序列极值统计模型及其在气候-水文变化研究中的应用综述. 水利学报, 2017, 48(4): 379-389.] |
| [12] |
Sang YF, Xie P, GU HT et al. Discussion on several major issues in the studies of hydrological nonstationarity. Chinese Science Bulletin, 2017(4): 254-261. [桑燕芳, 谢平, 顾海挺等. 水文过程非平稳性研究若干问题探讨. 科学通报, 2017(4): 254-261.] |
| [13] |
Liang ZM, Hu YM, Wang J et al. Estimation of design flood using equivalent reliability method under changing environment. Advances in Water Science, 2017, 28(3): 398-405. [梁忠民, 胡义明, 王军等. 基于等可靠度法的变化环境下工程水文设计值估计方法. 水科学进展, 2017, 28(3): 398-405.] |
| [14] |
Du H, Xia J, Zeng SD et al. Temporal and spatial variations and statistical models of extreme runoff in Huaihe River Basin. Acta Geographica Sinica, 2012, 67(3): 398-409. [杜鸿, 夏军, 曾思栋等. 淮河流域极端径流的时空变化规律及统计模拟. 地理学报, 2012, 67(3): 398-409. DOI:10.11821/xb201203011] |
| [15] |
Wei FY, Zhang T. Study on oscillation characteristics of summer precipitation in Huaihe River Basin and its relationship with climate background. Science China Earth Sciences, 2009, 10: 1360-1374. [魏凤英, 张婷. 淮河流域夏季降水的振荡特征及其与气候背景的联系. 中国科学:地球科学, 2009, 10: 1360-1374.] |
| [16] |
Liu SM, Wang H, Yan DH et al. Spatial-temporal evolution of isolated rainstorm events in Huai River basin under the background of climate change. Glacier Permafrost, 2016, 38(5): 1264-1272. [刘思敏, 王浩, 严登华等. 气候变化背景下淮河流域场次暴雨事件时空演变分析. 冰川冻土, 2016, 38(5): 1264-1272.] |
| [17] |
Pettitt AN. Anon-parametric approach to the change-point problem. Journal of the Royal Statistical Society, 1979, 28(2): 126-135. |
| [18] |
Zhang HB, Yu YH, Nan ZN et al. TFPW-BS-Pettitt method for detection of multiple change-points in the mean of hydrological series. Journal of Hydroelectric Engineering, 2017, 36(7): 14-22. [张洪波, 余荧皓, 南政年等. 基于TFPW-BS-Pettitt法的水文序列多点均值跳跃变异识别. 水利发电学报, 2017, 36(7): 14-22.] |
| [19] |
Beaulieu C, Chen J, Sarmiento JL. Change-point analysis as a tool to detect abrupt climate variations. Philosophical Transactions, 2012, 370: 1228-1249. DOI:10.1098/rsta.2011.0383 |
| [20] |
Rigby RA, Stasinopoulos DM. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society, 2010, 54(3): 507-554. |
| [21] |
Vogel RM, Yaindl C, Walter M. Nonstationarity:Flood magnification and recurrence reduction factors in the United States. Jawra Journal of the American Water Resources Association, 2011, 47(3): 464-474. DOI:10.1111/j.1752-1688.2011.00541.x |
| [22] |
Anhui Local Chronicles Compilation Committee. Anhui volunteers:Natural environment. Beijing: Fangzhi Press, 1999. [安徽省地方志编委会. 安徽省志:自然环境志. 北京: 方志出版社, 1999.]
|
| [23] |
Ye JY, Huang Y, Zhang CL et al. Spatial-temporal variations of climate change of the Huai River Basin during recent 50 years. Journal of Eco-environment, 2016, 25(1): 84-91. [叶金印, 黄勇, 张春莉等. 近50年淮河流域气候变化时空特征分析. 生态环境学报, 2016, 25(1): 84-91.] |
| [24] |
Lu YY, Wu BW, Tian H et al. Spatial and temporal variability characteristic of precipitation in Huai River Basin during 1961-2005. Resources and Environment in the Yangtze Basin, 2011, 20(5): 567-573. [卢燕宇, 吴必文, 田红等. 基于Kriging插值的1961-2005年淮河流域降水时空演变特征分析. 长江流域资源与环境, 2011, 20(5): 567-573.] |
| [25] |
Huang R. Research on evolution and countermeasures of droughts-floods abrupt alternation events in Huai River basin[Dissertation]. Beijing: China Water Resources and Hydropower Research Institute, 2015. [黄茹. 淮河流域旱涝急转事件演变及应对研究[学位论文]. 北京: 中国水利水电科学研究院, 2015. http://cdmd.cnki.com.cn/Article/CDMD-82301-1015346307.htm ]
|
| [26] |
Gu XH, Zhang Q, Wang ZZ. Evaluation on stationarity assumption of annual maximum peak flows during 1951-2010 in the Pearl River Basin. Journal of Natural Resources, 2015, 30(5): 824-835. [顾西辉, 张强, 王宗志. 19512010年珠江流域洪水极值序列平稳性特征研究. 自然资源学报, 2015, 30(5): 824-835. DOI:10.11849/zrzyxb.2015.05.010] |
| [27] |
Jiang C, Xiong LH. Trend analysis for the annual discharge series of the Yangtze River at the Yichang Hydrological Station based on GAMLSS. Acta Geographica Sinica, 2012, 67(11): 1505-1514. [江聪, 熊立华. 基于GAMLSS模型的宜昌站年径流序列趋势分析. 地理学报, 2012, 67(11): 1505-1514. DOI:10.11821/xb201211007] |
| [28] |
Ministry of Water Resources of the People's Republic of China. Water and Hydropower Engineering Design Flood Calculation Specification SL44-2006. Beijing: China WaterPower Press, 2006. [中华人民共和国水利部. 水利水电工程设计洪水计算规范SL44-2006. 北京: 中国水利水电出版社, 2006.]
|
| [29] |
Xiang SK. Land resources overview and analyses of structure and condition of land use in Anhui Province. Guangdong Agricultural Sciences, 2010, 37(8): 349-353. [项思可. 安徽土地资源概况及土地利用结构与状况分析. 广东农业科学, 2010, 37(8): 349-353.] |
 2018, Vol. 30
2018, Vol. 30 


