(2: 苏州市气象局, 苏州 215131)
(2: Suzhou Meteorological Bureau, Suzhou 215131, P. R. China)
水体浊度是表征水中介质对光衰减能力的物理量,是悬浮物浓度及其特征(尺度分布、折射指数)、水色等的函数[1].引起悬浮物浓度变化的再悬浮、沉降及输移等物理过程既是影响水体中营养盐时空变换的关键,也是改变水下光场的重要组成部分[2].与悬浮物浓度相比,水体浊度因涵盖溶解态的物质而能更好地指示生态系统变化,同时更为客观地表征其对水生生态系统的影响作用[3-4].因此,探究水体浊度的变化规律及其影响机制有着重要意义.
水体中的悬浮物的总量是决定水体浊度的最主要因子[5],主要由沉积物的再悬浮、沉降过程以及沉积物特征(组成、密度等)等控制[6].在河流中,河底坡度是造成水体流动、产生切应力的关键,进而造成底泥再悬浮.与河流相比,风场是控制太湖动力的关键[7],也影响其底泥再悬浮、沉降的过程[8].此外,风生流是影响水体中悬浮物及溶解有机质时空分布及维持自然水体中背景浊度的主要动力[9-10].可见, 风场是影响大型浅水湖泊中水体浊度的关键因素.
尽管水体浊度对湖泊水体生态环境有着重要影响,但由于风场对水体浊度变化的影响机制复杂、且不同湖泊的特征差异导致对风场的响应效果不同,因此,风场影响水体浊度的相关机制尚不清楚.近期有学者基于动力模式分别对在美国的Lake Okeechobee[11]、Salton Sea[12]以及中国太湖[8]等进行了水体浊度或沉积物浓度模拟,但在模式应用过程中需要大量的参数,同时还需要诸多观测结果以校正模拟结果,使得模式难以移植和推广. Wu等[9]基于对湖泊动力参数(有效波高、流速等)和水体浊度(或悬浮物浓度)的观测,构建了水体浊度模型,确定了沉积物再悬浮的临界风速及临界切应力[5],但由于观测时段较短,未能探讨风向及持续时间对水体浊度的影响及湖流水平输移的效应.此外,对于内陆湖泊而言,由于风向及边界、地形等的作用,使得由风场产生的湖流及波浪空间分异明显,Howick等[13]利用风值(耦合了风场的时间累积及深度)提高了水体浊度与风值的相关性,且这种相关性随深度圆环面积增大而提高,但这种以深度覆盖的圆环面积难以描述近岸的浊度.正由于风向、时间累积效应对水体浊度的影响难以定量描述,限制水体浊度模拟的精度[9],甚至造成风速与浊度的负相关性[6].总之,由于风速和风向的高频变化、不同水生生态系统的地形特征及沉积物组成差异等因素造成水体浊度变化机制难以厘清;另一方面由于波浪及湖流等参数难以长时间、多点观测,使得模拟水体浊度的模型难以得到推广应用.
太湖是一大型浅水富营养化湖泊,平均水深为1.9 m,风浪作用显著,水华频发[8].本研究基于临近2个站点的长时间序列的浊度观测及附近气象站的风场系列数据,探讨风速、风向及风场累计时间对水体浊度的影响机制,进而探究水体浊度的水平输移特征,为太湖水体浊度预测及太湖水生生态系统恢复奠定基础.
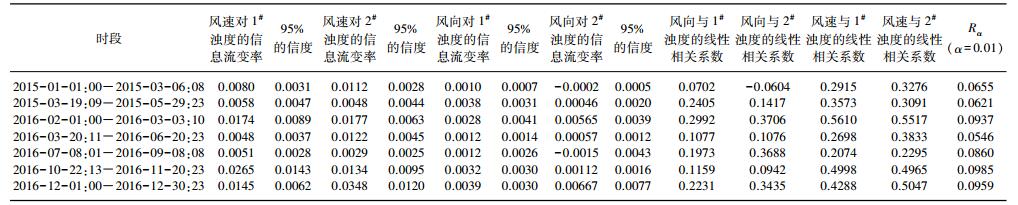
1 材料与方法 1.1 数据获取两个浊度观测站点位于金墅(1#点; 31.411°N, 120.33°E)和上山村(2#点; 31.23°N, 120.26°E)(图 1),分别位于贡湖湾湖心和湾口附近.观测仪器为多参数水质检测仪YSI(美国产的6600V2多参数水质检测仪).有效观测时段为:2015-01-01 0:00-2015-03-06 08:00、2015-03-19 09:00-2015-05-29 23:00、2016-02-01 00:00-2016-03-03 10:00、2016-03-20 11:00-2016-06-20 23:00、2016-07-08 01:00-2016-09-08 08:00、2016-10-22 13:00-2016-11-20 23:00、2016-12-01 00:00-2016-12-30 23:00.观测深度位于水面以下35 cm左右.风场(风速、风向)数据采用苏州市东山气象站(31.11°N, 120.43°E)的观测数据.浊度和风场的观测频率均为逐小时.
|
图 1 太湖浊度观测点示意 Fig.1 Sampling locations in Lake Taihu |
基于两点之间的浊度时间序列的信息流变率,确定二者之间的因果关系, 即平流输送.信息流时间变率的计算公式为[14]:
| $ {T_{2 \to 1}} = \frac{{{C_{11}}{C_{12}}{C_{2, d1}}- C_{12}^2{C_{1, d1}}}}{{C_{11}^3{C_{22}}- {C_{11}}C_{12}^2}} $ | (1) |
| $ {C_{i, j}} = \overline {({X_i}- \overline {{X_i}} )({X_j}- \overline {{X_j}} )} $ | (2) |
| $ {C_{i, dj}} = \overline {({X_i}- \overline {{X_i}} )({{\dot X}_j}- \overline {{{\dot X}_j}} )} $ | (3) |
| $ \dot X = \frac{1}{N}\sum \frac{{{X_{i, n + 1}}- {X_{i, n}}}}{{\Delta t}} $ | (4) |
式中,T2→1表示从上山村到金墅的浊度信息流变率,X1和X2分别为金墅和上山村两站的水体浊度时间序列,C是样本协方差,X是时间序列X的平均值,N为时间序列的样本数,Δt是时间序列中的时间间隔.
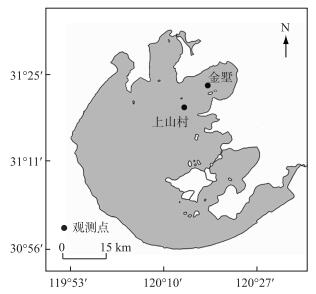
2 结果 2.1 太湖风场特征分析太湖地处亚热带季风区,季节特征明显. 2015-03-19 09:00-2015-05-29 23:00和2016-03-20 11:00-2016-06-20 23:00基本属于冬夏过渡期,风向分布相对离散,东南风所占比例略大,风速相对较小,其平均风速为3 m/s左右,介于3~5 m/s的风速占比最大,1~3 m/s的占比次之,5~8 m/s的占比最小;西北风比例较小,但平均风速相对较大. 2016-07-08 01:00-2016-09-08 08:00主要处于夏季,主导风向为东南风,平均风速为3.2 m/s,多数风速介于3~5 m/s;尽管西偏北风的比例较小,但其风速较大,其中5~8 m/s占比较大,平均风速为4.2 m/s. 2016-10-22 13:00-2016-11-20 23:00属于秋季,风向相对分散,以大风过程以偏北风为主,平均风速为2.3 m/s, 且风速介于3~5 m/s的比例也较小. 2015-01-01 00:00-2015-03-06 08:00、2015-12-15 14:00-2016-03-03 10:00、2016-12-01 00:00-2016-12-30 23:00基本处于冬季,主导风向为西北风,平均风速在所有时段中最大,说明大风过程以偏北风为主(图 2).
|
图 2 太湖风场玫瑰图 Fig.2 Wind field rose figure in Lake Taihu |
总之,春、夏两季主导风向以东南风为主,但风速相对较弱;秋、冬季以西北风为主,平均风速最大;另一方面,由于太湖处于内陆,且风场观测高度为10 m,因而造成风场受边界层地形等的作用显著,加之逐时的风场是整点前10分钟的观测结果(气象局观测规范),造成风场(尤其是风向)呈现高频变化,更多地体现风场的变化特征,而掩盖其部分规律性,从而使得风向较为分散,规律性相对较弱,季节性的变化规律性也相对较弱.
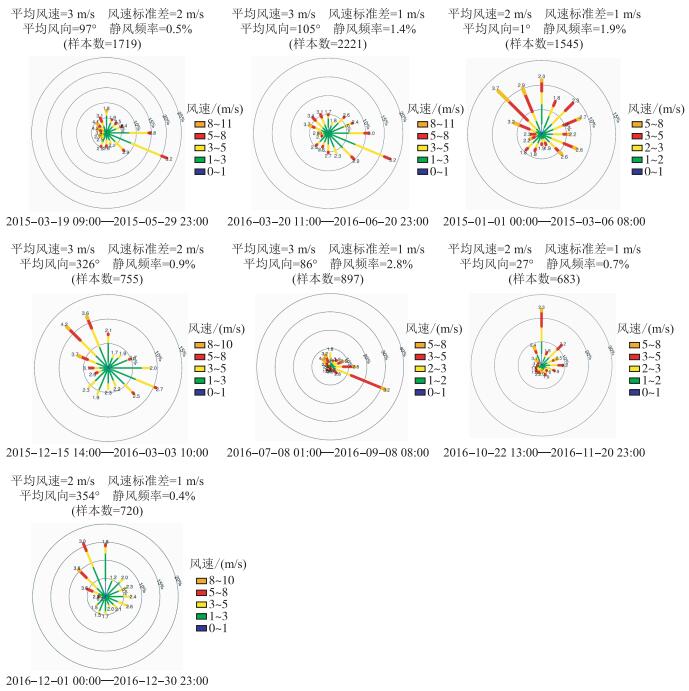
2.2 贡湖湾的水体浊度特征2016-03-20 11:00-2016-06-20 23:00,季风由冬向夏转换的过渡时段,该时段天气多不稳定,造成无论是风场还是浊度(1#点、2#点)的变率明显(图 3);2016-10-22 13:00-2016-11-20 23:00,处于夏季风向冬季风过渡时段,风场变率与春季类似,但程度较弱.冬季(2015-01-01 00:00-2015-03-06 8:00、2015-12-15 14:00-2016-03-03 10:00、2016-12-01 00:00-2016-12-30 23:00)和夏季(2016-07-08 01:00-2016-09-08 08:00)天气相对较稳定,风场和浊度的变率也相对较弱;冬季浊度的变化及浓度均较夏季明显.尽管水体浊度呈现一定的季节差异,但其主要表现在水体浊度的变化频率方面.
|
图 3 浊度及风场时序特征 Fig.3 Temporal characteristics of turbidity and wind field in Lake Taihu |
从金墅(1#点)和上山村(2#点)浊度时序变化特征来看, 2个站点的浊度在不同季节的变化频率也基本相同.二者之间的变化趋势基本类似,如图 4的a、f、g和h等的区域,但二者在变化程度上存在显著差异,如h和g区域.另外有些时段2个站点之间的变化位相同样也存在显著差异,如b、c区域.
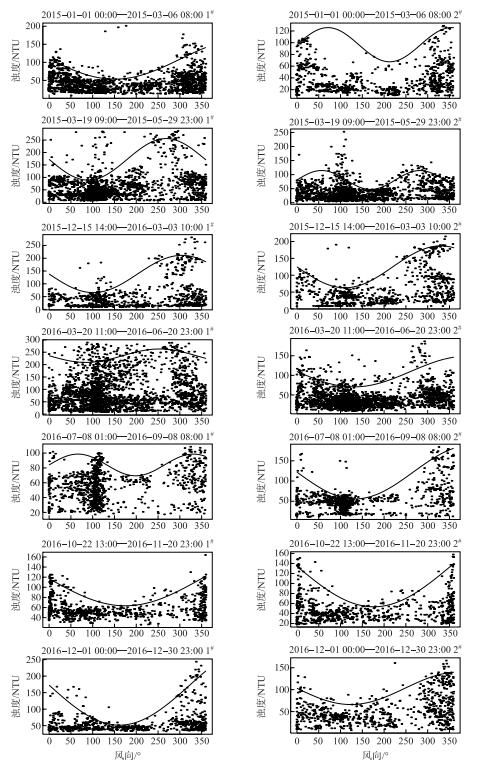
|
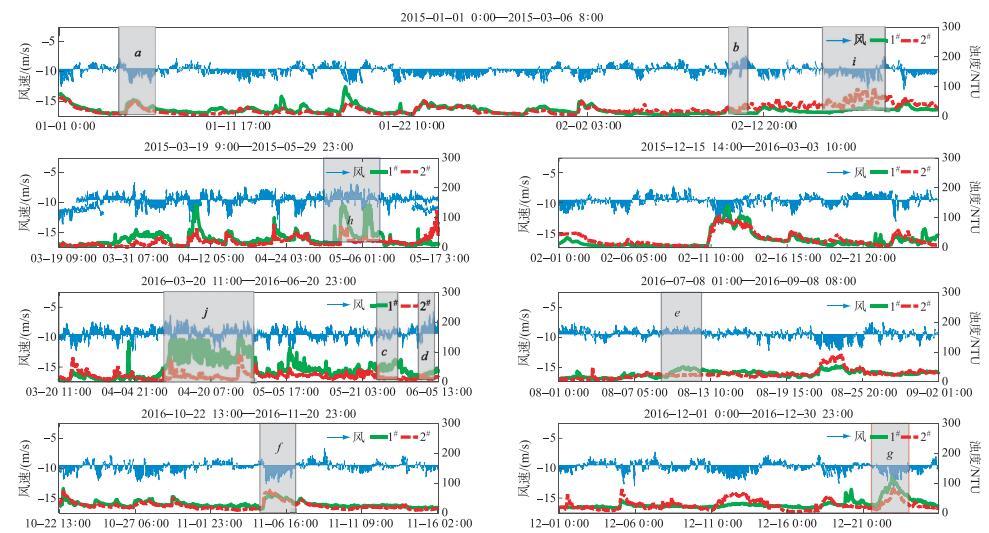
图 4 水体浊度随风向的变化 Fig.4 Water turbidity variation with wind direction |
尽管影响水体浊度的直接因素是湖流和波浪,然而对于太湖这类换水周期较长的湖泊而言,其动力主要来源于风场的驱动,因而在几何距离较近的2个站点,其风场基本一致, 是二者浊度变化趋势及变化频率类似的基础.然而风场对湖流和波浪驱动作用还受到周边地形等的影响,从而可能造成风场对水体浊度的影响存在空间差异,所以风场要素对空间差异的定量影响及机制有待进一步探讨.
2.3 风向对水体浊度的影响鉴于风向玫瑰图主要表征的是风场统计特征,难以刻画风场对水体浊度的影响.因此采用风场和浊度的时序特征描述水体浊度对风场的响应.
从图 3可以看出:2个站点的绝大多数浊度峰值出现在偏北风向情况(如a、f、g等区域),其中f区为东北风、g区为西北风,西北风对应的浊度大于东北风情况,两个区域的风速大小范围相近;少数的弱峰值区对应偏南风向(如b、d、e区域);但2个站点浊度峰值对风场响应的差异较大:如b区域,风场偏南、风速相对较大、持续时间相对较短;2#点浊度呈现弱峰、1#点的浊度基本维持不变,d区与b区基本相反;e块矩形区域(风向偏南、风速相对较弱、持续时间相对较长),1#点浊度呈弱峰,2#点却基本维持不变;可见,偏北风对1#、2#点的浊度影响较大,同时风速大小、方向和持续时间均为影响其水体浊度变化差异的关键因素,但对水体浊度的影响程度却也存在显著的差异.
浊度时间序列线性相关性结果表明, 2个站点之间浊度总体变化趋势一致,但变化过程中存在一定细微差别(图 3).如C区域,1#点的浊度上升而2#点却呈下降趋势;图 3中i区域,2015年2月20日左右,尽管2个站点的浊度变化趋势类似,但2#点的浊度远大于1#点.在相应时段,风向偏南,风速从逐渐增大而随后逐渐减小.浊度变化趋势与风速变化趋势类似,但二者的区别在于偏南风向下2#点吹程效应远大于1#点,由此可能造成上述二者之间的浊度差异;j区域,2016年4月20日前后,1#点的浊度较长时间维持在150 NTU左右且远高于2#点.此时段中风速特征并不突出,但风向变化频繁,因而弱化了风场对处于开阔区域(如1#点相对较大的吹程)的作用、强化了湖流垂直切变引起的再悬浮效应,并进而可能造成1#点的浊度较2#点高而持久.鉴于两站点几何距离近,故其气象场基本一致,由此推断,地形边界及风向转变频率(或风场持续时间)可能是造成两站点差异的关键.
基于2个站点浊度时间序列的信息流的时间变率进一步探讨2个站点浊度之间是否存在输移关系(表 1).春、夏、秋三季中,贡湖湾口(2#点)的水体浊度对湾中心(1#点)的浊度信息流的时间变率均为正且通过95 %的信度检验,这说明贡湖湾外的水体浊度对湾区内的浊度有平流输移的作用,即湾外的浊度向湾内水平输移;在冬季的三个时段中,均存在湾内浊度水平向外输移.但在2016-12-01 00:00-2016-12-30 23:00时段,湾内-湾外互为因果,即水体浊度在湾内与湾外互为水平输移补充.鉴于风速不能表征方向,不可能解释水体浊度的平流作用,由此推断,风向在水体浊度的平流输送方面起到了关键作用.诚然,水体浊度的输移关系仅停留在推断层面,有待于直接观测结果予以验证.
| 表 1 金墅(1#点)和上山村(2#点)水体浊度之间的因果(平流输送)关系 Tab.1 The causal relationship (advection) between turbidity in 1# and 2# sites |
总之,风速对水体浊度有重要影响作用,影响太湖水体浊度的关键因子也涵盖风向及相应风场的持续时间.
图 4中位于上包络线附近的水体浊度与风向的相关性较高,而其下部的水体浊度与风向的相关性较弱,推断可能受到其他要素影响相对较大.依据水体浊度随风向的变化,水体浊度随风向的上包络线基本呈现单谷型、双峰型、峰谷型及谷峰型特征.基于外包络线的形状,利用高分位非线性拟合回归法,采用形如X=a·sin(bα)+c(X为水体浊度时间序列, α为风向(度))的函数描述水体浊度对风向响应关系. 7个时段中2个站点的浊度拟合的分位数均为0.95(P < 0.0001),回归参数见表 2.可见,水体浊度对风向的响应呈现较明显的方向特征,该函数能较好地定量表征其响应特征.
| 表 2 水体浊度随风向变化的分位(0.95)回归参数 Tab.2 Quantile regression parameters of turbidity variation with wind direction |
位于贡湖湾内的金墅站,秋、冬季,北风和西北风对该站点浊度的影响最为明显;春季,西风对其浊度的影响较显著;夏季表现为东北风和西北风对其浊度的影响显著.位于贡湖湾口的上山村站,北风均对水体浊度产生显著的影响,2015年冬季水体浊度对西北风及东风较敏感.仅风向而言, 北风对水体浊度影响显著,西北风影响尤甚;同时,春季东、西向风对水体浊度的影响也较为突出.
拟合的三角函数的振幅(a)可以表达浊度对风向依赖程度的差异,其绝对值越大,风向的影响效应越明显(如2016年12月1#点).冬季,贡湖湾内(1#点)的风向对水体浊度的影响较2#点明显;夏、秋两季,贡湖湾口区域(2#)的水体浊度对风向的响应较湾区内明显(1#点);春季却无明显规律.
尽管风向对水体浊度的影响效应呈季节性变化,但水体浊度对风向有着较强依赖性,尤其是偏北风和东、西向风对水体浊度影响显著;另一方面,不同时间、空间的水体浊度对风向的响应程度具有较明显的差异.
2.4 风向、风速及其时间累计效应分析大型浅水湖泊中水动力过程的能量主要来源于风场,因而风速大小、风向及其持续时间决定了水体获取能量的大小.风向效应呈现随角度变化的趋势,持续时间是决定风能向水体传输能量的又一关键要素.基于风向影响下的风速及其持续时间,探讨风速、风向修正下的风速及其不同持续时间与对应时段的水体浊度的相关性,并以此为依据深入探讨风向及持续时间的效应.
鉴于风向对水体浊度的影响,构建风向修正风速对水体浊度影响的函数WD=WS{[a·sin(bα)+c]/[a+c]},并在此基础上进一步耦合了时间累积效应的风值(WDI),可表达为
为验证WDI的效应,将各时间基准点的WDI与水体浊度的线性相关系数分别与各时间基准点的风速进行比较,以进一步探讨风向、时间累积对水体浊度的影响效应.
如图 5所示,WD、WDI及WS与水体浊度的相关系数均通过0.99的检验. 2个站点的7个时段中, 风速与水体浊度之间均存在显著的相关性.另由于样本数较大,从首次测定时间开始,依次减少1~24个样本,对相关性影响较小,因而二者之间的相关性基本维持不变.冬秋两季相关性大于春夏两季,且上山村(2#)的相关性比贡湖湾内金墅(1#)更为显著.
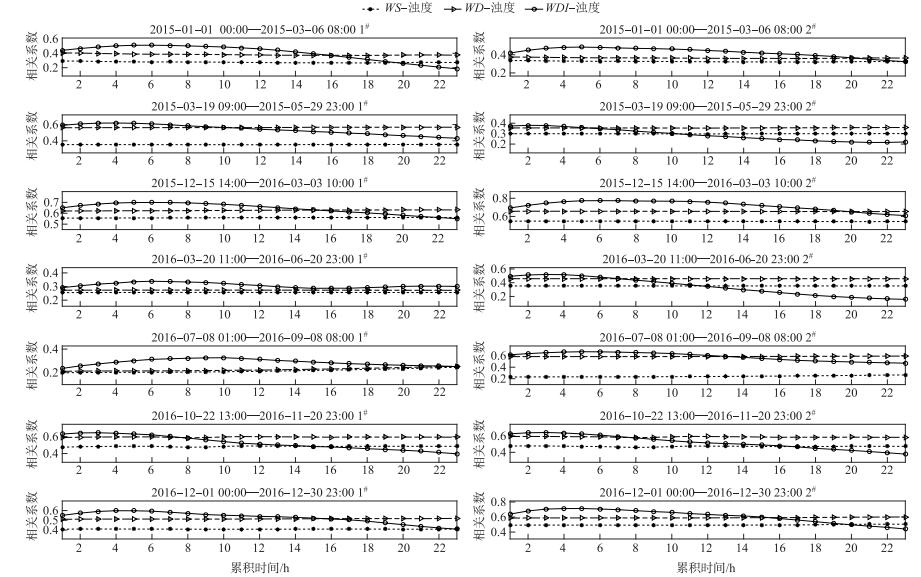
|
图 5 1#和2#点风向、风速及其持续时间与水体浊度的线性相关系数 Fig.5 Linear correlation coefficients of wind direction, wind direction, wind speed and its duration with turbidity in 1# and 2# sites |
从风向的作用来看,依据风向效应对风向角度的依赖程度,建立风向对风速效应的修正函数,并计算耦合风向效应的风值(WD).类似于风速与浊度的相关性,在从首次测定时间开始依次减少1~24 h,WD与水体浊度的相关性也基本维持为直线.耦合风向效应的WD与水体浊度的相关性呈现两种情况:其一:湾内2016年春、夏两季的WD值与浊度的相关性略有提高,即此两时段该区域的风向影响效应较弱;其二,其他时段,风向效应的影响均较显著.总体而言,耦合风向效应的风值能更好地表征风场对水体浊度的影响.
耦合风向后的累积风速(累积时间从1~23 h)与水体浊度的相关性随累积时间增加基本呈现先升后降的变化趋势,上升期的相关性均较WD显著.就时间累计效应的差异而言,湾内冬季时间累积效应最为显著;上山村,2015年春季及2016年秋季时间累积效应较弱,其他时段较显著.累积效应随累积时段变化呈现显著的时空差异,风场对水体浊度的最有效累积时段为2~9 h;相同时段,湾口处和湾内的最有效的累积时段差异较为明显.这也证实水体浊度明显受前期风场的影响,且前期时间累积效应的有效时段小于10 h.
总之,风速是水体浊度变化的主要驱动力,风向通过对风速效应的修正或调整,影响风速对水体浊度的效应,同时,耦合前期风场效应(时间累积)可以显著提高基于风场对水体浊度的预测,有效的时间累积时段为2~9 h.
3 讨论太湖水体换水周期长,出、入流较小,由水压差引起的湖流作用基本可忽略,而风场是驱动太湖动力过程(即湖流和波浪)的主要来源[15].可见,影响水体浊度变化的重要过程之一——底泥再悬浮的动力主要来源于风场.摩擦作用使得风能向水体传输,从而产生风生流和波浪等.能量转化的过程受风速大小、摩擦过程经由的距离(即吹程)以及摩擦过程持续的时间等因素控制[5-6, 9].可见,针对换水周期长的浅水湖泊而言,风速和风向及其持续时间是通过影响湖流、波浪的切应力继而影响底泥再悬浮及水平输移,是水体浊度变化的关键动力,即说明风速、风向及其持续时间是影响水体浊度的三个关键因素.另一方面, 鉴于水体流速、波浪及其相互作用的作用机制异常复杂(郎缪尔环流、波浪破碎等的能量传递),长时间的野外观测费时费力,加之这类湖泊湖流流速小及波浪多为中高频波,使得针对流速及波浪数值模拟的误差难以得到有效控制,因而通过气象局对风场的业务观测资料探讨水体浊度的变化更具有实际应用和推广意义.
3.1 风速对水体浊度的关键作用机制风速是影响风能向水体传输关键因素,它不仅影响底泥再悬浮和沉积物沉降,同时也是影响湖流及其水体悬浮物输送的关键要素.贡湖湾内的金墅(1#点)和湾口的上山村(2#点)处水体浊度在不同季节的位相与频率变化基本相似,及其与风场的相应特征也基本类同;另一方面,2个站点的所有时段的水体浊度与风速均呈现出的显著的正相关,证实了二者间的密切关系(表 3);另一方面,从风速对水体浊度信息流的时间变率及其置信度来看,风速是造成2个站点所有时段水体浊度变化的关键因素.
| 表 3 风速、风向对水体浊度信息流的时间变率及与浊度的相关系数 Tab.3 Time variability of information flow from wind speed or wind direction to turbidity, linear correlation coefficients between wind speed(or wind direction) and turbidity |
鉴于太湖在冬季及深秋,蓝藻水华基本消亡[16],也就是水体中有机质含量相对较少,从而导致风能引起再悬浮的底泥占水体浊度的权重增大,进而使得在冬、秋季的风速引起水体浊度变化的效应更显著,即风速对水体浊度的正向反馈作用更为突出.
风速引起水体浊度变化的反馈作用往往与研究的时间尺度和风速特征密切相关:在24~48 h的时间内,因风速变化引起水体中表层悬浮物累积、扩散等原因可能导致逐时风速与水体浊度存在负相关性,而在包含上述时段的20天时间跨度内,逐日平均风速对水体浊度存在明显的正反馈作用[6].而在本研究中的所有时段内,逐时风速对水体浊度变化的正反馈作用是稳健的,即证实了风速是引起太湖水体中浊度变化的关键原因.
3.2 风向与风速耦合作用下水体浊度变化机制影响风能引发的水体波、流的另一个重要参数是吹程,其主要受到风向及湖面边界的影响.通常湖泊边界较为稳定,而风向却是一快变物理量.风向决定和影响风生流等的方向,进而影响水体中浊度的水平输移.
通过2个站点的风向与对应水体浊度的相关性分析(表 3)发现:风向与水体浊度的相关性整体低于风速与水体浊度的相关性,风向与水体浊度的相关关系也远弱于风速:贡湖湾口内的1#点风向对水体浊度变化存在相关关系的仅有2016年的2016-02-01 00:00-2016-03-03 10:00、2016-03-20 11:00-2016-06-20 23:00、2016-07-08 01:00-2016-09-08 08:00,其他时段无明显相关关系存在;而在湾口外的2#点仅在2016-02-01 00-2016-03-03 10:00时段内,风向与水体浊度存在相关关系,其他时段均不存在相关关系.因1#点位于湾区内,湖泊边界条件对吹程的影响较位于湾区外的2#点大,造成两空间点上风向对水体浊度的相关关系存在差异,即湾区内风向的作用较湾区外明显;另一方面,由于水体浊度不仅受到底泥再悬浮的影响,同时还受到风向引起的风生流对水体中悬浮物质输移的差异影响(尤其是较轻的有机悬浮质),加之风向多变,以及风向与风速在数值上的配合难以稳定一致,使得风向对水体浊度的影响较风速弱、且复杂,难以定量描述.总之,风向通过影响吹程及风生流等作用而间接影响水体浊度,但其影响弱于风速的直接作用.
鉴于风速对水体浊度影响强于风向,使得难以从中分离风向的定量影响,正因为如此,针对短时间段的大风过程,水平输移对水体浊度的影响常被忽略[5, 9].基于长时段的气象场及水体浊度的观测,证实了1#和2#站点之间的水体浊度可能存在水平输移(表 1),但其规律性相对较弱.由于“引江济太”工程引起贡湖湾区湖流的影响,使得湖流与纯由风场驱动的流场相偏离,影响两点之间的平流输送关系,进而使得两观测点之间的浊度因果关系更为复杂.可见,风向不仅通过风速影响水体浊度,而且也可能是影响水体浊度输移的重要因素,其中平流输送有待于以后进一步考证.
由于本文所观测数据覆盖时段较长,包含了不同风速、风向及水体浊度,为利用高分位回归法描述风向对水体浊度的影响提供了保障.高分位确保了从众多样本中挑选出风向对水体浊度影响显著的样本,其拟合函数X=a·sin(bα)+c刻画了水体浊度随风向角度变化规律.鉴于上述拟合函数仅针对水体浊度对风向敏感的样本,为此,结合风速与水体浊度呈显著的线性相关特点,构建了WD=WS{[a·sin(bα)+c]/[a+ c]},由此既表达了风速对水体浊度影响的关键作用,也表达了风向对风速效应的修正作用.构建函数计算的风值与水体浊度的线性相关性的提高证实了耦合风向作用的有效性,耦合风向的风速与水体浊度的线性关系也得到显著提高(图 5),可见,就风场对水体浊度影响而言,风向与风速的耦合作用是通过风向对风速效应修正作用来表达的.
3.3 风场的时间累积效应对水体浊度的影响机制除风速、风向外,影响风场对水体能量转换及对水体悬浮物平流输送的另一个重要因素是风场作用时间. Cózar等[6]利用日平均的风速与水体浊度代替逐时数据以规避风速与水体浊度负相关关系和风场的累积时间效应;Howick等[13]基于24 h的时间累积探讨了风场累积对水体浊度的影响.然而不同湖泊有着不同的地理边界、水深、底泥组成的空间分异等不同特征,以及不同时段水体中有机质含量的差异,因而风场对其时间累计效应也不可能雷同.太湖贡湖湾中心及湾外的两个空间点的时间累计效应从2~10 h左右.耦合风向和时间累积的风场与水体浊度的相关性得到进一步提高,为研究水体浊度变化机制及基于风场对水体浊度预测奠定了基础.
诚然,由于影响水体动力过程的风场采用的10 m高的观测结果,该高度属于贴地层,其风向受地形等影响强烈,因而弱化了风场的季节特征;另一方面,由于水体中影响水体浊度的诸因子在时空上也呈现多变状态,因而在一定程度上弱化了风场对水体浊度的影响规律,但也从侧面证实了水体浊度变化机制的复杂性.本文仅从风场的角度(风速、风向及累积时间)探究了其影响规律,为进一步厘清水体浊度变化机制奠定了基础.同时也为通过相对易得的风场数据对湖泊浊度预测提供了新途径,具有较强的移植和推广性.
4 结论1) 在以风场驱动为主要动力来源的大型浅水湖泊中,春、秋两季的风场、水体浊度的变化频率高于夏、冬两季,且春季变率更为突出;冬季风场和水体浊度的变率均较夏季明显; 风场通过沉积物再悬浮、水平输移等物理过程,驱动营养盐循环、水下光能流动等,进而影响水生生态系统的演变.
2) 风场是影响水体浊度变化关键因素,其包括风速、风向及其累积时间.其中风速是最为关键的决定性因子;且风速对水体浊度的驱动效应呈季节变化,对秋、冬季尤其是冬季的影响最为突出.
3) 风向影响水体浊度函数通过三角函数(X=a·sin(bα)+c)表征,风速、风向及累计时间的耦合形式为:
| [1] |
Mukundan R, Pierson DC, Schneiderman EM et al. Factors affecting storm event turbidity in a New York City water supply stream. Catena, 2013, 107: 80-88. DOI:10.1016/j.catena.2013.02.002 |
| [2] |
Horppila J, Kaitaranta J, Nurminen L. Application of littiral Baltic Sea resuspension model in a eutrophic lake—Factors behind differences in the model performance. International Journal of Sediment Research, 2015, 30: 100-106. DOI:10.1016/j.ijsrc.2015.03.005 |
| [3] |
Bessell-Browne P, Negri AP, Fisher R et al. Impacts of turbidity on corals: The relative importance of light limitation and suspended sediments. Marine Pollution Bulletin, 2017, 117: 161-170. DOI:10.1016/j.marpolbul.2017.01.050 |
| [4] |
Pérez GL, Lagomarsino L, Zagarese HE. Optical properties of highly turbid shallow lakes with contrasting turbidity origins: The ecological and water management implications. Journal of Environmental Management, 2017, 130: 207-220. |
| [5] |
Zheng SS, Wang PF, Wang C et al. Sediment resuspension under action of wind in Lake Taihu, China. International Journal of Sediment Research, 2015, 30: 48-62. DOI:10.1016/S1001-6279(15)60005-1 |
| [6] |
Cózar A, Gálvez JA, Hull V. Sediment resuspension by wind in a shallow lake of Esteros del Iberá (Argentina): a model based on turbidity. Ecological Modelling, 2005, 186: 63-76. DOI:10.1016/j.ecolmodel.2005.01.020 |
| [7] |
Anderson J, Reitzel K, De Barbanere H et al. Relationships between wind-driven and hydraulic flow in Lake St. Clair and the St. Clair River Delta. Journal of Great Lakes Research, 2011, 37(1): 147-158. DOI:10.1016/j.jglr.2010.11.007 |
| [8] |
Qin BQ, Hu WP, Gao G et al. Dynamic mechanism and conceptual model of inner load release of sediments suspension from Lake Taihu. Chinese Science Bulletin, 2003, 48(17): 1822-1831. [秦伯强, 胡维平, 高光等. 太湖沉积物悬浮的动力机制及内源释放的概念性模式. 科学通报, 2003, 48(17): 1822-1831. DOI:10.3321/j.issn:0023-074X.2003.17.002] |
| [9] |
Wu TF, Qin BQ, Zhu GW et al. Modeling of turbidity dynamics caused by wind-induced waves and current in the Lake Taihu. International Journal of Sediment Research, 2013, 28: 139-148. DOI:10.1016/S1001-6279(13)60026-8 |
| [10] |
Zhao QH, Qin BQ. Mechanism and characteristics of spatial distribution of colored dissolved organic matter in Lake Taihu between summer and winter. China Environmental Science, 2008, 28(4): 289-293. [赵巧华, 秦伯强. 太湖有色溶解有机质光谱吸收空间的分异特征. 中国环境科学, 2008, 28(4): 289-293. DOI:10.3321/j.issn:1000-6923.2008.04.001] |
| [11] |
Jin KR, Ji ZG. Calibration and verification of a spectral wind-wave mode for Lake Okeechobee. Ocean Engineering, 2001, 28(5): 571-584. DOI:10.1016/S0029-8018(00)00009-3 |
| [12] |
Chung EG, Bombardelli FA, Schladow G. Modeling linkages between sediment resuspension and quality in a shallow eutrophic wind-exposed lake. Ecological Modeling, 2009, 220: 1251-1265. DOI:10.1016/j.ecolmodel.2009.01.038 |
| [13] |
Howick GL, Wlihm J. Turbidity in Lake Carl Blackwell: Effects of water depth and wind. Proc Okla Acad Sci, 1985, 65: 51-57. |
| [14] |
Liang XS. Unraveling the cause-effect relation between time series. Physical Review, 2014, 90: 052150. |
| [15] |
Pang Y, Pu PM. Numerical simulation of three-dimensional wind-driven current in Lake Taihu. Geography Journal, 1996, 51(4): 322-328. [逄勇, 濮培民. 太湖风生流三维数值模拟试验. 地理学报, 1996, 51(4): 322-328. DOI:10.3321/j.issn:0375-5444.1996.04.005] |
| [16] |
Zhang M, Duan HT, Shi XL et al. Contributions of meteorology to the phenology of cyanobacterial blooms: Implications for future climate change. Water Research, 2012, 46: 442-452. DOI:10.1016/j.watres.2011.11.013 |
 2018, Vol. 30
2018, Vol. 30