(2: 河海大学水安全与水科学协同创新中心, 南京 210098)
(2: National Cooperative Innovation Center for Water Safety & Hydro-Science of Hohai Universtiy, Nanjing 210098, P. R. China)
洪水预报在防洪决策方面发挥着重要作用[1],利用水文模型进行洪水预报是一种常用的预报方法.水文模型输入存在不确定性,而降雨资料是水文模型输入的最重要资料之一,所以研究降雨资料的不确定性具有重要的理论和实践价值.使用模型研究降雨输入的不确定性,可为延长洪水预报的预见期和提高洪水预报的精度提供可靠方法.目前,利用数值降雨预报信息驱动水文模型,可以有效延长预见期,提高预报精度[2-4]. Verbunt等[5]利用高分辨率的气象集合预报系统驱动水文模型,对莱茵河流域进行研究,并探讨了气象集合预报的可利用性.高兵等[6]采用中尺度数值天气模式WRF和分布式水文模型对三峡流域进行了研究,结果表明水文气象耦合模型在洪水预报中具有应用潜力.李致家等[7]将雷达测雨数据应用于新安江模型,进行实时洪水预报,发现使用雷达测雨数据作为洪水预报输入具有广泛的应用前景.徐炜等[8]将全球系统发布的未来10 d数值降雨预报信息作为新安江模型和多元线性回归模型的降雨输入,发现预报结果高于不考虑降雨预报信息的径流预报.将数值预报信息作为水文模型的降雨输入进行洪水模拟研究时,需要对预报降雨进行不确定性和误差分析.降雨不确定性[9-10]主要体现在3个方面:暴雨中心位置偏差、降雨量数值偏差以及降雨时间偏差[11-12],研究其对洪水预报结果的影响,可以为预报数值降雨产品应用于水文模型提供理论依据和参考,具有比较重要的理论意义和实用价值.
我国河流众多,其中中小河流近9000条.近年来,受气候变化影响,由局地强降水造成的中小河流突发性洪水频繁发生,已成为造成人员伤亡的主要灾种.由于中小河流源短流急、站网偏稀,洪水具有暴雨强度大、历时短、难预报、难预防等特点,同时中小河流实测水文资料匮乏,因而难以满足现有水文模型参数率定的需要,导致中小河流洪水预报成为国内外研究难点.多年来我国在大江大河洪水预报研究中取得了比较丰富的成果,而中小河流洪水预报的研究与应用则刚刚起步.另外,本文采用的新安江模型主要应用在湿润流域,且得到了很好的模拟效果[13],而在半湿润流域的应用较少[14].因此,对中小流域和半湿润地区的研究具有重要的现实意义.
本文以陈河流域和大河坝流域为研究区域,结合新安江模型,研究降雨输入的不确定性[15-16].首先,分别将不考虑未来降雨资料和考虑未来降雨的资料作为输入,进行实时预报洪水模拟,分析不同预见期对预报精度的影响.然后分别将考虑未来降雨的降雨量误差和降雨时间误差作为输入,分析降雨量误差和降雨时间误差对模拟结果的影响.
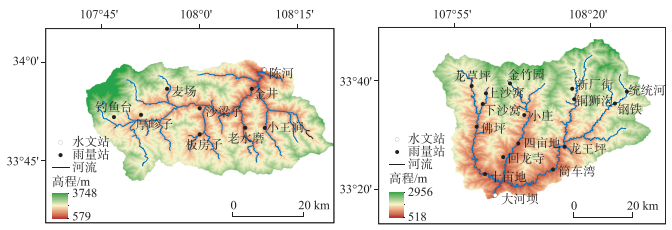
1 流域介绍、模型选择与参数率定陕西省陈河流域和大河坝流域均位于半湿润地区,属中小河流[17-18].陈河流域位于北温带,属于大陆性季风气候,流域面积1380 km2,河长126 km,多年平均降雨量800 mm,流域河流水量主要系雨水补给,该流域发生洪水的主要原因是局部暴雨[19-20].流域平均径流深度100~500 mm,径流系数0.2~0.5,为相对较高产流区.陈河水文站以上流域有8个雨量代表站,分别为厚畛子、沙梁子、老水磨、金井、陈河钓鱼台、麦场、板房子和小王涧.大河坝流域[21]位于秦岭南麓,流域面积2198 km2,多年平均降雨量约900 mm,属山溪性河流,主要流经秦岭深山区,流域呈扇形.流域地势北高南低,沟壑纵横.大河坝水文站以上流域有15个雨量代表站,分别为佛坪、钢铁、回龙寺、金竹园、龙草坪、龙王坪、十亩地、上沙窝、四亩地、铜狮沟、统统河、筒车湾、小庄、新厂街和大河坝.陈河流域和大河坝流水系图见图 1.
|
图 1 流域水系与站网分布:(a)陈河流域;(b)大河坝流域 Fig.1 The streams and gauges in Chenhe Basin (a) and Daheba Basin (b) |
新安江模型作为我国最重要的流域水文模型之一,已经在洪水预报方面发挥了非常大的作用.新安江模型蒸散发计算采用三层模型,产流计算采用蓄满产流模型,水源划分为地表径流、壤中流和地下径流,流域汇流采用线性水库,河道汇流采用马斯京根分段连续演算.新安江模型中一共涉及到17个参数,采用人工优选法和SCE-UA自动优选法结合对新安江模型参数进行率定[22].利用SCE-UA方法对蒸散发折算系数K、自由水容量SM和河网水流消退系数CS等敏感参数进行率定.利用人工优选法,根据流域特征和经验方法对蓄水容量分布曲线指数B、深层蒸散发扩散系数C、不透水面积比例IM、自由水容量分布曲线指数EX、地下水出流系数KG和地下水消退系数CG等非敏感参数进行率定.陈河流域和大河坝流域新安江模型次模参数率定结果见表 1.
| 表 1 新安江模型次模参数 Tab. 1 Hourly model parameters of Xin'anjiang Model |
本文研究的预见期根据洪水资料的不同,可分为历史洪水预见期和洪水预报的预见期.历史洪水预见期可根据历史洪水资料(实测的流域平均降雨和流量过程)分析确定[23-24],本文以降雨量明显增大的时刻至洪峰出现的时刻作为历史洪水预见期,同时也作为降雨误差分析的预报开始时间.而洪水预报的预见期是指洪水能提前预测的时间.选取陈河流域和大河坝流域4场典型洪水进行模拟,因研究区域为半湿润地区的中小河流山区流域,由于中小河流多产生暴雨,汇流时间短,对于洪峰准确预报更为重要.因此在本文中,选择洪峰相对误差和峰现时间误差为主要评价指标,洪量相对误差和确定性系数DY[23]作为辅助评价指标.预报选取的4场洪水的起止时间和模拟结果见表 2和图 2.
| 表 2 洪水起止时间和模拟结果 Tab. 2 The beginning and ending of the flood and simulation results of flood |

|
图 2 4场洪水实测和模拟结果 Fig.2 Measured and simulation results of four floods |
历史洪水预见期分析:(a)陈河流域洪号2003090319场次洪水:2003年9月3日19:00开始,2003年9月9日12:00结束,历时138 h,洪水预见期为9 h,预报开始时间选择9月6日3:00;(b)陈河流域洪号2011091520场次洪水:2011年9月15日20:00开始,2011年9月23日1:00结束,历时174 h,洪水预见期为10 h,预报开始时间选择9月18日9:00;(c)大河坝流域洪号2013052508场次洪水:2013年5月25日8:00开始,2013年5月28日2:00结束,历时67 h.该场次洪水的预见期为7 h,预报开始时间为5月25日8:00(d)大河坝流域洪号2013052803场次洪水:2013年5月28日3:00开始,2005年6月1日8:00结束,历时102 h,洪水预见期为10 h,预报开始时间选择5月29日10:00(表 2和图 2).
3 研究方法本文采用不考虑未来降雨、考虑未来降雨、考虑预报降雨的降雨量误差和降雨时间误差共4种方法,对实时预报及降雨输入不确定性进行研究,具体方法介绍如下:
1) 不考虑未来降雨逐时段预报:从选取的预报时刻开始,不考虑未来降雨资料,以现有的实测降雨资料作为模型输入,对洪水过程进行逐时段预报分析.该方法以现有的实测降雨资料模拟洪水过程,分析不同预报预见期下的预报精度以及新安江模型不考虑未来降雨时的最长预报预见期.
2) 考虑未来降雨逐时段预报:对于本文选取的研究区域,流域面积较小,天气预报降雨不能精确到每个雨量站,因此本文以实测雨量在研究流域的面积加权平均值作为实时预报中的未来预报降雨量,不考虑与未来实测雨量之间的误差.从选取的预报时刻开始,以现有的实测资料以及未来降雨量作为模型输入,对洪水过程进行逐时段预报分析,研究不同预报预见期下的预报精度以及新安江模型降雨输入的不确定性.
3) 考虑预报降雨的降雨量误差预报:预报降雨会出现预报雨量误差,该方法考虑预报降雨误差的不确定性,在实测降雨观测资料上人为设置一些误差,降雨资料按照同倍比缩小增大方法,分析降雨资料在±5 %、±10 %、±15 %、±20 %、±25 %、±30 %误差下的预报精度,分析不同降雨量误差对评价指标的影响和降雨量误差对模型预报的影响.
4) 考虑预报降雨的降雨时间误差预报:预报降雨会出现预报时间误差,该方法考虑预报降雨时间的不确定性,将降雨系统时间的整体推迟或提前,对于一场降雨过程,将实测的降雨资料分别整体提前和滞后1、2、3、4、5 h,驱动新安江模型,分析不同降雨时间误差的预报精度.
4 计算结果分析与比较本文对不考虑未来预报降雨进行模拟预报分析,对考虑未来降雨、考虑预报降雨的降雨量误差和降雨时间误差进行实时预报分析.另外,文中提到的最长预报预见期是指不考虑未来预报降雨时使预报合格得到的最大预见期.实时预报的思路是:当前时刻,利用已观测到的前期流量、前期降雨量和未来24 h预报降雨量预测未来24 h每一时刻的流量;下一时刻,继续向后预报24 h流量,依次类推,实现实时洪水滚动预报.因此对于模拟预报的洪水,需要根据洪水预见期选择不同预见期的预报时间,预报模拟时段长均为1 h.
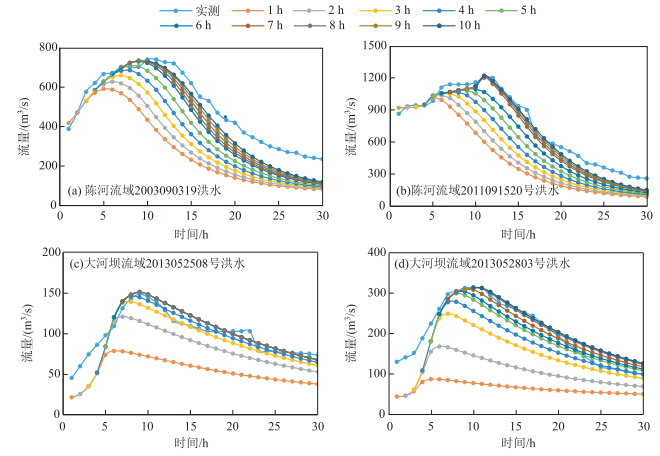
4.1 不考虑未来降雨的实时预报结果分析不考虑未来降雨逐时段预报分析,4场洪水分别以选取的预报时刻开始,以现有的实测资料作为模型输入进行逐时段预报,每隔1 h驱动一次模型,直至预见期为1 h,预报结果见图 3和表 3.
|
图 3 不考虑未来降雨的不同预报预见期预报结果 Fig.3 Forecasting results without consideration of weather forecast of rainfall in different periods |
| 表 3 不考虑未来降雨的不同预报预见期预报结果* Tab. 3 Forecasting results without consideration of weather forecast of rainfall in different periods |
从表 3可以看出,在不考虑未来预报降雨的情况下,4场洪水的最长预报预见期均在7~8 h之间,预报预见期较长时,模拟流量过程整体偏小,预报精度低,随着预报预见期的缩短预报精度逐渐增高.从图 3中可以看出,随着预报预见期增长,陈河流域两场洪水预报精度稳定下降,而大河坝流域两场洪水在预报预见期分别超过7与9 h后精度显著下降.分析降雨资料可以看出,陈河流域两场洪水降雨中心位于流域上游,而大河坝流域两场洪水降雨中心位于流域下游附近,洪水汇流时间短,因此预报预见期增长会引起预报精度显著降低.
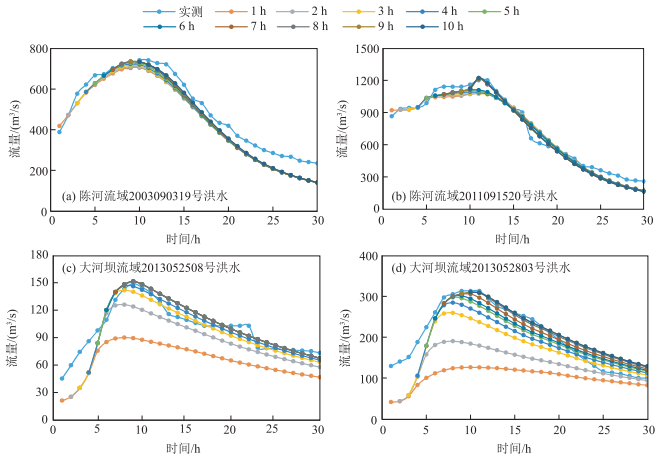
4.2 考虑未来降雨的实时预报结果分析考虑未来降雨逐时段预报分析,4场洪水分别以选取的预报时刻开始,以现有的实测资料以及未来降雨量作为模型输入进行逐时段预报,每隔1 h驱动一次模型,直至预见期为1 h,预报结果见图 4和表 4.
|
图 4 考虑未来预报降雨的不同预报预见期预报结果 Fig.4 Forecasting results with consideration of weather forecast of rainfall in different periods |
| 表 4 考虑未来预报降雨的不同预报预见期预报结果 Tab. 4 Forecasting results with consideration of weather forecast of rainfall in different periods |
由图 4和表 4可以看出,在陈河流域,不同预报预见期下的预报模拟过程基本重合,且预报精度较高;而在大河坝流域,即使在考虑未来预报降雨的情况下,当预报时刻距离洪峰出现时刻较长时,预报过程基本不合格,预报精度低,随着实测资料逐时段的输入,预报精度逐渐提高,这主要是由于在大河坝流域,暴雨主要集中在流域下游,以面平均雨量作为未来降雨输入时,降雨均化对洪水预报精度影响较大,当选择预报预见期较长的预报时段时未来降雨输入的时段更长,降雨均化带来的影响更大,所以预报精度较低.
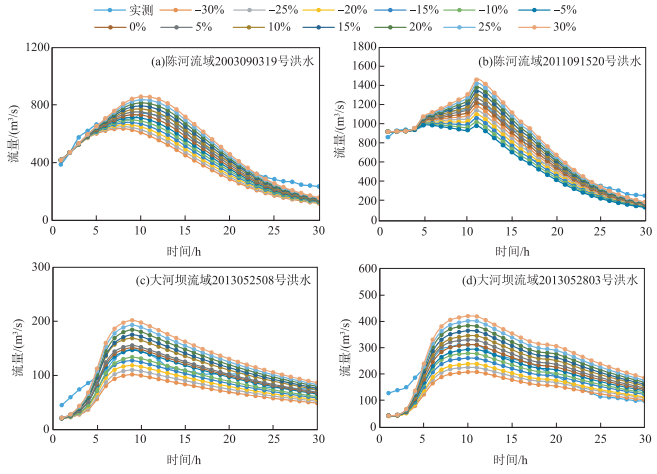
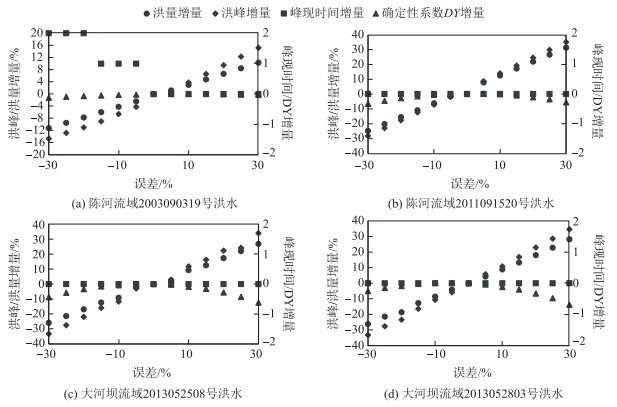
4.3 考虑降雨的降雨量误差预报结果分析考虑降雨量误差预报分析结果见图 5和附录Ⅰ.由图 5和附录Ⅰ中可知,降雨误差越大,预报精度越低,整体拟合情况越差,降雨量误差主要对洪量相对误差和洪峰相对误差影响较大,对峰现时间误差和确定性系数影响较小.陈河流域洪号2003090319场次洪水在±30 %的误差条件下,预报结果仍然合格,洪号2011091520场次洪水的正最大允许误差为25 %,但在-30 %的误差条件下预报仍然合格,大河坝流域的两场洪水降雨量最大允许误差为±15 %,超过则预报不合格.由此可见,陈河流域的降雨量允许误差大于大河坝流域,这是由于陈河流域暴雨中心位于流域上游,而大河坝流域的暴雨中心位于流域下游,对于暴雨中心在流域上游的,降雨量增大或者减少,经过流域的调蓄作用汇流到流域出口断面,会削弱降雨量误差带来的影响,因此陈河流域场次洪水的降雨量允许误差大.以降雨量误差为0时的模拟过程为参考标准,分析不同降雨量误差下各评价指标误差增量(图 6).
|
图 5 考虑预报降雨量误差预报结果 Fig.5 Forecasting results with consideration of weather forecast of rainfall error |
| 附录Ⅰ 考虑预报降雨量误差预报结果 Appendix Ⅰ Forecasting results with consideration of weather forecast of rainfall error |
|
图 6 评价指标随降雨误差变化增量 Fig.6 The increment of evaluation index with the variation of rainfall error |
由图 6可知,以不同的降雨量误差作为新安江模型的输入,降雨量误差的变化对洪量和洪峰的影响较大,对峰现时间误差和确定性系数影响较小;分析其原因,降雨量误差的设置是呈同倍比增大或缩小,降雨量的输入增大或减少,会直接影响洪峰和洪量的数值,但降雨模式和暴雨中心位置并未改变,因此对峰现时间误差影响较小.对图 6中洪峰相对误差增量、洪量相对误差增量和确定性系数进行趋势线拟合,可以看出相关系数都非常接近1,洪峰和洪量的拟合公式为线性一次函数,确定性系数的拟合公式为非线性二次函数(表 5).
| 表 5 洪峰和洪量增量随降雨误差拟合公式 Tab. 5 Formula of flood peak and flooding increment with rainfall error |
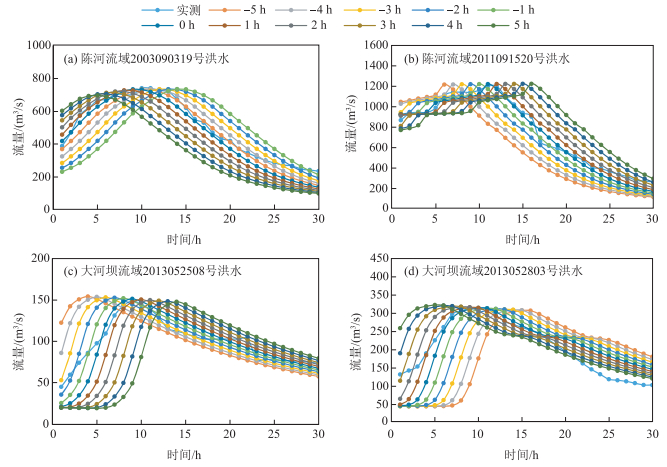
考虑预报降雨的降雨时间误差预报结果见图 7和表 6.由图 7和表 6可知,降雨时间误差越大,预报精度越低,整体拟合情况越差,降雨时间误差导致模拟过程线整体平移.以降雨时间误差为0时的模拟过程为参考标准,分析不同降雨时间误差下各评价指标误差增量(图 8).
|
图 7 考虑预报降雨时间误差预报结果 Fig.7 Forecasting results with consideration of weather forecast of rainfall error |
| 表 6 考虑预报降雨时间误差预报结果 Tab. 6 Forecasting results with consideration of weather forecast of rainfall error |
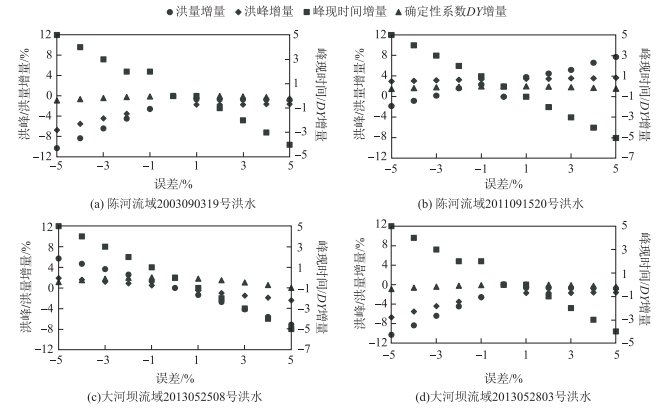
|
图 8 评价指标随降雨时间误差变化增量 Fig.8 The increment of evaluation index with the variation of rainfall time error |
洪量误差增量、洪峰误差增量,峰现时间误差增量和确定性系数增量基本上呈线性变化,本文降雨时间误差设置从-5~5 h呈等步长(1 h)增加,由图 8可知,以不同的降雨时间误差作为新安江模型的输入,降雨时间误差的变化对峰现时间误差影响最大,对洪量相对误差、洪峰相对误差峰现时间误差和确定性系数影响较小.降雨时间误差的设置是将降雨过程整体前移或推后,因此对峰现时间误差影响较大,对其他评价指标影响较小.
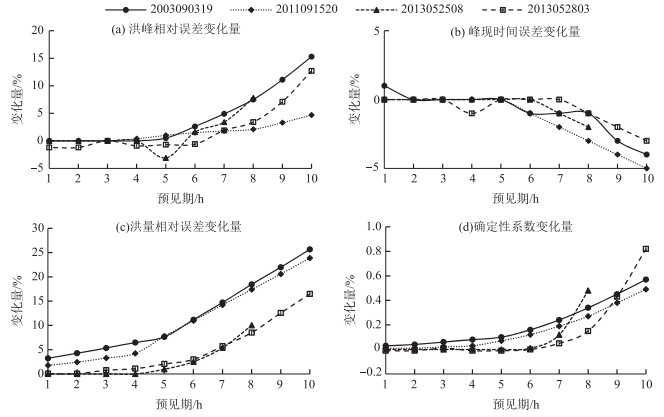
4.5 分析与比较以上基于4种方法对降雨输入不确定性进行了研究.其中,在不同的预见期下分析不考虑未来降雨方法和考虑未来降雨方法的预报模拟精度.对比不考虑未来降雨的实时预报结果,考虑未来降雨的预报方法精度显著增高,表 7和图 9列出了两种方法在不同的预见期各指标的变化量(考虑未来降雨结果减不考虑未来降雨结果).
| 表 7 4场洪水实时预报结果各评价指标变化量 Tab. 7 The increment of evaluation indexes of four flood forecasts |
|
图 9 4场洪水实时预报结果各指标变化量 Fig.9 The increment of evaluation indexes of four flood forecasts |
从表 7和图 9可以看出,在8~10 h预见期内,各指标增大显著,洪峰相对误差最大增长量和最小增长量分别为15.3 %和2.1 %,平均增长量为7.5 %;洪量相对误差最大增长量和最小增长量分别为25.66 %和8.52 %,平均增长量17.55 %;峰现时间误差最大增长量和最小增长量分别为-5和-1,平均增长量为-2.8;确定性系数最大增长量和最小增长量分别为0.82和0.15,平均增长量为0.438;在1~7 h预见期内,各指标增长变幅较小且基本趋于稳定,由此可见,在超过不考虑未来降雨方法得到的最长预报预见期时,考虑未来降雨方法能有效延长预见期,提高预报精度.另外,暴雨中心位置不同对两种预报方法的结果影响显著,暴雨中心位于流域上游时,受到的流域调蓄作用较强,不考虑未来降雨情况,预报精度随预见期的缩短稳定增大,考虑未来降雨情况,不同预见期情况下预报基本重合且预报精度较高;暴雨中心位于流域下游时,流域汇流时间短,不考虑未来降雨情况,预报精度随预见期的缩短显著增大,考虑未来降雨时,在长预见期内,洪水预报精度仍然不合格.
考虑降雨的降雨量误差方法和降雨时间误差方法,分析不同误差条件下的模拟预报精度.其中,降雨量误差主要对洪量相对误差和洪峰相对误差影响较大,对峰现时间误差和确定性系数影响较小,且对洪量和洪峰的影响是线性的,对确定性系数的影响是非线性的二次函数;降雨时间误差主要对峰现时间误差影响较大,对洪量相对误差、洪峰相对误差峰现时间误差和确定性系数影响较小.另外,暴雨中心位置对考虑降雨量误差方法预报结果影响显著,对考虑降雨的降雨时间误差预报结果影响不明显.考虑降雨量误差方法情况,由于暴雨中心位置的不同,经过流域汇流的调蓄作用后,会削弱或者增强降雨量误差对预报精度的影响,因此暴雨中心在流域上游的降雨量允许误差大于暴雨中心在下游的降雨量允许误差;考虑降雨的降雨时间误差方法,降雨系统的滞后或提前主要影响峰现时间,对洪峰流量的影响很小,相当于整个预报过程线的整体平移.
5 结论与展望本文以半湿润的陈河流域和大河坝流域为研究区域,探索不同降雨输入条件下预报结果误差和不同预报预见期的预报精度.研究表明:
1) 采取不考虑未来降雨和考虑未来降雨这两种方法作为模型输入,两个流域得出基本相同的结论,即预报预见期越长,预报精度越低,反之亦然.另外,预报预见期较长时,考虑未来降雨方法比不考虑未来降雨方法的预报精度提高较多,预报预见期较短时,考虑未来降雨比不考虑未来降雨预报精度提高较少.
2) 采取降雨量误差和降雨时间误差预报作为模型输入.相同结论在于设置误差跨度越大,预报精度越低,拟合效果越差.不同之处在于降雨量误差主要影响洪量误差和洪峰误差,且随降雨量误差的增大(减小)呈线性增加(减小),但对确定性系数的影响呈非线性的二次函数,而降雨时间误差主要影响峰现时间误差.
3) 暴雨中心位置对预报精度影响较大.暴雨中心位于流域上游时,受到的流域调蓄作用强,会削弱降雨误差的影响,而暴雨中心位于流域下游时,流域汇流时间短,会增强降雨误差的影响.
4) 本文针对降雨误差,分析了降雨量误差、降雨时间误差和暴雨中心位置对预报精度的影响,研究发现降雨量误差对洪量相对误差和洪峰相对误差的影响呈线性变化,对于这一结论还需在机理上进行更深入的研究.另外,还需对模型参数不确定性和模型结构不确定性进行研究,为数值天气预报产品应用于水文模型提供参考及理论依据.
6 附录附录见电子版(DOI:10.18307/2019.0104).
| [1] |
Wang W, Ma J. Review on some methods for hydrological forecasting. Advances in Science and Technology of Water Resources, 2005, 25(1): 56-60. [王文, 马骏. 若干水文预报方法综述. 水利水电科技进展, 2005, 25(1): 56-60. DOI:10.3880/j.issn.1006-7647.2005.01.018] |
| [2] |
Wang LL, Chen DH, Zhao LN. Application of GRAPES meteorological and hydrological coupled model to flood forecast. Journal of Applied Meteorological Science, 2012, 23(3): 274-284. [王莉莉, 陈德辉, 赵琳娜. GRAPES气象-水文模式在一次洪水预报中的应用. 应用气象学报, 2012, 23(3): 274-284. DOI:10.3969/j.issn.1001-7313.2012.03.003] |
| [3] |
Zhao TTG. Study on reservoir based on hydrological forecast: Uncertainty analysis and optimization[Dissertation]. Beijing: Tsinghua University, 2013. [赵铜铁钢.考虑水文预报不确定性的水库优化调度研究[学位论文].北京: 清华大学, 2013. ]
|
| [4] |
Bao HJ, Zhao LN. Flood forecast of Huaihe River based on TIGGE ensemble predictions. Journal of Hydraulic Engineering, 2012, 43(2): 216-224. [包红军, 赵琳娜. 基于集合预报的淮河流域洪水预报研究. 水利学报, 2012, 43(2): 216-224.] |
| [5] |
Verbunt M, Walser A, Gurtz J et al. Probabilistic flood forecasting with a limited-area ensemble prediction system:Selected case studies. Journal of Hydrometeorology, 2007, 8(4): 897-909. DOI:10.1175/JHM594.1 |
| [6] |
Gao B, Yang DW, Gu XQ et al. Flood forecast of Three Gorges reservoir based on numerical weather forecast model and distributed hydrologic model. Journal of Hydroelectric Engineering, 2012(1): 22-28. [高冰, 杨大文, 谷湘潜等. 基于数值天气模式和分布式水文模型的三峡入库洪水预报研究. 水力发电学报, 2012(1): 22-28.] |
| [7] |
Li ZJ, Liu JT, Ge WZ et al. Coupling of weather radar rainfall data with hydrological model and its application to flood forecasting. Journal of Hohai University:Natural Sciences, 2004, 32(6): 601-606. [李致家, 刘金涛, 葛文忠等. 雷达估测降雨与水文模型的耦合在洪水预报中的应用. 河海大学学报:自然科学版, 2004, 32(6): 601-606.] |
| [8] |
Xu W, Peng Y. Medium-term river runoff forecast model using data of quantitative precipitation forecasts. Journal of Hydroelectric Engineering, 2016, 35(6): 11-19. [徐炜, 彭勇. 基于数值降雨预报信息的中期径流预报方法研究. 水力发电学报, 2016, 35(6): 11-19.] |
| [9] |
Liang ZM, Jiang XL, Cao YX et al. Probabilistic flood forecasting considering rainfall uncertainty. Journal of Hohai University:Natural Sciences, 2016(1): 8-12. [梁忠民, 蒋晓蕾, 曹炎煦等. 考虑降雨不确定性的洪水概率预报方法. 河海大学学报:自然科学版, 2016(1): 8-12.] |
| [10] |
Li ML. Uncertainty estimation of hydrological models under a Bayesian framework[Dissertation]. Beijing: Tsinghua University, 2012: 41-45. [李明亮.基于贝叶斯统计的水文模型不确定性研究[学位论文].北京: 清华大学, 2012: 41-45. ]
|
| [11] |
Ye JY, Zhang JT, Huang Y et al. Evaluation of precipitation forecasts for Dabie Mountain area and application counter-measures for the reservoirs regulation. J Lake Sci, 2017, 29(6): 1528-1537. [叶金印, 张锦堂, 黄勇等. 大别山库区降水预报性能评估及应用对策. 湖泊科学, 2017, 29(6): 1528-1537. DOI:10.18307/2017.0625] |
| [12] |
Gupta HV, Beven KJ, Wagener T. Model calibration and uncertainty estimation. Encyclopedia of Hydrological Sciences. John Wiley & Sons, Ltd, 2006.
|
| [13] |
Zhao RJ. Hydrological modeling of watershed. Beijing: Water Resources and Electric Power Press, 1984: 1-10. [赵人俊. 流域水文模拟. 北京: 水利电力出版社, 1984: 1-10.]
|
| [14] |
Huo WB, Li ZJ, Li QL. Hydrological models comparison and ensemble forecasting in semi-humid watersheds. J Lake Sci, 2016, 29(6): 1491-1501. [霍文博, 李致家, 李巧玲. 半湿润流域水文模型比较与集合预报. 湖泊科学, 2016, 29(6): 1491-1501. DOI:10.18307/2017.0621] |
| [15] |
Orth D. The rivers handbook:Hydrological and ecological principles. Transactions of the American Fisheries Society, 1992, 125(3): 486-488. |
| [16] |
Li ZJ, Jiang TT, Huang PN et al. Impact and analysis of watershed precipitation and topography characteristics on model simulation results. Advances in Water Science, 2015, 26(4): 000473-480. [李致家, 姜婷婷, 黄鹏年等. 降雨和地形地貌对水文模型模拟结果的影响分析. 水科学进展, 2015, 26(4): 473-480.] |
| [17] |
Willems P. A time series tool to support the multi-criteria performance evaluation of rainfall-runoff models. Environmental Modelling & Software, 2009, 24(3): 311-321. DOI:10.1016/j.envsoft.2008.09.005 |
| [18] |
Zhou L, Li ZJ, Han T. Study on the parameter regularity of Nash Unit Hydrograph based on DEM and geomor-phic data. J Lake Sci, 2016, 28(5): 1141-1147. [周莉, 李致家, 韩通. 基于地形地貌资料的Nash单位线参数规律研究. 湖泊科学, 2016, 28(5): 1141-1147. DOI:10.18307/2016.0525] |
| [19] |
Tong BX, Yao C, Li ZJ et al. A method to obtain the spatial distribution of free water storage capacity based on topographic indel. J Lake Sci, 2017, 29(5): 1238-1244. [童冰星, 姚成, 李致家等. 一种通过地形指数提取流域自由水蓄水容量空间分布的方法. 湖泊科学, 2017, 29(5): 1238-1244. DOI:10.18307/2017.0522] |
| [20] |
Tong BX, Li ZJ, Wen YH et al. Construction and application of geomorphologic instantaneous unit hydrograph confluence model in Chenhe catchment. Water Power, 2017(10): 19-22. [童冰星, 李致家, 温娅惠等. 基于地貌单位线的汇流模型在陈河流域的构建与应用. 水力发电, 2017(10): 19-22.] |
| [21] |
Liu SC. Distributed simulation of surface evapotranspiration in the Wu-Jin River watershed, Hanjiang River[Dissertation]. Nanjing: Nanjing University, 2004. [刘三超.汉江子午河流域地表蒸散发分布式模拟研究[学位论文].南京: 南京大学, 2004. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y810566 ]
|
| [22] |
Li ZJ. Modern hydrological modeling and forecasting techniques. Nanjing: Hohai University Press, 2010: 1-4. [李致家. 现代水文模拟与预报技术. 南京: 河海大学出版社, 2010: 1-4.]
|
| [23] |
Bao WM. Hydrologic Forecasting. Beijing: China Water Power Press, 2009: 151-159. [包为民. 水文预报. 北京: 中国水利水电出版社, 2009: 151-159.]
|
| [24] |
Nemec J ed. Hydrological forecasting. Wiley, 1985.
|
 2019, Vol. 31
2019, Vol. 31 

