(2: 河海大学水安全与水科学协同创新中心, 南京 210098)
(2: National Cooperative Innovation Center for Water Safety & Hydro-Science of Hohai University, Nanjing 210098, P.R.China)
自2003年PUB(Predictions in Ungauged Basins)计划[1]被提出以来,无资料地区的水文研究激起了广大水文学者的兴趣.对于无资料地区水文现象的研究,水文模型是必不可少的工具.然而,由于历史实测资料缺乏,在无资料地区模型参数难以率定与检验,因此解决模型参数问题是无资料地区水文预报的关键所在.目前应用最广泛的参数确定方法是参数移植[2],但参数移植只能根据流域的水文相似性进行,不适用所有流域,只有从参数物理意义出发[3],找出模型参数规律,才是解决模型在无资料地区应用的根本.
新安江模型是根据长期实践和水文机理分析基础上构建的概念性水文模型[4],在我国湿润、半湿润地区应用广泛,取得了良好的模拟效果.深入挖掘新安江模型的潜力,发展模型的理论,具有重要的研究意义与实用价值[5].河网蓄水消退系数(Cs)[6]是新安江模型汇流计算模块中一个极其敏感的参数,反映流域退水速率的快慢,主要控制洪峰的形状,对模拟结果影响较大[7],在新安江模型实际应用中Cs的确定尤为关键,但Cs与河网形态及地形地貌特征密切相关,而不同流域河网及下垫面特征千变万化,没有统一规律,因此在无资料地区Cs难以移植,模型应用困难.为了使新安江模型在无资料地区得以应用,许多学者试图建立Cs与河网结构和地貌特征之间的关系.例如,赵人俊[8]在1991年提出了Cs随时间、流量变化的方程.徐倩等[9]依据实测资料得出每个流域与Cs之间的经验关系.陆旻皎[10]提出用蓄泄系数与地貌因子与水力因子的关系探求消退系数的参数规律.但以上方法只是经验公式,难以推广应用到任意流域. 2016年李致家等[11]推导Cs与河网结构之间的关系,通过构建描述河网汇流动态变化的微分方程,用数值法求得方程的解,从而建立了Cs具有物理意义的计算方法,并在25个流域上对该计算方法做了验证,但研究仅限于求得整个流域的Cs值,每个单元流域还是采用相同的Cs值进行计算,没有深入探讨流域分块后Cs的变化规律以及每个单元流域采用不同的Cs值进行汇流计算对模拟结果的影响.
本文以提高新安江模型在无资料地区预报精度为出发点,从Cs的物理意义出发,采用了基于自相似河网结构Cs计算方法[11]推求出整个流域Cs值与单元流域Cs值,深入探讨单元流域Cs值与全流域Cs之间的关系,以及各单元流域Cs值之间的参数规律,在此基础上修改了新安江模型汇流计算过程,根据每个单元流域的Cs计算值进行单元流域的汇流演算,并将修改后的模型与新安江模型进行比较分析以探讨修改后模型的合理性.
1 Cs计算方法河网消退系数反映了流域退水速率的快慢,可直接由时段初与时段末实测流量比值确定,但在无资料地区由于实测资料的缺乏,难以直接用实测流量来确定.本文借鉴基于自相似河网结构的Cs估算方法,将河网假设为自相似结构,对河链建立水量平衡方程和槽蓄方程,推求出槽蓄量与出口流量之间的关系式,并引入一个无量纲时间t′:
| $ t\prime = v \cdot t/L $ | (1) |
式中,v为平均河道流速,m/s;t为次洪模拟时间,h;L为平均河链长,m,递推出流域出口河链蓄量方程.从而将Cs值转化为用流域出口河链的槽蓄量比值来表示.本文所采用的新安江模型取1 h为次洪模型计算时段,因此文中所有Cs值都是以1 h为时段长定义的.
1.1 基本假设① 认为河网结构为二叉树结构,对河链编号:某河链的编号等于该条河链的上游总链数+1,从河源出发的河链编号都为1;若某河链的编号为n,则上游共含有n-1条河链(图 1、2);②假设每条河链长度相等;③当降雨空间分布均匀、河道坡降分布均匀、河床形态一致时,将平均河道流速v看作定值;④当各河链无支流时,河链的区间入流量为零.
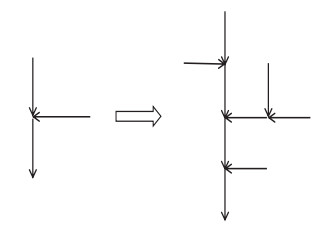
|
图 1 自相似河网结构示意图 Fig.1 Schematic diagram of self-similar channel network structure |
|
图 2 河链编号示意图 Fig.2 Schematic diagram of river chain number |
根据质量守恒定律可得,编号为k的河链槽蓄量变化满足下列方程:
| $ \frac{{{\rm{d}}W\left( {k, t} \right)}}{{{\rm{d}}t}} = I\left( {k, t} \right)-O\left( {k, t} \right)\;\;\;\;\;\left( {k = 1, 2, \ldots, n} \right) $ | (2) |
式中,t表示时间;W(k, t)为k链蓄量,m3;I(k, t)为k链入流量,m3/s;O(k, t) 为k链出流量,m3/s.
对于二叉树河网,k链入流量I(k, t)由以下两部分组成:
| $ I\left( {k, t} \right) = O({k_1}, t) + O({k_2}, t) $ | (3) |
式中,k1、k2分别为k链上游两条链编号;O(k1, t)和O(k2, t)分别为k1、k2链的出流量,m3/s.
假设河道为矩形河道,则k链的出流量O(k, t) = B ·D ·v,槽蓄量W(k, t) = D ·B ·L.其中,B为平均河链宽,m;D为平均水深,m;v为平均河道流速,m/s;L为平均河链长,m.由以上公式可推求出如下关系式:
| $ O\left( {k, t} \right) = \frac{v}{L}W\left( {k, t} \right) $ | (4) |
假定各河链的初始时刻蓄水量都为W0,将公式(3)、(4)代入公式(2),得到:
| $ \frac{{{\rm{d}}W\left( {k, t} \right)}}{{{\rm{d}}t}} = \frac{v}{L}W({k_1}, t) + \frac{v}{L}W({k_2}, t)-\frac{v}{L}W\left( {k, t} \right) $ | (5) |
为求得上述方程,在此引入t′,将W(k, t)、W(k1, t)及W(k2, t)转换为以t′为时间变量的形式F(k, t′)、F(k1, t′)及F(k2, t′),则式(5)可以转化为:
| $ \frac{{{\rm{d}}F\left( {k, t\prime } \right)}}{{{\rm{d}}t}} = \frac{v}{L}F({k_1}, t\prime ) + \frac{v}{L}F({k_2}, t\prime )-\frac{v}{L}F\left( {k, t\prime } \right) $ | (6) |
则式(6)可以化简为:
| $ \frac{{{\rm{d}}F\left( {k, t\prime } \right)}}{{{\rm{d}}t\prime }} = F({k_1}, t\prime ) + F({k_2}, t\prime )-F\left( {k, t\prime } \right) $ | (7) |
由此,便可求解出递推形式的河链蓄量的解析表达式,河网中k链的蓄量通式为:
| $ F\left( {k, t\prime } \right) = {{\rm{e}}^{- t\prime }}\left\{ {{W_0} + \int_0^{t'} {{{\rm{e}}^\tau }\left[{F({k_1}, \tau ) + F({k_2}, \tau )} \right]{\rm{d}}\tau } } \right\} $ | (8) |
由上式得编号为1的外链,式(8)积分方程中F(k1, τ)和F(k2, τ)均为0,则编号为1的河链蓄量方程为:
| $ F\left( {1, t\prime } \right) = {W_0}{{\rm{e}}^{-t\prime }} $ | (9) |
若取小时作为时间t的单位,经过单位转换后,t′的表达式为:
| $ t\prime = 3.6v \cdot t/L $ | (10) |
在水文资料缺乏地区采用经验流速公式. Bras等根据Eagleson的思路,以运动波理论为基础[12],推出如下流速公式:
| $ v = 0.665{\alpha ^{0.6}}{({i_r} \cdot A)^{0.4}} $ | (11) |
| $ \alpha = \frac{{{S_0}^{\frac{1}{2}}}}{{n \cdot {B^{\frac{2}{3}}}}} $ | (12) |
式中,ir为降雨强度,cm/h;A为流域面积,km2;B为平均河宽,m;S0为河道坡降;n为曼宁糙率系数.据研究表明[13],曼宁糙率系数全部取0.025,对结果影响不大.
1.3 最小二乘法确定Cs河网蓄水消退系数反映退水速率的快慢,可直接由计算时段(Δh = 1)始、末的两个实测流量来确定,即:
| $ Cs = \frac{{O({t_m})}}{{O({t_0})}} $ | (13) |
式中,t0表示计算时段开始时刻,tm表示计算时段结束时刻.将式(4)代入式(13),则式(13)可以转换为:
| $ Cs = \frac{{W({t_m})}}{{W({t_0})}} $ | (14) |
| $ Cs = \frac{{F(t\prime {_m})}}{{F(t\prime {_0})}} $ | (15) |
式中,t0、tm分别表示与t′0、t′m所对应的无量纲时间,W(t0)、F(t′0)表示流域出口所在的河链t0时刻的蓄量,W(tm)、F(t′m)表示流域出口所在的河链tm时刻的蓄量.
Cs是随时间变化的变量,若仅用一组数值[F(t′0), F(t′m)]来确定Cs,会引起参数估计误差.为尽量消除这一影响,选择n组数据[F(t′0), F(t′1)],[F(t′1), F(t′2)],…,[F(t′n-1), F(t′n)]采用最小二乘法计算Cs:
| $ Cs = \frac{{\sum\limits_{i = 0}^{n-1} {F(t\prime {_i})F(t\prime {_{i + 1}})} }}{{\sum\limits_{i = 0}^{n-1} {{F^2}(t\prime {_i})} }} $ | (16) |
以图 2所示流域为例,计算该流域的Cs值.
1) 递推出流域出口所在河链,即编号13的河链的蓄量表达式.
河链1:式(8)中F(k1, τ)和F(k2, τ)均为0,F(1, t′) = W0e-t′
河链3:
河链5:
河链11:
河链13:
2) 利用ArcGIS提取出该流域流域面积、河道平均坡降、河宽、平均河链长,根据实测雨量资料计算雨强,根据公式(11)、(12)求出河道平均流速.
3) 取1 h为次洪模型的计算时段,根据式(10)将实际时间0, 1, …, n转化为相应的无量纲时间t′0,t′1,…,t′n,代入到河链13的蓄量表达式,即可得一系列时段始末的蓄量值:F(t′0),F(t′1),…,F(t′n).
4) 用最小二乘法求出该流域次洪模型的Cs值.
2 Cs计算方法应用与分析 2.1 研究流域概况本次研究从安徽、浙江、陕西三省选取了11个湿润、半湿润及半干旱典型流域作为试验流域.数字高程资料(DEM)来自美国地质调查局(USGS)免费提供的全球90 m×90 m的原始DEM数据,运用ArcGIS软件通过填洼、确定流向、水系提取等处理,得到流域面积、河道坡降、平均河链长等资料,获取资料主要用于新安江模型的输入及Cs的计算.洪水摘录、降雨摘录、日流量、日雨量、时段流量、时段雨量蒸发资料和土壤墒情数据等由当地水文局提供.各研究流域的基本概况和资料情况见表 1.
| 表 1 研究流域基本概况 Tab. 1 General situation of experimental catchments |
按照基于自相似河网结构的Cs估算方法求出11个流域的全流域Cs计算值和各子流域Cs计算值.为了检验该方法的适用性及可靠性,对每个流域分别根据历史资料用新安江模型进行次洪参数率定,得到每个流域Cs率定值,然后将子流域Cs均值作为模型中的Cs输入值,对其余参数利用次洪结果进行率定. 表 2为两种方法得到的Cs值及与相应模拟结果的比较.
| 表 2 研究流域下垫面提取数据及Cs率定值、计算值 Tab. 2 The extraction data of the underlying surface and calculated values and calibrated values of Cs |
11个流域全流域Cs计算值与流域面积的关系见图 3;图 4a为11个流域的子流域Cs计算均值与率定值的散点图;图 4b为11个流域用率定值与计算均值模拟得到的确定性系数均值散点图.由图 4a、b可知,两幅图的大部分散点都均匀落在45°虚线的两侧且与该线非常靠近,这表明子流域Cs计算均值与率定值非常接近,通过各子流域Cs计算均值与新安江模型率定取得的模拟效果也十分相近.所以,从整体上来说,本文提出的Cs计算方法是有效的.在无资料地区,可直接采用该计算方法求得Cs值,降低模型应用中参数的不确定性.随着面积的增大,全流域Cs计算值有增大的趋势(表 2和图 3).这种结果是合理的,因为流域的调蓄功能与流域面积呈正相关,Cs代表着流域对洪水的坦化作用,流域调蓄功能越强,Cs值也就越大.众所周知,新安江模型在进行流域分块时,并不能确保每个单元的面积相等,因此也不能保证每个单元的Cs值相等,而在率定中却采用相同的Cs值进行汇流演算,这与流域汇流规律不相符,因此有必要考虑每个单元流域采用各自的Cs值进行汇流计算.
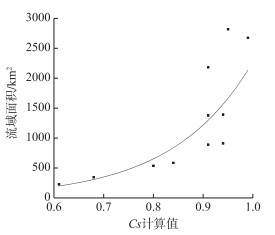
|
图 3 Cs计算值与流域面积的关系 Fig.3 Scatter plot of calculated Cs values with catchment area |
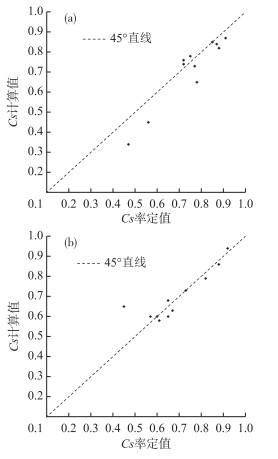
|
图 4 Cs计算值与率定值散点图(a)及对应的确定性系数均值散点图(b) Fig.4 Scatter plot of calculated Cs values with calibrated Cs values (a) and corresponding mean deterministic coefficient (b) |
选取陕西黑河的陈河流域及安徽屯溪流域作为研究流域.其中,陈河流域多年平均降水量700~900 mm,属于半湿润地区,流域山高、坡陡、水流湍急.河流水量主要来自雨水补给,局部暴雨是发生洪水的主要原因.陈河水文站(33°58′23″N,108°09′52″E)建于1996年5月,地处陕西省周至县陈河乡木江河村,实测最高水位608.07 m(2002年),实测最低水位603.13 m(2004年),实测流量年最大值为1750 m3/s(2005年),最小值为196 m3/s(2004年).屯溪流域属于湿润地区,邻近中国东南沿海,位于亚热带季风气候区,年平均温度17℃,冬季盛行西北风,天气晴冷干燥;夏季多东南风,气温高,光照强,空气湿润;春、秋两季气旋活动频繁,冷暖变化大.年平均降水量1600 mm,其中4 6月多雨,占50 %,易发生洪涝灾害;7 9月,占20 %,旱灾频繁.河川径流年内、年际变化较大.屯溪和陈河流域的DEM资料见图 5.
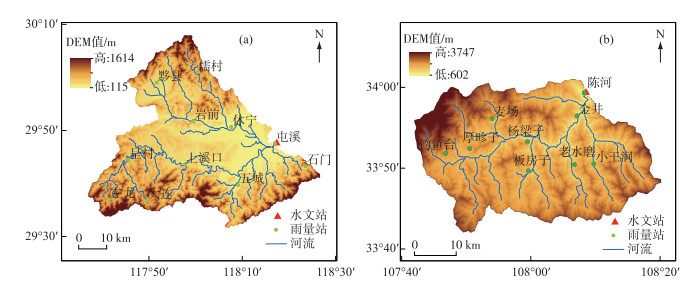
|
图 5 屯溪(a)和陈河(b)流域DEM资料 Fig.5 DEM data of Tunxi (a) and Chenhe (b) catchments |
由于流域下垫面及降雨空间分布不均匀,在新安江模型中,对于面积较大的流域要先进行分块然后进行产汇流计算,通常采用的分块方法为泰森多边形法和自然子流域分块法.泰森多边形法往往会将不同分水岭的支流划分到一起,这与河道汇流演算规律不符.而按自然子流域划分,是依据河网结构将流域分为多个小单元,与下垫面特征更贴合,因此本文是采用自然子流域划分.将水系及流域提取之后,按照雨量站点对流域进行自然子流域的划分,使每个子流域中含有一个雨量站,其中划分遵循二叉树的自相似结构,不能将不同分水岭的支流划分在同一子流域.划分之后的陈河流域及屯溪流域自然子流域提取图见图 6.
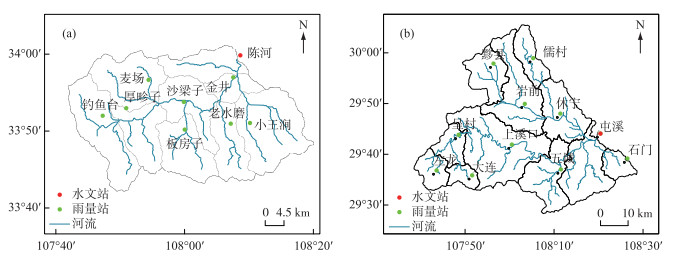
|
图 6 陈河流域(a)及屯溪流域(b)子流域提取图 Fig.6 Map of the sub-catchment and river networks in Chenhe (a) and Tunxi (b) catchments |
由表 3可知,一些面积较大的单元流域Cs值会比面积较小的单元流域Cs值小,例如休宁和岩前,由图 7也可以直观地看出,屯溪流域Cs值随着单元面积的增大而呈现增大的趋势,而陈河流域Cs值随着单元面积的增大而呈现减小的趋势,这与上节得出的面积越大Cs值越大的结论相违背.这是因为Cs除了与面积密切相关外,还与河链数、距离出口断面数、河道坡降及河宽等因素有关.由图 8、9可以看出,两个流域子流域Cs值与出口断面距离呈负相关,与河宽呈正相关. Cs是反映流域调节作用的一个指标,Cs值越大,则代表流域的调蓄能力越强,退水速率越慢.对于一个流域,面积越大,河网级数越高,则流域内水滴到达流域出口处的路径越长,水滴到达出口断面时间就越长,退水就越慢,Cs也就越大.从河宽的角度来看,河道越宽,则河道的调蓄功能就越强,因此Cs值就越大.另外,一般下游河道的河底比降比上游河道的河底比降小得多,下游河宽也比上游大,位于下游的河道即距离出口断面近的子流域河槽的调蓄作用大,因此距离出口断面近的Cs偏大,距离出口断面远的Cs值偏小.
| 表 3 屯溪和陈河子流域Cs计算值 Tab. 3 Calculated Cs values of Tunxi and Chenhe sub-catchments |

|
图 7 各单元流域面积与Cs计算值的关系 Fig.7 Scatter plot of calculated Cs values with sub-catchment area |
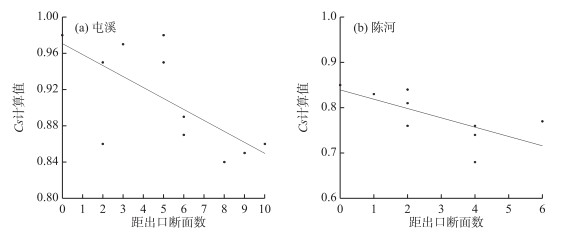
|
图 8 各单元距离出口断面数与Cs计算值关系 Fig.8 Scatter plot of calculated Cs with distance between each sub-catchmet and outlet section |
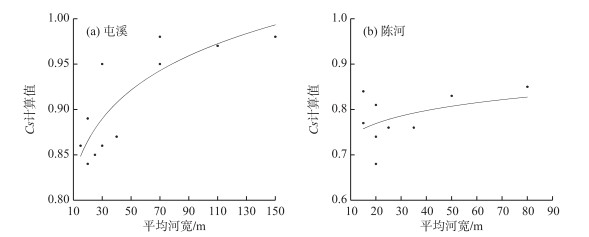
|
图 9 各单元流域平均河宽与Cs计算值散点图 Fig.9 Scatter plot of calculated Cs with sub-catchment average river width |
陈河全流域Cs计算值为0.94,屯溪全流域Cs计算值为0.99(表 2),将其与对应的子流域Cs值(表 3)比较可以发现,流域分块后每个单元流域的Cs值均小于等于全流域的Cs值.这种结果是合理的,因为分块以后每个单元的面积比全流域面积小,调蓄功能也相应变小,另外从模型结构来说,流域分块之后,除了每个单元用Cs进行滞后演算对出口流量进行调节以外,还需采用马斯京根分段演算法对每个单元出口以下的河段进行河道汇流演算,这部分河道演算分担了一部分调蓄功能,因而单元流域的Cs值比全流域的Cs值小.
4 模型应用及分析在汇流计算参数中,河网消退系数Cs是极其敏感参数,反映了退水速率的快慢,因此Cs值越小,洪峰越大.由上文分析可知,Cs值与流域面积、河链数及地形地貌特征密切相关,而每个流域内部的单元流域水系及下垫面条件都有所不同,因此每个单元的Cs值也存在差异.在传统新安江模型中没有考虑各个单元流域的Cs值差异,只采用单一的Cs值对出口流量进行调节,容易引起次洪模拟尤其是洪峰流量的较大误差.为了使模拟精度进一步提高,将模型汇流计算过程进行了修改,并在半湿润地区陈河流域和湿润地区屯溪流域进行了验证.
4.1 模型汇流计算框架新安江模型是分散性模型[14],它将全流域分为若干单元流域,对每个单元进行产汇流计算.分水源之后每种径流成分的入流量确定并进入汇流计算阶段.在汇流计算中,先对每个单元流域的产流量用相同Cs值进行滞后演算,然后对出口断面的流量运用马斯京根分段流量演算法进行河道汇流演算,最后将所有单元流域的流量进行汇总得流域出口流量.滞后演算计算公式为:
| $ {Q_t} = Cs \cdot {Q_{t-1}} + \left( {1-Cs} \right) \cdot R \cdot U $ | (17) |
式中,Qt为t时刻的出口断面流量,m3/s;Qt-1为t-1时刻的出口断面流量,m3/s;R为径流量,mm;U为单位换算系数,
在流域分块之后,各单元流域下垫面特征及河网形态存在差异,对应的Cs值也应取值不同,但新安江模型进行产汇流计算时每个单元采用同一套参数,由空间变异对参数取值的影响考虑不完全.为了使新安江模型在无资料地区预报精度进一步提高,本文对新安江模型汇流计算进行了修改.考虑到模型是分散性模型,所以先根据本文所采用的Cs计算方法计算出每个单元流的Cs值,用对应的Cs值对每个单元出口流量进行调节,再分别用马斯京根分段流量演算法进行河道汇流演算,得到每个单元对出口流量的贡献量,最后累加得到出口断面的流量.假设将整个流域分为两个子流域,修改后新安江模型汇流计算结构见图 10.
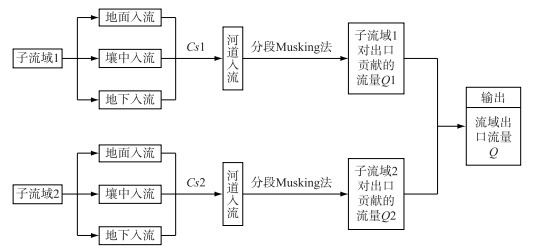
|
图 10 修改后新安江模型汇流计算结构 Fig.10 Structure of confluence calculation in the modified Xin'anjiang model |
为检验改进后模型的适用性,选取陈河流域及屯溪流域的历史洪水进行模拟分析.在选择洪水时保证大、中、小洪水全面选择,并且各种峰形及历时长短的洪水尽量覆盖.陈河流域选取2003 2012年共20场洪水进行模拟计算.前14场用于率定期,后6场用于验证.屯溪流域选取了1981 2005年共34场洪水进行模拟计算,前20场用于率定,后14场用于验证.分别采用如下3种方案进行洪水模拟:
方案1:将研究流域用传统新安江模型率定,进行次洪模拟.
方案2:将方案1的Cs率定值改为各子流域计算值的均值,再调节其他参数,进行次洪模拟.
方案3:用改进后的新安江模型,将研究流域每一子流域的Cs改为计算值,并重新率定其他参数值进行次洪模拟.
根据《水文情报预报规范》(GB/T 22482 2008)选取了洪量合格率、洪峰合格率、确定性系数以及峰现时间误差4个指标作为评价标准,图 11、12分别为陈河(CH)、屯溪(TX)流域用3种方案(表示为1、2、3)模拟得到的率定期(C)与验证期(V)洪峰相对误差(RPE)、洪量相对误差(RRE)、确定性系数(NSE)和峰现时间(PTE)箱线图. 表 4列出了陈河和屯溪采用3种方案得到的率定期及验证期所有次洪模拟特征值的统计. 图 13为陈河2005070106号洪水和屯溪1983052908号洪水用以上3种方案得到的洪水流量过程线.
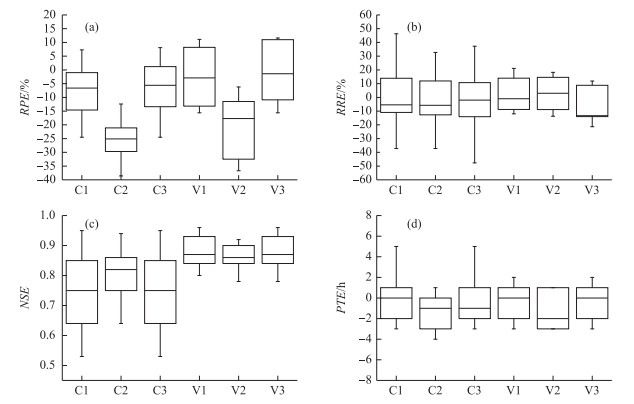
|
图 11 陈河流域洪峰相对误差、洪量相对误差、确定性系数及峰现时间箱线图 Fig.11 Box plots of the RPE, RRE, NSE and PTE statistics of all hourly simulations, including both calibration and validation events with three methods in Chenhe catchment |
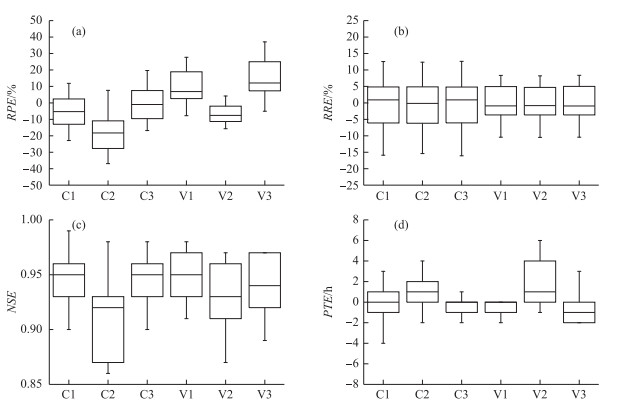
|
图 12 屯溪流域洪峰相对误差、洪量相对误差、确定性系数及峰现时间箱线图 Fig.12 Box plots of the RPE, RRE, NSE and PTE statistics of all hourly simulations, including both calibration and validation events with three methods in Tunxi catchment |
| 表 4 次洪模拟结果特征值统计 Tab. 4 Characteristic statistics of the results of flood event simulation in Chenhe and Tunxi catchments |
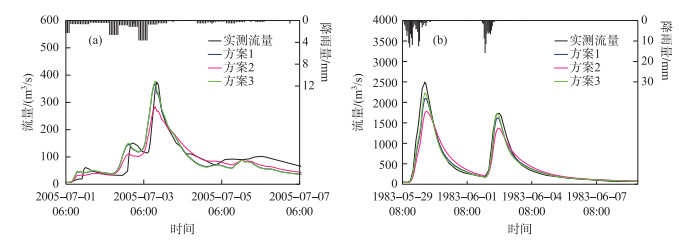
|
图 13 陈河流域2005070106号洪水(a)和屯溪流域1983052908号洪水(b)过程线 Fig.13 Observed and simulated hydrographs of flood 2005070106 in Chenhe catchment (a) and flood 1983052908 in Tunxi catchment (b) |
由陈河流域模拟结果(图 11、表 4)可知,3种方案在洪量相对误差及峰现时间这两个指标上相差不大,这是因为Cs主要是对洪峰有重要影响,对洪量及峰现时间影响不大.但从洪峰相对误差来看,陈河流域3种方案率定期洪峰相对误差大致范围分别为-25 % ~10 %、-40 % ~-10 %和-25 % ~10 %,验证期洪峰相对误差大致范围分别为-15 % ~10 %、-40 % ~10 %和-15 % ~10 %;方案2洪峰模拟误差普遍比方案1、方案3偏大,即预报洪峰比实测洪峰普遍偏小,这说明方案2中采用的Cs值偏大.因此,在陈河流域方案1与方案3可行,方案2不可行.由屯溪流域模拟结果(图 12、表 4)可得,屯溪流域3种方案率定期洪峰相对误差范围分别为-22.9 % ~26.7 %、-36.9 % ~7.6 %和-16.8 % ~19.7 %,验证期洪峰相对误差范围分别为-7.8 % ~27.7 %、-15.7 % ~4.2 %和-3 % ~35.5 %,除了方案2在率定期预报洪峰比实测洪峰稍有偏小之外,在率定期与验证期分别采用这3种方案的洪峰相对误差、洪量相对误差、确定性系数、峰现时间结果相差不大,均在可接受范围之内.因此这3种方案在屯溪流域均适用.
从两个流域模拟情况来看,陈河流域方案2的洪峰模拟效果极差,洪峰相对误差合格率只有21 %,而屯溪流域方案2模拟效果相对好一些,洪峰相对误差合格率为55 % (表 4).通过比较两个流域的DEM数据(图 5)可以发现,陈河流域变化范围为602~3747 m,屯溪流域变化范围为115~1614 m,从面积大小来看,陈河流域面积比屯溪流域小,即陈河流域数字高程空间变化要比屯溪大,所以,陈河流域各单元Cs值差值比屯溪各单元差值大.从地形因素也可以看出,陈河流域位于山区,地势起伏不平,河道坡降变化大,下垫面条件差异性比屯溪大,单元流域Cs差异越大,子流域Cs均值往往就不具有代表性,不能反映流域的综合调蓄能力,所以在陈河使用方案2模拟效果不佳,而屯溪流域各子流域Cs值相近,洪峰模拟相对较好.
综上所述,这3种方案均有可取之处,但方案2适用于子流域下垫面条件相似的地区,所以方案1和方案3比方案2更好.但在无资料地区,方案1率定较为困难,难以应用,不具优势.方案3不仅模拟效果好,而且参数Cs物理意义更明确,模型将参数与流域空间变异性联系起来,使模型结构更加合理,因此在无资料地区应用方案3会更胜一筹.
5 结论1) Cs计算均值与率定值在研究区湿润、半湿润和半干旱地区11个流域模拟效果十分相近,这说明本文所采用的Cs计算方法是有效的,在无资料地区可采用此方法来确定模型汇流参数Cs值.
2) Cs值与流域面积、河链数以及河宽呈正相关,与子流域距离出口断面远近呈负相关.流域分块后每个单元流域的Cs值均小于等于全流域的Cs值,流域分块后每个单元的面积比全流域面积小,调蓄功能也相应变小.另外从模型结构来说,流域分块之后,除了每个单元用Cs对出口流量进行调节以外,还需采用马斯京根分段演算法对每个单元出口以下的河段进行河道汇流演算,这部分河道演算分担了一部分的调蓄功能,因而单元流域的Cs值比全流域的Cs值小.
3) 由3种方案的模拟结果可得,3种方案均可行,但方案1在无资料地区难以率定,方案2建议在子流域下垫面条件相似地区使用,方案3修改后的新安江模型结构更加合理,Cs物理意义明确,进一步考虑了流域空间变异性,根据每个单元流域属性差异取相应的Cs进行滞后演算,模型物理机制增强,这是修改后的新安江模型最大的优势所在.但在不能修改模型的条件下,退而求其次使用方案2尚可.因此,本文所提出的Cs计算方法、区域参数规律及新安江模型汇流计算过程修改方法对新安江模型在无资料地区的应用具有指导意义.
| [1] |
Sivapalan M, Takeuchi K, Franks SW et al. IAHS decade on predictions in ungauged basins (PUB), 2003-2012: Shaping an exciting future for the hydrological sciences. International Association of Scientific Hydrology Bulletin, 2003, 48(6): 857-880. DOI:10.1623/hysj.48.6.857.51421 |
| [2] |
Wagener T, Wheater HS, Gupta HV. Rainfall-runoff modelling in gauged and ungauged catchments. London: Imperial College Press, 2004: 332.
|
| [3] |
Rui X, Ling Z, Liu N et al. Origin of Xin'anjiang model and its further development. Advances in Science and Technology of Water Resources, 2012, 32(4): 1-5. [芮孝芳, 凌哲, 刘宁宁等. 新安江模型的起源及对其进一步发展的建议. 水利水电科技进展, 2012, 32(4): 1-5.] |
| [4] |
Li ZJ. Application and research of hydrological modelling. Nanjing: Hohai University Press, 2008: 76-88. [李致家. 水文模型的应用与研究. 南京: 河海大学出版社, 2008: 76-88.]
|
| [5] |
Li JT, Song HQ, Zhang XN et al. A discussion on advances in theories of Xin'anjiang Model. Journal of China Hydrology, 2014, 34(1): 1-6. [刘金涛, 宋慧卿, 张行南等. 新安江模型理论研究的进展与探讨. 水文, 2014, 34(1): 1-6.] |
| [6] |
Zhao RJ. Proceedings of Zhao Renjun on hydrological forecasting. Beijing: Water Resources and Electric Power Press, 1994: 120-135. [赵人俊. 赵人俊水文预报文集. 北京: 水利电力出版社, 1994: 120-135.]
|
| [7] |
Li ZJ, Li LR, Huang PN et al. Effect of watershed subdivision on confluence parameter. Journal of Hohai University: Natural Sciences, 2014, 42(4): 283-288. [李致家, 李兰茹, 黄鹏年等. 流域分块对汇流参数的影响. 河海大学学报:自然科学版, 2014, 42(4): 283-288.] |
| [8] |
Zhao RJ. Watershed concentration flow of linear time-varying system. Journal of China Hydrology, 1994(4): 1-6. [赵人俊. 时变线性系统流域汇流模型. 水文, 1994(4): 1-6.] |
| [9] |
Xu Q, Li ZJ, Chen XD. Study on the parameter laws of watershed flow concentration of Xin'anjiang model. Boutique of China Science and Technology Papers Online, 2009, 2(4): 1-6. [徐倩, 李致家, 陈向东. 新安江模型流域汇流参数规律研究. 中国科技论文在线精品论文, 2009, 2(4): 1-6.] |
| [10] |
Lu JW. New approach to synthesization of recession coefficients in Xin'anjiang model. Journal of Hydroelectric engineering, 2016, 35(9): 1-6. [陆旻皎. 关于新安江模型河网蓄水消退系数规律的建议. 水力发电学报, 2016, 35(9): 1-6.] |
| [11] |
Li ZJ, Liang K, Kan GY et al. A method for deriving the river network flow concentration parameter Cs of the Xin'anjiang model. Advances in Water Science, 2016, 27(5): 652-661. [李致家, 梁珂, 阚光远等. 新安江模型中河网汇流参数Cs的一种计算方法. 水科学进展, 2016, 27(5): 652-661.] |
| [12] |
Li Q, Wen K. Dynamical factors in general formulas of geomorphologic unit hydrograph: research of velocity calculation. Haihe River Water Conservancy, 1989(1): 6-12. [李琪, 文康. 地貌单位线通用公式中动力因子—流速计算的研究. 海河水利, 1989(1): 6-12.] |
| [13] |
Li ZJ, Li LR, Huang PN et al. Effect of watershed subdivision on confluence parameter. Journal of Hohai University: Natural Sciences, 2014, 42(4): 283-288. [李致家, 李兰茹, 黄鹏年等. 流域分块对汇流参数的影响. 河海大学学报:自然科学版, 2014, 42(4): 283-288.] |
| [14] |
Singh VP. Computer models of watershed hydrology. Colorado: Water Resources Publications, 1995, 443-476. |
 2019, Vol. 31
2019, Vol. 31 

