(2: 广东省华南地区水安全调控工程技术研究中心, 广州 510275)
(3: 北京师范大学环境演变与自然灾害教育部重点实验室, 北京 100875)
(2: Center of Water Security Engineering and Technology in Southern China of Guangdong, Guangzhou 510275, P.R.China)
(3: Key Laboratory of Environmental Change and Natural Disaster, Beijing Normal University, Beijing 100875, P.R.China)
全球气候变化加大了降水径流等气象水文要素的空间分布差异,影响着多江流域水资源及气象水文极值的组合特征[1].丰枯遭遇实质是气象水文变量的多区域组合问题,涉及到降水的分区组合[2-4]、流域干流和其支流的径流组合[5]、多条河流的径流组合[6]或极值流量组合[7]、调水工程水源区和受水区的降水或径流组合[8-9]、多个水库的来水量组合[10]等.
通常认为丰枯遭遇的各区域气象水文变量是个随机过程,但它们之间又存在相依性.多维随机变量构造函数Copula在反映单个随机变量分布特征的同时又能呈现变量之间的相依性,现已被广泛应用于洪水特性分析、干旱特性分析、水文过程模拟、气象水文变量多维联合分布模拟等[11-21].其中,基于Copula函数的径流丰枯遭遇研究[5],是通过构建多条河流的径流Copula模型,分析径流丰枯组合的联合概率特征.径流丰枯遭遇联合分布模拟多为二维模型和三维模型[6],冯平[22]等运用四元Copula函数研究了南水北调西线工程水源区河流与受水区黄河上游的丰枯遭遇问题,同一流域三变量以上的丰枯遭遇研究较少.同一流域涉及多条河流来水时,变量的维数变高,问题变复杂,Copula函数的应用使丰枯遭遇的问题简单化.
鄱阳湖为中国最大的淡水湖,接纳饶河、抚河、信江、赣江和修水的五江来水,经过湖盆调蓄后汇入长江[23].作为国际重要湿地和长江干流重要调蓄性湖泊,鄱阳湖水量的丰枯变化影响着湖区生物多样性保护及长江中下游的洪水调蓄等[24].前人对鄱阳湖水量的研究多集中在流域单一变量的水文特征分析方面,如径流变化[25-27]、枯水特征[28]、水文干旱特征[23]和流域旱涝规律[28]等.近些年,有学者也开始利用Copula函数研究鄱阳湖极值流量的遭遇特征和枯水多特征的联合分布[29]等,但均为两变量联合分布模拟.受全球气候变化的影响,鄱阳湖流域水资源量发生变化,流域内出现极端干旱事件,旱涝灾害频繁[30].研究表明,5大水系来水变化与湖区干旱等水文极值事件有密切关系[31].因此,研究5大水系来水丰枯规律,能加强流域内的水量调控,对区域防洪抗旱有重要意义.为加强流域内水量调控,需分析流域各条河流来水量之间的相互关系,传统方法是建立变量之间的相关关系或选取若干典型年[32].为保证调水方案的合理性,需要分析各水系水量的丰枯遭遇概率,传统方法无法回答遭遇概率大小的问题,Copula函数的引入能很好地解决此问题.对于多条河流来水的鄱阳湖水系来说,多维分布可对鄱阳湖流域局部至流域整体的径流规律进行研究.
因此,本文基于鄱阳湖5大水系径流,运用Copula函数构建二维至五维的联合分布模型,探讨多条河流来水丰枯遭遇的多维模拟方法,从多个维度上分析鄱阳湖水系径流丰枯遭遇特征变化,为流域水资源管理及水旱灾害预防提供依据.
1 方法和数据 1.1 径流多维联合分布某一河流在一定时间尺度上的径流,如年径流、汛期径流和非汛期径流,其逐年变化一般认为是个随机过程.一个流域面积较大的河湖水系(如鄱阳湖水系),其水量变化同时受到多条河流的影响.受地理位置及气候条件影响,同属一个水系的多条河流之间,其径流过程具有一定的相依性.因此,同一流域多条河流径流丰枯遭遇分析的前提是构建多维联合分布模型[6].现已广泛应用于多维联合分布的Copula函数,在水文多变量联合分布中模拟较好[33],可用于径流丰枯遭遇的多维联合分布.
有d条河流的径流系列(X1, …, Xd),其边缘分布函数分别为F(x1), …, F(xd).根据Sklar定理,d维联合分布函数H(x1), …, F(xd)可定义为:
| $ H\left( {{x_1}, \cdots , {x_d}} \right) = C\left[ {F\left( {{x_1}} \right), \cdots , F\left( {{x_d}} \right)} \right] = C\left( {{u_1}, \cdots , {u_d}} \right) $ | (1) |
式中,C(u1), …, F(ud)为边缘分布在[0, 1]区间的Copula联结函数;u1=F(x1), …, ud=F(xd)为各单变量的边缘分布,即累积频率;d为联合分布的维数,即变量个数.
Copula函数构造多样,其中Meta-Gaussian Copula在降水径流的多变量联合分布模拟中具有良好效果[4]. d维Meta-Gaussian Copula的分布函数C(u1), …, F(ud)和密度函数c(u1), …, F(ud)分别为:
| $ C\left( {{u_1}, \cdots , {u_d}} \right) = \int_{ - \infty }^{{b_1}} { \cdots \int_{ - \infty }^{{b_d}} {g\left( {{\omega _1}, \cdots , {\omega _d}} \right){\rm{d}}{\omega _1} \cdots {\rm{d}}{\omega _d}} } $ | (2) |
| $ c\left( {{u_1}, \cdots , {u_d}} \right) = {\left| \Sigma \right|^{ - 1/2}}\exp \left( { - {\zeta ^T}{\Sigma ^{ - 1}}\zeta /2 + {\zeta ^T}\zeta /2} \right) $ | (3) |
其中:
| $ g\left( {{\omega _1}, \cdots , {\omega _d}} \right) = {\left( {2{\rm{ \mathsf{ π} }}} \right)^{ - d/2}}{\left| \Sigma \right|^{ - 1/2}}\exp \left( { - {\omega ^T}{\Sigma ^{ - 1}}\omega /2} \right) $ | (4) |
式中,b1=Φ-1(u1), …, bd=Φ-1(ud);ω为被积函数变量矩阵ω=[ω1, …, ωd]T;ζ=[b1, …, bd]T; Σ为相关系数矩阵,即:
| $ \Sigma = \left[ {\begin{array}{*{20}{c}} 1& \cdots &{{\rho _{ij}}}\\ \vdots&\ddots&\vdots \\ {{\rho _{ij}}}& \cdots &1 \end{array}} \right], {\rho _{ij}} = \left\{ {\begin{array}{*{20}{c}} {1, i = j}\\ {{\rho _{ij}}, i \ne j} \end{array}} \right. $ | (5) |
式中,ρij∈[-1, 1];i=1, …, d; j=1, …, d, 为任意两个变量之间的相关系数.
各径流系列的边缘分布可采用水文统计分析较为常用模型进行拟合,即伽马分布(GAMMA)、对数正态分布(LOGN)、韦布尔分布(WBL)、广义极值分布(GEV)、广义Logistic(GLO)、广义正态(GNO)、皮尔逊Ⅲ型(P-Ⅲ).采用Pearson-γ计算河流之间的径流相关性.多个维度的联合分布及其边缘分布模型拟合,分别通过基于Rosenblatt变换的Cramervon Mises检验之一的Sn(B)[34]和Anderson-Darling(A-D)法的An2进行检验.边缘分布模型综合考虑均方根误差(RMSE)、赤池信息准则(AIC)和统计量的P值,进行优选[35].联合分布及边缘分布模型参数均采用最大似然法估计.经验分布频率采用次序统计累积频率并进行适当的变换[36-37].
1.2 径流丰枯分类在水资源分析中,基于降水或径流的丰枯分类并没有统一的划分方法和标准.一种方法是基于距平百分率,划分丰、平、枯的标准[38].更为常用的方法是根据径流频率,如以频率37.5 %和62.5 %划分丰、平、枯3种水平年[2],也有的采用25 %和75 %作为分界线划分丰、平、枯[5].
在《水文基本术语和符号标准》(GB/T 50095—2014)设计年径流中,提出了特枯水年(年降水量或年河川径流量为历年最小值或接近历年最小值的年份)、枯水年(年降水量或年河川径流量显著小于多年均值的年份)、平水年(年降水量或年河川径流量接近多年均值的年份)、丰水年(年降水量或年河川径流量显著大于多年均值的年份).这说明在年径流设计实践中,有时需要更为精细分类,以关注特枯水年或特丰水年的水资源状况.
综上分析,本文拟采用从小到大的累积频率12.5 %、37.5 %、62.5 %和87.5 %为分界值,将径流系列分为特枯水年P≤12.5 %、偏枯水年12.5 % < P≤37.5 %、平水年37.5 % < P≤62.5 %、偏丰水年62.5 % < P≤87.5 %和特丰水年P>87.5 %.
1.3 径流丰枯遭遇单一河流的径流丰枯划分,呈现的是径流的概率区间.丰枯遭遇是指多条河流的径流在不同概率区间的组合事件.若d条河流各自的径流概率区间边界为[ai, bi], i=1, 2…, d,ai∈[0, 1]、bi∈[0, 1]且ai≤bi,d维丰枯遭遇概率则为:
| $ P\left( {{a_1} \le {u_1} \le {b_1}, \cdots , {a_i} \le {u_i} \le {b_i}, \cdots , {a_d} \le {u_d} \le {b_d}} \right) = \\ \sum\limits_{{i_1}}^2 { \cdots \sum\limits_{{i_j}}^2 { \cdots \sum\limits_{{i_d}}^2 {{{\left( { - 1} \right)}^{{i_1} + \cdots {i_j} + \cdots {i_d}}}C\left( {{u_{1, {i_1}}}, \cdots {u_{i, {i_j}}}, \cdots {u_{d, {i_d}}}} \right)} } } $ | (6) |
式中,ij=1, 2;j=1, 2, …, d;ui, 1=ai;ui, 2=bi.
根据概率容斥原理[39],式(6)可解释为:
| $ \begin{array}{l} P\left( {{a_1} \le {u_1} \le {b_1}, \cdots , {a_i} \le {u_i} \le {b_i}, \cdots , {a_d} \le {u_d} \le {b_d}} \right)\\ = C\left( {{b_1}, {b_2}, \cdots , {b_d}} \right)\\ \;\;\; - \left[ {C\left( {{a_1}, {b_2}, {b_3}, \cdots , {b_d}} \right) + C\left( {{b_1}, {b_2}, \cdots , {b_{d - 1}}, {a_d}} \right)} \right]\\ \;\;\; + \left[ {C\left( {{a_1}, {b_2}, {b_3}, \cdots , {b_d}} \right) + C\left( {{b_1}, {b_2}, \cdots , {b_{d - 2}}, {a_{d - 1}}, {a_d}} \right)} \right]\\ \;\;\;\; \vdots \\ \;\;\; + {\left( { - 1} \right)^k}\left[ {C\left( {{a_1}, {a_2}, \cdots , {a_k}, {b_{k - 1}}, \cdots , {b_d}} \right) + C\left( {{b_1}, {b_2}, \cdots , {b_{d - k}}, {a_{d - k + 1}}, \cdots , {a_d}} \right)} \right]\\ \;\;\;\; \vdots \\ \;\;\; + {\left( { - 1} \right)^d}C\left( {{a_1}, {a_2}, \cdots , {a_d}} \right) \end{array} $ | (7) |
式中,k=0, 1, 2, …, d,第k+1项中有
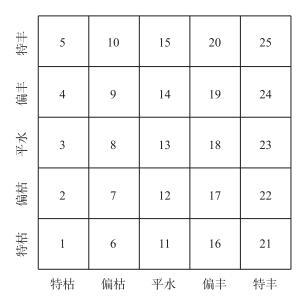
依据上述的特枯、偏枯、平水、偏丰和特丰,共5个概率区间,d条河流的丰枯遭遇情况共有5d个组合,即2、3、4和5条河流的丰枯遭遇组合数分别为25、125、625和3125个.为分析不同组合的概率变化,对多条河流不同概率区间组合的编号顺序按照每条河流从特枯至特丰依次变化.以d=2为例,丰枯组合及编号如图 1所示.因此,多条河流概率区间的组合即同特枯、同偏枯、同平、同偏丰和同特丰的编号分别是:2条河流为1、7、13、19、25,3条河流为1、32、63、94、125,4条河流为1、157、313、469、625,5条河流为1、782、1563、2344、3125.
|
图 1 2条河流的径流区间概率组合编号 Fig.1 Numbering for combination of interval probability of two rivers |
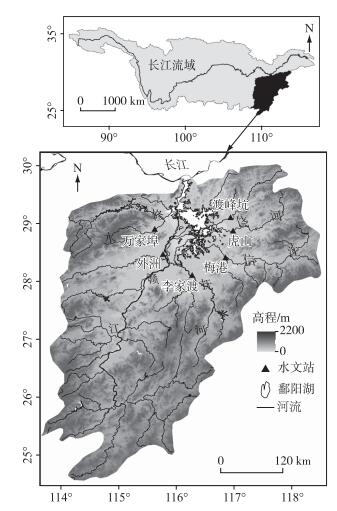
鄱阳湖位于长江中游江西省北部,属于长江流域(图 2).鄱阳湖水系为辐射状,流域面积约为16.22万km2.由于地处中国亚热带湿润季风气候区,雨量充沛,但存在明显的年内变化,通常每年4—9月为汛期,10月至次年3月为非汛期.
|
图 2 鄱阳湖水系地理位置及其河流和水文站点 Fig.2 Location of Lake Poyang Basin and its rivers and gauging stations |
鄱阳湖水系五大河流的水文控制站分别为饶河的渡峰坑和虎山、信江的梅港、抚河的李家渡、赣江的外洲、修水的万家埠和虬津.选用各站1955—2001年共47年(水文年)的逐月径流资料,分析年径流、汛期径流和非汛期径流3个系列的丰枯遭遇特征.部分缺失数据通过选取邻近的水文站资料采用线性插值进行插补,饶河采用渡峰坑和虎山两站径流叠加数据.由于虬津站资料缺失,修水选用其支流潦河万家埠站的径流数据,集水面积约占修水的26.4 %.
2 结果与讨论 2.1 各条河流的径流常规统计特征鄱阳湖五大水系的径流基本特征见表 1,将饶河、信江、抚河、赣江和修水5条河流分别编号.从径流量均值上看,由于赣江集水面积较大,径流量远大于其他河流;修水支流潦河集水面积小,其径流量远小于其他河流.信江和抚河的集水面积相差很小,但前者的径流量明显大于后者.从径流模数上看,信江最大,其次为饶河和修水,抚河和赣江的径流模数较小.从径流量的年际变差系数来看,赣江明显小于其他河流;非汛期径流变差系数大于年径流系列和汛期径流系列.以上结果表明:在单位面积上单位时间所产生的径流量和径流年际变化程度上,北部河流大于南部河流;在时间变化上,非汛期径流的年际变化程度明显大于年径流和汛期径流.
| 表 1 鄱阳湖五大河流的集水面积及径流特征 Tab. 1 Drainage area of five rivers and streamflow statistics in Lake Poyang Basin |
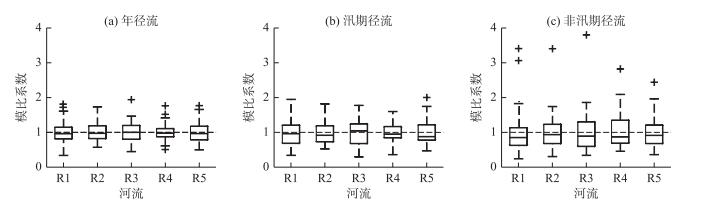
各径流系列的箱形统计如图 3.模比系数等于1的虚线为样本的均值线,箱内实线为中位值. 5条河流的年径流均值与中位值非常接近,非汛期径流均值均大于中位值.抚河的汛期径流均值略小于中位值,其他河流的汛期径流均值大于中位值. 图 3中上下框边界分别对应上四分位数Q1和下四分位数Q3,两端沿虚线延伸出的边界分别对应着Q1-1.5(Q3-Q1)和Q3+1.5(Q3-Q1),在此区间内的值通常认为是正常值,区间外的则被认为是异常值(如图中十字符号所示).除了非汛期径流出现了异常最大值,大部分径流数据均在正常值范围内.
|
图 3 径流统计的箱形图特征 Fig.3 Box plot of streamflow statistics |
每条江各径流系列所有模型拟合检验P值均大于显著性检验水平0.05(表 2),表明常用的7种单变量分布模型均可作为备选的边缘分布.基于RMSE和AIC最小原则,饶河、抚河、信江、赣江和修水的径流系列最优分布:年径流分别为GLO、GLO、GLO、GLO、GNO,汛期径流分别为GNO、P-Ⅲ、GEV、GEV、GNO,非汛期径流分别为GLO、LOGN、GAMMA、GNO、LOGN.为便于对比各条河流径流分布特征差异,同一种径流系列选用同一种模型模拟,即5条河流的年径流、汛期径流、非汛期径流的边缘分布分别选用GLO、GNO、LOGN模型.选用模型和最优模型的RMSE和AIC值差别均较小,对径流系列概率计算影响甚微.
| 表 2 径流统计分布模型拟合检验 Tab. 2 Goodness-of-fit test of statistic distributions of streamflow |
5条河流的年径流形态参数均为负值,其绝对值较小.抚河的汛期径流形态参数为很小的正值,其他河流均为负值,其中饶河、信江和修水的汛期径流形态参数的绝对值较大(表 3).结合选用模型的概率密度曲线(图 4),年径流趋向于对称的分布,汛期径流、非汛期径流均呈现正偏态分布(右偏),水文现象中大多数都属于正偏.
| 表 3 径流分布模型参数 Tab. 3 Parameters of statistical distribution of streamflow |

|
图 4 径流统计分布的概率密度曲线 Fig.4 Curves of theoretical probability density for streamflow statistics |
两条河流之间的径流相关性及联合分布参数如表 4所示,其中饶河与抚河、赣江的相关系数相对较小,其次为修水与抚河、赣江.但从总体上来说,鄱阳湖水系5条河流之间呈现较高的相关性,其中北部与南部河流之间的相关性相对要低些.另外,河流之间的非汛期径流相关性高于年径流和汛期径流. Gaussian Copula模型参数反映了各变量之间的相关性,与相关系数接近.
| 表 4 两条河流的径流相关性及联合分布参数 Tab. 4 Dependence of streamflow for a pair of rivers and parameters of joint distributions |
多维径流联合分布模拟检验P值,均大于显著性检验水平0.05(表 5),表明Gaussian Copula能够很好地模拟鄱阳湖水系多条河流之间的径流联合分布.
| 表 5 径流多维联合分布模拟 Tab. 5 Goodness-fit test of multivariate joint distribution of streamflow |
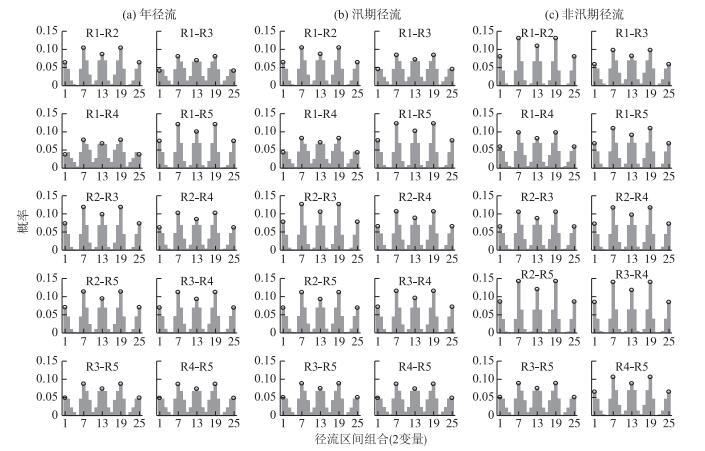
基于各径流系列联合分布,2~5条河流多个维度的丰枯遭遇概率如图 5~8.中空圆圈标注的是同一概率区间遭遇的联合概率,即丰枯同步概率,沿横坐标方向依次表示为同特枯、同偏枯、同平、同偏丰和同特丰.由于1条河流的特枯和特丰的区间概率相等、偏枯和偏丰的区间概率相等,分别为0.125和0.25,选用的Gaussian Copula函数具有对称性,即以同平组合为中心,丰枯两侧对称.因此,多条河流组合的同特枯和同特丰的联合概率相等、同偏枯和同偏丰的联合概率相等.以此类推,如2条河流的特枯与偏枯组合的联合概率等于偏枯与特枯组合的联合概率,5条河流的特枯、偏枯、平水、偏丰与特丰组合的联合概率等于特丰、偏丰、平水、偏枯与特枯组合的联合概率.
|
图 5 2河径流概率区间的联合概率 Fig.5 Joint probability of probability intervals of streamflow for two rivers |

|
图 6 3河径流概率区间的联合概率 Fig.6 Joint probability of probability intervals of streamflow for three rivers |
|
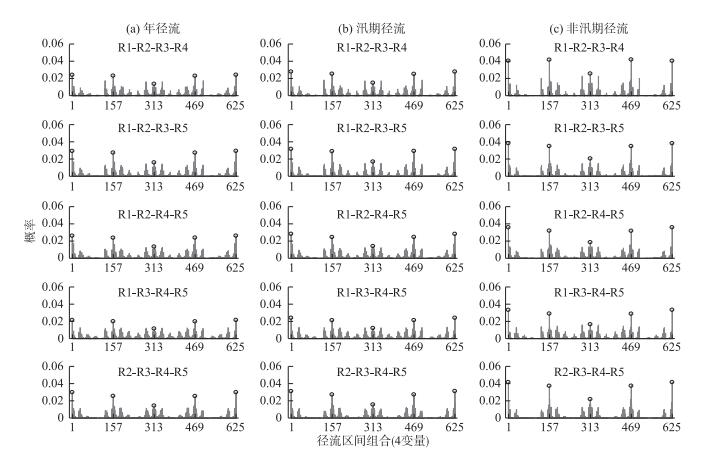
图 7 4河径流概率区间的联合概率 Fig.7 Joint probability of probability intervals of streamflow for four rivers |
|
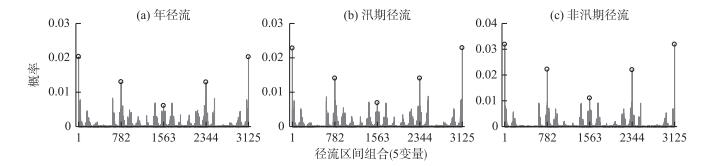
图 8 5河径流概率区间的联合概率 Fig.8 Joint probability of probability intervals of streamflow for five rives |
对比不同概率区间的同步联合概率,2条河流组合的联合概率:同偏枯或同偏丰>同平>同特枯或同特丰;3条河流组合的联合概率:同偏枯或同偏丰>同特枯或同特丰>同平;4条或5条河流组合的联合概率:同特枯或同特丰>同偏枯或同偏丰>同平.也就是说,尽管对每1条河流概率区间设置时,偏枯、平水和偏丰的区间概率相对较大,均为0.25;特枯和特丰的区间概率相对较小,为0.125;但是2条或3条河流的同偏枯或同偏丰的联合概率明显大于同平的联合概率,4条或5条河流同特枯或同特丰、同偏枯或同偏丰的联合概率均明显大于同平的联合概率,且5条河流的同特枯或同特丰的联合概率也明显大于同偏枯或同偏丰的联合概率.以上结果表明,多条河流丰枯遭遇随着维数的增加,丰枯同步的最大联合概率值由同偏枯或同偏丰趋向于丰枯两端的同特枯或同特丰.另外,对于相同的概率区间,非汛期径流的丰枯同步联合概率明显大于年径流和汛期径流,而年径流和汛期径流之间的丰枯同步联合概率差别较小.
2条河流组合丰枯完全异步即1条河特丰1条河特枯概率区间对应的联合概率接近于0.1条河流特丰(特枯)另1条河流偏枯(偏丰)组合的联合概率相比丰枯同步概率相差较大.相邻2条河流组合的丰枯异步概率小于非相邻2条河流组合丰枯异步的概率.对比图 5~8,多条河流丰枯遭遇随着维数的增加,丰枯异步的组合变复杂,但遭遇概率变化趋势是一致的.
5条河流多维的丰枯同步联合概率计算结果见表 6.
| 表 6 多维径流丰枯同步联合概率 Tab. 6 Joint probability of identical probability intervals of streamflow for multiple rivers |
从2条河流丰枯遭遇空间组合上来看,年径流丰枯同步最大联合概率为饶河与修水同偏枯或同偏丰的0.121,其次为信江与抚河的同偏枯或同偏丰的0.119;汛期径流丰枯同步最大联合概率为信江与抚河的同偏枯或同偏丰的0.126,其次为饶河与修水的0.123;非汛期径流丰枯同步最大联合概率为信江与抚河同偏枯或同偏丰的0.142,其次为抚河与赣江的0.140.年径流、汛期径流和非汛期径流的丰枯同步最小联合概率,均为饶河与赣江的同特枯或同特丰,分别为0.037、0.043和0.050;其次均为饶河与抚河的同特枯或同特丰,分别为0.041、0.045和0.058.总体上来说,饶河与信江、饶河与修水、信江与抚河、抚河与赣江之间的丰枯同步概率相对大些,而河流之间其他组合情况下的丰枯同步概率相对小些.
对于3条河流的丰枯遭遇空间组合,年径流丰枯同步最大联合概率为饶河、信江与修水的同偏枯或同偏丰的0.058,其次为信江、抚河与赣江的同偏枯或同偏丰的0.056;汛期径流丰枯同步最大联合概率为信江、抚河与赣江的同偏枯或同偏丰的0.061,其次为饶河、信江与修水的0.058;非汛期径流丰枯同步最大联合概率为信江、抚河与赣江的同偏枯或同偏丰的0.081,其次为饶河、信江与抚河的0.073.年径流和汛期径流的丰枯同步最小联合概率均为饶河、抚河与赣江的同平,分别为0.026和0.028;其次均为抚河、赣江与修水的同平,分别为0.028和0.029;非汛期径流的丰枯同步最小联合概率为饶河、抚河与修水同平的0.031,其次为饶河、赣江与修水同平的0.032.
对于4条河流的丰枯遭遇空间组合,年径流、汛期径流和非汛期径流的丰枯同步最大联合概率均为信江、抚河、赣江与修水的同特枯或同特丰,分别为0.030、0.031和0.042;丰枯同步最小联合概率均为饶河、抚河、赣江与修水的同平,分别为0.011、0.012和0.016.
对于5条河流即全流域的丰枯遭遇,年径流、汛期径流和非汛期径流丰枯同步最大联合概率分别为0.020、0.023和0.032,均为同特丰或同特枯;丰枯同步最小联合概率分别为0.006、0.007和0.011,均为同平.
以上结果表明,同处于流域北部河流(如饶河、信江与修水)或南部河流(如抚河与赣江)或相邻河流(如信江与抚河),它们之间组合的同步联合概率相对要大些,而南北河流组合(如饶河与赣江、修水与赣江)的同步联合概率相对要小.
另外,多条河流丰枯遭遇随着维数的增加,丰枯组合数也增加,丰枯同步的联合概率明显下降.
3 结论运用Gaussian Copula函数,构建了鄱阳湖流域5条河流径流二维至五维的联合分布.基于特枯、偏枯、平水、偏丰和特丰的径流丰枯分类,计算了年径流、汛期径流和非汛期径流的多条河流的多维丰枯遭遇联合概率,分析探讨了多维丰枯同步联合概率的变化特征.主要结论如下:
鄱阳湖水系河流之间具有较高的相关性,Gaussian Copula函数能较好地模拟二维至五维的径流联合分布.由于选用的Gaussian Copula函数具有对称性,即以同平组合为中心,丰枯两侧对称.
多条河流的丰枯遭遇随着维数的增加,丰枯同步的最大联合概率趋向于丰枯两端的概率区间.如5条河流的同特枯或同特丰的联合概率明显大于同偏枯或同偏丰的联合概率,同偏枯或同偏丰的联合概率明显大于同平的联合概率.
对于相同的概率区间,非汛期径流的丰枯同步联合概率明显大于年径流和汛期径流的同步联合概率,而年径流和汛期径流之间的丰枯同步联合概率差别较小.
同处于流域北部河流(如饶河、信江与修水)或南部河流(如抚河与赣江)或相邻河流(如信江与抚河)之间组合,其同步联合概率相较于其他组合大,而南部与北部河流组合(如饶河与赣江、修水与赣江)的同步联合概率相对较小.另外,多条河流丰枯遭遇随着维数的增加,丰枯组合数也增加,丰枯同步的联合概率明显下降.
总之,本文通过构建多维的径流联合分布模型,从多个维度分析了水系径流丰枯遭遇,主要是同步联合概率的情况及空间特征,对区域防洪抗旱以及流域内水资源协调利用有重要意义.但由于Gaussian Copula函数的对称性限制,研究结论未能反映丰枯两侧的差异性.因此,在多维Copula函数的选择方面,需要进一步研究和探讨.
| [1] |
Yao MT, Gao C, Lu M et al. The intensity and frequency characteristics of extreme runoff over the Huaihe River Basin during 1959-2008. Geographical Research, 2015, 34(8): 1535-1546. [姚梦婷, 高超, 陆苗等. 1959-2008年淮河流域极端径流的强度和频率特征. 地理研究, 2015, 34(8): 1535-1546. DOI:10.11821/dlyj201508011] |
| [2] |
Zheng HX, Liu CM. Analysis on asynchronism synchronism of regional precipitation in planned South-to-North Water Transfer Areas. Journal of Geographical Sciences, 2000(5): 523-532. [郑红星, 刘昌明. 南水北调东中两线不同水文区降水丰枯遭遇性分析. 地理学报, 2000(5): 523-532. DOI:10.11821/xb200005002] |
| [3] |
Wang ZG, Luo YZ, Wu MY et al. Synchronous-asynchronous encounter probability analysis on precipitation in the Haihe River Basin during the last five decades. Journal of Natural Resource, 2013, 28(10): 1685-1693. [王中根, 罗燏辀, 吴梦莹等. 近50 a海河流域降水丰枯遭遇分析. 自然资源学报, 2013, 28(10): 1685-1693. DOI:10.11849/zrzyxb.2013.10.004] |
| [4] |
Du YL, Tu XJ, Du XX et al. Analysis of regional irrigation water demand based on high-dimensional Gaussian Copula function. Journal of Hydraulic Engineering, 2018, 49(3): 323-331. [杜奕良, 涂新军, 杜晓霞等. 基于高维Gaussian Copula函数的区域农田灌溉需水分析. 水利学报, 2018, 49(3): 323-331.] |
| [5] |
Mo SH, Sheng B, Zhang XW et al. Synchronous asynchronous encounter probability of rich-poor runoff based on copula function. Journal of Northwest A & F University: Natural Science Edition, 2009, 37(6): 131-136. [莫淑红, 沈冰, 张晓伟等. 基于Copula函数的河川径流丰枯遭遇分析. 西北农林科技大学学报:自然科学版, 2009, 37(6): 131-136.] |
| [6] |
Guan S, Zha XN, Ding B et al. Wetness-dryness encountering of runoff of the pearl river basin based on copula functions. Tropical Geography, 2015, 35(2): 208-217. [关帅, 查悉妮, 丁波等. 基于Copula函数的珠江流域河川径流丰枯遭遇. 热带地理, 2015, 35(2): 208-217.] |
| [7] |
Sun P, Zhang Q, Cheng XH. Copula-based evaluation of high-and low-flows frequency of the Lake Poyang Basin and the risk assessment. J Lake Sci, 2011, 23(2): 183-190. [孙鹏, 张强, 陈晓宏. 基于Copula函数的鄱阳湖流域极值流量遭遇频率及灾害风险. 湖泊科学, 2011, 23(2): 183-190. DOI:10.18307/2011.0204] |
| [8] |
Xie H, Luo Q, Huang JS. Synchronous asynchronous encounter analysis of multiple hydrologic regions based on 3D copula function. Advances in Water Science, 2012, 23(2): 186-193. [谢华, 罗强, 黄介生. 基于三维copula函数的多水文区丰枯遭遇分析. 水科学进展, 2012, 23(2): 186-193.] |
| [9] |
Tu XJ, Chen XH, Diao ZJ et al. Copula runoff model and risk of water shortage in west-to-east water transfer of Pearl River Delta, China. Transactions of the CSAE, 2016, 32(18): 162-168. [涂新军, 陈晓宏, 刁振举等. 珠江三角洲Copula径流模型及西水东调缺水风险分析. 农业工程学报, 2016, 32(18): 162-168. DOI:10.11975/j.issn.1002-6819.2016.18.022] |
| [10] |
Liu ZF, Tan SL, Luo YQ et al. Study of the wetness-dryness encountering of inflow of the three biggest reservoirs in the Dongjiang River basin based on Copula functions. J Lake Sci, 2015, 27(2): 361-370. [刘祖发, 谭圣林, 罗勇强等. 基于Copula函数的东江流域3大水库丰枯遭遇分析. 湖泊科学, 2015, 27(2): 361-370. DOI:10.18307/2015.0222] |
| [11] |
Chen L, Guo S, Zhang HG et al. Flood coincidence probability analysis for the upstream Yangtze River and its tributaries. Advances in Water Science, 2011, 22(3): 323-330. [陈璐, 郭生练, 张洪刚等. 长江上游干支流洪水遭遇分析. 水科学进展, 2011, 22(3): 323-330.] |
| [12] |
Yan BW, Guo S, Chen L et al. Applicability analysis of copula function in hydrological estimation. Mathematics in Practice and Theory, 2008, 42(3): 85-93. [闫宝伟, 郭生练, 陈璐等. Copula函数在水文计算中的适用性分析. 数学的实践与认识, 2008, 42(3): 85-93.] |
| [13] |
Zhang T, Zhao CW, Luo WS. Random simulation of flood hydrographs based on Copula function. Engineering Journal of Wuhan University, 2008, 41(4): 1-4. [张涛, 赵春伟, 雒文生. 基于Copula函数的洪水过程随机模拟. 武汉大学学报:工学版, 2008, 41(4): 1-4.] |
| [14] |
Chen L, Guo S. Copula-based method for multisite monthly and daily streamflow simulation. Journal of Hydrology, 528: 369-384. DOI:10.1016/j.jhydrol.2015.05.018 |
| [15] |
Chen L, Singh VP, Guo S et al. Drought analysis using copulas. Journal of Hydrologic Engineering, 18(7): 797-808. DOI:10.1061/(ASCE)HE.1943-5584.0000697 |
| [16] |
Guo SL, Yan BW, Xiao Y et al. Multivariate hydrological analysis and estimation. Hydrology, 2008, 28(3): 1-7. [郭生练, 闫宝伟, 肖义等. Copula函数在多变量水文分析计算中的应用及研究进展. 水文, 2008, 28(3): 1-7.] |
| [17] |
Tu XJ, Du XX, Du YL et al. Multivariate joint design of hydrological drought and impact of water reservoirs. J Lake Sci, 2018, 30(2): 509-518. [涂新军, 杜晓霞, 杜奕良等. 水文干旱多变量联合设计及水库影响评估. 湖泊科学, 2018, 30(2): 509-518. DOI:10.18307/2018.0222] |
| [18] |
Zhou YL, Yuan XC, Jin JL et al. Reginal Hydrological drought frequency based on copulas. Scientia Geographica Sinica, 2011, 31(11): 1383-1388. [周玉良, 袁潇晨, 金菊良等. 基于Copula的区域水文干旱频率分析. 地理科学, 2011, 31(11): 1383-1388.] |
| [19] |
Ma MW, Song SB. Elliptical copulas for drought characteristics analysis of Xi'an gauging station. Journal of China Hydrology, 2010, 30(4): 36-42. [马明卫, 宋松柏. 椭圆型Copulas函数在西安站干旱特征分析中的应用. 水文, 2010, 30(4): 36-42. DOI:10.3969/j.issn.1000-0852.2010.04.009] |
| [20] |
Tu X, Singh VP, Chen X et al. Uncertainty and variability in bivariate modeling of hydrological droughts. Stochastic Environmental Research and Risk Assessment, 2016, 30(5): 1317-1334. DOI:10.1007/s00477-015-1185-3 |
| [21] |
Ma M, Song S, Ren L et al. Multivariate drought characteristics using trivariate Gaussian and Student t copulas. Hydrological Processes, 2013, 27(8): 1175-1190. DOI:10.1002/hyp.8432 |
| [22] |
Feng P, Niu YJ, Zhang Y et al. Analysis of wetness-dryness encountering probability among water source rivers and the Yellow River in the Western Route of South-to-North Water Transfer Project. Journal of Hydraulic Engineering, 2010, 39(8): 900-907. [冯平, 牛军宜, 张永等. 南水北调西线工程水源区河流与黄河的丰枯遭遇分析. 水利学报, 2010, 39(8): 900-907.] |
| [23] |
Cheng YQ, Sun P, Zhang Q et al. Copula-based analysis of hydrological drought frequency in Poyang Lake Basin. Journal of Natural Disasters, 2013, 22(1): 75-84. [陈永勤, 孙鹏, 张强等. 基于Copula的鄱阳湖流域水文干旱频率分析. 自然灾害学报, 2013, 22(1): 75-84. DOI:10.13577/j.jnd.2013.0111] |
| [24] |
Guo H, Hu Q, Zhang Q et al. Annual variations in climatic and hydrological processes and related flood and drought occurrences in the Poyang Lake Bain. Journal of Geographical Sciences, 2012, 67(5): 699-709. [郭华, HU Qi, 张奇等. 鄱阳湖流域水文变化特征成因及旱涝规律. 地理学报, 2012, 67(5): 699-709.] |
| [25] |
Ye XC, Zhang Q, Liu J et al. Impacts of climate change and human activities on runoff of Poyang Lake Catchment. J Glaciol Geocryol, 2009, 31(5): 835-842. [叶许春, 张奇, 刘健等. 气候变化和人类活动对鄱阳湖流域径流变化的影响研究. 冰川冻土, 2009, 31(5): 835-842.] |
| [26] |
Ye XC, Zhang Q, Liu J et al. Natural runoff change characteristics and flood/drought disasters in Poyang Lake catchment basin. J Nat Disaster, 2012(1): 140-147. [叶许春, 张奇, 刘健等. 鄱阳湖流域天然径流变化特征与水旱灾害. 自然灾害学报, 2012(1): 140-147.] |
| [27] |
Cui T, Xu XF, Liu L et al. Variation characteristics of annual average runoff and evolution law of high and low in Poyang Lake Basin. Water Resources and Power, 2014, 32(8): 22-25. [崔同, 许新发, 刘凌等. 鄱阳湖流域年际径流及丰枯变化分析. 水电能源科学, 2014, 32(8): 22-25.] |
| [28] |
Li SQ, Min Q, Tan GL et al. Cause analysis of low water characteristics of Poyang Lake in 2006. Hydrology, 2008, 28(6): 73-76. [李世勤, 闵骞, 谭国良等. 鄱阳湖2006年枯水特征及其成因研究. 水文, 2008, 28(6): 73-76. DOI:10.3969/j.issn.1000-0852.2008.06.022] |
| [29] |
Hong XJ, Guo SL, Li TY. Multivariate analysis on low flow frequency at Duchang station in Poyang Lake using copula function. Journal of Yangtze River Scientific Research Institute, 2014, 31(12): 11-16. [洪兴骏, 郭生练, 李天元. 基于Copula函数的鄱阳湖都昌站枯水多变量频率分析. 长江科学院院报, 2014, 31(12): 11-16. DOI:10.3969/j.issn.1001-5485.2014.12.003] |
| [30] |
Liu YB, Zhao XS, Wu GP. A primary investigation on the formation of frequent drought in the Poyang lake basin in recent decade. Resources and Environment in the Yangtze Basin, 2014, 23(1): 131-138. [刘元波, 赵晓松, 吴桂平. 近十年鄱阳湖区极端干旱事件频发现象成因初析. 长江流域资源与环境, 2014, 23(1): 131-138. DOI:10.11870/cjlyzyyhj201401019] |
| [31] |
Gan XY, Liu CL, Huang XM. Study on the drought in Poyang Lake. Journal of Anhui Agri Sci, 2011, 39(24): 14676-14678. [甘小艳, 刘成林, 黄小敏. 鄱阳湖干旱分析. 安徽农业科学, 2011, 39(24): 14676-14678. DOI:10.3969/j.issn.0517-6611.2011.24.059] |
| [32] |
Fei YF. A method for estimating the conditional probability of multi-random variables and its application in hydrology. Journal of Hydraulic Engineering, 1995(8): 60-66. [费永法. 多元随机变量的条件概率计算方法及其在水文中的应用. 水利学报, 1995(8): 60-66. DOI:10.3321/j.issn:0559-9350.1995.08.009] |
| [33] |
Renard B, Lang M. Use of a Gaussian copula for multivariate extreme value analysis: Some case studies in hydrology. Advances in Water Resources, 2007, 30(4): 897-912. DOI:10.1016/j.advwatres.2006.08.001 |
| [34] |
Dobri J, Schmid F. A goodness of fit test for copulas based on Rosenblatt's transformation. Computational Statistics & Data Analysis, 2007, 51(9): 4633-4642. |
| [35] |
Genest C, Rémillard B, Beaudoin D. Goodness-of-fit tests for copulas: A review and a power study. Insurance Mathematics & Economics, 2009, 44(2): 199-213. |
| [36] |
Tu X, Du YL, Singh VP et al. Joint distribution of design precipitation and tide and impact of sampling in a coastal area. International Journal of Climatology, 2017, 38(S1): e290-e302. DOI:10.1002/joc.5368 |
| [37] |
Gringorten II. A plotting rule for extreme probability paper. Journal of Geophysical Research, 1963, 68(3): 813-814. DOI:10.1029/JZ068i003p00813 |
| [38] |
Ministry of Water Resources, People's Republic of China ed. Standard for essential technical terms and symbols in hydrology. Beijing: China Planning Press, 1999. [中华人民共和国水利部. 水文基本术语和符号标准. 北京: 中国计划出版社, 1999.]
|
| [39] |
Salvadori G, Durante F, Michele CD. Multivariate return period calculation via survival functions. Water Resources Research, 2013, 49(4): 2308-2311. DOI:10.1002/wrcr.20204 |
 2019, Vol. 31
2019, Vol. 31 


