(2: 黄河勘测规划设计研究院有限公司, 郑州 450003)
(2: Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003, P. R. China)
黄河口属于多沙弱潮型河口,相对于径流动力,河口海洋动力较弱,从黄河中下游挟带来的大量泥沙淤积在河口处.自1976年清水沟流路改道以来,黄河口利津站多年平均来沙量约3.9×108 t/a(1976—1998年),大量泥沙淤积在口门处[1],并在河口形成了广阔的黄河三角洲.与此同时龙羊峡水库的运用(1986年)使得进入黄河口的水沙条件发生较大改变,在自然与人为因素的共同作用下,黄河尾闾段始终处于自然淤积状态[2]. 1999年以后小浪底水库开始进行蓄水拦沙,对黄河下游及其尾闾段的水沙过程与河床冲淤产生了较大影响,主要表现为:水沙系列表现为枯水少沙,含沙量大幅减少,且泥沙主要集中在汛期输移;河床冲刷显著,断面形态朝窄深方向发展[3-4].因此,为确保黄河尾闾段的防洪安全,建立能够精确模拟水沙演进及河床冲淤过程的数学模型具有重要的意义,采用一维水沙数学模型是一条很重要的研究途径.
目前国内外对河口段一维水动力模型有较为深入的研究.如Hossain等[5]采用流量加权法建立了适用于河口段的一维非恒定水动力模型;戴文鸿等[6]在尾闾段河网水流运动特点的基础上,建立一维河网水动力模型研究沿程水位变化;李亦芳等[7]基于实测洪水资料,采用SOEBK的一维水动力学模块计算水位变化.在河口段防洪能力研究中,除了需要掌握河道洪水位变化,还需要分析河床冲淤的影响.一维水沙数学模型一般用于模拟长河段及长时段的水沙演进及河床冲淤过程[8-9].目前部分学者对一维水沙数学模型的计算方法及关键参数取值等问题进行了比较深入的研究,并应用于黄河口尾闾段洪水演进及河床冲淤过程计算.如陈界仁等[10]综合考虑断面水沙分布和冲淤不均匀分布、阻力变化、三角洲淤积延伸等问题,建立了尾闾段(利津至十八公里)一维水沙数学模型.
上述研究表明,现有尾闾段一维水沙数学模型通常将水流过程与河床冲淤过程分开计算,不适用于河床冲淤速率较大的情况.考虑到黄河尾闾段断面形态沿程变化与汛期冲淤变化较大的特点,本文首先建立了一维非恒定流非均匀沙耦合水沙数学模型;然后采用2003年利津—西河口段及2015年利津—汊3段实测资料分别对该模型进行率定及验证;最后基于2015年研究河段的水沙及地形资料,反演不同断面间距下的洪水过程,分析不同断面间距对洪水位及河段冲淤量等计算结果的影响.
1 一维水沙耦合数学模型黄河口属于典型的陆相弱潮河口,感潮段极短.已有研究表明,黄河尾闾段受海洋动力影响较小,在一维模型计算中可不考虑潮汐作用、盐度等影响[10].除此之外,由于水流运动的非恒定特性,结合非均匀泥沙的不平衡输移,尾闾段汛期河床冲淤较为显著[2].故此处采用一维非恒定、非均匀沙的水沙耦合数学模型研究尾闾段的水沙输移及河床冲淤过程.由于该模型仅用于模拟汛期洪水过程,未模拟长时间的冲淤变形,因此可以忽略河口段淤积延伸或蚀退导致的回水影响.
1.1 一维模型控制方程基于不规则断面的一维水沙耦合控制方程,可写为如下形式[8].
水流连续方程:
| $ \frac{\partial Q}{\partial x}+B \frac{\partial Z}{\partial t}=q_{1}-\frac{\partial A_{0}}{\partial t} $ | (1) |
水流动量方程为:
| $ \begin{array}{c} \frac{{\partial Q}}{{\partial t}} + \left( {gA - {\alpha _f}B\frac{{{Q^2}}}{{{A^2}}}} \right)\frac{{\partial Z}}{{\partial x}} + 2{\alpha _f}\frac{Q}{A}\frac{{\partial Q}}{{\partial x}} + gA\left( {{J_f} + {J_l}} \right) + \frac{{{\rho _1}{q_1}{u_1}}}{{{\rho _m}}} = \\ {\left. {\frac{{{Q^2}}}{{{A^2}}}\frac{{\partial A}}{{\partial x}}} \right|_z} - \frac{1}{{{\rho _m}}}\frac{{\Delta \rho }}{{{\rho _s}}}\left( {Q\frac{{\partial S}}{{\partial t}} + \left( {\frac{{{Q^2}}}{A} + gA{h_c}} \right)\frac{{\partial S}}{{\partial x}}} \right) \end{array} $ | (2) |
悬沙输移方程:
| $ \frac{\partial}{\partial t}\left(A S_{\kappa}\right)+\frac{\partial}{\partial t}\left(A U S_{\kappa}\right)=B \omega_{\kappa} \alpha_{\kappa}\left(S_{* \kappa}-S_{\kappa}\right)+S_{l \kappa} q_{1} $ | (3) |
河床冲淤方程:
| $ {\rho ^\prime }\frac{{\partial {A_0}}}{{\partial t}} = \sum\limits_{k = 1}^N B {\omega _\kappa }{\alpha _\kappa }\left( {{S_\kappa } - {S_{*\kappa }}} \right) $ | (4) |
式中,Q为流量;Z为水位;A0、A分别为河床冲淤面积和过水断面面积;B为河宽;αf为水流动量修正系数;S为断面平均含沙量;ρm为浑水密度,ρm=ρf+(Δρ/ρs)S,其中Δρ=ρs-ρf,ρs、ρf分别为泥沙密度和清水密度;ρ1、q1、u1分别为单位河长侧向入出流密度和入出流的流量、侧向入出流流速在主流方向的分量;Jf为水力坡度;Jl为断面扩收引起的局部阻力;hc为过水断面形心淹没深度;g、x、t分别为重力加速度、沿程距离和时间;U为断面平均流速;N为悬沙分组数;Slκ为侧向入出流分组含沙量;ρ′为床沙干密度;S*κ、Sκ分别为第k粒径组悬沙的分组挟沙力和含沙量;ωκ、ακ分别为第κ粒径组悬沙的浑水沉速及恢复饱和系数.
1.2 数值解法及关键问题处理 1.2.1 数值解法该一维数学模型中的浑水控制方程采用非守恒形式,求解微分方程式(1)、(2)时,通常采用Preissmann四点偏心隐格式进行离散,这种格式的数值稳定性及质量守恒性较好,国内外应用较为普遍[8].采用Preissmann四点偏心隐格式进行离散时,利用追赶法求解离散方程中各水流变量,如水位、流量等,进而得出其他水力要素.对于非均匀悬沙不平衡输移方程(式(3)),则直接采用显式迎风格式离散.张晓雷等[9]采用一维水沙数学模型,分析了不同冲淤面积分配模式对黄河下游河道冲淤等计算结果的影响,结果表明等厚度分配模式的计算效果相对较好.因此,河床冲淤方程式(4)采用显格式离散,得到冲淤面积后,按等厚冲淤模式分配确定冲淤后断面上各节点高程.在这里需指出,等厚冲淤模式分配是指当河床冲刷时,仅对主槽区域进行等厚冲刷修正,当河床淤积时,淤积面积沿湿周等厚分布.因此,采用该模式计算冲淤量对水位计算精度影响较小,对流量、含沙量以及河道冲淤特性的计算精度有一定的影响[9].除此之外,此模型还根据不同粒径组的冲淤厚度,采用床沙活动层与分层记忆层考虑冲淤过程中的床沙级配调整[11].
1.2.2 关键问题处理黄河尾闾段沿程断面的滩槽高差变化较大,河床冲淤过程复杂.因此需要事先对这几个关键问题进行处理:滩槽划分及糙率系数、恢复饱和系数以及悬移质水流挟沙力等.
1) 滩槽划分及糙率系数取值.
黄河尾闾段断面形态比较复杂,河床冲淤幅度相对较大,同一断面的滩槽阻力差异较大,因此需要在计算断面上划分出主槽与滩地,进而对主槽与滩地的节点分别用不同代码特征值表示(滩地用1表示,主槽用0表示),如图 1所示.

|
图 1 黄河尾闾段的典型断面形态 Fig.1 Typical cross-sectional profiles at Lijin and Xihekou Stations in the Yellow River Estuary |
糙率是一维水沙模型的关键参数之一,其取值大小不仅能够影响水力计算精度,而且还影响河床冲淤量的计算精度.但糙率确定目前尚无通用的方法,必须根据具体情况率定.现有研究表明,黄河尾闾段糙率的取值范围为n=0.009~0.025,因此糙率率定时应在该范围内取值[12].在实际计算中,通常用流量与糙率关系确定主槽糙率,而高滩与低滩的糙率则取一固定值.根据黄河口实测水沙数据拟定若干组流量级,然后确定各控制断面在不同流量级下的糙率值,通过模型计算结果再调整糙率,直至使水位计算值与实测值拟合较好.
2) 恢复饱和系数取值.
黄河下游及河口段的悬移质泥沙输移经常处于非平衡状态.恢复饱和系数ak表示悬移质含沙量恢复至挟沙力的速率,其取值越大表示含沙量向挟沙力靠近越快,反之则越慢. ak的取值直接影响河床冲淤速率.关于恢复饱和系数的研究,韩其为等[13]给出了在河床冲淤强平衡条件下有关参数及恢复饱和系数的表达式;方红卫等[14]在建立一维全沙输移数学模型时,讨论了恢复饱和系数在不同河床边界条件下的求解方法;张红武等[15]则通过引入非饱和系数与附加系数,对河床变形方程进行了改进.针对黄河尾闾段的水沙及河床冲淤特性,本文采用韦直林等[16]提出的公式进行恢复饱和系数计算:
| $ a_{k}=\frac{m}{\omega_{k}^{n}} $ | (5) |
式中,m取0.001;当冲刷时,n=0.74;当淤积时,n=0.28.
3) 悬移质水流挟沙力计算.
悬移质水流挟沙力是河床冲淤计算的重要基础,其取值是否合理将直接影响河床冲淤的计算精度.本文采用Zhang等[17]提出的黄河水流挟沙力的通用公式,该公式充分考虑了高含沙量对挟沙力的影响,可表示为:
| $ {S_*} = 2.5{\left[ {\frac{{\left( {0.0022 + {S_v}} \right){U^3}}}{{\kappa \frac{{{\rho _s} - {\rho _m}}}{{{\rho _m}}}gh{\omega _m}}}\ln \left( {\frac{h}{{6{D_{50}}}}} \right)} \right]^{0.62}} $ | (6) |
式中,h为断面平均水深;κ为与含沙量相关的卡门常数;Sv为体积比含沙量;D50为床沙中值粒径;ωm为非均匀悬沙的代表沉速,
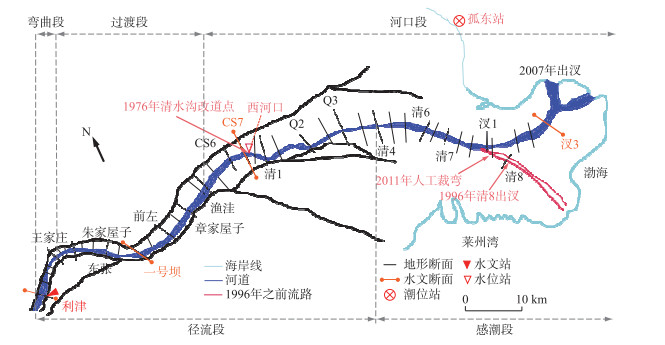
黄河口属于弱潮陆相型河口,位于莱州湾与渤海湾之间,潮差沿黄河三角州海岸分布呈马鞍形,平均潮差约1.5 m[18].黄河尾闾段上起利津,下至渤海湾,总长约106 km,如图 2所示.按照河床演变特点不同,黄河尾闾段可分为弯曲段、过渡段及河口段.利津-王家庄河段为弯曲段,约10 km,主河槽窄深,滩槽高差较大(4~7 m),沿岸控导工程使主要河湾得到控制,因此主槽横向摆动不明显;渔洼以下为河口段,约66 km,主槽宽浅,滩槽高差较小(2~3 m),清4断面以下无控导工程,因此河势变化较剧烈[2];王家庄-渔洼为弯曲段向河口段发展的过渡型河段,约30 km,滩槽高差约4~5 m,沿岸控导工程较少,主槽摆动频繁.根据研究,黄河口感潮段极短,在西河口断面水流运动已不受海洋动力的影响[20].故如果以水动力特点划分尾闾河段时,则可将利津-清4区间划分为径流段,清4-口门区间划为感潮段[21].近年来黄河口实测水沙资料不齐全,且西河口断面以下未再设置水位站,仅在黄河入海口北侧约15 km处设置有孤东潮位站.已有研究表明,黄河口海区底部坡度较小, 平均比降仅0.1 ‰ [18-19],在此范围内海区的潮位变化很小,且汊3断面临近黄河入海口,可以认为该断面水位过程基本与潮位过程一致,故该站实测潮位资料可近似作为汊3断面的潮位资料.本研究选取利津-西河口段具有较全实测水沙资料的年份对该模型进行详细率定,再用利津-汊3河段的实测资料对该模型进行验证.
|
图 2 黄河尾闾河道平面示意 Fig.2 Planview of the Yellow River Estuary |
黄河尾闾利津-西河口河段包含了弯曲段、过渡段和河口段,全长约50 km. 2003年该河段布设有利津水文站、一号坝和西河口两个水位站(同时为临时水文站),以及11个淤积观测断面.根据实测资料分析,1990-2000年利津-西河口段处于持续淤积状态,累计淤积量达3991万m3;小浪底水库进行蓄水拦沙运用后,尾闾段经历了持续冲刷过程,2000-2015年累计冲刷量达4010万m3,其中2003年冲刷量最大,达1677万m3.这是由于该年度出现了多次较大洪水过程,导致黄河尾闾段河床冲刷严重,故本文采用2003年实测水沙及地形资料率定该数学模型.
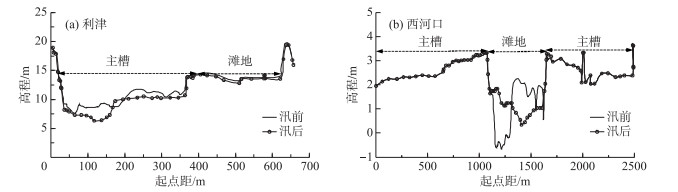
3.1 2003年洪水过程及计算条件在黄河尾闾段,2003年9-10月发生了多次较大的洪水过程,洪水形成原因包括自然降水及小浪底水库调水调沙形成的人造洪水,因此该年汛期尾闾段洪水特点为大流量、长历时. 9月利津站洪峰流量为2790 m3/s,最大含沙量为85.4 kg/m3,悬沙中值粒径为0.025 mm;10月利津站洪峰流量为2890 m3/s,最大含沙量为33.1 kg/m3,本月洪水泥沙组成较粗,悬沙中值粒径达0.035 mm.在经历了长时间的洪水过程后,利津-西河口段冲刷严重,实测冲刷量达1677万m3. 图 3给出了2003年研究河段内利津和西河口2个典型断面的汛前与汛后形态调整.
|
图 3 2003年黄河尾闾段利津和西河口实测断面形态调整 Fig.3 Variation in typical cross-sectional profiles at Lijin and Xihekou Stations in the Yellow River Estuary in 2003 |
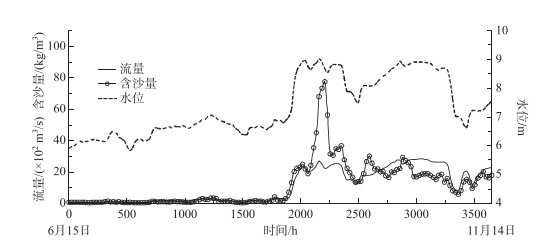
本模型采用该河段2003年6月实测的11个断面作为初始地形,并在维持原断面形态的基础上适当进行概化处理.总模拟时长为3648 h(6月15日-11月14日),计算时间步长取120 s.上游进口边界采用2003年利津站实测流量及含沙量过程,下游出口边界采用2003年西河口站实测水位过程,如图 4所示.
|
图 4 模型率定时的进出口边界条件(2003年) Fig.4 Boundary conditions used in the model calibration in 2003 |
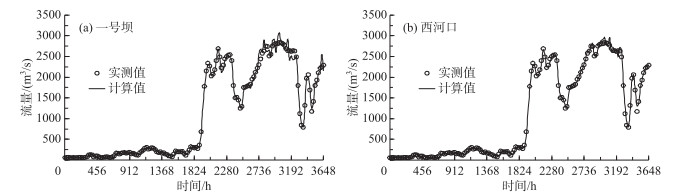
采用建立的一维水沙耦合数学模型计算了2003年尾闾段的洪水演进及河床冲淤过程.从图 5可知,一号坝及西河口两断面的流量计算过程与实测值总体比较符合,计算的洪峰传播时间与实际传播时间基本一致,但计算值略大于实测值,其中一号坝断面计算值的平均相对误差为0.08 %,西河口断面的平均相对误差为0.17 %.在一号坝断面(图 5a),计算洪峰最大流量为3069 m3/s,而实测值为2840 m3/s,计算值比实测值偏大8.1 %;在西河口断面(图 5b),计算洪峰最大流量为2953 m3/s,仍大于实测最大流量(2840 m3/s),但仅偏大3.9 %.值得注意的是,该模型暂未考虑洪水演进过程中含沙量大小及床沙级配调整等因素对糙率的影响,当前仅考虑了流量大小对河床糙率的影响,这可能是造成本次洪峰流量的计算值相较于实测值均产生一定的偏差的原因.因此,还需结合黄河口尾闾段的水沙过程与河床演变特点,选择合适的动床阻力公式进一步完善该一维水沙耦合数学模型.
|
图 5 2003年汛期一号坝(a)和西河口(b)典型断面流量的计算与实测过程对比 Fig.5 Comparisons between the simulated and measured discharge hydrographs at Yihaoba(a) and Xihekou(b) Stations during the flood season in 2003 |
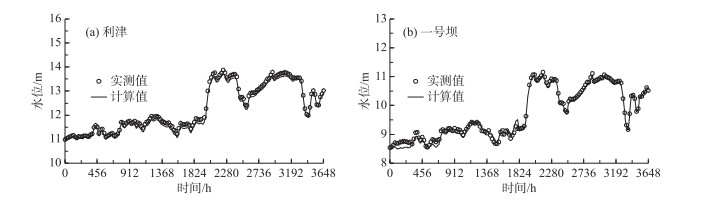
2003年汛期典型断面的水位计算值与实测值拟合较好(图 6).在利津断面(图 6a),计算最高水位为11.0 m,而实测为11.1 m,计算值仅比实测值偏小0.9 %;在一号坝断面(图 6b),计算最高水位为13.7 m,小于实测最高水位(13.9 m),但两者误差为1.4 %.由于河段沿程水位变化与河床变形有直接的关系,因此水位计算值与实测值符合较好也能间接说明河床变形模拟结果与实际过程基本符合.
|
图 6 2003年汛期利津(a)和一号坝(b)典型断面水位的计算与实测过程对比 Fig.6 Comparisons between the simulated and measured water level hydrographs at Lijin(a) and Yihaoba(b) Stations during the flood season in 2003 |
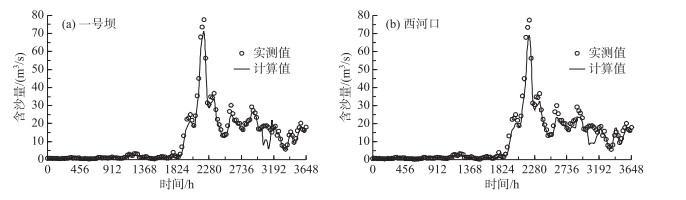
一号坝及西河口断面的含沙量计算过程与实测过程符合较好.在一号坝断面(图 7a),计算最大含沙量为71 kg/m3,相较于实测最大含沙量(77 kg/m3)偏小7.8 %;在西河口断面(图 7b),计算含沙量过程与实测过程拟合较好,计算最大含沙量为20 kg/m3,而实测为21 kg/m3,两者误差仅4.8 %.这两个典型断面的最大含沙量计算值均小于实测值,这主要是由于该模型计算的利津至一号坝河段冲刷量偏小,因此洪水演进到西河口时计算的含沙量峰值偏大.
|
图 7 2003年汛期典型一号坝(a)和西河口(b)断面含沙量计算与实测过程对比 Fig.7 Comparisons between the simulated and measured concentration hydrographs at Yihaoba(a) and Xihekou(b) Stations during the flood season in 2003 |
2003年洪水过程使黄河尾闾段冲刷严重.从分河段冲刷量来看,各分河段计算结果均为冲刷.从河段总冲淤量来看,利津-西河口河段实测冲刷量1677万m3,数学模型计算结果为1601万m3,因此计算的河段冲刷量与实测值较为接近.从上述模型率定结果看,该模型经率定后的各水文断面的流量、水位、含沙量及累计河段冲淤量的计算结果均与实测值较为一致.因此,率定后的模型可用于计算黄河尾闾段其他年份的洪水演进及河床冲淤过程.
4 模型验证采用黄河尾闾段2015年汛期的实测水沙资料,对所建立的一维水沙数学模型进行验证.由于实测资料有限,验证过程仅比较典型断面的水位过程与河段冲淤量数据.此外以往研究表明:断面间距的变化对一维水沙数学模型计算结果会产生较大影响[22-23],在模型中采用的断面数量越多(即断面间距越小),模型的计算精度越好;但另一方面,增加实测断面的数量无疑也增加了测量成本.因此,在数学模型中如何确定合适的断面数量来保证计算精度,这方面的研究非常重要. 2004年以后,黄河尾闾段实测断面数量由原来的18个增至41个,且在2015年汛期河床淤积较为显著(淤积量为425万m3).故此处还采用验证后的数学模型,以2015年汛期水沙过程为例,模拟不同断面间距对利津-西河口河段水沙演进及河床冲淤结果的影响.
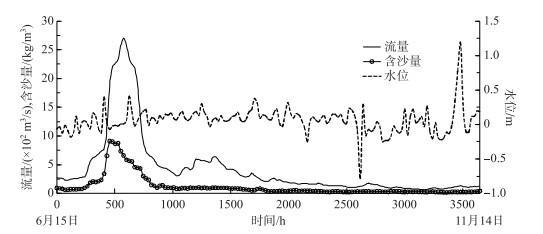
4.1 2015年洪水过程及计算条件据统计,2015年汛期洪水过程受到尾闾段上游降雨的影响,其中7月利津站洪峰流量达2700 m3/s,最大含沙量为9.09 kg/m3. 2015年黄河尾闾河段洪水挟带的含沙量较低,且悬沙较细,中值粒径仅为0.009 mm.采用利津至汊3河段2015年汛前实测的41个断面地形作为初始地形,总模拟时长为3648 h(6月15日-11月14日),计算时间步长取120 s. 图 8所示为模型验证中采用的上、下游边界条件,上游进口边界采用2015年利津站实测的流量与含沙量过程,下游出口边界采用孤东站实测潮位过程.从图 8还可以看到,孤东站实测潮位总体在-0.8~1.2 m之间变化(这里还需指出,孤东站的潮位资料已换算到大沽高程系统).
|
图 8 模型验证所用的进出口边界条件(2015年) Fig.8 Boundary conditions used in the model verification in 2015 |
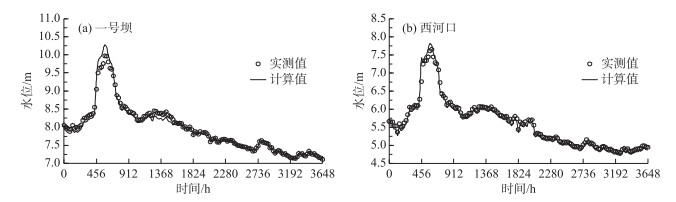
采用率定后的一维水沙数学模型反演了黄河尾闾段2015年的洪水演进与河床变形过程.由于2015年一号坝及西河口两个水位站未测流量及含沙量等数据,故无法比较这些水沙要素的计算与实测过程.从河段水位变化过程可以看到,计算与实测水位过程符合较好,在一定程度上说明模型很好地反映了黄河尾闾河段水沙运动特性(图 9).在一号坝断面(图 9a),水位计算值与实测值的绝对误差范围在0.01~0.81 m之间,最大误差不超过6.9 %;在西河口断面(图 9b),计算值与实测值的绝对误差范围在0~0.81 m之间,最大误差不超过8.8 %.此外利津和一号坝两断面计算的最高水位较实测值略有偏大.综合分析可知,导致出现上述差异的可能原因是两断面所在河段水位变化受河势调整及主流顶冲等影响较大,在局部位置造成了壅水现象[24].
|
图 9 2015年汛期一号坝(a)和西河口(b)典型断面水位计算与实测过程比较 Fig.9 Comparisons between the simulated and measured water level hydrographs at Yihaoba(a) and Xihekou(b) Stations during the flood season in 2015 |
表 1给出了利津至汊3段冲淤量计算值与实测值的对比.从整体上看,研究河段内冲淤量的模拟结果与实测值相差较小.根据实测数据,该计算时段内研究河段的累计淤积量达425万m3,而数学模型计算结果为440万m3.从分河段冲淤量来看,利津(LJ)至一号坝(YHB)、一号坝(YHB)至汊3(C3)段模型计算的淤积量与采用断面法计算的淤积量的绝对误差分别为41万和26万m3,其中利津至一号坝段淤积量的计算值与实测值差异较为明显.综合分析导致以上误差原因有以下几点:由于实测冲淤量的测量精度与冲淤量的大小有关,冲淤量越大则测量相对误差越小.除此之外,本文在统计分河段冲淤量采用的是断面法,本身就存在一定的误差.有关黄河冲淤量计算方法的研究成果很多,如申冠卿等[25]对断面法计算冲淤量的误差来源进行了总结,包括:断面测量本身有精度误差,即由测量方法或测量技术引起;淤积断面代表性误差,即断面位置布设及断面疏密情况的影响.因此,这些因素可能是造成河段冲淤量计算结果与实测值产生差异的原因.
| 表 1 利津至汊3段累计淤积量的计算值与实测值比较 Tab. 1 Comparisons between the simulated and measured channel evolution volumes in the Lijin-C3 reach |
详细的河道断面地形资料是开展一维水沙数学模型研究的基础,通常减小断面间距能适当提高计算精度[22].对于一维水沙数学模型而言,影响计算精度的主要因素包括关键参数的处理、数值计算方法及足够的断面数量.而现有一维数学模型研究成果多从关键参数的处理和数值计算方法上分析对计算结果的影响,如Guo等[26]建立了基于非均匀沙不平衡输沙理论的一维恒定流模型,用于计算黄河下游河段的一般洪水与高含沙洪水的河床变形过程,通过在动量方程中加入一个额外项来计算侧向分汇流对水沙输移的影响,提高了模型的适用性.黄河尾闾段断面形态复杂且沿程变化较大,本文采用的一维水沙耦合数学模型已充分考虑了数值计算方法与关键参数的处理,采用2015年汛期的实测资料验证了该模型.此处在保持其他计算条件不变的情况下,进一步分析不同断面间距对沿程水位及河段冲淤量结果的影响.
4.3.1 计算工况介绍小浪底水库运用前,黄河口尾闾段布设了若干淤积统测断面,但数量较少. 2004年以前尾闾段统测断面数量仅19个,断面最大间距6.84 km,平均间距5.11 km. 2004年后为准确计算尾闾段的冲淤量,不仅延伸了测量范围且对淤积断面数量进行了加密,统测断面延伸至汊3断面,断面数量增至41个,平均间距2.36 km.此处以利津至汊3段的41个计算断面(CS41)的计算结果作为参照,并将现有41个计算断面依次减少为37、31、28、22和15个,同时保证在断面数量减少的同时相邻两断面间距相对变化不大.这五种不同工况分别定义为CS37、CS31、CS28、CS22和CS15,相应的平均断面间距(Δx)分别为2.62、3.14、3.41、4.49和7.08 km(表 2),为方便计算结果比较,每个工况都包含了一号坝和西河口断面.
| 表 2 不同计算工况断面参数及计算结果 Tab. 2 Simulated results for the cases with different numbers of cross-sections |
为分析断面间距对计算结果的影响,不同工况计算时所有关键参数保持不变.采用上述数学模型计算了不同工况下尾闾段(利津-汊3)2015年汛期的洪水演进与河床冲淤过程.为方便分析,图 10仅给出利津与一号坝两断面在CS41与CS15工况下水位过程的计算结果.
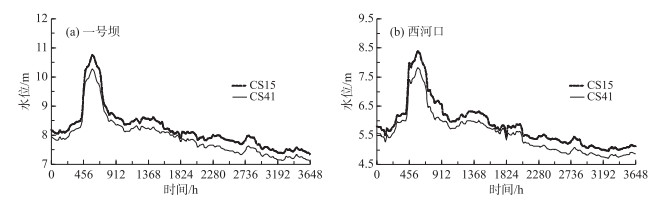
|
图 10 一号坝(a)和西河口(b)不同断面间距下水位过程的计算结果对比 Fig.10 Comparisons between simulated and measured water levels for cases of CS41 and CS15 at Yihaoba(a) and Xihekou(b) Stations |
从表 2及图 10中可以看出,不同工况的水位计算结果相差不大.其中一号坝断面CS41工况计算的最高水位值(Zmax)最小(10.11 m);CS22工况计算的最高水位值最大(10.92 m);西河口断面CS41工况计算的最高水位值最小(7.77 m),CS22工况计算的最高水位值最大(8.85 m).与CS41工况计算的最高水位值相比,其他工况下一号坝与西河口断面最高水位的最大绝对误差分别为0.81和1.08 m.
无论从分河段还是河段总冲淤量(Ved)来看,断面间距对计算结果均影响较大.以LJ-YHB分河段为例,该河段冲淤量实测值为235万m3,表现为淤积,CS41、CS37、CS31、CS28、CS22和CS25工况下计算的LJ-YHB河段冲淤量分别为286万、136万、116万、98万、-20万和-16万m3,可以看出LJ-YHB分河段在CS22及CS15这两个工况下计算值出现了明显的偏差.从河段总冲淤量来看,上述五个工况的计算值均表现为淤积,但CS15工况与实测值差异最大.
综合以上分析可知,对于黄河尾闾段2015年汛期水沙过程而言,不同断面间距对一维数学模型计算结果有一定的影响:断面间距的增加或减少对水位计算结果影响较小,而对河段冲淤量的计算结果影响较大.综上,对于黄河尾闾段复杂的河道断面形态,采用一维水沙数学模型计算时应考虑断面间距的影响.就黄河尾闾段2015年汛期水沙过程而言,断面间距不应超过3.41 km.但在这里需特别指出:黄河尾闾段的河道断面形态随河床冲淤变化(包括河口段的淤积延伸和蚀退)一直处于动态的调整过程中,但该模型暂时还未考虑断面形态的横向调整[27],故这方面的模拟功能需要在后续研究中进一步完善.
5 结论本文采用一维水沙耦合数学模型计算黄河尾闾段不同类型的洪水演进及河床冲淤过程,同时分析了不同断面间距对该模型计算结果的影响,主要得到以下结论:
1) 针对黄河尾闾段复杂断面形态及水沙运动特点,建立了基于耦合解法的一维水沙数学模型.该模型的控制方程采用了含动量附加项的圣维南方程组、非均匀沙不平衡输移方程及河床变形方程,能够考虑河床冲淤对水流运动的影响;此外,该模型还考虑了潮流对水沙输移的影响,适用于模拟黄河尾闾段在径流与潮流共同作用下的洪水演进及河床冲淤过程.
2) 采用黄河尾闾利津-西河口段2003年汛期实测洪水过程资料详细率定了该一维数学模型,结果表明各水文断面的流量、水位、含沙量及累计河段冲淤量的计算值均与实测值总体符合较好.然后采用尾闾段(利津-汊3)2015年汛期实测洪水过程资料验证了该模型,结果表明典型断面的水位及累计河段冲淤量的计算值与实测值较为一致.说明该模型经率定及验证后可较精确地计算尾闾段复杂断面形态下的洪水演进及河床冲淤过程.
3) 通过不同工况下黄河尾闾段(利津-汊3)2015年汛期洪水过程,分析了不同断面间距对该河段内沿程水位及河床冲淤量计算结果的影响.结果表明断面间距越小,计算结果与实测值越符合;考虑到黄河尾闾段水沙输移及河床变形的复杂特性,就该场次洪水过程而言,计算断面间距不应超过3.41 km.
| [1] |
Li G, Wei H, Han Y et al. Sedimentation in the Yellow River delta, part Ⅰ:Flow and suspended sediment structure in the upper distributary and the estuary. Marine Geology, 1998, 149(1/2/3/4): 93-111. |
| [2] |
Hou ZJ, You BH, Li SG. Erosion and deposition characteristic analysis of tail reaches in the Yellow River Estuary in recent years. Journal of Sediment Research, 2009(1): 48-53. [侯志军, 由宝宏, 李士国. 近年来黄河尾闾河道冲淤特性分析. 泥沙研究, 2009(1): 48-53. DOI:10.3321/j.issn:0468-155X.2009.01.008] |
| [3] |
Ru YY, Wang KR, Hou ZJ. Response of the reach near the Yollow River Estuary to the operation of Xiaolangdi Reservoir. Journal of Sediment Research, 2008(3): 63-68. [茹玉英, 王开荣, 侯志军. 黄河口河道对小浪底水库运用的响应. 泥沙研究, 2008(3): 63-68. DOI:10.3321/j.issn:0468-155X.2008.03.009] |
| [4] |
Chen JG, Zhou WH, Han SS. Ponderations and suggestions on operation mode of Xiaolangdi Reservoir in its second stage of sediment retaining. Journal of Hydraulic Engineering, 2015, 46(5): 574-583. [陈建国, 周文浩, 韩闪闪. 黄河小浪底水库拦沙后期运用方式的思考与建议. 水利学报, 2015, 46(5): 574-583.] |
| [5] |
Hossain S, Eyre B, Mcconchie D. Suspended sediment transport dynamics in the sub-tropical micro-tidal Richmond River estuary, Australia. Estuarine Coastal & Shelf Science, 2001, 52(5): 529-541. |
| [6] |
Dai WH, Zhang Y, Gao S et al. Application of 1-D mathematical model of lower river networks. Hydro-Science and Engineering, 2011, 27(4): 97-101. [戴文鸿, 张云, 高嵩等. 尾闾段河网一维水流数学模型应用研究. 水利水运工程学报, 2011, 27(4): 97-101. DOI:10.3969/j.issn.1009-640X.2011.04.015] |
| [7] |
Li YF, Lei GE, Wang X et al. Applicability of a one-dimensional hydraulic model in Yellow River estuary based on SOBEK. Journal of China Hydrology, 2011, 31(5): 72-75. [李亦芳, 葛雷, 王新功等. 基于SOBEK的黄河口一维水力学模型适用性研究. 水文, 2011, 31(5): 72-75. DOI:10.3969/j.issn.1000-0852.2011.05.014] |
| [8] |
Xia JQ, Zhang XL, Wang ZH et al. Modelling of hyperconcentrated flood and channel evolution in a braided reach using a dynamically coupled one-dimensional approach. Journal of Hydrology, 2018, 561. |
| [9] |
Zhang XL, Xia JQ, Li J et al. Influence of cross section area distribution modes of erosion and deposition to results of one-dimensional morphodynamic model for the Lower Yellow River. Journal of Sediment Research, 2017, 42(1): 53-59. [张晓雷, 夏军强, 李洁等. 冲淤面积分配模式对黄河下游一维模型计算结果的影响. 泥沙研究, 2017, 42(1): 53-59.] |
| [10] |
Chen JR, Chen GX. One dimensional mathematical model of water and sediment routing in the Yellow River Mouth Reach. Advances in Water Science, 1995, 6(4): 297-303. [陈界仁, 陈国祥. 黄河河口段一维水流泥沙数学模型. 水科学进展, 1995, 6(4): 297-303. DOI:10.3321/j.issn:1001-6791.1995.04.006] |
| [11] |
Xia JQ, Zhang XL, Deng SS et al. Modelling of hyperconcentrated floods in the lower Yellow River using a coupled approach. Advances in Water Science, 2015, 26(5): 686-697. [夏军强, 张晓雷, 邓珊珊等. 黄河下游高含沙洪水过程一维水沙耦合数学模型. 水科学进展, 2015, 26(5): 686-697.] |
| [12] |
Cao WH, Hu CH, Jiang NS et al. Experimental study on reactions of mouth bar of the Yellow River on the upstream river channel. Journal of Sediment Research, 2005(1): 1-6. [曹文洪, 胡春宏, 姜乃森等. 黄河口拦门沙对尾闾河道反馈影响的试验研究. 泥沙研究, 2005(1): 1-6. DOI:10.3321/j.issn:0468-155X.2005.01.001] |
| [13] |
Han QW. A study on coefficient of saturation recovery. Journal of Sediment Research, 1997, (3):32-40. [韩其为, 何明民.恢复饱和系数初步研究.泥沙研究, 1997, (3):32-40. http://www.cnki.com.cn/Article/CJFDTotal-NSYJ703.004.htm ]
|
| [14] |
Fang HW, Wang GQ. 1-D Numerical simulation for total sediment transport and its application. Journal of Basicence & Engineering, 2000, 8(2): 154-164. [方红卫, 王光谦. 一维全沙泥沙输移数学模型及其应用. 应用基础与工程科学学报, 2000, 8(2): 154-164. DOI:10.3969/j.issn.1005-0930.2000.02.007] |
| [15] |
Zhang HW, Huang YD, Zhao LJ et al. A mathematical model for unsteady sediment transport in the lower Yellow River, Ⅰ, model equations and numerical method. Advances in Water Science, 2002, 13(3): 265-270. [张红武, 黄远东, 赵连军等. 黄河下游非恒定输沙数学模型-Ⅰ模型方程与数值方法. 水科学进展, 2002, 13(3): 265-270. DOI:10.3321/j.issn:1001-6791.2002.03.001] |
| [16] |
Wei ZL, Zhao LK. Research on mathematical model for sediment in Yellow River. Journal of Wuhan University of Hydraulic & Electric Engineering, 1997(5): 21-25. [韦直林, 赵良奎. 黄河泥沙数学模型研究. 武汉大学学报:工学版, 1997(5): 21-25.] |
| [17] |
Zhang HW, Huang YD, Zhao LJ et al. A mathematical model for unsteady sediment transport in the lower Yellow River. International Journal of Sediment Research, 2001, 16(2): 150-158. |
| [18] |
Chen ZR. The tidal range of the modern Yellow River Estuary. Transactions of Oceanology and Limnology, 1988(4): 85-88. [陈彰榕. 黄河现行河口的潮区界. 海洋湖沼通报, 1988(4): 85-88.] |
| [19] |
Huang YC, Liu AJ. Characteristics of tidal in the seaport of Yellow River. Advances in Marine Science, 1989(2): 69-73. [黄易畅, 刘爱菊. 黄河海港海域的潮汐特征. 海洋科学进展, 1989(2): 69-73.] |
| [20] |
Wang KR, Huang HJ, Zhang YP. Shrinkage on riverbed form of the tail of Yellow River Mouth in Qingshuigou course. Marine Geology & Quaternary Geology, 2008, 28(2): 15-22. [王开荣, 黄海军, 张永平. 黄河清水沟流路河口尾闾段河床形态萎缩特征. 海洋地质与第四纪地质, 2008, 28(2): 15-22.] |
| [21] |
Yu X, Wang WZ, Li Y et al. Processes of the Yellow River Estuary since operation of the Xiaolangdi Reservoir. Journal of Sediment Research, 2016(6): 8-11. [余欣, 王万战, 李岩等. 小浪底水库运行以来黄河口演变分析. 泥沙研究, 2016(6): 8-11.] |
| [22] |
Castellarin A, Baldassarre GD, Bates PD et al. Optimal cross-sectional spacing in Preissmann Scheme 1D Hydrodynamic Models. Journal of Hydraulic Engineering, 2009, 135(2): 96-105. DOI:10.1061/(ASCE)0733-9429(2009)135:2(96) |
| [23] |
Zhang XL, Xia JQ, Deng SS et al. Effect of different cross-sectional spacing on simulation results of hyperconcentrated floods in Lower Yellow River. Journal of Zhejiang University:Engineering Sciences, 2016, 50(4): 735-743. [张晓雷, 夏军强, 邓珊珊等. 断面间距对黄河下游高含沙洪水模拟结果影响. 浙江大学学报:工学版, 2016, 50(4): 735-743.] |
| [24] |
Shen GQ, Qu SJ, Zhang YF et al. Effect of cross section regulation in flood period on the capacity of conveyance flood of the lower Yellow River. Journal of Sediment Research, 2001(6): 33-38. [申冠卿, 曲少军, 张原锋等. 黄河下游洪水期断面调整对过洪能力的影响. 泥沙研究, 2001(6): 33-38. DOI:10.3321/j.issn:0468-155X.2001.06.006] |
| [25] |
Shen GQ, Jiang NQ, Zhang YF et al. Comparison of the calculated sedimentation amount by different methods in the Lower Yellow River. Journal of Sediment Research, 2006(1): 32-37. [申冠卿, 姜乃迁, 张原锋等. 黄河下游断面法与沙量法冲淤计算成果比较及输沙率资料修正. 泥沙研究, 2006(1): 32-37. DOI:10.3321/j.issn:0468-155X.2006.01.005] |
| [26] |
Guo QC, Hu CH, Koniyoshi T et al. Numerical modeling of hyper-concentrated sediment transport in the lower Yellow River. Journal of Hydraulic Research, 2008, 46(5): 659-667. DOI:10.3826/jhr.2008.3009 |
| [27] |
Zheng S, Han SS, Tan GM et al. Morphological adjustment of the Qingshuigou channel on the Yellow River Delta and factors controlling its avulsion. Catena, 2018, 166: 44-55. DOI:10.1016/j.catena.2018.03.009 |
 2019, Vol. 31
2019, Vol. 31 


