(2: 广西防灾减灾与工程安全重点实验室, 南宁 530004)
(2: Guangxi Key Laboratory of Disaster Prevention and Reduction and Engineering Safety, Nanning 530004, P. R. China)
随着我国经济的高速发展,越来越多沿江城市在穿城河流的支流入汇口附近修建了大量防洪排涝闸、防洪堤等,此类修建在干、支流交汇河口处支流上的水利工程,不仅会受到支流洪水的直接影响,而且还会受到干流洪水的顶托作用,其防洪设计水位确定应该考虑干流、支流洪水的共同作用,同时还需要考虑水利工程行洪与洪水的耦合关系.目前,针对此类水利工程的防洪设计水位的确定并无成熟的计算方法.在实际设计中,一般采用的是经验组合的方法[1],如采用“干流达频洪水+支流平均洪水”或者“支流达频洪水+干流平均洪水”的组合,并进行调洪计算得到防洪设计水位.该方法缺乏理论依据,无法区分不同干、支流洪水的特性,会导致计算的防洪设计水位不确定,将带来未知的的防洪风险.
干、支流洪水也可以看做是多变量洪水事件,可采用多变量水文理论进行处理,即在建立干、支流洪水的联合分布的基础上,根据设计洪水重现期确定设计洪水组合,进而计算水利工程的防洪设计水位.其中最常用的方法为利用Copula函数建立洪水联合分布模型[2],然后根据“OR”重现期或“AND”重现期确定设计洪水组合,由于同一个“OR”重现期或者“AND”重现期对应的洪水组合有无数种,具体采用哪种洪水组合作为设计洪水组合仍有争议,其中采用最多的洪水组合为设计同频组合[3-6]以及最大可能组合[7-10],也有学者采用了最不利组合[11-13],具体应该采用何种组合作为设计组合仍未能取得统一.修建在干、支流交汇河口处支流上的水利工程同时受到干、支流洪水的共同作用,不管采用经验组合还是设计洪水同现期对应的特征组合进行设计,都未能考虑干、支流洪水与水利工程行洪的相互作用.最近有学者[14-17]针对设计洪水过程线的峰、量组合问题,提出了结构荷载重现期的概念,指出考虑水库与洪水的交互作用才能保证水库防洪能力达到防洪标准.国内外有关研究仍处于起步阶段,对于受到多重洪水共同作用的设计洪水组合问题,尚未有相关研究.
本文在探讨防洪标准本质的基础上,利用Copula-蒙特卡罗模拟方法计算得到干、支流洪水共同作用下的防洪设计水位,并以西江流域的桂平航运枢纽水闸为例进行分析,与已有的洪水重现期方法、经验组合方法的计算结果进行了对比,为修建在支流入汇口处受干、支流洪水共同影响的水利工程的防洪设计提供更合理的思路.
1 研究方法与理论 1.1 Copula联合分布模型干、支流洪水的边缘分布采用P-Ⅲ型曲线进行拟合,其表达式为:
| $ f\left( x \right) = \frac{{{\beta ^\alpha }}}{{\Gamma \left( \alpha \right)}}{\left( {x - {a_0}} \right)^{\alpha - 1}}{{\rm{e}}^{ - \beta \left( {x - {a_0}} \right)}} $ | (1) |
式中,Γ(α)是伽玛函数;α为P-Ⅲ型分布函数的形状参数,β为P-Ⅲ型分布函数的尺度参数,a0为P-Ⅲ型分布函数的位置参数,其中α>0, β>0.
将干、支流洪水共同影响下的洪水组合问题按二变量联合分布进行处理.设干流洪水系列X,支流洪水系列Y为连续的随机变量,F(x)和F(y)分别为系列X和Y的边缘累计分布函数.则根据Sklar定理,干、支流洪水的联合分布函数F(x, y)定义为[18]:
| $ F\left( {x,y} \right) = C\left[ {F\left( x \right),F\left( y \right)} \right] = C\left( {u,v} \right) $ | (2) |
式中,C(u, v)是边缘分布为[0, 1]的Copula联合分布函数,其中u=F(x),v=F(y).
Copula函数类型众多,常用的二维Copula函数有椭圆Copula函数、Plackett Copula函数以及阿基米德Copula函数,阿基米德Copulas因其构造简单、计算简便,已在水文领域获得广泛应用[19].本文采用已被证明可有效描述多变量洪水事件的Clayton、Frank、Gumbel-Hougaard及Ali-Mikhail-Haq(AMH)4种阿基米德Copula作为干、支流洪水的联合分布的备选模型函数,Copula函数模型的相关参数θ用Kendall秩相关系数τ来估算[20].
1.2 干、支流共同作用下的洪水重现期以及特征洪水组合假定干、支流洪水分别为X和Y,其边缘分布函数分别为u=F(x),v=F(y), 其联合分布为C[F(x), F(y)]=C(u, v),用Copula函数表征.
其联合概率分布可以表示为:
| $ F\left( {x,y} \right) = P\left( {X < x,Y < y} \right) = \int {_{ - \infty }^y} \int {_{ - \infty }^x} f\left( {u,v} \right){\rm{d}}u{\rm{d}}v $ | (3) |
则对于干、支流洪水事件来说,“OR”重现期是指干流或支流洪水中至少有一个大于其指定洪水时的重现期;“AND”重现期则是指干流和支流洪水同时大于指定洪水时的重现期,其表达式可分别表示为:
干、支流洪水“OR”重现期TO:
| $ {T_{\rm{O}}} = \frac{1}{{P\left( {X > x \cup Y > y} \right)}} = \frac{1}{{1 - C\left( {u,v} \right)}} $ | (4) |
干、支流洪水“AND”重现期TA:
| $ {T_{\rm{A}}} = \frac{1}{{P\left( {X > x \cap Y > y} \right)}} = \frac{1}{{1 - u - v + C\left( {u,v} \right)}} $ | (5) |
显然,同一洪水重现期对应的洪水组合(X, Y)有无数种,已有相关研究常采用同频组合、最大可能组合、最不利组合等特征组合作为设计组合进行防洪设计.同频组合是指公式(4)和(5)中的u=v, 即干流洪水与支流洪水同频率[3-6];最可能组合可以表示如下[21]:
| $ \left( {{u_{\rm{m}}},{v_{\rm{m}}}} \right) = \arg \;\max \;f\left( {u,v} \right) $ | (6) |
| $ f\left( {u,v} \right) = c\left( {u,v} \right)f\left( x \right)f\left( y \right) $ | (7) |
式中,c(u, v)为干、支流洪水联合分布的概率密度函数,f(x)和f(y)则是其边缘分布的概率密度函数.在干、支流洪水共同作用下的同一洪水重现期对应的组合有无数个,则对应的防洪水位也有无数个,则防洪水位最大、最小值对应的组合分别为最大、最小水位组合.
1.3 考虑防洪标准本质的Copula-蒙特卡罗模拟水利工程防洪标准为T设年一遇,本质上应该是指其防洪能力F设足够,洪水破坏力F破坏超过防洪能力的平均间隔时间为T设年,或者洪水破坏力F破坏超过防洪能力F设的概率为1/T设.在洪水作用下,水利工程的行洪水位z超过防洪设计水位z设, 说明洪水破坏能力F破坏超过了水利工程的设计防洪能力F设, 因此有:
| $ P\left( {z > {z_设}} \right) = P\left( {{F_{破坏}} > {F_设}} \right) = 1/{T_设} $ | (8) |
根据水利工程防洪设计的一般方法,首先根据洪水重现期计算与防洪标准对应的设计洪水,然后根据设计洪水调洪计算即可得到水利工程的防洪设计水位z设.
在单个洪水作用情况下,一般假定洪水破坏力F破坏与洪水重现期T洪呈正比,有:
| $ \begin{array}{l} P\left( {z > {z_设}} \right) = P\left( {{F_{破坏}} > {F_设}} \right) = 1/{T_设} = P\left( {z\left( x \right) > z\left( {{x_设}} \right)} \right) = \\ P\left( {X > {x_设}} \right) = {T_{设洪}} \end{array} $ | (9) |
在洪水破坏力F破坏与洪水重现期T洪呈正比的条件下,设计洪水的重现期T设洪与水利工程防洪的设计重现期T设一致,可以利用洪水重现期为T设=T设洪对应的设计洪水直接调洪计算得到防洪设计水位z设.对于干、支流洪水共同作用下的水利工程,其防洪水位不但与干、支流的洪水组合关系有关,还与水利工程的行洪特性有关,公式(8)仍然成立,但满足同一洪水重现期T洪对应的洪水组合有无数种,且这些洪水组合的破坏力并不一致,洪水破坏力F破坏与洪水重现期T洪不再呈正比,因此难以确定具体应该采用哪种组合进行调洪计算得到防洪设计水位.
已有部分学者针对水库洪水的峰、量组合事件进行研究,将水库坝前最高水位超过设定阈值的事件定义为危险事件,以坝前最高水位超过设定阈值的概率衡量水库的防洪标准,并将坝前最高水位超过设定阈值的概率的倒数定义为结构荷载重现期[13-17].其本质就是不考虑洪水事件本身的概率,跳过洪水重现期,直接对公式(8)进行求解.由于公式(8)涉及调洪计算,难以直接求解,一般采用蒙特卡罗模拟的方法进行求解[17].
本文结合防洪标准的本质,在建立描述干、支流洪水的Copula联合分布模型的基础上,采用蒙特卡罗模拟的方法利用公式(8)对修建在支流入汇口处受干、支流洪水共同作用的水利工程的防洪水位进行计算(下文简称F-C-M法).假定干、支流洪水分别为X和Y,其边缘分布为u和v, 利用Copula函数建立的联合分布为C(u, v), 则有条件概率:
| $ C\left( {v|u} \right) = \frac{\partial }{{\partial v}}C\left( {u,v} \right) $ | (10) |
利用F-C-M法计算干、支流洪水共同作用下的水利工程防洪设计水位的步骤为:
1) 建立干、支流洪水的边缘分布u=F(x), v=F(y), 及联合干、支流洪水的联合分布C(u, v);
2) 在(0, 1)中产生两个随机数n1和n2, 并令n1=u;
3) 通过解方程n2=C(v|u), 而求解出与u相关的v;
4) 利用各自的边缘分布函数,根据随机概率组合计算出干、支流洪峰的随机组合(x, y);
5) 对随机模拟的洪水组合(x, y)进行调洪计算即可得到该场随机洪水对应的行洪水位z;
6) 重复步骤(2)~(5),随机模拟足够多场次的洪水组合(x, y), 并对相应的行洪水位z进行排序,容易根据P(z>z设)=1/T设计算得到水利工程的防洪设计水位z设.
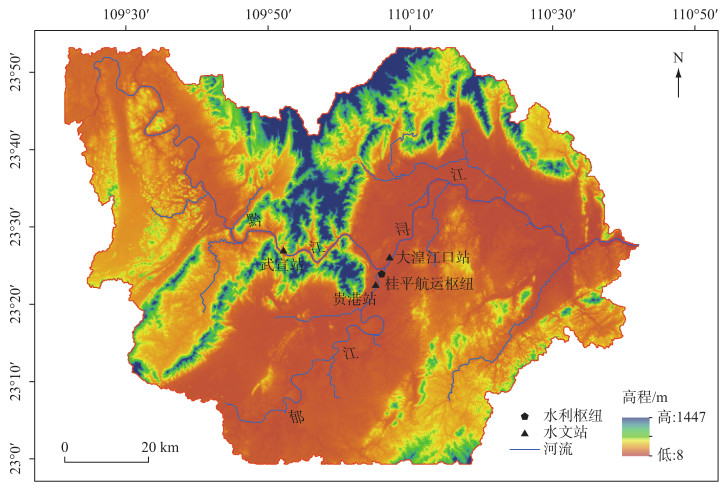
2 研究工程概况桂平航运枢纽工程位于珠江的西江流域(图 1)桂平市的郁江、黔江交汇口附近的郁江河段,是一个以通航为主,集航运、发电、灌溉、交通功能于一体的综合利用性航运枢纽工程,主要由航运船闸、溢洪坝及水闸组成.其中溢流坝长296 m,总溢流面宽度为238 m,设置17孔泄流,孔口净宽14 m,堰顶高程21 m.非洪水时期,溢流坝水闸关闭,枢纽坝上水位抬高以保证航运水位以及发电;洪水时期,溢洪坝水闸打开,洪水通过溢洪坝水闸下泄.桂平航运枢纽同时受到郁江和西江干流洪水的作用,汇合口的郁江上游附近有贵港水文站、干流下游附近有大湟江口站水文站[22].桂平航运枢纽水闸设计重现期为100年一遇,设计时采用大湟江口站重现期为100年的洪峰流量与0.2倍该洪峰值作为溢洪坝坝址设计洪水组合,并经过调洪计算得到溢洪坝水闸设计洪水位为43.48 m.
|
图 1 桂平航运枢纽工程位置 Fig.1 Location of Guiping Shipping Hub project |
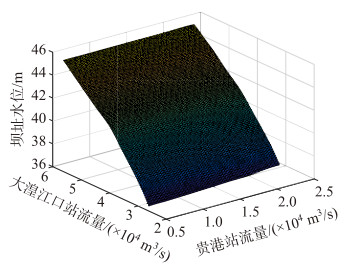
坝址自然水位同时受到郁江和西江干流洪水的作用,枢纽原设计过程中利用“贵港站流量-大湟江口站流量坝址自然水位”关系(图 2)插值计算得到不同的设计洪水组合下的闸下水位,再根据公式(11)计算得到闸上水位[23],即为水闸防洪设计水位.
| $ Q = \sigma \cdot \varepsilon \cdot M \cdot B\sqrt {2g} H_0^{\frac{3}{2}} $ | (11) |
|
图 2 贵港站流量-大湟江口站流量-坝址自然水位关系 Fig.2 Traffic volume of Guigang Railway Station: Natural water level relation of runoff to dam site at Great Huangjiangkou Station |
式中,σ为淹没系数;B为单个闸孔的净宽, m;H0为闸顶的总水头, m;ε为侧收缩系数;
干、支流洪水的边缘分布均采用P-Ⅲ型分布,采用线性矩(L-矩)方法对参数进行估计,模型拟合结果见表 1.大湟江口站与贵港站的洪水分布模型在位置参数上存在较大的差异,尺度参数较为接近.
| 表 1 干、支流洪水边缘分布计算结果 Tab. 1 Calculation results of marginal distribution of main and tributary floods |
通过计算,得到Kendall秩相关系数τ为0.1585,说明桂平航运枢纽干、支流洪水相关性较弱.根据Copula函数参数θ与Kendall秩相关系数τ之间的相关计算公式,求出本文所采用的4种Copula函数的参数值分别为0.5943、0.3767、1.1884以及1.46(AMH、Clayton、GH和Frank).干、支流洪水的联合分布的拟合优度评价结果(表 2)表明,4种Copula模型的AIC值与OLS值的变化范围不大,综合两种优度评价结果来看,AIC值与OLS值最小的均为Clayton Copula.因此,选择Clayton Copula作为联合分布特征的最优Copula模型.
| 表 2 Copula函数优度评价结果 Tab. 2 Copula function goodness evaluation result |
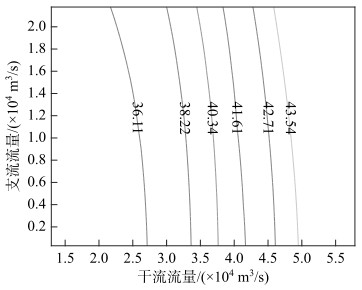
蒙特卡罗模拟方法具有随着模拟的次数越多,结果越精确的特点.本文随机模拟100万组干、支流洪水的洪峰组合,利用水闸设计过程中的调洪计算方法计算不同洪水组合对应的防洪水位,并采用F-C-M法计算给定不同防洪要求对应的防洪水位设计值.通过F-C-M法计算得到的结果如图 3所示. 图 3中的曲线为满足不同设计重现期下干、支流洪水组合的连线,曲线上的数值代表该设计重现期下防洪设计水位.根据计算结果,桂平航运枢纽水闸平均100年、50年、20年、10年、5年以及2年出现一次的闸上洪水位分别为43.54、42.71、41.61、40.34、38.22和36.11 m,分别对应防洪标准为100年、50年、20年、10年、5年的防洪设计水位,符合水利工程防洪标准越高设计水位越高的一般工程特性.
|
图 3 不同防洪标准对应的洪水位及洪水组合线 Fig.3 Flood location and flood combination line corresponding |
由图 3可见,同一防洪标准对应的防洪设计水位只有一个,但对应的干、支流设计洪水组合可以有无数个,这些洪水组合对水闸的行洪威胁一致,以其中任何一种组合作为设计洪水组合,得到的设计水位一致,不会出现防洪设计水位不确定的问题;不同防洪标准下的洪水位等值线与干流洪峰流量坐标轴接近垂直,防洪的标准越高,等值线越趋于直线(对比2年和100年水位等值线),说明桂平航运枢纽水闸洪水位受干流洪水影响大于支流洪水的影响,符合桂平航运枢纽水闸受干流洪水顶托严重的自然规律.
采用F-C-M法对水闸的防洪水位进行计算,考虑了干、支流洪水的组合特性及其与水闸的行洪耦合关系,计算的防洪设计水位可以保证达到防洪标准的要求.
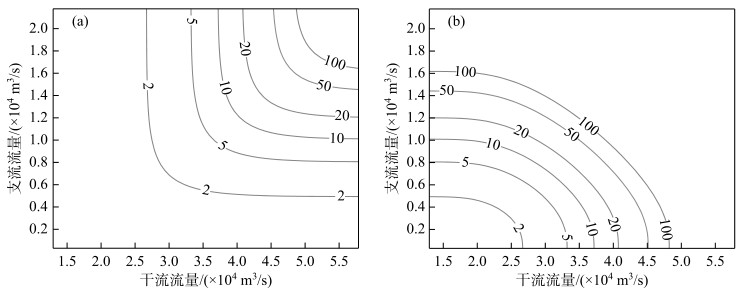
3.3.2 与利用“OR”重现期、“AND”重现期计算的防洪设计水位对比分别绘制干、支流洪水100年、50年、20年、10年、5年、2年一遇的“OR”重现期、“AND”重现期的洪水组合等值曲线(图 4).由图 4可以看出,满足某一特定重现水平年的“OR”重现期或“AND”重现期的干、支流洪水组合有无数个,这些组合基本沿纵、横坐标呈对称分布,即干、支流洪水对水闸的防洪水位作用起同等作用,说明利用“OR”重现期、“AND”重现期计算防洪设计水位的方法无法反映出干、支流洪水的组合特性及其与水闸行洪的耦合关系.
|
图 4 “OR”重现期(a)及“AND”重现期(b)洪水组合等值线图 Fig.4 Recurrent flood contour map of the "OR" (a) and "AND" (b) return period |
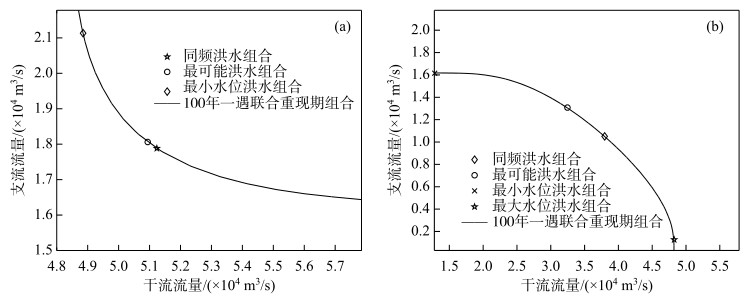
进一步计算100年一遇洪水重现期对应的同频组合、最可能组合、最大水位组合、最小水位组合及其对应的防洪设计水位,并与F-C-M法计算结果进行对比(图 5、表 3). 100年一遇“OR”重现期对应各种组合的防洪水位全部大于44.25 m,100年一遇“AND”重现期对应的各种组合的防洪水位在31.65~43.27 m之间.可见,利用“OR”重现期、“AND”重现期计算防洪设计水位时,采用不同特征组合进行设计得到的防洪设计水位不同,且差别很大,因此导致设计结果具有巨大的不确定性.
|
图 5 100年一遇“OR”重现期(a)和“AND”重现期(b)的特征洪水组合 Fig.5 100-year characteristic flood combination with "OR" (a) and "AND" (b) return period |
| 表 3 不同方法计算的100年一遇防洪设计水位结果对比 Tab. 3 Comparison of design water level results of 100-year flood control calculated by different methods |
利用F-C-M法计算得到的防洪标准100年一遇的防洪设计水位为43.54 m,保证了设计水位确定且可达到防洪标准的要求,比直接采用洪水重现期确定防洪设计水位的方法更加合理. F-C-M法计算的桂平航运枢纽工程100年一遇设计洪水组合等值线位于100年一遇的“OR”重现期洪水组合等值线和“AND”重现期组合等值线之间,说明以“AND”重现期计算得到的设计水位值偏小,达不到防洪标准的要求;而以“OR”重现期计算得到的防洪设计水位则偏大.目前各文献中推荐采用最多的同频组合及最可能组合,以“OR”重现期的同频组合及最可能组合计算得到的防洪设计水位分别偏高1.06 m和1.01 m,以“AND”重现期的同频组合及最可能组合计算得到的防洪设计水位分别偏低-2.8 m和-4.69 m,其偏差已经完全偏离合理误差的范围,可以认为以其进行计算得到的防洪设计水位是错误的.
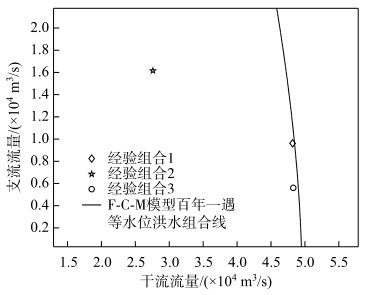
3.3.3 与经验组合确定的防洪设计水位对比将工程设计中采用的3种经验组合(组合1:干流达频+支流多年平均洪峰;组合2:支流达频+干流多年平均洪峰;组合3:桂平航运枢纽水闸设计过程中采用的干流达频+支流0.2倍干流达频洪峰)及其对应的防洪水位与本次F-C-M法计算结果进行对比(图 6、表 4). 3个特征组合对应的设计防洪水位均小于F-C-M法计算得到的水位.其中经验组合1对应的设计水位与F-C-M法计算结果相差0.18 m,其结果不安全,经验组合2对应的设计水位为36.02 m,远小于F-C-M法计算结果,经验组合3对应的设计水位为43.48 m,略小于F-C-M法计算结果.经验组合1和经验组合2为工程中最常采用的经验组合,但其无法反映出具体干、支流洪水的特性,更无法反映出干、支流洪水与水闸行洪的耦合关系,因此以其进行设计无法保证达到防洪标准要求;经验组合3为桂平航运枢纽水闸设计过程中经过充分分析干、支流洪水与行洪特征关系的基础上提出来的,因此具有较好的合理性,计算结果也与本次F-C-M法计算结果接近,该方法是经过充分定性分析后采用的设计组合,可以保证定性上具有一定的合理性,但无法保证定量上一定能达到防洪标准的要求,同时该经验组合仅针对桂平航运枢纽水闸提出,缺乏普适性.
|
图 6 工程设计采用的100年一遇洪水组合 Fig.6 100-year flood combination used in engineering design |
| 表 4 不同洪水组合下的设计水位值 Tab. 4 Design water level values under different flood combinations |
针对干、支流共同作用下的水利工程的防洪设计水位计算缺乏有效方法的问题,以防洪标准的本质为基础,采用F-C-M法对其进行研究,并以广西桂平航运枢纽水闸为例进行了对比分析,得到如下结论:
1) 现行的根据设计洪水重现期确定设计洪水组合,或者根据经验给定经验设计组合,继而计算防洪设计洪水位的方法不能充分考虑干、支流洪水组合特点及其与水利工程行洪特性的耦合关系,以其计算得到的防洪设计水位具有不确定性,且无法保证符合防洪标准要求.
2) 本文构建的F-C-M法可充分考虑干、支流洪水及其与水利工程行洪特性的耦合关系,计算得到的防洪设计水位唯一,且符合防洪标准对水利工程防洪能力的要求.
3) 将本文构建的方法运用到广西桂平航运枢纽水闸中,得到该水闸防洪标准100年一遇对应的防洪设计水位为43.54 m,略大于工程实际采取的百年一遇水位43.48 m,说明工程基本满足防洪标准的要求;100年一遇洪水重现期对应的各种洪水组合的防洪水位在31.65~44.60 m之间,以设计洪水重现期的特征组合计算得到的防洪设计水位完全偏离了合理的误差范围;以经验洪水组合计算在无法反映出不同洪水组合的特性及与工程的相互作用.
在干、支流洪水共同作用下,不宜采用设计洪水重现期确定水利工程的防洪设计水位,建议采用F-C-M法进行计算.
| [1] |
Fan KX, Xu CJ. Research on meeting of floods from Wujiang River and Three Gorges. Journal of China Hydrology, 2010, 30(4): 63-65. [范可旭, 徐长江. 乌江洪水与长江三峡洪水遭遇研究. 水文, 2010, 30(4): 63-65.] |
| [2] |
Guo SL, Yan BW, Xiao Y et al. Multivariate hydrological analysis and estimation. Journal of China Hydrology, 2008, 28(3): 1-7. [郭生练, 闫宝伟, 肖义等. Copula函数在多变量水文分析计算中的应用及研究进展. 水文, 2008, 28(3): 1-7.] |
| [3] |
Li TY, Guo SL, Yan BW et al. Derivative design flood hydrograph based on tri-variate joint distribution. Journal of Hydroelectric Engineering, 2013, 32(3): 10-14. [李天元, 郭生练, 闫宝伟等. 基于多变量联合分布推求设计洪水过程线的新方法. 水力发电学报, 2013, 32(3): 10-14.] |
| [4] |
Li TY, Guo SL, Liu ZJ et al. Design flood estimation based on bivariate joint distribution of flood peak and volume. Journal of Hydraulic Engineering, 2014, 45(3): 269-276. [李天元, 郭生练, 刘章君等. 基于峰量联合分布推求设计洪水. 水利学报, 2014, 45(3): 269-276.] |
| [5] |
Guo SL, Liu ZJ, Xiong LH. Advances and assessment on design flood estimation methods. Journal of Hydraulic Engineering, 2016, 47(3): 302-314. [郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价. 水利学报, 2016, 47(3): 302-314.] |
| [6] |
Xiao Y, Guo SL, Liu P et al. Derication of design flood hydrograph based on Copula function. Engineering Journal of Wuhan University, 2007, 4: 13-17. [肖义, 郭生练, 刘攀等. 基于Copula函数的设计洪水过程线方法. 武汉大学学报:工学版, 2007, 4: 13-17.] |
| [7] |
Yin JB, Guo SL, Liu ZJ et al. General formula of the most likely composition method for flood peaks and volumes estimation. Journal of Sichuan University:Engineering Science Edition, 2017, 49(2): 69-76. [尹家波, 郭生练, 刘章君等. 设计洪水峰量最可能组合法的计算通式. 工程科学与技术, 2017, 49(2): 69-76.] |
| [8] |
Yin JB, Guo SL, Liu ZJ et al. Deriving feasible interval estimation for seasonal design flood. Engineering Journal of Wuhan University, 2017, 50(1): 18-24. [尹家波, 郭生练, 刘章君等. 分期设计洪水的估计区间. 武汉大学学报:工学版, 2017, 50(1): 18-24.] |
| [9] |
Tu XJ, Du YL, Chen XH et al. Modeling and design on joint distribution of precipitation and tide in coastal city. Advances in Water Sciences, 2017, 28(1): 49-58. [涂新军, 杜奕良, 陈晓宏等. 滨海城市雨潮遭遇联合分布模拟与设计. 水科学进展, 2017, 28(1): 49-58.] |
| [10] |
Yan BW, Guo SL, Guo J et al. Regional design flood composition based on Copula function. Journal of Hydroelectric Engineering, 2010, 29(6): 60-65. [闫宝伟, 郭生练, 郭靖等. 基于Copula函数的设计洪水地区组成研究. 水力发电学报, 2010, 29(6): 60-65.] |
| [11] |
Lu YJ, Liu DF, Xie BT et al. Calculation of design flood for the Three Gorges Project. Periodical of Ocean University of China, 2007, 37(3): 497-502. [逯义军, 刘德辅, 谢波涛等. 多维联合概率理论对三峡工程设计洪水的计算. 中国海洋大学学报:自然科学版, 2007, 37(3): 497-502.] |
| [12] |
Chen JH, Guo SL, Liu P et al. Research on the design flood calculation method Based on reliability theory. Yellow River, 2008, 39(18): 1-3. [陈炯宏, 郭生练, 刘攀等. 基于可靠度理论的设计洪水计算方法研究. 人民长江, 2008, 39(18): 1-3. DOI:10.3969/j.issn.1001-4179.2008.18.001] |
| [13] |
Xie J, Xu R. Analysis of the impact of upstream construction on the design of the Tutun River Reservoir. Yellow River, 2010, 32(2): 53-54. [谢蕾, 徐仁. 上游建库对头屯河水库设计洪水的影响分析. 人民黄河, 2010, 32(2): 53-54. DOI:10.3969/j.issn.1000-1379.2010.02.024] |
| [14] |
Requena AI, Mediero L, Garrote L. A bivariate return period based on copulas for hydrologic dam design:accounting for reservoir routing in risk estimation. Hydrology and Earth System Sciences, 2013, 17(8): 3023-3038. DOI:10.5194/hess-17-3023-2013 |
| [15] |
Volpi E, Fiori A. Hydraulic structures subject to bivariate hydrological loads:Return period, design, and risk assessment. Water Resources Research, 2014, 50(2): 885-897. DOI:10.1002/2013WR014214 |
| [16] |
Salvadori G, Durante F, Michele CD et al. A multivariate copula-based framework for dealing with hazard scenarios and failure probabilities. Water Resources Research, 2016, 52(5): 3701-3721. DOI:10.1002/2015WR017225 |
| [17] |
Liu ZJ, Guo SL, Xu XF et al. Bivariate structure load return period and joint flood quantile estimation. Journal of Hydraulic Engineering, 2018, 49(8): 956-965. [刘章君, 郭生练, 许新发等. 两变量洪水结构荷载重现期与联合设计值研究. 水利学报, 2018, 49(8): 956-965.] |
| [18] |
Nelsen RB. An introduction to Copulas. 2nd Edition. New York: Springer, 2006.
|
| [19] |
Salvadori G, Michele CD. Frequency analysis via copulas:theoretical aspects and applications to hydrological events. Water Resources Research, 2004, 40(12): 229-244. |
| [20] |
Genest C, Rivest LP. Statistical inference procedures for bivariate Archimedean Copulas. Journal of the American Statistical Association, 2012, 88(423): 1034-1043. |
| [21] |
Salvadori G, Michele CD, Durante F. On the return period and design in a multivariate framework. Hydrology and Earth System Sciences, 2011, 15(11): 3293-3305. DOI:10.5194/hess-15-3293-2011 |
| [22] |
Gan FW, Hu XY, Liu X et al. Analysis on flood characteristics of the Xijiang River in Guangxi. Journal of Guangxi University:Natural Science Edition, 2015, 40(1): 244-250. [甘富万, 胡秀英, 刘欣等. 广西境内西江流域洪水特性分析. 广西大学学报:自然科学版, 2015, 40(1): 244-250.] |
| [23] |
Hu P. Study on the design flood combination and flood control water level under combined action of main stream and tributary floods[Dissertation]. Nanning: Guangxi University, 2017. [胡泊.干、支流洪水作用下的水闸设计洪水组合及设计水位研究[学位论文].南宁: 广西大学, 2017. ]
|
 2020, Vol. 32
2020, Vol. 32 

