(2: 湖北省水利水电勘测设计院, 武汉 430064)
(2: Hubei Provincial Water Resources and Hydropower Planning Survey and Design Institute, Wuhan 430064, P. R. China)
目前,关于洪涝灾害风险的研究主要包含灾害危险性分析[1-4]、承灾体易损性分析[5-7]、灾损评估[8-10]和风险应对决策[11-13]4个方面.其中,洪涝灾害的危险性受到天文、气象、水文、人类活动等多重因子的影响,仅采用单变量对其分析不能够清楚描述各因子之间的相互作用,难以有效地解决洪涝灾害问题,因此寻求多变量的联合分布就成为了洪涝灾害危险性分析的热点.
多变量联合分布模型根据边际分布函数的特点,可分为两类,第一类是具有相同边际分布的多变量分布模型[14-16],第二类是具有不同边际分布的多变量分布模型[17-19].根据洪涝灾害影响因子的实际情况,第二类多变量分布模型的适用性较强,因此相关学者的研究成果也更为丰富,但第二类模型中有些具体模型(如Meta-Gaussian模型和FGM模型)对变量间的相关性有要求,使它们的适用范围受到了限制.相比之下,同属第二类模型的Copula函数优势就更为明显,它不仅可以描述变量之间的线性关系还可以描述变量间的非线性关系,可以更好地表征洪涝灾害因子之间的相互结构.目前,经国内外广大学者对Copula函数的类型选取、参数估计、拟合优度等各方面的深入研究,其在水文中的应用已日渐成熟,主要包含两个部分,第一对水文气象变量的多特征属性进行频率分析(如洪水历时、洪峰、洪量,降水历时、降水量、降水强度等)[20-21],第二是各种水文事件的遭遇组合问题(如台风梅雨遭遇问题,干支流丰、平、枯组合问题等)[22-24].而洪涝灾害危险性分析研究在两类应用中均有涉及.
在多重天气系统的影响下,太湖流域降水类型分为梅雨和台风雨.不同的天气系统带来时空分布各异的降水,给该地区城镇防洪排涝工作造成了巨大的挑战.以往学者采用Copula函数对太湖流域汛期洪涝灾害危险性分析时,关注点主要集中于梅雨和台风的遭遇问题[25],且所选用的研究时段多为整个汛期[26].但相比梅雨和台风的遭遇的情况,在汛期,梅雨或台风等天气系统单独或交替影响整个流域降水的情况仍是大概率事件,并且由于梅雨或台风等天气系统的成因不同,造成降水在流域的时空分布情况也大不相同,因此造成的洪涝灾害危险性也有所差异.
本文在以往研究的基础上,将汛期划分为梅雨影响主导期(梅汛期)和台风影响主导期(台汛期),并采用Copula函数,研究不同时期下降水的空间分布情况,之后结合太湖流域防洪规划制定排涝不利情境,对流域梅汛期和台汛期的洪涝风险进行分析,为流域设计暴雨的调整、洪水资源的利用以及防洪排涝实时调度的决策提供科学参考.
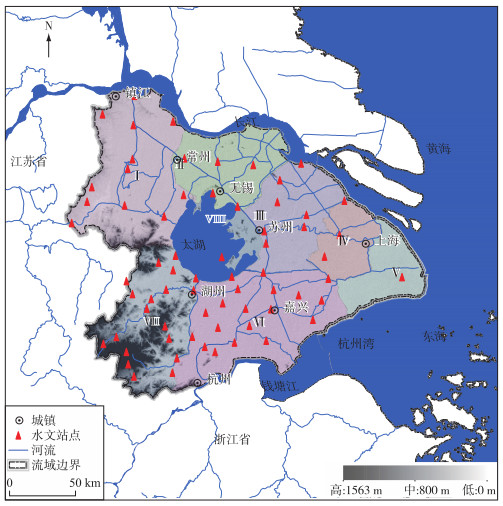
1 研究区与数据 1.1 流域概况太湖流域(30°28′~32°15′N,119°11′~121°53′E)北抵长江,东临东海,南濒杭州湾,西以天目山、茅山等山区为界,流域总面积约36895 km2.流域属亚热带季风气候,多年平均降水量为1177 mm,降水年内分布不均匀,主要集中在汛期.流域地形为一碟形洼地,周边高,中央低,水面面积2336.8 km2的太湖位于流域中央,流域平原低洼处通常低于汛期河湖水位,上游洪水和流域降雨汇集于低洼地区,极易产生洪涝灾害[27].流域内河网密布,湖泊众多,天然调蓄量大,但上游坡陡水急,来水迅速,下游地势平坦,水面较平缓,又受周边江海潮位顶托,泄水不畅,河湖水位一旦抬高,退落缓慢.根据水文和地理拓扑关系,太湖流域通常被分为8个水文分区,分别是湖西区(Ⅰ)、武澄锡虞区(Ⅱ)、阳澄淀泖区(Ⅲ)、浦西区(Ⅳ)、浦东区(Ⅴ)、杭嘉湖区(Ⅵ)、浙西区(Ⅶ)和太湖湖区(Ⅷ),各个分区的地理位置如图 1所示.
|
图 1 太湖流域水系地理位置及其河流和水文站点 Fig.1 Location of the Taihu Basin and its rivers and gauging stations |
本文所用到的数据资料包含:1962-2011年太湖流域67个代表站点的日降水资料、1962-2011年太湖水位数据、1962-2011年太湖流域梅雨发生时间数据和1962-2011年发源于西太平洋历史台风资料.其中,降水、水位和梅雨数据均来自中华人民共和国水利部太湖流域管理局,台风资料来源于中国气象局.
2 方法 2.1 基于降水主导因素的汛期分期本文选择太湖流域梅汛期的开始时间和结束时间来描述梅汛期的时间特征,利用台风登录太湖流域的时间来刻画台汛期的时间特征[25].采用水文领域中常用的Norm、Lnorm、Gamma、Beta、Logistic、Weibull 6种分布来拟合入梅时间(STP)、出梅时间(ETP)、台风登录时间(ITT)的分布函数.采用柯尔莫可洛夫斯米洛夫检验(K-S)、概率点距相关系数检验法(PPCC)、平方绝对误差(MAE)、均方根误差(RMSE)、确定性系数(DC)依次对入梅时间、出梅时间和台风登录时间等3个变量的6种分布线型进行拟合检验.各检验方法的表达式如下:
| $ PPCC = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \overline x } \right)\left( {{y_i} - \overline y } \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \overline x } \right)}^2}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \overline y } \right)}^2}} } } }} $ | (1) |
| $ RMSE = \frac{1}{n}\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} } $ | (2) |
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{x_i} - {y_i}} \right|} $ | (3) |
| $ DC = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{x_i} - \overline x } \right)}^2}} }} $ | (4) |
式中,xi和yi分别为经验频率和理论频率,x和y分别为经验频率和理论频频的均值,n为样本的个数.
太湖流域的前汛期以梅雨型降水为主,后汛期以台风型降水为主,但在主汛期甚至整个汛期梅雨型降水和台风型降水是有一定遭遇概率的,因此本文以入梅时间分布的累积概率为90 %处的时间点作为梅汛期的起点,即历史上90 %的年份在该日以后已经进入梅汛期;同样以台风登录时间分布的累积概率为90 %处的时间点作为台汛期的终点,即历史上百分之九十的台风在该日之前已经登录太湖流域.对于梅汛期和台汛期的时间节点的划分,通过构造梅台比重系数ω进行划分计算:
| $ \omega = F_{\left( x \right)}^{{\rm{plum}}}\left( {1 - F_{\left( x \right)}^{{\rm{typhoon}}}} \right) $ | (5) |
式中,ω为梅台比重系数,F(x)plum为出梅时间累积概率分布函数;F(x)typhoon为台风登录时间累积概率分布函数.
ω系数代表每个时间节点中梅雨和台风雨对降水的综合贡献率,取太湖流域主汛期ω值最大的时间节点作为梅汛期和台汛期的分界点,使得梅雨型降水和台风型降水能够在其各自的时间段内保持较好的主导性和典型性.选择太湖水位作为降水的响应变量,检验梅汛期和台汛期时间划分的合理性.根据太湖超警戒水位发生时间(TWL)的双峰特征,采用混合正态分布模型及其参数估计方法,对太湖警戒水位发生时间分布进行拟合和参数估计,具体公式如下:
| $ X \sim {\alpha _1}N\left( {{\mu _1}, \sigma _1^2} \right) + {\alpha _2}N\left( {{\mu _2}, \sigma _2^2} \right) $ | (6) |
式中,α1和α2为权重系数,且α1+α2=1;μ1和μ2为均值,σ1和σ2为均方差.
2.2 流域子区域聚类分析根据水系特征和径流关系,太湖流域被划分为8个水文分区.但不同的水文分区可能具有相似的降水规律,因此本文根据这一假设,对太湖流域8个水文分区进行聚类,合并成更具有特点的降水空间分区.这种方法既维持了区域之间的水力联系,又考虑了降水在空间上的分布情况.在水文分区多次聚合之后,会产生多个区域聚类结果,但流域洪涝灾害形成机理复杂,不仅仅由降水造成,因此最优的降水聚类结果并不一定最能反映流域洪涝特性.根据太湖流域实际情况,各区降水与太湖水位的关系是流域洪涝风险控制的核心因素,也是本文进行洪涝危险性分析的基础,因此,在每次聚合之后采用Copula函数拟合各区降水与太湖水位的联合分布函数,同时考虑完全不聚类(8个水文分区)和完全聚类(整个流域作为一个整体)的两种极端情况,通过经验概率与理论概率的对比分析,确定最优的区域聚类方案.此外,本文在区域聚类过程中,将梅汛期和台汛期分别考虑.
2.2.1 基于降水相关性的区域聚类首先,利用泰森多边形法分别统计梅汛期和台汛期8个分区的面降水量数据,之后通过皮尔森法(Pearson)、斯皮尔曼法(Spearman)计算各个分区之间的降水相关性,将降水相关性较强的区域依次合并聚类.
2.2.2 基于联合分布效果的区域聚类优选Copula函数是定义在[0, 1]均匀分布的多维联合分布函数,根据Sklar理论[28],令H为一个n维分布函数,各变量的边缘分布为F1, F2, …, Fn,那么存在一个n-Copula函数C,使得对任意的x属于Rn,满足:
| $ H\left( {{x_1}, {x_2}, \cdots , {x_n}} \right) = {C_\theta }\left( {{F_1}\left( {{x_1}} \right), {F_2}\left( {{x_2}} \right), \cdots , {F_n}\left( {{x_n}} \right)} \right) $ | (7) |
式中,θ为Copula函数的参数;若F1, F2, …, Fn是连续的,则函数C是唯一确定的.
对称Archimedean Copulas由于具有简单的函数构造,仅含一个参数,求解容易等特性,被广泛应用于水文多变量频率分析计算.本文选取Archimedean Copulas中的Clayton Copula、Gumbel Copula和Frank Copula这3种常用类型作为候选函数,并采用最大似然法进行参数估计[29].此外,为了能够找出最能反映降水与水位关系的区域聚类结果,采用赤池信息准则(Akaike Information Criterion)和贝叶斯信息准则(Bayesian Information Criterion)对联合分布进行拟合优度检验,每次区域聚类后,选择最优的Copulas函数类型[30].本文选用的拟合优度检验公式如下:
| $ {\rm{AIC}} = 2k + n\ln \left( {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{P_{ei}} - {P_i}} \right)}^2}} } \right) $ | (8) |
| $ {\rm{BIC}} = \ln \left( n \right)k + n\ln \left( {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{P_{ei}} - {P_i}} \right)}^2}} } \right) $ | (9) |
式中,Pei为联合经验频率,Pi为Copula函数联合分布值,k为模型中所含的参数,n为样本数,检验值AIC和BIC越小,表示Copula分布值Pi越靠近联合分经验概率值Pei,拟合精度越高.
通过对比分析每次聚类之后区域降水与太湖水位的联合分布,根据Copula函数拟合效果的优劣,确定梅汛期和台汛期最终的区域聚类划分结果.
2.3 基于Copula的洪涝风险分析根据太湖流域管理局与流域各省市有关单位编制的《太湖流域防洪规划》,到2025年,流域达到防御不同降雨典型100年一遇的洪水标准;区域基本达到防御50年一遇洪水标准.太湖警戒水位3.8 m,太湖保证水位4.65 m.根据梅汛期和台汛期的区域聚类结果,如果流域降水不分区,说明流域降水的空间分布不明显,整体降水较为均匀,则采用流域整体防洪标准、太湖警戒水位、保证水位进行洪涝风险情境设定.如果流域降水分为不同的区域,说明流域降水在空间上呈现差异性,则采用区域防洪标准、太湖警戒水位进行洪涝风险情境设定.之后,通过Copula函数拟合多元变量的联合分布函数[31],分析各区域或流域多种降水频率与太湖水位状态的遭遇概率,对梅汛期和台汛期流域洪涝风险进行分析.
3 结果和分析 3.1 汛期分期结果及分析根据K-S检验(表 1)和PPCC值、MAE值、RMSE值和DC值的大小(表 2和表 3),可知太湖流域入梅时间和出梅时间,台风登录时间拟合最好的函数类型分别为Weibull分布、Lognormal分布和Norm分布,具体参数值见表 4.
| 表 1 6种分布函数的K-S检验结果 Tab. 1 K-S test results of random variables with six reference distributions |
| 表 2 出梅时间和入梅时间的拟合优选 Tab. 2 The goodness of fit tests for the time distribution of the plum rain |
| 表 3 台风登录时间的拟合优选 Tab. 3 The goodness of fit tests for the time distribution of the typhoon |
| 表 4 6种分布函数的参数 Tab. 4 Parameters of six reference distributions |
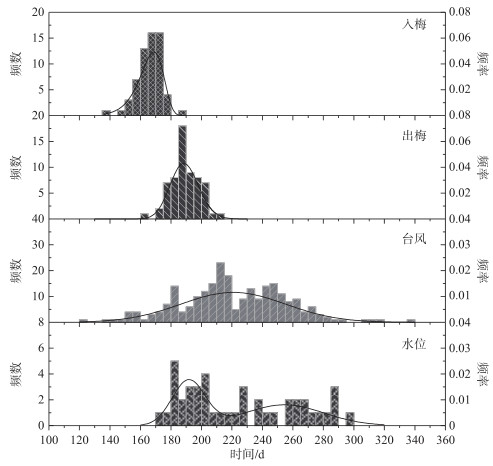
从图 2可知,梅汛期的起止时间为:6月24日(一年中的第175天,下同)至7月21日(202天);台汛期的起止时间为:7月22日(203天)至9月22日(265天).根据《太湖流域洪水与水量调度方案》(下面简称‘方案’),将全年划分为6个时段,其中,第4个时段为梅汛期(6月16日-7月20日),第5个时段为台汛期(7月21日-9月30日).本文计算的时段均处于‘方案’划分时段之内.此外,通过分析图中超警戒水位发生时间,可以得到以下3个结论:1)在第170~180天期间,超警戒水位发生概率迅速增大,说明在这时间段降水量明显增大,太湖流域已经入梅,验证了我们划分的第175天的入梅期是合理的;2)第191天为梅汛期超汛限水位发生概率最大的时间点,说明由梅雨主导的降水的结束点应该在这天之后,因此验证了我们划分的第202天是合理的;在第210~220天期间内,超警戒水位的发生概率最小,说明该期间为梅汛期尾期,台汛期初期,考虑到水位和降雨响应关系的延迟性,梅汛期和台汛期的分界点可以适当提前;3)梅汛期超警戒水位分布形状高且瘦,台汛期超警戒水位分布矮且胖,符合梅雨和台风的时长和频次的发生特点.梅汛期降雨量小且时间长,导致多年水位涨落过程集中;台汛期降雨量大且时间短,次数多,导致多年水位涨落过程分散叠加.
|
图 2 太湖流域入梅、出梅、台风和超警戒水位发生时间的理论概率关系 Fig.2 Probability density functions of random variables(STP, ETP, ITT and TWL) |
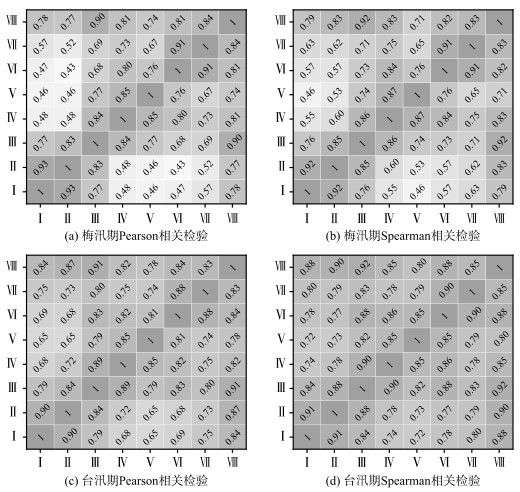
根据图 3分析各分区降水相关性,考虑地理拓扑关系和上下游水流走向,进行第1次聚类:在梅汛期,可将水利分区由原来的8个区域重新划分为湖西区与武澄锡虞区(Ⅰ & Ⅱ)、阳澄淀泖区与太湖湖区(Ⅲ & Ⅷ)、浦西区与浦东区(Ⅳ & Ⅴ)、浙西区和杭嘉湖区(Ⅵ & Ⅶ)4个区域.在台汛期,可以将水利分区由原来的8个区域重新划分为湖西区与武澄锡虞区(Ⅰ & Ⅱ)、阳澄淀泖区,太湖湖区与浦西区(Ⅲ & Ⅳ & Ⅷ)、浦东区(Ⅴ)、浙西区和杭嘉湖区(Ⅵ & Ⅶ)4个区域.
|
图 3 太湖流域梅汛期和台汛期8个水利分区降水量的相关关系 Fig.3 The correlation results of precipitation between eight hydrological sub-regions in Taihu Basin |
根据图 4分析各分区降水相关性,进行第2次聚类:在梅汛期可以发现阳澄淀泖和太湖湖区(Ⅲ & Ⅷ)与浦西和浦东区(Ⅳ & Ⅴ)的相关性仍然很大,在Pearson和Spearman检验下能够达到0.86和0.84,考虑地理拓扑关系和上下游水流走向关系,可以将这两个分区继续合并,因此整个太湖流域被分成:湖西区与武澄锡虞区(Ⅰ & Ⅱ),阳澄淀泖区、太湖湖区、浦西区与浦东区(Ⅲ & Ⅷ & Ⅳ & Ⅴ),浙西区和杭嘉湖区(Ⅵ & Ⅶ)3个区域.分析台汛期各分区降水相关性,可以发现4个区域降水的相关性仍然很大,特别是湖西区与武澄锡虞区(Ⅰ & Ⅱ),阳澄淀泖区、太湖湖区、浦西区(Ⅲ & Ⅷ & Ⅳ),浙西区和杭嘉湖区(Ⅵ & Ⅶ)三者之间在Pearson和Spearman检验下相关系数达到0.87及以上,呈现出整个区域的聚合性.但为了与梅汛期对比,在台汛期,太湖流域汛期分区结果与梅汛期一致.

|
图 4 太湖流域梅汛期和台汛期4个水利分区降水量的相关关系 Fig.4 The correlation results of precipitation between four hydrological sub-regions in Taihu Basin |
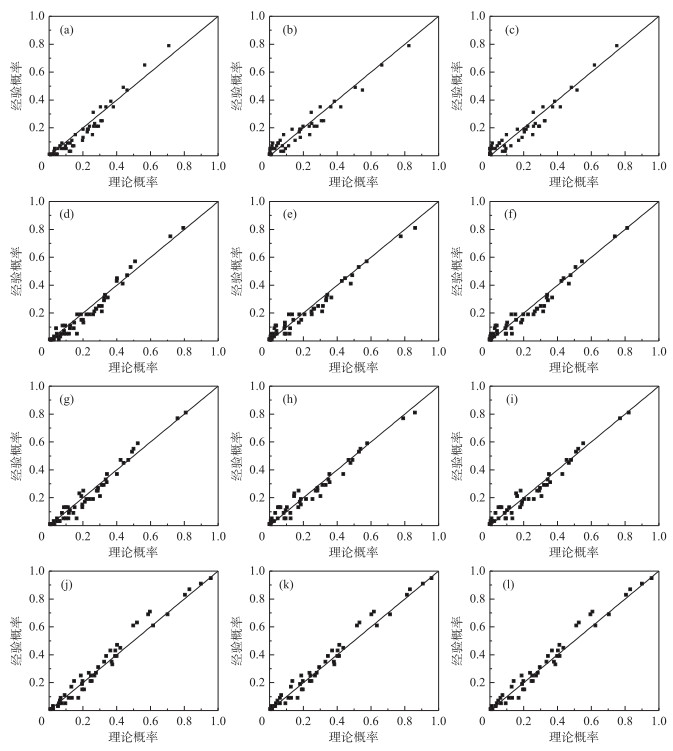
梅汛期,在9维、5维、4维联合分布函数中,Clayton Copula取得了最好的拟合效果;在整个太湖流域降水和太湖水位的2维联合分布函数中,AIC和BIC一致认为Gumbel Copula取得了最好的拟合效果(图 5、表 5);台汛期,在8个水利分区和太湖水位的9维联合分布函数中,Gumbel Copula取得了最好的拟合效果;在5维和4维水利分区降水和太湖水位的联合分布函数中,Clayton Copula取得了最好的拟合效果,在整个太湖流域降水和太湖水位的二维拟合关系中,AIC和BIC一致认为Gumbel Copula取得了最好的拟合效果(图 6、表 5).从各维度拟合效果来看,梅汛期、湖西区与武澄锡虞区(Ⅰ & Ⅱ),阳澄淀泖区、太湖湖区、浦西区与浦东区(Ⅲ & Ⅷ & Ⅳ & Ⅴ),浙西区和杭嘉湖区(Ⅵ & Ⅶ)3个区域的降水和太湖水位的4维联合分布最能反映区域降水和太湖水位的关系.台汛期,整个太湖流域降水和太湖水位的2维联合分布最能反映太湖流域降水和太湖水位的关系.太湖流域梅汛期和台汛期聚类划分结果如图 7所示.
|
图 5 太湖流域梅汛期降雨和太湖水位P-P图(图(a)、图(b)、图(c)是8水利分区降水和太湖水位的九维联合分布P-P图;图(d)、图(e)、图(f)是4水利分区降水和太湖水位的五维联合分布P-P图;图(g)、图(h)、图(i)是3水利分区降水和太湖水位的四维联合分布P-P图;图(j)、图(k)、图(l)是太湖流域降水和太湖水位的二维联合分布P-P图;图(a)、图(d)、图(g)、图(j)是Clayton Copula拟合的结果;图(b)、图(e)、图(h)、图(k)是Gumbel Copula拟合的结果;图(c)、图(f)、图(i)、图(l)是Frank Copula拟合的结果) Fig.5 The probability-probability (P-P) plots in the plum rain period in Taihu Basin |
| 表 5 汛期不同时段降雨和水位各维度联合概率分布函数的拟合优度评价 Tab. 5 The goodness of fit tests for the Copula functions in the plum rain period and typhoon period |

|
图 6 太湖流域台汛期降雨和太湖水位P-P图(各图序号定义与图 5一致) Fig.6 The probability-probability (P-P) plots in the typhoon period in Taihu Basin |

|
图 7 太湖流域梅汛期和台汛期聚类划分结果 Fig.7 The results of regional clustering in the plum rain period and typhoon period |
在梅汛期,通过对太湖警戒水位和区域防洪标准的分析,认为在太湖超过3.8 m警戒水位时,4个分区中只要有1个分区遭遇50年一遇以上暴雨即为排涝不利.因为各分区在遭遇超过本区域防洪能力的暴雨时,必将通过向区域外排放洪水,以减轻本区域水利工程的防洪压力和减少本区域洪涝灾害,而太湖是流域内主要的蓄水区域,但此时若太湖水位超过警戒值,不宜蓄水或水位过高难以接纳各分区涝水,则必然造成流域或流域部分区域排涝不利的情境.
在台汛期,通过对太湖警戒水位和流域防洪标准的分析,认为在太湖超过3.8 m警戒水位时,流域遭遇100年一遇以上暴雨即为排涝不利;在太湖超过4.65 m保证水位时,流域遭遇50年一遇以上暴雨即为排涝不利.
到2025年,根据设定的排涝不利情景,太湖流域在梅汛期和台汛期出现排涝不利的概率分别为2.4 %和1.1 % (表 6~8),与太湖流域防洪规划相比,结果基本吻合.相比以往洪涝风险分析方法(如MIKE模型[32]、太湖流域模型[33]),本文注意到不同天气系统导致洪涝风险差异性的现象,并利用较少的数据,最大程度上反映太湖流域防洪排涝的真实情况,在流域规划层面上,可以为流域区域防洪排涝协调性评估、防洪排涝工程布局等工作提供参考.
| 表 6 太湖流域梅汛期各区域不同降水和太湖水位遭遇概率计算结果(一)* Tab. 6 The calculation of encounter probability during the plum rain period in Taihu Basin (part.1) |
| 表 7 太湖流域梅汛期各区域不同降水和太湖水位遭遇概率计算结果(二)* Tab. 7 The calculation of encounter probability during the plum rain period in Taihu Basin (part.2) |
| 表 8 太湖流域台汛期不同降水和太湖水位遭遇概率计算结果* Tab. 8 The calculation of encounter probability during the typhoon period in Taihu Basin |
以往对降水时间分布不均匀性的研究多集中在年时间尺度,研究成果多以汛期和非汛期两阶段展示,而在汛期内,对由于复杂天气系统所造成降水时空差异性的研究较少,基于此的洪涝灾害危险性分析研究成果也不多.本文通过拟合天气系统中各降水主导因素的发生时间,将流域汛期划分为梅汛期和台汛期,并利用Copula函数对流域的水文分区进行聚类,探究不同时期,太湖流域各区域降水和太湖水位的关系.在此基础上,对梅汛期和台汛期流域洪涝风险进行分析.本文主要的结论如下:
1) 由于气象原因,太湖流域的梅雨和台风发生时间也呈现出一定的规律性,根据各自的发生时间规律,太湖流域汛期可以被分成梅汛期(6月24日-7月21日)和台汛期(7月22日-9月22日).
2) 在不同天气系统的影响下,降水的空间不均匀性也是不一致的.在梅汛期,太湖流域划分为P-Ⅰ区、P-Ⅱ区和P-Ⅲ区,采用4维的Clayton Copula函数来构建3个区域降水和太湖水位的联合分布最能反映流域实际洪涝情况;在台汛期,整个流域不分区,太湖流域降水作为一个整体进行流域洪涝风险分析.
3) 在2025年,梅汛期和台汛期,太湖流域出现排涝不利情景的风险概率分别为2.4 %和1.1 %.太湖流域年降水量虽然集中在汛期,但受复杂天气系统影响,汛期内降水的时空分布是不同的,因此梅雨期和台风期的洪涝灾害风险也不同,我们应该制定相应的应急预案来预防洪水灾害.
本文的研究区域是太湖流域,但对受台风和梅雨影响的台湾、辽东半岛、日本等东亚沿海地区均可以采用类似的方法进行防洪排涝风险分析,对东亚沿海地区设计暴雨的调整,洪水资源的利用,防洪排涝实时调度的决策具有一定的参考意义.此外在下一步研究中,可以结合具体的水动力学等数值模型,在不同时期、降水情境以及区域划分方案下,展开具体的数值模拟工作,为流域洪涝风险评估工作提供更为具体的技术支持.
| [1] |
Favre AC, El Adlouni S, Perreault L et al. Multivariate hydrological frequency analysis using copulas. Water Resources Research, 2004, 40(1): W01101. DOI:10.1029/2003WR002456 |
| [2] |
Karmakar S, Simonovic S. Bivariate flood frequency analysis:Part 1. Determination of marginals by parametric and nonparametric techniques. Journal of Flood Risk Management, 2008, 1(4): 190-200. DOI:10.1111/j.1753-318X.2008.00022.x |
| [3] |
Karmakar S, Simonovic S. Bivariate flood frequency analysis. Part 2:a copula-based approach with mixed marginal distributions. Journal of Flood Risk Management, 2009, 2(1): 32-44. DOI:10.1111/j.1753-318X.2009.01020.x |
| [4] |
Shabri A, Jemain AA. Regional flood frequency analysis for S outhwest P eninsular M alaysia by LQ-moments. Journal of Flood Risk Management, 2013, 6(4): 360-371. DOI:10.1111/jfr3.12023 |
| [5] |
Bhattacharjee K, Behera B. Determinants of household vulnerability and adaptation to floods:Empirical evidence from the Indian State of West Bengal. International Journal of Disaster Risk Reduction, 2018, 31: 758-769. DOI:10.1016/j.ijdrr.2018.07.017 |
| [6] |
Pandey AC, Singh SK, Nathawat MS. Waterlogging and flood hazards vulnerability and risk assessment in Indo Gangetic plain. Natural Hazards, 2010, 55(2): 273-289. DOI:10.1007/s11069-010-9525-6 |
| [7] |
Romanescu G, Hapciuc O, Minea I et al. Flood vulnerability assessment in the mountain-plateau transition zone:a case study of Marginea village (Romania). Journal of Flood Risk Management, 2018, 11: 502-513. DOI:10.1111/jfr3.12249 |
| [8] |
Bonasia R, Areu-Rangel O, Tolentino D et al. Flooding hazard assessment at Tulancingo (hidalgo, Mexico). Journal of Flood Risk Management, 2018, 11: 1116-1124. DOI:10.1111/jfr3.12312 |
| [9] |
Feng P, Cui GT, Zhong Y. On the evaluation and prediction of urban flood economic loss. Journal of Hydraulic Engineering, 2001, 8(3): 64-68. |
| [10] |
Smith DI. Flood damage estimation-A review of urban stage-damage curves and loss functions. Water Sa, 1994, 20(3): 231-238. |
| [11] |
Fakhruddin S, Kawasaki A, Babel MS. Community responses to flood early warning system:Case study in Kaijuri Union, Bangladesh. International Journal of Disaster Risk Reduction, 2015, 14: 323-331. DOI:10.1016/j.ijdrr.2015.08.004 |
| [12] |
McCallum I, Liu W, See L et al. Technologies to support community flood disaster risk reduction. International Journal of Disaster Risk Science, 2016, 7(2): 198-204. DOI:10.1007/s13753-016-0086-5 |
| [13] |
Zaw T N, Lim S. The military's role in disaster management and response during the 2015 Myanmar floods:A social network approach. International Journal of Disaster Risk Reduction, 2017, 25: 1-21. DOI:10.1016/j.ijdrr.2017.06.023 |
| [14] |
Bacchi B, Becciu G, Ottegoda N. Bivariate exponential model applied to intensities and durations of extreme rainfall. Journal of Hydrology, 1994, 155(1/2): 225-236. |
| [15] |
Goel N, Seth S, Chandra S. Multivariate modeling of flood flows. Journal of Hydraulic Engineering, 1998, 124(2): 146-155. DOI:10.1061/(ASCE)0733-9429(1998)124:2(146) |
| [16] |
Yue S, Ouarda TBMJ, Bobée B et al. The Gumbel mixed model for flood frequency analysis. Journal of Hydrology, 1999, 226(1/2): 88-100. |
| [17] |
Long D, Krzysztofowicz R. Farlie-Gumbel-Morgenstern bivariate densities:Are they applicable in hydrology?. Stochastic Hydrology & Hydraulics, 1992, 6(1): 47-54. |
| [18] |
Kelly KS, Krzysztofowicz R. A bivariate meta-Gaussian density for use in hydrology. Stochastic Hydrology & Hydraulics, 1997, 11(1): 17-31. |
| [19] |
Salvadori G. Bivariate return periods via 2-Copulas. Statistical Methodology, 2004, 1(1/2): 129-144. |
| [20] |
Shiau JT, Wang HY, Tsai CT. Bivariate frequency analysis of floods using copulas. Jawra Journal of the American Water Resources Association, 2010, 42(6): 1549-1564. |
| [21] |
Liu Y, Wang YT, Hu QF et al. Characteristics analysis of Plum rains in Taihu Lake basin based on joint distribution. Hydro-Science and Engineering, 2015(4): 98-105. [刘勇, 王银堂, 胡庆芳等. 基于联合分布的太湖流域梅雨特征研究. 水利水运工程学报, 2015(4): 98-105.] |
| [22] |
Lian JJ, Xu K, Ma C. Joint impact of rainfall and tidal level on flood risk in a coastal city with a complex river network:a case study of Fuzhou City, China. Hydrology and Earth System Sciences, 2013, 17(2): 679-689. DOI:10.5194/hess-17-679-2013 |
| [23] |
Ai P, Yuan D, Xiong C. Copula-based joint probability analysis of compound floods from rainstorm and typhoon surge:A case study of jiangsu coastal areas, China. Sustainability, 2018, 10(7): 2232. DOI:10.3390/su10072232 |
| [24] |
Fang B, Guo SL, Xiao Y et al. Annual maximum flood occurrence dates and magnitudes frequency analysis based on bivariate joint distribution. Advances in Water Science, 2008, 19(4): 505-511. [方彬, 郭生练, 肖义等. 年最大洪水两变量联合分布研究. 水科学进展, 2008, 19(4): 505-511. DOI:10.3321/j.issn:1001-6791.2008.04.009] |
| [25] |
Hu SY, Wang ZZ, Wang YT et al. Encounter probability analysis of typhoon and plum rain in the Taihu Lake Basin. Science China Technological Sciences, 2011(4): 426-435. [胡四一, 王宗志, 王银堂等. 太湖流域台风与梅雨遭遇概率分析. 中国科学:技术科学, 2011(4): 426-435.] |
| [26] |
Deng PX, Hu QF, Wang YT et al. Heterogeneity study of rainfall in the Taihu Lake basin. Hydro-Science and Engineering, 2014(5): 34-40. [邓鹏鑫, 胡庆芳, 王银堂等. 太湖流域降水不均匀性研究. 水利水运工程学报, 2014(5): 34-40. DOI:10.3969/j.issn.1009-640X.2014.05.006] |
| [27] |
Wang TS. Flood control and water resource management in Taihu Basin. Beijing: China Water & Power Press, 2006: 3-13. [王同生. 太湖流域防洪与水资源管理. 北京: 中国水利水电出版社, 2006: 3-13.]
|
| [28] |
Sklar A. Random variables, distribution functions, and copulas:a personal look backward and forward. Lecture notes-monograph series, 1996, 1-14. |
| [29] |
Hofert M, Mächler M, McNeil AJ. Likelihood inference for Archimedean copulas in high dimensions under known margins. Journal of Multivariate Analysis, 2012, 110: 133-150. DOI:10.1016/j.jmva.2012.02.019 |
| [30] |
Genest C, Rémillard B, Beaudoin D. Goodness-of-fit tests for copulas:A review and a power study. Insurance:Mathematics and economics, 2009, 44(2): 199-213. DOI:10.1016/j.insmatheco.2007.10.005 |
| [31] |
Omelka M, Veraverbeke N, Gijbels I. Bootstrapping the conditional copula. Journal of Statistical Planning and Inference, 2013, 143(1): 1-23. DOI:10.1016/j.jspi.2012.06.001 |
| [32] |
Zhang NQ, Li N, Wang J et al. Study on urban flood inundation analysis model for plain tidal river network region. Water Resources and Hydropower Engineering, 2017, 48(5): 23-29. [张念强, 李娜, 王静等. 平原感潮河网区域城市洪涝分析模型研究. 水利水电技术, 2017, 48(5): 23-29. DOI:10.3969/j.issn.2095-0144.2017.05.007] |
| [33] |
Cheng WH, Wang CH, Zhu Y. Taihu Basin model. Nanjing: Hohai University Press, 2006: 111-115. [程文辉, 王船海, 朱琰. 太湖流域模型. 南京: 河海大学出版社, 2006: 111-115.]
|
 2020, Vol. 32
2020, Vol. 32 


