当风吹行于水体表面时,能经过水气相互作用的传递产生风浪.风浪可导致湖泊堤坝工程护坡的损坏和淘刷,是影响湖泊防波堤安全、防洪以及水上安全作业的关键因素.在浅水湖泊中,风浪是表征湖泊水动力过程最为重要的因子.国内外研究结果显示,浅水湖泊风浪作用是沉积物再悬浮最重要的驱动因素[1-8],湖泊底泥再悬浮是影响和控制内源释放的关键物理过程[9-15],也是影响生长层内部结构和生物数量变化、光学的吸收衰减等化学、生物过程的重要因素[16-18].因此,风浪研究对于湖泊防洪、建筑物设计、水上安全作业和湖泊生态系统研究都具有重要意义.
湖泊风浪研究与海洋风浪研究类似,主要通过现场观测和数值模拟手段.早期,一些学者[19-23]根据实测资料,通过数据分析,得出了一些重要的结论.但湖泊风浪现场观测研究主要是基于局部观测点的观测数据得出经验公式,进而应用到全湖的风浪分布研究,这些结果为了解湖泊风浪要素的分布及认识风浪谱提供了依据,但是仅由部分观测点的数据得到的风浪特征必定受区域边界的影响,其结论是否适合整个湖泊水域还有待研究.近年来随着风浪模型的成熟和完善,数值模拟方法逐渐成为研究风浪发展和传播的主要手段.李一平等[24]在太湖实际风浪观测的基础上,利用SWAN模型对太湖风浪进行数值模拟,研究了太湖风浪的主要影响因素.陶蓉茵[25]利用SWAN模型开展了太湖风浪模拟,分析了太湖风浪谱的时空分布特征.许遐祯等[26]以空间均匀的实际风场为驱动,利用SWAN模式开展太湖风浪场模拟,分析了太湖风浪频率分布特征以及不同区域风浪谱对风时、风区、水深等因素的敏感性.王震等[27]利用SWAN模型开展了太湖自然风条件下不同湖区风浪季节变化特征. Jin和Ji[28]进行了SWAN模型在奥基乔比湖风浪模拟中的可靠性验证,结果显示模型可很好地再现湖泊中风浪的变化趋势与波动特征. Graf等[29]开展了SWAN模型在苏黎世湖应用研究,验证了突变风况下SWAN模型计算波浪场的可靠性,分析了风场的时间分辨率对该湖风浪特征的影响.这些研究表明数值模拟手段可以很好地揭示湖泊风浪的影响因素和分布特征以及补充原位观察在研究湖泊风浪空间分布时的不足.
目前有关巢湖的风浪观测分析与数值模拟工作较为缺乏,不利于巢湖水环境的综合整治、防洪和船泊航运安全.巢湖地处内陆,较少受到台风的影响,而台风过程往往伴随着强烈的大风过程,一旦遭遇台风过境势必引起强烈的风浪过程.本文基于巢湖实测风浪资料,结合SWAN风浪模型,对2018年8月第14号台风“摩羯”和第18号台风“温比亚”过境巢湖时的风浪变化情况进行分析,探讨巢湖不同区域巢湖风浪的变化和分布特征,为我们正确认识大风情况下巢湖风浪情况提供指导.
1 研究概况 1.1 研究区域巢湖(31°25′28″~31°43′28″N, 117°16′54″~117°51′46″E)地处安徽省中部,常水位8.50 m(吴淞高程,下同)时水面面积为769.60 km2,平均水深约为2.79 m,流域面积为1.35万km2,是我国长江流域五大淡水湖之一.巢湖东西长54.50 km,南北宽15.10 km,最大宽度约21.00 km,巢湖的地形如图 1所示.巢湖流域地处西南季风区,属北亚热带季风气候,受亚热带季风气候影响,巢湖流域内平均风速4.1 m/s,盛行E、NE风,频率30.0 %.冬季多NE、NW风,夏季多偏S风;平均每年8级以上大风日数18.8 d,历史最大风速为34.0 m/s(1958年8月10日).
|
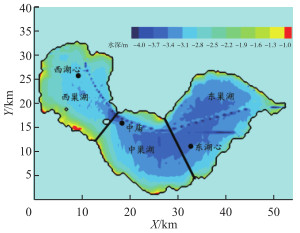
图 1 巢湖地形及观测站布置(横坐标代表东西宽度,纵坐标代表南北宽度,颜色等值线代表水深等值线,黑色实心点代表监测点位) Fig.1 The topography and observation stations in Lake Chaohu (Horizontal ordinates represent the width in east-west direction, the longitudinal coordinates represent the width in north-south direction, the color isolines represent the water depth isolines, and the black solid dots represent observation stations) |
2018年8月8日14时,第14号台风“摩羯”生成,其中心位于19.4°N,133.5°E,强度等级为热带风暴级,中心附近最大风力达8级(18 m/s),8月13日8:00进入安徽境内,于8月13日12:00-15:00从巢湖东北部掠过;2018年8月15日14时,第18号台风“温比亚”在东海东南部海面形成,强度等级为热带风暴级,8月17日13:00进入安徽境内,并于8月17日16:00-21:00从巢湖南部掠过.台风过程伴随着较大的风速,过境各处时往往在上百公里内产生大于6级的风,因此当台风过境巢湖时势必带来大风过程,故而会在巢湖引起强烈的风浪过程,对巢湖生态系统、防洪以及船舶航行安全产生较大的影响.
2 台风期间气象与风浪测量 2.1 气象监测为获得风浪观测期间湖面风场特征,分别在东湖心、中庙、西湖心3个站位布置了气象站(图 1),气象站位于湖中间平台上,可测定风速、风向、降雨、大气辐射等参数,气象站采用太阳能与蓄电池供电,可保证长期稳定工作.其中风速传感器分辨率为0.1 m/s,测量范围为0~60 m/s;风向传感器分辨率为1°,测量范围为0°~359°.
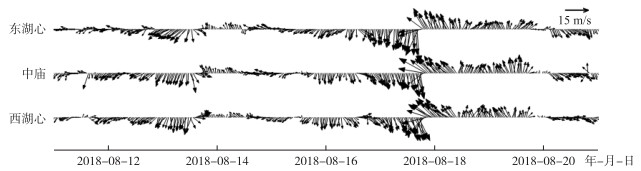
通过观测获得了2018年8月份的巢湖湖面风速与风向情况,表 1为3个测站风速统计特征,图 2为巢湖湖面2018年8月东湖心、中庙、西湖心3个测站处风速风向变化情况.可以看出,3个测站处湖面风速大小与方向变化趋势相似,在风速大小与风向转变时刻会略有差异.在台风“摩羯”(8月13日)和“温比亚”(8月17日)过境时,出现了较大的风速过程,其中台风“摩羯”8月13日9:00在东湖心引起了12.7 m/s的大风,且较大风速过程主要为东北向大风;在中庙与西湖心引起的最大风速分别为12.7和11.3 m/s,明显大于8月份巢湖各测站平均风速(表 1),最大风速出现时刻分别为8月13日12:40和12:50,较东湖心最大风速出现时间明显滞后,而且较大风速过程的风向介于北偏东和北偏西间;由图 2可以看出,台风“摩羯”过境时,由于巢湖一直处于台风“摩羯”左侧,因此风向逐渐由东北向逆时针转为南向.台风“温比亚”的影响更为显著,3个测站8月份最大风速都出现在“温比亚”过境时,其中8月17日16:30在东湖心产生了24.7 m/s的北风,中庙与西湖心测站最大风速分别为19.7和18.6 m/s,风向分别为东南和北偏西;由图 2可以看出,台风“温比亚”过境前,风向主要为西北风,过境后主要呈东南风,且这种风向突变时刻东湖心最早,其次为中庙,最后为西湖心,这是因为过境前巢湖位于台风“温比亚”左侧,随着向巢湖南侧移动,巢湖逐渐处于了台风“温比亚”右侧. 8月份巢湖平均风速看,东湖心测站最大为4.8 m/s,其次为中庙站的4.6 m/s,西湖心最小为4.4 m/s.
| 表 1 2018年8月巢湖3个观测站的风速统计特征 Tab. 1 Statistical characteristics of wind speed at 3 observation stations in Lake Chaohu on August, 2018 |
|
图 2 2018年8月巢湖3个观测站风矢量的变化 Fig.2 The changes of wind vector at three observation stations in Lake Chaohu during August of 2018 |
风浪观测仪器采用WaveStar雷达测波仪,该仪器是一款高精度、非接触式风浪测量仪器,采用FMCW雷达测距原理,可以进行全天候测量.其测量原理为:传感器发射微波脉冲后在空气中传播,被水面反射的信号又被传感器接收,通过精确计算传播时间和数字信号处理技术,精确计算出传感器距离反射面的距离,由此获得湖面波动数据.波面数据通过仪器自身软件处理后可以获得观测点不同统计特征的波高(如有效波高、最大波高、平均波高等)和周期(如平均波周期、最大波周期).仪器安装在西湖心的固定平台上,如图 1所示,其位置为31°39′9.73″N,117°22′21.17″E,仪器距离水面5.5 m,风浪观测时间为2018年8月9日12:00-8月31日23:30,时间间隔为30 min,采样频率为4 Hz,每次采集波面数为2048(约为8.53 min波面过程).
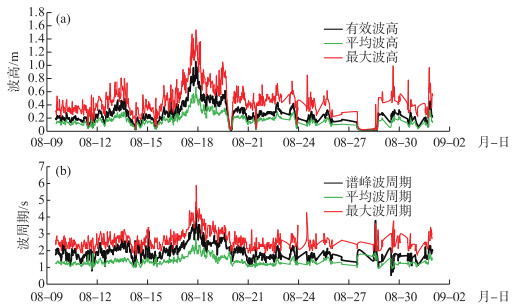
观测期间,由于连续阴雨天气导致太阳能供电中断会出现缺测值,同时剔除异常数值,共取得有效数据755条,图 3a为波高(有效波高、平均波高、最大波高)随时间变化情况,图 3b为周期(谱峰波周期、平均波周期、最大波周期)随时间变化情况,表 2为风浪要素统计情况.可以看出,在台风“摩羯”和“温比亚”过境巢湖流域时,分别出现两次较大的风浪过程,两次台风过程间隙风浪强度较小.其中台风“摩羯”过境时可在西湖心监测站处产生最大0.29 m的平均波高、0.49 m的有效波高和0.80 m的最大波高,平均波周期、谱峰波周期和最大波周期的最大值可分别达1.59、3.25和2.67 s,较8月份平均值(表 2)明显偏大;而“温比亚”过境时风浪强度更为显著,可在西湖心监测站处产生最大0.66 m的平均波高、1.05 m的有效波高和1.53 m的最大波高,平均波周期、谱峰波周期和最大波周期的最大值可分别达2.68、4.57和5.88 s,为巢湖8月份监测到的最大风浪强度(表 2),进一步表明8月份巢湖最大风浪出现在台风“温比亚”过境时.风浪要素最大值出现在台风“温比亚”过境巢湖流域时,发生时间较最大风速出现时间滞后约5 h(表 1).监测期间,西湖心有效波高平均值为0.28 m,平均波周期平均值为1.38 s,实测值为我们认识巢湖风浪强度提供了基础.
|
图 3 实测浪高(a)和实测周期(b)(测量时间:2018年8月9日12:30-8月31日23:30) Fig.3 The observation wave height (a) and wave period (b) (Observation time: August 9th, 12:30-August 31st, 23:30, 2018) |
| 表 2 2018年8月巢湖观测站风浪要素统计值 Tab. 2 The statistics of wind wave elements at observation stations in Lake Chaohu during August 2018 |
SWAN风浪模式(Simulating Waves Nearshore)是适用于海岸和内陆水体的第3代风浪模型,由荷兰Delft大学土木工程系的Booij等[30]开发并由SWAN团队发展和完善.除了包含其他3代风浪模式(如WAVEWATCH[31]、WAM[32])中的风生成项、白浪耗散项、四波相互以及底部耗散项外,还增加了三波相互作用和浅水区域水深变浅引起的风浪破碎耗散影响.
由于流存在时,波谱能量密度不守恒,而波作用量谱守恒,因此SWAN风浪模式跟其他3代风浪模式相似,采用波作用量密度谱对风浪进行描述.波谱作用量密度谱的变化率可以用作用量平衡方程来表示:
| $ \frac{{\partial N}}{{\partial t}} + \nabla \cdot \left[ {\left( {{{\overrightarrow C }_g} + \overrightarrow V } \right)N} \right] + \frac{{\partial {C_\sigma }N}}{{\partial \sigma }} + \frac{{\partial {C_\theta }N}}{{\partial \theta }} = \frac{{{S_{{\rm{tot}}}}}}{\sigma } $ | (1) |
其中,N是波作用量密度谱,N=S/σ,S为能量密度;t为时间;σ、θ为相对波频和波向;Cσ和Cθ为风浪在谱空间(σ, θ)传播速度;
对于源项,通常包含以下几项:
| $ {S_{{\rm{tot}}}} = {S_{{\rm{in}}}} + {S_{{\rm{nl3}}}} + {S_{{\rm{nl4}}}} + {S_{{\rm{ds, w}}}} + {S_{{\rm{ds, b}}}} + {S_{{\rm{ds, br}}}} $ | (2) |
式中,Sin为风能输入项,Snl3为三波相互作用,Snl4为四波相互作用,Sds, w为白浪耗散项,Sds, b为由于底部摩阻引起的耗散,Sds, br为水深变浅引起的破碎导致的耗散项.风能向风浪的转换可以利用共振[33]和反馈[34]机制来阐述.其中共振机制主要作用在风浪生成的初始阶段,随时间线性增长;而反馈机制主要反映着波能随时间呈指数增长.其他诸如白浪耗散、四波相互、三波相互、水深变浅破碎及底摩阻耗散等源项的计算可参考SWAN技术手册[35],这里不再赘述.
3.2 模型配置此处建立东西54.4 km、南北长34 km的巢湖模拟区域,采用二维非恒定模型.模型的空间分辨率为400 m×400 m,计算时间步长取5 min,计算时间范围为2018年8月1日00:00-9月1日00:00.根据巢湖实测的周期范围,拟定频率范围为0.1~2.0 Hz,分成40个频率段.方向沿整个圆周方向均分为36份,即方向分辨率为10°.模型物理过程中,风输入考虑了线性增长和指数增长两部分,线性增长采用Caraler和Malanotte-Rizzoli公式[36],增长部分采用Yan公式[37].底摩擦引起的消耗采用JONSWAP模型,系数取0.067.浅水风浪破碎系数在计算时取其均值0.73.由于入湖河道对太湖风浪影响不大,此处计算时不考虑入湖河流影响.模型中考虑了浅水中三波相互作用,其他采用默认值.
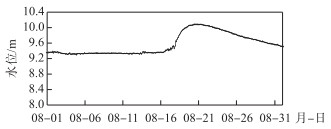
巢湖整体水位受防洪、航运、灌溉等任务控制较显著,且受季节变化影响,据资料统计显示,巢湖年内水位变幅最小为1.44 m(1966年),最大可达6.48 m(1954年).水位的变化势必导致巢湖绝对水深的变化,而水深是影响风浪形成和发展的重要因素之一,因此计算巢湖风浪情况时,考虑水位波动的影响是十分必须的.为此收集整理了巢湖周边塘西、槐林镇、巢湖闸3个水位站2018年8月逐时水位数据,并取3个站的平均值作为水位值输入到SWAN模型中,图 4为3站平均的巢湖水位变化情况,最高水位为10.10 m(2018年8月20日11:00),最低水位为9.29 m(2018年8月4日20:00),水位变化幅度为0.81 m.模型计算中,将东湖心、中庙、西湖心3个测站处所观测风速矢量在整个计算区域进行距离插值,得到模型计算所需的非均一风场,输入SWAN模型中.
|
图 4 2018年8月1-31日巢湖平均水位的变化 Fig.4 Average water levels at Lake Chaohu during 1-31 August, 2018 |
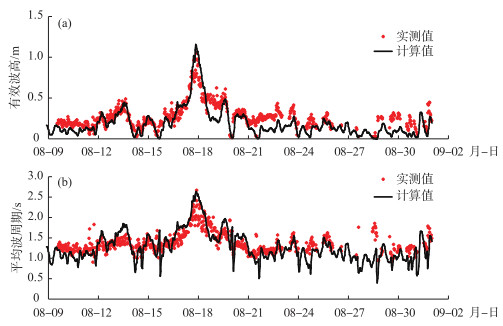
为了验证模式计算结果,将2018年8月9日12:30-8月31日23:30期间观测站位的模拟计算结果与实测数据进行对比,对比结果如图 5所示.由验证结果可以看出,模拟值与实测值吻合良好,其中有效波高相关系数为0.84,平均波周期相关系数为0.74,表明模型能较准确地反映出有效波高与平均周期随时间的变化情况.由此可见,利用SWAN风浪模型模拟的巢湖波高和周期,能够很好地反映出巢湖的实际风浪情况,可以较好地模拟出巢湖的风浪特征,因此可以采用SWAN风浪模型开展巢湖风浪特征的模拟研究与分析.
|
图 5 2018年8月9日12:30-8月31日23:30期间风浪计算有效波高(a)和平均波周期(b)与实测值的对比 Fig.5 The comparison between the calculated value and the observation value of the significant wave height (a) and average wave period (b) during August 9th, 12:30 and August 31st, 23:30, 2018 |
浅水湖泊在风浪作用下一方面可以引起底泥再悬浮和水体污染内源的释放,严重影响湖泊的水质,另一方面会导致水体垂向混合增加,进一步对藻类的垂向迁移产生影响,风浪的强度、范围和时间决定了蓝藻水华的时空分布.风浪的有效波高和平均波周期是表征风浪强度的重要波要素,本节将重点分析台风过程时该两种风浪要素的变化情况.
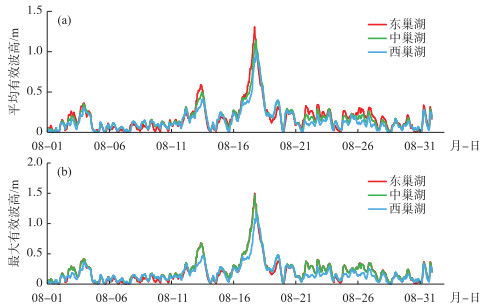
4.1 有效波高变化及分布特征图 6为2018年8月巢湖分湖区统计的平均有效波高和最大有效波高随时间变化情况.整体看,8月东巢湖有效波高平均值最大,为0.18 m,中巢湖略小,西巢湖最小为0.15 m,从图 6中不同湖区平均有效波高变化也可以明显看出,东巢湖和中巢湖有效波高较西巢湖大;月内最大有效波高规律略有差异,总体中巢湖最大,东巢湖与中巢湖接近,西巢湖最小,8月最大有效波高平均值分别为0.21、0.22和0.18 m.从图 6可以看出台风“摩羯”和“温比亚”过境时,明显产生了强烈的风浪过程,其中台风“摩羯”过境时东巢湖、中巢湖和西巢湖平均有效波高最大值分别为0.59、0.50和0.41 m,出现时刻为2018-8-13 10:00、11:00和13:00,最大有效波高最大值为0.68、0.67和0.48 m,出现时刻为2018-8-13 10:00、10:00和13:00,根据路径图可知,以上极值出现在台风“摩羯”刚进入安徽境内至巢湖市北部这段时间内,随着台风“摩羯”继续北上和强度减弱,巢湖风浪强度快速减小,至台风“温比亚”抵达前,巢湖风浪强度较弱(各湖区有效波高平均值和最大值都小于0.22 m).台风“温比亚”过境时,风浪强度增大,在东巢湖、中巢湖和西巢湖平均有效波高最大值分别达到1.31、1.15和1.02 m,最大有效波高最大值分别为1.50、1.47和1.19 m,出现时刻分别为2018-8-17 17:00、17:00和20:00,即东巢湖和中巢湖首先受台风影响,根据路径图可知,当“温比亚”抵达安徽省芜湖市无为县红庙镇,即巢湖东南侧时,对东巢湖与中巢湖的影响达到最大,随后随着“温比亚”继续前进,抵达安徽省合肥市肥西县三河古镇附近时,对西巢湖的影响达到最大,而后“温比亚”逐渐远离巢湖流域,影响逐渐减弱.
|
图 6 2018年8月1日-31日巢湖平均有效波高(a)和最大有效波高(b)的变化 Fig.6 The changes of average significant wave height (a) and maximum significant wave height (b) for Lake Chaohu during 1-31 August, 2018 |
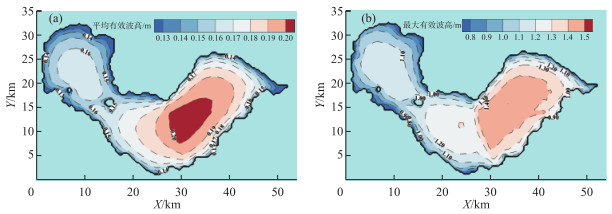
图 7为8月份月均有效波高和月最大有效波高在整个巢湖的分布情况.可以看出,月均有效波高最大值出现在东巢湖与中巢湖接洽的中心水域,而月最大有效波高则出现在东巢湖湖心附近水域,即台风“温比亚”过境时对整个巢湖影响最大的区域位于东巢湖湖心水域.受地形、水深、风区长度影响,近岸附近水域有效波高较小,较大值主要出现在各湖区湖心水深较大的水域;整体看,西巢湖产生的风浪强度最小,中巢湖次之,东巢湖最大,这与不同测站测得的风速相对应(表 1、图 2),即东巢湖测站出现了最大的风速过程,且风向为东北向,在东巢湖产生较大的风区长度,因此相应的东巢湖出现的风浪强度最大;中巢湖风速次之,相应的风浪强度也比东巢湖小;西巢湖风速过程最小,相应的风浪强度也最小.根据统计,8月东巢湖、中巢湖和西巢湖月最大有效波高大于1.0 m的面积分别为254.88、201.44和152.64 m2,分别各个湖区总面积的93 %、89 %和66 %,进一步表明台风“温比亚”过境时对东巢湖的影响最为显著,中巢湖次之,西巢湖最小.因此台风过境或大风天气时,湖心水域尤其是东巢湖与中巢湖连通的大面积湖心水域要密切注意防范大风浪下作业安全问题.
|
图 7 巢湖2018年8月1日-31日平均有效波高(a)和最大有效波高(b)的空间分布 Fig.7 Spatial distribution of average significant wave height (a) and maximum significant wave height (b) for Lake Chaohu during 1-31 August, 2018 |
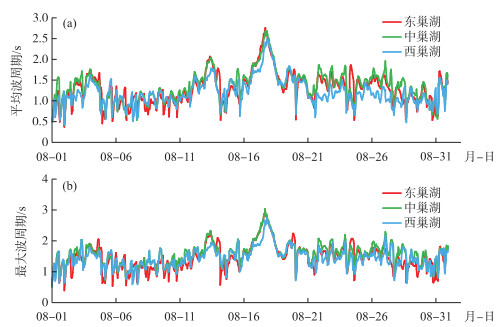
图 8为2018年8月巢湖分湖区统计的平均波周期和最大波周期随时间变化情况(此处波周期为平均波周期T1).可以看出,不同湖区波周期略有差异,但差异性较有效波高明显偏小.总体8月份东巢湖、中巢湖和西巢湖波周期平均值为1.29、1.35和1.21 s,最大波周期平均值为1.46、1.57和1.45 s,总体中巢湖最大,东巢湖次之,西巢湖最小.由图 9可以明显看出,台风“摩羯”和“温比亚”过境时,出现了较大的波周期;其中台风“摩羯”过境时东巢湖、中巢湖和西巢湖平均波周期最大分别为2.07、2.05和1.79 s,最大波周期为2.25、2.33和1.95 s,出现时刻均为2018-8-13 9:00、10:00和11:00,相较有效波高峰值,东巢湖和西巢湖略有提前,分别提前了1和2 h,而中巢湖波周期峰值与有效波高峰值同步出现;台风“温比亚”过境时影响更为显著,东巢湖、中巢湖和西巢湖平均波周期最大分别为2.76、2.69和2.49 s,最大平均波周期为2.99、3.04和2.74 s,出现时刻均为2018-8-17 17:00、17:00和20:00,与有效波高峰值时刻同步.
|
图 8 2018年8月1日-31日巢湖平均波周期(a)和最大波周期(b)的月变化 Fig.8 The changes of average wave period (a) and maximum wave period (b) for Lake Chaohu during 1-31 August, 2018 |

|
图 9 2018年8月1日-31日巢湖平均波周期(a)和最大波周期(b)的空间分布 Fig.9 Spatial distribution of average wave period (a) and maximum wave period (b) for Lake Chaohu during 1-31 August, 2018 |
图 9为8月份波周期平均值和波周期最大值在整个巢湖的空间分布情况.可以看出8月月均平均波周期和月最大波周期较大值主要出现在东巢湖与中巢湖连通的湖心水域,由此可知台风过境时会在东巢湖与中巢湖连通的大片湖心水域出现较大的波周期分布区域,需要格外注意.月均平均波周期最大值和月最大波周期最大值均出现在靠近东巢湖的中巢湖湖心水域,最大值分别为1.39和3.08 s;西巢湖月均波周期较大值主要出现在南半湖水域,北半湖水域周期相对较小,而月最大波周期则在湖心附近较大,近岸区域相对较小.以上分析可以看出,台风过境时不同湖区湖心水域由于水深大、风区长度长,往往是出现最大风浪强度的区域,如在台风“温比亚”过境时,有较长时间的大的东北向风速过程出现(图 2),此时东巢湖与中巢湖连通的湖心水域的风浪风区长度可达20 km以上,而此处水深又较大(约3.5 m左右),有利于较大风浪过程产生,因此在开展极端天气下湖泊作业以及生态环境影响分析时需要重点注意.
5 结论本文基于实测和数值模拟手段,开展了台风“摩羯”和“温比亚”过境的2018年8月巢湖风浪变化及分布特征分析,得到以下结论:
1) 台风过境时,实测结果显示在巢湖产生了较大的风速和风浪过程;台风“摩羯”过境时,数值计算结果表明在东巢湖、中巢湖和西巢湖平均有效波高最大值分别为0.59、0.50和0.41 m,最大有效波高最大值为0.68、0.67和0.48 m;台风“温比亚”过境时,风浪强度更大,数值计算结果表明在东巢湖、中巢湖和西巢湖平均有效波高最大值分别达到1.31、1.15和1.02 m,最大有效波高最大值分别为1.50、1.47和1.19 m.台风过境时对整个巢湖影响较大的区域位于东巢湖与中巢湖连接的湖心水域,总体对东巢湖的影响最为显著,中巢湖次之,西巢湖最小.
2) 台风“摩羯”过境时,数值计算结果显示东巢湖、中巢湖和西巢湖平均波周期最大值分别为2.07、2.05和1.79 s,最大平均波周期最大值为2.25、2.33和1.95 s;台风“温比亚”过境时东巢湖、中巢湖和西巢湖平均波周期最大值分别为2.76、2.69和2.49 s,最大平均波周期最大值为2.99、3.04和2.74 s.波周期较大值主要出现在东巢湖与中巢湖联通的湖心水域,台风“温比亚”期间出现了3.08 s的最大波周期.
致谢: 感谢本研究团队(王岩、彭兆亮、朱金格、郭西亚、崔健)在野外观测中给予的帮助.
| [1] |
Sheng YP, Lick W. The transport and resuspension of sediments in a shallow lake. Journal of Geophysical Research Atmospheres, 1979, 84(C4): 1809-1826. DOI:10.1029/JC084iC04p01809 |
| [2] |
Bailey MC, Hamilton DP. Wind induced sediment resuspension:a lake-wide model. Ecological Modelling, 1997, 99: 217-228. DOI:10.1016/S0304-3800(97)01955-8 |
| [3] |
Havens KE, Schelske CL. The importance of considering biological processes when setting total maximum daily loads (TMDL) for phosphorus in shallow lakes and reservoirs. Environmental Pollution, 2001, 113(1): 1-9. DOI:10.1016/S0269-7491(00)00235-9 |
| [4] |
Fan CX, Zhang L, Qu WC. Lake sediment resuspension and caused phosphate release-a simulation study. Journal of Environmental Sciences, 2001, 13(4): 406-410. |
| [5] |
Qin BQ, Fan CX. Exploration of conceptual model of nutrient release from inner source in large shallow lake. China Environmental Science, 2002, 22(2): 150-153. [秦伯强, 范成新. 大型浅水湖泊内源营养盐释放的概念性模式探讨. 中国环境科学, 2002, 22(2): 150-153. DOI:10.3321/j.issn:1000-6923.2002.02.013] |
| [6] |
Qin BQ, Hu WP, Gao G et al. Dynamic mechanism of sediment suspension in Taihu Lake and conceptual model of internal source release. Chinese Science Bulletin, 2003, 48(17): 1822-1831. [秦伯强, 胡维平, 高光等. 太湖沉积物悬浮的动力机制及内源释放的概念性模式. 科学通报, 2003, 48(17): 1822-1831. DOI:10.3321/j.issn:0023-074X.2003.17.002] |
| [7] |
Luo LC, Qin BQ. Comparison between wave effects and current effects on sediment re-suspension in Lake Taihu. Hydrology, 2003, 23(3): 1-4. [罗潋葱, 秦伯强. 太湖波浪与湖流对沉积物再悬浮不同影响的研究. 水文, 2003, 23(3): 1-4.] |
| [8] |
Luo LC, Qin BQ, Hu WP et al. Sediment re-suspension under different hydrodynamic disturbances in Lake Taihu. J Lake Sci, 2004, 16(3): 273-276. [罗潋葱, 秦伯强, 胡维平等. 不同水动力扰动下太湖沉积物的悬浮特征. 湖泊科学, 2004, 16(3): 273-276. DOI:10.18307/2004.0313] |
| [9] |
Mihelčić G, Aurija B, Juračić M et al. History of the accumulation of trace metals in sediments of the saline Rogoznica Lake (Croatia). Science of the Total Environment, 1996, 182: 105-115. DOI:10.1016/0048-9697(95)05058-2 |
| [10] |
Pejrup M, Valeur J, Jensen A. Vertical fluxes of particulate matter in Aarhus Bight, Denmark. Continental Shelf Research, 1996, 16(8): 1047-1064. DOI:10.1016/0278-4343(95)00044-5 |
| [11] |
Loeff MMRV, Boudreau BP. The effect of resuspension on chemical exchanges at the sediment-water interface in the deep sea-A modelling and natural radiotracer approach. Journal of Marine Systems, 1997, 11: 305-342. DOI:10.1016/S0924-7963(96)00128-5 |
| [12] |
Matthai C, Birch GF, Jenkinson A et al. Physical resuspension and vertical mixing of sediments on a high energy continental margin (Sydney, Australia). Journal of Environmental Radioactivity, 2001, 52(1): 67-89. DOI:10.1016/S0265-931X(00)00104-1 |
| [13] |
Luettich RA, Harleman DRF. Dynamic behavior of suspended sediment concentrations in a shallow lake perturbed by episodic wind events. Limnology & Oceanography, 1990, 35(5): 1050-1067. DOI:10.4319/lo.1990.35.5.1050 |
| [14] |
Søndergaard M, Jensen JP, Jeppesen E. Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia, 2003, 506-509(1): 135-145. DOI:10.1023/B:HYDR.0000008611.12704.dd |
| [15] |
Brzáková M, Hejzlar J, Nedoma J. Phosphorus uptake by suspended and settling seston in a stratified reservoir. Hydrobiologia, 2003, 504(1): 39-49. DOI:10.1023/B:HYDR.0000008506.29287.11 |
| [16] |
Hawley N, Chang HL. Sediment resuspension and transport in Lake Michigan during the unstratified period. Sedimentology, 1999, 46(5): 791-805. DOI:10.1046/j.1365-3091.1999.00251.x |
| [17] |
Hamilton DP, Mitchell SF. An empirical model for sediment resuspension in shallow lakes. Hydrobiologia, 1996, 317(3): 209-220. DOI:10.1007/BF00036471 |
| [18] |
Luettich RA, Harleman DRF. Dynamic behavior of suspended sediment concentrations in a shallow lake perturbed by episodic wind events. Limnology & Oceanography, 1990, 35(5): 1050-1067. DOI:10.4319/lo.1990.35.5.1050 |
| [19] |
Qiao SL, Du JP, Chen GP et al. Calculation method and characteristics of wind-wave in lake. Hydro-Science and Engineering, 1996(3): 189-197. [乔树梁, 杜金曼, 陈国平等. 湖泊风浪特性及风浪要素的计算. 水利水运工程学报, 1996(3): 189-197.] |
| [20] |
Pang Y, Pu PM, Hu WP et al. Analysis of the wind wave spectrum character in the north bank of Taihu Lake. Oceanologia et Limnologia Sinica, 1996, 27(5): 531-537. [逄勇, 濮培民, 胡维平等. 太湖北岸风浪谱的特征分析. 海洋与湖沼, 1996, 27(5): 531-537. DOI:10.3321/j.issn:0029-814X.1996.05.013] |
| [21] |
Luo LC, Qin BQ, Hu WP et al. Wave characteristics in Lake Taihu. Journal of Hydrodynamics, 2004, 19(5): 664-670. [罗潋葱, 秦伯强, 胡维平等. 太湖波动特征分析. 水动力学研究与进展, 2004, 19(5): 664-670. DOI:10.3969/j.issn.1000-4874.2004.05.016] |
| [22] |
Hu WP, Hu CH, Zhang FB et al. On the empirical wind-wave height model in northern Lake Taihu, China. J Lake Sci, 2005, 17(1): 41-46. [胡维平, 胡春华, 张发兵等. 太湖北部风浪波高计算模式观测分析. 湖泊科学, 2005, 17(1): 41-46. DOI:10.18307/2005.0107] |
| [23] |
Fan CX ed. Environmental geochemistry and eutrophication of lakes in the middle and lower reaches of the Yangtze River. Beijing: Science Press, 2007. [范成新. 长江中下游湖泊环境地球化学与富营养化. 北京: 科学出版社, 2007.]
|
| [24] |
Li YP, Pang Y, Liu XP et al. Numerical modeling of waves in Lake Taihu. J Lake Sci, 2008, 20(1): 117-122. [李一平, 逄勇, 刘兴平等. 太湖波浪数值模拟. 湖泊科学, 2008, 20(1): 117-122. DOI:10.18307/2008.0118] |
| [25] |
Tao RY. Analysis of wave characteristics and application on wave simulation with wind fields in Lake Taihu[Dissertation]. Nanjing: Nanjing University of Information Science & Technology, 2012. [陶蓉茵.不同风场条件下太湖波浪数值模拟的研究及其应用[学位论文].南京: 南京信息工程大学, 2012. ]
|
| [26] |
Xu XZ, Tao RY, Zhao QH et al. Wave characteristics and sensitivity analysis of the wind field in a large shallow lake-Lake Taihu. J Lake Sci, 2013, 25(1): 55-64. [许遐祯, 陶蓉茵, 赵巧华等. 大型浅水湖泊太湖波浪特征及其对风场的敏感性分析. 湖泊科学, 2013, 25(1): 55-64. DOI:10.18307/2013.0108] |
| [27] |
Wang Z, Wu TF, Zou H et al. Changes in seasonal characteristics of wind and wave in different regions of Lake Taihu. J Lake Sci, 2016, 28(1): 217-224. [王震, 吴挺峰, 邹华等. 太湖不同湖区风浪的季节变化特征. 湖泊科学, 2016, 28(1): 217-224. DOI:10.18307/2016.0125] |
| [28] |
Jin KR, Ji ZG. Calibration and verification of a spectral wind-wave model for Lake Okeechobee. Ocean Engineering, 2001, 28(5): 571-584. DOI:10.1016/S0029-8018(00)00009-3 |
| [29] |
Graf M, Sprenger M, Lohmann U et al. Evaluating the suitability of the SWAN/COSMO-2 model system to simulate short-crested surface waves for a narrow lake with complex bathymetry. Meteorologische Zeitschrift, 2013, 22(3): 257-272. DOI:10.1127/0941-2948/2013/0442 |
| [30] |
Booij N, Ris RC, Holthuijsen LH. A third-generation wave model for coastal regions:1. Model description and validation. Journal of Geophysical Research Oceans, 1999, 104(C4): 7649-7666. DOI:10.1029/98JC02622 |
| [31] |
Tolman HL. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. Journal of Physical Oceanography, 1991, 21(6): 782-797. DOI:10.1175/1520-0485(1991)021<0782:ATGMFW>2.0.CO;2 |
| [32] |
The WAMDI Group. The WAM model-a third generation ocean wave prediction model. Journal of Physical Oceanography, 1988, 18(12): 1775-1810. DOI:10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2 |
| [33] |
Phillips OM. On the generation of waves by turbulent wind. Journal of Fluid Mechanics, 1957, 2(5): 417-445. DOI:10.1017/S0022112057000233 |
| [34] |
John W. On the generation of surface waves by shear flows. Journal of Fluid Mechanics, 1957, 3(3): 185-204. DOI:10.1017/S0022112057000567 |
| [35] |
SWAN Team. SWAN Cycle Ⅲ version 40.51 user manual. Delft University of Technology. The Netherlands:Faculty of Civil Engineering and Geosciences, Environmental Fluid Mechanics Section, 2006. |
| [36] |
Luigi C, Malanotte RP. Wind wave prediction in shallow water:Theory and applications. Journal of Geophysical Research:Oceans, 1981, 86(C11): 10961-10973. DOI:10.1029/JC086iC11p10961 |
| [37] |
Yan L. An improved wind input source term for third generation ocean wave modelling. De Bilt, 1987. |
 2020, Vol. 32
2020, Vol. 32 

