(2: 台州市水文站, 台州 318001)
(3: 青山水库管理处, 杭州 311305)
(2: Taizhou Hydrological Station, Taizhou 318001, P. R. China)
(3: Qingshan Reservoir Management Office, Hangzhou 311305, P. R. China)
黄土地区泥沙问题是目前水文研究的重点问题之一.研究黄河水沙变化、把握黄河水沙变化规律,对于进一步完善治黄方略、实施流域水资源配置与管理及重大水利工程布局,意义重大[1].目前泥沙模型的研究取得了较为丰硕的成果,主要包括经验相关模型和物理成因模型.经验相关模型中,Wischmeier WH等[2]提出了著名的通用土壤侵蚀方程USLE.基于物理机理的流域水沙模型研究较多,汤立群等[3]基于坡面径流侵蚀量计算公式提出了流域产沙模型;WEPP、LISEM、EUROSEM等模型[4-6]基于土壤侵蚀过程的物理描述,模拟了流域侵蚀过程,在许多国家被成功推广应用.已有的大多数流域产沙模型未能考虑不同流域尺度的泥沙规律,模型模拟精度以及使用范围受到了很大限制.因此,包为民[7]基于流域自然地理特性,在对黄土地区产沙机制进行概化的基础上,提出了结构和参数均具有物理意义的流域水沙模拟概念模型.该模型经黄土地区不同流域尺度的实际流域和前期大量的试验流域验证,可以很好地模拟黄土高原地区流域的水沙规律[8].
水沙模拟中重要的动力条件是水流,因此水流模拟的精度直接影响流域产沙和汇沙过程,进而影响水沙模型的模拟精度和效果[9].水流模拟的主要技术手段是依赖于水文模型.水文模型计算误差来源有很多,其中包括重要输入项降雨资料、下垫面条件、流域初始状态值、模型本身误差等[10].由于降雨是水文预报模型计算的重要输入项,因此降雨资料直接影响模型产流,进而影响模型的模拟精度[11].在水沙模型计算过程中,基于黄土区域自然地理特性,流域面平均雨量大多采用“以点带面”的方式进行计算,即利用雨量站点的观测资料代表该雨量站所代表的单元面上的降雨,这种方式不可避免的给流域降雨带来误差.同时,部分降雨资料由于观测等因素存在时段均化现象,伴有一定程度的缺测、漏测和误测问题,降雨资料由插补展延而来, 造成模型模拟误差.因此需要对输入水沙模型进行计算的流域面平均雨量进行修正,从而提高洪水和泥沙的模拟精度.国内外学者对降雨资料观测误差的分析与估计,目前研究较多的是对雷达测雨资料误差进行的修正,然而以遥测系统为观测手段,对流域尺度范围的降雨观测资料误差进行分析和研究则开展得较少,在国外几乎很少涉及[12-15].为提高模型模拟精度,司伟等[16-17]首先提出了动态系统响应曲线修正方法,该方法是向误差源头追溯的动态反馈修正方法,具有物理基础强和不损失预见期等优点[18].将该方法应用在新安江模型降雨误差估计中,对流域面平均雨量进行修正以提高预报精度,取得了非常好的修正效果[10, 19-21].基于以上研究,为了更精确模拟黄土区域水沙规律,本文尝试将该方法应用在水沙模拟概念模型中,通过矫正降雨误差,以提高水流和泥沙的模拟精度.
因此在水沙模拟概念模型计算中引入降雨动态系统响应曲线修正方法,对流域面平均雨量进行修正,建立面平均雨量和流域流量之间的响应关系.降雨和产汇流过程是流域产沙汇沙过程的动力来源,水流是泥沙运移和输送的载体,水流模拟精度与流域出口断面的输沙率过程息息相关.鉴于此,本研究尝试通过对面平均雨量进行修正,将修正后面平均雨量系列输入模型进行计算重新得到新的流量和输沙率过程,以达到提高水沙模型模拟精度的目的.
1 水沙模拟概念模型介绍水沙模拟概念模型是包为民教授在20世纪末研究黄土地区流域泥沙提出的概念性模型,并被用于模拟蛇家沟和水旺沟流域等20多个小流域以及皇甫和河口镇-龙门镇区间等中大流域的水沙变化,取得了较好的模拟效果.模型结构简单,物理概念清晰,适用于黄土区域干旱半干旱地区,以满足水土保持措施效益分析和黄河中游水沙变化原因分析等问题研究的大尺度、长系列模拟的需要,为人类活动和气候变化对流域水沙变化的影响提供基础数据[22].
该模型根据水沙在流域上产生、运动各个环节机制的差异,分为水流模拟和泥沙模拟两大部分[23].水流模拟分为产流、坡面汇流和沟道汇流3部分;泥沙模拟分为面蚀产沙、沟蚀产沙、坡面汇沙和沟道汇沙4部分.产流机制采用垂向混合产流模式,坡面汇流采用线性水库法,沟道汇流采用马斯京根河道演算法;面蚀产沙采用土壤抗侵蚀能力分布曲线,沟蚀产沙采用拜格诺河道水流悬移质泥沙公式,坡面汇沙和沟道汇沙采用泥沙汇集概念模拟公式.
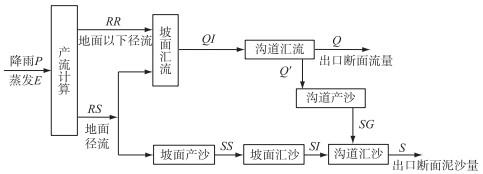
模型输入为降雨P和蒸发E资料,主要输出为流域出口断面的流量过程和泥沙过程.模型主要结构和参数如图 1和表 1所示.
|
图 1 水沙模拟概念模型结构图 Fig.1 Structural chart of conceptual model of water and sediment simulation |
| 表 1 水沙模拟概念模型参数 Tab. 1 Parameters of conceptual model of water and sediment simulation |
动态系统响应曲线修正方法是用于水文预报模型中的误差修正技术,以模型输入或某中间变量与输出之间的对应关系建立响应曲线.由于降雨是模型的重要输入项,降雨误差会在模型计算中进行传递[24].因此通过修正流域面平均雨量,提高模型的模拟精度.
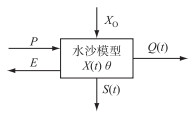
本文将该方法用于水沙模拟概念模型中,将模型的水流模拟部分概化为一个系统(图 2),建立动态系统响应曲线函数[17]:
|
图 2 水沙模型概化系统 Fig.2 Generalization system of conceptual model of water and sediment simulation |
| $ Q(t) = f[X(t),\theta ,t] $ | (1) |
式中,Q=[Q1, Q2, Q3……Qn]T为流域出口断面流量过程(m3/s);S= [S1, S2, S3……Sn]T为流域出口断面输沙率过程(kg/s);P=[P1, P2, P3……Pn]T为流域降雨系列(mm);E=[e1, e2, e3……en]T为蒸发(mm);X(t)为模型的输入变量和中间变量,XO为模型变量初始状态值;θ为模型参数,在一定时期内不随时间变化;t为时间,n为系列长度.
在本文中,只考虑降雨对水沙模型流量的响应过程,因此降雨动态系统响应曲线函数简化为:
| $ Q(P) = f(P) $ | (2) |
所谓降雨动态系统响应曲线,即对某时段的降雨Pi增加一个单位值,将新的降雨系列输入模型进行计算得到的流量与原始计算流量之间的差值.
把降雨输入作为自变量对流量求全微分,并将观测流量系列代入式中,则其矩阵表达式为:
| $ Q(P) \approx QC\left( {{P_0}} \right) + U\Delta P + W $ | (3) |
式中,ΔP是需求解的降雨系列误差(mm);W是经过实时修正后的预报系统残差(m3/s);U为系统响应矩阵.
U矩阵如下:
| $ U = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {Q_1}(P)}}{{\partial {P_1}}}}& \cdots &{\frac{{\partial {Q_1}(P)}}{{\partial {P_m}}}}\\ {\frac{{\partial {Q_2}(P)}}{{\partial {P_1}}}}& \cdots &{\frac{{\partial {Q_2}(P)}}{{\partial {P_m}}}}\\ \cdots & \cdots & \cdots \\ {\frac{{\partial {Q_n}(P)}}{{\partial {P_1}}}}& \cdots &{\frac{{\partial {Q_n}(P)}}{{\partial {P_m}}}} \end{array}} \right] $ | (4) |
计算降雨动态系统响应曲线的步骤如下:
(1) 假设流域有降雨系列PO,实测流量为QO,PO输入模型计算得到流域原始计算流量系列为QC.
(2) 流域各站点降雨系列PO中第i个时段Pi,在其余时段各站点降雨均不变的情况下,增加一个单位值,得到新的降雨系列PCi.
(3) 将新的降雨系列PCi输入模型进行计算,得到新的计算流量过程QCi.
(4) 将新的流量过程QCi与原始计算流量QC相减,其差值为Pi的系统响应曲线,属于U矩阵中的第i列.
(5) 依次计算U矩阵中的每一列,最终建立降雨系列PO的动态系统响应曲线.运用最小二乘法,计算得到降雨的修正误差值:
| $ \Delta P = {\left( {{U^{\rm{T}}}U} \right)^{ - 1}}{U^{\rm{T}}}\left( {{Q_{\rm{O}}} - {Q_{\rm{C}}}} \right) $ | (5) |
(6) 修正后的降雨系列:
| $ {P_{\rm{U}}} = {P_{\rm{O}}} + \Delta P $ | (6) |
输入模型进行计算,新的流域出口断面流量和输沙率过程即该流域流量和输沙率的修正值.
3 应用检验检验方法修正效果,具体采用以下4个指标来衡量修正效果:
(1) 径流深相对误差ΔR,本文取误差绝对值:
| $ \Delta R = \left| {\frac{{{R_{\rm{C}}} - {R_{\rm{O}}}}}{{{R_{\rm{O}}}}} \times 100\% } \right| $ | (7) |
(2) 产沙量相对误差ΔS,本文取误差绝对值:
| $ \Delta S = \left| {\frac{{{S_{\rm{C}}} - {S_{\rm{O}}}}}{{{S_{\rm{O}}}}} \times 100\% } \right| $ | (8) |
(3) 纳什效率系数NS:
| $ NS = 1 - \frac{{\sum\limits_i^n {{{\left[ {{y_{{\rm{C}}i}} - {y_{{\rm{O}}i}}} \right]}^2}} }}{{\sum\limits_i^n {{{\left[ {{y_{{\rm{O}}i}} - \overline {{y_{\rm{O}}}} } \right]}^2}} }} $ | (9) |
(4) 纳什效率系数提高幅度INS:
| $ INS = \frac{{N{S_{\rm{U}}} - N{S_{\rm{O}}}}}{{N{S_{\rm{O}}}}} \times 100\% $ | (10) |
式中,RC为径流深预报值(mm);RO为径流深实测值(mm);SC为产沙量预报值(t);SO为产沙量实测值(t);yCi为观测变量第i个时段预报值;yOi为观测变量第i个时段实测值;$\overline{y_{\rm{o}}}$为观测变量实测值的均值;n为资料系列长度;NSO为修正前纳什效率系数;NSU为修正后纳什效率系数.
3.1 理想案例检验在理想案例中,假设模型的输入、输出、参数和初始状态值已知.假设一个降雨系列PO,将其输入水沙模型计算得到的流量和输沙率QO和SO,作为理想案例的实测系列.随机给定一组服从零均值分布的降雨误差值ΔP,误差值不超过降雨系列的±80 %,将加上误差值的新的降雨系列PC输入模型计算得到计算流量QC和计算输沙率SC.其中,
| $ {P_{\rm{C}}} = {P_{\rm{O}}} + \Delta P $ | (11) |
对PC系列降雨进行动态系统响应修正,修正得到降雨误差值为-ΔP′,修正的降雨系列为:
| $ {P_{\rm{U}}} = {P_{\rm{C}}} - \Delta {P^\prime } = {P_{\rm{O}}} + \Delta P - \Delta {P^\prime } $ | (12) |
PU输入模型计算得到修正后流量QU和输沙率SU.分别将修正降雨误差值-ΔP′与给定降雨误差值ΔP进行对比,比较两者相关性,检验该方法是否能够精确反演降雨误差;分别将修正后流量、输沙率和计算流量、输沙率与实测流量、输沙率进行对比分析,检验修正后的模型模拟精度是否得到提高.
在本研究中,理想案例降雨系列采用曹坪流域1962年7月23日场次洪水降雨资料,流域面积187 km2,有30个雨量站,洪水汇流演算马斯京根演算法河段数为10.给定随机降雨误差值建立理想案例,表 2为理想案例的径流深和产沙量修正情况,图 3为理想案例给定降雨误差和修正降雨误差值对比图,图 4为理想案例降雨数据的修正效果,图 5为理想案例水流和泥沙修正效果.
| 表 2 理想案例流量和输沙率修正效果 Tab. 2 Correction effect of flow and sediment transport rate of ideal case |
|
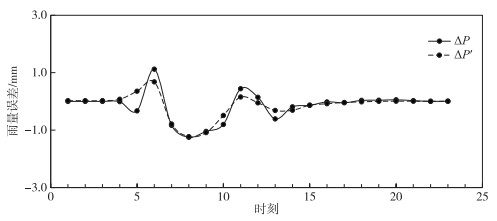
图 3 理想案例给定雨量误差ΔP及修正雨量误差ΔP′值(图中1个时刻为模型计算时间尺度0.5 h) Fig.3 Given rainfall error ΔP and corrected rainfall error ΔP′ of ideal case |
|
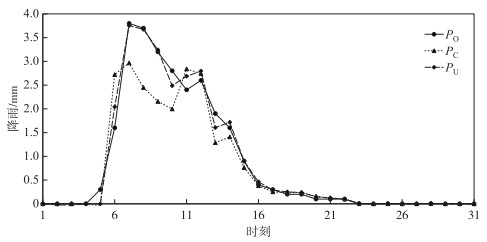
图 4 理想案例修正前后降雨值(图中1个时刻为模型计算时间尺度0.5 h) Fig.4 Rainfall values before and after revision of ideal case |
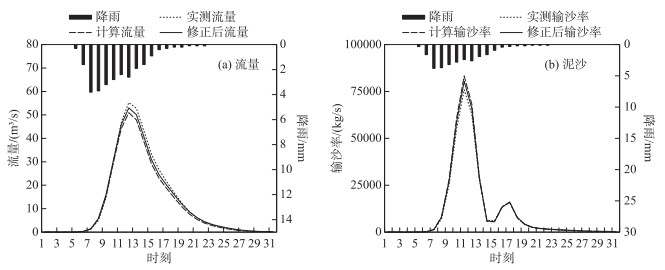
|
图 5 理想案例修正效果(图中1个时刻为模型计算时间尺度0.5 h) Fig.5 Correction effect of ideal case |
从表 2可以看出,应用降雨动态系统响应曲线后,理想案例水流部分径流深误差由8.29 %降低到2.67 %,纳什效率系数由0.989提高到0.997;泥沙部分产沙量相对误差由6.96 %降低到4.77 %,纳什效率系数由0.990提高到0.996.从图 3可以看出,给定降雨误差与修正得到的降雨误差之间NS系数为0.821,相关系数为0.908,二者非常接近.从图 4可以看出,相比较有误差的降雨系列PC,修正后的降雨系列PU更接近于降雨基准数据PO系列,这说明本文中所采用的降雨误差估计方法能够准确地估计出给定的降雨误差,精确反演降雨误差.从图 5可以看出,修正后的流量和输沙率更接近流量真值和输沙率真值,流量和输沙率拟合过程都有所改善.这说明降雨动态系统响应曲线修正方法能够同时提高水沙模型的水流和泥沙模拟精度,可以进一步用于实际流域的应用检验.
3.2 实际流域应用本文选取黄土地区曹坪流域作为实验流域.曹坪流域位于黄河大理河流域中下游地区,流域大部分为黄土丘陵沟壑区域,植被稀疏,水土流失严重.是典型的大陆性季风气候区,夏季炎热潮湿多暴雨,冬季寒冷干燥.降雨年内变化大,降雨多集中在7-9月.流域多年平均降雨量447 mm,多年平均气温7.8~9.6℃,流域泥沙侵蚀模数为2.2万t/(km2 ·a).
研究流域曹坪(岔巴沟)为干旱半干旱气候,产流模式符合混合产流模式,可以运用水沙概念模拟模型进行计算.用于计算修正的资料系列为1961-1989年的13场洪水资料,模型计算时间尺度为0.5 h,流域水系及站网布设见图 6.
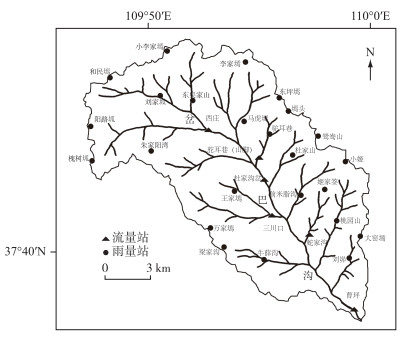
|
图 6 曹坪流域水系及站网布设 Fig.6 Layout of water system and station network in Caoping Basin |
水沙模型经函数曲面参数率定方法[25]进行参数率定后,对降雨进行动态系统响应修正,检验模型的修正效果.模型参数率定情况见表 3.13场洪水水流和泥沙修正结果分别见表 4和表 5.
| 表 3 水沙模型曹坪流域参数率定 Tab. 3 Calibration of parameters of Caoping Basin for conceptual model of water and sediment simulation |
| 表 4 曹坪流域水流修正效果 Tab. 4 Correction effect of the water simulation part of Caoping Basin |
| 表 5 曹坪流域泥沙修正效果 Tab. 5 Correction effect of the sediment simulation part of Caoping Basin |
从表 4洪水修正效果来看,应用降雨动态系统响应曲线后,修正后的径流深相对误差与修正前相比都有所减小,纳什效率系数均有所提高.平均径流深相对误差由2.48 %降低到0.62 %,纳什效率系数由0.689提高到0.810,纳什效率系数提高幅度为17.56 %.从表 5泥沙修正效果来看,产沙量经修正后相对误差全部降低,纳什效率系数全部提高.平均产沙量相对误差从1.71 %降低到1.28 %,纳什效率系数从0.643提高到0.745,纳什效率系数提高幅度为15.86 %.从图 7洪水的纳什效率系数修正效果来看,修正后的纳什效率系数均比修正前有显著提升.选取第8场次洪水的流量和输沙率修正结果查看修正效果,从图 8可以看出,洪水修正后的流量和输沙率更接近流量真值和输沙率真值,流量和输沙率拟合过程也有所改善.这说明降雨动态系统响应曲线修正方法应用于水沙模型后,能够减小模型径流深和产沙量的相对误差,提高纳什效率系数,最终提高模型的模拟精度.
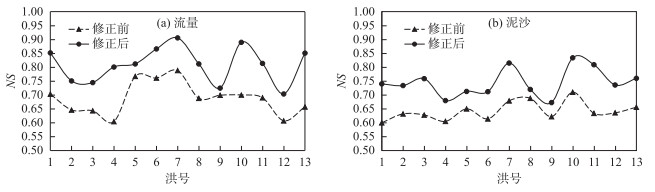
|
图 7 曹坪流域13场洪水纳什效率系数修正前后对比 Fig.7 Contrast of NS coefficient before and after correction of 13 floods in Caoping Basin |
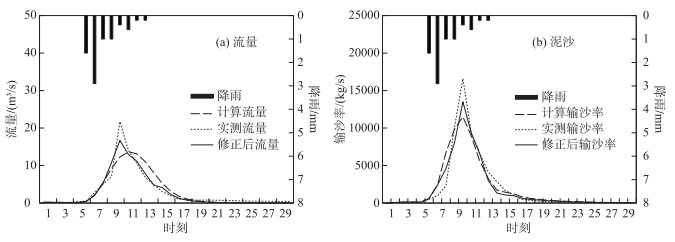
|
图 8 第8场次洪水修正效果(图中1个时刻为模型计算时间尺度0.5 h) Fig.8 Correction effect of flood 8 |
在现今应用的黄河流域土壤侵蚀产沙模型中,流域的复杂性和资料的制约,造成模型模拟结果精度欠佳的不足[26].流域面平均雨量的误差,影响了模型的模拟精度,使模型初始模拟效果没有想象中理想.用于降雨动态系统响应修正的13场洪水降雨大多分为两种情况:一是由于原始降雨资料存在降雨时段均化、缺测、漏测等问题,部分降雨数据由插补展延而来导致降雨误差.这种类型降雨输入模型进行计算后,相比实际流量和输沙率过程,计算洪水流量和输沙率过程相对呈现“矮胖型”,洪水缓涨缓落,洪峰、沙峰偏低,模型模拟精度不高.二是由于原始资料存在误测等问题,某些时刻降雨数据明显偏大或者偏小,造成降雨数据误差.这部分降雨数据输入模型后也会造成计算误差,使计算流量和输沙率过程与实际过程不相符合,模型模拟精度较低.降雨是模型计算的重要输入项,也是模型误差的重要来源之一.因此,在使用水沙模型模拟黄土区域水沙时,对于有误差的降雨资料,尤其针对以上两种降雨分布情况的洪水场次,可以应用降雨动态系统响应曲线修正方法,通过修正面平均雨量,以提高模型模拟精度.
4 结论水沙模拟概念模型物理概念清楚,实用性强,适用于黄土区域干旱半干旱地区.应用于黄土地区流域,合理地模拟了流域水沙变化规律.降雨是水沙模型的重要输入项,降雨误差能够直接造成模型误差,从而影响模型的模拟精度.因此,本文将降雨动态系统响应曲线修正方法与水沙模型相结合,通过修正面平均雨量,将修正后降雨输入模型进行计算重新得到新的流量和输沙率过程,以达到减小模型误差的目的.结果表明,在对降雨进行修正后,水沙模型水流径流深更接近实际值,流量过程纳什效率系数提高;产沙量误差降低,输沙率过程纳什效率系数提高.说明水沙模型应用降雨动态系统响应曲线修正方法后,能够提高模型的模拟精度,最终水流和泥沙模拟平均提高幅度分别是17.56 %和15.86 %,其修正效果是显著的.
降雨动态系统响应曲线修正方法能够很好地提高水沙模型的模拟精度,但是由于水文系统毕竟是非线性系统,影响因素比较复杂,降雨误差因素并非模型误差的唯一来源.考虑到本文仅修正面平均雨量一个变量,因此,对于如何细化降雨误差,以及综合考虑降雨和其他影响因素之间量化关系有待进一步研究.根据流域降雨分布情况,选择降雨动态系统响应曲线修正方法应用于水沙模型模拟中,可以为研究黄河水沙变化规律提供一定的技术指导和理论支撑.
| [1] |
Yao WY, Jiao P. Water and sediment variations and research prospect in the Yellow River. Soil and Water Conservation in China, 2016(9): 55-63, 93. [姚文艺, 焦鹏. 黄河水沙变化及研究展望. 中国水土保持, 2016(9): 55-63, 93. DOI:10.3969/j.issn.1000-0941.2016.09.020] |
| [2] |
Wischmeier WH, Smith DD. Predicting rainfall-erosion losses from cropland east of the Rocky Mountain. Agriculture Handbook, 1965, 282: 47. |
| [3] |
Tang LQ. Study on sediment yield model of basin. Advances in Water Science, 1996(1): 47-53. [汤立群. 流域产沙模型的研究. 水科学进展, 1996(1): 47-53. DOI:10.3321/j.issn:1001-6791.1996.01.008] |
| [4] |
Laflen JM, Lane LJ, Foster GR. WEPP:A new generation of erosion prediction technology. Journal of Soil & Water Conservation, 1991, 46(1): 34-38. |
| [5] |
De Roo APJ, Jetten VG. Calibrating and validating the LISEM model for two data sets from the Netherlands and South Africa. Catena, 1999, 37(3/4): 477-493. |
| [6] |
Morgan RPC, Quinton JN, Smith RE et al. The European soil erosion model (EUROSEM):a dynamic approach for predicting sediment transport from fields and small catchments. Earth Surface Processes and Landforms, 1998(23): 527-544. |
| [7] |
Bao WM. A conceptual modelling study for small basin sediment yields in Loess Region. Advances in Water Science, 1993(1): 44-50. [包为民. 黄土地区小流域产沙概念性模拟研究. 水科学进展, 1993(1): 44-50. DOI:10.3321/j.issn:1001-6791.1993.01.007] |
| [8] |
Bao WM, Hou L, Shen DD et al. Application of flow-sedimentation coupled model in Dali River Basin of Loess Plateau. J Lake Sci, 2019, 31(4): 1120-1131. [包为民, 侯露, 沈丹丹等. 黄土高原大理河流域水沙耦合模型应用研究. 湖泊科学, 2019, 31(4): 1120-1131. DOI:10.18307/2019.0407] |
| [9] |
Bao WM. Conceptual model of water and sediment simulation and application in Loess Region. Nanjing: Press of Hohai University, 1995. [包为民. 黄土地区流域水沙模型模拟概念模型与应用. 南京: 河海大学出版社, 1995: 170.]
|
| [10] |
Si W, Bao WM, Qu SM. Runoff error correction in real-time flood forecasting based on dynamic system response curve. Advances in Water Science, 2013, 24(4): 497-503. [司伟, 包为民, 瞿思敏. 洪水预报产流误差的动态系统响应曲线修正方法. 水科学进展, 2013, 24(4): 497-503.] |
| [11] |
Si W, Yu HH, Bao WM et al. Area-mean rainfall updating by system response curve method and application to real-time flood forecasting of Fuchunjiang basin. Journal of Hydroelectric Engineering, 2016, 35(1): 38-45. [司伟, 余鸿慧, 包为民等. 面平均雨量的系统响应曲线修正方法及其在富春江流域洪水预报中的应用. 水力发电学报, 2016, 35(1): 38-45.] |
| [12] |
Yang Y, Zhang JY, Qi JG et al. Review and prospect on the application of weather radar in hydrology. Advances in Water Science,, 2000(1): 92-98. [杨扬, 张建云, 戚建国等. 雷达测雨及其在水文中应用的回顾与展望. 水科学进展, 2000(1): 92-98. DOI:10.3321/j.issn:1001-6791.2000.01.017] |
| [13] |
Collier CG. Applications of weather RADAR system. England: Praxis publishing Ltd, 1996.
|
| [14] |
Artan G, Gadin H, Smith JL et al. Adequacy of satellite-derived rainfall data for streamflow. Natural: Hazards, 2007, 43: 167-185. DOI:10.1007/s11069-007-9121-6 |
| [15] |
Berenguer M, Corral C, Sanchez-Diezma R. Hydrological validation of a radar-based nowcasting technique. Journal of Hydrometeorology, 2005, 6: 532-550. DOI:10.1175/JHM433.1 |
| [16] |
Si W, Bao W, Wang H et al. The research of rainfall error correction based on system response curve. Applied Mechanics and Materials, 2013, 368-370: 335-339. DOI:10.4028/www.scientific.net/AMM.368-370.335 |
| [17] |
Si W, Bao W, Gupta HV. Updating real-time flood forecasts via the dynamic system response curve method. Water Resources Research, 2015, 51(7): 5128-5144. DOI:10.1002/2015WR017234 |
| [18] |
Shu HL, Bao WM, Yang SS et al. Application of runoff error correction based on dynamic system response curve. Water Power, 2016, 42(4): 22-26. [束慧连, 包为民, 杨姗姗等. 产流误差动态系统响应曲线修正方法的应用. 水力发电, 2016, 42(4): 22-26.] |
| [19] |
Sun Y, Bao W, Jiang P et al. Development of multivariable dynamic system response curve method for realtime flood forecasting correction. Water Resources Research, 2018, 54(7): 4730-4749. DOI:10.1029/2018WR022555 |
| [20] |
Si W, Gupta HV, Bao W et al. Improved dynamic system response curve method for real-time flood forecast updating. Water Resources Research, 2019. |
| [21] |
Si W, Bao WM, Qu SM et al. Real-time flood forecast updating method based on mean areal rainfall error correction. J Lake Sci, 2018, 30(2): 533-541. [司伟, 包为民, 瞿思敏等. 基于面平均雨量误差修正的实时洪水预报修正方法. 湖泊科学, 2018, 30(2): 533-541. DOI:10.18307/2018.0224] |
| [22] |
Bao WM, Chen YT. A conceptual flow-sedimentation coupled simulation model for large basins. Advances in Water Science, 1994(4): 287-292. [包为民, 陈耀庭. 中大流域水沙耦合模拟物理概念模型. 水科学进展, 1994(4): 287-292. DOI:10.3321/j.issn:1001-6791.1994.04.005] |
| [23] |
Si W, Bao W, Jiang P et al. A semi-physical sediment yield model for estimation of suspended sediment in loess region. International Journal of Sediment Research, 2017, 32(1): 12-19. DOI:10.1016/j.ijsrc.2015.10.002 |
| [24] |
Qu SM, Bao WM. Comprehensive correction of real-time flood forecast. Advances in Water Science, 2003(2): 167-171. [瞿思敏, 包为民. 实时洪水预报综合修正方法初探. 水科学进展, 2003(2): 167-171. DOI:10.3321/j.issn:1001-6791.2003.02.008] |
| [25] |
Lai SZ, Qu SM, Bao WM et al. Application of parameter calibration method based on parameter function surface in SAC model. Journal of Hydraulic Engineering, 2014, 45(8): 973-983. [赖善证, 瞿思敏, 包为民等. 函数曲面参数率定方法在SAC模型中的应用. 水利学报, 2014, 45(8): 973-983.] |
| [26] |
Li JY, Zhang N, Wang RB. Soil erosion and sedimentation model in the Yellow River basin:state-of-the-art review. Progress in Geography, 2006(2): 103-111. [李景玉, 张楠, 王荣彬. 黄河流域土壤侵蚀产沙模型研究进展. 地理科学进展, 2006(2): 103-111. DOI:10.3969/j.issn.1007-6301.2006.02.012] |
 2020, Vol. 32
2020, Vol. 32 


