由于自然过程的复杂性和人类认识水平的局限性,使得单一预报结果不可避免的存在不确定性,因此发展起来了集合预报与概率预报[1].集合预报给出了预报量可能的结果集,是采用集合形式量化预报的不确定性.而概率预报,顾名思义,估计了预报量(如流量)的概率分布,通过概率形式量化预报的不确定性.一方面,集合预报仅提供了预报量有限的可能结果,而概率预报量化了预报量所有结果的可能性,因此,概率预报是集合预报的一种“升华”,较集合预报提供更为全面的信息.另一方面,由于很难直接估计预报量的理论分布函数,因此,往往采用预报量有限的可能结果集来近似替代其分布函数,估计其预报不确定性,即集合预报可以视为概率预报的一种表现形式[2].本文将集合预报视作概率预报的一种表现形式,对洪水概率预报结果的评价体系开展研究.
就方法而言,目前的洪水概率预报方法可以大致分为两类途径:全要素耦合途径和总误差分析途径.
全要素耦合途径是指分别识别、量化洪水预报过程中各阶段的不确定性,并将其与确定性预报模型耦合,从而实现洪水概率预报.这些不确定性一般包括输入(如降雨)[3-4]、模型结构[5]、模型参数和模型状态[6]的不确定性.代表性方法包括贝叶斯总误差分析方法BATEA[7](BAyesian Total Error Analysis)、贝叶斯综合不确定性估计方法IBUNE[8](Integrated Bayesian UNcertainty Estimator)等.这类方法虽然可以量化洪水预报过程中的各类不确定性要素,识别不确定性来源,但往往计算耗时,不利于生产实际应用.总误差分析途径是指不识别洪水预报具体过程的不确定性,仅对最终预报结果进行分析,量化其不确定性,进而实现概率预报[9-10].常用的方法包括水文不确定性处理器HUP[11](Hydrologic Uncertainty Processor)、模型条件处理器MCP[12](Model Conditional Processor)、三维误差矩阵[13]等.这一途径避免了处理洪水预报子过程的不确定性,往往计算省时,结构灵活,可以与各类确定性预报模型进行衔接,但是无法溯源预报的不确定性.
随着洪水概率预报方法研究的进展,其评价问题也得到重视,但相较而言,对洪水概率预报评价的研究相对滞后,尚未形成较完整的评价指标体系. Murphy[14]构建了概率预报制定-应用过程的检验框架:从一致性(Consistency)、预报质量(Quality)和预报价值(Value)三方面进行检验.其中“预报质量”指预报结果与观测数据的一致性,即一般意义上预报结果的好坏. Murphy就观测分布f(Qobs)、预报分布f(Qsim)、条件分布f(Qobs|Qsim)和f(Qsim|Qobs)的关系总结了偏差(Bias,预报分布与观测分布均值的差异)、技巧(Skill,相对的预报精度)、分辨率(Resolution,预报条件分布与观测分布的差异)等一系列评价预报质量的指标,为后续的概率预报评价研究提供了理论基础.而在实际洪水概率预报研究中,往往关注条件分布f(|Qsim)(以确定性预报为条件的实际流量的分布函数)对实际观测值Qobs的“拟合情况”,如任政等[15]采用区间覆盖率(预报区间覆盖实测流量的比例)、区间平均宽度和区间对称性对概率预报区间进行评估;徐兴亚等[6]采用60 %和90 %置信度预报区间的落入频率(即覆盖率)对河道洪水概率预报的区间预报进行评价;王艳兰等[16]采用90 %置信度的覆盖率和平均离散度评估概率预报结果,并给出了Q50分位数预报的洪峰误差、洪量误差和纳什系数;徐炜等[17]采用单位区间离散化系数对比评估了两个概率预报模型的90 %置信度预报区间的合理性;梁忠民等[18]采用90 %置信度覆盖率、平均相对带宽(即平均离散度)和平均相对偏移度对洪水概率预报结果进行评价,并计算了中位数预报的洪峰误差和纳什系数.此外,随着水文气象研究的深入,气象集合预报的评价方式在水文领域得到了发展,如Alfieri等[19]采用连续排序概率得分CRPS和连续排序概率技能得分CRPSS对集合流量预报结果进行了评价.
尽管洪水概率预报评价指标研究得到了一定程度的发展,但仍存在一些问题:如不同研究中采用的评价指标,有些虽然名称不同,但含义相同,尚欠缺相关研究对现有的评价指标进行归纳总结;这些指标大多仅对某一置信度条件下的区间预报结果进行合理性评估,如90 %置信度区间预报的覆盖率、离散度等,尚没有一种评价指标可以对概率预报的整体合理性做出估计(即同时考虑所有置信度区间预报的合理性);不同研究对概率预报结果的侧重各有不同,采用的评价指标亦有所差异,尚没有形成一套通用的系统的概率预报评价指标体系.为此,本文根据实际洪水概率预报研究和应用的需要,针对条件分布f($\hat{Q}$|Qsim)对实际观测值Qobs“拟合情况”的评价问题,分析并总结了现有研究中常见的评价指标,形成了洪水概率预报“精度-可靠度”联合评价指标体系,并在可靠度评价指标中,提出一个新的评价指标-覆盖率判定系数,用以评估概率预报的整体合理性(同时考虑各个置信度的区间预报).在淮河王家坝区间流域,对“精度-可靠度”联合评价指标体系进行应用研究.
1 概率预报“精度-可靠度”联合评价指标体系传统的洪水确定性预报提供了每一时刻预报量的预测值,可以通过比较预测值与观测值的差异来评价确定性预报结果的准确性,即精度评价.以流量预报为例,t时刻真实流量
本节首先对现有的精度评价指标和可靠度评价指标进行分析和总结,在可靠度评价指标中,提出覆盖率判定系数用以评价概率预报的整体可靠度.在此基础上,建立了洪水概率预报“精度-可靠度”联合评价指标体系.
1.1 精度评价指标对任一预报时刻,可以通过条件分布f(
(1) 洪峰相对误差REP(%)和洪量相对误差REV(%).
《水文情报预报规范》[20]规定:降雨径流预报以实测洪峰流量的20 %作为许可误差.因此,REP的许可误差为±20 %.
将洪量平铺于流域面积,可以计算出相应的径流深,因此,径流深误差与洪量误差相等. 《水文情报预报规范》[20]规定:径流深预报以实测值的20 %作为许可误差.因此,可以认为REV的许可误差为±20 %.
REP和REV均评价了预报结果的偏差(Bias,预报是否偏大/偏小于观测).
(2) 洪峰滞时ET.
洪峰滞时指预测洪峰滞后于实测洪峰的时段长. 《水文情报预报规范》[20]规定:滞时绝对值的许可误差为预见期的30 %,许可误差小于3 h或一个计算时段长时,则以3 h或一个计算时段长作为许可误差.
(3) 确定性系数/纳什系数[21](Deterministic Coefficient/Nash-Sutcliffe Efficiency,NSE).
| $ NSE = 1 - \frac{{\sum\limits_{i = 1}^N {{{\left[ {{Q_{{\rm{obs}}}}(i) - {Q_{{\rm{pre}}}}(i)} \right]}^2}} }}{{\sum\limits_{i = 1}^N {{{\left[ {{Q_{{\rm{obs}}}}(i) - {{\bar Q}_{{\rm{obs}}}}} \right]}^2}} }} $ | (1) |
式中,Qobs(i)为第i时刻的实测流量,m3/s;Qpre(i)为第i时刻的倾向值预报流量,m3/s;Qobs为实测流量的平均值,m3/s;N为洪水过程时段数.
NSE评价了洪水过程的拟合效果,其取值范围是(-∞, 1],NSE越接近于1,表明洪水过程的拟合效果越好.除了NSE以外,均方误差(Mean Squared Error,MSE)[22]也可以用来评估洪水过程的拟合情况:
| $ MSE = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {{Q_{{\rm{obs}}}}(i) - {Q_{{\rm{pre}}}}(i)} \right]}^2}} $ | (2) |
理论上,NSE与MSE存在转化关系[22]:
| $ NSE = 1 - \frac{{MSE}}{{\sigma _{{\rm{obs}}}^2}} $ | (3) |
式中,σobs2为实测流量的方差.
由公式(2)和(3)可知,MSE的取值受到了流量级别的影响,不利于对比不同量级洪水过程的拟合效果;而NSE在一定程度上消除了流量量级的影响,因此,在实际应用中NSE比MSE应用更为广泛,更具说服力.对NSE进行分解,可以将NSE分解为3个评价因子[22]:
| $ NSE = 2 \cdot \alpha \cdot r - {\alpha ^2} - {\beta ^2} $ | (4) |
| $ \alpha = \frac{{{\sigma _{{\rm{pre}}}}}}{{{\sigma _{{\rm{obs}}}}}} $ | (5) |
| $ \beta = \frac{{{\mu _{{\rm{pre}}}} - {\mu _{{\rm{obs}}}}}}{{{\sigma _{{\rm{obs}}}}}} $ | (6) |
| $ r = \frac{{Co{v_{{\rm{pre,obs}}}}}}{{{\sigma _{{\rm{obs}}}} \cdot {\sigma _{{\rm{pre}}}}}} $ | (7) |
式中,σpre为倾向值预报的标准差;σobs为实测流量的标准差;μpre为倾向值预报的均值;μobs为实测流量的均值;Covpre, obs为倾向值预报与实测流量的协方差;α为方差因子;β为均值因子;r为预报与实测的线性相关系数.
由公式(4)~(7)可知,NSE评估了倾向值预报与实测流量之间均值和标准差的差异,同时考虑了两者的线性相关程度.当倾向值可以完美拟合实测流量过程时(完美预报),两者的均值相等、标准差相等、线性相关程度最高,即α=1;β=0;r=1,此时NSE=1.根据NSE的评价因子(β、α、r),Gupta等[22]提出了Kling-Gupta Efficiency (KEG)评价指标:
| $ KGE = 1 - \sqrt {{G_1} + {G_2} + {G_3}} $ | (8) |
| $ {G_1} = {\left( {\frac{{{\sigma _{{\rm{pre}}}}}}{{{\sigma _{{\rm{obs}}}}}} - 1} \right)^2} $ | (9) |
| $ {G_2} = {\left( {\frac{{{\mu _{{\rm{pre}}}}}}{{{\mu _{{\rm{obs}}}}}} - 1} \right)^2} $ | (10) |
| $ {G_3} = {(r - 1)^2} $ | (11) |
式中, 变量含义与式(5)~(7)中变量相同. KGE的取值范围为(-∞, 1],KGE越接近于1,表明洪水过程的拟合效果越好.
类似于NSE,KGE也考虑了均值因子G2、方差因子G1和线性相关性因子G3共3个评价因子.不同于NSE,KGE中因子对KGE的影响关系更直观:KGE与3个因子均为单调递减关系.因此,通过计算KGE及其评价因子,可以提供预报流量更细致的精度评价.
(4) 基准系数[23](Benchmark Efficiency,BE).
| $ BE = 1 - \frac{{\sum\limits_{i = 1}^N {{{\left[ {{Q_{{\rm{obs}}}}(i) - {Q_{{\rm{pre}}}}(i)} \right]}^2}} }}{{\sum\limits_{i = 1}^N {{{\left[ {{Q_{{\rm{obs}}}}(i) - {Q_{\rm{b}}}(i)} \right]}^2}} }} $ | (12) |
式中,Qb(i)为基准预报流量,m3/s;其他变量含义同前.
基准系数BE评价了模型的预报技巧(Forecast Skill,预报相对于某一标准是否具有较高的精度),一般用于对比倾向值预报Qpre与基准预报Qb在洪水过程拟合中的相对好坏:BE=0说明Qpre与Qb在洪水过程拟合中表现相当;BE>0说明Qpre比Qb更优;BE < 0说明Qpre比Qb拟合效果差. BE在形式上与NSE相似,可以认为NSE是以实测平均值作为基准预报的BE值.
1.2 可靠度评价指标Murphy[14]将预报量条件分布函数f(
| $ DI = \frac{{\sum\limits_{i = 1}^N D (i)}}{N} $ | (13) |
式中,DI指某一置信度条件下预报区间的平均离散度;N为预报时刻数;D(i)指第i时刻预报区间的离散度(预报区间宽度与实测的比值),具体计算如下:
| $ D(i) = \frac{{{q_{\rm{u}}}(i) - {q_{\rm{d}}}(i)}}{{{Q_{{\rm{obs}}}}(i)}} $ | (14) |
式中,qu(i)、qd(i)指预报区间的上限和下限,m3/s;其他变量含义同前.
D(i)的计算过程消除了流量级别对区间宽度(b(i)=qu(i)-qd(i))的影响,因此DI的取值不受流量级别影响,可用以对比不同量级洪水的区间预报结果:离散度越小区间预报效果越好,但是有关DI阈值的研究仍较为匮乏.我国《水文情报预报规范》[20]中规定洪峰预报允许误差为20 %,借鉴这一概念,本文将洪峰处的区间离散度定义为洪峰离散度Dpeak,并确定其阈值如下:
将洪峰预报区间边界与实测洪峰相对距离的最大允许值定为0.2,即:
| $ \frac{{\left| {{q_{{\rm{u,peak}}}} - {Q_{{\rm{obs}},{\rm{peak}}}}} \right|}}{{{Q_{{\rm{obs}},{\rm{peak}}}}}} \le 0.2 $ | (15) |
| $ \frac{{\left| {{Q_{{\rm{obs,peak}}}} - {q_{{\rm{d,peak}}}}} \right|}}{{{Q_{{\rm{obs,peak}}}}}} \le 0.2 $ | (16) |
式中,qu,peak和qd, peak分别为洪峰预报区间的上下边界,m3/s;Qobs, peak为洪峰观测流量,m3/s.
当qd, peak≤Qobs, peak≤qu,peak时,即实测洪峰位于区间预报范围内,将式(15)和(16)相加可知,洪峰离散度
(2) 区间覆盖率[24-25](Containing Ratio, CR):
| $ CR = \frac{{\sum\limits_{i = 1}^N k (i)}}{N} $ | (17) |
| $ k(i) = \left\{ {\begin{array}{*{20}{l}} {1,\left( {{q_{\rm{d}}}(i) \le {Q_{{\rm{obs}}}}(i) \le {q_{\rm{u}}}(i)} \right)}\\ {0,\left( {{Q_{{\rm{obs}}}}(i) < {q_{\rm{d}}}(i)\;aaa\;{Q_{{\rm{obs}}}}(i) > {q_{\rm{u}}}(i)} \right)} \end{array}} \right. $ | (18) |
理论上来说,CR值越接近区间置信度,概率预报结果越合理.如置信度为90 %的区间预报结果,其CR值越接近90 %,该预报区间越合理.
(3) 覆盖率判定系数(Containing Ratio Coefficient, CRC).
区间覆盖率CR只能考虑某一个置信度(如90 %)预报区间包含实测的情况,并不能代表整个概率预报结果的合理性,因此,本文提出覆盖率判定系数CRC评价指标,对所有置信度区间预报结果做出整体评估.
根据区间覆盖率的含义,当概率预报为完美预报时,对所有的置信度X=0, …, 100%,其对应的覆盖率CR,应满足CR=X.点绘(X, CR)时,所有的点据应位于45°线上.然而,实际中不可能做到完美预报,(X, CR)点往往散落在45°线附近,此时,可以计算这些点据与45°线的确定性系数R(即CRC),来判断概率预报的合理性,覆盖率判定系数计算公式如下:
| $ CRC = 1 - \frac{{\sum\limits_{j = 1}^F {{{\left( {C{R_j} - {X_j}} \right)}^2}} }}{{\sum\limits_{j = 1}^F {{{\left( {{X_j} - \bar X} \right)}^2}} }} $ | (19) |
式中,Xj为置信度, Xj∈(0, 100%];X为置信度的均值;CRj是对应于置信度Xj的区间覆盖率;F为置信度个数,理论上F应取无穷大,即Xj为无穷多个,实际应用时,建议置信度Xj在[10%,90%]区间内间隔5 %选取,即Xj=90%、85%、……、15%、10%,此时F=17.
CRC的取值范围是(-∞,1],CRC=1为完美概率预报.当CRC大于某一阈值时,线性关系CR=X显著,概率预报结果合理,而这一阈值随实际研究问题不同而变化,应通过统计检验来确定.在水文实际应用中,一般认为相关系数r≥0.8时变量存在较显著线性相关性,根据r与确定性系数R的关系(r2=R),本文认为在不便于采用统计检验方式确定CRC阈值时,可以将0.64作为CRC的阈值,认为CRC≥0.64时45°线可以较好的拟合(X, CR)点据,即概率预报结果合理.
由CRC计算公式可知,CRC同时考虑了所有置信度条件下的区间预报结果,可以衡量概率预报的整体合理性.
就思路而言,CRC与Q-Q(Quantiles-Quantiles)图方法[27]、概率图(Probability Plot)法[28]类似,三者的45°线均代表了完美预报.然而,Q-Q图方法评价的是各个分位数的合理性,概率图法评价了累计概率的合理性,CRC考虑的是区间覆盖率的合理性,三者的关注点不同.考虑到实际洪水概率预报中多关注区间预报的覆盖率,因此本文认为CRC方法较Q-Q图方法、概率图方法更适用于实际生产应用.
(4) 单位区间离散化系数.
一般而言,区间宽度越大,离散度越大,区间覆盖率越大,反之亦然,区间离散度和覆盖率在某种程度上是一组矛盾的评价指标.为了解决这一矛盾,提出了单位区间离散化系数[17, 29](Percentage of observations bracketed by the Unit Confidence Interval,PUCI),用以描述“平均相对区间宽度”所包含的实测点据比例.
| $ PUC{I_j} = \frac{{1 - \left| {C{R_j} - {X_j}} \right|}}{{D{I_j}}} $ | (20) |
式中变量含义同前.理论上,PUCI的取值范围是[0, ∞). PUCI值越大,表明该置信度的区间预报结果合理性越差.
对不同置信度预报区间的PUCI值进行平均,可以得到平均单位区间离散化系数(ACI):
| $ ACI = \frac{1}{F}\sum\limits_{j = 1}^F P UC{I_j} $ | (21) |
式中变量含义同前.通过计算ACI值,可以估计区间预报的整体合理性:ACI越小,概率预报结果越合理.然而,由于ACI的允许误差很难界定,因此不建议采用ACI对概率预报结果合理性进行评估.
(5) 连续排位评分(Continuous Ranked Probability Score, CRPS)和连续排位技巧评分(Continuous Ranked Probability Skill Score, CRPSS)
CRPS[30-31]评估了概率预报的预报能力.对任一时刻,CRPS计算方式如下:
| $ CRPS = \int_{ - \infty }^\infty {{{\left[ {\tau (y) - {\tau _0}(y)} \right]}^2}} {\rm{d}}y $ | (22) |
式中,y为预报量,即流量;τ(y)为该时刻的预报累计概率分布;
CRPS值[31-32]越小,说明预测分布在观测值附近越呈现“尖瘦”形态,预测分布的“准确性”越高.但目前研究尚未给出CRPS的合理阈值,往往采用CRPS比较多个预报的相对预报能力[33],进而提出了CRPSS[19],其计算公式如下:
| $ CRPSS({\rm{fore,ref}}) = \frac{{CRP{S_{{\rm{ref}}}} - CRP{S_{{\rm{fore}}}}}}{{CRP{S_{{\rm{ref}}}}}} $ | (23) |
式中,CRPSfore为待评价概率预报的CRPS值;CRPSref为参考预报的CRPS值,对于确定性预报,其CRPS值即为平均绝对误差[30].
连续排位技巧评分CRPSS是一种技巧(Skill)评分指标,取值范围是(-∞,1].当CRPSS>0时,概率预报较参考预报具有更高的预报能力;当CRPSS < 0时,待评价概率预报的“准确性”不如参考预报;当CRPSS=0时,待评价概率预报与参考预报预报能力相当.
(6) 区间对称度和对称比
对称度[24]Λ1评估了某一置信度预报区间关于实测流量的对称性,其计算公式如下:
| $ {\mathit{\Lambda }_1} = \frac{1}{N}\sum\limits_{i = 1}^N {{\lambda _1}} (i) $ | (24) |
| $ {\lambda _1}(i) = \left| {h(i) - 0.5} \right| $ | (25) |
| $ h(i) = \frac{{{q_{\rm{u}}}(i) - {Q_{{\rm{obs}}}}(i)}}{{b(i)}} $ | (26) |
式中变量含义同前.由Λ1计算公式可知,当i时刻的预报区间关于实测流量对称时,h(i)=0.5,λ1(i)=0. Λ1值越小,预报区间关于实测对称性越强.一般的,要求Λ1 < 0.5.此外,还可以采用平均对称度Λ2对区间对称性进行评价:
| $ {\mathit{\Lambda }_2} = \frac{1}{N}\sum\limits_{i = 1}^N {{\lambda _2}} (i) $ | (27) |
| $ {\lambda _2}(i) = {\left( {\frac{{\left| {{{\left( {{q_{\rm{u}}}(i) - {Q_{{\rm{obs}}}}(i)} \right)}^3} - {{\left( {{q_{\rm{d}}}(i) - {Q_{{\rm{obs}}}}(i)} \right)}^3}} \right|}}{{b(i)}}} \right)^{\frac{1}{3}}} $ | (28) |
式中变量含义同前.Λ2值越小,预报区间关于实测对称性越强,当Λ2=0时,预报区间关于实测流量完全对称.一般的,要求Λ2 < 1.
区间对称比[15]Λ3采用实测值大于区间上界的个数与小于区间下界个数的比值来衡量预报区间关于实测流量的对称性:
| $ {\mathit{\Lambda }_3} = \frac{{\sum\limits_{i = 1}^N {{J_u}} (i)}}{{\sum\limits_{i = 1}^N {{J_{\rm{d}}}} (i)}} $ | (29) |
| $ {J_{\rm{u}}} = \left\{ {\begin{array}{*{20}{l}} {1\left( {{Q_{{\rm{obs}}}}(i) > {q_{\rm{u}}}(i)} \right)}\\ {0\left( {{Q_{{\rm{obs}}}}(i) \le {q_{\rm{u}}}(i)} \right)} \end{array}} \right. $ | (30) |
| $ {J_{\rm{d}}} = \left\{ {\begin{array}{*{20}{l}} {1\left( {{Q_{{\rm{obs}}}}(i) < {q_{\rm{d}}}(i)} \right)}\\ {0\left( {{Q_{{\rm{obs}}}}(i) \ge {q_{\rm{d}}}(i)} \right)} \end{array}} \right.\]w $ | (31) |
由于区间预报结果往往并不要求对称,同时,区间覆盖率与离散度已经在某种程度上反映了预报区间相对实测流量的对称性.因此,对称性评价指标(对称度和对称比)在实际生产中的应用较少.
1.3 建议的“精度-可靠度”联合评价指标由于洪水概率预报结果一般可以分为倾向值预报和区间预报两个部分,因此,应采用“精度-可靠度”联合评价方式对洪水概率预报结果进行评估,即分别评价倾向值预报的准确性(精度评价)和区间预报的合理性(可靠度评价),具体评价指标如下:
在精度评价时,根据前文的介绍与分析,参考《水文情报预报规范》[20]的相关规定,建议采用:纳什系数NSE评价洪水过程,洪峰误差REF、洪峰滞时ET评价洪峰拟合情况,洪量误差REV评估水量平衡情况,基准系数BE比较不同定值预报(倾向值/确定性)对洪水过程的拟合情况.当需要对定值预报过程进行更为细致的评价时,可以采用KGE及其3个评价因子G1、G2、G3对洪水过程的拟合效果进行评价.
在“可靠度”评价时,常关注置信度为90 %的区间预报结果,因此,建议采用:洪峰处区间离散度Dpeak、单位区间离散化系数PUCI和覆盖率CR对该区间预报结果进行评价.由于90 %预报区间仅是众多预报区间中的一个,并不能代表其他置信度的预报区间结果,因此,应采用覆盖率判定系数CRC给出概率预报结果合理性的整体评估.此外,可以采用连续排位技巧评分CRPSS对比多个概率预报结果的相对预报能力.
相关评价指标的具体计算公式见前文,此处不再赘述.
2 洪水概率预报评价指标应用以淮河王家坝区间流域为例,在新安江模型预报基础上,采用水文不确定性处理器(Hydrologic Uncertainty Processor,HUP)[11]进行洪水概率预报,并采用“精度-可靠度”联合评价指标体系对洪水概率预报结果进行评估.
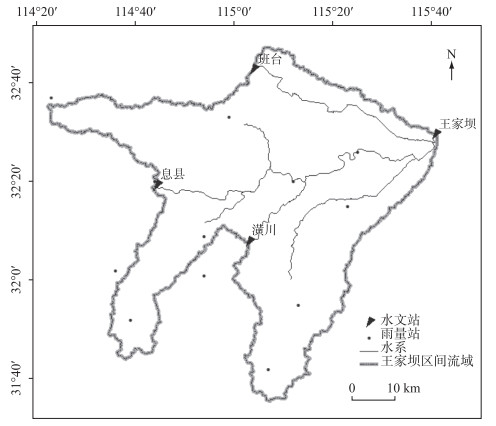
2.1 研究区概况王家坝区间流域集水面积为7110 km2.区域内年平均降水量800~1200 mm,降水年际变化大,时空分布不均匀.洪水主要来源为上断面(息县、潢川、班台)河道来水和区间降雨产生的径流,区间降雨的汇流时间约72 h(雨峰至洪峰出现时间).研究区域示意图见图 1.
|
图 1 研究区域示意图 Fig.1 The sketch of research area |
新安江模型是河海大学赵人俊[34]教授设计的国内第一个完整的流域水文模型.三水源新安江模型蒸散发计算采用三层模型;产流计算采用蓄满产流模型;采用自由水蓄水库结构将总径流划分为地表径流、壤中流和地下径流3种;流域汇流计算采用线性水库;河网汇流采用滞洪演算法;河道汇流采用马斯京根分段连续演算法.三水源新安江模型共有17个参数,包括7个产流参数、10个汇流参数.
以王家坝区间流域洪水为研究对象,上断面河道来水采用马斯京根法进行汇流计算.选用1990-2013年共24年的资料进行日模型率定,对其间的12场洪水资料进行次洪模型计算(其中8场洪水用于率定,4场洪水用于验证),本文以计算时段为3 h为例开展相关研究,新安江模型参数见表 1,确定性预报精度统计见表 2.
| 表 1 王家坝区间流域新安江模型参数 Tab. 1 The parameters of Xinanjiang model in Wangjiaba subbasin |
| 表 2 新安江模型精度统计 Tab. 2 The performance of Xinanjiang model |
由表 2可知:王家坝区间流域新安江模型预报的洪峰误差在4 % ~31 %,最小洪峰误差为4.07 %,有两场洪水洪峰误差超过20 %,合格率为83 %. 12场洪水的洪量误差均在15 %以内;洪峰滞时在3个时段(9 h)以内;确定性系数均大于0.75.综合而言,新安江模型预报洪水精度尚可.
2.3 概率预报模型HUP模型[11]由Krzysztofowicz和Herr(2001年)提出,已被广泛用于洪水概率预报研究中[35-38],本文仅对该模型进行简单介绍,其他细节可参考文献[11, 39-40].
HUP模型中,首先采用正态分位数转换技术[41](Normal Quantile Transform)将确定性预报(新安江模型预报)结果与实测结果转换至正态空间.然后在正态空间进行线性似然函数假定,并根据贝叶斯理论推求预报量的后验分布函数.最后通过正态分位数逆转换过程,将正态空间的预测分布函数转换至原始空间,进而实现概率预报.预报量hn的后验概率密度函数可以表示为:
| $ \Phi \left( {{h_n}|{s_n},{h_0}} \right) = {\Omega ^{ - 1}}\left( {\frac{{\Omega \left( {{\mathit{\Gamma }_n}\left( {{h_n}} \right)} \right) - {A_n}\Omega \left( {{\mathit{\Gamma }_s}\left( {{s_n}} \right)} \right) - {D_n}\Omega \left( {{\mathit{\Gamma }_0}\left( {{h_0}} \right)} \right) - {B_n}}}{{{T_n}}}} \right) $ | (32) |
式中, sn为n时刻的预报量;n代表预见期,本文预见期为3 h(与确定性预报一致);h0为起报时刻实测流量值;An、Bn、Dn、Tn为模型参数,结果见表 3;Ω(·)表示正态分位数转换,Ω-1(·)表示正态分位数的逆转换过程;Γ(·)表示新安江模型预报或实测流量的边际分布,一般采用三参数对数威布尔分布,对数威布尔分布函数形式如下:
| 表 3 HUP模型相关参数 Tab. 3 The parameters of HUP model |
| $ F(x) = 1 - {{\rm{e}}^{ - {{\left( {\frac{{{\rm{ln}}(x) - c}}{a}} \right)}^b}}} $ | (33) |
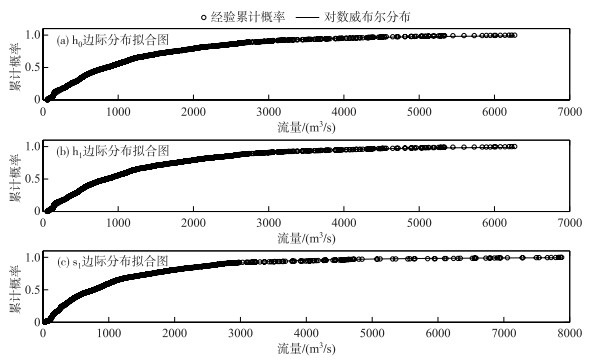
式中, x为新安江模型预报流量或实测流量;a、b、c为对数威布尔分布的3个参数.采用上述8场洪水率定HUP模型相关参数,参数率定结果见表 3,边际分布拟合情况如图 2所示.
|
图 2 边际分布拟合图 Fig.2 Fitting graph of marginal distribution |
由图 2可知,对数威布尔分布理论概率曲线可以很好地拟合流量的经验累积概率.计算对数威布尔分布与经验概率的平均绝对值误差:h0、h1和s1的平均绝对值误差均不超过0.02,因此,概率预报模型的边际分布拟合效果较好.
2.4 概率预报评价在精度评价中,采用洪峰误差REF、洪量误差REV、洪峰滞时ET对HUP模型的倾向值预报(Q50预报值和均值预报)进行评估,并采用基准系数BE对比倾向值预报与新安江模型预报结果,相关数据见表 4.
| 表 4 洪水概率预报精度评价 Tab. 4 The accuracy assessment of probabilistic flood forecast |
由表 4可知:倾向值预报的REF在6 %以内,小于新安江模型洪峰误差;倾向值预报的REV在7 %以内;洪峰滞时ET在1个时段(3 h)以内.通过倾向值预报的REF、REV和ET比较结果可知,概率预报的Q50和均值预报均比新安江模型预报精度更高.此外,倾向值预报的BF均大于0,说明Q50预报和均值预报的洪水过程拟合效果比新安江模型更好.为了更细致的对比倾向值预报的精度,分别计算了新安江模型和倾向值预报(Q50和均值)的KGE及其3个评价因子取值,见表 5.
| 表 5 倾向值预报KGE计算结果 Tab. 5 The KGE of preferred prediction |
由表 5可知:概率预报倾向值预报(Q50和均值)的KGE均比新安江模型大,说明Q50和均值对实际流量过程的拟合精度较新安江模型预报更高.此外,新安江模型的3个评价因子取值较小,说明新安江模型预报在方差、均值和线性相关性方面的模拟精度较高,而倾向值预报(Q50和均值)的3个评价因子几乎都小于新安江预报,说明倾向值预报在均值、方差和线性相关性的模拟精度都大于新安江模型.
在可靠度评价中,采用洪峰处区间离散度Dpeak、覆盖率CR和单位区间离散化系数PUCI对置信度为90 %的区间预报结果进行评价,并采用覆盖率判定系数CRC对概率预报结果进行整体评估.概率预报可靠度评价结果见表 6. 图 3点绘了验证期4场洪水置信度分别为90 %、85 %、……、10 %时,对应的区间覆盖率.
| 表 6 洪水概率预报可靠度评价 Tab. 6 The reliability assessment of probabilistic flood forecast |

|
图 3 验证期洪水置信度与覆盖率的关系 Fig.3 X vs. CR for verification floods |
由表 6可知,置信度为90 %的区间预报:洪峰离散度均在20 %以内;覆盖率在80.36 % ~95.45 %,接近90 %;单位区间离散化系数PUCI在0.35以内,数值较小.因此认为概率预报置信度90 %区间预报结果较为合理.同时,CRC均在0.64以上,因此,概率预报结果整体上是合理的.
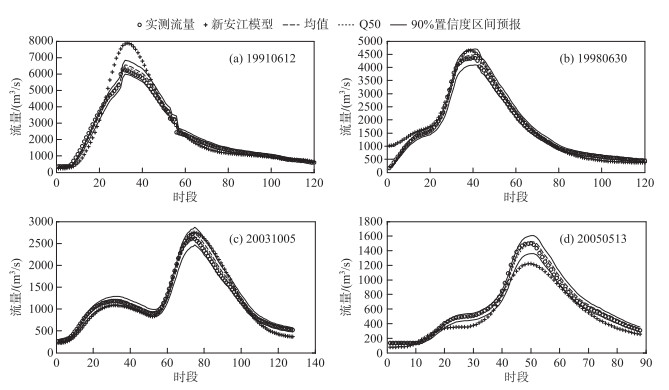
由图 3可知:4场洪水的点据总体上位于45°线(图中实线)附近,仅在置信度小于50 %左右时,(X, CR)点据与45°线的距离有所偏大.总体而言,验证期4场洪水的概率预报结果比较合理. 图 4以90 %置信度的区间预报为例,给出了验证期4场洪水的概率预报过程图.
|
图 4 验证期洪水概率预报过程(计算时段为3 h) Fig.4 The hydrograph of probabilistic forecast for verification floods |
本文分析并总结了目前洪水概率预报研究中常用的评价指标,在此基础上,建立了“精度-可靠度”联合评价指标体系.在淮河王家坝区间流域,采用新安江模型作为确定性预报模型,采用HUP模型进行洪水概率预报,对“精度-可靠度”联合评价指标体系进行应用,主要结论如下:
在“精度”评价时,采用洪峰误差、洪量误差、洪峰滞时和基准系数指标对倾向值预报(Q50和均值)进行评价,结果表明:Q50和均值在洪峰流量、径流量、洪峰出现时间和洪水过程预报中的表现均优于初始确定性预报.
在“可靠度”评价时,采用洪峰离散度、覆盖率和单位区间离散化系数指标可以评价某一置信度(以90 %为例)的区间预报结果的合理性.覆盖率判定系数指标同时考虑了多个置信度的区间预报结果,可以用以估计概率预报结果的整体合理性.
“精度-可靠度”联合评价指标体系分别量化了概率预报倾向值的准确性和区间预报的合理性,实现了洪水概率预报结果的综合评价.
| [1] |
Ye SZ, Xia J. Cenntury's retrospect and looking into the future of hydrological science. Advances in Water Science, 2002, 13(1): 93-104. [叶守泽, 夏军. 水文科学研究的世纪回眸与展望. 水科学进展, 2002, 13(1): 93-104. DOI:10.3321/j.issn:1001-6791.2002.01.017] |
| [2] |
Cloke HL, Pappenberger F. Ensemble flood forecasting:A review. Journal of Hydrology, 2009, 375(3/4): 613-626. DOI:10.1016/j.jhydrol.2009.06.005 |
| [3] |
Wen YH, Li ZJ, Sun MK et al. Influence of rainfall input on real-time flood forecasting accuracy and forecast period. J Lake Sci, 2019, 31(1): 39-51. [温娅惠, 李致家, 孙明坤等. 降雨输入对实时洪水预报精度与预见期的影晌. 湖泊科学, 2019, 31(1): 39-51. DOI:10.18307/2019.0104] |
| [4] |
Zhao LN, Liu Y, Dang HF et al. The progress on application of ensemble prediction to flood forecasting. Journal of Applied Meteorological Science, 2014, 25(6): 641-653. [赵琳娜, 刘莹, 党皓飞等. 集合数值预报在洪水预报中的应用进展. 应用气象学报, 2014, 25(6): 641-653. DOI:10.11898/1001-7313.20140601] |
| [5] |
Liu KL, Hu YB, Wang YJ et al. Performance and parameterization of the BMA model applied in the Huaihe River Basin. J Lake Sci, 2017, 29(6): 1520-1527. [刘开磊, 胡友兵, 汪跃军等. BMA集合预报在淮河流域应用及参数规律初探. 湖泊科学, 2017, 29(6): 1520-1527. DOI:10.18307/2017.0624] |
| [6] |
Xu XY, Fang HW, Zhang YF et al. A real-time probabilistic channel flood forecasting model and application based on particle filters. Advances in Water Science, 2015, 26(3): 356-364. [徐兴亚, 方红卫, 张岳峰等. 河道洪水实时概率预报模型与应用. 水科学进展, 2015, 26(3): 356-364.] |
| [7] |
Kavetski D, Kuczera G, Franks SW. Bayesian analysis of input uncertainty in hydrological modeling:1. Theory. Water Resources Research, 2006, 42(3). DOI:10.1029/2005WR004368 |
| [8] |
Ajami NK, Duan QY, Sorooshian S. An integrated hydrologic Bayesian multimodel combination framework:Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resources Research, 2007, 43(1): W1403. DOI:10.1029/2005WR004745 |
| [9] |
Han SS, Coulibaly P. Bayesian flood forecasting methods:A review. Journal of Hydrology, 2017, 551: 340-351. DOI:10.1016/j.jhydrol.2017.06.004 |
| [10] |
Liu ZJ, Guo SL, He SK et al. Multivariate hydrologic uncertainty processor based on Copula function. Shuili Xuebao, 2018, 49(3): 332-342. [刘章君, 郭生练, 何绍坤等. 基于Copula函数的多变量水文不确定性处理器. 水利学报, 2018, 49(3): 332-342.] |
| [11] |
Krzysztofowicz R, Herr HD. Hydrologic uncertainty processor for probabilistic river stage forecasting:precipitation-dependent model. Journal of Hydrology, 2001, 249(1/2/3/4): 46-68. DOI:10.1016/S0022-1694(01)00412-7 |
| [12] |
Todini E. A model conditional processor to assess predictive uncertainty in flood forecasting. International Journal of River Basin Management, 2008, 6(2): 123-137. DOI:10.1080/15715124.2008.9635342 |
| [13] |
Van Steenbergen N, Ronsyn J, Willems P. A non-parametric data-based approach for probabilistic flood forecasting in support of uncertainty communication. Environmental Modelling & Software, 2012, 33: 92-105. DOI:10.1016/j.envsoft.2012.01.013 |
| [14] |
Murphy AH. What is a good forecast an essay on the nature of goodness in weather forecasting. Weather and Forecasting, 1993(2): 281-293. |
| [15] |
Ren Z, Sheng D. Study on Uncertainty of Xin'anjiang model parameters based on Multi-objective GLUE Method. Water Resources and Power, 2016, 34(3): 15-18. [任政, 盛东. 基于多目标GLUE算法的新安江模型参数不确定性研究. 水电能源科学, 2016, 34(3): 15-18.] |
| [16] |
Wang YL, Liang ZM, Wang K et al. Probabilistic flood forecasting based on multi-model MCP. South-to-North Water Transfers and Water Science & Technology, 2018, 16(6): 39-45. [王艳兰, 梁忠民, 王凯等. 基于多模型MCP方法的洪水概率预报. 南水北调与水利科技, 2018, 16(6): 39-45.] |
| [17] |
Xu W, Jiang HG, Yang X et al. Efficiency of Bayesian probabilistic hydrological forecast system based on Box-Cox transformation. Journal of Hydroelectric Engineering, 2018, 37(11): 15-23. [徐炜, 姜宏广, 杨洵等. 基于Box-Cox变换的贝叶斯概率水文预报效率. 水力发电学报, 2018, 37(11): 15-23. DOI:10.11660/slfdxb.20181102] |
| [18] |
Liang ZM, Jiang XL, Cao YX et al. Probabilistic flood forecasting considering rainfall uncertainty. Journal of Hohai University:Natural Sciences, 2016, 44(1): 8-12. [梁忠民, 蒋晓蕾, 曹炎煦等. 考虑降雨不确定性的洪水概率预报方法. 河海大学学报:自然科学版, 2016, 44(1): 8-12.] |
| [19] |
Alfieri L, Pappenberger F, Wetterhall F et al. Evaluation of ensemble streamflow predictions in Europe. Journal of Hydrology, 2014, 517: 913-922. DOI:10.1016/j.jhydrol.2014.06.035 |
| [20] |
GB/T 22482-2008, Standard for hydrological information and hydrological forecasting. GB/T 22482-2008, [水文情报预报规范. ]
|
| [21] |
Nash J, Sutcliffe J. River flow forecasting through conceptual models. Part Ⅰ:A discussion of principles. Journal of Hydrology, 1970(10): 282-290. |
| [22] |
Gupta HV, Kling H, Yilmaz KK et al. Decomposition of the mean squared error and NSE performance criteria:Implications for improving hydrological modelling. Journal of Hydrology, 2009, 377(1/2): 80-91. DOI:10.1016/j.jhydrol.2009.08.003 |
| [23] |
Schaefli B, Gupta HV. Do Nash values have value?. Hydrological Processes, 2007, 21(15): 2075-2080. DOI:10.1002/hyp.6825 |
| [24] |
Xiong LH, Wan M, Wei XJ et al. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation. Hydrological Sciences Journal, 2009, 54(5): 852-871. DOI:10.1623/hysj.54.5.852 |
| [25] |
Li L, Xia J, Xu CY et al eds. Analyse the sources of equifinality in hydrological model using GLUE methodology. In: Hydroinformatics in Hydrology, Hydrogeology and Water Resources. Italy: IAHS Press, 2009: 130-138.
|
| [26] |
Jin XL, Xu CY, Zhang Q et al. Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. Journal of Hydrology, 2010, 383(3/4): 147-155. DOI:10.1016/j.jhydrol.2009.12.028 |
| [27] |
Renard B, Kavetski D, Kuczera G et al. Understanding predictive uncertainty in hydrologic modeling:The challenge of identifying input and structural errors. Water Resources Research, 2010, 46(5). DOI:10.1029/2009WR008328 |
| [28] |
Laio F, Tamea S. Verification tools for probabilistic forecasts of continuous hydrological variables. Hydrol Earth Syst Sci, 2007, 11: 1267-1277. DOI:10.5194/hess-11-1267-2007 |
| [29] |
Li L, Xu CY, Xia J et al. Uncertainty estimates by Bayesian method with likelihood of AR (1) plus Normal model and AR (1) plus Multi-Normal model in different time-scales hydrological models. Journal of Hydrology, 2011, 406(1/2): 54-65. DOI:10.1016/j.jhydrol.2011.05.052 |
| [30] |
Matheson JE, Winkler RL. Scoring rules for continuous probability distributions. Management Science, 1976, 22: 1087-1095. DOI:10.1287/mnsc.22.10.1087 |
| [31] |
Hersbach H. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather and Forecasting, 2000, 15(5): 559-570. DOI:10.1175/1520-0434(2000)015<0559:DOTCRP>2.0.CO;2 |
| [32] |
Biondi D, De Luca DL. Performance assessment of a Bayesian Forecasting System (BFS) for real-time flood forecasting. Journal of Hydrology, 2013, 479: 51-63. DOI:10.1016/j.jhydrol.2012.11.019 |
| [33] |
Pappenberger F, Ramos MH, Cloke HL et al. How do I know if my forecasts are better? Using benchmarks in hydrological ensemble prediction. Journal of Hydrology, 2015, 522: 697-713. DOI:10.1016/j.jhydrol.2015.01.024 |
| [34] |
Zhao RJ. Basin hydrological simulation-Xinanjiang model and Shanbei model. Beijing: Water Resources and Electric Power Press, 1984. [赵人俊. 流域水文模拟-新安江模型和陕北模型. 北京: 水利电力出版社, 1984.]
|
| [35] |
Zhang Y, Liang ZM. Application research of BFS to flood forecasting. Water Resources and Power, 2009(5): 44-47. [张宇, 梁忠民. BFS在洪水预报中的应用研究. 水电能源科学, 2009(5): 44-47. DOI:10.3969/j.issn.1000-7709.2009.05.014] |
| [36] |
Biondi D, Versace P, Sirangelo B. Uncertainty assessment through a precipitation dependent hydrologic uncertainty processor:An application to a small catchment in southern Italy. Journal of Hydrology, 2010, 386(1/2/3/4): 38-54. DOI:10.1016/j.jhydrol.2010.03.004 |
| [37] |
Xing ZX, Rui XF, Fu Q et al. Nash model parameter uncertainty analysis by AM-MCMC based on BFS and probabilistic flood forecasting. Chinese Geographical Science, 2011, 21(1): 74-83. DOI:10.1007/s11769-010-0433-1 |
| [38] |
Wang J, Liang ZM, Hu YM. Application and improvement of BFS in flood forecasting. Journal of Hohai University:Natural Sciences, 2012(1): 52-58. [王军, 梁忠民, 胡义明. BFS在洪水预报中的应用与改进. 河海大学学报:自然科学版, 2012(1): 52-58.] |
| [39] |
Zhang HG. Bayesian probability hydrological forecasting system and its application[Dissertation]. Wuhan: Wuhan University, 2005. [张洪刚.贝叶斯概率水文预报系统及其应用研究[学位论文].武汉: 武汉大学, 2005. ]
|
| [40] |
Jiang XL, Liang ZM, Wang CQ et al. Application of BFS-HUP model to flood probabilistic forecasting of Tongguan Station. Yellow River, 2015, 37(7): 13-15. [蒋晓蕾, 梁忠民, 王春青等. BFS-HUP模型在潼关站洪水概率预报中的应用. 人民黄河, 2015, 37(7): 13-15. DOI:10.3969/j.issn.1000-1379.2015.07.004] |
| [41] |
Krzysztofowicz R. Transformation and normalization of variates with specified distributions. Journal of Hydrology, 1997, 197(1/2/3/4): 286-292. |
 2020, Vol. 32
2020, Vol. 32 


