(2: 长江水利委员会水文局, 武汉 430010)
(2: Bureau of Hydrology, Changjiang River Water Resources Commission, Wuhan 430010, P. R. China)
分汊河段在长江中下游大量存在,占总河长的75%以上[1].分汊河段具有主流摆动频繁,洲滩消长,主、支汊兴衰交替的演变特征[2-3].在以悬移质运动为主的冲积河流中,汊道分流很大程度上决定了汊道分沙[4],分流比的变化会引发各汊输沙动力强弱的改变,造成汊道的消长.中枯水分流比反映了基本河槽的分流状况,因此被作为判断汊道发展状态的重要指标[5].显然,研究汊道分流比在不同水沙、地形边界条件下的变化规律,对于研究汊道冲淤演变机理和航道治理实践具有重大意义[6].
从1940s开始,陆续有学者通过水槽试验来研究明渠分汊的水流结构. Lakshmana等[7]和Ramamurthy等[8]先后建立了直角明渠分汊中支汊分流比的计算式,但这些公式仅适用于直角分汊,无法应用于边界条件更为复杂的分汊河流.天然汊道中分流比可基于水面线的推求[9]或数学模型计算[10-11]获得,但对计算结果影响巨大的河道阻力分布大多通过实测资料率定反求[12]或直接用经验公式[13]计算,难以反映水沙、地形边界条件改变后阻力发生的调整.而由河床演变基本理论基于各种假设推求的分流比计算式[14-16],在已知单个汊道断面内各汊的过水面积、水深、糙率、比降等数值后即可计算得到分流比,避免了复杂的流场求解,但对糙率、比降不同的处理方式造成了各分流比计算式精度的差异.可见,无论是通过求解汊道段流场分布还是利用分流比计算公式来求得分流比,汊道阻力分布的确定都是重难点所在.
三峡水库蓄水后,水沙条件显著的变化造成下游各分汊河段主、支汊的趋势性调整[1, 17].坝下游首个沙质河床段——荆江沙市段是典型的分汊河段[3],其汊道冲淤调整响应较为剧烈[18],可作为研究建坝影响下分流比变化的典型河段.以沙市段为例,用实测资料检验现有分流比计算式的可靠性,探索提高分流比公式计算精度的方法,提出改进后的分流比计算式.
本文研究仅限于双分汊河段的分流比计算式.
1 研究区域与研究方法 1.1 研究河段沙市段位于上荆江河段,上起陈家湾、下至玉和坪,总长约18 km(图 1).河段进口左岸有沮漳河入汇,右岸有太平口分流,自上而下根据平面外形的不同可分为太平口顺直分汊和三八滩微弯分汊两个河段,其中太平口分汊段由太平口心滩分为北(左)槽和南(右)槽,三八滩分汊段由三八滩分为北(左)汊和南(右)汊.各分汊段的形态特征指标见表 1.
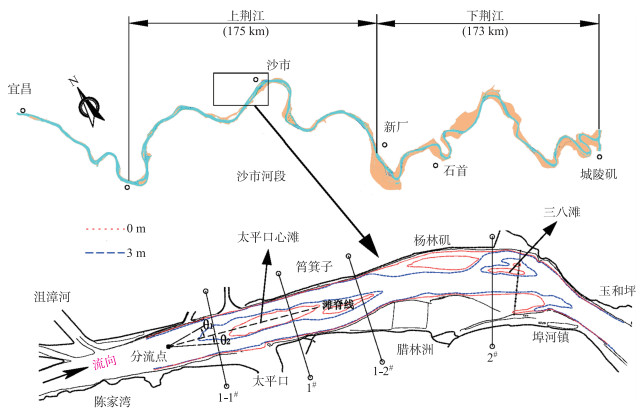
|
图 1 长江荆江河段沙市段河势图 Fig.1 Sketch of the Jingjiang River and Shashi anabranching reach |
| 表 1 研究河段汊道形态特征 Tab. 1 Morphological characteristics of the study anabranching reaches |
研究数据包括2003-2019年沙市段两分汊段典型断面1#、2#(断面位置见图 1)在不同流量下测得的流速、水位、比降、河宽等,其中,1#断面有3500~27000 m3/s流量下共23个测次的数据,2#断面有6000~8000 m3/s流量下共12个测次的数据.上述35个测次数据中,24个包含有比降实测值.研究还收集了2003-2018年沙市段地形图.
分析计算过程中,过水面积由水深沿河宽积分得到,过水面积除以水面宽得到平均水深,汊道流量则由单宽流量(垂线平均流速与水深之积)沿汊宽积分得到,分流比根据两汊的流量求出.沿两汊深泓线从分流点到汇流点间的距离作为相应的汊长,心滩滩头脊线与分流点处两汊水动力轴线的夹角为相应的偏转角(图 1),1-1#~1#、1#~1-2#、1-1#~1-2#之间的比降分别为汊道进口段、出口段和整个汊道段的平均比降.
本文的研究方法为:采用实测数据检验并对比现有分流比计算公式的精度,在此基础上,针对基于曼宁公式建立的分流比计算式,分析糙率、比降不同表达方法对分流比计算精度的影响,提出改进后的分流比计算公式型式,利用实测数据率定公式的参数后得到新的分流比计算经验公式,并进一步分析沙市段汊道的分流比变化特点.
2 分流比计算公式的比较 2.1 分流比计算公式 2.1.1 基于曼宁公式的分流比计算式基于曼宁公式较易得到如下的分流比计算式[14]:
| $ {\eta _1} = {\left[ {1 + \frac{{{A_2}}}{{{A_1}}}{{\left( {\frac{{{H_2}}}{{{H_1}}}} \right)}^{2/3}}\frac{{{n_1}}}{{{n_2}}}{{\left( {\frac{{{J_2}}}{{{J_1}}}} \right)}^{1/2}}} \right]^{ - 1}} $ | (1) |
式中,A、H、n和J分别表示汊道断面过水面积、平均水深、综合糙率系数和纵比降,下标1、2分别表示两汊.两汊综合糙率系数表征了两汊的综合阻力,由于缺乏天然河道糙率实测数据,因此采用以下的近似处理办法:
1) 假定两汊糙率、比降均相差不大,即n1/n2(J2/J1)1/2≈1.汊道分流比可利用水力几何变量(A和H)计算得到[14]:
| $ {\eta _1} = {\left[ {1 + \frac{{{A_2}}}{{{A_1}}}{{\left( {\frac{{{H_2}}}{{{H_1}}}} \right)}^{2/3}}} \right]^{ - 1}} $ | (2) |
2) 假定从分流点至汇流点两汊水头差相等,即Δh1=Δh2,J2/J1=(Δh2/L2)/(Δh1/L1)=L1/L2,其中L表示汊长,h表示水位.此法较为常用,也称等水位差法[14],利用相对较易测量的汊长代替比降,即可得到分流比计算式:
| $ {\eta _1} = {\left[ {1 + \frac{{{A_2}}}{{{A_1}}}{{\left( {\frac{{{H_2}}}{{{H_1}}}} \right)}^{2/3}}\frac{{{n_1}}}{{{n_2}}}{{\left( {\frac{{{L_1}}}{{{L_2}}}} \right)}^{1/2}}} \right]^{ - 1}} $ | (3) |
等动量法也称动量平衡法,由童朝锋[15]最先提出.他认为分流段两分流水体在垂直于河道主轴方向上的动量相等,即Q1·U1·sinθ1=Q2·U2·sinθ2,其中Q和U分别表示汊道流量和平均流速,θ表示偏转角.将Q=U·A代入上式,即可得等动量法分流比计算式:
| $ {\eta _1} = {\left[ {1 + {{\left( {\frac{{{A_2}}}{{{A_1}}} \cdot \frac{{{H_2}}}{{{H_1}}}} \right)}^{3/4}}{{\left( {\frac{{\sin {\theta _1}}}{{\sin {\theta _2}}}} \right)}^{1/2}}} \right]^{ - 1}} $ | (4) |
文献[16]指出,对于河床相对稳定的分汊河段,各汊的含沙量是比较接近的.而处于平衡状态的河流,含沙量近似等于其挟沙力.根据张瑞瑾挟沙力计算公式可得到:
| $ {K_0}{\left( {\frac{{U_0^3}}{{g \cdot {H_0} \cdot {\omega _0}}}} \right)^{{m_0}}} = {K_1}{\left( {\frac{{U_1^3}}{{g \cdot {H_1} \cdot {\omega _1}}}} \right)^{{m_1}}} = {K_2}{\left( {\frac{{U_2^3}}{{g \cdot {H_2} \cdot {\omega _2}}}} \right)^{{m_2}}} $ | (5) |
式中,下标0表示上游单一段,K和m分别为挟沙力系数和指数,一般可认为变化不大.进一步假设分汊前后泥沙粒径不变,则各汊内泥沙沉速相等.将Q=U·A代入上式后,即可得到等含沙量法分流比计算式[15]:
| $ {\eta _1} = {\left[ {1 + \frac{{{A_2}}}{{{A_1}}}{{\left( {\frac{{{H_2}}}{{{H_1}}}} \right)}^{1/3}}} \right]^{ - 1}} $ | (6) |
用含有比降的实测数据检验各公式的计算精度,分别计算北槽和北汊的分流比并与实测值作比较,结果见图 2.
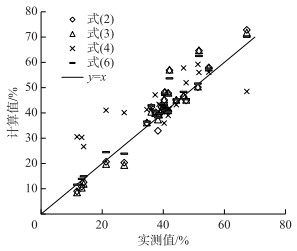
|
图 2 分流比计算结果对比 Fig.2 Measured versus calculated flow division ratio |
以计算值与实测值的平均绝对值差值
| 表 2 分流比计算式计算误差 Tab. 2 Calculation error of different flow division ratio formulas |
式(2)不考虑两汊糙率和比降的差异,最大计算偏差可达15%,中、洪水流量下计算值与实测值之间的吻合程度高,计算偏差不超过3%,说明枯水流量下忽略糙率、比降差异会造成较大的偏差,中洪水流量下影响不大;式(3)中保留式(2)n1≈n2的假设用汊长代替比降后,计算误差略有减小,但变化不大;式(4)在4个公式中计算误差最大,说明偏转角θ不能全面反映两汊糙率、比降对分流比的影响;式(6)与式(2)形式相同,仅水深之比的指数不同,其最大计算偏差约为11%.
总体上,现有分流比计算公式考虑两汊糙率和比降差异的程度不够,虽然型式简单,但精度不高.
3 分流比计算式的改进准确反映两汊糙率和比降的差异是提高分流比计算公式精度的关键.本节将主要探讨分流比计算中如何选取代表性比降以及能够综合反映糙率、比降差异的参数.
3.1 选取不同的比降对分流比计算精度的影响汊道内比降沿程变化[5],进口段、出口段和整个汊道段的平均比降不同,选择不同的比降计算分流比结果不同.将式(1)中取n1/n2=1,然后分别采用进口段、出口段和汊道的平均比降计算分流比,即在式(2)的基础上考虑比降差异的影响,太平口心滩分汊段计算结果见图 3和表 3.可以看出:和不考虑比降影响的式(2)相比,采用进口段比降和汊道平均比降后,分流比的计算误差均有所减小,其中采用进口段比降计算,误差相对更小;但只考虑比降的差异,计算结果仍存在着较大的偏差(最大偏差约为9%).
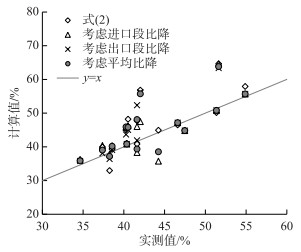
|
图 3 考虑不同的比降对分流比计算结果的影响 Fig.3 Impacts on flow division ratio calculation by considering different water surface slopes |
| 表 3 分流比计算式计算误差 Tab. 3 Calculation error of different flow division ratio formulas |
对两汊分别运用曼宁公式相除后可得到:
| $ \frac{{{n_1}}}{{{n_2}}}{\left( {\frac{{{J_2}}}{{{J_1}}}} \right)^{1/2}} = \frac{{{A_1}}}{{{A_2}}} \cdot \frac{{{Q_2}}}{{{Q_1}}}{\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^{2/3}} = {\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^{2/3}}\frac{{{U_2}}}{{{U_1}}} \approx \frac{{{F_{r2}}}}{{{F_{r1}}}}{\left( {\frac{{{H_1}}}{{{H_2}}}} \right)^{1/6}} $ | (7) |
定义n/J1/2为糙率比降综合影响系数C(后文简称综合系数),则上式表达的是综合系数之比C1/C2,与水力半径之比和流速之比相关,也与两汊的平均水深之比和Froude数之比相关,而水深与Froude数之间存在着内在联系.分别点绘综合系数比与平均水深比和Froude数比之间的关系(图 4).
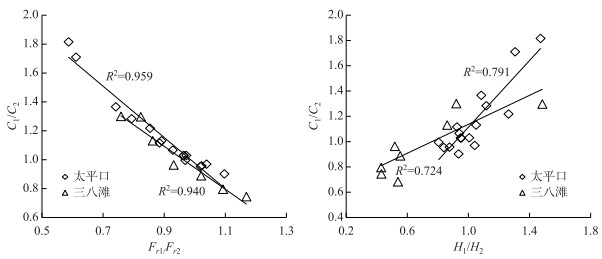
|
图 4 Froude数之比、平均水深之比与综合系数之比的相关关系 Fig.4 Relationships between Fr1/Fr2 and C1/C2, H1/H2 and C1/C2 |
可以看出,两汊综合系数比与Froude数之比高度相关、与平均水深比强相关,虽然Froude数之比能更充分反映综合系数差异对分流比的影响,但由于Froude数中显含流速U,而分流比的计算实际上就是要确定U,因此本文选取平均水深之比来反映综合系数比对分流比的影响.对图 4中24组数据拟合后可得平均水深之比与综合系数之比的经验表达式,将其代入式(1)中可得到:
| $ {\eta _1} = {\left[ {1 + \frac{{{A_1}}}{{{A_2}}}{{\left( {\frac{{{H_2}}}{{{H_1}}}} \right)}^{2/3}}\left( {a\frac{{{H_1}}}{{{H_2}}} + b} \right)} \right]^{ - 1}} $ | (8) |
式(8)即为采用平均水深之比代替综合系数之比的分流比计算式,其中,a、b可通过实测资料线性拟合得到.采用实测数据对该公式进行验证,结果见表 3和图 5.由图表可见,该计算式的计算误差显著减小,各级流量下的分流比计算偏差均小于5%.
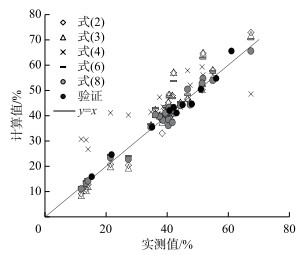
|
图 5 改进后分流比计算式计算结果对比 Fig.5 Measured versus calculated flow division ratio by the improved formula and other ones |
顺直分汊段和微弯分汊段的平面形态不同,a、b的取值会有明显的差异.以2010年4月-2018年3月冲淤变化引起的水深比、综合系数比的改变为例,太平口心滩分汊段北槽冲刷(图 6),北槽与南槽水深之比(H1/H2)增加约15%,两汊综合系数比(C1/C2)增长约28%,北槽枯水分流比增加约17%;与之相反,三八滩北汊大幅萎缩(图 6),北汊与南汊水深之比H1/H2减小约36%,C1/C2仅减小约21%,北汊枯水分流比减小达64%.显然,不同类型的汊道内,两汊水深之比的变化对综合系数之比和分流比的改变程度不同,主、支均势的顺直分汊段分流比对于汊道冲淤的敏感度较低[19],A1/A2、H1/H2小幅度的增加往往引起C1/C2显著的增加,因而η1增幅较小;而主、支差异明显的微弯分汊段,分流比受断面冲淤变化的调节作用更为明显,当北汊冲刷发展(或淤积萎缩)时,随着A1/A2、H1/H2的增加(或减小),C1/C2的增幅(或减幅)相对较小,η1随之发生显著的增加(或减小).
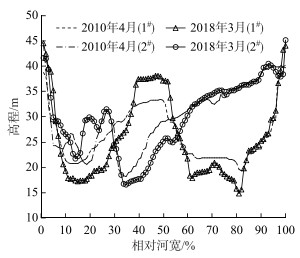
|
图 6 分汊断面2010年4月-2018年3月冲淤变化 Fig.6 Variations in the branching cross-section profiles from April of 2010 to March of 2018 |
综上所述,本文提出的分流比计算式可准确地反映分汊河段汊道冲淤变化条件下的分流比变化,由于不同的分汊河段内,两汊水深之比的变化对综合系数之比和分流比的改变程度不同,因此应用在具体的分汊河段时,须采用实测资料率定公式中的系数a、b.
4 三峡水库蓄水后沙市段分流比变化特点分析 4.1 汊道分流比随水位的变化利用式(8),计算1#断面处A1/A2、H1/H2和η1随水位的变化过程.结果显示,当计算所选取的地形边界不同时,η1随水位的变化情况是不同的,有先增后减、先减后增、逐渐增加和逐渐减小等多种变化趋势(图 7),与以往研究认为支汊分流比随流量的增加而增加[20]并不相同.这是因为在自然条件下枯水期主流流经主汊,随着流量的增加,主流所具有的“小水坐弯,大水趋直”的特性使得其在一定程度上偏离主汊、偏向支汊,因而支汊的分流比随流量的增加而增加.而在两汊差别不大,主流摆动频繁的顺直分汊段,上游来沙减少引起汊道剧烈的冲淤调整,汊道冲淤交替导致主汊位置的不固定,使得顺直分汊段分流比随水位的变化规律呈多样性.尽管不同地形边界下,分流比随水位的变化趋势有所不同,但H1/H2与η1的变化趋势总体较为一致.
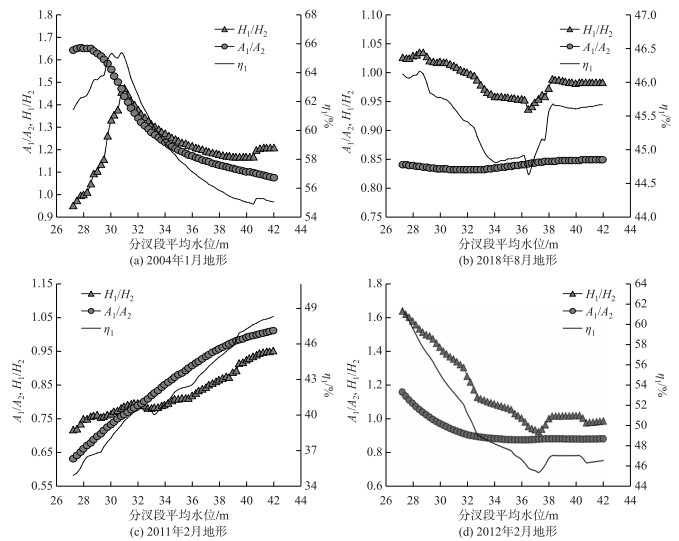
|
图 7 不同地形边界下A1/A2、H1/H2和η1随水位的变化 Fig.7 Variation curves of A1/A2, H1/H2 and η1 versus water level under different channel boundaries |
利用式(8)计算不同地形边界下枯、中、洪水流量分流比的变化,分析蓄水后不同流量级分流比的年际变化特征.方法为:针对不同的实测1#、2#断面地形,利用相应的沙市水文站水位流量关系确定枯、中、洪水流量(8000、12000和25000 m3/s)所对应的水位,由此得到各地形边界下的A1/A2和H1/H2.代入式(8)计算η1,结果见图 8.
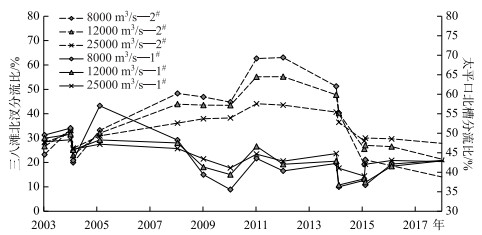
|
图 8 沙市分汊段不同流量分流比的年际变化 Fig.8 Temporal variations in flow division ratio of different flow discharges at the Shashi anabranching reach |
可以看出,三峡水库蓄水后,太平口北槽洪、中、枯水分流比均呈总体减小的趋势.蓄水初期,北槽枯水分流比经历了从低于50%增加到超过50%,而后又减小至低于50%的转变,即主支汊发生了较频繁的易位. 2008年三峡水库试验性蓄水后,各流量下北槽分流比有所减小,2010年后有增有减,整体变化不大,现枯水分流比稳定在40% ~45%;蓄水初期,三八滩分汊段各流量下分流比变化较小,始终保持南汊占优的局面. 2005-2008年和2010-2012年,北汊分流比经历了两次明显的增加,中枯水分流比超过50%. 2013年后,北汊分流比迅速减小,至2015年小于50%,也发生了主支汊易位,其后减小趋势仍在继续,但速度放缓,现枯水分流比低于20%.
可见,太平口北槽、三八滩北汊分流比在三峡水库蓄水初期变化剧烈,后期由于连续实施的航道整治工程对河势的控制作用逐渐显现,加上上游来水持续偏枯,因而分流比调整的剧烈程度降低.随着上游梯级水库群的建成运用,下游分汊河段趋势性调整仍将延续这一特点,特别是三八滩北汊继续趋于萎缩.但在出现大洪水时,河段内分流比的变幅会增大.
比较不同流量下分流比变化过程可发现,不管是顺直还是微弯分汊段,流量越大,分流比变化越小,流量越小,分流比的调整则越剧烈.这主要是因为蓄水后汊道冲淤主要集中于枯水河槽[18],同时枯水位明显降低[21],使得两汊枯水流量下水深变幅较大,对分流的影响也更大.
4.3 同一流量下汊道分流比随汊道冲淤的变化对同流量下某一固定的汊道断面,设t1时刻左、右汊过水面积为A1、A2,左汊分流比为η1,t2时刻分别为A1′、A2′和η1′,则该时段内两汊单位河长发生的冲淤体积可分别表示为(A1′- A1)×1和(A2′- A2)×1.令ER= A1′- A1-(A2′- A2),Δη1=η1′-η1,不同流量下Δη1与ER的关系如图 9所示.
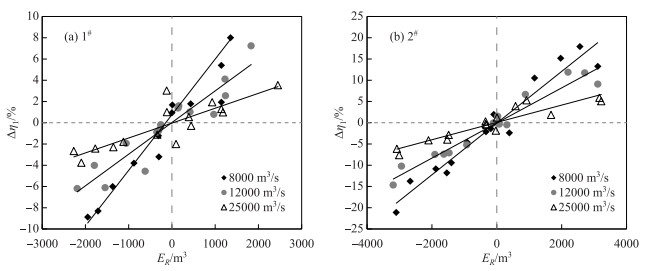
|
图 9 不同流量下Δη1随ER的变化 Fig.9 Variations of Δη1 with ER at different flow discharges |
由图 9可见,ER与左汊分流比变化之间呈较好的线性关系,左汊相对于右汊的冲刷发展(或淤积萎缩)会改善(或恶化)其入流条件,分流比随之增加(或减小).拟合出Δη1与ER之间的线性关系表达为:
| $ \Delta {\eta _1}' = {k_1} \cdot {E_R} + {k_2} $ | (9) |
式中,k1和k2分别表示直线斜率和截距,线性拟合的相关系数R及k1的取值见表 4.
| 表 4 线性拟合参数 Tab. 4 Fitting parameters of the linear fitting |
从表 4可以看出,随着流量的增加,k1逐渐减小,说明冲淤变化对分流比的影响趋于减小,枯水分流比对于河道冲淤变化的敏感程度要大于洪水分流比.各级流量下,微弯分汊段k1取值均大于顺直分汊段,进一步反映了两汊分流差异较大的微弯分汊段内,冲淤变化对于分流比的影响要大于顺直分汊段[19].
5 结论1) 汊道分流比计算公式中,两汊糙率、比降差异的准确反映与否是影响其计算精度的关键.完全忽略糙率、比降差异的影响会给枯水分流比的计算结果带来较大的偏差;只考虑两汊比降差异而忽略糙率差异的影响,分流比计算精度仍然较低.
2) 两汊平均水深之比可较全面反映河道阻力、比降的差异,与糙率、比降综合影响系数之比高度相关,将平均水深之比与糙率、比降综合影响系数之比引入到分流比计算公式,得到了较高精度的分流比计算式,各流量下计算偏差不大于5%.
3) 三峡水库蓄水后,沙市段汊道枯水分流比的变化较为剧烈,洪水分流比变化较小.汊道冲淤变化对枯水分流比的影响强于洪水分流比,对主、支差异较大的微弯分汊段分流比的影响强于主、支均势的顺直分汊段.
| [1] |
Li M, Hu CH. Study on processes of braided river downstream of the Three Gorges Reservoir. Journal of Sediment Research, 2017, 42(6): 1-7. [李明, 胡春宏. 三峡工程运用后坝下游分汊型河道演变与调整机理研究. 泥沙研究, 2017, 42(6): 1-7.] |
| [2] |
Zhang W, Li YT, Jiang L. Fluvial process change of the typical multi-branched meandering reach in the Mid-Down Yangtze River after Three Gorges Dam impoundment. Journal of Sichuan University:Engineering Science Edition, 2008, 40(4): 17-24. [张为, 李义天, 江凌. 三峡水库蓄水后长江中下游典型分汊浅滩河段演变趋势预测. 四川大学学报:工程科学版, 2008, 40(4): 17-24.] |
| [3] |
Zhu LL, Zhang W, Ge H. Evolution trend and caused of the typical braided middle Yangtze reach after Three Gorges reservoir impoundment. Journal of Hydroelectric Engineering, 2011, 30(5): 106-113. [朱玲玲, 张为, 葛华. 三峡水库蓄水后荆江典型分汊河段演变机理及发展趋势研究. 水力发电学报, 2011, 30(5): 106-113.] |
| [4] |
Han QW, He MM, Chen XW. The suspended sediment diversion model at the bifurcation. Journal of Sediment Research, 1992(1): 44-54. [韩其为, 何明民, 陈显维. 汊道悬移质分沙的模型. 泥沙研究, 1992(1): 44-54.] |
| [5] |
Yu WC. Some characteristics of water flow and sediment transportation at the entrance region of the braided channel with stable islands in the Middle and Lower Yangtze River. Journal of Yangtze River Scientific Research Institute, 1987(1): 14-25. [余文畴. 长江分汊河道口门水流及输沙特性. 长江水利水电科学研究院院报, 1987(1): 14-25.] |
| [6] |
Chen L, Zhou YJ, Yan X et al. Research on erosion adjustment features of different types of braided reaches downstream the Three Gorges Project. Journal of Hydroelectric Engineering, 2011, 30(3): 109-116. [陈立, 周银军, 闫霞等. 三峡下游不同类型分汊河段冲刷调整特点分析. 水力发电学报, 2011, 30(3): 109-116.] |
| [7] |
Lakshmana RNS, Sridharan K, Baig MYA. Experimental study of the diversion of flow in an open channel. Sydney: Conference on Hydraulics and Fluid Mechanics, 1968.
|
| [8] |
Ramamurthy AS, Duc MT, Carballada LB. Dividing flow in open-channels. Journal of Hydraulic Engineering, 1990, 116(3): 449-455. DOI:10.1061/(ASCE)0733-9429(1990)116:3(449) |
| [9] |
He SH. Caculation of the water surface and flow volume diversion in anabranching channels. Hydrology, 2000, 20(1): 51-52.
|
| [10] |
Bao Y, Xu WM. Two-dimensional numerical simulation of the whole Pearl River estuary and and the study on diversion ratio. Hohhot: 14th China Ocean (Cosatal) Engineering Symposium, 2009. [包芸, 许炜铭. 珠江河口二维整体数值模拟及分流比研究. 呼和浩特: 第十四届中国海洋(岸)工程学术讨论会, 2009.]
|
| [11] |
Ramamurthy AS, Qu JY, Vo D. Numerical and experimental study on dividing open-channel flows. Journal of Hydraulic Engineering, 2007, 133(10): 1135-1144. DOI:10.1061/(ASCE)0733-9429(2007)133:10(1135) |
| [12] |
Mahashati H, Nuerxiaxi M. Analysis of the methods for determing the roughness of natural river course. Energy and Energy Conservation, 2017(4): 94-95. [玛哈沙提哈孜哈力, 努尔夏西曼斯尔. 天然河道的糙率确定方法分析. 能源与节能, 2017(4): 94-95. DOI:10.3969/j.issn.2095-0802.2017.04.046] |
| [13] |
Shen WW, Chen YF, Shen ZD. Inverse problems of river roughness:research review and project. Zhejiang Hydrotechnics, 2017, 45(4): 1-3. [沈五伟, 陈一帆, 申振东. 河道糙率反问题研究回顾与展望. 浙江水利科技, 2017, 45(4): 1-3.] |
| [14] |
Ding JS, Qiu FL. Calculation of flow and sediment diversion in anabranching channels. Journal of Sediment Research, 1981(2): 58-64. [丁君松, 丘凤莲. 汊道分流分汊计算. 泥沙研究, 1981(2): 58-64.] |
| [15] |
Tong CF. Study on flow and sediment movement of bifurcation area and related application of 3-D numerical flow model[Dissertation]. Nanjing: Hohai University, 2005. [童朝锋.分汊口水沙运动特征及三维水流数学模型应用研究[学位论文].南京: 河海大学, 2005. ]
|
| [16] |
Wang CJ. River Dynamics. Beijing: China Communications Press, 2001. [王昌杰. 河流动力学. 北京: 人民交通出版社, 2001.]
|
| [17] |
Han JQ, Zhang W, Yuan J et al. Responses of riverbed morphology to the hydrological regime in anabranching reaches of the downstream Three Gorges Reservoir. Advances in Water Science, 2018, 29(2): 186-195. [韩剑桥, 张为, 袁晶等. 三峡水库下游分汊河道滩槽调整及其对水文过程的响应. 水科学进展, 2018, 29(2): 186-195.] |
| [18] |
Chen F, Chen L, Zhang W et al. Responses of channel morphology to flow-sediment variations after dam construction:A case study of the Shashi Reach, middle Yangtze River. Hydrology Research, 2019, 50(5): 1359-1375. DOI:10.2166/nh.2019.066 |
| [19] |
Yao SM, Yu WC, Dong YH. Characteristics of water flow and sediment motion in braided river and their effects on fluvial evolution. Journal of Yangtze River Scientific Research Institute, 2003, 20(1): 7-9. [姚仕明, 余文畴, 董耀华. 分汊河道水沙运动特性及其对河道演变的影响. 长江科学院院报, 2003, 20(1): 7-9. DOI:10.3969/j.issn.1001-5485.2003.01.002] |
| [20] |
Luo HC. Characteristics of fluvial processes and stability of the braided channel in the middle and lower reaches of the Yangtze River. Shuili Xuebao, 1989(6): 10-19. [罗海超. 长江中下游分汊河道的演变特点及稳定性. 水利学报, 1989(6): 10-19. DOI:10.3321/j.issn:0559-9350.1989.06.002] |
| [21] |
Han JQ, Sun ZH, Yang YP. Flood and low stage adjustment in the middle Yangtze River after impoundment of the Three Gorges Reservoir (TGR). J Lake Sci, 2017, 29(5): 1217-1226. [韩剑桥, 孙昭华, 杨云平. 三峡水库运行后长江中游洪、枯水位变化特征. 湖泊科学, 2017, 29(5): 1217-1226. DOI:10.18307/2017.0520] |
 2020, Vol. 32
2020, Vol. 32 

