(2: 水利部信息中心(水利部水文水资源监测预报中心), 北京 100053)
(3: 黄河水利委员会河南水文水资源局, 郑州 450003)
(4: 宁波市镇海区建筑(交通)工程安全质量管理站, 宁波 315202)
(5: 北京水文总站, 北京 100089)
(2: Information Center(Hydrology Monitor and Forecast Center), Ministry of Water Resources, Beijing 100053, P. R. China)
(3: Henan Bureau of Hydrology and Water Resources, Yellow River Conservancy Commission, Zhengzhou 450003, P. R. China)
(4: Construction(Transportation) Project Safety and Quality Supervision Station of Zhenhai District, Ningbo 315202, P. R. China)
(5: Beijing Hydraulic Center, Beijing 100089, P. R. China)
暴雨与洪水灾害严重威胁人民的生命财产安全,如何系统地研究两者间的联系并及时准确做出水文气象预报一直是研究的热点难点问题[1].一般地,暴雨事件可通过大气数值模式模拟[2-3],如WRF模式[3-5];而洪水一般通过水文模型预报[6-7],如新安江模型[8]和TOPMODEL模型[9]等.事实上,大气模式和水文模型尺度不尽相同,前者一般尺度较大,后者网格较精细.近些年来,出现了将两者相耦合的建模方法(即陆气耦合模型),该法可显著延长洪水预报的预见期,为暴雨洪水的模拟和预报提供有力工具[10-12].例如,高冰等[11]将WRF模式与分布式水文模型GBHM进行耦合,较好地模拟三峡库区入库洪水过程.但多数研究均采用单向的陆气耦合方式,即仅将大气模式的输出作为水文模型的输入,而未考虑后者对前者的反馈机制.双向耦合的水文气象模型可以较好地考虑两个过程间的交互作用,更合理地模拟水文气象状态,提供更可靠的暴雨洪水预报.
WRF-Hydro模型[13]是有物理基础的、多尺度的、多参数化方案的、可与大气模式进行单向或双向耦合的、新一代的分布式水文气象预报系统,能定量研究流域内大气-陆面水热交换过程[14]. WRF-Hydro模型以较大尺度的陆面模式[2]为基础,加入基于精细网格的汇流模块,以解决某些陆面模式中未考虑侧向流的问题.同时可以更好地模拟土壤水的分布情况,为大气模式提供更合理的下边界条件.此外,该模型在不同的水文气象过程中能提供多个参数化方案以供选择,如河道演算模块提供马斯京根法、马斯京根-康吉法与扩散波演算法[13].近4年来,国外学者对该系统进行了深入研究.例如Yucel等[15]探究了该模型的参数率定和移植方法,发现在无资料流域利用移植的参数和WRF同化数据所得的模拟结果误差较小. Senatore等[16]发现WRF/WRF-Hydro双向耦合系统的模拟结果略优于仅使用WRF模式的结果. Naabil等[17]认为WRF-Hydro模型在降水模拟、洪水预报、水文水资源管理等各个领域都有应用潜力.而在实际应用之前,从水文学角度研究WRF-Hydro模型在我国汇流时间较短的中小流域中的表现及适用性很有必要.
为了评价该模型在中小流域的表现和适用性,本文利用在我国湿润半湿润地区应用较好的新安江模型进行对比分析.新安江模型是经典的概念性半分布式水文模型,也经常作为工具来评价其他模型在水文方面的表现[11-12, 18].例如谢帆等[19]在淮河的息县流域对半分部式水文模型TOPMODEL模型和新安江模型进行对比,发现两者均可达到精度要求.李致家等[20]在新安江的呈村流域分别利用分布式水文模型TOPKAPI模型[21]和新安江模型进行洪水模拟,发现两者精度相差不大,均可用于水文过程的模拟与评价.
本文分别利用陆气耦合模型WRF-Hydro模型和新安江模型对陈河流域4年共16场洪水进行模拟分析,讨论WRF-Hydro模型在研究流域的表现及适用性,以及两个模型在结构、参数、输入输出和模拟结果方面的差异性.考虑到尺度问题,引入土层厚度乘子ZSOILFAC对WRF-Hydro模型的次表面层的厚度进行调节,以合理地提高模拟精度.同时利用新安江模型反推的包气带厚度与调节后的次表面层厚度进行对比分析,进一步论证ZSOILFAC的必要性与合理性.此外,探究WRF-Hydro模型在陈河流域中合适的计算步长,并分析可能的原因,为之后利用单向或双向耦合的WRF-Hydro模型在中小流域进行水文模拟和实时洪水预报提供参考.
1 研究流域与方案 1.1 陈河流域概况选取陕西省渭河右岸一级支流黑河的陈河水文站以上集水区域为研究流域(简称陈河流域).陈河流域地处陕西省中南部,流域面积约为1380 km2,流域内黑河干流河长约为105 km.该流域恰好位于“秦岭-淮河”的北部,为典型的半湿润流域,流域径流深100~500 mm.多年平均降水量为800 mm,且多集中在夏、秋两季,易形成洪水.夏季降雨历时较短,雨强较大;秋季降雨历时较长,雨强较小.该流域地处秦岭褶皱带,地形以山地为主,其中秦岭主峰太白山位于流域西北部.海拔高程约为600~3500 m,落差较大.流域平均坡度为26.73°,其中坡度为10°~50°的面积约占总面积的95.3 %,而20°~40°的面积约占68.2 %.根据美国地质勘探局(USGS)资料[22],陈河流域的表层土壤均为壤土,主要土地利用类型有:稀树草原(60.9 %)、草地(12.3 %)、混合林(8.9 %)和落叶阔叶林(7.9 %).流域内有8个雨量站和1个水文站(图 1).
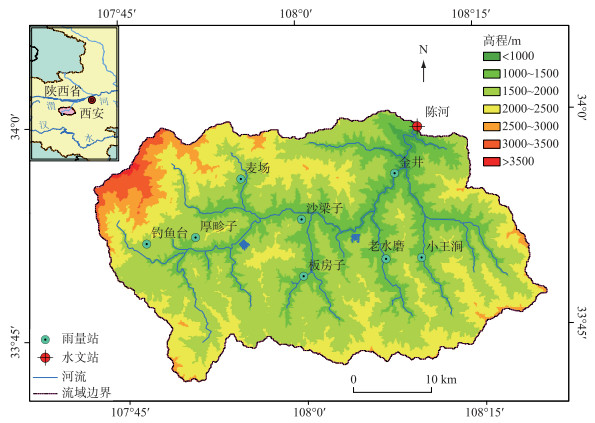
|
图 1 陈河流域水系及水文站的分布 Fig.1 Geographic location of rain/flow stations and main rivers in Chenhe Basin |
流域内可用资料为2003-2012年的日流量资料和以小时为尺度的部分洪水资料,其中洪水事件共计24场.而2003、2006、2010、2011年内有记录的洪水共16场,占总场次的66.7 %,其余年份仅有1~2场.考虑计算成本和效率问题,选择这4年6-10月为研究时段,详细信息见表 1.注意到本研究中所有洪水事件均以1 h时段资料为基础.根据WRF-Hydro模型的相关研究[15-16],将2003和2006两年共6场洪水作为率定期,2010和2011两年共10场洪水作为检验期. WRF-Hydro模型需要预热以获得与实际较为相符的流域初始状态.对于每一年,预热期的跨度为汛期中有记录的第一场洪水的前一个月左右.利用全球再分析资料FNL(Final Operational Global Analysis)驱动WRF模式,所获得的初始状态场视为WRF-Hydro模型预热期的初始状态场.其中FNL资料来源于https://rda.ucar.edu/.相对于假设的模型状态场,这种方法可以获得相对准确的初始场,适当地缩短预热期长度,提高计算效率. WRF-Hydro模型所需的土地利用、土壤类型和反射率等均源于WRF模式前处理系统WPS的数据库http://www2.mmm.ucar.edu/wrf/.此外该模型需要的高分辨率数字高程资料源自http://www.gscloud.cn/.
| 表 1 预热期、模拟期和研究洪水事件信息 Tab. 1 The information of spin-up period, simulated period and research events |
由于WRF-Hydro模型是基于陆面模式的水文模型系统,需要大量的气象强迫数据,包括近地面的气温、气压、比湿、风速、向下长波辐射、向下短波辐射和降水率(雨强).一方面,陈河流域目前没有可以获得以上全部资料的观测站点,这为驱动模型带来很大困难.而全球陆面数据同化系统(GLDAS)提供全球范围内较大尺度的气象再分析资料,为资料匮乏地区提供宝贵的强迫数据.本文利用分辨率为3 h,0.25°的GLDAS资料,时间上经线性插值,空间上经双线性插值[23],得到陈河流域1 h、1 km的强迫数据场.另一方面,在洪水模拟中,降雨的时空分布往往起很大的作用.因此,利用反距离权重法(以下简称IDW法)对雨量站观测数据进行空间插值,得到1 h、1 km的降雨时空分布场.将处理后的强迫数据场中的非降雨场与利用IDW法插值后的降雨场结合,得到最终的模型强迫数据.
新安江模型的主要输入是站点的降雨数据和蒸发皿观测数据.蒸发皿蒸发数据源于流域外黑峪口站(位于流流域出口东北方向约9 km处),经换算得到流域蒸发能力.对于雨量数据,将整个流域按照每个自然子流域有且仅有一个观测站的原则进行划分.在每个自然子流域内,对IDW法插值后的降雨场求面平均值作为模型输入,以保证两个模型降雨的一致性.
1.3 评价指标本文选取径流深误差(AErd)、洪峰相对误差(REfp)、峰现时间误差(AEpt)及纳什系数(NSE)作为评价模型表现的主要指标,具体计算方法见文献[24].在模拟和实测过程之间,AErd反映两者洪量的差异,REfp与AEpt则综合评价了模型在洪峰方面的表现,NSE表示模拟与实测过程在线型上的拟合程度.此外计算合格洪水数与总洪水数之比(即合格率)以整体衡量模型的表现.当某场洪水的径流深误差小于径流深许可误差(PAErd)时,则径流深预报合格;当洪峰相对误差在20 %以内时,则洪峰预报合格[24].其中PAErd是实测径流深的函数:当实测径流深小于15 mm时,PAErd取3 mm;当实测径流深大于15 mm小于100 mm时,PAErd取实测径流深的20 %;当实测径流深大于100 mm时,PAErd取20 mm[25].此外,在陈河流域内,若相邻时刻流量增量大于10 m3/s,且后续时刻至洪水极大值处流量持续增加,则将第一个时刻定义为洪水起涨时刻.模拟过程与实测过程的洪水起涨时刻的差值定义为洪水起涨点误差,单位为h.
2 模型与参数 2.1 WRF-Hydro模型 2.1.1 模型简介WRF-Hydro模型是美国国家气象研究中心(NCAR)开发的陆气耦合模型系统,主要包括不同尺度的陆面模式和汇流模块[13].陆面模式的相关过程均在尺度较大的网格(如1 km,简称陆面模式网格)进行,如下渗等;水文汇流的相关过程均在尺度较小的网格(如100 m,简称汇流网格)进行,如地表径流等.在模型运行过程中,变量或参数需要在两个不同尺度间相互转换,具体方法见文献[13]和[23].模型的本质是在陆面模式的基础上添加汇流模块以更精细地考虑水文过程.本文中WRF-Hydro模型各个部分的选取方案见表 2.
| 表 2 WRF-Hydro模型系统的主要物理过程配置方案* Tab. 2 The main physical process configuration scheme of WRF-Hydro modeling system |
Noah陆面模式主要模拟大气下层、植被冠层和浅层土层之间的水量和能量的交互过程[2, 27].冠层截留[26]、超渗地面径流、土壤含水量和蒸散发均在陆面模式网格中计算. Noah模式的浅层土层被称为次表面层,主要计算水量能量的分布情况.其总厚度为2.0 m,共4层,每层默认厚度由上至下分别为0.1、0.3、0.6、和1.0 m.当雨强大于最大下渗率(式1)时,地表出现超渗地面径流.
| $ {I_{{\rm{max}}}} = {P_{\rm{d}}}\frac{{{D_{\rm{x}}}\left[ {1 - {{\rm{e}}^{ - kdt{\delta _{\rm{i}}}}}} \right]}}{{{P_{\rm{d}}} + {D_{\rm{x}}}\left[ {1 - {{\rm{e}}^{ - kdt{\delta _{\rm{i}}}}}} \right]}}\;\;\;kdt = kd{t_{{\rm{ref}}}}\frac{{{K_{\rm{s}}}}}{{{K_{{\rm{ref}}}}}} $ | (1) |
式中,Imax为最大下渗率(m/s),Pd为经冠层截留后的雨强(m/s),Dx为次表面层总缺水量(m/s),Ks为饱和水力传导度(m/s),Kref=2.0×10-6m/s,kdtref为可调参数,δi为与时段转换有关的系数,δi与Dx的计算详见文献[26].次表面层的湿度和温度分别由Richard方程和热扩散方程计算. Noah模式的总蒸发分为地表直接蒸发、冠层截留量蒸发和植物根系散发3部分,蒸发能力由Penman公式计算[27].
汇流网格主要计算次表面径流(即壤中流)、坡面流、地下径流和河网汇流等.利用达西定律计算侧向饱和壤中流:
| $ {Q_{\rm{i}}} = \frac{{{K_{\rm{s}}} \cdot d \cdot w}}{n}{\left( {1 - \frac{h}{d}} \right)^n}\left( {\sum\limits_x {{\alpha _x}} + \sum\limits_y {{\alpha _y}} } \right) $ | (2) |
式中,Qi为饱和壤中流的流量(m3/s),αx和αy分别为x和y方向的水面坡度,d为土层厚度(m),w为网格边长(m),h为水面深度(m),n为可调参数,默认为1.在计算步长Δt内,根据水量平衡计算当前网格的水深变化Δh.模型认为每个网格的地表积水由3部分构成:超渗地面径流、饱和地面径流及与其他网格的水量交换.当且仅当网格水深hs超过参数地表积水深hret时,出现可自由流动的地表径流.地表径流由浅水波的扩散波方程计算,详见文献[6, 13].其中,单宽流量与糙率的关系由曼宁公式计算:
| $ q = \frac{1}{{{n_{{\rm{ov}}}}}}h_{\rm{s}}^{\frac{5}{3}}S_{\rm{f}}^{\frac{1}{2}} $ | (3) |
式中,q为单宽流量(m2/s),nov为坡面的曼宁糙率,Sf为摩阻坡度.使用概念性水箱模型描述流域对次表面层以下基流(即地下径流)的调蓄作用,该水箱的水深并不代表真实含水层中的水深[13].水箱的入流量为次表面层最下层向下的渗透量,出流量采用经验蓄泄关系计算,详见文献[13].河道形状均采用等腰梯形,其底宽、边坡系数、糙率为河道等级的函数,在相关参数文件中有预定值,也可在随后过程中率定.河道演算采用一维扩散波方程:
| $ Q = - \frac{1}{{{n_{{\rm{ch}}}}}}{\mathop{\rm sgn}} \left( {\frac{{\partial H}}{{\partial x}}} \right)A \cdot {R^{\frac{2}{3}}}\sqrt {\left| {\frac{{\partial H}}{{\partial x}}} \right|} $ | (4) |
式中,A为过水断面面积(m2),Q为河道流量(m3/s),nch为河道曼宁糙率,H为河道水面高程(m),R为水力半径(m),sgn(·)为符号函数.
2.1.2 参数率定WRF-Hydro模型可调参数较多,主要分为陆面网格参数(如土层的田间持水量SMCREF)和汇流网格参数(地表糙率乘子参数).模型中多利用乘子参数在整个空间范围内对某些属性值(如地表糙率)进行合理地等比缩放.考虑到次表面层是针对大尺度的陆面或天气模式而设计的,其厚度可能不适用于中小流域的洪水模拟.因此,本文借鉴其他乘子参数,引入土层厚度乘子ZSOILFAC.利用该参数在合适范围内等比例地对整个次表面层厚度进行调节.相比于文献[16]将次表面层厚度直接定为0.05、0.2、0.45和0.8 m,经过ZSOILFAC修改的厚度更加合理.综上,本文选取5个主要参数进行率定,分别是土层厚度乘子ZSOILFAC、渗透参数REFKDT(kdtref)、地表截流深乘子RETDEPRTFAC(hret的乘子参数)、地表糙率乘子OVROUGHRTFAC(nov的乘子参数)和河道曼宁糙率乘子MANNFAC(nch的乘子参数).其中,前3个参数主要控制径流分配和洪水水量,后两个参数主要控制洪峰和洪水过程线的形状.
调参的目的是使率定期内尽可能多的模拟洪水与实测过程充分接近,使AErd和REfp较小,同时使NSE较大.考虑到计算成本,对主要参数使用手动逐步逼近法调参,以避免消耗大量时间[15].手动逐步逼近法是指对某一参数在合理的范围内以适当的步长分别驱动模型,结合指标定量评价模拟结果,从而确定最佳的参数. WRF-Hydro模型在陈河流域的参数率定结果见表 3.
| 表 3 WRF-Hydro模型系统的主要参数及率定数值 Tab. 3 The main parameters of WRF-Hydro modeling system and theirs values |
三水源新安江模型是经典的概念性半分布式水文模型,在我国湿润和半湿润地区有较好的应用.模型结构包含三层蒸散发、蓄满产流、三水源划分和流域汇流4个模块[6, 8].鉴于新安江模型在陈河流域有较好的应用,本文使用该模型对16场洪水进行模拟,并与WRF-Hydro模型的结果比较,评价后者的表现与适用性.利用自然子流域分割法将陈河流域分为9块,每块有且只有1个雨量/水文站,以此考虑降水的空间差异性.新安江模型的主要参数率定结果见表 4.
| 表 4 新安江模型的主要参数及率定数值 Tab. 4 The main parameters of XAJ Model and theirs values |
WRF-Hydro模型是基于物理的分布式水文模型系统,可定量考虑下垫面属性的空间差异,并与WRF模式有很好的相容性.新安江模型虽然是概念性半分布式水文模型,但对实际过程进行合理概化,使得其在土壤含水量较高的地区得以广泛应用.两个模型的结构对比结果见表 5.
| 表 5 WRF-Hydro模型和新安江模型结构对比* Tab. 5 The structure comparison between WRF-Hydro model and XAJ model |
鉴于在陈河流域内对WRF-Hydro模型与新安江模型模拟结果进行对比的目的,本部分以率定期和检验期为基础分别对它们的模拟结果和评价指标进行分析.此外发现文献[13]推荐的WRF-Hydro模型的计算步长不适用于陈河流域,需要重新寻找使模拟结果稳定的计算步长,并分析造成这一现象的可能原因.本研究中WRF-Hydro模型为3.0版本,陆面模式网格分辨率为1 km,汇流网格为100 m.如无特殊声明,本文所涉及单位及符号采用国际单位制(SI).
3.1 模型计算步长选取对计算结果的影响由于需使用差分格式或一阶牛顿迭代法对坡面浅水波方程组与河道的扩散波方程组求近似解,所以WRF-Hydro模型的汇流网格的计算步长选取是影响模型计算稳定性的重要因素.该计算步长的选取往往与网格空间分辨率有关,且对模拟结果的稳定性影响较大.尤其对水深较深的河道洪水演算而言,模拟结果受时间计算步长影响更大[13].为了保证模型的计算稳定性,WRF-Hydro模型用户手册[13]给出了不同汇流网格分辨率对应的计算步长.如100 m的汇流网格对应的时间计算步长为6 s.然而,经数值实验发现该时间步长并不适用于陈河流域,如图 2中红色虚线所示.因此,需要在建议的基础上进一步缩小计算步长.以两场模拟洪水060926和110804为例,图 2描述这两场洪水的计算步长分别取6、3和1 s时,WRF-Hydro模型的模拟结果.当Δt=6 s时,两场洪水在洪峰段与退水段均出现数值波动现象;Δt=3 s时退水段模拟结果显著提升,但在洪峰段仍偶尔存在波动;Δt=1 s时洪水过程表现平滑.注意到110804洪水在Δt取3 s和6 s时相对于1 s洪峰整体向后坦化,随后又于8月5日20:00时陡落,但洪量整体保持一致.这说明若Δt选取不合适,甚至可能对洪峰模拟造成较大偏差,增加模型不确定性.
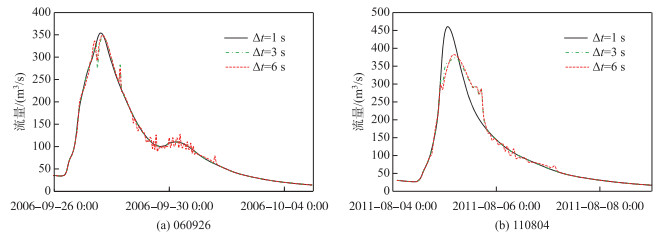
|
图 2 模型计算步长Δt的选取(模拟结果输出步长:1 h) Fig.2 The determination of values of calculation step Δt (the time step of simulation results: 1 h) |
地形起伏较大、坡度和比降较陡,可能是默认时间空间步长关系在陈河流域不适用的主要原因.当坡度或河道比降较大时,导致重力沿坡面的分力对洪水波运动影响较大.水量相同的情况下导致流速变大,洪水波传播速度c可能变快.根据Courant数的定义Cn=cΔt/Δx,如果波速增大且保持空间分辨率Δx不变,则计算步长Δt需要适当减小以保证Courant数数值不变.进一步说明在陈河流域适当减小计算步长的必要性.综上,在陈河流域中利用当前版本的WRF-Hydro模型进行洪水模拟时,若要与100 m的汇流网格相对应,计算步长须取1 s才能保证模型计算的稳定性.
3.2 率定期结果分析本研究中率定期共由6场洪水构成,即2003年的3场和2006年的3场,两个模型的评价指标结果见表 6. WRF-Hydro模型的径流深合格率和洪峰合格率均为66.7 %,而新安江模型均为83.3 %.在2003年WRF-Hydro模型的模拟效果整体较好,NSE均值为0.91,而2006年模拟效果欠佳,NSE均值仅为0.03.总体而言,率定期内WRF-Hydro模型各场洪水均方根误差均值为49.3 m3/s,新安江模型为53.3 m3/s.在66.7 % (6场中的4场)的洪水中,前者的均方根误差小于后者.说明前者的模拟结果误差较小,且NSE表现尚可;后者模拟效果相对稳定.选取030828、030916、060827、060925为代表洪水,其过程线如图 3所示.
| 表 6 WRF-Hydro模型和新安江模型在率定期的模拟结果* Tab. 6 The simulation results of WRF-Hydro model and XAJ model in calibration period |
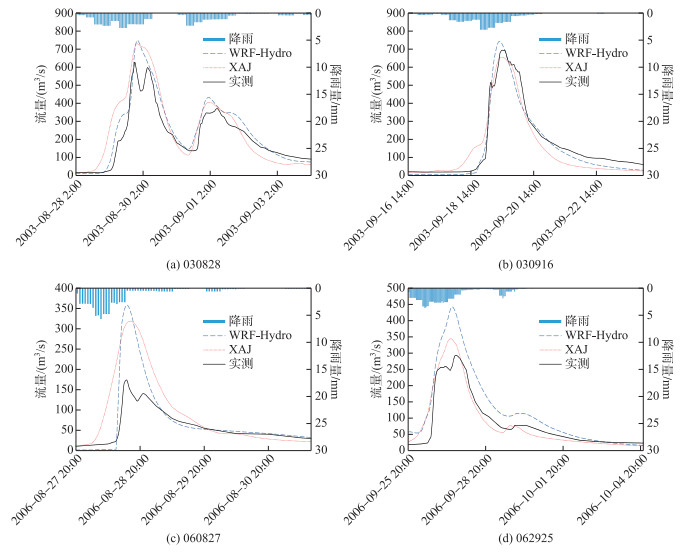
|
图 3 两个模型在率定期内4场代表洪水的对比(输入输出数据时间步长:1 h) Fig.3 The simulation results of four events in calibration period of two models (the time step of data: 1 h) |
030828和030916号洪水的径流深和洪峰均合格,而且两个模型的模拟效果较好. WRF-Hydro模型模拟洪峰误差略大于新安江模型,但AErd和NSE整体优于新安江模型.对于多峰洪水030828(图 3a),由起涨段至第一个洪峰处,WRF-Hydro模型与观测过程较为贴合,相关系数为0.9578;而新安江模型模拟过程出现较早的抬升,相关系数为0.9409.两个模型模拟洪峰偏大15 % ~20 %,表现较接近.最后的退水段,新安江模型退水幅度过大,模拟水量偏小.对于单峰洪水030916(图 3b),由起涨段至洪峰处,WRF-Hydro模型仍然在起涨时间和趋势上模拟较好,相关系数为0.9834;而新安江模型再次出现较早抬升,相关系数为0.9656.洪峰处WRF-Hydro模型模拟洪峰偏大7.6 %;而新安江模型偏小7.3 %.退水阶段与前场洪水相似,新安江模型低估退水段水量.综合两场洪水发现WRF-Hydro模型对洪水过程的起涨过程和退水过程的模拟较好,其中洪水起涨点与实测过程几乎重合;而新安江模型的洪水起涨点比实测过程提前8 h,且有高估涨洪段水量、低估退水段水量的特点.
对于洪水060827,结合图 3c发现,两个模型均未成功模拟洪水过程.根据洪水起涨点误差和退水段的相关系数,WRF-Hydro模型在洪水起涨时刻和退水过程与实测过程相当接近,但模拟洪峰大幅偏大.虽然新安江模型对洪峰高估程度略小于WRF-Hydro模型,但其对整个洪水过程的模拟效果很不理想.对于洪水060925(图 3d),WRF-Hydro模型的初始流量为56.8 m3/s,是实测流量(18.0 m3/s)的3倍;新安江模型的初始流量为26.6 m3/s,是实测流量的近1.5倍.在整个洪水过程中,WRF-Hydro模型模拟的洪量和洪峰显著偏大;新安江模型在起涨段和洪峰处偏大,在退水段偏小,使径流深误差较小,仅为0.7 mm.这两场洪水模拟效果偏差的原因将在第4.3节讨论.
综合率定期所有洪水,发现虽然WRF-Hydro模型的径流深合格率低于新安江模型,但在4场径流深模拟较好的洪水中(030828、030903、030916和060903),有3场NSE高于新安江模型.而且该模型善于刻画洪水的细节,例如率定期洪水起涨点误差均在3 h之内,而新安江模型在4~10 h间.新安江模型整体表现较稳定,有较高的径流深合格率和洪峰合格率,66.7 % (6场中的4场)的NSE大于0.8.事实上,结合图 3可知,新安江模型在洪水起涨段和退水段均存在偏差,起涨段为正偏差,退水段为负偏差.因此,在计算整体的径流深误差时部分偏差被抵消,可能使其在洪量方面表现较好.
3.3 检验期结果分析检验期由2010年和2011年共10场洪水组成,两个模型的评价指标结果见表 7. WRF-Hydro模型的径流深合格率和洪峰合格率均分别为60.0 %和50.0 %,而新安江模型均为50.0 %.率定期内WRF-Hydro模型的均方根误差均值为115.7 m3/s,新安江模型为80.0 m3/s.其中60 % (10场中的6场)的WRF-Hydro模型的均方根误差小于新安江模型,且这些洪水多为两个指标均合格的洪水.在两个指标均合格的洪水中,WRF-Hydro模型的均方根误差均值为54.8 m3/s,新安江模型为68.6 m3/s,且前者的AErd、REfp和NSE整体优于后者.其他洪水多为不合格洪水,其中前者的均方根误差的均值为207.1 m3/s,后者为97.1 m3/s.说明WRF-Hydro模型在洪峰洪量表现好的洪水中误差较小,NSE较高;在其他洪水中,偏离程度较明显.新安江模型对峰现时间的刻画较好,表现相对稳定;对洪峰洪量误差较大的洪水模拟效果也较差,但优于WRF-Hydro模型.选取100812、100823、110728、110909为代表洪水,其过程线如图 4所示.
| 表 7 WRF-Hydro模型和新安江模型在检验期的模拟结果* Tab. 7 The simulation results of WRF-Hydro model and XAJ model in validation period |

|
图 4 两个模型在检验期内4场代表洪水的对比(输入输出数据时间步长:1 h) Fig.4 The simulation results of four events in verification period of two models (the time step of data: 1 h) |
两个模型对100823和110909号洪水模拟结果较好(图 4a,图 4b).在洪水100823的起涨段,WRF-Hydro模型与观测过程较为贴合,相关系数为0.9876;新安江模型高估洪水的初始状态,从而模拟的起涨过程水量偏大,相关系数为0.9285.两个模型对洪峰模拟效果都很出色,WRF-Hydro模型的REfp为2.1 %,新安江模型的REfp为-1.9 %.退水段,WRF-Hydro模型表现出色,相关系数为0.9981;新安江模型在退水前期和后期略微高估洪量,在退水中期低估洪量,相关系数为0.9872.对于洪水110909,WRF-Hydro模型和新安江模型的NSE分别达到了0.96和0.92,模拟结果相当出色.在洪水起涨段,WRF-Hydro模型受前场洪水退水过程影响,模拟流量过程偏大,相关系数为0.9819;新安江模型对洪量模拟较好,相关系数为0.9468. WRF-Hydro模型模拟洪峰较准确,REfp和AEpt分别为9.0 %和0 h.在退水段,WRF-Hydro模型仍与观测过程较接近,相关系数为0.9965;而新安江模型低估退水中后期的洪量.此外,WRF-Hydro模型甚至能较准确模拟出9月14日2:00时的小洪水波,表现该模型在退水段的优秀性能,这可能是该模型可利用的信息较丰富导致的.
两个模型对另外两场洪水的模拟效果欠佳. 100812和110728号洪水与060827号洪水相似,WRF-Hydro模型模拟的洪量和洪峰仍然大幅偏大;新安江模型也大幅偏大,但偏离程度小于WRF-Hydro模型.这两场洪水模拟效果偏差的原因也将在第4.3节讨论.
综合检验期所有洪水,发现WRF-Hydro模型的径流深合格率和洪峰合格率平于甚至优于新安江模型.在多数两个指标均合格的洪水中(100820、100822和110909),前者的均方根误差小于后者;在其他洪水中,前者模拟过程的误差很大. WRF-Hydro模型检验期起涨时刻误差均值为1.3 h,而新安江模型为5 h;在70 % (10场中的7场)的洪水中,前者模拟的退水段的相关系数大于后者.说明WRF-Hydro模型善于模拟洪水的细节;新安江模型在整体上的表现非常稳定,很少出现大幅度的偏差.
3.4 模拟结果对比在所有洪水事件中,WRF-Hydro模型的径流深合格率和洪峰合格率分别为62.5 %和56.3 %,均方根误差均值为90.8 m3/s;新安江模型径流深合格率和洪峰合格率均为62.5 %,均方根误差均值为70.0 m3/s.这说明WRF-Hydro模型的径流深和洪峰合格率平于或略低于新安江模型,且均方根误差均值稍大.在径流深和洪峰指标均合格的洪水中(030828、030902、030916、060903、100820、100822和110909;共7场),WRF-Hydro模型均方根误差均值为43.5 m3/s,NSE的均值为0.87,其中在57.1 % (7场中的4场)的事件中,NSE达到0.9以上;新安江模型均方根误差均值为55.4 m3/s,NSE的均值为0.84,其中在42.9 % (7场中的3场)的事件中,NSE达到0.9以上.在其他洪水中,WRF-Hydro模型均方根误差均值为127.6 m3/s;新安江模型均方根误差均值为81.3 m3/s.由此发现WRF-Hydro模型在两个指标均合格的洪水中均方根误差均值比新安江模型小21.5 %,而在其他洪水中,前者均方根误差均值比后者大56.2 %.
在两个指标均合格的洪水事件中,可能WRF-Hydro模型需要的资料信息较多,相对于新安江模型更加善于模拟洪水过程线的细节,使模拟洪水的误差较小,NSE较高.但是,在其他表现效果较差的事件中,大量信息中的不确定性可能对WRF-Hydro模型的模拟过程产生较大影响,使模拟洪水的偏离幅度较大.新安江模型反而因为未使用大量的资料,模拟过程的偏离幅度小于WRF-Hydro模型.综上,WRF-Hydro模型可以较好地模拟洪水过程,刻画洪水细节,但可能对资料质量较为敏感.新安江模型误差整体较小,模拟效果较稳定.此外,WRF-Hydro模型在洪水起涨处模拟较好,其涨洪点误差均值为-1 h,而新安江模型为-5.7 h.这可能是由于WRF-Hydro模型利用地形、糙率等信息获得了更为精细的模拟结果.
4 对比讨论本部分主要从模型参数和输入输出信息对WRF-Hydro模型和新安江模型进行对比讨论,最后对模拟效果较差洪水进行分析.
4.1 参数对比WRF-Hydro模型可调参数较多,主要包含植被参数(如冠层持水能力等)、土壤特性参数(如水力传导度)、下垫面参数(如地表糙率等)及汇流参数(如河道糙率等)[15, 29].三水源新安江模型约有17个参数,主要分为产流参数(如流域平均张力水容量等)、蒸散发参数(如流域蒸散发折算系数等)、分水源参数(如表层自由水蓄水容量等)和汇流参数(如河网消退系数等)[6, 8, 24].
4.1.1 产流参数两个模型在概化流域土壤时有较大差异.对于大尺度的天气或陆面模式,通常只考虑包气带中对天气过程影响较大的部分.如在Noah陆面模式中,认为地表至地下2 m之间的土层对天气过程影响较显著,而2 m以下的土层对模拟的影响可忽略不计.而WRF-Hydro模型是基于Noah陆面模式发展而来,继承了这一特点,即只考虑近地面2 m深的土层内水量分配情况,其余土层内的水视为地下径流.但是对于小尺度的水文模拟而言,默认的次表面层厚度可能不适用于中小流域.需要经过土层厚度乘子ZSOILFAC对其进行调节,以控制模拟过程中土层的含水量.此外,几乎每层土层内的土壤水都会受渗透率REFKDT和蒸散发影响,各层水量平衡利用Richard方程计算[26-27].而对于新安江模型,其着重研究包气带中的水量平衡,并将土壤水划分为张力水和表层自由水,分别由张力水蓄水容量WM和自由水蓄水容量SM控制. WM影响土壤含水量和产流计算,SM影响地表径流、壤中流、地下径流3种径流成分的比例[6, 8].
此外,研究发现经过ZSOILFAC调节后的次表面土层厚度和新安江模型反推的包气带厚度有较好的关系.后者的计算过程如下.由于张力水蓄水容量存在空间差异,故对于任意汇流网格,假设其张力水蓄水容量为WM(i, j),且可由式(5)估计[6]:
| $ {W_{\rm{M}}} = \left( {{\theta _{{\rm{fc}}}} - {\theta _{{\rm{wp}}}}} \right){L_{\rm{a}}} $ | (5) |
式中,θfc和θwp分别为田间持水量和凋萎含水量,均为体积含水量,La为当前网格的包气带厚度(mm).根据(5)式,利用WM的最大值和最小值即可反推出包气带厚度的分布范围. WM的最大值为流域最大张力水蓄水容量Wmax,可由式(6)[6, 24]计算:
| $ {W_{\max }} = \left( {1 + B} \right){W_{\rm{M}}} $ | (6) |
式中,B为张力水蓄水容量曲线的指数,取0.3;WM取180 mm(表 4).由式(6)可知,Wmax=234 mm.根据(5)式及壤土的属性(θfc=0.3, θwp=0.1),与Wmax相对应的La的最大值为1.17 m.根据流域变动产流理论[6, 9],在湿润地区河道附近包气带较薄,河流上游坡地的包气带相对较厚[30-31].故假设河道附近网格几乎饱和,相应的包气带厚度为0.综上,由新安江模型反推的流域包气带厚度分布在0~1.17 m内,均值为0.8 m.而次表面层经ZSOILFAC调节后,厚度为0.4 m,与包气带厚度均值接近.由此说明,经ZSOILFAC作用后的次表面层厚度与新安江模型反推所得的包气带厚度有较好的一致性,进一步说明在中小流域中利用ZSOILFAC调节次表面层厚度的合理性与必要性.
4.1.2 汇流参数WRF-Hydro模型主要利用扩散波方程,并结合OVROUGHTFAC和MANNFAC两个参数考虑地表和河道的调蓄作用;次表面径流主要可以由侧向水力传导度LKSATFAC调节[16];地下径流调蓄作用可利用概念水箱模型[13]调节.新安江模型在流域汇流方面主要利用线性水库考虑流域调蓄作用,如壤中流消退系数(CI)和地下水消退系数(CG);子流域河网汇流利用滞后演算法,如CS和滞时L[6, 24]. WRF-Hydro模型的OVROUGHTFAC和MANNFAC与新安江模型的CS均可以调整洪水形状,有相似的作用.
4.2 输入输出信息对比两个模型在各个过程的输入输出信息见表 8.作为基于物理的分布式水文模型,WRF-Hydro模型需要大量的气象强迫和下垫面属性数据,对资料依赖性和计算机性能要求较高.基于高质量的强迫数据及高性能服务器,该模型可以很好地描述各个水文气象变量的空间不均匀性,获得较精细的输出结果.作为概念性半分布式水文模型,新安江模型合理地简化实际产汇流情况,如分别利用自然子流域分割法和蓄水容量曲线考虑降水和土壤水的空间分布不均匀性[6, 8, 24].该模型能在保证一定模拟精度的基础上降低计算量.但正是由于对实际过程简化,无法获得精细土壤水空间分布及各个河道的流量.两个模型输入信息量和计算量的巨大差别导致计算精度存在一定差别.
| 表 8 WRF-Hydro模型和新安江模型输入输出对比 Tab. 8 The inputs and outputs of WRF-Hydro model and XAJ model |
表 9对模拟结果较差的洪水进行归纳.根据成因不同,可将洪水分为两类:060827、100812和110728为第1类,060925和110731为第2类.对于第1类洪水,两个模型模拟的洪峰和洪量均偏大,而实测径流量与降雨量的比值较小,均小于0.2,说明大部分降雨被流域保持.可能有以下两点原因:1)因为这类洪水事件前期缺少降水,洼地、库塘闸坝未蓄满,使这类洪水的实测值较小. 2)由于缺少有效降水,可能导致土层相对干燥、腐殖质层松软、地下水位偏低、包气带偏厚.进行参数率定时未考虑这些洪水事件产流的差异性,使模型低估了实际的下渗率和土壤调蓄能力,导致模拟过程偏大.此外,该类型洪水在率定期内只包含060827,针对该问题考虑较少.综上,实测值较小且模拟过程偏大,导致两个模型模拟的径流量与洪峰偏大. WRF-Hydro模型利用更多的降水空间分布的下垫面信息,使其更易受影响.
| 表 9 WRF-Hydro模型和新安江模型主要不合格洪水统计* Tab. 9 The main information of unqualified flood events in WRF-Hydro model and XAJ model |
第2类洪水的实测径流量与降雨量的比值均大于0.35.虽然两个模型模拟的洪水过程偏大,但新安江模型的表现整体较好.对于洪水060925,WRF-Hydro模型的参数可能低估了洪水开始前的包气带厚度、下渗率和糙率,导致洪水初始时刻模拟流量偏大近3倍.当降雨达到极值后,仍以较小的雨量持续近5天,进一步促使WRF-Hydro模型模拟结果偏高.而新安江模型的初始状态源于日模型,对前期水量和径流成分模拟较好.洪水110731与洪水060925的原因相似.
总体而言,上述洪水模拟效果较差的可能原因是流域初始状态和其他洪水有较大差异,如包气带厚度、土壤含水量、下渗率、地表糙率和河道糙率等.这种情况下仍使用相同的参数,可能导致两个模型模拟的径流量与洪峰偏大.此外,WRF-Hydro模型需要大量的资料输入,这些资料的误差可能在模拟流域状态和洪量过程时传递,增加不确定性.新安江模型需要资料较少,由资料误差引起不确定性的概率稍低.改善这类问题主要有3点:1)利用高质量高空间分辨率的资料或融合数据驱动WRF-Hydro模型,提高模拟结果的精度与可靠性;2)尽可能地延长预热期,把握好计算成本和预热期长度的平衡;3)增加率定期洪水场次数,在计算成本和率定期洪水场次数之间寻找平衡.
5 结论与展望在半湿润区中小流域陈河流域中,利用GLDAS非降水数据场与IDW降雨场的结合数据驱动WRF-Hydro模型,利用站点的降雨数据和蒸发皿观测数据驱动新安江模型.探究WRF-Hydro模型在陈河流域的表现及适用性,对比分析两个模型的结构、主要参数、输入输出和模拟结果,并对模拟效果较差洪水进行讨论.研究表明:
1) 在陈河流域中,需要在建议的基础上进一步缩小计算步长的值,以满足稳定性的要求.本文中汇流网格的空间分辨率为100 m,对应的计算时间步长应取1 s.原因可能是陈河流域地形起伏较大、坡度和比降较陡.
2) 借鉴WRF-Hydro模型的其他乘子参数,在中小流域中引入土层厚度乘子ZSOILFAC,对整个次表面层的厚度等比缩放,使次表面层与包气带建立联系.经过ZSOILFAC调节后的次表面土层厚度和新安江模型反推的包气带厚度空间分布场有较好的关系,进一步说明在中小流域中利用ZSOILFAC调节次表面层厚度的合理性与必要性.
3) WRF-Hydro模型能够较好地模拟实测洪水过程,捕捉洪水的细节.其涨洪点误差均值为-1 h,比新安江模型小82.5 %.这可能是WRF-Hydro模型可利用大量信息,提高洪水模拟效果,但同时可能带来较大的不确定性.该模型与新安江模型性能相近,表现出在半湿润地区中小流域内实际应用的潜力.
4) 对于所有洪水,WRF-Hydro模型的径流深合格率和洪峰合格率分别为62.5 %和56.3 %,均方根误差均值为90.8 m3/s;新安江模型均为62.5 %,均方根误差均值为70.0 m3/s.说明WRF-Hydro模型的径流深和洪峰合格率平于或略低于新安江模型,且均方根误差均值稍大;新安江模型整体误差小于WRF-Hydro模型,模拟效果相当稳定.
5) 在径流深和洪峰指标均合格的洪水事件中,WRF-Hydro模型均方根误差均值比新安江模型小21.5 %;但在其他事件中,前者均方根误差均值比后者大56.2 %.可能是WRF-Hydro模型对信息质量较为敏感,信息质量较好时善于模拟洪水细节;反之,资料的不确定性以及参数与某些洪水实际情况不匹配将对模拟过程产生较大影响.
本研究使用GLDAS资料的分辨率相对较粗,下一步将对多种资料或组合资料进行对比研究,如WRF模拟资料、降水融合资料等,以寻找更适用于WRF-Hydro模型的资料,为之后的实时预报提供理论基础.研究洪水场次较少,后期研究需要适当增加洪水场次.而针对讨论部分提出的率定参数可能与某些洪水实际状态不匹配的问题,需要在预热期长度、率定期洪水场次数和计算成本之前寻找平衡. WRF-Hydro模型作为新一代陆气耦合的分布式水文模型系统,在水文模拟、洪水预报和水资源评估等方面有较大应用的潜力,同时也为水文气象研究提供新的思路.
致谢: 感谢NCAR的喻炜博士对WRF-Hydro模型参数调整的指导与建议.
| [1] |
Li MS, Li S, Li YH. Analysis of flood disaster in the past 50 years in China. Chinese Journal of Agrometeorology, 2004, 25(1): 38-41. [李茂松, 李森, 李育慧. 中国近50年洪涝灾害灾情分析. 中国农业气象, 2004, 25(1): 38-41. DOI:10.3969/j.issn.1000-6362.2004.01.011] |
| [2] |
Wang CH, Long X, Yang Y. Atmospheric numerical model and simulation. Beijing: Meteorology Press, 2011: 1-293. [王澄海, 隆霄, 杨毅. 大气数值模式及模拟. 北京: 气象出版社, 2011: 1-293.]
|
| [3] |
Hong SY, Lee JW. Assessment of the WRF model in reproducing a flash-flood heavy rainfall event over Korea. Atmospheric Research, 2009, 93(4): 818-831. DOI:10.1016/j.atmosres.2009.03.015 |
| [4] |
Syed TH, Famiglietti JS, Rodell M et al. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resources Research, 2008, 44(2): 339-356. DOI:10.1029/2006wr005779 |
| [5] |
Caldwell P, Chin HNS, Bader DC et al. Evaluation of a WRF dynamical downscaling simulation over California. Climatic Change, 2009, 95(3/4): 499-521. DOI:10.1007/s10584-009-9583-5 |
| [6] |
Li ZJ, Kong FZ, Wang D et al. Modern hydrological modelling and forecasting techniques. Nanjing: Hohai University Press, 2010: 29-104. [李致家, 孔凡哲, 王栋等. 现代水文模拟与预报技术. 南京: 河海大学出版社, 2010: 29-104.]
|
| [7] |
Huo WB, Li ZJ, Li QL. Hydrological models comparison and ensemble forecasting in semi-humid watersheds. J Lake Sci, 2017, 29(6): 1491-1501. [霍文博, 李致家, 李巧玲. 半湿润流域水文模型比较与集合预报. 湖泊科学, 2017, 29(6): 1491-1501. DOI:10.18307/2017.0621] |
| [8] |
Zhao RJ. Hydrological modeling of watershed. Beijing: Water Resources and Electric Power Press, 1984: 106-130. [赵人俊. 流域水文模拟. 北京: 水利电力出版社, 1984: 106-130.]
|
| [9] |
Beven KJ, Kirkby MJ. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d'appel variable de l'hydrologie du bassin versant. Hydrological Sciences Bulletin, 1979, 24(1): 43-69. DOI:10.1080/02626667909491834 |
| [10] |
Hao CF, Jia YW, Wang H. Atmospheric and hydrological models' coupling and application in flood forecasting of the Weihe Basin. Journal of Hydraulic Engineering, 2012, 43(9): 1042-1049. [郝春沣, 贾仰文, 王浩. 气象水文模型耦合研究及其在渭河流域的应用. 水利学报, 2012, 43(9): 1042-1049.] |
| [11] |
Gao B, Yang DW, Gu XQ et al. Flood forecast of Three Gorges reservoir based on numerical weather forecast model and distributed hydrologic model. Journal of Hydroelectric Engineering, 2012, 31(1): 20-26. [高冰, 杨大文, 谷湘潜等. 基于数值天气模式和分布式水文模型的三峡入库洪水预报研究. 水力发电学报, 2012, 31(1): 20-26.] |
| [12] |
Lu GH, Wu ZY, Lei W et al. Application of a coupled atmospheric-hydrological modeling system to real-time flood forecast. Advances in Water Science, 2006, 17(6): 847-852. [陆桂华, 吴志勇, 雷 Wen等. 陆气耦合模型在实时暴雨洪水预报中的应用. 水科学进展, 2006, 17(6): 847-852. DOI:10.3321/j.issn:1001-6791.2006.06.016] |
| [13] |
Gochis DJ, Yu W, Yates DN et al. The WRF-Hydro model technical description and user's guide, version 3.0. NCAR Technical Document, 2015: 1-120. http://www.ral.ucar.edu/projects/wrf_hydro/.
|
| [14] |
Kerandi N, Arnault J, Laux P et al. Joint atmospheric-terrestrial water balances for East Africa:A WRF-Hydro case study for the upper Tana River basin. Theoretical and Applied Climatology, 2018, 131(3/4): 1337-1355. DOI:10.1007/s00704-017-2050-8 |
| [15] |
Yucel I, Onen A, Yilmaz KK et al. Calibration and evaluation of a flood forecasting system:Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. Journal of Hydrology, 2015, 523: 49-66. DOI:10.1016/j.jhydrol.2015.01.042 |
| [16] |
Senatore A, Mendicino G, Gochis DJ et al. Fully coupled atmosphere-hydrology simulations for the central Mediterranean:Impact of enhanced hydrological parameters values for short and long time scales. Journal of Advances in Modeling Earth Systems, 2015, 7(4): 1693-1715. DOI:10.1002/2015ms000510 |
| [17] |
Naabil E, Lamptey B, Arnault J et al. Water resources management using the WRF-Hydro modelling system:Case-study of the Tono dam in West Africa. Journal of Hydrology:Regional Studies, 2017, 12: 196-209. DOI:10.1016/j.ejrh.2017.05.010 |
| [18] |
Wen YH, Li ZJ, Sun MK et al. Influence of rainfall input on real-time flood forecasting accuracy and forecast period. J Lake Sci, 2019, 31(1): 39-51. [温娅惠, 李致家, 孙明坤等. 降雨输入对实时洪水预报精度与预见期的影响. 湖泊科学, 2019, 31(1): 39-51. DOI:10.18307/2019.0104] |
| [19] |
Xie F, Li ZJ, Yao C. The application and comparative study of TOPMODEL and Xin'anjiang Model. Water Power, 2007, 33(10): 14-18. [谢帆, 李致家, 姚成. TOPMODEL和新安江模型的应用比较. 水力发电, 2007, 33(10): 14-18. DOI:10.3969/j.issn.0559-9342.2007.10.005] |
| [20] |
Li ZJ, Wang XQ, Lv YX et al. Application of TOPKAPI model and comparison with Xin'anjiang Model. Water Power, 2013, 39(11): 6-10. [李致家, 王秀庆, 吕雁翔等. TOPKAPI模型的应用及与新安江模型的比较研究. 水力发电, 2013, 39(11): 6-10.] |
| [21] |
Liu Z, Todini E. Towards a comprehensive physically-based rainfall-runoff model. Hydrology and Earth System Sciences, 2002, 6(5): 859-881. DOI:10.5194/hess-6-859-2002 |
| [22] |
Yu XH, Ding KY, Li Y et al. Overview of the real-time data products of USGS. China Mining Magazine, 2018, 27(z2): 19-22. [于晓荷, 丁克永, 李越等. 美国地质调查局实时数据产品概述. 中国矿业, 2018, 27(z2): 19-22.] |
| [23] |
Gochis DJ, Chen F. Hydrological enhancements to the community Noah land surface model. NCAR Technical Note, NCAR/TN-454+STR, 2003, 68. |
| [24] |
Bao WM. Hydrological forecasting. Beijing: China Water Power Press, 2009: 327-330. [包为民. 水文预报. 北京: 中国水利水电出版社, 2009: 327-330.]
|
| [25] |
Ministry of Water Resources Hydrology Bureau. GB/T 22482-2008 Standard for hydrological information and hydrological forecasting. Beijing: China Standard Press, 2008: 5-6. [水利部水文局. GB/T 22482-2008水文情报预报规范. 北京: 中国标准出版社, 2008: 5-6.]
|
| [26] |
Chen F, Dudhia J. Coupling an advanced land surface-hydrology model with the Penn state-NCAR MM5 modeling system. Part Ⅰ:model implementation and sensitivity. Monthly Weather Review, 2001, 129(4): 569-585. DOI:10.1175/1520-0493(2001)1290569:caalsh>2.0.co;2 |
| [27] |
Tian J, Su HB, Sun XM et al. Accuracy test for the application of GDAS data and NOAH land surface model to China. Progress in Geography, 2011, 30(11): 1422-1430. [田静, 苏红波, 孙晓敏等. GDAS数据和NOAH陆面模式在中国应用的精度检验. 地理科学进展, 2011, 30(11): 1422-1430. DOI:10.11820/dlkxjz.2011.11.013] |
| [28] |
Wigmosta MS, Vail LW, Lettenmaier DP. A distributed hydrology-vegetation model for complex terrain. Water Resources Research, 1994, 30(6): 1665-1679. DOI:10.1029/94wr00436 |
| [29] |
Yao C, Li ZJ, Bao HJ et al. Application of a developed grid-xinanjiang model to Chinese watersheds for flood forecasting purpose. Journal of Hydrologic Engineering, 2009, 14(9): 923-934. DOI:10.1061/(asce)he.1943-5584.0000067 |
| [30] |
Tong BX, Yao C, Li ZJ et al. A method to obtain the spatial distribution of free water storage capacity based on topographic index. J Lake Sci, 2017, 29(5): 1238-1244. [童冰星, 姚成, 李致家等. 一种通过地形指数提取流域自由水蓄水容量空间分布的方法. 湖泊科学, 2017, 29(5): 1238-1244. DOI:10.18307/2017.0522] |
| [31] |
Silver M, Karnieli A, Ginat H et al. An innovative method for determining hydrological calibration parameters for the WRF-Hydro model in arid regions. Environmental Modelling & Software, 2017, 91: 47-69. DOI:10.1016/j.envsoft.2017.01.010 |
 2020, Vol. 32
2020, Vol. 32 


