自从农药发明并应用以来,由于对农业社会经济发展的巨大推动作用,使其在全世界范围内大量的生产和使用.目前,世界上化学农药年产量约200万吨,共有约1000多种人工合成化合物被用作杀虫剂、除草剂等各类农药[1].然而,随着农药使用规模的不断扩大,农药残留问题日趋严重.农药一方面在杀灭农业有害生物中发挥重要作用,另一方面由于其本身的性质,部分不易降解的农药容易在环境不同介质中迁移,同时在农作物或者生物链中传递、富集和放大,使得施用之后残留在环境中的农药及其衍生物不仅对自然环境中的动植物产生危害,破坏生态系统的结构与功能,影响生态系统服务功能,而且对人类自身的健康也构成了严重威胁[2-3].因此,深入研究农药施用之后在环境中的多介质归趋特点尤为关键.
湖泊及其流域是人类的主要生境之一.流域内的水、土地、生物及矿产等资源维系着人类的生存和发展,河流、湖泊、水库和湿地等作为栖息地为物种多样性的维持提供了保障[4].湖泊流域生态系统是以流域为基本单元,经由河流廊道将湖泊、平原(包含城市与农村)和山地相连接,形成的一个具有整体性、动态性、层级性和复杂性的综合体[5].湖泊是其流域最低侵蚀基准面,是污染物汇聚的重要场所;流域内的城市及农村的工业废水、生活污水,以及农田中施用的农药残留等污染物易通过降雨径流和土壤侵蚀等作用进入河流,最终汇聚于湖泊,造成多种水体污染问题,如富营养化、重金属污染和杀虫剂污染等.湖泊沉积物-水界面结构和相内、相间迁移过程的特殊性对污染物在湖泊生态系统多介质归趋具有重要影响.湖泊沉积物水界面结构不仅受水深和水动力的影响,而且受沉积物活性层厚度、质地、有机质含量等理化性质的影响;污染物在沉积物主相内存在孔隙水子相与固相颗粒子相之间的迁移,而污染物在水沉积物两个主相间的跨界面迁移即受控于分子扩散过程,也受颗粒物沉降和再悬浮过程的影响.
近年来,我国的主要湖泊如鄱阳湖、太湖、巢湖等在周边农业及工业活动的影响下,水环境污染严重,持久性有机污染物尤其是农药在湖泊水体、悬浮物及沉积物中的残留水平及分布特征有较多报道[6-12].以巢湖为例,贺勇等[9]对巢湖的微量有机污染物研究进展进行了综述,大量研究表明OCPs广泛存在于巢湖水体、大气、悬浮物和沉积物中.巢湖水体中OCPs残留的空间分布特征为中部湖区>西部湖区>东部湖区,其原因可能与来自于农业区的入湖河流丰乐河杭埠河的入河径流有关[10];水体悬浮物中OCPs含量夏季最高,其可能与降雨径流造成的颗粒物增加以及藻类暴发造成的颗粒物有机碳含量增加有关[11];入湖河口中沉积物中的OCPs污染最为严重[13],而河口沉积物往往由入湖径流中的悬浮颗粒物在河口沉积而形成,这表明巢湖内的OCPs主要来自于湖泊流域内的农业排放通过地表径流入湖.王雁等[12]对巢湖的OCPs来源进行了解析,发现巢湖生态系统中OCPs的主要来源为流域内农业活动中长时间的大量使用. Li等[14]对巢湖沉积物中OCPs的污染历史及其影响因素进行了分析.结果表明,沉积物中OCPs残留水平与TOC含量、沉积物粒径、营养成分和重金属含量具有显著的相关性,自然沉积条件和人类活动对沉积物中OCPs的残留与分布具有重要影响.王卿梅等[11]根据沉积物OCPs的质量基准(SQGs)对巢湖悬浮物中OCPs的潜在生态风险进行了评估.结果表明,巢湖悬浮物中氯丹、p,p’-DDD、七氯浓度低于阈值效应浓度(TECs),不会对水生生物产生不利影响;而p,p’-DDT和o,p’-DDT的浓度高于潜在效应浓度(PECs),可能会对水生生物产生不利影响.因此,研究农药在湖泊流域内的多介质归趋,评估其长期残留水平,对于农药的合理施用以及流域生态系统的保护尤为重要.
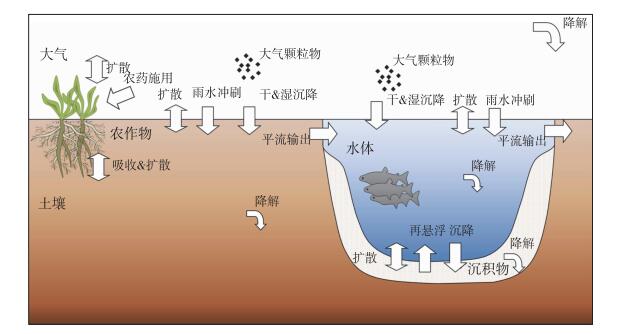
环境多介质模型是1980s发展起来的污染物环境模型,其核心思想为环境系统的性质和污染物自身的物理化学属性共同决定了污染物在环境各介质中的浓度分布和迁移转化过程,在污染生态学、持久性有毒污染物的生物地球化学循环与生态风险评价、环境管理及污染防治等方面得到广泛应用[15-16].加拿大多伦多大学环境研究中心Donald Mackay教授在环境多介质模型的基础上,使用逸度的概念代替了传统的浓度,提出基于逸度的污染物多介质模型,使得模型在结构上更加简单,对污染物环境行为的描述也更加简洁[17-19].逸度模型所模拟的环境一般包含水体、大气、土壤(沉积物)、植物等环境介质(图 1),污染物如农药进入环境系统后,在大气-植物-土壤间存在植物吸收、气/土间扩散、干湿沉降交换等迁移转化过程,由雨水冲刷、径流作用进入湖泊后,在大气-水体-沉积物间迁移以及水生生物的吸收传递.通过将这些不同环境介质内污染物的迁移转化过程与污染物跨介质的迁移过程相联系,可模拟农药在环境系统中的残留水平及污染特征,有助于区域环境的生态风险评价和农药管理.本文对湖泊流域农药多介质模型研究进展进行了简要介绍,重点针对基于逸度的环境多介质模型的发展,以及在湖泊流域农药多介质归趋研究中的应用和前景进行阐述.
|
图 1 湖泊流域农药多介质归趋过程示意 Fig.1 Transport and fate of pesticides in a lake watershed |
农药在农业生态系统中的广泛使用使得大量的农药在农田环境中残留,并且在生物中累积或者放大,直接影响了自然环境、生态系统和人类的健康[20].农药迁移模型对理解农药在农业系统中的行为、建立更好的农药管理策略有重要的意义[21].对农药的多介质归趋的模型研究,已经实现了从温室尺度[22]、田块尺度[23]到流域与区域尺度[24]的跨越.目前已有部分农药多介质模型得到了较为广泛的应用,比如PRZM系列模型、RZWQM模型和PEARL模型等.
PRZM模型(pesticide root zone model)主要用来模拟农药在土壤/沉积物表面径流、水体平流、扩散、植物吸收、土壤吸附、生物和化学降解等关键过程.模型最早在美国纽约附近的农业系统中使用,根据农药Aldicarb(涕灭威)的实际观测数据对模型参数进行校正[25].校正后的模型参数均在理论范围之内,表明该模型可以有效地模拟农药在作物土壤的农业系统中的迁移过程.
PRZM-2是在PRZM模型的基础上改进,将PRZM与VADOFT(vadose zone transport model)模型进行结合. PRZM-2模型与前一代模型相比,可以模拟土壤的温度、农药在土壤中的挥发迁移、土壤灌溉、微生物的降解等.该模型也采用了新的算法解决了数值计算中的一些问题.不仅如此,PRZM-2模型还可以同时模拟农药及其最多两个衍生物的环境归趋. VADOFT模型主要用来模拟土壤不饱和层的水流,从而更加精确的模拟农药在土壤中的迁移过程[26].另外,PRZM-2可以进行模型的不确定性分析[26].而PRZM-3模型与前代模型相比,主要增加了农田生态系统中的氮循环的模拟,可以跟踪氮素在土壤环境和地下水中的迁移转化过程[27].
RICEWQ (rice water quality model)模型同样可以与VADOFT模型进行结合,模拟农药在水稻田中的归趋和迁移过程[28].该模型根据意大利北部的实际观测数据进行校正,模拟结果与实测结果吻合.研究显示19 %的农药会进入包气带,但是由于土壤的吸附和转化,极少量农药(< 0.1 %)会进入地下水.土壤渗透能力和农业水源管理对农药的归趋有显著影响.该模型为农药在水稻田系统中的暴露风险提供了有效的工具[28].
RZWQM(root zone water quality model)模型是RICEWQ模型的升级版,是基于物理原理的农业系统综合模型,主要可用于模拟农业系统中水循环迁移过程,另外还可模拟热平衡、植物生长、有机质/氮的循环、农药的环境行为、以及预测农业管理措施对上述过程的影响[21].在综合评价了多项相关研究后发现,该模型的土壤浅层模块、农药吸附参数和农药降解速率是准确预测农药环境行为的关键参数.
近年来开发的模型进一步考虑了农业活动对农药多介质归趋的影响,如农作物的收割、多种农作物的混合种植等,代表性的模型为农作物模型STICS-Pest[29]等.在加入了农药模块以后,该模型可以模拟农药和氮元素在农业系统中的归趋.模型根据欧洲地区的典型农业系统中观测数据进行校正,并与其他类似的模型进行了比较.结果表明该模型与其他模型模拟结果接近,同时其优势体现在能够模拟农作物的生长,因此可更好地模拟长时间尺度下作物收割等农业活动带来的影响[29].另一个代表性模型为PEARL[30-31].该模型模拟农药在土壤植物系统中的行为以及其向环境中的排放过程(包括大气、水体等).该模型与水动力模型SWAP(soil-water-atmosphere-plant)进行了耦合,可以模拟不同的农药使用方式导致的农药环境分配结果[31].
dynamiCROP(dynamic assessment model for human health impacts due to crop uptake of organic pollutants)模型是用于模拟农药等有毒化学品在多介质的植物环境系统中的动态变化过程.模拟结果显示农业系统中果实、植物表面和土壤是农药环境的重要介质.该模型将复杂的农药环境行为过程分解为几个简单的过程,大大简化了模型的结构和参数的数量[32].该模型还可用于计算农药的人体暴露水平,结果表明不同农药使用在不同作物中,对人体健康的影响水平量化差别最高可达到10个数量级.因此,对农药的环境健康评价要根据实际情况进行判断.同时,农药的使用要考虑与收割的时间间隔和农药的降解速率[33-34].使用该模型对欧洲地区的模拟结果显示,90 %的健康风险仅来自于13种农药在3种农作物上的使用,造成了欧洲人平均寿命减少2.6小时[35].
2 基于逸度的多介质模型研究进展1901年,美国化学家Gilbert N. Lewis提出了逸度(Fugacity)的概念,表征物质在某一相中存在向相邻相逃逸的趋势,其用f表示.在理想条件下,物质的浓度和逸度有着以下关系:
| $ C = Z \cdot f $ | (1) |
式中,C是浓度(mol/m3),f是逸度(Pa),Z是逸度容量(mol/(m3 ·Pa)).加拿大多伦多大学的Mackay等学者首次把这一概念应用于环境多介质模型研究中,以逸度作为判断环境相间是否达到平衡的标准,并总结了逸度容量在不同环境介质中的计算方法(表 1)[36].在逸度模型的计算中,当化学物质在环境各相间分配平衡时,各相中的逸度相同:
| 表 1 逸度容量在不同介质中的计算方法 Tab. 1 Equations of fugacity capacity in different medias |
| $ M = f\sum {{V_i} \cdot {Z_i}} $ | (2) |
式中,M为进入环境系统的化学物质总量(mol),Vi、Zi分别为第i相的体积和逸度容量,通过平衡逸度f与逸度容量Z就可计算出各介质中的浓度.这样的计算方式很容易用计算机列表或程序来进行,当环境相数增加时数学运算的复杂性并不增加,因此基于逸度的多介质模型在对复杂环境系统中的模拟中具有巨大的优势.
逸度模型可根据其复杂程度将其分为Ⅰ~Ⅳ共4个等级,用来模拟不同情境下化学品在环境介质中的浓度分布、质量平衡、迁移转化等行为,使得人们估算化学品的使用导致的环境暴露量提供了方法. Ⅰ级模型为稳态、平衡、封闭的系统,污染物在环境介质内均匀分布,且在多环境介质间分配达到平衡,假设在环境介质内不发生任何化学反应,没有物质的流入或流出. Ⅱ级模型为稳态、平衡、开放的系统,考虑了目标物质在目标区域中流入和流出,以及目标物在该系统中与降解去除相关的反应过程. Ⅰ、Ⅱ级模型都假设污染物在各个环境介质中的处于平衡状态,但在真实环境条件下系统内很少处于平衡状态,因此其适用性范围十分有限. Ⅲ级模型为稳态、非平衡、开放的系统,考虑污染物在目标区域的流入、流出和降解过程之外,还考虑了污染物在环境介质之间的迁移过程. Ⅳ级模型为非稳态、非平衡、开放的系统,在Ⅲ级模型基础上,进一步考虑污染物输入速率和浓度等随时间变化,更全面、动态地描述了污染物在环境介质中的迁移转化和降解反应.
在模型研究的开始阶段,多介质逸度模型往往将待评估环境单元抽象为水体(含悬浮物)、空气(含气溶胶)、沉积物、土壤、生物几大环境分室(compartment).随着后期的不断深入,越来越多的研究将生物圈涉及的主要动植物尽可能的包含在模型中,更细致的考虑了污染物在环境中的迁移转化过程,使逸度模型的结构由简单变为复杂.研究表明,大气、水、土壤和沉积物中的有机污染物能够迁移到植物、无脊椎动物、鱼类、哺乳动物等生物体中,并且在食物网中传递,这就导致了这些污染物在食物网高营养级动物体内的富集,进而威胁这些生物的健康[37].环境毒理学的发展使得单物种的生物富集模型由定性走向定量,这为逸度模型与生物相的进一步结合打下了基础. Mackay[38]提出了生物累积因子KB(生物相浓度与环境介质浓度之比)和辛醇水分配系数KOW及水中溶解度CL之间的存在的比例关系,并且以一组鱼的数据为例得出了KB=0.048KOW和KOW=1795/CL的简单关系.之后,Mackay等[39]基于逸度概念,提出了描述鱼类对有机化学品的吸收、释放和选择性毒性效应的三参数等式(扩散、非扩散和反应参数),结果表明化学品的生物吸收和清除时间常数与其辛醇水分配系数(KOW)有关,高憎水性的化学品达到平衡的时间更长.将逸度引入生物相使得相应的模型更为简洁和易于解释. Connolly等[40]分别利用逸度模型和食物链模型研究水生生物对化学品的生物放大,得到了完全不同的结论.研究结果推翻了逸度模型中逸度比(生物体:水)不会超过1的假设,表明食物链的传递是由于生物体摄食导致内脏中存在的逸度梯度,这为利用逸度方法研究生物累积提供了理论基础.为了进一步解释生物放大的机理,Gobas等[41]用逸度模型研究了化学品在鱼类消化系统中的吸收过程,实验室和场地实验均表明消化道中化学品的逸度要比食物中的高出7~8倍,其原因主要是由于消化道中食物吸附导致化学品浓度增高,而食糜的逸度容量下降.因此,无论是在实验室研究还是在场地研究,食物的消化和吸附是生物放大因子和食物吸收效率的决定性因素.这项研究加深了人们对有机化学品的生物放大过程的理解,也降低了化学品食物吸收参数的不确定性.植物的生物累积潜力的一直是环境多介质模型中的限制因素. Calamari等[42]首次将陆生植物相引入逸度模型,提出了其生物量计算公式,分别考虑了植物作为一个整体和将植物分为树叶、树干和树根两种计算方法,并利用改进的逸度模型估算了3种农药在空气、水、土壤、底泥、悬浮物、水生生物、陆生植物共7个环境相中的分布. Paterson等[43]建立了植物对土壤和空气中的有机污染物的多介质逸度模型,同样将植物分为树叶、树干和树根.该模型全面的考虑了植物与环境介质间化学品的交换过程,提供了可以由化学品的性质、土壤和大气中的浓度和植物生理性质来估算植物不同组织中化学品浓度的方法. Hung等[44]用一个较为简单的模型考虑了农业草本植物吸收有机化学品随时间的变化情况,由于农作物常被人类摄食,因此该研究结果对人体健康风险评价有积极意义. Mckone等[45]总结了植物生物浓缩因子(BCF)的各种模型和实验估计方法,研究了模型结果和实验结果的不确定性对总不确定性的贡献,并以某化学品的81个BCF数据为例,发现模型结构的不确定性相对更大.这项成果为农作物BCF更为准确的估计提供了基础.
随着研究的深入,越来越多的学者使用Ⅳ级逸度模型研究化合物在一个时间段内的连续变化,由稳态模拟转变为动态模拟. Ⅳ级模型可模拟非稳定污染源排放的状况,并能得出环境系统对污染物排放变化所作出的响应时间. Wania等[46]建立了POPs在全球分配的Ⅳ级多介质逸度模型,并对HCB、MCBP、γ-HCH以及DDT四种POPs进行了模拟和验证.研究特别关注了POPs全球分布的影响因素,并认为温度是POPs全球分布的重要因素.而温度变化下大量物化参数的变化数据还不完善,为这类研究带来了一定程度的不确定性. Diamond等[47]模拟计算了某海湾地区As、PCP和PCBs的环境归趋,并计算了在减少排放的情况下,水和沉积物的恢复相应时间,为污染物的控制提供了相应的措施,其中还建立了一个结合了食物链的Ⅲ级稳态模型. Tao等[48]将Ⅲ级与Ⅳ级模型结合起来,模拟了天津地区1953-2001年γ-HCH的环境分布,并预测随着2001年γ-HCH的施用和排放彻底结束,2020年环境各介质中的浓度将会下降1.7~1.9个数量级. Liu等[49]利用Ⅳ级模型模拟了辽河盆地1952 2001年间γ-HCH的浓度分布,同样得到土壤为最大汇,土壤中降解和大气平流输出为最主要的去除过程,并观察到环境中浓度和排放值间存在较大相关性. Valle等[50]关注了气候变化对POPs全球分布的影响.气候变化,如温度升高、风向和降水类型的改变、海平面和冰面的变化都会通过影响环境系统的特性改变POPs的全球分布状况.研究选定PCBs和PCDFs作为目标化合物,模拟结果显示,虽然气候的变化会对使得环境中污染物总量减少,但仍然会通过增加其移动性而增加风险.研究同样指出,这样的结果仅仅考虑了气候变化的直接影响,环境系统的真实变化要来得更加复杂,并同样忽略了各地的空间差异,还有待后续研究的深化和完善.
对于具有持久性,长距离迁移能力的污染物如POPs等,研究其排放后在较大尺度区域内的迁移、残留状况及其生态风险具有重要的意义.近年来,越来越多的研究将逸度模型与地理信息系统、大气传输模型等相结合,对研究区域的细化与整合,实现了对化学品空间迁移转化分析[51-52]. MacLeod等[53]用BETR-North America模型模拟了北美地区毒杀芬的环境归趋,该模型将北美环境系统基于流域边界划分为24个生态区域,利用地理信息系统(GIS)技术结合水文和气象数据,模拟大气、淡水和沿海水域污染物的区域间运输.曹红英等[54]在稳态假设条件下研究了菲在天津市的多介质分布和相间迁移.在探讨了废气排放、土壤有机质含量和土壤中菲降解速率常数的空间变异的基础上, 建立了具有空间变异特征的多介质模型.模型包括气、水、土和沉积物4个主相, 各主相根据情况细分为气、水和固等子相.结果表明,与无空间变异模型估算结果相比,在大气相和土壤相引入空间变异后, 得到的平均浓度与实测结果更加接近,大气、水和土壤3相绝对误差分别为0.14、0.48和0.13对数单位, 其中大气和土壤预测精度大大改善.相比于一般的逸度模型,具有空间分辨率的逸度模型适用于在较大区域甚至全球尺度上具有较高环境持久性和流动性的污染物的多介质归趋模拟,模型结果的准确性并不仅仅取决于模型结构的复杂性和空间分辨率, 也需要输入数据和参数达到相应的精度和准确性要求[51].
3 逸度模型在区域(湖泊流域)农药多介质归趋模拟中的应用农药使用后易通过降雨径流以及大气沉降的作用进入到区域土壤、湖泊中,破坏当地生态环境.逸度模型自提出以来经十几年的发展改进已逐渐趋于成熟,在农药多介质归趋研究以及区域性农药使用评估等领域都得到了广泛的使用.徐晓白[55]利用Ⅲ级逸度模型模拟了池塘生态系统中单甲眯在大气、植物(根、茎、叶)、沉积物、水和鱼中的稳态平衡分布、稳态非平衡分布和排放强度随时间变化时的动态分布;Jean-Marc等[56]使用Ⅲ级逸度模型模拟了4种新烟碱类农药的多介质归趋,结果表明大部分噻虫嗪、吡虫啉(约40 %)会下渗至土壤孔隙水中,而噻虫胺、啶虫脒则主要通过径流作用从农田流失(约80 %),这些农药不易被植物吸收或降解,主要由渗透和径流作用污染周围环境. Kong等[57-58]利用Ⅳ级逸度模型模拟了巢湖α-HCH和γ-HCH(林丹)的多介质归趋及其动态变化,并预测了禁止使用农药林丹后至今巢湖湖泊系统中林丹残留的去除过程.然而,总体来说我国目前在湖泊流域农药环境模型研究方面的成果较少,尤其是对流域内农业生态系统污染物多介质归趋的模型开发较少,这可能与现研究阶段国家的科研关注与经费投入力度不足,以及在污染物环境行为和归趋基础研究不足有关.模拟在真实环境中的降解过程,需要掌握污染物在自然环境中的半衰期,而自然环境中的半衰期测定需要较长时间序列环境介质浓度数据支撑.此外,我国在污染物多介质迁移过程的研究较缺乏,如土气交换、水气交换、水沉降物交换等界面过程的研究报导较少.所以这些基础研究不足,无法提供符合我国国情的可靠的模型参数,如土气交换污染物迁移速率等,弱化了多介质环境模型结果的可信度.因此,开展自然环境中污染的降解过程研究和多介质间的迁移过程研究,是推进我国环境多介质模型发展的基础.开发出针对农药污染、适用于流域生态系统的逸度模型,对我国未来农村农业管理、流域生态系统管理有着十分重要的理论指导意义.
3.1 QWASI模型Mackay等[59-60]在1983年开发了QWASI(定量水、空气和沉积物相互作用,Quantitative Water Air Sediment Interaction)模型,最初被用于模拟湖泊和河流系统中化学物质的归趋.在该模型中,环境系统由水、沉积物和空气三个部分组成,在这些环境介质中污染物的迁移过程包括平流、相间传输和降解. QWASI模型需要输入参数主要为环境参数(包括湖泊尺寸、水体流量、湖水中颗粒物浓度、空气中颗粒物浓度、表层沉积物固体体积分数、大气沉积参数等),以及化学物质的物化参数(如亨利常数、降解速率等),以计算化学物质在湖泊环境体系各介质中浓度、停留时间、迁移速率等. Warren等[61]将其用于印度Rihand水库中,使用QWASI的不同版本(包括平衡态和非平衡态,稳态和动态等模式)对农药林丹进行模拟,其结果验证了该模型的可行性. Di Guardo等[62]在QWASI模型的基础上进行了一些改进,开发了DynA模型,使其适用于输入量等参数在每日变化或是周期性变化下的环境场景.他们进而将模型运用在意大利湖泊中农药DDT的近似排放量估算中,显示该湖泊系统对不同排放情景下的响应,包括达到分配平衡的时间等,并提供了DDT排放的合理估计,为农药的管理控制提供了依据.
Kong等[57]将QWASI模型用于中国湖泊巢湖的农药α-HCH模拟,使用敏感性分析确定各个参数对于模拟结果的影响,以及蒙特卡罗模拟来评估模型的不确定性.模型还考虑了季节性变化的影响,结果表明巢湖的α-HCH的主要来源为大气输入,主要输出大气平流和沉积物降解;沉积物是α-HCH的一个重要的汇,温度变化对模型输出的影响较大.随后,Kong等[58]还进一步对巢湖γ-HCH的长期动态变化进行了模拟(1984 2020年),并且模拟了禁止使用农药林丹后对于γ-HCH分布产生的影响. 1984 1993年,林丹在我国全面禁用前,环境中γ-HCH浓度均处于稳定状态,1993年林丹被禁用后至今,γ-HCH的浓度下降了3个多数量级,并且在大约10年后变化速度变慢, 该模拟结果与2010年和2011年的观测数据保持一致.该模型预测到2020年,巢湖γ-HCH的残留水平将继续缓慢下降,但仍将保持与目前类似的水平.因此,QWASI在农药长期残留问题上的模拟,尤其在湖泊生态系统中的模拟具有优越性,有助于生态风险评估和环境管理.
3.2 EQC模型EQC模型(EQuilibrium Criterion)是由加拿大环境建模和化学品中心根据Mackay的逸度模型理论和等量浓度平衡准则建立的[59]. EQC模型根据化学物质的物理化学性质如蒸汽压、辛醇/水分配系数等,应用Ⅰ级、Ⅱ级、Ⅲ级逸度模型,系统地揭示化学物质在理想环境中的行为特征的环境归宿[63].该模型的特点是模拟非真实环境中化学品的行为,即在模型中环境条件是固定的,输入变量仅为化学品性质相关参数[64].模型基于Excel程序进行计算,并且允许用于根据需要选择Ⅰ、Ⅱ、Ⅲ级的模拟. EQC模型在农药使用后的迁移归趋模拟有很好的应用,如Matamoros等[65]将EQC模型运用于厄瓜多尔香蕉种植园中农药如丙环唑、草甘膦等的暴露浓度模拟,模型预测值与实际检测值相近;汤亚飞等[66]应用LevelⅡ级别的EQC模型模拟了甲基对硫磷等5种有机磷农药投入使用后的分布及归趋,计算出安全使用量,为农药施用的管理控制提供了参考.
此外,该模型根据化学物质的不同性质将其分为3类:分配于所有环境介质、不挥发性物质和不溶于水的物质[63].对于第1类和第3类化学品,模型将选择使用逸度平衡准则进行归趋的模拟;对于第2类化学物质,模型选择使用浓度平衡准则进行模拟.因此,EQC的一个重要优点是,它可以模拟不同类型的化学物质,包括非极性有机化学物质[63, 67].
在农业生态系统的模拟中,许多学者对EQC模型进行了一些改进,如Batiha等[68-69]在EQC模型的基础上结合生态相对风险(EcoRR)方法,建立了农业归趋与风险评估模型(agricultural fate and risk assessment model,MAFRAM).该模型将农业生态系统分为农场内外两个区域,每个区域中的环境介质包括空气、水、土壤、沉积物、地上植物和根系. MAFRAM模型根据农药的物化特性、生物种群数据和环境特性进行模拟,可以得到农药在各个介质间的转移率、主要损失机制、浓度、停留时间以及各个介质中的生态风险.
3.3 BETR模型BETR(Berkeley-Trent)模型是由MacLeod等[70]在2001年提出的基于逸度模型的理论和计算方法,用于研究化学物质区域多介质分配和归趋模拟的模型. BETR模型将研究区域根据地理特征、政治边界等进行划分或是由固定栅格划分.最初BETR模型被用于北美地区(BETR-North America),其根据流域划分为24个生态区域,每个区域内使用包含7种环境介质的逸度模型研究化学物质的归趋,利用地理信息系统(GIS)技术结合水文和气象数据,模拟大气、淡水和沿海水域污染物的区域间运输.这种基于流域的划分考虑到流域内的河流分布和走向,可以大大简化划分后区块内及区块间河流流量及流向计算. Macleod等[53]在2002年使用BETR对北美地区杀虫剂毒杀芬的大陆尺度动态质量进行了估算,其结果表明在1945-2000年期间,北美使用了5.34亿kg毒杀芬作为杀虫剂和杀鱼剂,模型结果与目前和历史上报道的空气、水、土壤和沉积物中毒杀芬的浓度存在较好的一致性.且结果表明2000年北美环境中仍有1500万kg的毒杀芬处于活跃的生物地球化学循环中,其中大多数毒杀芬残留于美国南部和墨西哥的土壤中;大气沉积到五大湖的毒杀芬总量中,约有70 %来自于五大湖盆地以外的污染源,模型实现了对于污染物在大陆尺度上多介质分配的估算.
Prevedouros等[71]研究欧洲大陆的农药林丹的稳态归趋,以BETR-North America模型为基础,在区域分割上采用固定的栅格进行分割,将欧洲分割为50个区域以及4个缓冲区域,结合1998年林丹的排放数据,考虑各区域的化学分配和降解,以及在稳态或完全动态条件下的区域间运输,实现了对林丹在整个欧洲大气和表层土壤分布模拟.此外,也有学者认为在区域的划分中城市地区和农村地区存在着一些差异性,Song等[72]认为城市和农村地区对于POPs的排放量不同,排放的差异将影响其迁移的行为,因此利用土地覆盖等信息,将BETR模型转化为BETR-Urban-Rural模型来模拟城市与农村之间持久性有机污染物的运输,为制定控制城乡人口增长的政策提供了的指导.而农药在城市区域和农村区域的排放也存在着很大的差异,这样的划分方式也适用于农药的迁移模拟中.
BETR模型不同于其他的多介质模型,其对于研究区域空间的划分,考虑到了空间上的大气传输和地表径流的传输,可进行空间迁移分析[51].对于一些挥发性较强的,尤其是属于POPs的农药,其具有长距离迁移能力,在大规模、大面积的使用后会在一个较大的区域进行传输,对其进行区域性的迁移模拟尤为重要.因此BETR模型在较大范围内的污染物归趋模拟中有着明显的优势.
3.4 G-CIEMS模型G-CIEMS模型(Grid-Catchment Integrater Environmental Modeling System)[73]是一种在地理信息系统(GIS)的基础上,基于空间分辨率的动态多介质逸度模型,模型中包含的环境介质包括空气、淡水(河流、湖泊)、淡水沉积物、森林、土壤、海水及其沉积物,其中土壤介质还包含七种土地用途类型(水田、农田、灌丛、非植被区、森林、建筑用地及其他土地类型).该模型的优点是基于不同地理形状的介质之间的投影面积或投影长度来对于不同栅格的分割和整合.比如,在空气介质中可以认为其分布均匀,可向四周扩散,以网格单元的方式划分;河流介质中以线段结构的方式划分,其传输具有方向性;土壤介质中根据其流域结构和地理信息进行划分,而不同环境介质间的物质传输则借助于GIS分析工具进行分析计算[73].因此该模型可以用于较为复杂的区域内化学物质分布的模拟研究.如Imaizumi等[74]利用G-CIEMS模型结合农药化学物高分辨估计方法PeCHREM来研究农药对当地水生生态系统构成潜在风险,研究中对25种水稻除草剂在施用后河流中每日的环境浓度变化进行了最高浓度和出现时间的预测,并利用监测数据对结果进行了验证,结果表明,在全日本,不同除草剂的空间分布存在着较大差异,预测和观察的结果相似,最高浓度的差异小于一个数量级的占66 %,出现时间差异小于两周的占79 %.
4 基于浓度和基于逸度的农药多介质模型比较 4.1 两类主要模型的特点比较本文对比了各模型涉及的环境介质、研究区域尺度、优点及适用范围见表 2.相比于基于浓度的农业生态系统中的农药模型(如PRZM系列等),逸度模型在农药的多介质归趋模拟中有着明显的优越性,在农药管理、风险评估等方面也有十分重要的参考价值.逸度模型的优点体现在如下几个方面:
| 表 2 湖泊流域农药多介质模型的对比 Tab. 2 Comparison of several multimedia models for pesticides in lake watersheds |
1) 逸度模型用逸度的概念代替了传统的浓度,在模型结构上更加简单,所需参数更少,计算更加便捷,结果表示更加直观,有助于质量平衡方程的编制和求解,且其计算方法可推广到任意数目的环境介质.因此,将逸度模型应用在农业生态系统的农药多介质归趋研究中,其考虑的环境介质更多,考虑农药的影响范围更广(包括农业生态系统中的水系统,如灌溉系统、池塘等).
2) 在基于浓度的多介质模型中,农药在各环境相中的残留浓度是根据各相间的分配系数进行计算,但当所模拟的环境尺度增大,结构更为复杂时,如湖泊中农药多介质归趋的模拟中,包含着的大气、大气颗粒物、水体、悬浮物、鱼类、沉积物等诸多环境介质,其分配系数的计算量和所需的参数就会大量增加,原则上,对于一个拥有10个相的环境系统,我们可以定义90个分配系数,其中某些分配系数还可能从其他分配系数中导出,这将使得对复杂环境的模拟变得十分困难[36].而在基于逸度的多介质模型中,使用逸度容量代替分配系数,模型参数更少,计算量降低,以至于参数的可获性增强,参数的灵敏度分析更方便.
3) 逸度方法在研究生物对化学品的吸收、释放、以及食物链传递过程中有着明显的优势,将逸度引入生物相对于生物放大等一些过程更易于解释,能够使得模型的结构更为清晰.因此在农药对生态环境的影响,尤其是对水生生物的影响及其生物放大效应的研究中,使用逸度模型进行评价也更为具体全面.
4) 逸度的概念便于连接所分割的空间单元,提高了模型处理空间差异性的能力.如对于一些平流、扩散等环境过程,使用逸度的方法进行描述更加简洁和统一.因此,逸度模型可用于空间大尺度的研究,比如在农业生态系统中对于农药施用后区域性的空间分配过程的研究.
5) 在模型迁移通量的计算上,浓度模型由于参数多,计算复杂,较少有计算各环境过程的迁移通量.在逸度模型中,迁移通量T由迁移速率D与介质的逸度差来决定,迁移速率D值是通过逸度容量、传质系数、扩散系数等参数来计算,如对于化学物质在环境相中的降解过程(符合一级动力学方程),有Di=Vi ·Zi ·ki,其中Vi、Zi、ki分别为该相的体积、逸度容量和化学物质在该相的降解速率.迁移速率D的引入将大量庞杂的细节归纳在一起,有利于构建相当复杂的模型来描述化学品在几个介质间通过多个途径的迁移,使逸度模型对环境过程的模拟更为具体,易于揭示化学物质在系统中的迁移行为.
4.2 两类主要模型的应用价值比较各模型在对不同尺度的环境模拟中,其主要模拟过程存在着许多差异,模拟结果对农业污染管理也有着不同的实践和指导意义(表 3).在小尺度范围内如水稻田的模拟中,由于逸度模型参数表示的是时间和空间平均值,在一个环境介质内环境过程以恒定和相同的速率发生.因此,逸度模型在反映小尺度环境变化方面,尤其是农药在稻田中的短期扩散、吸收等以及农业生产活动及管理措施如晒田、收割等行为的模拟能力有限.相比较而言,基于浓度的STICS-Pest等模型在这些方面有优势.
| 表 3 部分湖泊流域农药多介质模型的实际应用价值 Tab. 3 Practical values of different multimedia models for pesticides in lake watersheds |
在区域模拟中,逸度模型适用于模拟更加复杂的环境过程.如QWASI模型用于湖泊的多介质模拟,不仅包括污染物在湖泊内水体-悬浮物-沉积物的分配过程,还考虑了通过大气沉降、河水径流的输入以及水生生物捕食富集的作用,这些过程的模拟都使得模型结构更接近真实环境.因此,区域尺度的逸度模型更适用于模拟农药在区域中各环境介质的残留水平,评估其暴露风险和生态风险.此外,季节性变化、地形地貌、降水、气温、风向风速等因素会影响农药的迁移过程,进而影响农药的多介质归趋.在模型中可以通过灵敏度分析来判断各因素的影响程度. Kong等[58]在用QWASI模型对巢湖HCH多介质归趋研究中,对模型中所用的静态参数和动态参数进行了敏感性分析,发现亨利常数是最敏感的静态参数,在预测持久性有机污染物的环境行为中起着基础性作用[75];温度是最敏感的动态参数, 对污染物在湖泊系统各介质间的迁移过程有着重要影响,而逸度模型可以有效减少温度差异的影响.
而在更大尺度上的模拟中,将逸度模型与地理信息系统(GIS)结合,对模拟区域进行划分与整合,可实现对农药在区域内空间迁移以及跨区域传输过程的模拟.目前基于GIS的逸度模型大多以流域边界或固定栅格的方式进行空间划分,如BETR-Europe模型以流域进行空间划分,侧重应用于土壤和河流等非均质介质在污染物迁移中占主导作用时, 得到的模拟结果更容易进行局部区域的污染来源分析;BETR-North America模型基于栅格的划分更能体现出大气在污染物迁移中的作用, 更易分析出污染物在整个研究区域中的整体分布情况[51].流域内农业耕作方式(水田、旱田)、农作物种类及用地类型(农田、灌丛、森林、城市用地等)的差异、排放源的空间分布特性、水文条件等因素均会影响农药在区域内的迁移与转化,以及河流下游水体或湖泊中的残留水平.例如水稻田不同于传统的旱田种植,在水稻生长期间,稻田往往处于被水淹没的状态,农药施用后会在土壤-水体中分配,并通过周期性注水、排水作用下从农田流失进入区域水体[76-77].对于不同的农作物,其农药的使用强度和流失率也存在差异,Wei等[78]调查了1990-2011年我国主要农作物品种的农药使用情况,其中蔬菜、果树的农药施用强度最大,旱田粮食作物的农药使用量和流失量最高,尤其在我国中部和东部地区.利用GIS技术,结合区域内不同耕地类型的农药排放特性及空间分布特征进行流域内农药归趋模拟,分析主要排放源,有利于对流域内农业活动的管理.但目前逸度模型较少有考虑到具体的作物类型和农业活动,因此结合农业生产特点,实现对多种耕作方式的模拟,也是将来农业多介质模型发展的一个方向.
相比于如QWASI等研究单一区域的模型,基于GIS的逸度模型可以很好地模拟污染物在流域内的空间分布规律,对流域污染管理有着重要的指导意义.但同时大尺度的多介质模拟计算量庞大,建模所考虑的微观环境过程往往比一般的逸度模型要少,其模拟的环境更接近理想的状态,且研究的尺度越大,其结果精度越低,因此在实际应用的过程中,需要根据研究目的选择适合的逸度模型进行模拟分析.
5 湖泊流域农药多介质逸度模型研究展望基于上述分析和讨论,本文对逸度模型在湖泊流域农药多介质模拟研究中,提出以下几点展望:
1) 已有的基于逸度的多介质模型中,很少有模型专门考虑农业生态系统.对于农业生态系统,如水稻田系统,研究水稻、稻田水(水体和悬浮物)和稻田土壤(土壤固体)中农药的多介质归趋,对农药的环境风险和人体健康风险评价,农药施用的管理等都有非常重要的作用.因此在流域、区域尺度上的逸度模型中,若有大量的人类农业生产活动,这些农业系统应当作为一个生态系统的整体进行考虑,并在模型构型上考虑这些系统的特点(如季节变化、农业种植规律等).
2) 流域内具体的农业生产活动,往往存在耕种方式、农药施用方式以及不同农作物对农药吸收、转化的差异,这些差异均会影响区域内农药的多介质归趋行为.因此对于农业生态系统的多介质模型应该考虑这些差异性,并在不同的情境下使用不同的方式进行模拟,使结果更为真实.未来需要结合多介质逸度模型和传统的农业生态系统模型(如STICS-Pest等)的不同优势进行下一代模型开发.
3) 目前的研究中基于地理信息系统(GIS)技术开发的逸度模型较少.农业活动的面源排放是流域内农药污染的主要来源,不同农业活动的排放特点以及空间分布特性、区域地形地貌和水文气象条件、土地利用/覆盖变化均会影响农药在湖泊流域生态系统内的迁移过程.开发具有空间分辨率的农药多介质逸度模型,结合研究区域的地理信息分析农药的多介质归趋,将有助于掌握湖泊流域生态系统内农药污染的时空分布特征,识别主要污染源,进行农药污染防治,评价农药施用的生态与健康风险,为农村农业活动管理、农药合理施用方面提供科学与技术支持.
4) 逸度模型应当继续扩展其适用性,满足更多的需求.开发相应的软件平台,嵌入基本的模型分析工具(参数灵敏度和模型不确定性分析)和常见农药的参数数据库,以期为农药的环境行为研究和管理提供有效的应用工具.
| [1] |
Tomlin CD. The pesticide manual:A world compendium. British Crop Production Council, 2009. |
| [2] |
Jeyaratnam J. Acute pesticide poisoning:a major global health problem. World Health Statistics Quarterly, 1990, 43(3): 139-144. |
| [3] |
Rosenstock L, Keifer M, Daniell WE et al. Chronic central nervous system effects of acute organophosphate pesticide intoxication. The Lancet, 1991, 338: 223-227. DOI:10.1016/0140-6736(91)90356-T |
| [4] |
Liu Y, Guo HC, Huang K et al. The theories and methods of lake-watershed ecosystem management(LWEM). Acta Ecologica Sinica, 2007(12): 5352-5360. [刘永, 郭怀成, 黄凯等. 湖泊-流域生态系统管理的内容与方法. 生态学报, 2007(12): 5352-5360. DOI:10.3321/j.issn:1000-0933.2007.12.048] |
| [5] |
Liu Y, Guo HC, Zhou F et al. Watershed approach as a framework for lake-watershed pollution control. Acta Scientiae Circumstantiae, 2006(2): 337-344. [刘永, 郭怀成, 周丰等. 基于流域分析方法的湖泊水污染综合防治研究. 环境科学学报, 2006(2): 337-344. DOI:10.3321/j.issn:0253-2468.2006.02.029] |
| [6] |
Li QY, Zhao ZH, Jiang Y et al. Vertical distribution characteristics of organochlorine pesticides and polycyclic aromatic hydrocarbons in a sedimentary core from Zhouxi Bay, Lake Poyang. J Lake Sci, 2016, 28(4): 765-774. [郦倩玉, 赵中华, 蒋豫等. 鄱阳湖周溪湾沉积物中有机氯农药和多环芳烃的垂直分布特征. 湖泊科学, 2016, 28(4): 765-774. DOI:10.18307/2016.0409] |
| [7] |
Zhu JY, Wang D, Wang YK. Comprehensive analysis and ecological and health risk assessment of persistent organic pollutants in Taihu Lake Basin. Journal of Nanjing University:Natural Sciences, 2016, 52(2): 370-381. [朱洁羽, 王栋, 王远坤等. 太湖流域持久性有机污染物特征分析和生态与健康风险评价. 南京大学学报:自然科学, 2016, 52(2): 370-381.] |
| [8] |
Yu YP, Liu M. Distribution characteristics and ecological risk assessment of organochlorine pesticides in water sources of Taihu Lake Basin. Environmental Pollution & Control, 2017, 39(8): 829-834, 840. [于英鹏, 刘敏. 太湖流域水源地有机氯农药分布特征与生态风险评价. 环境污染与防治, 2017, 39(8): 829-834, 840.] |
| [9] |
He Y, Xu FL, He W et al. Progresses in the studies on trace organic contaminants in Lake Chaohu ecosystem. Asian Journal of Ecotoxicology, 2016, 11(2): 111-123. [贺勇, 徐福留, 何伟等. 巢湖生态系统中微量有机污染物的研究进展. 生态毒理学报, 2016, 11(2): 111-123.] |
| [10] |
Liu WX, He W, Qin N et al. Residues, distributions, sources, and ecological risks of OCPs in the water from Lake Chaohu, China. The Scientific World Journal, 2012. DOI:10.1100/2012/897697 |
| [11] |
Wang QM, He QS, Wang Y et al. Distribution, source identification and risk assessment of organochlorine pesticides (OCPs) in suspended particulate matter (SPM) from Lake Chaohu. J Lake Sci, 2014, 26(6): 887-896. [王卿梅, 何玘霜, 王雁等. 巢湖悬浮物中有机氯农药的分布、来源与风险. 湖泊科学, 2014, 26(6): 887-896. DOI:10.18307/2014.0611] |
| [12] |
Wang Y, He W, Qin N et al. Residual levels and ecological risks of organochlorine pesticides in surface sediments from Lake Chaohu. Acta Scientiae Circumstantiae, 2012, 32(2): 308-316. [王雁, 何伟, 秦宁等. 巢湖表层沉积物中有机氯农药的残留与风险. 环境科学学报, 2012, 32(2): 308-316.] |
| [13] |
Liu WX, He W, Qin N et al. The residues, distribution, and partition of organochlorine pesticides in the water, suspended solids, and sediments from a large Chinese lake (Lake Chaohu) during the high water level period. Environmental Science and Pollution Research, 2013, 20(4): 2033-2045. DOI:10.1007/s11356-012-1460-5 |
| [14] |
Li CC, Huo SL, Xi BD et al. Historical deposition behaviors of organochlorine pesticides (OCPs) in the sediments of a shallow eutrophic lake in Eastern China:Roles of the sources and sedimentological conditions. Ecological Indicators, 2015, 53: 1-10. DOI:10.1016/j.ecolind.2015.01.018 |
| [15] |
Cohen Y. Modeling of pollutant transport and accumulation in a multimedia environment. The Conference on Geochemical and Hydrologic Processes and their Protection, Council on Environmental Quality, 1984, September 25, Washington, D.C.
|
| [16] |
Mackay D ed. Multimedia environmental models:The fugacity approach, seconded. New York: Lewis Publishers, 2001.
|
| [17] |
Mackay D, Paterson S. Fugacity revisited. Environmental Science & Technology, 1982, 16: 654A-660A. |
| [18] |
Sattler C, Kächele H, Verch G. Assessing the intensity of pesticide use in agriculture. Agriculture, Ecosystems & Environment, 2007, 119: 299-304. DOI:10.1016/j.agee.2006.07.017 |
| [19] |
Malone, R W, Ahuja LR, Ma L et al. Application of the Root Zone Water Quality Model (RZWQM) to pesticide fate and transport:an overview. Pest Management Science:Formerly Pesticide Science, 2004, 60: 205-221. DOI:10.1002/ps.789 |
| [20] |
Katsoulas N, Boulard T, Tsiropoulos N et al. Experimental and modelling analysis of pesticide fate from greenhouses:The case of pyrimethanil on a tomato crop. Biosystems Engineering, 2012, 113: 195-206. DOI:10.1016/j.biosystemseng.2012.07.007 |
| [21] |
La N, Lamers M, Nguyen VV et al. Modelling the fate of pesticides in paddy rice-fish pond farming systems in northern Vietnam. Pest Management Science, 2014, 70: 70-79. DOI:10.1002/ps.3527 |
| [22] |
Zhang C, Cui F, Zeng GM et al. Quaternary ammonium compounds (QACs):a review on occurrence, fate and toxicity in the environment. Science of the Total Environment, 2015, 518: 352-362. |
| [23] |
Carsel RF, Mulkey LA, Lorber MN et al. The pesticide root zone model (PRZM):A procedure for evaluating pesticide leaching threats to groundwater. Ecological Modelling, 1985, 30: 49-69. DOI:10.1016/0304-3800(85)90036-5 |
| [24] |
Mullins J, Carsel R, Scarbrough J et al. PRZM-2, a model for predicting pesticide fate in the crop root and unsaturated soil zones: User's manual for release 2. 0. AScI Corp., Athens, GA (United States), 1993.
|
| [25] |
Carsel R. PRZM-3, a model for predicting pesticide and nitrogen fate in the crop root and unsaturated soil zones. Users manual for release 3.0. 1998.
|
| [26] |
Miao Z, Cheplick MJ, Williams MW et al. Simulating pesticide leaching and runoff in rice paddies with the RICEWQ-VADOFT Model. Journal of Environmental Quality, 2003, 32: 2189-2199. DOI:10.2134/jeq2003.2189 |
| [27] |
Queyrel W, Habets F, Blanchoud H et al. Pesticide fate modeling in soils with the crop model STICS:Feasibility for assessment of agricultural practices. Science of the Total Environment, 2016, 542: 787-802. DOI:10.1016/j.scitotenv.2015.10.066 |
| [28] |
Leistra M, Van Den BF. Volatilization of parathion and chlorothalonil from a potato crop simulated by the PEARL model. Environmental Science & Technology, 2007, 41: 2243-2248. |
| [29] |
Van den Berg, Tiktak FA, Boesten J et al. PEARL model for pesticide behaviour and emissions in soil-plant systems. Statutory Research Tasks Unit for Nature & the Environment, 2016, 2352-2739. |
| [30] |
Fantke P, Wieland P, Wannaz C et al. Dynamics of pesticide uptake into plants:From system functioning to parsimonious modeling. Environmental Modelling & Software, 2013, 40: 316-324. |
| [31] |
Fantke P, Juraske R, Antón A et al. Dynamic multicrop model to characterize impacts of pesticides in food. Environmental Science & Technology, 2011, 45: 8842-8849. DOI:10.1021/es201989d |
| [32] |
Fantke P, Wieland P, Juraske R et al. Parameterization models for pesticide exposure via crop consumption. Environmental Science & Technology, 2012, 46: 12864-12872. |
| [33] |
Fantke P, Friedrich R, Jolliet O. Health impact and damage cost assessment of pesticides in Europe. Environment International, 2012, 49: 9-17. DOI:10.1016/j.envint.2012.08.001 |
| [34] |
Mackay D. Multimedia environmental models:the fugacity approach(The second edition). Beijing: Chemical Industry Press, 2007. [唐纳德·麦凯. 环境多介质模型:逸度方法(第二版). 北京: 化学工业出版社, 2007.]
|
| [35] |
Sharpe S, Mackay D. A framework for evaluating bioaccumulation in food webs. Environmental Science & Technology, 2000, 34: 2373-2379. |
| [36] |
Mackay D. Correlation of bioconcentration factors. Environmental Science & Technology, 1982, 16: 274-278. |
| [37] |
Mackay D, Hughes AI. 3-parameter equation describing the uptake of organic-compounds by fish. Environmental Science & Technology, 1984, 18: 439-444. DOI:10.1021/es00124a009 |
| [38] |
Connolly JP, Pedersen CJ. A thermodynamic-based evaluation of organic-chemical accumulation in aquatic organisms. Environmental Science & Technology, 1988, 22: 99-103. DOI:10.1021/es00166a011 |
| [39] |
Gobas F, Wilcockson JB, Russell RW et al. Mechanism of biomagnification in fish under laboratory and field conditions. Environmental Science & Technology, 1999, 33: 133-141. |
| [40] |
Calamari D, Vighi M, Bacci E. The use of terrestrial plant biomass as a parameter in the fugacity model. Chemosphere, 1987, 16: 2359-2364. DOI:10.1016/0045-6535(87)90293-1 |
| [41] |
Paterson S, Mackay D, McFarlane C. A model of organic-chemical uptake by plants from soil and the atmosphere. Environmental Science & Technology, 1994, 28: 2259-2266. |
| [42] |
Hung H, Mackay D. A novel and simple model of the uptake of organic chemicals by vegetation from air and soil. Chemosphere, 1997, 35: 959-977. DOI:10.1016/S0045-6535(97)00182-3 |
| [43] |
McKone TE, Maddalena RL. Plant uptake of organic pollutants from soil:Bioconcentration estimates based on models and experiments. Environmental Toxicology and Chemistry, 2007, 26: 2494-2504. DOI:10.1897/06-269.1 |
| [44] |
Wania F, Mackay D. A global distribution model for persistent organic-chemicals. Science of the Total Environment, 1995, 160/161: 211-232. DOI:10.1016/0048-9697(95)04358-8 |
| [45] |
Diamond ML, MacKay D, Poulton DJ et al. Assessing chemical behavior and developing remedial actions using a mass balance model of chemical fate in the Bay of Quinte. Water Research, 1996, 30: 405-421. DOI:10.1016/0043-1354(95)00161-1 |
| [46] |
Tao S, Yang Y, Cao H et al. Modeling the dynamic changes in concentrations of γ-hexachlorocyclohexane (γ-HCH) in Tianjin region from 1953 to 2020. Environmental Pollution, 2006, 139: 183-193. DOI:10.1016/j.envpol.2004.12.013 |
| [47] |
Liu ZY, Quan X, Yang FL. Long-term fate of three hexachlorocyclohexanes in the lower reach of Liao River basin:Dynamic mass budgets and pathways. Chemosphere, 2007, 69: 1159-1165. DOI:10.1016/j.chemosphere.2007.03.072 |
| [48] |
Valle MD, Codato E, Marcomini A. Climate change influence on POPs distribution and fate:A case study. Chemosphere, 2007, 67: 1287-1295. DOI:10.1016/j.chemosphere.2006.12.028 |
| [49] |
Liu SJ, Lu YL, Shi YJ. Advances in spatially explicit environmental multimedia fate models of POPs. Asian Journal of Ecotoxicology, 2011, 6(2): 129-137. [刘世杰, 吕永龙, 史雅娟. 持久性有机污染物环境多介质空间分异模型研究进展. 生态毒理学报, 2011, 6(2): 129-137.] |
| [50] |
Zhang SX, Zhang B, Zhang QQ et al. Chemical environmental fate models and their applications. Environmental Chemistry, 2019, 38(8): 1684-1707. [张少轩, 张冰, 张芊芊等. 化学品环境归趋模型及应用. 环境化学, 2019, 38(8): 1684-1707.] |
| [51] |
MacLeod M, Woodfine D, Brimacombe J. A dynamic mass budget for toxaphene in North America. Environmental Toxicology and Chemistry, 2002, 21: 1628-1637. DOI:10.1002/etc.5620210813 |
| [52] |
Cao HY, Tao S, Wang XL et al. Multimedia fate modeling with spatial resolution for phenanthrene in Tianjin. Environmental Science, 2003(5): 54-59. [曹红英, 陶澍, 王喜龙等. 天津地区菲的空间分异多介质归趋模型. 环境科学, 2003(5): 54-59.] |
| [53] |
Xu XB ed. Changes and ecological effects of typical chemical pollutants in environment. Beijing: Science Press, 1998. [徐晓白. 典型化学污染物在环境中的变化及生态效应. 北京: 科学出版社, 1998.]
|
| [54] |
Jean-Marc B, Dominique AN, Heron M et al. A survey and risk assessment of neonicotinoids in water, soil and sediments of Belize. Environmental Pollution, 2019, 249: 949-958. DOI:10.1016/j.envpol.2019.03.099 |
| [55] |
Kong X, He W, Qin N et al. Simulation of the fate and seasonal variations of α-hexachlorocyclohexane in lake chaohu using a dynamic fugacity model. The Scientific World Journal, 2012. DOI:10.1100/2012/691539 |
| [56] |
Kong X, He W, Qin N et al. Modeling the multimedia fate dynamics of γ-hexachlorocyclohexane in a large Chinese lake. Ecological Indicators, 2014, 41: 65-74. DOI:10.1016/j.ecolind.2014.01.024 |
| [57] |
Mackay D, Joy M, Paterson S. A quantitative water, air, sediment interaction (QWASI) fugacity model for describing the fate of chemicals in lakes. Chemosphere, 1983, 12: 981-997. DOI:10.1016/0045-6535(83)90251-5 |
| [58] |
Mackay D, Paterson S, Joy M. A quantitative water, air, sediment interaction (QWASI) fugacity model for describing the fate of chemicals in rivers. Chemosphere, 1983, 12: 1193-1208. DOI:10.1016/0045-6535(83)90125-X |
| [59] |
Warren CS, Mackay D, Bahadur NP et al. A suite of multi-segment fugacity models describing the fate of organic contaminants in aquatic systems:application to the Rihand Reservoir, India. Water Research, 2002, 36: 4341-4355. DOI:10.1016/S0043-1354(02)00161-6 |
| [60] |
Di Guardo A, Ferrari C, Infantino A. Development of a dynamic aquatic model (DynA Model):Estimating temporal emissions of DDT to Lake Maggiore (N. Italy). Environmental Science and Pollution Research, 2006, 13: 50-58. DOI:10.1065/espr2006.01.009 |
| [61] |
Mackay D, Di Guardo A, Paterson S et al. Evaluating the environmental fate of a variety of types of chemicals using the EQC model. Environmental Toxicology and Chemistry, 1996, 15: 1627-1637. DOI:10.1002/etc.5620150929 |
| [62] |
Qing DH, Xu YP, Wang ZJ. The evolution of environmental fugacity models on chemical exposure and risk assessment. Asian Journal of Ecotoxicology, 2018, 13(6): 13-29. [青达罕, 许宜平, 王子健. 基于环境逸度模型的化学物质暴露与风险评估研究进展. 生态毒理学报, 2018, 13(6): 13-29.] |
| [63] |
Matamoros D, Vanrolleghem PA. Pesticide assessment of the banana sector in an Ecuadorian watershed. Mededelingen Faculteit Landbouwkundige en Toegepaste Biologische Wetenschappen Universiteit Gent, 2001, 66(2B): 863-872. |
| [64] |
Tang YF, Wang YX, Cai HS. Transportation and fate of pesticide in surface water environment. J Wuhan Inst Chem Tech, 2005(4): 13-15, 22. [汤亚飞, 王焰新, 蔡鹤生. 地表水环境中农药迁移与归宿. 武汉化工学院学报, 2005(4): 13-15, 22. DOI:10.3969/j.issn.1674-2869.2005.04.005] |
| [65] |
Cousins IT, Staples CA, Kleĉka GM et al. A multimedia assessment of the environmental fate of bisphenol A. Human and Ecological Risk Assessment:An International Journal, 2002, 8(5): 1107-1135. DOI:10.1080/1080-700291905846 |
| [66] |
Batiha MA, Kadhum AAH, Batiha MM. MAFRAM-A new fate and risk assessment methodology for non-volatile organic chemicals. Journal of Hazardous Materials, 2010, 181: 1080-1087. DOI:10.1016/j.jhazmat.2010.05.125 |
| [67] |
Batiha MM, Ramadan A, Kadhum AAH. Generalization of the MAFRAMmethodology for semi-volatile organic agro-chemicals. Water, Air, and Soil Pollution, 2014, 225: 1789. DOI:10.1007/s11270-013-1789-5 |
| [68] |
MacLeod M, Woodfine DG, Mackay D. BETR North America:A regionally segmented multimedia contaminant fate model for North America. Environmental Science and Pollution Research, 2001, 8: 156-163. DOI:10.1007/BF02987379 |
| [69] |
Prevedouros K, MacLeod M, Jones KC. Modelling the fate of persistent organic pollutants in Europe:parameterisation of a gridded distribution model. Environmental Pollution, 2004, 128: 251-261. DOI:10.1016/j.envpol.2003.08.041 |
| [70] |
Song S, Su C, Lu Y et al. Urban and rural transport of semivolatile organic compounds at regional scale:a multimedia model approach. Environmental Science, 2016, 39: 228-241. DOI:10.1016/j.jes.2015.12.005 |
| [71] |
Suzuki N, Murasawa K, Sakurai T et al. Geo-referenced multimedia environmental fate model (G-CIEMS):Model formulation and comparison to the generic model and monitoring approaches. Environmental Science & Technology, 2004, 38: 5682-5693. |
| [72] |
Imaizumi Y, Noriyuki S, Shiraishi F et al. Development and validation of a simulation method, PeCHREM, for evaluating spatio-temporal concentration changes of paddy herbicides in rivers. Environmental Science-Processes & Impacts, 2018, 20: 120-132. |
| [73] |
Odabasi M, Cetin B, Demircioglu E et al. Air-water exchange of polychlorinated biphenyls (PCBs) and organochlorine pesticides (OCPs) at a coastal site in Izmir Bay, Turkey. Mar Chem, 2008, 109: 115-129. DOI:10.1016/j.marchem.2008.01.001 |
| [74] |
Wang RY, Luo YZ, Chen HJ et al. Environmental fate and impact assessment of thiobencarb application in California rice fields using RICEWQ. Science of the Total Environment, 2019, 664: 669-682. DOI:10.1016/j.scitotenv.2019.02.003 |
| [75] |
Wang RY, Yuan YP, Yen H et al. A review of pesticide fate and transport simulation at watershed level using SWAT:Current status and research concerns. Science of the Total Environment, 2019, 669: 512-526. DOI:10.1016/j.scitotenv.2019.03.141 |
| [76] |
Wei OY, Cai GQ, Huang WJ et al. Temporal-spatial loss of diffuse pesticide and potential risks for water quality in China. Science of the Total Environment, 2016, 541: 551-558. DOI:10.1016/j.scitotenv.2015.09.120 |
 2020, Vol. 32
2020, Vol. 32 

