(2: 河海大学浅水湖泊综合治理与资源开发教育部重点实验室, 南京 210098)
(2: Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes, Ministry of Education, Hohai University, Nanjing 210098, P. R. China)
内源污染是湖泊不可忽视的污染来源之一,对长期受到污染的湖泊,底泥可作为存储库将污染物从水中移除,但也会受到扰动向上覆水释放污染物,因此底泥释放成为湖泊富营养化发生的潜在因素.尤其针对大型浅水湖泊,易受表层风应力和底层切应力的作用影响[1],底泥长期处于动态释放过程.
氮、磷是研究者最关注的引起水域富营养化的“罪魁祸首”.与磷不同的是,氮的化学形态多样且相关生化反应复杂,无机盐均呈溶解态,容易自由迁移转化,沉积物-水界面动态的氧化还原环境和微生物活性影响着硝化-反硝化作用,最终部分氮也能以气体形式被去除.但随着人类活动频繁,大量氮元素被不断输送到水体[2],导致湖泊初级生产增长,进一步加剧氮盐的湖相循环[3].环境数值模型是模拟水质的有效工具,已成功应用于水资源管理、水质预测领域[4],然而模拟时底泥释放速率通常被设置为常数[5],分区设置可以进一步减少空间差异带来的底泥释放模拟误差,但对于大型浅水湖泊并不适用,对底泥释放进行精细化模拟十分必要.沉积成岩模型可有效模拟内源释放的动态变化,多用于研究河口和沿海区域沉积物-水界面的营养交换[6-7]. Chen等[8]建立沉积成岩模型来表征小型潮汐沼泽底栖生物的养分通量,Prakash等[9]为CE-QUAL-W2开发沉积成岩模型以研究矿坑湖沉积物-水界面生物气体的生成和释放.目前沉积成岩理论在淡水湖的应用很少,在常见的水质模型中,只有CE-QUALICM/TOXI模型和EFDC模型开发了沉积成岩模块[10].现用沉积成岩模型模拟太湖内源磷释放已有成功案例[11],但对氮的内源释放模拟还有待研究.
本文基于EFDC(Environmental Fluid Dynamic Code)模型建立太湖沉积成岩模型,以太湖5个湖区为研究对象,从沉积成岩模型中选取与氮模拟密切相关的18个参数,运用拉丁超立方抽样(LHS)排列出200组参数组合,使用概率统计方法分析参数对氨氮和硝态氮的不确定性影响,采用标准秩回归分析法定量衡量参数敏感性,识别底泥释放的关键物理生化过程和沉积成岩模型的敏感参数,为大型浅水湖泊的底泥释放研究提供参考.
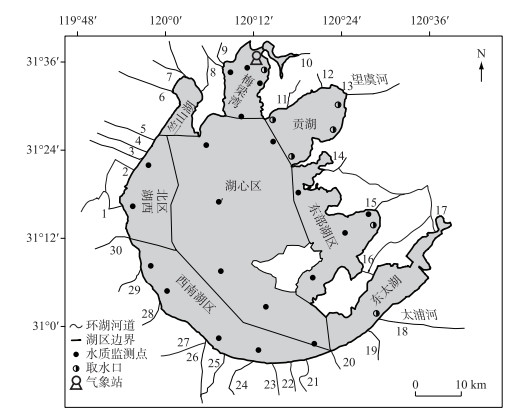
1 研究区域太湖(30°55′~31°32′N,119°52′~120°36′E)是我国第三大淡水湖,位于长江三角洲南部,水域面积2338 km2,平均水深1.9 m,属于典型的大型浅水湖泊.长期以来,工业活动向太湖输入大量营养物质,太湖水体和底泥中积累了丰富的含氮化合物.营养元素的不均匀分布使太湖呈现“草-藻”型生态系统共存格局[12],污染严重的西部湖区呈现明显的藻型特征,东部湖区水质较清呈现草型特征.为研究氮在太湖不同类型湖区的分布特征,将太湖划分为8个湖区(图 1),并选取藻型湖区梅梁湾、西北湖区、西南湖区,草型湖区东部湖区、湖心区共5个湖区作为主要研究区.
|
图 1 太湖湖区划分及监测点位 Fig.1 Lake Taihu area division and monitoring points |
本案例选用开发有沉积成岩模块的EFDC模型进行模型构建,将太湖水平划分为4464个矩形网格,网格尺寸750 m×750 m,东西横跨89个网格,南北纵跃95个网格.边界条件包括太湖出入湖流量、水温水质、风场气象的时间序列.气象和温度数据来自中国科学院太湖湖泊生态系统研究站的气象监测站,流量和水质监测数据来自监测站点(位置见图 1),水质指标为氨氮和硝态氮,监测频率为每月一次,水质数据采用2004年湖区30个采样点每月一次的表层水样的实测值.为简化模型将太湖沿岸河流概化为30条作为出入湖边界[13].模型计算初始日期2004年1月1日,模拟周期365天,采用动步长计算方式,初始时间步长10 s,安全因子0.2.水动力[13]、水质[14]和成岩参数已得到率定验证,氨氮和硝态氮浓度在梅梁湾的相对误差分别是30.46 %、27.54 %,在竺山湾的相对误差分别是33.36 %、32.57 %,在湖心区的相对误差分别是28.06 %、27.32 %.
2.2 沉积成岩模型原理EFDC的沉积成岩模块以DiToro和Fitzpatrick为切萨皮克湾开发的沉积模型为基础,其原理基于质量守恒定律,包含沉降通量、成岩通量、沉积通量三类通量,这些通量将耦合到水质模块中.如图 2所示,水体中颗粒态有机氮在重力作用下沉降到底泥形成沉降通量①,底泥中颗粒态有机氮中易降解的部分被成岩作用分解为氨氮和硝态氮,产生成岩通量②,氨氮、硝态氮受浓度梯度驱动扩散到上覆水中产生沉积通量③.沉积成岩模型假设底泥分为两层:上层是好氧或缺氧,下层总是厌氧,下层的厚度远远大于上层(厚度约0.1 cm[15]).三类通量的具体计算公式如下[15]:

|
图 2 沉积成岩模型中氮的三类通量 (PON表示颗粒态有机氮,LPON表示易降解颗粒有机氮,RPON表示难降解颗粒有机氮) Fig.2 Three types of fluxes of nitrogen in diagenesis module (PON represents granular organic nitrogen, LPON represents organic nitrogen of easily degraded particles, and RPON represents organic nitrogen of refractory particles) |
沉降通量:
| $ {{J_{{\rm{PON}},i}} = FNL{P_i}W{S_{LP}}LPO{N^\mathit{N}} + FNR{P_i}W{S_{RP}}RPO{N^\mathit{N}} + \sum\limits_{x = c,d,g} F N{B_{x,i}}AN{C_x}W{S_x}B_x^N} $ | (1) |
成岩通量:
| $ {{J_{{\rm{PON}},{i_2}}} = {K_{{\rm{PON}},i}}\theta _{{\rm{PON}},i}^{T - 20}{H_2} - W{G_{{\rm{PON}},i}} + {H_2}\frac{{\partial {G_{{\rm{PON}},{\rm{i}}}}}}{{\partial t}}} $ | (2) |
沉积通量包括氨氮和硝态氮的沉积通量,氨氮的沉积通量:
| $ {{J_{aq}} = KL\left( {C{t_2} - C{t_1}} \right) - WC{t_1} - \frac{{\kappa _{1,{\rm{NH}}}^2}}{s}N{H_{4l}} = s\left( {C{t_1} - f{d_0}C{t_0}} \right)} $ | (3) |
| $ {\kappa _{1,{\rm{N}}{{\rm{H}}_2}}^2 = \frac{{D{O_0}}}{{2K{M_{{\rm{N}}{{\rm{H}}_,},{0_2}}} + D{O_0}}}\frac{{K{M_{{\rm{N}}{{\rm{H}}_4}}}}}{{K{M_{{\rm{N}}{{\rm{H}}_ + }}} + N{H_{41}}}}\kappa _{{\rm{N}}{{\rm{H}}_4}}^2\theta _{{\rm{N}}{{\rm{H}}_4}}^{T - 20}} $ | (4) |
| $ {{H_2}\frac{{\partial C{t_2}}}{{\partial t}} = - KL\left( {C{t_2} - C{t_1}} \right) + W\left( {C{t_1} - C{t_2}} \right) + \sum\limits_{i = 1}^2 {{K_{{\rm{PON}},i}}} \theta _{{\rm{PON}},i}^{T - 20}{G_{{\rm{PON}},i}}{H_2}} $ | (5) |
硝态氮的沉积通量:
| $ {{J_{aq}} = KL\left( {C{t_2} - C{t_1}} \right) - WC{t_1} - \frac{{\kappa _{{\rm{N}}{{\rm{O}}_{3,1}}}^2\theta _{{\rm{N}}{{\rm{O}}_3}}^{T - 20}}}{s}N{H_{41}} = s\left( {C{t_1} - f{d_0}C{t_0}} \right)} $ | (6) |
| $ {{H_2}\frac{{\partial C{t_2}}}{{\partial t}} = - KL\left( {C{t_2} - C{t_1}} \right) + W\left( {C{t_1} - C{t_2}} \right) - {\kappa _{{\rm{N}}{{\rm{O}}_{3,2}}}}\theta _{{\rm{N}}{{\rm{O}}_3}}^{T - 20}C{t_2}} $ | (7) |
由于氮气通量从水体中去除对水质没有影响,故未列出计算公式,式中各符号的物理意义见表 1.
| 表 1 公式中各符号物理意义* Tab. 1 The meanings of the symbols in the formula |
根据沉积物-水界面的物理生化作用及沉积成岩模型原理,选取18个参数作为不确定性和敏感性分析的输入参数(表 2),假设参数服从均匀分布,参数取值综合参考海湾、河流、浅水湖泊的相关文献[16-19].
| 表 2 沉积成岩模型输入参数取值范围 Tab. 2 The range of input parameters of diagenesis model |
拉丁超立方抽样(LHS)是一种分层抽样方法[20],能使抽样结果均匀覆盖到可行区间,且能反应样本的概率分布[21],是不确定分析的常见抽样方法. LHS假设参数之间相互独立,若待抽样组数为n,有k个输入变量,则抽样步骤为[22]:①对每个输入变量X1、X2…Xk在其可行区间内均匀分成n个互不重合的小区间,在每个小区间内按变量的概率密度分布随机抽样,则对第k个变量Xk而言有n个取值;②将变量X1产生的n个取值与X2的n个取值随机配对,再与X3的n个取值随机组合,依次类推,最终得到一组n个抽样数的k维变量组值.由于LHS在取样上的优越性,当抽样组数大于变量个数的4/3时可得到稳定的输出结果[23],本案例在参数的抽样组数上进行鲁棒性实验,结合计算时长的消耗和不确定性结果的稳定性综合考虑,选取抽取组数200组[11, 13-14](n≈11k).
2.3.3 不确定性分析方法不确定性分析采用概率统计方法[24]:①将LHS产生的n个变量值代入EFDC模型计算产生n个模拟值;②将n个模拟值按大小排列,分配给每个模拟值出现的概率为1/n,所有模拟值出现的概率之和为1,得到模拟值的累积经验分布函数;③累积经验分布函数提供了模拟值的分位值,即p/n×100 %是第p个模拟值的分位点.本文以5 %、95 %分位点作为氮浓度不确定性边界[25],以均值与5 %、95 %分位点的差值分别求得不确定性的下宽度与上宽度,以氮浓度的方差定量衡量不确定性.
2.3.4 敏感性分析方法标准秩回归分析方法是典型的回归分析方法,假设变量之间相互独立,可解决变量与模拟值间的非线性关系,先将参数值和模拟值排序得秩,最小值为秩1,接着用秩排序代替原始数据进行回归分析,计算公式如下[26]:
1) 对n组输入变量值和模拟值进行回归分析:
| $ {\hat y_i} = {b_0} + \sum\nolimits_j {{b_j}} {x_{ij}} + {\varepsilon _i}(i = 1,2, \cdots ,n;j = 1,2, \cdots ,k) $ | (8) |
式中, n为抽样次数,k为参数个数,ŷi是模拟值yi的估计量,b0、bj是回归系数,xij是第j个参数的第i个参数组的值,εi是误差.
2) 将回归结果进行标准化:
| $ \frac{{\hat y - \bar y}}{{\hat s}} = \sum\limits_{j = 1}^n {\left( {{b_j}{{\hat s}_j}/\hat s} \right)} \left( {{x_j} - {{\bar x}_j}} \right)/{\hat s_j} $ | (9) |
式中, xj、ŝj是参数xj的平均值和标准差,y、ŝ是模拟值的平均值和标准差,bjŝj/ŝ是回归系数(SRRC),SRRC越大表明输入变量越敏感,对模型结果不确定性的贡献率越大.
3) 计算决定系数:
| $ {R^2} = \sum\limits_{j = 1}^k S RRC_j^2 $ | (10) |
式中, SRRCj2是输入变量j对氮浓度方差的贡献率,R2表征不确定性回归模型分析的可行性程度,R2越大回归分析越可行,一般大于0.7认为回归分析合理.本例分别对氨氮、硝态氮浓度作回归分析,决定系数R2大于0.7的网格占比超过75 %,认为回归分析可行.
3 结果与讨论太湖表层底泥中的有机氮主要来自藻类[27],藻类生长从水体吸收大量硝态氮和氨氮,死亡后沉降到底泥,有机质被降解为无机氮,水体和底泥中不同形态的氮含量与藻类生长密切相关.根据藻类休眠-复苏-生物量增加-上浮及聚集四阶段理论[28],选取藻类休眠、生物量增加、上浮及聚集三个时期所在的2月、5月和7月为时间点,分别对应模型的第50天(冬季)、第150天(春季)和第200天(夏季),以氨氮和硝态氮为水质目标探究藻类不同生长期下水质的不确定性和参数敏感性差异.
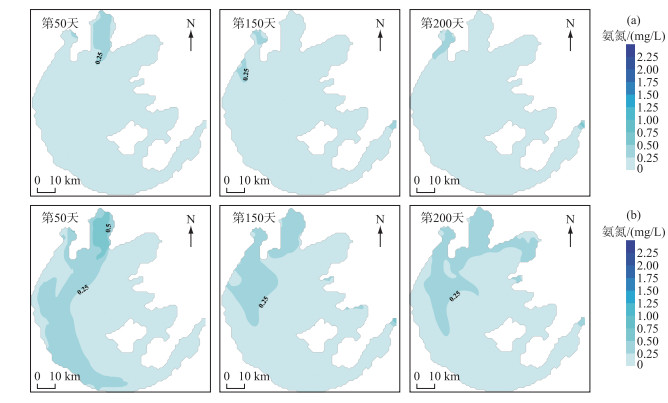
3.1 不确定性分析氨氮浓度分布表现出显著的时空差异性,西北湖区(1.34~2.51 mg/L)和梅梁湾(0.42~2.66 mg/L)浓度较高,东部湖区(0.03~0.08 mg/L)浓度较低,氨氮浓度自西北至东南方向递减,西北湖区>梅梁湾>西南湖区>湖心区>东部湖区,氨氮的时间变化特征表现为冬季高、夏秋低,这与已有对太湖氨氮浓度分布的研究一致[29].使用氨氮浓度的上宽度与下宽度得到不确定性的时空分布特征(图 3),第50天氨氮浓度5 %、95 %分位点与均值的差异不大,西北湖区和西南湖区第150天的95 %分位点分别比均值高0.27、0.14 mg/L,第200天分别比均值高0.17、0.14 mg/L;西北湖区第150天、第200天的5 %分位点低于均值的13.4 % ~17.5 %,梅梁湾分别低于均值的76.1 % ~85.7 %.第50天梅梁湾、西北湖区、西南湖区的氨氮下宽度较上宽度较大,第150天和第200天氨氮浓度的不确定性主要集中在梅梁湾和西北湖区,参数的不确定性导致氨氮浓度整体偏低.对比上宽度和下宽度,参数不确定性对水体中氨氮浓度的不确定性有显著的时空差异性.
|
图 3 氨氮浓度第50天、150天、200天的上宽度(a)、下宽度(b) Fig.3 Top width (a) and bottom width (b) of ammonia nitrogen concentration on day 50, 150 and 200 |
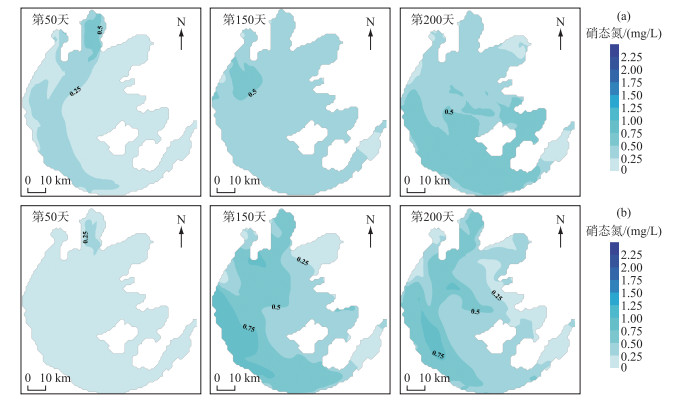
硝态氮浓度同样呈现时空差异性,在西北湖区(0.3~2.51 mg/L)和梅梁湾(0.87~1.38 mg/L)较高,在东部湖区(0.12~0.34 mg/L)较低,自西北至东南方向递减,西北湖区>梅梁湾>西南湖区>湖心区>东部湖区,时间上同样表现为冬季高、夏秋低.硝态氮浓度不确定性的时空分布特征(图 4)表明,第50天梅梁湾的硝态氮浓度上下边界分别偏离均值0.51、0.33 mg/L,西北湖区的硝态氮浓度上下边界分别偏离均值0.49、0.22 mg/L,这两个湖区第150天和第200天硝态氮浓度上下边界分别偏离均值的19.09 % ~72.14 %和27.50 % ~84.62 %.第50天硝态氮浓度的上宽度大于下宽度,参数的不确定性导致第50天硝态氮浓度偏高,第150天和第200天氨氮浓度的不确定性主要集中在梅梁湾、西北湖区、西南湖区.参数导致的硝态氮浓度的不确定性与时间、空间显著相关,且不确定性明显大于氨氮.
|
图 4 硝态氮浓度第50天、150天、200天的上宽度(a)、下宽度(b) Fig.4 Top width (a) and bottom width (b) of nitrate nitrogen concentration on day 50, 150 and 200 |
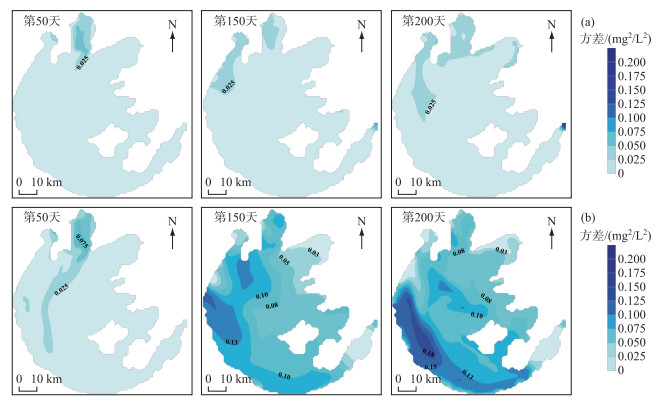
计算同一点位200组水质浓度的方差(图 5)定量衡量不确定性,方差越大表示不确定性越大.氨氮浓度方差为0.0002~0.035 mg2/L2,梅梁湾和西北湖区不确定性较大,方差均大于0.01 mg2/L2,其余湖区方差均小于0.01 mg2/L2;硝态氮浓度方差为0.001~0.146 mg2/L2,第50天和第150天梅梁湾的不确定性最大,方差分别为0.050和0.102 mg2/L2,第200天西南湖区的不确定性最大,方差为0.146 mg2/L2,湖心区方差为0.078 mg2/L2.两种氮浓度的不确定性均表现为夏季>春季>冬季,硝态氮浓度不确定性大于氨氮.
|
图 5 氨氮(a)、硝态氮(b)浓度第50、150、200天的方差 Fig.5 Variance of concentration of ammonia nitrogen (a) and nitrate nitrogen (b) on day 50, 150, and 200 |
不确定性的上下边界和水质浓度方差都表明硝态氮的不确定性大于氨氮,污染严重的梅梁湾、西北湖区、西南湖区的不确定性较大.水质指标和湖区间的不确定性差异揭示了一个重要因素是水质本底浓度,水质浓度越高其不确定性越大.不确定性大小随时间的响应特征为夏季>春季>冬季.冬季水温较低、光照条件很弱,藻类生长处于休眠期,沉积物-水界面的物理生化反应缓慢,沉积成岩过程对水质的影响很小.春季温度回升,微生物活性逐渐增强,沉积物-水界面生化反应加快,处于生物量增加期的藻类对氮需求急增,通过改变沉积物pH和氧化还原环境促进沉积物中有机氮分解[30],使氨氮进入间隙水进而向上覆水扩散,其中涉及的生化反应和动力过程对上覆水中氮浓度影响很大.夏季温度持续上升,剧烈的生化反应、藻类聚集上浮的扰动对底泥释放起促进作用.
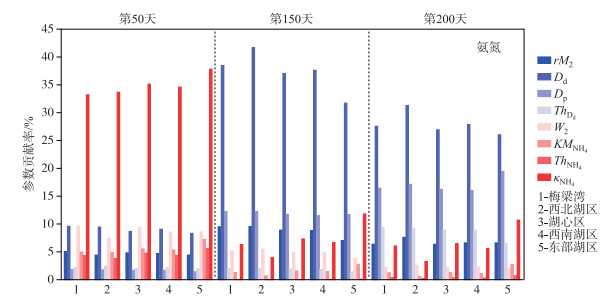
3.2 敏感性分析筛除贡献率低于5 %的弱敏感参数得到氨氮各敏感参数的贡献率(图 6),8个敏感参数(rM2、Dd、Dp、ThDd、W2、KMNH4 、ThNH4 、kNH4 )对氨氮浓度不确定性的贡献率之和超过70 %,起主导作用的敏感参数随藻类生长而变化.冬季20℃时的最优硝化反应速率(kNH4 )最敏感,对各湖区氨氮的不确定性贡献率为33.21 % ~37.82 %,约占参数贡献率的一半,孔隙水扩散系数(Dd)和底泥覆盖速率(W2)分别排第二和第三,贡献率均超过7.4 %.春季最敏感参数变为Dd,贡献率41.68 % ~31.73 %,颗粒物混合表面扩散系数(Dp)和下层(第二层)固体浓度(rM2)次之,贡献率均超过7 %.夏季最敏感参数依然是Dd,其贡献率下降到26.03 % ~31.29 %,Dp的贡献率15.99 % ~19.47 %,其余参数的贡献率均小于10 %.各湖区间氨氮的敏感参数排序高度一致,春、夏季孔隙水扩散系数(Dd)敏感,冬季最优硝化反应速率(kNH4)最敏感.
|
图 6 沉积成岩模型参数对各湖区氨氮浓度不确定性贡献率 Fig.6 The contribution of diagenesis model parameters to the uncertainty of ammonia nitrogen concentration in each lake area |
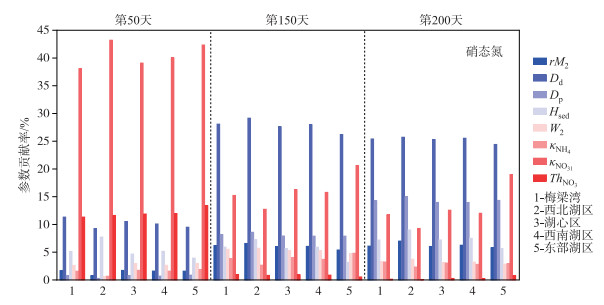
硝态氮的8个敏感参数(rM2、Dd、Dp、Hsed、W2、kNH4、KNO31、ThNO3)的不确定性贡献率超过71.3 % (图 7),主要敏感参数也随时间变化.冬季硝态氮的最敏感参数是20℃时表层反硝化作用反应速率(kNO31 ),对各湖区硝态氮的不确定性贡献率为38.06 % ~43.21 %,超过参数贡献率的一半,孔隙水扩散系数Dd排列第二,反硝化速率的温度调节系数(ThNO3)排列第三,贡献率均超过9.25 %.春季最敏感参数是Dd,贡献率为26.22 % ~29.15 %,KNO31和Dp次之,贡献率均超过7.89 %.夏季的参数敏感性排序与春季相同,主要敏感参数Dd的贡献率26.03 % ~31.29 %,次敏感参数是Dp和ThDd,不同的是Dp的贡献率上升到15.99 % ~19.47 %,其余参数敏感性排序均与春季相同.春、夏季硝态氮的主要敏感参数是孔隙水扩散系数(Dd),冬季的最敏感参数是表层反硝化作用反应速率(kNO31).
|
图 7 沉积成岩模型参数对各湖区硝态氮浓度不确定性贡献率 Fig.7 The contribution of diagenesis parameters to the uncertainty of nitrate nitrogen concentration in each lake area |
同一水质目标下各湖区参数敏感性排序一致,氨氮、硝态氮的敏感参数主要与沉积物-水界面的硝化速率、反硝化速率和扩散过程有关.氨氮的主要敏感参数是孔隙水扩散系数(Dd)和最优硝化反应速率(kNH4);硝态氮的敏感参数是Dd和表层反硝化作用反应速率(kNO31 ).产生影响的硝化和反硝化作用均发生在底泥表层,这是因为表层底泥可以为生化反应提供好氧或缺氧环境,反应产物直接扩散到上覆水中,对水质的影响更为直接;水动力方面,底泥中氮释放的原理是无机盐先进入到孔隙水再受浓度梯度驱动扩散到上覆水中,Dd对氮盐释放起直接影响,敏感参数在模型率定中需予以重点关注.现有研究中对磷模拟得到的敏感参数排序在湖区间并不一致[11],对藻类模拟筛选出的是敏感的光照和温度参数[31],与氮敏感参数的空间排序和类别均有差异,这与氮盐多通道的转化途径和氮释放所受动力影响大于生化反应影响有关.至于敏感参数随时间的变化,春、夏季节藻类生长对氮的需求加速了氮盐从底泥扩散到上覆水的过程,藻类上浮和聚集过程产生扰动,水动力影响很大,冬季沉积物-水界面较为平静,动力参数影响的弱化放大了生化反应参数的敏感性,这意味着在不考虑藻类生长的数值模拟中应把kNH4 和kNO31放在优先调整的地位.
根据筛选出的氨氮和硝态氮的敏感参数,将参数范围缩小到氮浓度90 %置信度不确定性下参数的取值区间,优化后的参数范围见表 3.
| 表 3 敏感参数的取值范围 Tab. 3 Possible range of sensitive parameters |
1) 对于大型浅水湖泊,沉积物-水界面的硝化作用、反硝化作用和扩散过程对氮浓度的不确定性影响较大.太湖氮浓度不确定性的空间特征为梅梁湾>西北湖区>西南湖区>湖心区>东部湖区,时间特征为夏季>春季>冬季,硝态氮浓度的不确定性大于氨氮;氮浓度的不确定性受藻类生长影响.
2) 在藻型湖泊底泥释放模拟中,随着藻类生长生化反应参数的敏感性逐渐减弱,动力参数的敏感性逐渐增强.氨氮的最敏感参数是最优硝化反应速率(冬季)和孔隙水扩散系数(春夏季),硝态氮的最敏感参数是表层反硝化作用反应速率(冬季)和孔隙水扩散系数(春夏季),这些参数与沉积物-水界面硝化作用、反硝化作用和孔隙水的扩散过程有关,在率定时需予以着重考虑.
3) 对于大型浅水湖泊尤其是藻草型特征共存的湖泊,在底泥释放模拟中若涵盖藻类生长过程应优先调整动力参数,若不考虑藻类生长过程则优先调整生化反应参数.
4) 敏感性分析提供了参数调整的优先级,对优化参数区间以进一步减小模型的不确定性、提高模型精度有参考意义.
| [1] |
Qin BQ. Progress and prospect on the eco-environmental research of Lake Taihu. J Lake Sci, 2009, 21(4): 445-455. [秦伯强. 太湖生态与环境若干问题的研究进展及其展望. 湖泊科学, 2009, 21(4): 445-455. DOI:10.18307/2009.0401] |
| [2] |
Gruber N, Galloway JN. An earth-system perspective of the global nitrogen cycle. Nature, 2008, 451(7176): 293-296. DOI:10.1038/nature06592 |
| [3] |
Zhang YP, Wan Y, Nie Q et al. Biogeochemical process and its ecological significance of nitrogen in lake systems. Journal of Nanjin University:Nature Sciences, 2016, 52(1): 5-15. [张亚平, 万宇, 聂青等. 湖泊水体中氮的生物地球化学过程及其生态学意义. 南京大学学报:自然科学, 2016, 52(1): 5-15.] |
| [4] |
Zhu W, Feng GY, Liu YF. Influence of environmental dredging on the water quality and studies on sensitive parameters of a typical deep reservoir (Tongjiqiao Reservoir). J Lake Sci, 2019, 31(4): 930-940. [朱伟, 冯甘雨, 刘毅璠等. 深水型水库环保疏浚对水质的影响及敏感参数研究——以通济桥水库为例. 湖泊科学, 2019, 31(4): 930-940. DOI:10.18307/2019.0419] |
| [5] |
Zou R, Wu Z, Zhao L et al. Nutrient cycling flux of Lake Dianchi:A three-dimensional water quality modelling approach. J Lake Sci, 2017, 29(4): 819-826. [邹锐, 吴桢, 赵磊等. 湖泊营养盐通量平衡的三维数值模拟. 湖泊科学, 2017, 29(4): 819-826. DOI:10.18307/2017.0405] |
| [6] |
Testa JM, Brady DC, Di Toro DM et al. Sediment flux modeling:Simulating nitrogen, phosphorus, and silica cycles. Estuarine, Coastal and Shelf Science, 2013, 131: 1-19. DOI:10.1016/j.ecss.2013.07.010 |
| [7] |
Paraska DW, Hipsey MR, Salmon SU. Sediment diagenesis models:Review of approaches, challenges and opportunities. Environmental Modelling & Software, 2014, 61: 297-325. |
| [8] |
Yan C, Rui Z, Han S et al. Development of an integrated water quality and macroalgae simulation model for tidal marsh eutrophication control decision support. Water, 2017, 9(4): 277. DOI:10.3390/w9040277 |
| [9] |
Prakash S, Vandenberg JA, Buchak EM. Sediment diagenesis module for CE-QUAL-W2 Part 2:numerical formulation. Environmental Modeling & Assessment, 2015, 20(3): 249-258. |
| [10] |
Li YP, Shi YY, Jiang L et al. Advances in surface water environment numerical models. Water Resources Protection, 2019, 35(4): 1-8. [李一平, 施媛媛, 姜龙等. 地表水环境数学模型研究进展. 水资源保护, 2019, 35(4): 1-8.] |
| [11] |
Shi YY, Li YP, Cheng Y et al. Uncertainty and sensitivity analysis of phosphorus model parameters in large shallow lakes. Environmental Science, 2019, 40(10): 4478-4486. [施媛媛, 李一平, 程月等. 大型浅水湖泊磷模型参数不确定性及敏感性分析. 环境科学, 2019, 40(10): 4478-4486.] |
| [12] |
Wang YP, Zhu GW, Hong DL. Environmental characteristics of sediment-water interface of phytoplankton and macrophyte dominated zones in Lake Taihu. J Lake Sci, 2013, 25(2): 199-208. [王永平, 朱广伟, 洪大林等. 太湖草/藻型湖区沉积物-水界面环境特征差异. 湖泊科学, 2013, 25(2): 199-208. DOI:10.18307/2013.0204] |
| [13] |
Li YP, Tang CY, Yu ZB et al. Uncertainty and sensitivity analysis of large shallow lake hydrodynamic models. Advances in Water Science,, 2012, 23(2): 271-277. [李一平, 唐春燕, 余钟波等. 大型浅水湖泊水动力模型不确定性和敏感性分析. 水科学进展, 2012, 23(2): 271-277.] |
| [14] |
Li YP, Tang CY, Zhu TJ et al. Parametric uncertainty and sensitivity analysis of hydrodynamic processes for a large shallow freshwater lake. Hydrological Sciences Journal, 2015, 60(6): 1-18. |
| [15] |
Ji ZG. Hydrodynamics and water quality: Modeling rivers, lakes, and estuaries. Tetra Tech Inc Wiley Interscience, John Wiley & Sons, Inc., 2017: 292-293.[ [季振刚.水动力学和水质——河流、湖泊及河口数值模拟.北京: 海洋出版社, 2017: 292-293.] ]
|
| [16] |
Di Toro DM, Fitzpatrick JJ. Chesapeake bay sediment flux model. Hydro Qual, Inc., 1993.
|
| [17] |
Testa JM, Brady DC, Di Toro DM. Sediment flux modeling:Simulating nitrogen, phosphorus, and silica cycles. Estuarine, Coastal and Shelf Science, 2013, 131: 245-263. DOI:10.1016/j.ecss.2013.06.014 |
| [18] |
Zhang ZL, Sun BW, Johnson BE. Integration of a benthic sediment diagenesis module into the two dimensional hydrodynamic and water quality model-CE-QUAL-W2. Ecological Modelling, 2015, 297: 213-231. DOI:10.1016/j.ecolmodel.2014.10.025 |
| [19] |
Moore PA, Reddy KR, Fisher MM. Phosphorus flux between sediment and overlying water in Lake Okeechobee, Florida:Spatial and temporal variations. Journal of Environment Quality, 1998, 27(6): 1428-1439. |
| [20] |
Wan HP, Ren WX, Wang NB. A Gaussian process model based global sensitivity analysis approach for parameter selection and sampling methods. Journal of Vibration Engineering, 2015, 28(5): 714-720. [万华平, 任伟新, 王宁波. 高斯过程模型的全局灵敏度分析的参数选择及采样方法. 振动工程学报, 2015, 28(5): 714-720.] |
| [21] |
Wang Y, Lu WX, Bian JM et al. Surrogate model of numerical simulation model of groundwater based on Wavelet Neural Network. China Environmental Science, 2015, 35(1): 139-146. [王宇, 卢文喜, 卞建民等. 基于小波神经网络的地下水流数值模拟模型的替代模型研究. 中国环境科学, 2015, 35(1): 139-146.] |
| [22] |
Helton JC, Davis FJ. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliability Engineering and System Safety, 2003, 81: 23-69. DOI:10.1016/S0951-8320(03)00058-9 |
| [23] |
Manache G, Melching C. Sensitivity of latin hypercube sampling to sample size and distributional assumptions. In:Proceedings CD-ROM, 32nd Congress of the International Association of Hydraulic Engineering and Research, Venice, Italy, 2007, 1-6. |
| [24] |
Li YP, Qiu L, Tang CY et al. Uncertainty and sensitivity analysis of input conditions in large shallow lake hydrodynamic model. China Environmental Science, 2014, 34(2): 410-416. [李一平, 邱利, 唐春燕等. 湖泊水动力模型外部输入条件不确定性和敏感性分析. 中国环境科学, 2014, 34(2): 410-416.] |
| [25] |
Shi XQ, Wu JC, Jiang BL et al. Uncertainty analysis of groundwater models based on the Latin Hypercube Sampling technique. Hydrogeology and Engineering Geology, 2009, 36(2): 1-6. [施小青, 吴吉春, 姜蓓蕾等. 基于LHS方法的地下水流模型不确定性分析. 水文地质工程地质, 2009, 36(2): 1-6.] |
| [26] |
Pan F, Zhu JT, Ye M et al. Sensitivity analysis of unsaturated flow and contaminant transport with correlated parameters. Journal of Hydrology, 2011, 397: 238-249. DOI:10.1016/j.jhydrol.2010.11.045 |
| [27] |
Ni ZK, Li YJ, Wang SR. The sources of organic carbon and nitrogen in sediment of Taihu Lake. Acta Ecologica Sinica, 2011, 31(16): 4661-4670. [倪兆奎, 李跃进, 王圣瑞等. 太湖沉积物有机碳与氮的来源. 生态学报, 2011, 31(16): 4661-4670.] |
| [28] |
Kong FX, Gao G. Hypothesis on cyanobacteria bloom-forming mechanism in large shallow eutrophic lakes. Acta Ecologica Sinica, 2005(3): 589-595. [孔繁翔, 高光. 大型浅水富营养化湖泊中蓝藻水华形成机理的思考. 生态学报, 2005(3): 589-595.] |
| [29] |
Lu WW, Yao X, Zhang BH et al. Temporal-spatial distribution of nitrogen and phosphorus nutrients in Lake Taihu based on geostatistical analysis. Environmental Science, 2019, 40(2): 590-602. [吕伟伟, 姚昕, 张保华等. 基于地统计学分析的太湖颗粒态和溶解态氮、磷营养盐时空分布特征及来源分析. 环境科学, 2019, 40(2): 590-602.] |
| [30] |
Geng Xue, Wen SL, Sun PR et al. Environmental significance of phosphorus fractions of phytoplankton and macrophyte dominated zones in Taihu Lake. Environmental Science, 2019(12): 1-16. [耿雪, 文帅龙, 孙培荣等. 太湖草藻型湖区磷赋存特征及其环境意义. 环境科学, 2019(12): 1-16.] |
| [31] |
Jiang L, Li YP, Zhang SS et al. Parameter sensitivity analysis of algal model in large shallow lakes. J Lake Sci, 2018, 30(3): 693-700. [姜龙, 李一平, 章双双等. 大型浅水湖泊藻类模型参数敏感性分析. 湖泊科学, 2018, 30(3): 693-700. DOI:10.18307/2013.0204] |
 2020, Vol. 32
2020, Vol. 32 


