水生植被广泛分布于河流、湖泊以及滨海湿地等浅水域中，为鱼类、底栖动物和其他水生动物提供食物和栖息地^[1-3].水生植被可以吸收水体过剩营养物质，净化水质改善透明度；通过植物根系稳定河床保护河岸；还可衰减波浪，避免海岸带遭受侵蚀^[4-5].在浅水域，沉积物易受风生波影响导致再悬浮，加剧悬浮颗粒中营养物和污染物的释放，从而导致水体营养物质的增加以及水质恶化^[6].太湖的原位观测实验表明，太湖底泥沉积物再悬浮的临界剪切应力为0.03~0.04 N/m²，风生浪是导致太湖底泥沉积物再悬浮的主要驱动力，当风速达到6.5 m/s时，沉积物再悬浮含量以及水体氮磷营养物质浓度会急剧增加^[6].一方面，水生植被可以有效削减波浪并降低近床面波速^[7-8]，从而减少波浪驱动的沉积物再悬浮^[9]；另一方面，有研究表明波浪与植被的相互作用能增强近床面的紊流^[10-11]，而紊流的增加能增强沉积物的再悬浮作用.研究发现，柔性沉水植被的刚性叶鞘具有与挺水植被类似的性质，刚性叶鞘部分产生的近床面紊动能与波浪轨道运动半径(A_w)和植株间距(S)的比值(A_w/S)有关，当A_w/S > 0.5时，相比无植被情景，植被能有效增加近床面紊动能^[11].随机排列的红树林模型植被实验结果表明，波浪驱动的沉积物悬浮浓度与紊流强度之间存在正相关关系，再悬浮的临界波速在植被层内相对于光滑床面更低，其原因在于植被产生的紊流作用促进了沉积物再悬浮^[12].当植被产生的紊流强度增加了近床面的总紊流强度时，沉积物悬浮浓度也随之增强^[13].相比实验室研究，田间尺度上密集的鳗草冠层内波浪速度和紊流的减少，反过来减少了沉积物再悬浮^[14].同样，在浅水湖泊中，与无植被区域相比，沉水和挺水植物的存在使滇池福宝湾生态恢复区的底泥再悬浮量、氮磷释放量均削减了80 %以上^[9].田间观测和实验室观测之间互相矛盾的结果反映了植被对波浪衰减^[15]和紊流形成的双重影响^[11].即是植被产生的紊流可以局部增强沉积物再悬浮作用^[12-13]，但是大面积植被的波浪衰减可以有效减少沉积物的再悬浮^[14].本研究以植被茎干产生的紊流可局部增强沉积物再悬浮为切入点，旨在阐明波浪条件下刚性植被茎干产生的紊流如何影响沉积物再悬浮过程，提出沉积物再悬浮植被紊流模型，基于该模型预测沉积物再悬浮的临界波速，通过水槽试验的实测数据对该模型进行验证，并将其扩展到其他研究中.

1 植被紊流与临界波速的理论关系

植被产生的紊流涡旋将能量从平均流场转移到紊流中，单向水流中非淹没刚性植被产生的紊流模型k_tv可表示为^[16]：

$ {k_{tv}} = {\delta ^2}\left( {{C_D}\frac{{2\phi }}{{{\rm{ \mathit{ π} }}\left( {1 - \phi } \right)}}} \right){\rm{}}{^{2/3}}{U^2} $

(1)

式中，U为空间和时间平均的纵向速度，C_D为植被拖曳力系数，$ \phi $是植被固相体积分数，δ为比例因子.对圆柱形植被茎干而言，$ \phi $=mπd²/4，其中m为植被茎干密度(根/m²)，d为植被直径.公式(1)适用于d/S < 0.56的植被情景.

研究表明，近床面总紊动能(k_t)可表示为植被产生的紊动能(k_tv)与床面产生的紊动能(k_tb)之和，即是k_t=k_tv+k_tb^[17].在光滑床面的单向流动中，k_tb与水流产生的床面剪切应力τ_c之间存在线性关系，已有研究证实光滑床面τ_c/ρk_tb=0.19^[18].此外，床面剪切应力可以根据流速U和床面摩擦系数C_f估算，即τ_c=ρC_fU²，使得k_tb=C_bU²，其中C_b≈C_f/0.2.结合公式(1)，单向流中近床面总紊动能可表示为：

$ {k_t} = {\delta ^2}{\left( {{C_D}\frac{{2\phi }}{{{\rm{ \mathit{ π} }}\left( {1 - \phi } \right)}}} \right)^{2/3}}{U^2} + {C_b}{U^2} $

(2)

渠道内的流速结构或床面形态产生的紊流可以增强沉积物运动^[19]，植被产生的紊流也具有类似的影响.单向流中沉积物的初始运动由紊动能的临界值决定，根据公式(2)，光滑床面的临界总紊动能k_tc=C_bU_co²，式中，U_co为光滑床面沉积物颗粒运动的临界速度^[17].对于临界状态而言，沉积物再悬浮所需的临界紊动能k_tc为常数，即是光滑床面的临界紊动能等于有植被时近床面的临界总紊动能.等同于公式(2)对临界紊流水平的定义，变换公式(2)可得植被影响下沉积物运动的临界速度U_c：

$ \frac{{{U_c}}}{{{U_{co}}}} = \frac{1}{{\sqrt {1 + \frac{{{\delta ^2}}}{{{C_b}}}{{\left( {\frac{{2{C_D}}}{{\rm{ \mathsf{ π} }}}} \right)}^{2/3}}{{\left( {\frac{\phi }{{1 - \phi }}} \right)}^{2/3}}} }} $

(3)

对于单向流，沉积物运动的临界速度随植被固相体积分数($\phi $)的增加而减小. Tinoco和Coco^[12]结合Yang等^[17]的研究结果验证了沉积物输运模型(公式(3))，用单向流的Shields数描述波浪驱动的沉积物再悬浮过程，用波周期内临界波速最大值(即轨道波速U_w)代替临界流速，以描述无植被(U_{w, co})和植被(U_{w, c})情景下的沉积物再悬浮临界速度.假设波浪条件下光滑床面产生的紊流(k_{tb, w})与床面切应力τ_w也呈线性关系，Green and Coco^[20]已证实τ_w与波速平方U_w²呈正比(τ_w=ρ ·f_w ·U_w²/2)，f_w为波浪摩擦因子.因此，波浪条件下光滑床面产生的紊动能k_{tb, w}=C_{b, w}U_w²合理.

将公式(2)中的流速替换为波速，可得波浪驱动下的植被紊流方程为：

$ {k_{tw}} = {\delta ^2}{\left( {{C_D}\frac{{2\phi }}{{{\rm{ \mathit{ π} }}\left( {1 - \phi } \right)}}} \right)^{2/3}}U_w^2 + {C_{b, w}}U_w^2 $

(4)

本研究通过水槽试验，验证了公式(4)作为波浪条件下不同密度和直径的刚性植被层近床面紊流模型.假设波浪条件下的沉积物再悬浮紊流临界水平k_tc可以从光滑床面推断而来，即k_tc=C_{b, w}U_{w, co}²，则通过公式(4)可得圆柱形植被层内波浪驱动的沉积物再悬浮临界波速为：

$ \frac{{{U_{w, c}}}}{{{U_{w, co}}}} = \frac{{{\rm{ }}1{\rm{ }}}}{{\sqrt {1 + {\rm{ }}\frac{{{\delta ^2}}}{{{C_{b, w}}}}{{\left( {\frac{{2{C_D}}}{{\rm{ \mathit{ π} }}}} \right)}^{2/3}}{{\left( {\frac{\phi }{{1 - \phi }}} \right)}^{2/3}}{\rm{ }}} }} $

(5)

2 实验设计与方法

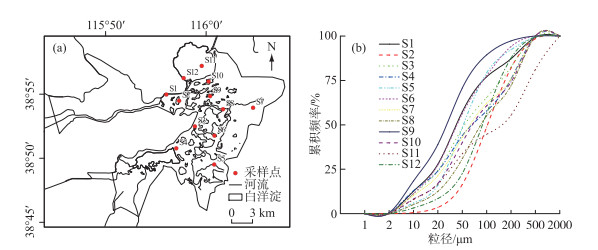
根据2016年对白洋淀春、夏、秋3个季节12个采样点的水生植被野外采样(图 1a)，S1~S12分别为东关码头、鸳鸯岛、淀头、端村、采蒲台、圈头、枣林庄、光淀张庄、王家寨、大口子、烧车淀以及旅游码头.结果显示，白洋淀挺水植被以芦苇和香蒲为主，芦苇株高为2.70±0.33 m，株茎为0.77±0.15 cm，沉水植被以金鱼藻、菹草、眼子菜科为优势种.同时采集12个采样点的沉积物，将其带回实验室物理风干后用激光粒度分析仪(Microtrac S3500 Particle Size Analyzer)进行粒径测量.结果表明，白洋淀12个采样点的沉积物平均中值粒径D₅₀ =0.076 cm，属于细砂，各采样点的沉积物粒径分布见图 1b.相比较而言，白洋淀沉积物粒径大于太湖(D₅₀=0.009 mm)、龙感湖(D₅₀ = 0.007 mm)以及巢湖的湖岸(D₅₀=0.007 mm)和湖中心(D₅₀=0.010 mm)^[21].

本试验在长24 m、宽38 cm、高60 cm的玻璃水槽中进行(图 2).为更好的阐述植被作用下近床面的沉积物再悬浮过程，同时防止流速测量仪和浓度测量仪对近床面波速和紊流结果的影响，选取长7 cm直径分别为0.32、0.64、1.26 cm的模型植被(圆木棒)用于水槽试验，以模拟浅水湖泊中的芦苇(d=0.77±0.15 cm)、滨海湿地中的红树林(根茎直径粗至2 cm^[22])，以及拥有此长度与直径刚性叶鞘的水生植被.研究结果表明，不同波浪条件下，淹没刚性植被茎干产生的紊动能(TKE)明显高于光滑床面，淹没植被上方无植被区域的紊动能与光滑床面近似，植被顶端并未出现紊动能峰值^[13].因此，7 cm的植被高度足以反映植被茎干紊流特性与沉积物再悬浮过程，同时兼顾测量仪器位置和测量效果.植被密度m=102~2121根/m²，固体体积分数$ \phi $ =0.002~0.099(表 1)，模型植被以交错排列方式插入长2 m、宽34 cm的PVC底板中，将底板置于水槽中间位置，相邻植被平均间距$ S = \sqrt {{\rm{ }}1/m} $.以中值粒径D₅₀=0.085±0.015 cm的模型沙模拟白洋淀沉积物在不同植被情景下的沉积物再悬浮规律，每组试验之前在植被前端下游60 cm处铺设长为100 cm、厚约0.5±0.2 cm的沉积物层，如图 2所示.

水槽前端通过液压驱动的垂直桨叶产生规则波浪，通过计算机程序控制波的振幅和频率，水槽末端设有1 :5的消能缓坡.试验平均水深h=40 cm，波浪周期T=2 s，振幅a_w=1.5~3.7 cm，所产生的波速为4~20 cm/s.波浪位移η(t)用频率为1000 Hz的电阻型波浪仪测定，波浪仪位于植被中部横向中间位置(图 2)，根据测量水面位移的均方根估算波幅，${a_w} = {\rm{ }}\sqrt 2 {\rm{ }}{\eta _{rms}} $.运用3D声学多普勒测速仪(ADV，Nortek Vectrino)以200 Hz的采样频率测量x(纵向)、y(横向)和z(垂直)3个方向的瞬时流速(u, v, w)，流速仪位于植被冠层中间位置.流速测量点为沙床上方1.3 cm水深处，每个流速情景下连续测量流速6 min，运用加速度阈值法去除速度数据噪点^[23].

波浪的瞬时速度u(t)可分解为时均流速U_c、震荡的波浪流速U_w(t)和紊动流速u′(t)(以u为例，对于v和w相同)：

$ u\left( t \right) = {U_c} + {U_w}\left( t \right) + u\prime \left( t \right) $

(6)

运用相位平均的方法，将不同周期内同一相位的瞬时流速进行时间平均，即可得到相位平均的流速$ \widetilde u\left( \varphi \right)$，时均流速则可表示为相位平均流速在一个波浪周期内的积分平均$({U_c} = \int_0^{2\pi } {\tilde u\left( \varphi \right){\rm{d}}\varphi /2{\rm{ \mathsf{ π} }}} ) $，波浪流速则用相位平均后流速值的均方根表示：

$ {u_{rms}} = \sqrt {\frac{1}{{{\rm{2\pi }}}}\int_0^{2{\rm{\pi }}} {{{\left[ {\widetilde u\left( \varphi \right) - {U_c}} \right]}^2}{\rm{d}}\varphi } } $

(7)

震荡的波浪速度也称轨道波速(U_w)，是波浪周期内相位平均流速的最大值，可表示为$ {U_w} = 2{\rm{ }}\sqrt {{u_{rms}}} $.紊动流速定义为瞬时流速u(t)与相位平均流速值$ \widetilde u\left( \varphi \right)$之间的偏差，每个相位内的均方根波动(u_rms，v_rms，w_rms)用于估计该相位内的紊动能，表示为：

$ TKE = (u_{rms}^2 + v_{rms}^2 + w_{rms}^2)/2 $

(8)

本文以TKE表示波周期内所有相位的时间平均的实测紊动能，以k_t表示植被紊流模型的计算紊动能.运用光学后向散射浊度仪(OBS，Seapoint Sensors Inc.)测量悬浮颗粒浓度，将其放置于植被层纵向和横向中间位置，浊度仪探头位于沙床上方5 cm处，探头朝下.每个波浪情景下，浊度仪以20 Hz的采样频率连续采集10 min，将电压输出结果转换为悬浮颗粒浓度.

3 结果与讨论 3.1 植被紊动能

对于单向流，淹没植被层顶部阻力不连续，通过剪切层不稳定性产生紊流相干结构，并在冠层顶部产生紊流峰值^[24].相比较而言，在波浪情景下，只有长波(T > 12 s)流经密度较大的植被层时会在冠层顶部产生剪切层不稳定性^[25].本研究所采用T=2 s的波浪情景未产生紊流相干结构，故仅考虑植被茎干产生的紊流.

在沙床以上1.3 cm处的测量结果表明，紊动能是波浪流速的平方(u_rms²)和植被固相体积分数($ \phi $)的函数，不同密度和直径的植被产生的紊动能随u_rms²的增加而增加，$ \phi $表示植被密度和直径对紊流的影响，如图 3所示. TKE随$ \phi $的增加呈增加趋势，对比不同直径同一$ \phi $的植被所产生的TKE发现，尽管在植被密度更大的情景下直径对TKE的影响更大，但整体上$ \phi $主导紊流的产生，如图 3中的$ \phi $=0.05和0.099.对于所有具有不同的$ \phi $和d的植被情景而言，TKE与u_rms²呈正线性关系，在波浪流速u_rms相对较低的情景下，即使在较大的直径范围内也会产生较小的TKE. 图 3中的线性关系也验证了公式(4)可以合理地描述植被对TKE的影响.

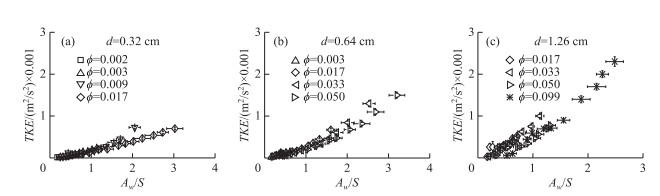
对于单一直径的植被(d=0.32、0.64或1.26 cm)，植被茎干$ \phi $越大所产生的TKE越大(图 4).对于相同的$ \phi $，直径仍然影响TKE，尤其是对于直径较大的植被，如$ \phi $=0.017和0.05，相同$ \phi $不同直径所产生的TKE差异更大.在图 4b, c中，植被固相体积分数$ \phi $=0.017的3种直径的植被层产生的TKE相近，但当$ \phi $=0.05时，直径d=0.64 cm(图 4b)和d=1.26 cm(图 4c)的植被层所产生的TKE则存在明显差异.此外，当波浪轨道运动半径与植被间距的比值A_w/S越大时(A_w=U_wT/2π)，刚性植被茎干所产生的紊动能越大，尤其是当A_w/S ≥ 1时，植被茎干产生的紊流可以传播到整个植被层，前人对沉水植被刚性叶鞘的研究也揭示了同样的结果^[11].而对于A_w/S < 0.5，本研究中茎干产生的紊流与前人研究中^[11]光滑床面产生的TKE相当，Zhang等的结果是基于$ \phi $=0.011~0.051^[11]，该植被$ \phi $范围小于本研究中的$ \phi $范围($ \phi $=0.0016~0.099).本研究中的A_w/S=0.16~3.21(图 4)，当A_w/S > 1时，植被阻力主导水流，导致冠层内的波速小于冠层外；相反，波的传播与主导惯性力有关，在A_w/S < 1的情况下冠层内的速度会变大^[13]，这表明植被所产生的TKE将根据A_w/S的不同分为两部分.

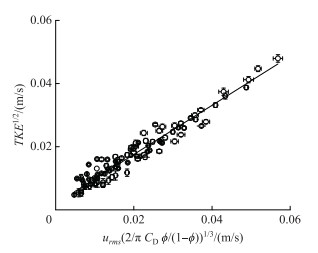
为确定植被紊流模型中紊流的比例因子δ²，将实测TKE与紊流模型预测值(公式(4)等式右边第一项)进行比较，比较结果如图 5所示.从图 3可知，$\phi $ =0.002和0.003的植被层具有与光滑床面($\phi $=0)相近的紊流水平，因此图 5中不考虑$\phi $=0.002和0.003的植被产生的紊动能.植被阻力系数C_D根据Keulegan-Carpenter数^[26](简称KC数，KC=U_wT/d)估算，得到3种直径的植被阻力系数C_D=1.5±0.3.实测紊动能与公式(4)中植被紊动能的预测值的线性拟合的斜率为δ =0.78±0.02(95 % CI)，即紊流比例因子δ²=0.61±0.02.

3.2 沉积物再悬浮浓度与临界速度

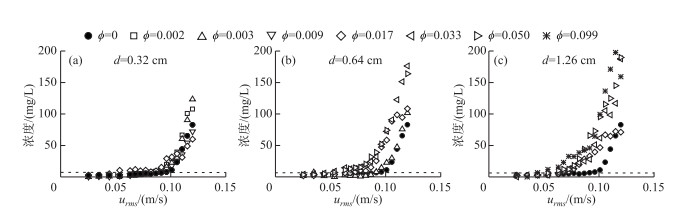
沉积物再悬浮浓度受植被固相体积分数和波浪条件共同影响，用$\phi $表示直径和密度的影响(图 6).当悬浮颗粒平均浓度高于OBS仪器噪声水平时，则认为沉积物开始悬浮，此时的波速为沉积物再悬浮的临界波速，仪器噪声水平即是不同植被情景下静水时测量浓度的平均值，为7 mg/L.本研究所用的模型沙的沉降时间为沙子在OBS测量深度(h′=5 cm)上的标准化沉降速度，即沉降速度w_s=0.4 cm/s，沉降时间h′/w_s=1.25 s.对于已经悬浮的颗粒沙，沉降时间小于波浪周期(T=2 s)，表明部分颗粒在较小的波浪条件下沉降.

除密度较小的植被情景($ \phi $ =0.002和0.003)外，其余植被情景下沉积物再悬浮的临界波速小于光滑床面的临界速度值，一旦沉积物重新悬浮，相同的波速下，悬浮浓度随植被固相体积分数$ \phi $的增加而增加(图 6).该结果表明，在大多数植被情景下，与光滑床面相比，植被的存在增强了沉积物再悬浮.同样的结果也曾被报道：悬浮浓度受到固体体积分数$ \phi $的影响，且具有较大$ \phi $的植被情景下沉积物再悬浮时间更早^[27].在直径更大(d=2 cm)的模型植被层中，单向水流下的沉积物再悬浮浓度随$ \phi $的增加而增加^[28]. Tinoco和Coco^[12]也阐明了植被层中的沉积物再悬浮浓度随$ \phi $($ \phi $=0、0.008、0.047、0.079)的增加而增加这一类似结论，在波浪扰动下，植被产生的紊动能比床面切应力更能促进沉积物再悬浮.

所有直径的植被层中沉积物再悬浮临界速度u_{rms, c}随固相体积分数$ \phi $的增加而降低(图 7)，由此可知，$ \phi $对沉积物再悬浮的重要性高于植被直径d，这一试验结果与植被茎干产生的紊流控制沉积物再悬浮理论一致(公式(4)右边第一项).因此，本研究将圆柱形植被层影响下的沉积物再悬浮临界速度的观测范围限定在植被直径d=0.32~1.26 cm.

光滑床面所测量的沉积物颗粒(D₅₀=85±21 μm)再悬浮的临界速度均值为u_{rms, co}=9.1 cm/s，则光滑床面沉积物再悬浮临界状态的最大波速即是轨道波速U_w = 12.8±0.9 cm/s. Shields数$\left( {\theta = {\tau _b}/\left( {{\rho _s} - \rho } \right)g{D_{50}}} \right) $与颗粒粒径相关，可用于确定颗粒运动的临界状态，当θ值大于临界θ时，可认为是沉积物再悬浮的初始状态^[29].由此可知，小颗粒的再悬浮临界速度较低.遵循Yang等^[17]与Tinoco和Coco^[12]的结论，植被产生的紊流是沉积物颗粒起动和再悬浮的主要驱动因素. 图 8比较了悬浮颗粒浓度和近床面的紊流水平，在大多数直径情景下(d=0.32、0.64、1.26 cm)，沉积物悬浮颗粒浓度在TKE≈3×10^-4 m²/s²时高于测量仪器噪声水平7 mg/L(图 8中的黑虚线).已有研究发现在d =2 cm的随机植被分布格局中，波浪扰动的植被情景下，沉积物再悬浮的植被紊动能阈值TKE ≈ 6×10^-4 m²/s2^[12].此TKE阈值略大于本研究中的阈值(TKE ≈ 3×10^-4 m²/s²)，其原因是该文献研究使用的沉积物颗粒(D₅₀=280 μm)稍大于本研究(D₅₀= 85±21 μm).

所有试验情景中有4种情景的沉积物再悬浮临界紊动能低于前文所述的临界水平(3×10^-4 m²/s²)，分别是光滑床面($ \phi $ =0)、直径d=0.32 cm的$ \phi $=0.002和$ \phi $=0.003(图 8a)，以及直径d=0.64 cm的$ \phi $=0.003(图 8b).可能的原因是，对于光滑床面和$ \phi $值较低的情景，床面产生的紊流是近床面总紊动能的最主要来源.因此，在推求沉积物再悬浮的临界紊动能时，不考虑上述4种情景的TKE.根据其余植被情景得到沉积物再悬浮的临界紊动能k_{t, c}=2.6±1.0(×10^-4 m²/s²)，其中k_{t, c}的不确定性为不同植被情景的标准偏差.

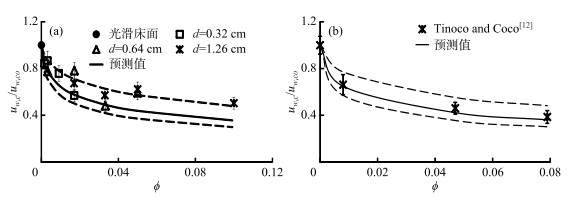
根据公式(4)的理论，特定沉积物颗粒的再悬浮临界紊动能为常数.由前文可知光滑床面沉积物再悬浮临界轨道波速U_{w, co}=12.8±0.9 cm/s，由此可得沙床粗糙度系数C_{b, w}=k_{t, c}/U_{w, co}²=0.02±0.01.从图 5可知δ²=0.61±0.02，将δ²和C_{b, w}代入公式(4)中，得到植被影响下沉积物再悬浮的临界波速U_{w, c}.将C_D=1.5±0.3代入公式(5)，得紊动能预测值与实测值的相互关系(图 9). 图 9a中U_{w, c}/U_{w, co}的预测值与实测值误差在20 %以内，该结果证实公式(5)的适用范围为固相体积分数小于10 % ($\phi $ < 0.1)的植被茎干紊流.运用Tinoco and Coco^[12]的水槽试验数据(淹没刚性植被直径d=2 cm，植被高度h_c= 21 cm，密度m=25~250根/m²，$\phi $=0.008~0.079，沙床粒径D₅₀=280 μm)对本模型进行验证，结果显示Tinoco and Coco^[12]的实测数据在本模型的预测范围内(图 9b)，表明本模型的沉积物颗粒适用范围从D₅₀=85 μm扩展至D₅₀=280 μm，植被茎干直径从d=0.32~1.26 cm扩展至d=2 cm.

本研究仅考虑具有单个周期(T=2 s)的波，对应野外的风生波，可近似于例如大型浅水湖泊太湖风生浪的波浪周期T = 1.2~1.8 s和波高(2 cm和10 cm)^[30].但本文提出的植被紊流模型可能不适用于流经植被层的长波，长波会在植被冠层顶部产生剪切紊流，并有助于再悬浮^[25]，如受海洋重力波等长波影响的潮滩植被.此外，本研究所提出的波浪驱动下刚性植被层中沉积物再悬浮模型，可与植被影响下的波浪衰减模型相结合，综合考虑植被层对波浪的衰减和沉积物再悬浮的抑制作用，以及植被茎干产生的紊流对沉积物再悬浮的促进作用，以此得到实际野外波浪扰动下植被对沉积物的综合影响，并得出基于沉积物沉降或再悬浮需求的适宜植被面积、植被密度和高度等分布特征，为浅水湖泊和滨海湿地生态修复与保护提供科学指导与关键参数.

4 结论

本研究通过室内水槽试验探究了刚性模型植被对波浪驱动的沉积物再悬浮的影响，植被层设定了3种直径(d=0.32、0.64和1.26 cm)、4种固相体积分数($\phi $)和不同的波浪条件.结果表明：1)植被改变波速结构并产生紊动能(TKE)，含植被近床面的总TKE由植被产生的紊流和床面粗糙度产生的紊流共同决定；2)植被层近床面TKE随$\phi $增大而增大，与波速均方根的平方(u_rms²)呈线性关系；3)$\phi $>0.003的植被茎干产生的紊流可局部增强沉积物再悬浮，当近床面总TKE大于2.6±1.0(×10^-4 m²/s²)时，沉积物开始悬浮，且$\phi $越大沉积物悬浮越早；3)构建并验证了公式(4)作为预测波浪驱动的沉积物再悬浮的植被紊流模型，基于植被近床面总TKE值确定了沉积物再悬浮的波速阈值(公式(5))，用于预测沉积物再悬浮的临界波速.该植被紊流模型适用于波浪驱动下沉积物颗粒粒径D₅₀=85~280 μm，植被茎干直径d=0.32~2 cm的刚性植被层沉积物再悬浮过程.