(2: 北京英特利为环境科技有限公司, 北京 100191)
(2: Beijing Inteliway Co., Ltd, Beijing 100191, P. R. China)
湖泊是重要的陆地景观单元,过量氮、磷营养物质输入所导致的湖泊富营养化是全球水环境领域面临的长期挑战.目前,全球范围内仍有超过60 %的湖泊处于不同程度的富营养化状态,而贫营养的湖泊则主要集中在中国青藏高原、北美高纬度区、南美南部高原等高海拔地区[1].湖泊会受到自然和人为活动的直接和间接影响[2-3],其中:直接影响主要包括居民生活、工业生产、农业种植活动排放的营养物质以及水利调控等[4],而间接影响则多指气候变化下降雨量与极端降雨增加所导致的冲击效应,使得水华暴发的时空异质性逐步增大[5].经过多年的治理,逐步形成了“负荷削减→污染防治→水质保护→生态系统管理”的湖泊管理模式,我国重点治理湖泊的水质得到明显提升,但水华暴发的强度与频次依然没有得到根本改善[6-7],湖泊富营养化防控将会面临更大挑战[8-9].
湖泊水环境与水生态系统对流域污染输入与负荷削减的响应关系非常复杂,表现为非线性、时滞性和时空异质性等特征,其背后的富营养化产生和变化机制仍在持续研究中.为应对以上特征,湖泊富营养化治理亦在循序渐进.湖泊与流域治理不同的是,湖泊治理要求以系统角度综合评估其复杂性与驱动因素,在水质水生态目标导向下制定有效的污染控制策略,再借助流域治理(如点源削减、非点源控制)、水量调度、生态修复等措施实现削减目标.如何定量识别上述特征并制定经济和高效的流域调控方案是湖泊治理的关键,其中模型模拟是常用的研究方法.模型基于实验和观测数据并克服其应用条件严格、周期长、成本高的瓶颈,在得到充分校验的基础上,可用于识别影响湖泊演化的重点驱动因素、量化水质和水生态响应关系及其时空变异性,为确定流域营养物质的控制目标提供科学依据[10].在湖泊富营养化治理决策中,模型的具体作用是:(1)量化水体的主要过程,包括水动力、泥沙、有毒物质、水质、浮游动植物等,表征系统的非线性、时滞性和时空异质性[10]; (2)基于模拟的各个物质之间的响应关系,解析得到各污染源对水质和水生态变化的贡献程度[11]; (3)情景分析、方案评估和流域调控决策优化[12]; (4)促进数据监测体系的完善并辅助机理过程解释[13-14].据此,可将模型分为两类:流域输入的湖泊富营养化响应模型和流域优化调控决策模型.湖泊富营养化响应模型的研究重点包括:基于统计回归和机器学习等模型的藻类-营养盐关系拟合[15-17],基于简单机理模型的大尺度环境空间模拟与适用性讨论[18],基于复杂机理的湖泊水动力-水质-水生态模拟模型开发[19-20]以及针对藻类、营养盐、溶解氧、沉积物等物质变化的模拟与应用[16, 21].与模型实际应用紧密相关的研究包括:湖泊生态动力学特征及其对治理策略和气候变化的响应模拟[22],模型输出对于输入数据的敏感性分析[23],水质、水生态模拟中的不确定性分析及策略应对[24-25].流域优化调控决策模型主要包括多目标、非线性、不确定性优化方法,并探究复杂机理模型简化及在优化治理决策中的应用[18],复杂模型的替代方法及评估[26-27]等.但已有的研究综述主要是针对模型构建、求解、不确定性分析及优化等传统方向进行总结,而缺乏针对现状富营养化最新治理背景下实现精准治污决策的进展综述,面临非线性表征、调控精准性与揭示长期演变趋势等新挑战,未来还需要对数据融合、模型方法研发、应用研究等做深入探索.因此,本文将从湖泊富营养化的当前状态和演变趋势出发,结合湖泊系统显著存在的非线性特征,对湖泊富营养化响应模拟与污染优化调控的模型方法进行综述,以期为湖泊富营养化控制提供模型研究支撑.
1 湖泊富营养化响应的模型研究进展 1.1 数据驱动的统计模型湖泊富营养化响应模拟中常用的统计模型包括:经典统计学模型、贝叶斯统计模型和机器学习模型等,这些模型都是由数据直接驱动的.经典统计学模型是指采用经典统计学的理论进行建模的方法,按照能否采用确定的有限参数建立模型,又可分为参数方法和非参数方法.参数方法为当前应用最普遍的统计学方法,包括线性回归模型、对数线性回归模型、广义线性回归模型、分位数回归模型、滑动平均模型、动态线性模型、混合效应模型以及多元统计分析方法等[28],其中滑动平均模型和动态线性模型多用于时间序列回归.非参数方法由于不需要预先设定参数的个数,因而对于拟合非线性关系具有很大优势,常见的方法包括局部加权回归、广义加性模型和时间序列分解模型等[29].
贝叶斯统计模型是指采用贝叶斯统计学理论进行参数估计的一类方法,其明显区别于经典统计学方法之处在于进行参数估计时需要给定先验分布以及参数视为分布(经典统计学理论认为参数具有唯一真值)[30].在湖泊富营养化响应模拟中应用较多的方法包括贝叶斯方差分析模型、贝叶斯层次模型和贝叶斯突变点模型等[31-33].贝叶斯统计学模型在参数和模型的不确定性分析中具有优势,因而常用于建立不确定性的响应关系和探究特定事件(如藻类暴发)的不确定性或风险.
机器学习模型是一类新兴的数据分析技术,该类方法直接从数据中挖掘信息,而无需依赖于预定的方程.常见的机器学习模型包括贝叶斯网络、人工神经网络、支持向量机、随机森林和递归神经网络等[34],其中递归神经网络(如长短期记忆神经网络)常用于时间序列变量的模拟[35].机器学习方法的主要优势在于对复杂非线性关系的拟合,随着监测数据的积累,建立可靠的机器学习模型来挖掘变量间的复杂非线性关系成为可能[36].因而,机器学习方法成为用于湖泊富营养化响应模拟中非常有前景的统计方法.但需要注意的是,机器学习模型需要大量的监测数据进行模型训练和验证,在应用时也需特别注意避免过拟合现象.
上述方法在应用中通常用于建立响应关系、时间序列特征分析以及敏感指标的预报预警.例如,根据建立的营养盐与叶绿素a(Chl.a)的响应关系来确定保证Chl.a在目标水平时的营养盐基准值[37];采用时间序列分解模型探究变量的趋势和周期性特征[38];采用长短期记忆模型建立Chl.a浓度与其他水质指标间的响应关系并进行短期预报[35].
1.2 因果驱动的机理模型机理模型包含流域的水文与污染物输移模拟以及对湖泊水文、水动力、水质、水生态等过程的模拟,本文的综述以后者为主.随着对湖泊物理、化学、生物等机理过程的深入研究以及计算性能的提升,多变量、跨尺度的湖泊水动力-水质-水生态机理模型在富营养化研究与控制决策中发挥了越来越重要的作用[39-41].它通常包含4种过程:(1)水动力过程,指水体在时空上的流动过程,因为环流、湍流和波浪运动是影响水体温度场、营养物质输移、溶解氧浓度、生物群落和生产力分布的主要因素;(2)热量交换过程,或称水温过程,指温度在时空上的分布规律,对水动力过程和水质过程都非常重要,如水体分层可导致营养物质、溶解氧在垂向上的显著差异;(3)水质过程,以水体中的碳、氮、磷等生源要素为对象,描述要素的输移与水质变化的动态响应关系;(4)水生态过程,主要包括生物因子驱动的生物光合作用、藻类生长、大型水生植物生长、浮游动物生长、鱼类生长、单种群增长和生态毒理过程,多基于种群尺度进行构建,以生物量为计算基础,其时间和空间分辨率通常比水动力和水质过程要低.在空间维度上,上述模型可实现零维、1维、2维和3维的过程模拟.此外,根据研究对象的不同,有的模型还包括泥沙输移过程、有毒物质模块和沉积物成岩过程等;这些过程相互作用、相互依赖,形成一个复杂的系统网络.目前常用的湖泊复杂机理模型包括Environmental Fluid Dynamics Code(EFDC)、CE-QUAL-W2、DELFT3D、MIKE3、RMA10、AQUATOX、Computational Aquatic Ecosystems Dynamic Model (CAEDYM)、Water Quality Analysis Simulation Program (WASP)、IWIND和MOHID等.针对每一种模型的模拟状态量、复杂程度、优势与不足、适用性可参考已有的研究综述[20].
机理模型的建模与应用要求严格,需要较多的输入数据,如:人口、地形、土地利用等基础数据以及气象、污染产生与输入等时间序列数据,并需具备对研究湖泊充分的了解和丰富的模型构建经验.例如,Zhao等[39]基于EFDC构建了异龙湖的水动力-水质模型,模拟湖泊的水动力循环、污染物迁移转化以及营养盐、浮游植物和大型植物之间的相互作用,量化水质对负荷削减强度和生态恢复措施的响应;Liu等[40]研究湖泊水质、水生态对流域生态补水和湖泊水位的响应关系,区分各种外界输入对湖泊水质变化的贡献.
流域是湖泊富营养化控制的基本单元,因此需要流域水文和污染物输移模拟以及湖体响应模型的耦合来实现多过程、跨时空尺度的应用,这增加了模型构建的难度.流域模拟模型为湖泊模型提供输入数据,而湖泊模型则模拟湖泊对流域负荷输入的响应,并为流域模型的反向校核提供参考.流域模型可以选择Soil & Water Assessment Tool(SWAT)、Hydrological Simulation Program-Fortran (HSPF)、Loading Simulation Program C++(LSPC)等,湖体响应模型可选择EFDC、WASP、CAEDYM等,以及将二者耦合在一起的综合模型平台,如MIKE-SHE、MIKE-11等.关于湖泊模型与流域模型的耦合研究数量较多,难以统一,实际研究中通常需要结合模拟目的、状态过程、模拟时空精度以及对模型熟悉程度等因素进行选择,这里仅举例说明.例如,Carraro等[11]以意大利北部的Pusiano湖为对象,将分布式流域水文模型SWAT和湖泊响应模型DYRESM-CAEDYM耦合,讨论并比较了不同情景结果的差异. Debele等[42]耦合水文和水质模型(SWAT和CE-QUAL-W2)来模拟高原流域和下游水体的水量和水质的综合过程;Zhang等[43]耦合SWAT-EFDC-WREM模拟加拿大Assiniboia流域水量、温度和氮磷、溶解氧等变化过程,结果表明该流域水生系统主要受氮限制,且沉积物通量在水库营养盐动态变化中起着至关重要的作用;Bai等[44]结合SWAT和EFDC模型模拟中国八里湖水质对污染源的响应情况,结果表明污染源对湖泊水质的贡献具有很强的空间异质性,为优化污染负荷控制方案提供了有用的信息.在治理决策优化过程中,机理模型又进一步作为评估优化方案的必要工具,形成“模拟-优化”体系[45-46].
机理模型尽管已得到广泛应用,但由于其具有时间精细化、空间多维化、机理过程多样、状态变量繁多、参数数量庞大和参数交互性强等特点,使得模型面临着敏感性分析、参数校验、模型不确定性的众多挑战.敏感性分析主要是识别对输出结果有重要影响的输入边界和模型参数[47-48],包括局部敏感性分析和全局敏感性分析.局部敏感性分析能快速地识别单因子的敏感性,但无法反映机理模型里多输入、多参数在全局空间的敏感程度[49].全局敏感性分析可探索所有关键参数在整个高维空间的影响,评估参数间的相互关联,适用于非线性的机理模型[50],但其需要高额的运算成本[51].参数校正是机理模型运用中必要的过程,由于机理模型参数的数量巨大(通常超过100个),需要在校正前筛选出对模拟结果有显著影响的敏感参数,再对其进行校正以更好地拟合湖泊的水动力、水质和水生态变化过程.模型的参数校正通常分为两类:①基于建模经验和试错法的参数手动调整法,需要建模者对湖泊的充足了解和对参数的深入认识;②自动优化算法,如遗传算法、贝叶斯推断法、Generalized Likelihood Uncertainty Estimation(GLUE)、Markov Chain Monte Carlo(MCMC)法、模拟退火法等,可一定程度上减少对模型开发经验的依赖,也有利于分析模型模拟的不确定性(表 1).但由于参数校正通常需要进行成千上万次机理模型的运行才能保证模拟误差达到可接受水平或达到自动校参算法的收敛条件,因此在复杂机理模型校正中采用自动校正的算法存在挑战[61].
| 表 1 机理模型校正中常用的参数校正方法 Tab. 1 Comparison of parameters calibration methods used in mechanism models |
在构建和应用机理模型时,模型数据不确定性与参数不确定性是影响模拟误差和方差的主要因素,因此对模型的不确定进行研究就显得尤为重要,尤其是决策支持模型.这些不确定性主要包括:湖沼学机理认识的经验表达与不确定性[63];模型结构中方程的概化与计算机数值求解方法产生的近似;模型网格和时空尺度的离散化形式;水质模型参数存在的“异参同效”现象;模型边界数据和观测数据的不确定性等[64].由于这些问题的存在,在过去的治理决策中往往更倾向于简单机理模型[18],但随着计算能力的提升以及对决策精度的更高要求,复杂模型的应用越来越广泛.但是无论采用简单还是复杂的机理模型,都需要根据模型服务目标对其进行不同层次的不确定性分析[65],并加强对模拟结果的解释与讨论[66].一些研究致力于提出统一的模型不确定性分析框架和应用规范[25, 67],包括模型过程表达、空间和时间尺度、模型参数取值、校正与验证策略、敏感性分析、不确定性、性能测量评估等全过程的重点建议,为模型应用提供了参考.
2 流域优化调控决策的模型研究进展以污染负荷削减为核心的流域调控是解决湖泊富营养化问题的根本,决策优化模型可以有助于寻找实现湖泊管理目标的最佳方案.由于湖泊流域系统具有非线性特征,将机理模型和优化模型建立在统一的框架之下,形成模拟-优化方法体系,这成为流域调控决策研究和应用的热点[45-46].其中,机理模型用来模拟湖泊和流域系统内部要素对外界驱动因素的响应关系,并对可能的状态变化进行预测;优化模型则通过迭代运行模拟模型,在约束条件下寻求实现目标的最优解集空间.优化模型有不同的形式,根据目标函数和约束函数的复杂度可采用线性优化和非线性优化形式;根据参数的形式可采用区间规划、模糊规划和随机规划;根据目标的数量可采用单目标优化和多目标优化等.模拟-优化耦合的一般形式为[68]:
| $ \min f(x) $ | (1) |
| $ \text { s.t. } g_{j}(x, y) \leqslant 0, j=1, 2, \cdots, m $ | (2) |
| $ h_{i}(x, y)=0, i=1, 2, \cdots, n $ | (3) |
| $ \begin{array}{c} y=U(x, w) \end{array} $ | (4) |
式中,x为决策变量的向量,hi(x, y)和gj(x, y)为优化模型的等式和不等式约束式,U(x, w)为模拟模型,w为模型的参数集合.
模拟-优化方法亦存在不确定性,对应的优化方法主要包括随机优化、区间优化等.随机优化是在求解过程中对不确定性参数采用蒙特卡洛随机采样,再转化成确定性的优化问题进行求解[69];区间优化是将不确定参数用区间数来表达,采取各种不同的求解形式寻找最优解[70].但近年来的研究表明,某些区间优化求解算法的结果难以确保系统满足约束条件[71].针对这一问题,出现了一些面向实际应用的算法,其中包括风险显性区间数线性规划(REILP)算法[72]. REILP算法基于极端情景和对应方案定义风险函数,从而使得在区间优化问题求解过程中,不管是约束问题的处理还是方案的优劣判断都具有明确的决策意义.
机理模型和优化模型可直接耦合,对于简单或可以显式表达的模拟模型,这种方式可以通过经典的启发式搜索算法(如遗传算法、粒子群算法)求出其近似解,但对于复杂的模拟模型而言却难以求解.尽管近年来计算速度大幅提升[55, 73-74],但是模拟-优化方法依然面临计算效率不足这一难题,因而通常选择将模拟模型进行并行计算[75]、简化[76]或者替代[77-78].替代模型是对原模型进行再次建模[79],拓展了机理模型在敏感性分析、参数估值、污染源水质贡献解析和模拟-优化方法等层次的应用[80].目前替代模型主要分为两类:①响应面模型,基于数据驱动建立原始模型输入输出的响应关系;②简单模型替代,拥有与原始模型相近的模拟过程但简化模型细节,删去不敏感性的物理过程、参数或对原模型进行降维处理.已有研究对替代模型进行了总结,在机器学习算法得到广泛关注前,替代模型主要是简单的统计模型,如多项式拟合、Moving Least-Squares、Radial Basis Functions、Support Vector Regression、Kriging等,Chen等[81]设计了7种对复杂模拟模型进行替代的统计模型,综述替代模型在实验抽样与拟合方面的最新进展;Forrester等[82]进一步结合多种统计算法推荐替代模型的构建框架,明确在初始抽样、噪声、嵌入方式和多目标等方面需要重点关注的问题以及应对办法;随着替代方法的拓展,Razavi等[26]将替代模型分为响应面替代和低复杂度替代模型,总结在水资源领域的应用,采用实例讨论各种方法的限制及样本量等问题,并提出缩减替代成本、强化替代不确定性将是未来更多替代方法出现会面临的新挑战.在模拟-优化方法中,有研究从近似求解的角度提出了一些高效求解非线性问题的替代模型,如Zou等[83]开发非线性区间映射重构(NIMS)的方法,与REILP算法结合,将非线性问题替代为线性规划,在显著提高计算效率的同时能够得到高度精确的解.
3 湖泊治理面临的挑战与模型研究展望 3.1 湖泊治理面临的挑战我国的湖泊治理已取得明显进展,但成效并不稳定[84-85],尤其是藻类水华的暴发强度与频次仍然很高,进一步的治理面临更大的挑战,更为迫切需要在对富营养化机制理解基础上的流域精准调控决策,并促进湖泊系统长期稳定的水质改善与生态健康.因此,如何表征响应的高度非线性,如何提高调控的精准性以及如何揭示湖泊生态系统演变的规律将成为制约湖泊治理成效的关键问题.
在非线性响应方面,湖泊是包含水动力传输、热量交换、沉降与释放、硝化与反硝化、固氮、生物生长与死亡等多种物质循环的复杂系统,对于大气沉降、流域输入等边界条件的响应关系多呈非线性[86].同时,非线性也增加了富营养化湖泊的治理难度,如入湖污染负荷的削减并不意味着水质等比例的改善,也更不意味着藻类生物量的同步下降[87].时滞性可作为非线性的一种表现形式,是指由于水体中物质传输及生物生长、死亡等生物地球化学过程的作用时间尺度不一致,导致了系统内的因果关联与响应关系具有时间上的滞后效应[88],例如物质循环可以小时作为响应的时间单元,但水生生物的生物量变化则需要在天或者更大的时间尺度上进行衡量.对单一湖泊而言,非线性响应可分为两种:外源输入的非线性叠加;湖泊内氮、磷、藻浓度的非均匀性变化.外源输入的非线性叠加是指在外部自然和人为(如负荷输入、短时冲击、水利调节等)的复合干扰下,湖泊呈现出的动态和非线性变化,其关键问题是能否定量解析各种干扰的贡献.非均匀性是指湖内生物地化循环对氮、磷、藻等产生的非等效影响,其关键问题是如何衡量外源输入与内部循环的关联及贡献[89].对多湖泊而言,非线性指的是其响应的时空异质性,也即不同湖泊对于负荷输入响应的敏感性存在的差异.即使是同一类型的湖泊,由于所处区域的地形、水动力条件、生态结构和物种组成不一致,在相同的外界干扰强调下也会表现出迥异的响应关系.
在湖泊治理调控的决策方面,当前遇到的瓶颈是流域总量减排与湖泊水质改善间的关联并不明晰[90-92],因此如何提升已有治理措施的水质改善效益、实施精准治污,是接下来治理的核心突破点.而以水质改善为目标的工程治理实践需要定量化表达出微观措施与宏观水质间的跨时空响应关系,以解决自下而上的工程总量削减与自上而下的水质管理目标两者之间的脱节问题.这种跨时空尺度的响应关系将会更加复杂,不仅要面临上述的非线性、不确定性与计算成本等问题,还需建立将陆域污染物迁移模型、河道水动力-水质模型、湖泊水动力-水质-水生态模型紧密相连、且具有高时空分辨率的模型系统,再耦合优化决策模型,以形成同时考虑“城市-流域-湖体”一体化监测、“工程-片区-河道-湖泊”系统评估、水质改善与负荷削减决策优化、湖泊治理工程科学设计等在内的精准治污决策系统,其面临的挑战集中表现为非线性响应的时空尺度转化与统筹、海量组合方案评估、模型运算成本与等效替代、工程运行与动态调度、不确定性分析与决策稳健性等.
在湖泊的长期生态演化方面,氮、磷、藻的含量是目前常用的表观监测指标,但由于它们是对湖泊变化的短期表征,因而难以反映生态系统的长期演化趋势、恢复潜力与系统稳定性[93].为此,能否以目前监测到的表观指标来衡量长期变化,能否评估湖泊富营养状态对短期氮、磷循环的反馈效应,以及能否寻求到其变化轨迹并定量分析其驱动因素,是制约湖泊治理的重要基础科学问题.在外部干扰条件变化下,湖泊的水质、生物群落、食物网结构均发生变化,并存在不同步性[88].需进一步揭示在不同的干扰条件下,湖泊生态系统内在的响应机制,如:营养盐的沉降、再悬浮、硝化、反硝化及其在浮游生境中的内循环速率,沉积物的源汇转换,食物网结构和不同生物组分间的营养拓扑结构与连接强度,生物群落的生产力、生物量和生物组成等,从而探究生态系统内部的响应过程和响应机制,探索湖泊在各种干扰下响应的特殊性和一般性规律.目前的研究方法主要是基于简单动力学模型[94],或采用统计学手段分析阈值和临界现象[95],但这些方法对湖泊演变机制和时滞性的假设过于强烈.未来的研究还需要将湖泊机理模型与食物网耦合,产生高精度的内部过程通量;并构建以弹性、持久性和变异性为核心的表征方法,用以探索生态复杂性对湖泊稳定性的影响.然而,由于湖泊生态系统稳定性的长短期效应不一致,在湖泊水动力-水质-食物网耦合上如何应对时空尺度独立与不匹配的问题是需要解决的技术难题.
3.2 湖泊响应与流域调控的模型研究展望1) 多源数据的融合
数据是模型的基础,无论数据驱动的统计模型,还是因果驱动的机理模型,抑或是决策导向的优化模型,均离不开可靠的数据.一方面,大量的环境监测数据为富营养化机制提供深入认识的依据,为湖泊治理提供了新的模型工具;另一方面,流域精细化管理对数据的数量、频次、广度、精确度提出了新的需求[12, 89].据此,湖泊富营养化的治理迫切需要多源数据的融合,结合大数据挖掘的机器学习方法,以建立更可靠的响应关系,进行更准确的预测,从而更好地为湖泊富营养化管理提供决策支撑.按照来源,数据可以分为原生数据和次生数据两种.
原生数据即为采用测量或监测手段直接获得的数据,主要包括自动监测站的高频监测数据[36]和基于遥感技术获得的高时空分辨率的影像数据等[96].高频监测数据包括气象、水文、水质等,具有数量大、频率高、自相关性强等特征,能够更加全面、准确地表征变量的动态变化,揭示常规监测所不能反映的规律[97].由于自动监测的数据量大,难免会存在数据异常和缺失的问题,而采用人工手检的质量控制效率低下.机器学习算法在原生数据的清洗中具有巨大的优势[98],可以实现自动的异常值识别和缺失值插补,获得较为可靠的数据集.次生数据是指采用可靠的机理模型产生的具有高频特征的数据,可反映机理模型中变量之间复杂的非线性关系.基于次生数据,可以进一步地探索湖泊系统的重要过程,如:已有研究根据机理模型输出的通量数据,分析了湖泊各个过程营养盐通量变化特征,更好地揭示了湖体内所发生的氮、磷转化过程[99],识别影响湖泊Chl.a浓度预测的主要水质指标[35].未来随着监测技术与模拟模型的发展与广泛应用,原生数据与次生数据融合将成为一种新的研究范式,前文已述的机理模型、统计模型亦将成为数据融合的常用方法并得以改进.
2) 生态系统动力学模型与个体行为驱动模型的耦合
传统意义上,湖泊生态系统动力学模型大多是基于生物功能群尺度而构建的以生物量为计算基础的过程模型.这类模型力图通过最简单的策略来揭示宏观规律,例如捕食关系和种群演替等[100],但模型的构建是基于一定假设的,也即种群的个体之间不存在差异,且个体与个体之间无法相互影响.尽管生态系统动力学模型可以很好地模拟并揭示系统层面的问题,但无法表达个体的差异性行为,且难以与高时空分辨率的三维的水动力-水质模型结合.个体模型(agent-based model)的出现在一定程度上弥补了生态系统动力学模型的不足[101-102],它是模拟种群内每个个体的特性、行为和相互作用的模型[103-104].如对藻类而言,个体特性包括细胞生物量、大小以及生理状态等;行为则包括营养盐的摄取、光合作用、蛋白质合成等;个体的相互作用则包括种间或种内竞争、协同等[105-106].这些过程可以通过连续的数学方程的形式,也可以通过离散和基于规则的形式在模型中表达.个体模型的优势在于可以对种群内部每个个体进行单独模拟,并允许个体间的差异以及发生相互作用.同时,全部个体的特性及行为也可以汇总表现为其种群的特性和行为,种群的特性及行为取决于种群内所有个体的表现.不同于以生物量为计算基础的生态系统动力学模型,个体模型可以直接利用实验的单细胞数据进行模型构建,并利用个体及种群不同尺度的数据进行模型校验[107].
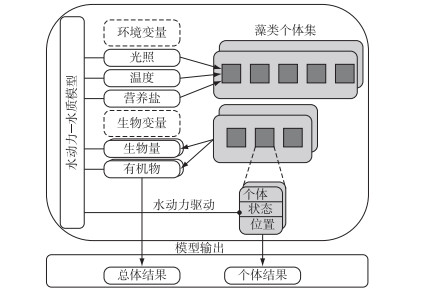
水动力-水质模型、生态系统动力学模型和个体模型各具优势,都是湖泊富营养化研究的必要工具,它们的耦合应用涉及到了不同的空间尺度,可通过降尺度的输入-输出耦合以及基于分布的升尺度输入-输出耦合来实现尺度融合.降尺度耦合方式的思想主要是通过插值等方法将水动力-水质模型及生态系统动力学模型结果的空间尺度降到适合个体模型的程度,作为个体模型的输入以驱动个体模型运算.升尺度耦合方式则主要是把个体模型中的个体根据其空间分布及机理模型的空间分辨率分成不同的集合,每个个体集合对应于相应的机理模型网格单元,从而做到输入和输出的匹配. Lange提出的机理模型耦合个体模型的框架(图 1)结合了降尺度和升尺度的方法,为水动力-水质-生态模型与个体模型的耦合提供了思路[108].
|
图 1 水动力-水质-生态模型与个体模型耦合的方法[108] Fig.1 Framework of agent-based model coupling with hydrodynamic and water quality model[108] |
3) 因果驱动模型与数据驱动模型的结合
因果驱动的机理模型能表达污染物的迁移转化过程,但复杂机理模型对数据要求较高、运行效率较低[109],且模拟的结果容易受到不确定性的影响[110],因此难以支持湖泊水质和水生态的短期预测[111].机器学习方法是当前最受关注的数据驱动模型,但由于它无法表达因果关系和机理过程而受到质疑[27].因此,将二者合理结合将为湖泊富营养化响应的模拟与短期预测提供新的路径.
机理模型和机器学习的结合可通过如下5个途径进行[27]:①采用机器学习方法提高机理模型参数的准确度;②采用机器学习方法来替代机理模型的子模型或模块;③采用机器学习方法揭示模拟残差的规律,修正机理模型的模拟偏差;④采用机器学习方法的输出结果来“约束”子模型,从而降低由于误差传递带来的不确定性和偏差;⑤采用机器学习方法作为复杂机理模型的替代模型.例如Liang等[35]采用长短期记忆模型模拟了复杂水质模型对Chl.a的预测效果,发现数据驱动的机器学习方法可以很好地实现对复杂水质模型预测预报的替代;Read等[112]采用水温与能量之间的关系约束机器学习模型,建立了过程指导的深度学习方法,成功拟合了湖泊温度随深度的变化关系,提高了水温预测的准确性.
将大量观测数据和模拟数据进行耦合的另一种方法是数据同化.数据同化方法的核心思想是把不同来源、不同分辨率的直接和间接的观测数据与模型模拟结果集成为具有时间一致性、空间一致性和物理一致性的各种状态的数据集,通过不断调整模型的运行轨迹来提高模型的短期预测能力[113].近年来,数据同化开始与水动力和生态模型结合以用于水质预警.数据同化主要分为变分同化和顺序数据同化方法,其中在复杂水质机理模型数据同化方案中使用较多的是集合卡尔曼滤波(EnKF)及其变体[114-115].但由于三维水动力-水质模型存在误差难以估计、误差高斯分布的假设难以满足、集合成员数目与时间成本的矛盾等问题,EnKF还难以实现水质预警的业务化应用.但随着模型内部机理的完善以及计算机运行能力的提高,数据同化在水质预警领域将有更广阔的应用空间.
当前,将机理模型与机器学习方法结合进行湖泊富营养化响应模拟尚处于探索阶段.尽管如此,已有的研究已经显示了将机理模型与机器学习方法结合在模拟效果和效率方面的潜在优势,未来研究应着眼于机理模型和机器学习方法结合方式(尤其是直接结合)的探索.
4) 多尺度融合的流域精准优化调控决策模型
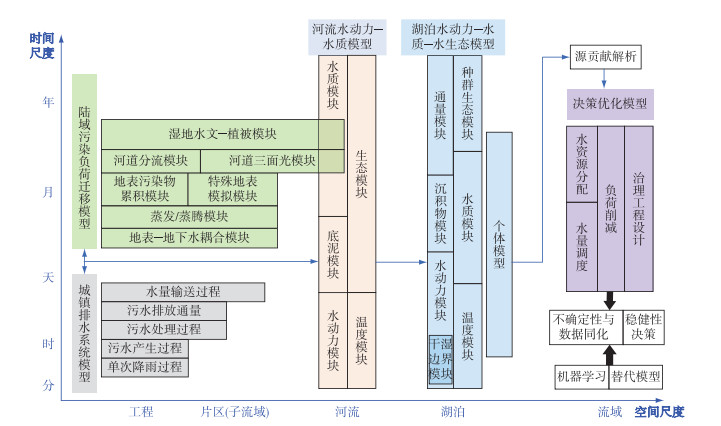
随着湖泊治理难度的加大,实施流域精准治理是必然的选择.精准治理以“工程-片区(子流域)-排口-河道-湖体”的水质响应关系评估为基础,为流域调控提供系统、精确、动态和科学的决策支撑.其模型体系主要包括城市排水系统模型、陆域污染物负荷迁移模型、河流水动力-水质模型、湖泊水动力-水质-生态模型和流域决策优化模型等.不同介质的各类模型彼此之间及其内部存在时空尺度不一致的挑战,如:城市排水系统模型中降雨过程主要以工程到片区为空间尺度,以分钟到小时为时间尺度;而排水系统的排放通量主要是以整个片区为空间尺度,以小时到天为时间尺度.陆域污染物负荷迁移模型中需要根据研究流域的实际情况决定是否开发或构建地表-地下水耦合、蒸发/蒸腾、地表污染物累积、特殊地表(边坡、农业大棚种植等)模拟、河道三面光、湿地等不同时空尺度的模块.湖泊水动力-水质模型以高时空分辨率的水动力、干湿边界、温度模拟为基础,耦合从小时到年的长时间尺度的水质模块,再与以小时到天为时间尺度的基于行为驱动的个体模型、以天到年为时间尺度的生态模型等集合,进行湖泊系统模拟.将城市排水系统模型、陆域污染物负荷迁移模型、河流水动力水质模型、湖泊水动力-水质-生态模型关联起来,形成机理模型体系,建立复杂的多尺度响应关系(图 2).在实际应用中,以研究问题为导向,根据复杂程度和计算成本,对机理模型体系进行一定程度的简化,对特征值与待预测数据进行采样,构建统计模型或机器学习模型实现点对点的拟合推演.机理模型与统计学习算法的联合可获取污染源水质贡献[89],并与决策优化模型耦合形成模拟-优化体系.优化模型以治理成本最小化、工程削减量最大化或水质和水生态改善最大化为目标函数,以治理措施的类型、规模和布局为决策变量,从海量方案组合中确定最优的方案集合.对于人为干预较强的湖泊-流域系统,水量调度将是未来提升措施水质效益的重要手段,包括生态补水的周期性调度、城市区域雨污水在多污水厂间转输、污水厂尾水排放等水量转移决策.与常规的优化决策不同的是,这是周期性更新且具有马尔科夫决策性质的动态决策问题,更适合使用基于深度学习的强化学习算法去解决[116].在复杂的流域精准治污决策模型系统中,当模型计算成本无法接受时,需要构建替代模型;使用多源数据对结果进行数据同化,以降低模型的不确定性;同时还应更重视决策的可靠性与稳健性分析.
|
图 2 流域精准治污模型体系 Fig.2 Framework of simulation on refined pollution control decisions on watershed |
1) 湖泊富营养化响应与流域优化调控决策模型分为数据驱动的统计模型、因果驱动的机理模型和决策导向的优化模型.其中,统计模型包含经典统计、贝叶斯统计和机器学习,常用于建立多指标间响应关系、时间序列特征分析以及敏感指标的预报预警,但对于机理规律解释不足.机理模型可实现不同时空尺度的流域和湖泊变化过程模拟,但由于存在时间精细化、空间多维化、机理过程多样、状态变量繁多、参数数量庞大和参数交互性强等特征,导致模型的敏感性分析、参数校验、不确定性分析等需要较高的计算成本.决策导向的优化模型结合机理模型形成“模拟-优化”体系,在不确定性条件下衍生出随机、区间优化等多种方法,可通过并行计算、简化与替代模型等方法应对计算成本过高的问题.
2) 湖泊富营养化治理依然面临较大的挑战,一是在外源输入非线性的叠加下如何定量解析各个污染源的贡献,如何衡量外源输入与内部循环的关联及贡献;二是工程总量减排与水质改善间的关联并不明晰,实现精准的污染治理需要解决非线性响应的时空尺度转化与海量组合方案评估、模型运算成本与等效替代、工程运行与动态调度、不确定性分析与决策稳健性等挑战;三是湖泊的氮、磷浓度等表观监测指标难以反映生态系统的长期演化趋势、恢复潜力与系统稳定性.
3) 为应对挑战,未来在模型方面仍需开展深入研究,主要包括:将原生数据、次生数据以及机器学习等算法进行融合,更加全面和准确地表征变量的动态变化,揭示常规监测不能反映的规律;将以生物量为基础单元的生态系统动力学模型与以个体行为驱动的个体模型进行升尺度或降尺度耦合,以表达物种间与物种内不同尺度的差异性;将机器学习算法与机理模型进行耦合,提高机理模型的参数准确度;将多介质的模型在时空尺度上进行融合,以综合评估从治理工程到湖体的多级响应关系,为湖泊治理提供系统、精确、动态和科学的决策支撑.
| [1] |
Wang SL, Li JS, Zhang B et al. Trophic state assessment of global inland waters using a MODIS-derived Forel-Ule index. Remote Sensing of Environment, 2018, 217: 444-460. DOI:10.1016/j.rse.2018.08.026 |
| [2] |
Ho JC, Michalak AM, Pahlevan N. Widespread global increase in intense lake phytoplankton blooms since the 1980s. Nature, 2019, 574(7780): 667-670. DOI:10.1038/s41586-019-1648-7 |
| [3] |
Sinha E, Michalak AM, Balaji V. Eutrophication will increase during the 21st century as a result of precipitation changes. Science, 2017, 357(6349): 405-408. DOI:10.1126/science.aan2409 |
| [4] |
Sutton MA, Oenema O, Erisman JW et al. Too much of a good thing. Nature, 2011, 472(7342): 159-161. DOI:10.1038/472159a |
| [5] |
Stevens CJ. Nitrogen in the environment. Science, 2019, 363(6427): 578-580. DOI:10.1126/science.aav8215 |
| [6] |
Huang JC, Zhang YJ, Arhonditsis GB et al. The magnitude and drivers of harmful algal blooms in China's lakes and reservoirs: A national-scale characterization. Water Research, 2020, 181: 115902. DOI:10.1016/j.watres.2020.115902 |
| [7] |
Chen JN, Zhang TZ, Du PF. Assessment of water pollution control strategies: A case study for the Dianchi Lake. Journal of Environmental Sciences, 2002, 14(1): 76-78. |
| [8] |
Carvalho L, McDonald C, de Hoyos C et al. Sustaining recreational quality of European lakes: Minimizing the health risks from algal blooms through phosphorus control. Journal of Applied Ecology, 2013, 50(2): 315-323. DOI:10.1111/1365-2664.12059 |
| [9] |
Cugier P, Billen G, Guillaud JF et al. Modelling the eutrophication of the Seine Bight (France) under historical, present and future riverine nutrient loading. Journal of Hydrology, 2005, 304(1/2/3/4): 381-396. DOI:10.1016/j.jhydrol.2004.07.049 |
| [10] |
Mooij WM, Trolle D, Jeppesen E et al. Challenges and opportunities for integrating lake ecosystem modelling approaches. Aquatic Ecology, 2010, 44(3): 633-667. DOI:10.1007/s10452-010-9339-3 |
| [11] |
Carraro E, Guyennon N, Hamilton D et al. Coupling high-resolution measurements to a three-dimensional lake model to assess the spatial and temporal dynamics of the cyanobacterium Planktothrix rubescens in a medium-sized lake//Salmaso N, Naselli-Flores L, Cerasino L et al eds. Phytoplankton responses to human impacts at different scales. Dordrecht: Springer, 2012: 77-95.
|
| [12] |
Ahlvik L, Ekholm P, Hyytiäinen K et al. An economic-ecological model to evaluate impacts of nutrient abatement in the Baltic Sea. Environmental Modelling & Software, 2014, 55: 164-175. DOI:10.1016/j.envsoft.2014.01.027 |
| [13] |
Ju WM, Gao P, Wang J et al. Combining an ecological model with remote sensing and GIS techniques to monitor soil water content of croplands with a monsoon climate. Agricultural Water Management, 2010, 97(8): 1221-1231. DOI:10.1016/j.agwat.2009.12.007 |
| [14] |
van Nes EH, Scheffer M. A strategy to improve the contribution of complex simulation models to ecological theory. Ecological Modelling, 2005, 185(2/3/4): 153-164. DOI:10.1016/j.ecolmodel.2004.12.001 |
| [15] |
Allawi MF, Jaafar O, Hamzah FM et al. Review on applications of artificial intelligence methods for dam and reservoir-hydro-environment models. Environmental Science and Pollution Research, 2018, 25(14): 13446-13469. DOI:10.1007/s11356-018-1867-8 |
| [16] |
Bhagowati B, Ahamad KU. A review on lake eutrophication dynamics and recent developments in lake modeling. Ecohydrology & Hydrobiology, 2019, 19(1): 155-166. DOI:10.1016/j.ecohyd.2018.03.002 |
| [17] |
Le Moal M, Gascuel-Odoux C, Ménesguen A et al. Eutrophication: A new wine in an old bottle?. Science of the Total Environment, 2019, 651: 1-11. DOI:10.1016/j.scitotenv.2018.09.139 |
| [18] |
Hong EM, Pachepsky YA, Whelan G et al. Simpler models in environmental studies and predictions. Critical Reviews in Environmental Science and Technology, 2017, 47(18): 1669-1712. DOI:10.1080/10643389.2017.1393264 |
| [19] |
Niu ZG, Wang XJ, Chen YX. Lake aquatic ecosystem models: A review. Chinese Journal of Ecology, 2013, 32(1): 217-225. [牛志广, 王秀俊, 陈彦熹. 湖泊的水生态模型. 生态学杂志, 2013, 32(1): 217-225.] |
| [20] |
Anagnostou E, Gianni A, Zacharias I. Ecological modeling and eutrophication—A review. Natural Resource Modeling, 2017, 30(3): E12130. DOI:10.1111/nrm.12130 |
| [21] |
Jørgensen SE. A review of recent developments in lake modelling. Ecological Modelling, 2010, 221(4): 689-692. DOI:10.1016/j.ecolmodel.2009.10.022 |
| [22] |
Vinçon-Leite B, Casenave C. Modelling eutrophication in lake ecosystems: A review. Science of the Total Environment, 2019, 651: 2985-3001. DOI:10.1016/j.scitotenv.2018.09.320 |
| [23] |
Pianosi F, Beven K, Freer J et al. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environmental Modelling & Software, 2016, 79: 214-232. DOI:10.1016/j.envsoft.2016.02.008 |
| [24] |
Uusitalo L, Lehikoinen A, Helle I et al. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environmental Modelling & Software, 2015, 63: 24-31. DOI:10.1016/j.envsoft.2014.09.017 |
| [25] |
Tscheikner-Gratl F, Bellos V, Schellart A et al. Recent insights on uncertainties present in integrated catchment water quality modelling. Water Research, 2019, 150: 368-379. DOI:10.1016/j.watres.2018.11.079 |
| [26] |
Razavi S, Tolson BA, Burn DH. Review of surrogate modeling in water resources. Water Resources Research, 2012, 48(7): W07401. DOI:10.1029/2011WR011527 |
| [27] |
Reichstein M, Camps-Valls G, Stevens B et al. Deep learning and process understanding for data-driven Earth system science. Nature, 2019, 566(7743): 195. DOI:10.1038/s41586-019-0912-1 |
| [28] |
Li YP, Tang CY, Yu ZB et al. Correlations between algae and water quality: Factors driving eutrophication in Lake Taihu, China. International Journal of Environmental Science and Technology, 2014, 11(1): 169-182. DOI:10.1007/s13762-013-0436-4 |
| [29] |
Wan YS, Wan L, Li YC et al. Decadal and seasonal trends of nutrient concentration and export from highly managed coastal catchments. Water Research, 2017, 115: 180-194. DOI:10.1016/j.watres.2017.02.068 |
| [30] |
Ellison AM. Bayesian inference in ecology. Ecology Letters, 2004, 7(6): 509-520. DOI:10.1111/j.1461-0248.2004.00603.x |
| [31] |
Qian SS, Shen ZH. Ecological applications of multilevel analysis of variance. Ecology, 2007, 88(10): 2489-2495. DOI:10.1890/06-2041.1 |
| [32] |
Liang ZY, Qian SS, Wu SF et al. Using Bayesian change point model to enhance understanding of the shifting nutrients-phytoplankton relationship. Ecological Modelling, 2019, 393: 120-126. DOI:10.1016/j.ecolmodel.2018.12.008 |
| [33] |
Liang ZY, Chen HL, Wu SF et al. Exploring dynamics of the chlorophyll a-total phosphorus relationship at the lake-specific scale: A Bayesian hierarchical model. Water, Air, & Soil Pollution, 2018, 229(1): 1-12. DOI:10.1007/s11270-017-3678-9 |
| [34] |
Chou JS, Ho CC, Hoang HS. Determining quality of water in reservoir using machine learning. Ecological Informatics, 2018, 44: 57-75. DOI:10.1016/j.ecoinf.2018.01.005 |
| [35] |
Liang ZY, Zou R, Chen X et al. Simulate the forecast capacity of a complicated water quality model using the long short-term memory approach. Journal of Hydrology, 2020, 581: 124432. DOI:10.1016/j.jhydrol.2019.124432 |
| [36] |
Crawford JT, Loken LC, Casson NJ et al. High-speed limnology: Using advanced sensors to investigate spatial variability in biogeochemistry and hydrology. Environmental Science & Technology, 2015, 49(1): 442-450. DOI:10.1021/es504773x |
| [37] |
Huo SL, Xi BD, Ma CZ et al. Stressor-response models: A practical application for the development of lake nutrient criteria in China. Environmental Science & Technology, 2013, 47(21): 11922-11923. DOI:10.1021/es4037034 |
| [38] |
Stow CA, Cha Y, Johnson LT et al. Long-term and seasonal trend decomposition of Maumee River nutrient inputs to western Lake Erie. Environmental Science & Technology, 2015, 49(6): 3392-3400. DOI:10.1021/es5062648 |
| [39] |
Zhao L, Li YZ, Zou R et al. A three-dimensional water quality modeling approach for exploring the eutrophication responses to load reduction scenarios in Lake Yilong (China). Environmental Pollution, 2013, 177: 13-21. DOI:10.1016/j.envpol.2013.01.047 |
| [40] |
Liu Y, Wang YL, Sheng H et al. Quantitative evaluation of lake eutrophication responses under alternative water diversion scenarios: A water quality modeling based statistical analysis approach. Science of the Total Environment, 2014, 468/469: 219-227. DOI:10.1016/j.scitotenv.2013.08.054 |
| [41] |
Chen Y, Zou R, Han S et al. Development of an integrated water quality and macroalgae simulation model for tidal marsh eutrophication control decision support. Water, 2017, 9(4): 277. DOI:10.3390/w9040277 |
| [42] |
Debele B, Srinivasan R, Parlange JY. Coupling upland watershed and downstream waterbody hydrodynamic and water quality models (SWAT and CE-QUAL-W2) for better water resources management in complex river basins. Environmental Modeling & Assessment, 2008, 13(1): 135-153. DOI:10.1007/s10666-006-9075-1 |
| [43] |
Zhang H, Huang GH, Wang DL et al. An integrated multi-level watershed-reservoir modeling system for examining hydrological and biogeochemical processes in small prairie watersheds. Water Research, 2012, 46(4): 1207-1224. DOI:10.1016/j.watres.2011.12.021 |
| [44] |
Bai H, Chen Y, Wang D et al. Developing an EFDC and numerical source-apportionment model for nitrogen and phosphorus contribution analysis in a lake basin. Water, 2018, 10(10): 1315. DOI:10.3390/w10101315 |
| [45] |
Reichold L, Zechman EM, Brill ED et al. Simulation-optimization framework to support sustainable watershed development by mimicking the predevelopment flow regime. Journal of Water Resources Planning and Management, 2010, 136(3): 366-375. DOI:10.1061/(asce)wr.1943-5452.0000040 |
| [46] |
Dong FF, Liu Y, Wu Z et al. Identification of watershed priority management areas under water quality constraints: A simulation-optimization approach with ideal load reduction. Journal of Hydrology, 2018, 562: 577-588. DOI:10.1016/j.jhydrol.2018.05.033 |
| [47] |
Chu-Agor ML, Muñoz-Carpena R, Kiker G et al. Exploring vulnerability of coastal habitats to sea level rise through global sensitivity and uncertainty analyses. Environmental Modelling & Software, 2011, 26(5): 593-604. DOI:10.1016/j.envsoft.2010.12.003 |
| [48] |
Tomassini L, Reichert P, Knutti R et al. Robust Bayesian uncertainty analysis of climate system properties using Markov chain Monte Carlo methods. Journal of Climate, 2007, 20(7): 1239-1254. DOI:10.1175/JCLI4064.1 |
| [49] |
Bar Massada A, Carmel Y. Incorporating output variance in local sensitivity analysis for stochastic models. Ecological Modelling, 2008, 213(3/4): 463-467. DOI:10.1016/j.ecolmodel.2008.01.021 |
| [50] |
Song XM, Zhang JY, Zhan CS et al. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. Journal of Hydrology, 2015, 523: 739-757. DOI:10.1016/j.jhydrol.2015.02.013 |
| [51] |
Yi X, Zou R, Guo HC. Global sensitivity analysis of a three-dimensional nutrients-algae dynamic model for a large shallow lake. Ecological Modelling, 2016, 327: 74-84. DOI:10.1016/j.ecolmodel.2016.01.005 |
| [52] |
Cooper VA, Nguyen VTV, Nicell JA. Evaluation of global optimization methods for conceptual rainfall-runoff model calibration. Water Science and Technology, 1997, 36(5): 53-60. DOI:10.1016/S0273-1223(97)00461-7 |
| [53] |
Dilks DW, Canale RP, Meier PG. Development of Bayesian Monte Carlo techniques for water quality model uncertainty. Ecological Modelling, 1992, 62(1/2/3): 149-162. DOI:10.1016/0304-3800(92)90087-U |
| [54] |
Borsuk ME, Higdon D, Stow CA et al. A Bayesian hierarchical model to predict benthic oxygen demand from organic matter loading in estuaries and coastal zones. Ecological Modelling, 2001, 143(3): 165-181. DOI:10.1016/S0304-3800(01)00328-3 |
| [55] |
Wu Z, Liu Y, Liang ZY et al. Internal cycling, not external loading, decides the nutrient limitation in eutrophic lake: A dynamic model with temporal Bayesian hierarchical inference. Water Research, 2017, 116: 231-240. DOI:10.1016/j.watres.2017.03.039 |
| [56] |
Beven K, Binley A. The future of distributed models: Model calibration and uncertainty prediction. Hydrological Processes, 1992, 6(3): 279-298. DOI:10.1002/hyp.3360060305 |
| [57] |
Andréassian V, Lerat J, Loumagne C et al. What is really undermining hydrologic science today?. Hydrological Processes, 2007, 21(20): 2819-2822. DOI:10.1002/hyp.6854 |
| [58] |
Blasone RS, Madsen H, Rosbjerg D. Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. Journal of Hydrology, 2008, 353(1/2): 18-32. DOI:10.1016/j.jhydrol.2007.12.026 |
| [59] |
Bates BC, Campbell EP. A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resources Research, 2001, 37(4): 937-947. DOI:10.1029/2000WR900363 |
| [60] |
Vrugt JA, ter Braak CJF, Diks CGH et al. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. International Journal of Nonlinear Sciences and Numerical Simulation, 2009, 10(3): 273-290. DOI:10.1515/ijnsns.2009.10.3.273 |
| [61] |
Liang SD, Jia HF, Xu CQ et al. A Bayesian approach for evaluation of the effect of water quality model parameter uncertainty on TMDLs: A case study of Miyun Reservoir. Science of the Total Environment, 2016, 560/561: 44-54. DOI:10.1016/j.scitotenv.2016.04.001 |
| [62] |
Wang XL, Sun YF, Song LG et al. An eco-environmental water demand based model for optimizing water resources using hybrid genetic simulated annealing algorithms. Part I. Model development. Journal of Environmental Management, 2009, 90(8): 2628-2635. DOI:10.1016/j.jenvman.2009.02.008 |
| [63] |
Park K, Jung HS, Kim HS et al. Three-dimensional hydrodynamic-eutrophication model (HEM-3D): Application to Kwang-Yang Bay, Korea. Marine Environmental Research, 2005, 60(2): 171-193. DOI:10.1016/j.marenvres.2004.10.003 |
| [64] |
Liu Y, Guo HC eds. Lake-watershed ecosystem management: Theory and application. Beijing: Science Press, 2008: 64. [刘永, 郭怀成. 湖泊-流域生态系统管理研究. 北京: 科学出版社, 2008: 64.]
|
| [65] |
Harmel RD, Smith PK, Migliaccio KW et al. Evaluating, interpreting, and communicating performance of hydrologic/water quality models considering intended use: A review and recommendations. Environmental Modelling & Software, 2014, 57: 40-51. DOI:10.1016/j.envsoft.2014.02.013 |
| [66] |
Matott LS, Babendreier JE, Purucker ST. Evaluating uncertainty in integrated environmental models: A review of concepts and tools. Water Resources Research, 2009, 45(6): W06421. DOI:10.1029/2008WR007301 |
| [67] |
Moriasi DN, Zeckoski RW, Arnold JG et al. Hydrologic and water quality models: Key calibration and validation topics. Transactions of the ASABE, 2015, 58(6): 1609-1618. DOI:10.13031/trans.58.11075 |
| [68] |
Srivastava P, Hamlett JM, Robillard PD et al. Watershed optimization of best management practices using AnnAGNPS and a genetic algorithm. Water Resources Research, 2002, 38(3): 2021-2034. DOI:10.1029/2001WR000365 |
| [69] |
Dong FF, Liu Y, Su H et al. Reliability-oriented multi-objective optimal decision-making approach for uncertainty-based watershed load reduction. Science of the Total Environment, 2015, 515/516: 39-48. DOI:10.1016/j.scitotenv.2015.02.024 |
| [70] |
Goberna MA, Jeyakumar V, Li G et al. Robust solutions to multi-objective linear programs with uncertain data. European Journal of Operational Research, 2015, 242(3): 730-743. DOI:10.1016/j.ejor.2014.10.027 |
| [71] |
Huang G, Cao M. Analysis of solution methods for interval linear programming. Journal of Environmental Informatics, 2011, 17(2): 54-64. DOI:10.3808/jei.201100187 |
| [72] |
Zou R, Liu Y, Liu L et al. REILP approach for uncertainty-based decision making in civil engineering. Journal of Computing in Civil Engineering, 2010, 24(4): 357-364. DOI:10.1061/(ASCE)CP.1943-5487.0000037 |
| [73] |
Maringanti C, Chaubey I, Popp J. Development of a multiobjective optimization tool for the selection and placement of best management practices for nonpoint source pollution control. Water Resources Research, 2009, 45(6): W06406. DOI:10.1029/2008WR007094 |
| [74] |
Jiang QS, Su H, Liu Y et al. Parameter uncertainty-based pattern identification and optimization for robust decision making on watershed load reduction. Journal of Hydrology, 2017, 547: 708-717. DOI:10.1016/j.jhydrol.2017.02.035 |
| [75] |
Gitau MW, Chiang LC, Sayeed M et al. Watershed modeling using large-scale distributed computing in Condor and the soil and water assessment tool model. Simulation, 2012, 88(3): 365-380. DOI:10.1177/0037549711402524 |
| [76] |
Xu M, van Overloop PJ, van de Giesen NC. Model reduction in model predictive control of combined water quantity and quality in open channels. Environmental Modelling & Software, 2013, 42: 72-87. DOI:10.1016/j.envsoft.2012.12.008 |
| [77] |
Fen C, Chan C, Cheng H. Assessing a response surface-based optimization approach for soil vapor extraction system design. Journal of Water Resources Planning and Management, 2009, 135(3): 198-207. DOI:10.1061/(ASCE)0733-9496(2009)135:3(198) |
| [78] |
Behzadian K, Kapelan Z, Savic D et al. Stochastic sampling design using a multi-objective genetic algorithm and adaptive neural networks. Environmental Modelling & Software, 2009, 24(4): 530-541. DOI:10.1016/j.envsoft.2008.09.013 |
| [79] |
Ge Q, Ciuffo B, Menendez M. Combining screening and metamodel-based methods: An efficient sequential approach for the sensitivity analysis of model outputs. Reliability Engineering & System Safety, 2015, 134: 334-344. DOI:10.1016/j.ress.2014.08.009 |
| [80] |
Ratto M, Castelletti A, Pagano A. Emulation techniques for the reduction and sensitivity analysis of complex environmental models. Environmental Modelling & Software, 2012, 34: 1-4. DOI:10.1016/j.envsoft.2011.11.003 |
| [81] |
Chen VCP, Tsui KL, Barton RR et al. A review on design, modeling and applications of computer experiments. ⅡE Transactions, 2006, 38(4): 273-291. DOI:10.1080/07408170500232495 |
| [82] |
Forrester AIJ, Keane AJ. Recent advances in surrogate-based optimization. Progress in Aerospace Sciences, 2009, 45(1/2/3): 50-79. DOI:10.1016/j.paerosci.2008.11.001 |
| [83] |
Zou R, Liu Y, Riverson J et al. A nonlinearity interval mapping scheme for efficient waste load allocation simulation-optimization analysis. Water Resources Research, 2010, 46(8): W08530. DOI:10.1029/2009WR008753 |
| [84] |
Zhou YQ, Ma JR, Zhang YL et al. Improving water quality in China: Environmental investment pays dividends. Water Research, 2017, 118: 152-159. DOI:10.1016/j.watres.2017.04.035 |
| [85] |
Tong Y, Zhang W, Wang X et al. Decline in Chinese lake phosphorus concentration accompanied by shift in sources since 2006. Nature Geoscience, 2017, 10(7): 507. DOI:10.1038/ngeo2967 |
| [86] |
Liang ZY, Liu Y, Chen HL et al. Is ecoregional scale precise enough for lake nutrient criteria? Insights from a novel relationship-based clustering approach. Ecological Indicators, 2019, 97: 341-349. DOI:10.1016/j.ecolind.2018.10.034 |
| [87] |
Phillips G, Kelly A, Pitt JA et al. The recovery of a very shallow eutrophic lake, 20 years after the control of effluent derived phosphorus. Freshwater Biology, 2005, 50(10): 1628-1638. DOI:10.1111/j.1365-2427.2005.01434.x |
| [88] |
Jeppesen E, Meerhoff M, Jacobsen BA et al. Restoration of shallow lakes by nutrient control and biomanipulation—the successful strategy varies with lake size and climate. Hydrobiologia, 2007, 581(1): 269-285. DOI:10.1007/s10750-006-0507-3 |
| [89] |
Rui Z, Su H, Yu YH et al. Object-Oriented Precise Decision-Making(OOPD) for water quality improvement in Lake Yilong. Acta Scientiarum Naturalium Universitatis Pekinensis, 2018, 54(3): 511-520. [邹锐, 苏晗, 余艳红等. 基于水质目标的异龙湖流域精准治污决策研究. 北京大学学报:自然科学版, 2018, 54(3): 511-520.] |
| [90] |
Schindler DW, Hecky RE. Eutrophication: more nitrogen data needed. Science, 2009, 324(5928): 721-722. DOI:10.1126/science.324_721b |
| [91] |
Schindler DW. The dilemma of controlling cultural eutrophication of lakes. Proceedings of the Royal Society B: Biological Sciences, 2012, 279(1746): 4322-4333. DOI:10.1098/rspb.2012.1032 |
| [92] |
Jarvie HP, Smith DR, Norton LR et al. Phosphorus and nitrogen limitation and impairment of headwater streams relative to rivers in Great Britain: A national perspective on eutrophication. Science of the Total Environment, 2018, 621: 849-862. DOI:10.1016/j.scitotenv.2017.11.128 |
| [93] |
Mollema PN, Antonellini M. Water and (bio) chemical cycling in gravel pit lakes: A review and outlook. Earth-Science Reviews, 2016, 159: 247-270. DOI:10.1016/j.earscirev.2016.05.006 |
| [94] |
Carpenter SR, Ludwig D, Brock WA. Management of eutrophication for lakes subject to potentially irreversible change. Ecological Applications, 1999, 9(3): 751-771. DOI:10.1890/1051-0761(1999)009%5b0751:MOEFLS%5d2.0.CO%3b2 |
| [95] |
Dakos V, Carpenter SR, van Nes EH et al. Resilience indicators: Prospects and limitations for early warnings of regime shifts. Philosophical Transactions of the Royal Society B: Biological Sciences, 2015, 370(1659): 20130263. DOI:10.1098/rstb.2013.0263 |
| [96] |
Albert MS, Janaki L, Joseph S et al. Determining the spatial variation of phosphorus in a lake system using remote sensing techniques. Lakes & Reservoirs: Research & Management, 2014, 19(1): 24-36. DOI:10.1111/lre.12054 |
| [97] |
Meinson P, Idrizaj A, Noges P et al. Continuous and high-frequency measurements in limnology: History, applications, and future challenges. Environmental Reviews, 2016, 24(1): 52-62. DOI:10.1139/er-2015-0030 |
| [98] |
Leigh C, Alsibai O, Hyndman RJ et al. A framework for automated anomaly detection in high frequency water-quality data from in situ sensors. Science of the Total Environment, 2019, 664: 885-898. DOI:10.1016/j.scitotenv.2019.02.085 |
| [99] |
Zou R, Wu Z, Zhao L et al. Nutrient cycling flux of Lake Dianchi: A three-dimensional water quality modelling approach. J Lake Sci, 2017, 29(4): 819-826. [邹锐, 吴桢, 赵磊等. 湖泊营养盐通量平衡的三维数值模拟. 湖泊科学, 2017, 29(4): 819-826. DOI:10.18307/2017.0405] |
| [100] |
Evans MR, Grimm V, Johst K et al. Do simple models lead to generality in ecology?. Trends in Ecology & Evolution, 2013, 28(10): 578-583. DOI:10.1016/j.tree.2013.05.022 |
| [101] |
Kreft JU, Plugge CM, Grimm V et al. Mighty small: Observing and modeling individual microbes becomes big science. PNAS, 2013, 110(45): 18027-18028. DOI:10.1073/pnas.1317472110 |
| [102] |
Hellweger FL, Bucci V. A bunch of tiny individuals—Individual-based modeling for microbes. Ecological Modelling, 2009, 220(1): 8-22. DOI:10.1016/j.ecolmodel.2008.09.004 |
| [103] |
DeAngelis DL, Mooij WM. Individual-based modeling of ecological and evolutionary processes. Annual Review of Ecology, Evolution, and Systematics, 2005, 36(1): 147-168. DOI:10.1146/annurev.ecolsys.36.102003.152644 |
| [104] |
Railsback SF, Grimm V eds. Agent-based and individual-based modeling: A practical introduction. Princeton: Princeton University Press, 2012: 3.
|
| [105] |
Sher D, Thompson JW, Kashtan N et al. Response of Prochlorococcus ecotypes to co-culture with diverse marine bacteria. The ISME Journal, 2011, 5(7): 1125-1132. DOI:10.1038/ismej.2011.1 |
| [106] |
Amin SA, Parker MS, Armbrust EV. Interactions between diatoms and bacteria. Microbiology and Molecular Biology Reviews, 2012, 76(3): 667-684. DOI:10.1128/mmbr.00007-12 |
| [107] |
Hellweger FL, Clegg RJ, Clark JR et al. Advancing microbial sciences by individual-based modelling. Nature Reviews Microbiology, 2016, 14(7): 461. DOI:10.1038/nrmicro.2016.62 |
| [108] |
Lange M ed. Embedding individual-based plankton ecosystem models in a finite element ocean model. London: Imperial College London, 2014.
|
| [109] |
Wellen C, Kamran-Disfani AR, Arhonditsis GB. Evaluation of the current state of distributed watershed nutrient water quality modeling. Environmental Science & Technology, 2015, 49(6): 3278-3290. DOI:10.1021/es5049557 |
| [110] |
Gal G, Makler-Pick V, Shachar N. Dealing with uncertainty in ecosystem model scenarios: Application of the single-model ensemble approach. Environmental Modelling & Software, 2014, 61: 360-370. DOI:10.1016/j.envsoft.2014.05.015 |
| [111] |
Elshorbagy A, Ormsbee L. Object-oriented modeling approach to surface water quality management. Environmental Modelling & Software, 2006, 21(5): 689-698. DOI:10.1016/j.envsoft.2005.02.001 |
| [112] |
Read JS, Jia XW, Willard J et al. Process-guided deep learning predictions of lake water temperature. Water Resources Research, 2019, 55(11): 9173-9190. DOI:10.1029/2019WR024922 |
| [113] |
Li X, Huang CL. Data assimilation: A new means for multi-source geospatial data integration. Science & Technology Review, 2004, 22(12): 13-16. [李新, 黄春林. 数据同化——一种集成多源地理空间数据的新思路. 科技导报, 2004, 22(12): 13-16. DOI:10.1016/S0958-2118(04)00281-2] |
| [114] |
Huang JC, Gao JF, Liu JT et al. State and parameter update of a hydrodynamic-phytoplankton model using ensemble Kalman filter. Ecological Modelling, 2013, 263: 81-91. DOI:10.1016/j.ecolmodel.2013.04.022 |
| [115] |
Chen C, Huang JC, Chen QW et al. Assimilating multi-source data into a three-dimensional hydro-ecological dynamics model using Ensemble Kalman Filter. Environmental Modelling & Software, 2019, 117: 188-199. DOI:10.1016/j.envsoft.2019.03.028 |
| [116] |
Neftci EO, Averbeck BB. Reinforcement learning in artificial and biological systems. Nature Machine Intelligence, 2019, 1(3): 133-143. DOI:10.1038/s42256-019-0025-4 |
 2021, Vol. 33
2021, Vol. 33 


