(2: 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室, 北京 100038)
(3: 深圳市水文水质中心, 深圳 518055)
(4: 深圳市东部水源管理中心, 深圳 518172)
(2: State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, P. R. China)
(3: Shenzhen Hydrology and Water Quality Center, Shenzhen 518055, P. R. China)
(4: Shenzhen Eastern Water Resources Management Center, Shenzhen 518172, P. R. China)
根据《2018年中国生态环境状况公报》,2018年全国地表水中Ⅳ类和Ⅴ类占比达22.3 %, 劣Ⅴ类占比6.7 %, 全国地下水水质监测点中Ⅳ类占70.7 %,Ⅴ类占15.5 % [1],我国地表及地下水面临着不同程度的污染.水污染控制和水环境保护的关键是控制污染物总量的排放,而其基础和关键是定量水体污染负荷总量[2].对于城市水环境而言,城市降雨径流污染是城市水质恶化的重要原因之一[3-4],定量计算城市降雨径流污染负荷,可为城市水环境治理和污染控制提供科学依据.
定量非点源污染负荷计算最早是美国在1960s-1970s开展的[5],中国始于1980s[6].目前,定量城市降雨径流污染负荷的计算方法较多,如浓度法[7-9]、统计方法[10]、推算方法[11]、反算方法[12-13],这些方法大多用于估算年污染负荷,通常需要监测多场场次径流污染负荷,监测难度和工作量大、费用高,且估算精度与监测的降雨场次有关.目前,关于估算场次降雨径流污染负荷研究相对较少.随着计算机的高速发展,数学模型的优势逐渐显现.目前,通用的计算模型较多,如SWMM[14]、STORM[15]、DR3M-QUAL[16]、SLAMM[17]、HydroWorks[18]、HSPF[19]、MOUSE[20-21]等.数学模型是定量分析非点源污染负荷的重要手段之一,通常利用有限场次降雨的监测数据便可估算研究区降雨径流污染负荷.数学模型存在的主要问题是建模和参数率定时间较长,并且在预测分析平原城市的污染负荷时存在子流域划分困难、河道流向难以确定等问题[22],导致径流量计算偏差较大,增加了污染物负荷计算的难度和预测精度.
为此,本文提出一种适用地区较广的快速估算场次降雨径流污染负荷的数学模型,即以污染物累积-冲刷理论为基础,提出了“特征面积”的概念和计算公式,构建了场次降雨径流污染负荷数学模型,并结合多个案例,对数学模型的有效性、预测精度和适用性等方面进行评价,以期为场次降雨径流污染负荷的计算提供一种快速估算方法.
1 场次降雨径流污染负荷估算方法地表径流污染负荷是指由降雨引起地表径流排放的污染物总量,其中由一场降雨引起的称为场次降雨污染负荷,由一年中多场降雨引起的称为年污染负荷[23].对于径流污染负荷,有学者采用径流量与对应污染物浓度的乘积进行计算,但数据需要现场监测,难度较大;另有学者通过多年监测数据统计出的估算模型进行计算,所需资料少,应用简便,如Schueler提出了城市开发区年地表径流污染物计算模型[10],该模型中污染负荷与地表径流系数、汇水区面积、降雨量和污染物径流量加权平均浓度呈正比.地表径流系数和污染物径流量加权平均系数对模型的精度影响甚大. Thomson等[24]研究表明,污染物径流量加权平均浓度的准确估算至少需要15~20场降雨径流观测数据.
污染物累积过程和降雨冲刷过程是决定降雨径流污染负荷的两个重要过程,描述累积过程的模型主要有线性、指数、对数等形式,其中以指数及一些变形形式相对比较成熟,而基于反映动力学假设的冲刷过程模型被人们广泛使用[25].应用广泛的SWMM模型中采用的是污染物线性累积模型和指数冲刷模型[26],见公式(1)和(2).该模型能较好地反映污染物负荷机理.
| $B=\frac{C_{1} \cdot t}{C_{2}+t} $ | (1) |
式中,C1为最大累积量,kg/m2;C2为半饱和常数(达到最大累积物一半时所用的时间), d;t为晴天时间,d.
| $W=c_{1} \cdot q^{c_{2}} \cdot B $ | (2) |
式中,c1为冲刷系数;c2为冲刷指数;q为单位面积径流速率,mm/h;B为污染物累积总量,kg/mm.
本文以污染物累积-冲刷理论为基础,提出“特征面积”概念,以表征污染物在各类土地上的污染负荷特性即污染物累积特性和冲刷特性.污染物累积特性用权重系数表示,即以污染物在各类土地上的最大累积量作为各类土地面积的权重,用以表征污染物累积强度,并以归一化的方式计算特征面积的权重系数,即各类土地面积的权重系数等于污染物在各类土地上的最大累积量与在研究区所有土地上最大累积量的最大值的比值.污染物冲刷特性用影响系数表示,以表征不同土地类型下降雨径流冲刷特性的差异.影响降雨冲刷特性的因素较多,主要可以分为两类:一是降雨的基本参数和雨型,二是降雨区域的相关特征,包括城市下垫面类型、功能区类型和排水体制类型等,其中,下垫面条件对径流量和径流污染负荷有非常重要的影响.本文将汇水区的土地利用类型分为透水区和不透水区两大类,分别设置透水区影响系数和不透水区影响系数.特征面积与污染物最大累积量、土地利用性质、汇水区面积、权重系数和影响系数有关,计算公式为:
| $S_{\mathrm{a}}=w_{\mathrm{im}} \cdot S_{\mathrm{im}}+w_{\mathrm{m}} \cdot S_{\mathrm{m}} $ | (3) |
式中,Sa为特征面积,hm2;Sim为不透水区特征面积,
根据污染物累积-冲刷模型,降雨径流污染负荷与降雨量、汇水面积、污染物累积量、地表径流系数等因素呈正比,而特征面积表征了污染物累积特性和不同土地利用类型的冲刷特性,因此,降雨径流污染负荷与降雨量和特征面积呈正比,降雨径流污染负荷数学模型可表示为:
| $M=k \cdot S_{\mathrm{a}} \cdot P+b=k_{1} \cdot S_{\mathrm{im}} \cdot P+k_{2} \cdot S_{\mathrm{m}} \cdot P+b $ | (4) |
式中,M为污染物负荷,kg;Sa为特征面积,hm2;Sim为不透水区特征面积,hm2;Sm为透水区特征面积,hm2;P为降雨总量,mm;k为斜率,kg/(hm2·mm);b为截距,kg. k1=k·wim,k2=k·wm.
斜率k1和k2表征降雨事件中不透水区和透水区降雨径流污染冲刷特性,其值与不透水率或径流系数有关.特征面积与降雨量的乘积具有体积单位,可定义为“特征体积”,因此,斜率k1和k2可理解为单位体积的降雨径流污染负荷.理论上讲,当降雨量为零时,污染量负荷为零,截距b也应该为零.但是,受模型简化和测量误差等因素的影响,截距可能并不等于零,因此,公式(4)中增加了截距项,以提高模型的预测精度.
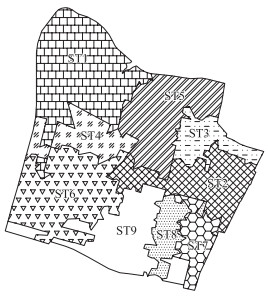
2 场次降雨径流污染负荷数学模型评价 2.1 材料与数据来源 2.1.1 研究区概况以安徽省某县城为例,研究区的总面积为43.6 km2,地势平缓,地面高程平均海拔26.5~33.5 m,地面自然坡降为1/9000.研究区分为9个汇水片区,分别为ST1、ST2、ST3、ST4、ST5、ST6、ST7、ST8和ST9,各汇水片区范围见图 1.研究区的土地类型分为路面、屋面和绿地,各汇水片区的面积及其包含各土地类型的占比和面积见表 1.
|
图 1 研究区各汇水区分布 Fig.1 Distribution of catchments |
| 表 1 各汇水区土地利用占比情况 Tab. 1 Land use proportion of catchments |
在建立场次降雨径流污染负荷数学模型时,需要多场污染负荷结果.由于SWMM非点源污染模型易于生成不同降雨径流条件下的污染负荷样本,因此本文采用SWMM非点源污染模型的模拟结果验证模型.以SWMM为平台,对研究区和排水系统进行概化,子汇水区690个,总面积为42.135 km2,管道876根,节点876个.各子汇水区的不透水率和坡度利用地形资料和遥感影像借助ArcGIS计算得到.管网计算选择动力波,下渗模型选择Horton模型,前期干旱时间选择10 d,清扫街道去除率为60 %,汇水区宽度系数、不透水区糙率、透水区糙率、不透水区洼蓄量、透水区洼蓄量、最大入渗率、最小入渗率、衰减常数、晴天时间分别取0.8、0.013、0.17、1 mm、3 mm、76.2 mm/h、3.81 mm/h、2 h-1、7 d[27].设计暴雨雨型选择芝加哥雨型[28],雨峰系数取0.4,设计重现期分别选取1、2、5、10、12、15和20 a(分别记为P1、P2、P5、P10、P12、P15、P20),根据当地的暴雨强度计算公式,各降雨重现期下的降雨量分别为51、76、108、132、138、146和156 mm.
选取COD、TP和TN 3种污染物作为参考研究区降雨径流污染负荷情况的指标.根据SWMM手册[26]和相关文献[29-30]得到污染物累积和冲刷的参数,分别见表 2和表 3.
| 表 2 污染物累积参数 Tab. 2 Build-up parameter of pollutants |
| 表 3 污染物冲刷参数 Tab. 3 Wash-off parameter of pollutants |
本文中使用的两个主要数据集:(1)研究区遥感数据,是从欧洲航天局(ESA,European Space Agency)的哨兵系列卫星科研数据中心(Sentinels Scientific Data Hub)中以10 m的空间分辨率检索土地利用数据(https://scihub.copernicus.eu/dhus/#/home);(2)研究区的地形数据,是当地人民政府提供的1 :1000城市地形规划图.
2.2 数学模型的有效性对7种重现期分别进行模拟,模拟时间为24 h(含退水时间).假定有i个汇水片区,各汇水片区包含j个排水口,根据SWMM模型模拟结果即各排水口地表径流量qi, j(τ)、对应的地表径流污染物含量ci, j(τ)和模拟的总时间,积分计算出一个排水口的污染负荷,对j个排水口的污染负荷进行累积,即可得到各汇水片区污染负荷MSTi,其计算公式见公式(5).研究区的污染负荷即所有汇水片区污染负荷的累加.以污染物COD为例,各汇水片区在不同降雨条件下污染负荷见表 4.各汇水片区在不同降雨重现期下污染负荷与“特征体积”之间的关系分别见图 2.
| 表 4 各汇水片区和研究区在不同降雨条件下的COD负荷 Tab. 4 Cumulated COD in each catchment and study area under different rainfall conditions |
|
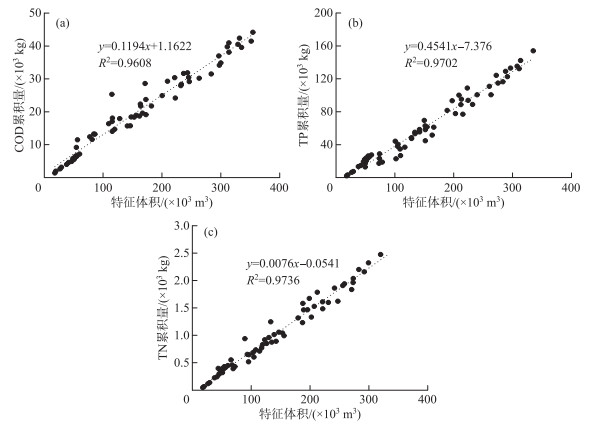
图 2 不同降雨条件下COD(a)、TP(b)和TN(c)累积总量与特征体积的关系曲线 Fig.2 The relationship between cumulated COD (a), TP (b) and TN (c) and characteristic volume under different rainfall conditions |
| $M_{\mathrm{ST}i}=\sum\limits_{j=1}^{n}\left(\int_{0}^{T} q_{i, j}(\tau) c_{i, j}(\tau)\right) \mathrm{d} \tau $ | (5) |
式中,T为模拟的总时间, s;qi, j(τ)为第i个汇水片区包含的第j个排水口对应汇水区径流量, m3/s;ci, j(τ)为第i个汇水片区包含的第j个排水口对应汇水区污染物浓度含量, mg/L.
从图 2中可见,降雨径流污染负荷与特征体积具有较好的线性关系,其中,TN和TP的相关系数为0.97,COD的相关系数为0.96,说明降雨径流污染负荷与“特征体积”即特征面积和降雨量的乘积呈正比,不同场次降雨下污染负荷可以用同一个公式进行描述,也从侧面说明了本文提出的估算模型是有效的.由于各相关系数并不等于1,所以本文提出的数学模型的预测精度还需要做进一步分析.
2.3 数学模型的预测精度研究区路面和屋面为不透水区,绿地为透水区,根据各汇水片区中各类土地面积(表 1)、污染物在各类土地上的最大累积量(表 2),结合公式(3),计算各汇水片区对应的不透水区特征面积和透水区特征面积;根据各降雨量和各汇水片区污染负荷(表 4),结合公式(4),率定场次降雨径流污染负荷数学模型.本文设置3种情景,即分别选择1场降雨(P5)、2场降雨(P5和P10)和3场降雨(P2、P5和P10)下的污染负荷,率定场次降雨径流污染负荷数学模型,预测其他场次降雨径流污染负荷,并与SWMM模型计算出的实际污染负荷进行对比,分析预测精度.
2.3.1 各汇水片区降雨径流污染负荷预测精度以COD为例,3种情景下的率定结果见表 5,各汇水片区的污染负荷预测误差如图 3所示.
| 表 5 模型系数和影响系数计算结果 Tab. 5 Model coefficients and influence coefficients |

|
图 3 各汇水片区污染物COD负荷预测误差(a:情景一;b:情景二;c:情景三) Fig.3 Prediction error of COD pollutant load under different storm frequencies in each catchment(a: scenario 1; b: scenario 2; c: scenario 3) |
从表 5中可以看出,不透水区影响系数几乎是透水区影响系数的两倍.透水区不仅能减少地表径流,也可控制降雨径流污染,低影响开发技术即是利用透水路面、植物透水砖、生物滞留池等技术增加透水区面积,降低降雨径流污染负荷.影响系数的差异也表明本文提出的“特征面积”的合理性,反映了汇水区上污染物累积特性和不透水率差异引起的地表径流冲刷特性的差异.
从图 3可以看出,3种情景下,P1和P2的降雨径流污染负荷的预测误差较大,P2以上的预测误差相对较小,预测精度较高.
2.3.2 研究区降雨径流污染负荷预测精度以整个研究区为对象,对3种情景下降雨径流污染负荷进行预测精度分析,计算误差如图 4所示.
|
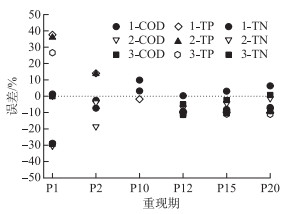
图 4 3种情景下各污染物在不同重现期下的预测误差 Fig.4 Prediction error of each pollutant load under the three scenarios and different storm frequencies |
从图 4中可以看出,对于COD,情景一时,P1的预测误差为-28.85 %, P2及以上的预测误差在-7.3 % ~9.8 %之间;情景二时,P2及以下的误差在-18.6 % ~30.0 %之间, P12及以上的预测误差在-1.4 % ~7.0 %之间;情景三时,P2及以下的误差在-29.2 %以内,P12及以上的预测误差在-5.0 % ~0.78 %之间.对于TP,情景一时,P1的预测误差为37.62 %, P2的预测误差为14.02 %,P10及以上的预测误差在-10.10 % ~-1.82 %之间;情景二时,P1的预测误差为36.02 %, P2的预测误差为13.7 %,P12及以上的预测误差在-9.6 % ~-9.2 %之间;情景三时,P1的预测误差为26.61 %, P12及以上的预测误差约为-11 %.对于TN,预测误差均在±11 %以内.
综上,本文提出场次降雨径流污染负荷数学模型,对于P2以上的降雨径流污染负荷预测精度较高,其相对误差小于±11 %,此外,降雨场次对数学模型的预测精度影响不大.模型中有3个系数需要率定,因此,利用3场以上场次污染负荷结果便可预测其他场次的污染负荷,从而大大减小获取污染负荷数据的工作量.对于2 a一遇以下的降雨情况,模型预测精度相对较低,其主要原因是:小降雨情况下,下垫面的洼蓄量和雨水下渗量在总降雨量中占比相对较大,采用大降雨事件的污染负荷结果率定模型参数与小降雨事件下有一定的差异,使得计算误差相对较大.因此,对于小降雨工况而言,可以采用降雨量相近的数据进行率定,以提高模型的预测精度.
2.4 数学模型的适用性选择武汉市和苏州市两个地区的实际案例进行分析和说明.
1) 案例一
潘璐[31]研究了武汉市典型校区的降雨径流污染负荷.研究区坡度在0.13 % ~0.50 %之间.经现场采样,TN和CODMn为主要污染物.地面分为路面、屋面、庭院/广场、操场和绿地,CODMn在对应土地类别上的最大累积量分别为80、60、45、45和30 kg/hm2;TN在对应土地类别上的最大累积量分别为6、4、6、6和10 kg/hm2.采用芝加哥雨型,雨峰系数0.4,降雨历时120 min,干旱时间10 d.研究区降雨总量和各降雨条件下的污染负荷等基础信息如表 6所示.
| 表 6 武汉市典型校区降雨径流污染负荷[31] Tab. 6 Rainfall runoff pollution load of the typical campus in Wuhan City |
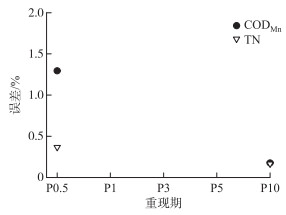
由于数据数量相对较少,因此,根据P1、P3、P5 3场降雨条件下的污染负荷结果率定模型,预测P0.5和P10下的污染负荷,预测精度均在98.5 %以内,精度较高,计算误差见图 5.
|
图 5 案例一中CODMn和TN污染负荷总量预测误差 Fig.5 Prediction error of total CODMn and TN pollution load of case 1 |
2) 案例二
祁继英[32]研究了苏州市南园水系排水区的降雨径流污染负荷.主要污染物为COD、TN和TP,地面分为屋面、绿地和交通道路.各污染物在对应土地类别上的最大累积量见表 2.采用芝加哥雨型,雨峰系数为0.367,降雨历时60 min,干旱时间10 d.研究区降雨总量和各降雨条件下的污染负荷总量等基础信息见表 7.
| 表 7 苏州南园水系降雨径流污染负荷[32] Tab. 7 Rainfall runoff pollution load of Nanyuan water system in Suzhou City |
根据P0.5、P1、P2 3场降雨条件下的污染负荷结果率定模型,预测P0.25、P3和P5下的污染负荷,预测精度均在99.5 %以内,精度较高,计算误差见图 6.

|
图 6 案例二中COD、TN和TP污染负荷总量预测误差 Fig.6 Prediction error of total COD and TN pollution load in case 2 |
本文构建了场次降雨径流污染负荷数学模型,预测精度较好,但其也有一定的局限性:
1) 对于小降雨事件,模型预测精度比其他降雨条件相对较低.为提高模型预测精度,建议采用降雨量相近的观测结果率定模型参数.
2) 降雨间隔影响污染物在地面上的最大累积量,而不同土地上的污染物最大累积量是影响场次降雨径流污染数学模型预测精度的关键参数,该参数与土地利用性质和状况、绿化条件、交通状况以及土地裸露程度直接相关[4],通常可在各类土地上选取有代表性的1 m2区域定时监测分析获得[33],也可参考相关文献,或根据经验确定(如查阅SWMM手册等).有分析表明[34],一场典型降雨48 h后地表污染物才能恢复原状.为此,对于连续降雨或者降雨间隔时间较短导致地面污染物在各类土地上的最大累积量发生变化,当全域最大累积量与局部最大累积量线性变化时,权重系数并不会发生较大变化,不会影响模型预测精度.倘若发生较大变化且不是线性变化时,为了提高模型的计算精度,模型还需重新率定.
3 结论本文以污染物累积-冲刷理论为基础,提出了反映污染负荷特性的“特征面积”,建立了场次降雨径流污染负荷数学模型,并结合多个案例,分析了数学模型的有效性、预测精度、适用性和局限性.主要结论如下:
1) 特征面积较好地反映了污染物在各类土地上的污染负荷特性即污染物累积特性和冲刷特性,经实例验证场次降雨径流污染负荷与特征面积和降雨量的乘积呈正比.
2) 利用3场及以上降雨径流污染负荷结果,可较好地率定场次降雨径流污染负荷数学模型,从而可快速且较准确地估算单场次降雨径流污染负荷.该方法简单实用,获取数据工作量小,适用地区广.
3) 对于小降雨事件,建议采用降雨量相近的观测结果对模型进行率定,以提高模型的预测精度.
| [1] |
Ministry of Ecology and Environment of the People's Republic of China. China eco-environment status bulletin 2018, 2019. http://www.mee.gov.cn/hjzl/sthjzk/zghjzkgb/201905/P020190619587632630618.pdf. [中华人民共和国生态环境部. 2018年中国生态环境状况公报, 2019. ]
|
| [2] |
Ma DM, Shi HH, Feng AP. Estimation of agricultural non-point source pollution based on watershed unit:A case study of LaizhouBay. Acta Ecologica Sinica, 2014, 34(1): 173-181. [麻德明, 石洪华, 丰爱平. 基于流域单元的海湾农业非点源污染负荷估算——以莱州湾为例. 生态学报, 2014, 34(1): 173-181.] |
| [3] |
Fucčík P, Kaplická M, Kvítek T et al. Dynamics of stream water quality during snowmelt and rainfall-runoff events in a small agricultural catchment. CLEAN-Soil, Air, Water, 2012, 40(2): 154-163. DOI:10.1002/clen.201100248 |
| [4] |
America Water Resources Association. Urban land runoff considerations urbanization and water quality control, 1995.
|
| [5] |
Ongley ED, Zhang XL, Tao Y. Current status of agricultural and rural non-point source pollution assessment in China. Environmental Pollution, 2010, 158(5): 1159-1168. DOI:10.1016/j.envpol.2009.10.047 |
| [6] |
Xia Q. Study on pollution system of urban runoff. Acta Scientiae Circumstantiae, 1982, 2(4): 271-278. [夏青. 城市径流污染系统分析. 环境科学学报, 1982, 2(4): 271-278. DOI:10.13671/j.hjkxxb.1982.04.001] |
| [7] |
Zhu YS, Jin GY. Urban hydrology. Beijing: China Science and Technology Press, 1991. [朱元甡, 金光炎. 城市水文学. 北京: 中国科学技术出版社, 1991.]
|
| [8] |
Li HE. Mean concentration method for estimation of nonpoint source load and its application. Acta Scientiae Circumstantiae, 2000, 20(4): 397-400. [李怀恩. 估算非点源污染负荷的平均浓度法及其应用. 环境科学学报, 2000, 20(4): 397-400. DOI:10.3321/j.issn:0253-2468.2000.04.003] |
| [9] |
Zhao JQ. Urban surface runoff pollution and control. Beijing: China Environmental Press, 2002. [赵剑强. 城市降雨径流污染与控制. 北京: 中国环境科学出版社, 2002.]
|
| [10] |
Akan AO ed. Urban stormwater hydrology. USA: Technomic Publishing Company Inc., 1993.
|
| [11] |
Wang RY. Pollution processes and management researches on urban rainfall runoff in Shanghai[Dissertation]. Shanghai: East China Normal University, 2005. [王和意.上海城市降雨径流污染过程及管理措施研究[学位论文].上海: 华东师范大学, 2005. ]
|
| [12] |
He BG, Zhou NS, Yuan XM. On contribution of sediment to secondary pollution of river. Environmental Pollution & Control, 1999, 21(3):41-43. [贺宝根, 周乃晟.底泥对河流的二次污染浅析.环境污染与防治, 1999, 21(3):41-43. ]
|
| [13] |
Wang DM, Zhang WY, Su XQ. Counter-measures of soil and water losses in urban area. Urban Studies, 2001(5): 49-53. [王冬梅, 张文艳, 苏新琴. 城市水土流失及其防治对策. 城市发展研究, 2001(5): 49-53.] |
| [14] |
Huber WC, Singh VP. EPA storm water management model SWMM 5.0. Computer Models of Watershed Hydrology, 1995. DOI:10.1201/9781420037432.ch14 |
| [15] |
US Army Corps of Engineers (USACE). Storage, Treatment, Overflow, Runoff model 'STORM': User's Manual. Hydrologic Engineering Center, Davis, CA, 1976.
|
| [16] |
Alley WM, Smith PE. Distributed routing rainfall-runoff model: versionⅡ. USA: United States Geological Survey, 1982. DOI: 10.3133/ofr82344.
|
| [17] |
Pitt R, Voorhees J. SLAMM, the source loading and management model//Field R, Sullivan eds. Wet-weather flow in the urban watershed. Boca Raton: Technology and Management CRC Press, 2002: 79-101. DOI: 10.1201/9781420012774.ch4.
|
| [18] |
Wallingford Software. Using hydroworks. United Kingdom: Wallingford Software, 1997.
|
| [19] |
Bicknell BR, Imhoff JC, Kittle JL. Hydrological simulation program-Fortran user's manual for release 11. USA: United States Environment Protection Agency, 1996.
|
| [20] |
D HI. MOUSE pipe flow, reference manual. Denmark: DHI Software, 2004.
|
| [21] |
D HI. MOUSE surface runoff models, reference manual. Denmark: DHI Software, 2004.
|
| [22] |
Li S, Zhang ZL, Sun YY. Simulation of non-point source pollution of nitrogen and phosphorus in Lake Nansi watershed using SWAT model. J Lake Sci, 2013, 25(2): 236-242. [李爽, 张祖陆, 孙媛媛. 基于SWAT模型的南四湖流域非点源氮磷污染模拟. 湖泊科学, 2013, 25(2): 236-242. DOI:10.18307/2013.0209] |
| [23] |
Li JK, Li YJ, Li HE. Study on the calculation method for urban surface runoff pollution load. Journal of Water Resources and Water Engineering, 2010, 21(2): 5-13. [李家科, 李亚娇, 李怀恩. 城市地表径流污染负荷计算方法研究. 水资源与水工程学报, 2010, 21(2): 5-13.] |
| [24] |
Thomson NR, McBean EA, Snodgrass W et al. Sample size needs for characterizing pollutant concentrations in highway runoff. Journal of Environmental Engineering, 1997, 123(10): 1061-1065. DOI:10.1061/(asce)0733-9372(1997)123:10(1061) |
| [25] |
Chen Q, Hu WP, Zhang JN. Advances in research on the build-up and rainfall runoff wash-off of urban surface pollutants. Resources and Environment in the Yangtze Basin, 2009, 18(10): 992-996. [陈桥, 胡维平, 章建宁. 城市地表污染物累积和降雨径流冲刷过程研究进展. 长江流域资源与环境, 2009, 18(10): 992-996. DOI:10.3969/j.issn.1004-8227.2009.10.019] |
| [26] |
Rossman LA, Huber WC. Storm water management model reference manual volume I, hydrology. United States Environment Protection Agency, 2015.
|
| [27] |
He SN, Chen WX, Chen KN et al. Analysis of drainage capacity and waterlogging characteristics of small and medium-sized cities-a case study of Guoyang Country. Water Resources and Hydropower Engineering, 2019, 50(9): 75-82. [何胜男, 陈文学, 陈康宁等. 中小城市排水系统排水能力和内涝特性分析——以涡阳县为例. 水利水电技术, 2019, 50(9): 75-82.] |
| [28] |
Cen GP, Shen J, Fan RS. Research on rainfall pattern of urban design storm. Advances in Water Science, 1998, 9(1): 42-47. [岑国平, 沈晋, 范荣生. 城市设计暴雨雨型研究. 水科学进展, 1998, 9(1): 42-47.] |
| [29] |
Ye M, Yang GS, Zhang WS et al. Study on urban non-point pollution characteristics and pollution loads prediction model. Environmental Science and Technology, 2006, 29(2): 67-69. [叶闽, 杨国胜, 张万顺等. 城市面源污染特性及污染负荷预测模型研究. 环境科学与技术, 2006, 29(2): 67-69.] |
| [30] |
Shi LC. Analysis on features of non-point source pollution in Chaohu City and research on load simulation[Dissertation]. Hefei: Jianzhu University, 2016. [施林超.巢湖市老城区非点源污染特性分析及负荷模拟研究[学位论文].合肥: 安徽建筑大学, 2016. ]
|
| [31] |
Pan L. Study on rainfall runoff pollution characteristics and pollution load in typical campus in Wuhan[Dissertation]. Wuhan: Hubei University of Technology, 2018. [潘璐.武汉典型校区降雨径流污染特征及污染负荷研究[学位论文].武汉: 湖北工业大学, 2018. ]
|
| [32] |
Qi JH. Quantity study on non-point source pollution of city[Dissertation]. Nanjing: Hohai University, 2005. [祁继英.城市非点源污染负荷定量化研究[学位论文].南京: 河海大学, 2005. ]
|
| [33] |
Guo L, Zeng GM, Cheng YL. Identity analysis of the surface sediment on the urban streets. Environmental Monitoring in China, 2003, 19(6): 40-42. [郭琳, 曾光明, 程运林. 城市街道地表物特性分析. 中国环境监测, 2003, 19(6): 40-42.] |
| [34] |
U·S University of Maryland. A mathematical model for estimating pollution loading sand removals for urban streets, 2000.
|
 2021, Vol. 33
2021, Vol. 33 


