(2: 合肥工业大学水资源与环境系统工程研究所, 合肥 230009)
(2: Institute of Water Resources and Environmental System Engineering, Hefei University of Technology, Hefei 230009, P. R. China)
水资源承载力是评判水资源与经济社会及生态环境之间是否协同发展的一项综合指标,研究水资源承载力对实现人水和谐具有重要意义,其内涵深化和概念延伸得到学界持续重视[1-4].随着我国社会经济的快速发展和生态环境保护意识的日益增强,区域水资源承载状态预测与控制已成为现代水资源系统管理研究的重要热点之一[5].早期的水资源承载力研究侧重于基于内涵的评价指标体系构建、评价方法探讨等,如夏军等[6]基于水资源承载力定义和水资源承载力系统关系,拟定了水资源承载力的度量和计算方法,并对变化环境下的流域水循环模拟研究、生态需水等进行重点讨论. Wang等[7]利用投影寻踪法将高维数据投影到低维空间,综合水资源承载力指数的特征并应用于流域水资源承载力的评价. Yang等[8]应用物元分析法、模糊综合评价法和投影寻踪综合评价法分别评价玛纳斯河流域水资源承载力,并对3种方法进行应用比较.段新光等[9]通过建立模糊综合评判模型对新疆水资源承载力现状进行评价. Naimi-Ait-Aoudia等[10]评估了阿尔及尔水资源在居民用水方面的承载能力.李云玲等[11]从水资源承载负荷和承载能力两个方向出发,构建了水资源承载能力评价指标体系,采用实物量指标对水资源承载能力各因素分别评价,采用“短板法”综合考虑各要素评价结果,得到水资源承载能力综合评价结果.随着水资源管理实践的演化和水资源承载力研究的深入,仅对现有水资源承载力系统进行静态综合评价已难以满足现代水资源管理的需求,开展承载力动态预测预警并针对性调控渐渐成为新的研究方向,如韩俊丽等[12]应用系统动力学模型(SD模型)对包头市水资源承载力进行模拟,并根据包头市现实状况和未来发展规划选择发展方案,进行仿真模拟来预测包头市水资源承载力.苏志勇等[13]将水资源承载力的研究纳入了生态经济系统的背景下进行综合集成研究,并根据模型的优化分析结果预测了黑河流域张掖地区未来20 a的水资源承载力.董涛等[14]提出从水资源支撑力、压力、调控力3个子系统选择指标,建立基于承载过程的水资源承载主客体耦合评价模型,并对安徽省水资源承载力进行了动态预测评价. Hu等[15]利用指标集方法对福建省流域水资源承载力进行预测,为规划部门决策提供辅助参考.车越等[16]以不同引水量和不同水资源策略为幕景,运用水资源承载力多幕景SD仿真模型,模拟预测崇明岛水资源承载力.赵筱青等[17]运用SD模型针对现状延续、提高水资源开发利用、节水对策、综合对策4种情景模拟预测2010—2020年昆明市水资源承载力.赵春丽[18]建立了河津市水资源承载力SD模型,并通过改变决策变量值设计了3种模拟方案,根据各方案对应的水资源承载力选取优化调控方案.
上述研究采取不同方法在区域水资源承载力动态预测方面进行了积极探索,但由于区域水资源承载力系统的高度复杂性,导致在优化调控理论和技术方法方面尚存在明显不足.目前,国内外水科学界对水资源承载的内涵深化、概念延伸、系统评价及模拟预测等理论与方法研究还在持续发展中,尤其是水资源承载力系统调控尚处于初步探索阶段.针对我国水资源短缺的现状,定性调控分析已经不能满足未来区域水资源承载力管理的需求.根据研究地区的水资源条件、经济发展水平、生态环境保护等现状及规划条件,提出适用于区域水资源承载能力提升与负荷定量调控的方案具有重要意义.需要指出的是,目前研究对象区域多偏向整体水系流域或省市行政区,往下细分到县域的承载力研究较少.笔者认为,我国县级行政区划是最基本的行政单元,基本上所有的社会、经济、环境等规划、设计及政策管理等都是以县(市)为基础,因此可以考虑以县域水资源承载力系统作为基本单元,逐级叠加、组合构成上一层级区域(市、省、自治区等)的水资源承载力系统,这样更能体现系统结构与功能的内在关系.目前对研究区域细分到县级区划作为单元的水资源承载力研究几乎还是空白,因此本文以巢湖流域作为研究对象,以县(市)为单元构建县域水资源承载力量质要素系统动力学动态模拟与预测模型;再从空间上耦合为巢湖流域整体模型以预测流域水资源承载状态;最后通过敏感性分析筛选量质调控指标,并采用正交试验方法确定优化调控方案,进行巢湖流域水资源承载力评价、预测及调控,为湖泊流域管理部门制定水资源管理政策提供理论参考.
1 区域概况巢湖流域(31°25′28″~31°43′28″N,117°16′54″~117°51′46″E)位于江淮之间、安徽省中部、长江中下游,总面积12938 km2,西北以江淮分水岭为界,东濒长江,南与菜子湖、白荡湖、陈瑶湖以及皖河流域毗邻.流域地貌多样,西为大别山,沿江沿湖为平原圩区,其余是丘陵山地,西南高,东北低.流域地处亚热带温润型季风气候,平均气温15~16℃,年均降雨1215 mm,流域内水系密布,水资源丰富,沿湖水系33条,主要支流杭埠河、丰乐河、派河、南淝河等自西向东注入[19].巢湖流域闸上区域行政区包括合肥、巢湖、肥东、肥西、长丰、舒城、庐江两市五县,是巢湖流域主要集水区,同时也是流域内人类社会经济活动影响最剧烈的地区,水资源承载状况复杂[19],因此作为本文研究的重点区域.
2 数据与方法 2.1 系统数据来源水资源承载力研究所需数据主要包含气象水文地理和社会经济两方面,具体数据来源参考《合肥市统计年鉴(2005—2016)》、《六安市统计年鉴(2005—2016)》、《合肥市水资源公报(2005—2016)》、《六安市水资源公报(2005—2016)》、《第一次全国污染源普查城镇生活源产排污系数手册》、《全国第二次污染源普查生活源产排污系数手册》.模型预测年份参数设置参考《合肥市城市总体规划(2006—2020)》、《六安市城市总体规划(2008—2030)》、《安徽省水资源综合规划报告(2010)》、《全国水资源综合规划(2010—2030)》等规划.
2.2 水资源承载力系统综合评价方法巢湖具有长江下游典型平原湖泊水面广、流速慢等特点,同时承担着大型省会城市日益增长的供水、排水任务.巢湖多年平均入湖径流量为36.51亿m3,但不同年份或不同季节差异明显,其中最大年径流量77.8亿m3,最小年径流量2.34亿m3.同时,由于1962年湖口建闸导致水体交换周期延长也进一步降低了湖泊水质净化能力,因此巢湖流域在水资源水量及水质要素方面均存在较大压力.水资源承载力可作为评判水资源与经济社会及生态环境之间是否协同发展的一项综合指标,因此通过水量来判断水资源与社会经济是否协同发发展;通过水质判断水资源与生态环境是否协同发展;二者结合,可较好地判断巢湖流域水资源承载状态.因此,本文选用水资源量质要素承载状态值作为水资源承载力表征指标,其计算公式分别为:
| $ {{S_{{\rm{W}}1}}\left( j \right) = {W_{\rm{U}}}\left( j \right)/{W_{\rm{A}}}\left( j \right)} $ | (1) |
式中,SW1(j)表示县(市)水量要素j年份承载状态值;WU(j)表示县(市)j年份用水总量;WA(j)表示县(市)j年份可利用水量.
| $ {{S_{{\rm{Q}}1}}\left( j \right) = {Q_{\rm{U}}}\left( j \right)/{Q_{\rm{A}}}\left( j \right)} $ | (2) |
式中,SQ1(j)表示县(市)水质要素j年份承载状态值;QU(j)表示县(市)j年份氨氮入河量;QA(j)表示县(市)j年份氨氮纳污能力.
| $ {{S_{{\rm{W}}2}}\left( j \right) = \sum\limits_{i = 1}^n {{W_{{\rm{U}}i}}\left( j \right)} \sum\limits_{i = 1}^n {{W_{{\rm{A}}i}}\left( j \right)} } $ | (3) |
式中,SW2(j)表示流域水量要素j年份承载状态值;n表示流域内县(市)个数;WUi(j)表示流域内第i个县(市)j年份用水总量;WAi(j)表示流域内第i个县(市)j年份可利用水量.
| $ {{S_{{\rm{Q}}2}}\left( j \right) = \sum\limits_{i = 1}^n {{Q_{{\rm{U}}i}}\left( j \right)} \sum\limits_{i = 1}^n {{Q_{{\rm{A}}i}}\left( j \right)} } $ | (4) |
式中,SQ2(j)表示流域水质要素j年份承载状态值;n表示流域内县(市)个数;QUi(j)表示流域内第i个县(市)j年氨氮入河量;QAi(j)表示流域内第i个县(市)j年份氨氮纳污能力.
流域整体及其内部县(市)的水量要素承载状态值评价标准为:< 0.9为可载;0.9~1.0为临界;>1.0为超载.水质要素承载状态值评价标准为:< 1.1为可载;1.1~1.2为临界;>1.2为超载[20].本文采用“短板法”评价区域水资源承载力,即采用水量、水质要素承载状态值中较差值作为水资源承载力的最终评价结果[11].
2.3 水资源承载力系统模拟预测方法系统动力学起于系统论,并吸收控制论、信息论的精髓,融结构与功能、物质与信息、科学与经验于一体,沟通了自然科学与社会科学的横向联系[21].它通过分析系统内部各变量间的反馈结构关系来研究系统整体行为,认为系统的行为是由系统的结构所决定的,并指出系统的结构是动态反馈结构从而可用控制论的方法来研究[22].系统动力学最突出的优点在于能处理高阶次、非线性、多重反馈、复杂时变的系统问题,而水资源承载力恰恰是一个包含模糊性、随机性、非线性等众多因素的复杂问题,因此系统动力学是较早应用于区域水资源承载力动态预测研究的重要方法[23-24].本文应用系统动力学构建巢湖流域水资源承载力量质要素系统动力学模型,来评价、预测巢湖流域水资源承载力.
2.3.1 巢湖流域水资源承载力系统动力学模型本文应用系统动力学方法构建流域内各县(市)水资源承载力量质要素承载状态模拟模型,再利用整体建模技术,空间耦合各县(市)模拟模型,构建流域水资源承载力量质要素承载状态模拟模型.
县域水资源承载力模拟模型由人口、经济、用水和水污染负荷排放4个子系统组成,可充分反映出县域水资源与社会发展、生态环境的变化情况.构建县域水资源承载力模拟模型的关键在于建立4个子系统之间的联系,从而建立各变量与水资源承载力量质要素间的联系,从机理上揭示量质要素演变规律.就子系统间的关系来看,人口、经济子系统为用水、水污染负荷排放子系统分别提供用水和污染排放数据.县域SD模型对量质要素承载状态值的模拟通过引入参数计算人口、产业经济的用水量和污染物产生量,整合得到区域用水总量、氨氮入河量,再根据区域水资源条件计算可利用水量,并查阅区域氨氮纳污能力,基于式(1)、(2)计算区域水资源量质要素承载状态值.
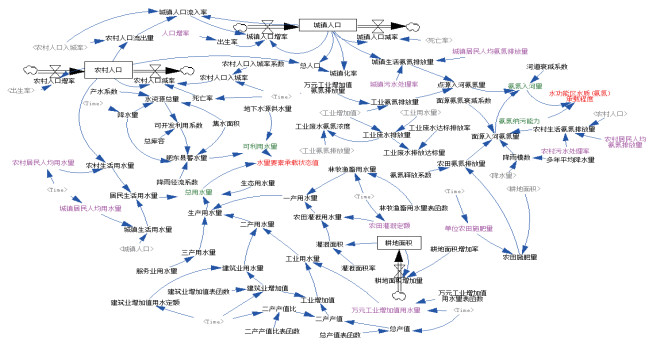
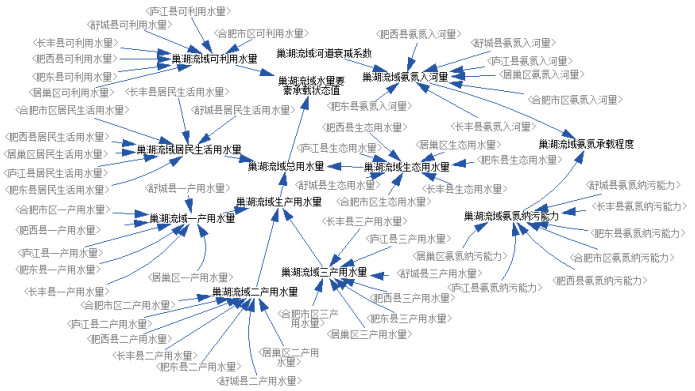
流域水资源承载力模拟模型就是采用整体建模技术,从人口、经济、用水和水污染负荷排放4个方面入手整合各县(市)的水资源承载力模拟模型,将县(市)域SD模型数据叠加得到流域的用水总量、可利用水量、氨氮入河量、氨氮纳污能力,基于式(3)、(4)计算流域水资源量质要素承载状态值.本文以巢湖流域作为研究对象,县(市)子模型及流域整体模型结构见图 1和图 2.
|
图 1 县域水资源承载力量质要素系统动力学模型 Fig.1 System dynamics model of water resources carrying capacity quantity and quality elements in county |
|
图 2 巢湖流域水资源承载力量质要素系统动力学模型 Fig.2 System dynamics model of water resources carrying capacity quantity and quality elements in Chaohu Basin |
模型中量质要素承载状态值相关主要方程为:
| $ 县域蓄水量 = 开发利用系数 \times \left( {县域降水量 \times 县域降雨径流系数 \times 县域集水面积/100000} \right) $ | (5) |
| $ 县域可利用水量 = 县域地下水源供水量 + 县域蓄水量 $ | (6) |
| $ 县域用水总量 = 县域生态用水量 + 县域生活用水量 + 县域生产用水量 $ | (7) |
| $ 县域点源氨氮入河量 = 县域城镇生活氨氮排放量 + 县域工业氨氮排放量 $ | (8) |
| $ 县域面源氨氮入河量 = \left( {农田氨氮排放量 + 农村生活氨氮排放量} \right) \times 面源氨氮衰减系数 \times 降雨模数 $ | (9) |
| $ 县域氨氮入河量 = \left( {区域点源氨氮入河量 + 面源氨氮入河量} \right) \times \left( {1 - 区域河道衰减系数} \right) $ | (10) |
本文以巢湖流域闸上区域行政区包括合肥、巢湖、肥东、肥西、长丰、舒城、庐江等两市五县作为研究对象.模型以2005—2016年的各区域人口、土地、水资源、生态环境和经济发展状况等历史数据为基础,确定模型参数和初始值,再对2017—2050年区域内各项数据以时间步长1 a进行模拟预测.模型的初始值和参数设置见附表 1.
| 表 1 2005—2016年巢湖流系统动力学模型有效性检验* Tab. 1 Validity test of system dynamics model of Chaohu Basin from 2005 to 2016 |
敏感性分析是指从定量分析的角度研究有关因素发生某种变化对某关键指标影响程度的一种不确定分析技术.这里采用单因素敏感分析法,通过逐一改变相关变量数值的方法来揭示关键指标受这些因素变动影响大小的规律,可用指标的敏感性来衡量指标对于评价目标的重要性.定义水资源承载力量质要素调控指标进行单位幅度的变化对承载状态值产生的影响称为指标敏感性.指标敏感性的计算公式为:
| $ {P_{{\rm{w}}ij}} = \left| {{S_{{\rm{w}}1}}\left( {i, j} \right) - {S_{{\rm{w}}0}}\left( {i, j} \right)} \right| $ | (11) |
式中,Pwij表示第i个指标对于j年份水量承载状态的敏感性;Sw1(i, j)表示第i个指标单位幅度变化后j年份水量要素承载状态值;Sw0(i, j)表示第i个指标未变化时j年份水量要素承载状态值.
| $ {P_{{\rm{Q}}ij}} = \left| {{S_{{\rm{Q}}1}}\left( {i, j} \right) - {S_{{\rm{Q}}0}}\left( {i, j} \right)} \right| $ | (12) |
式中,PQij表示第i个指标对于j年份水质承载状态的敏感性;SQ1(i, j)表示第i个指标单位幅度变化后j年份水质要素承载状态值;SQ0(i, j)表示第i个指标未变化时j年份水质要素承载状态值.
2.4 水资源承载力系统优化调控方法正交试验设计是研究多因素多水平的一种设计方法,它根据正交性从全面试验中挑选出了部分具有代表性的样本进行试验,是一种高效、经济、快速的实验设计方法[25-26].本文采用正交试验法来选取量质要素各调控指标的最优组合,以期满足调控目标的要求.首先根据各标准确定各调控指标的调控依据,按照大系统正交试验设计原理与方法以及调控依据,确定各调控指标水平数,将指标离散化;再根据指标个数以及指标水平数,选取合适的正交表,按正交表的调控方案分别进行调控,并计算各调控方案下量质要素承载状态值,最优量质要素承载状态值对应的调控方案为最优方案.限于篇幅,具体操作步骤及优化过程见相关文献[27-28].
3 结果与讨论 3.1 巢湖流域水资源承载力系统动力学模拟模型有效性分析系统动力学模型有效性检验的目的在于判断模型是否能够准确反映出系统的特征及变化规律[18].即利用水资源承载力系统动力学模型模拟2005—2016年的巢湖流域数据与真实数据对比来验证模型的有效性,当误差小于15 %时可以认为模型是有效的.本文变量较多,故选取人口、总用水量、氨氮入河量作为检验指标.
由表 1可知,模型对于3个指标的拟合误差均在允许范围内,SD模型拟合效果较好.
3.2 巢湖流域水资源承载力预测通过系统模拟,预测2017—2050年巢湖流域以及流域内各县(市)量质要素以及水资源承载力量质要素承载状态值.鉴于巢湖流域目前粗放型经济增长模式尚未根本性转变、城镇环境基础设施滞后于社会经济发展、水生态系统日渐退化以及环境监管能力不足,若不进行有效调控,预计水资源承载状态将进一步恶化.本文选取未来水平年2035、2050年来观察各要素的变化情况,具体预测结果见表 2.
| 表 2 巢湖流域量质要素承载状态值预测 Tab. 2 The prediction of quantity and quality elements carrying state value of Chaohu Basin |
由表 2可知,2035、2050年巢湖流域量质要素承载状态均为超载.且由于流域内人口增加以及生产规模的扩大与镇化率的提高,致使用水总量与氨氮入河量数值较大且逐年呈上升趋势,各县(市)及整个流域水资源承载力多处于超载且呈上升趋势.居巢区水量要素承载状态值有明显改善是由于2035年区域降雨量远小于2050年区域降雨量.肥西县水质要素承载状态有明显改善是因为其工业氨氮排放量占总体比重较大,随着生产技术的进步,万元工业增加值氨氮排放量降低.
3.3 巢湖流域水资源承载力调控模型构建 3.3.1 调控目标2035、2050年巢湖流域水资源承载力量质要素承载状态均达到临界.由表 2可知,巢湖流域水资源承载力急需调控,这里选取临界值作为调控目标,是因为可满足在对现有社会生产、生活状况最小变动的情况下保证流域水资源的合理使用.
3.3.2 调控机理及调控指标的初步确定由公式(1)、(2)可知,水资源量质要素承载状态值主要与用水总量、可利用水量、氨氮入河量、氨氮纳污能力等密切相关,根据图 1中SD模型选取与上述4个变量关联性较强的指标作为调控指标, 可以从生活、生产两方面入手,减小用水总量和氨氮入河量来改善区域水资源承载力.首先,利用敏感性分析对调控指标进行筛选.再以发展较好地区的各项指标作为各个调控指标的调控依据,并以此为基础进行正交试验,选取最优调控方案.
因以其他地区的指标作为调控依据,考虑到地区人口、面积等方面存在差异,故尽可能选取与这些因素无关的指标作为调控指标.同时考虑到巢湖流域用水量大、水质较差的特点,在水量要素调控方面选取农田灌溉定额、二产产值比、万元工业增加值用水量、农村居民人均用水量和城镇居民人均用水量5个指标;在水质要素调控方面选取城镇污水处理率、二产产值比、单位农田施肥量、城镇居民人均氨氮排放量、农村居民人均氨氮排放量和农村污水处理率6个指标.
3.3.3 筛选调控指标基于公式(11)、(12)计算各调控指标对应目标年份的敏感性,为避免偶然因素对指标敏感性的影响,以指标±5 %和±10 % 4种情况下2035年和2050年承载状态值变化幅度的均值来表征指标的敏感性,结果见表 3.
| 表 3 量质要素调控变量敏感性分析* Tab. 3 Sensitivity analysis of quantity and quality elements regulation variables |
选取敏感性较强(>1)的指标作为最终的调控指标,在水量要素方面选取亩均灌溉用水量、二产产值比、万元工业增加值用水量作为调控指标.在水质要素方面选取城镇污水处理率、二产产值比、城镇居民人均氨氮排放量、农村居民人均氨氮排放量作为调控指标.未来随着生产技术的发展和农业灌溉方式的进步,万元工业增加值以及亩均灌溉用水量将降低,污水处理效率必然得到提升;巢湖流域经济转型的根本任务是产业结构的调整,大力发展服务业势在必行,二产产值比将呈下降趋势;随着国民素质进一步提升,养成良好生活用水习惯,会使得生活污水中的氨氮进一步减少,分析可知上述6个指标均具有较好的调控性.调控的顺序为先调控水量要素再调控水质要素,二产产值比的调控在水量要素调控中进行.城镇污水处理率敏感性指标较大一是因为未来我国城镇化率进一步提升,导致城镇人口增加、农村人口减少;二是生产科技的进步,使得万元工业增加值氨氮排放量不断减小,因此城镇居民氨氮排放量占排放总量的比重进一步升高,城镇污水处理率对于氨氮排放量的影响程度也随之提升.
3.3.4 调控依据巢湖流域3个水量要素调控指标现状值为:亩均灌溉用水量329 m3;二产产值比0.544;万元工业增加值用水量43 m3.水量要素调控指标参照浙江省进行调控:亩均灌溉用水量280 m3;二产产值比0.5;万元工业增加值用水量35 m3.巢湖流域3个水质要素调控指标现状值为:城镇居民人均氨氮排放量45 g/(人·d);城镇污水处理率86.5 %;农村居民人均氨氮排放量20 g/(人·d).水质要素调控指标参考江苏省沿江城市典型生活小区数据:城镇居民人均氨氮排放量40 g/(人·d);城镇污水处理率93 %;农村居民人均氨氮排放量15 g/(人·d).
3.3.5 巢湖流域水资源承载力水量要素优化调控方案本文对巢湖流域进行整体调控,即对研究区域内7个县(市)的各个量质要素调控指标进行同倍比调控.根据现状条件下流域内的指标值及调控依据,按照大系统正交试验设计方法将水量要素的3个指标分成5个水平,即将调控依据值和现状指标值差值比上现状指标值,再进行五等分.量质要素调控指标均进行阶段性调控,即在2020年与2030年分别进行调控.水量要素试验设计见表 4.
| 表 4 巢湖流域水量要素试验设计 Tab. 4 Experimental design of water quantity elements in Chaohu Basin |
根据L25(53)正交表编制的25种方案进行调控,由表 2可知巢湖流域2050年水量要素承载状态值较大,故将各个调控方案下2050年的流域水量要素承载状态值与调控目标作比较,选取最优设计方案.
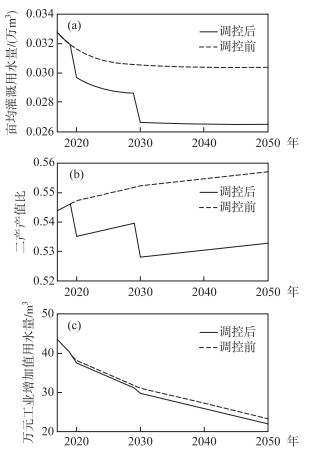
由附表Ⅱ可知,ABS最小值对应的最优调控方案为方案18,即亩均灌溉用水量削减12 %;二产产值比削减4.5 %;万元工业增加值需水量削减3 %.对应调控措施下巢湖流域水量要素调控指标变化情况见图 3.
|
图 3 巢湖流域水量要素调控 Fig.3 Regulation of water quantity elements in Chaohu Basin |
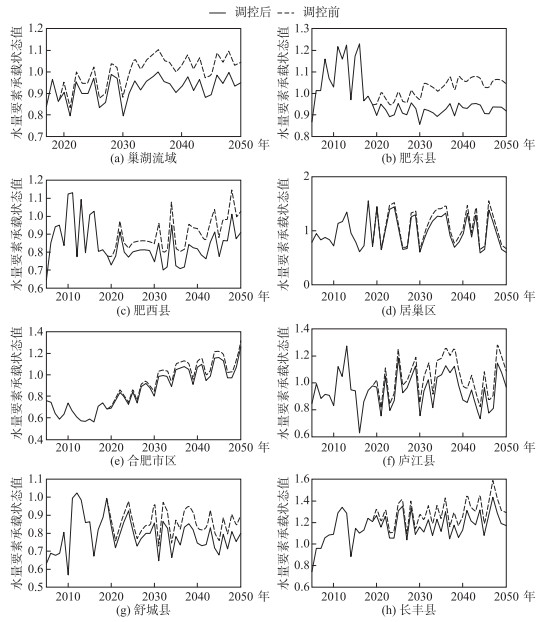
观察整体调控下,巢湖流域整体及流域内各县(市)水量要素承载状态值的变化情况,见图 4.
|
图 4 巢湖流域水量要素承载状态值变化情况 Fig.4 Change of carrying state value of water quantity elements in Chaohu Basin |
由图 4可知,在优化方案调控作用下,巢湖流域整体及各县(市)水量要素承载状态值得到明显改善. 2035年和2050年巢湖流域水量要素承载状态值分别为0.976和0.948,达到临界或可载;肥东县、肥西县和舒城县水量要素承载状态均达到可载/临界;其他县(市)均处于超载状态.图中虚线与实线所夹面积大小可反映调控方案对该区域的影响.合肥市区、居巢区调控效果不明显是因为区域内调控指标数值较小,在同倍比调控下,调控方案产生的影响较小.长丰县、庐江县仍处于超载一方面是因为区域内调控指标数值相对较小,另一方面是因为预测年份降雨量较小.
3.3.6 巢湖流域水资源承载力水质要素优化调控方案根据现状条件下流域内的水质要素调控指标值以及调控依据值,按照大系统正交试验设计方法及调控依据将水质要素的3个指标分成5个水平,水质要素试验设计见表 5.
| 表 5 巢湖流域水质要素试验设计 Tab. 5 Experimental design of water quality elements in Chaohu Basin |
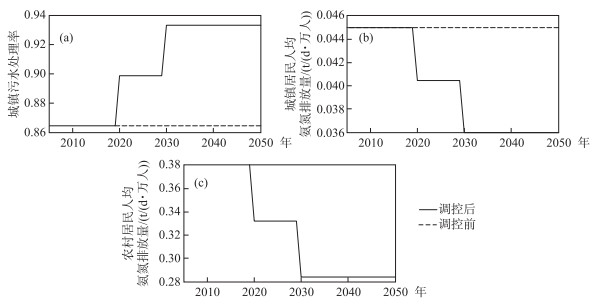
根据L25(53)正交表编制试验方案进行调控,计算各调控方案下2050年巢湖流域水质承载状态值并与调控目标进行比较选取最优方案.经优化可知巢湖流域水质要素调控指标最优调控方案为:在水量要素调控的基础上城镇污水处理率提升8 %;城镇居民人均氨氮排放量削减20 %;农村居民人均氨氮排放量削减15 %.巢湖流域水质要素调控指标变化情况如图 5所示.
|
图 5 巢湖流域水量要素调控 Fig.5 Regulation of water quality elements in Chaohu Basin |
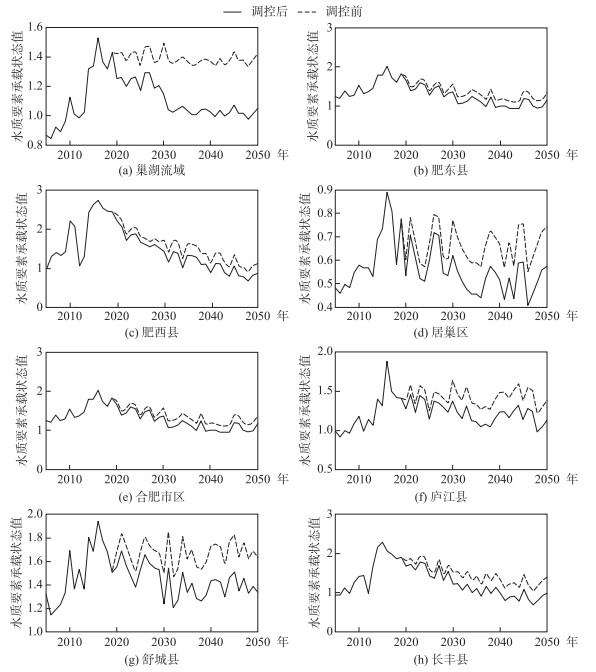
巢湖流域整体及流域内各县(市)的水质要素承载状态值在最优调控方案下的变化情况见图 6.
|
图 6 巢湖流域水质要素承载状态值变化情况 Fig.6 Change of carrying state value of water quality elements in Chaohu Basin |
由图 6可知,在水量调控措施的基础上进行水质调控,可明显改善巢湖流域水质要素承载状态. 2035年和2050年巢湖流域水质要素承载状态值经调控之后分别为1.0和1.1,达到临界/可承载状态;除舒城县外其他县(市)水质要素承载状态均达到临界/可载.舒城县水质要素承载状态超载一是因为氨氮纳污能力较弱;二是农村生活氨氮排放量占比较大,同倍比调控情况下,不能得到有效控制.
综上,在量质要素整体优化调控下,巢湖流域整体水资源承载状态达到临界/可载;合肥市区、居巢区、长丰县、庐江县及舒城县水资源承载力未达标,需对这些区域进行二次调控.
4 结论鉴于巢湖流域在水资源水量及水质方面存在较大压力,本文基于县(市)域系统动力学模型构建了巢湖流域量质要素系统动力学模型,预测了2017—2050年巢湖流域水资源承载力的变化趋势,采用正交试验设计优化了承载力调控方案,得到如下结果:
1) 在无调控情况下,随着巢湖流域未来产业规模的扩大以及城镇化率的提升,2017—2050年巢湖流域水资源承载状态值整体呈上升趋势,并于2030年后长期处于超载状态.
2) 在优化调控方案下,即亩均灌溉用水量削减12 %;二产产值削减4.5 %;万元工业增加值需水量削减3 %;城镇污水处理率提升8 %;城镇居民人均氨氮排放量削减20 %;农村居民人均氨氮排放量削减15 %,2035年和2050年巢湖流域水资源承载状态均处于临界/可载.
需要指出的是,整体调控措施虽然能使流域层面满足调控目标要求,但不能保证各县(市)局部承载状态均达标,但可起到一定的改善作用.巢湖流域水资源承载力具有明显能力的随机动态性和压力的长期渐增性,在局部区域或时段内当承载压力大于承载能力时,需要借助域内或域外的水量调入才能缓解纾困,即需要构建湖泊流域水资源承载力系统在时间和空间上应急调控机制,以保障区域生活、生产以及生态方面的安全.这样由整体到局部、由上而下的调控方法可以减少调控的繁琐程度,更快地满足区域整体及局部承载状态均可载的要求.
综上,本文提出的巢湖流域水资源承载力动态调控方案能促进当地水资源的有效流转与配置,提高其利用效率,降低由于水资源粗放式开发利用引发污染治理的经济成本,减小由于水资源过度开发带来的生态环境影响,有效改善当地的资源环境状况.
5 附录附表 Ⅰ、Ⅱ见电子版(DOI: 10.18307/2021.0106.)
| 附表Ⅰ 模型的初始值与参数设置* Appendix Ⅰ Initialization and parameter settings of the model |
| 附表Ⅱ 巢湖流域水资源承载力水量要素(2050年)正交试验分析 Appendix Ⅱ Orthogonal test analysis of water resources carrying capacity water quantity elements (2050) in Chaohu Basin |
| [1] |
Xinjiang Water Resources Soft Science Research Group. Water resources and its carrying capacity and development strategy in Xinjiang. Water Resources and Hydropower Engineering, 1989, 31(6): 2-9. [新疆水资源软科学课题研究组. 新疆水资源及其承载能力和开发战略对策. 水利水电技术, 1989, 31(6): 2-9.] |
| [2] |
Yao ZJ, Wang JH, Jiang D et al. Advances in study on regional water resources carrying capacity and research on its theory. Advances in Water Science, 2002, 13(1): 111-115. [姚治君, 王建华, 江东等. 区域水资源承载力的研究进展及其理论探析. 水科学进展, 2002, 13(1): 111-115.] |
| [3] |
Long TR, Jiang WC, He Q. Water resources carrying capacity:New perspectives based on eco-economic analysis and sustainable development. Journal of Hydraulic Engineering, 2004, 35(1): 38-45. [龙腾锐, 姜文超, 何强. 水资源承载力内涵的新认识. 水利学报, 2004, 35(1): 38-45.] |
| [4] |
Wang JH, Jiang DC, Xiao WH et al. Study on theoretical analysis of water resources carrying capacity:Definition and scientific topics. Journal of Hydraulic Engineering, 2017, 48(12): 1399-1409. [王建华, 姜大川, 肖伟华等. 水资源承载力理论基础探析:定义内涵与科学问题. 水利学报, 2017, 48(12): 1399-1409.] |
| [5] |
Chen SJ, Feng SY, Huo ZL et al.Research status and prospect of water resources carrying capacity in China//Chinese Society of Agricultural Engineering. Proceedings of 2005 annual meeting of Chinese society of agricultural engineering. Guangzhou, 2005. [陈绍军, 冯绍元, 霍再林等.我国水资源承载力研究现状及展望//中国农业工程学会. 2005年中国农业工程学会学术年会论文集.广州, 2005. ]
|
| [6] |
Xia J, Zhu YZ. The measurement of water resources security:A study and challenge on water resources carrying capacity. Journal of Natural Resources, 2002, 17(3): 262-269. [夏军, 朱一中. 水资源安全的度量:水资源承载力的研究与挑战. 自然资源学报, 2002, 17(3): 262-269. DOI:10.3321/j.issn:1000-3037.2002.03.002] |
| [7] |
Wang SJ, Hou Y, Zhang XL et al. Comprehensive evaluation method for water resources carrying capacity in river basins. Journal of Hydraulic Engineering, 2003, 34(1): 0088-0092. |
| [8] |
Yang G, Wang YJ, He XL et al. The study of three evaluation models of water resources carrying capacity in manas river basin. Advanced Materials Research, 2010, 113/114/115/116: 442-449. DOI:10.4028/www.scientific.net/amr.113-116.442 |
| [9] |
Duan XG, Luan FF. Evaluation of water resources carrying capacity in Xinjiang based on fuzzy comprehensive model. China Polulation. Resources and Environment, 2014, 24(S1): 119-122. [段新光, 栾芳芳. 基于模糊综合评判的新疆水资源承载力评价. 中国人口资源与环境, 2014, 24(S1): 119-122.] |
| [10] |
Naimi-Ait-Aoudia M, Berezowska-Azzag E. Algiers carrying capacity with respect to per capita domestic water use. Sustainable Cities and Society, 2014, 13: 1-11. DOI:10.1016/j.scs.2014.03.006 |
| [11] |
Li YL, Guo XN, Guo DY et al. An evaluation method of water resources carrying capacity and application. Progress in Geography, 2017, 36(3): 342-349. [李云玲, 郭旭宁, 郭东阳等. 水资源承载能力评价方法研究及应用. 地理科学进展, 2017, 36(3): 342-349.] |
| [12] |
Han JL, Duan WG, Li BS et al. Simulation and predication of arid area urban water resources bearing capacity based on SD model:a case study of Baotou City. Journal of Arid Land Resources and Environment, 2005(4): 188-191. [韩俊丽, 段文阁, 李百岁等. 基于SD模型的干旱区城市水资源承载力模拟与预测—以包头市为例. 干旱区资源与环境, 2005(4): 188-191.] |
| [13] |
Su ZY, Xu ZM, Zhang ZQ et al. Fundamental ecological economics study on the carrying capacity of water resources in Heihe river watershed. Journal of Glaciology and Geocryology, 2002, 24(4): 400-406. [苏志勇, 徐中民, 张志强等. 黑河流域水资源承载力的生态经济研究. 冰川冻土, 2002, 24(4): 400-406.] |
| [14] |
Dong T, Jin JL, Wu CG et al. Dynamic evaluation of water resources carrying capacity in Anhui Province based on carrying process. International Journal Hydroelectric Energy, 2018, 36(7): 17-21, 16. [董涛, 金菊良, 吴成国等. 基于承载过程的安徽省水资源承载力动态评价. 水电能源科学, 2018, 36(7): 17-21, 16.] |
| [15] |
Hu C, Chen G, Lu XH. Employing DPSIR conceptualization and PP clustering algorithm to predict water resources carrying capacity of river basins in Fujian, China, in 2020. Advanced Materials Research, 2012, 610/611/612/613: 2663-2670. DOI:10.4028/www.scientific.net/amr.610-613.2663 |
| [16] |
Che Y, Zhang MC, Yang K. Evaluation and predication of water resources carrying capacity based on SD model:A case study of Chongming island. Journal of East China Normal University:Natural Science, 2006(6): 67-74. [车越, 张明成, 杨凯. 基于SD模型的崇明岛水资源承载力评价与预测. 华东师范大学学报:自然科学版, 2006(6): 67-74.] |
| [17] |
Zhao XQ, Rao H, Yi Q et al. Study on water resources carrying capacity in Kunming City based on SD model. China Polulation. Resources and Environment, 2011, 21(S2): 339-342. [赵筱青, 饶辉, 易琦等. 基于SD模型的昆明市水资源承载力研究. 中国人口资源与环境, 2011, 21(S2): 339-342.] |
| [18] |
Zhao CL. Application of system dynamics method in regional water resources carrying capacity[Dissertation]. Xi'an: Xi'an University of Architecture and Technology, 2006. [赵春丽.系统动力学方法在区域水资源承载力中的应用研究[学位论文].西安: 西安建筑科技大学, 2006. ]
|
| [19] |
Ang CG. Chaohu yearbook. Hefei: Huangshan Publishing House, 2016. [昂朝桂. 巢湖年鉴. 合肥: 黄山书社, 2016.]
|
| [20] |
Jin JL, Dong T, Li JQ et al. Risk matrix method for evaluating regional water resources carrying capacity. North China Institute of Water Conservancy and Hydroelectric Power, 2018, 39(2): 46-50. [金菊良, 董涛, 郦建强等. 区域水资源承载力评价的风险矩阵方法. 华北水利水电大学学报:自然科学版, 2018, 39(2): 46-50.] |
| [21] |
Wang JH, Jiang D, Gu DF et al. Prediction of urban water resources carrying capacity in arid area based on SD model. Geography and Territorial Research, 1999, 15(2): 18-22. [王建华, 江东, 顾定法等. 基于SD模型的干旱区城市水资源承载力预测研究. 地理学与国土研究, 1999, 15(2): 18-22.] |
| [22] |
Xu GQ, Zou J. The method of system dynamics:Principle, characteristics and new development. Journal of Harbin Institute of Technology:Social Sciences Edition, 2006, 8(4): 72-77. [许光清, 邹骥. 系统动力学方法:原理、特点与最新进展. 哈尔滨工业大学学报:社会科学版, 2006, 8(4): 72-77.] |
| [23] |
Feng YL, Han WX, Wang HJ. Study on the region water resources carrying capacity. Advances in Water Science, 2003, 14(1): 109-113. [冯耀龙, 韩文秀, 王宏江等. 区域水资源承载力研究. 水科学进展, 2003, 14(1): 109-113.] |
| [24] |
Sun FX. Analysis and application of carrying capacity of water resources[Dissertation]. Nanjing: Hohai University, 2006. [孙富行.水资源承载力分析与应用[学位论文].南京: 河海大学, 2006. ]
|
| [25] |
Cheng JL, Guo YY. Optimization method of large scale system mathematical programming experiment and its application. Science in China:Series E, 1998(3): 254-258. [程吉林, 郭元裕. 大系统数学规划试验选优方法及其应用. 中国科学:E辑, 1998(3): 254-258.] |
| [26] |
Leung YW, Wang Y. An orthogonal genetic algorithm with quantization for global numerical optimization. IEEE Transactions on Evolutionary Computation, 2001, 5(1): 41-53. DOI:10.1109/4235.910464 |
| [27] |
Chen K. Experimental design and analysis. Beijing: Tsinghua University Press, 2005. [陈魁. 试验设计与分析. 北京: 清华大学出版社, 2005.]
|
| [28] |
Jiang SM, Cao XQ, Jin JL et al. Water resources regulation research of reservoirs and ponds combined irrigation system based on simulation optimization and orthogonal experiment. J Lake Sci, 2018, 30(2): 519-532. [蒋尚明, 曹秀清, 金菊良等. 基于模拟优化与正交试验的库塘联合灌溉系统水资源调控. 湖泊科学, 2018, 30(2): 519-532. DOI:10.18307/2018.0223] |
 2021, Vol. 33
2021, Vol. 33 


