在天然河流中,床面泥沙一般由非均匀沙组成,进而非均匀沙在水流冲刷的作用下发生分选输移,使得床沙不断调整(粗化或细化).三峡工程蓄水运用以来,大量泥沙在库前淤积,下泄水流含沙量处于严重不饱和状态[1],从而造成荆江段河床持续冲刷,床沙发生明显的粗化现象,其中沙市河段粗化程度较监利河段明显. 2002 2017年期间,荆江河段平滩河槽累计冲刷泥沙10.51×108 m3,年均冲刷量为0.701×108 m3,从冲淤量沿程分布来看,沙市、监利河段冲刷量分别占荆江冲刷量的24 %、18 %,进一步印证了床沙粗化现象[2].在新水沙条件下,年内床沙交换使得床沙组成不断调整,进而造成年际床沙粗化或细化,也对荆江段河床演变过程产生重要影响.因此,深入研究三峡工程下游沙质河段沙波运动规律与床沙交换、冲刷粗化之间的变化关系,可为进一步开展三峡工程下游非均匀悬移质泥沙沿程恢复机理与河床演变规律研究提供理论基础.
Chien和Wan认为[3],在沙波运动过程中,其床面形态随着输沙强度的不同而时刻变化,具有随机性及周期性;因此冲积河流床面沙波运动对推移质输沙率变化及河床演变的研究产生重要影响,国内外学者一直有着深入的探讨[4-9].在国内,尹学良[10]较早提出了清水冲刷条件下沙波运动与床沙交换、河床冲刷粗化之间的关系,发现沙质河床受清水冲刷后, 将通过水流扬沙的分选作用和泥沙的交换作用而发生粗化,并形成不稳定的粗化层.王士强[11-12]分析了多组水槽试验和河流实测资料,得到了推移质输沙率与沙波波高、波速等沙波要素之间的函数关系,提出了沙波法计算推移质输沙率的适用范围;在此基础上,提出床沙交换速度的概念,并得到了床沙调整变化与冲淤变化及床沙交换的计算关系式;但是,该计算模型所述的床沙交换指的是床沙与悬移质之间的相互交换,而忽略了推移质对床沙交换过程的影响.甘明辉等[13]建立了沙质河床平面二维水沙模型,从定性角度模拟了清水冲刷条件下粗化层的形成过程及河床变形、冲刷深度、含沙量及床沙级配等的变化,但该模型无法反映交换过程对床沙调整过程的影响.刘金梅等[14-15]通过水槽试验观察及分析长江、黄河等天然河流实测资料,提出床沙交换速率的概念,总结了非均匀沙河床冲刷过程中含沙量恢复饱和系数的简化计算式,并分析了表层床沙粗化对不平衡输沙的影响机理,但没有从理论角度深入分析床沙交换及粗化过程的影响.钟德钰等[16-18]基于冲积河流沙质河床表层床沙与推移质、悬移质泥沙在床面附近的掺混交换,以及混合活动层泥沙在沙波运动作用下的掺混交换过程,建立了混合活动层内床沙级配变化的动力学基本方程;在此基础上,结合悬移质不平衡输沙方程,计算了沙波运动影响下冲积河流悬移质冲刷不平衡输沙过程,模拟了沙质河床冲刷粗化过程,从理论角度进一步完善了计算模型,并用水槽试验资料对模型进行验证.另外,一些学者从不同角度出发,对沙波波高、沙波阻力、沙波形态等进行深入的探讨,使人们对沙波运动规律有了进一步的认识[19-23].综合以上分析可知,结合概率统计理论与沙波运动方法计算沙质河段床沙交换过程的研究还很少,也缺少从定量角度分析床沙交换方式的研究,如冲刷概率(床沙转换为推移质、悬移质的概率)以及淤积概率(推移质与悬移质转换为床沙的概率).
基于以上分析,本文采用力学分析、概率统计理论与沙波运动规律相结合的方法,引入Markov三态转移概率及非均匀沙隐暴系数,得到沙质河床上床沙级配的概率计算模式,能够同时考虑前期水沙条件、床沙起悬及冲淤过程对床沙交换及粗化过程的影响,进而可以将该模型应用到Parker和Wilcock[24-25]提出的表层床沙输移模型.最后分别采用荆江河段沙市、监利站实测流量过程、床沙级配、推移质级配、悬移质级配资料计算了沙质河床年际床沙粗化及年内床沙交换过程,并与2009-2014年实测资料进行比较.
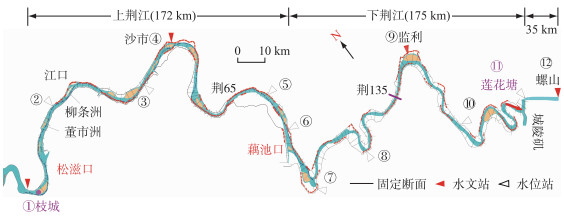
1 荆江河段概况 1.1 研究河段及数据来源如图 1所示,荆江河段上起枝城,下迄城陵矶,全程长约347 km;以藕池口为界分为上、下荆江,河长分别约为172、175 km.上荆江河段由枝城、江口、沙市等6个河湾及过渡段组成,属于微弯分汊型河道.其中,枝城江口河段为卵石夹沙河床,河床上有卵砾石洲滩分布;江口沙市河段为沙质河床,河床组成为中细沙.下荆江河段由石首、调关、监利等10个弯曲河段组成,属于典型的蜿蜒型河道;此河段为沙质河床,河床组成多为中细沙,床沙中值粒径约为0.18 mm,卵石层深埋在床面以下[1, 26].
|
图 1 荆江河段示意图 Fig.1 Sketch of the Jingjiang Reach |
本文收集整理的实测数据来源于长江中游荆江河段的沙市和监利水文站,均为沙质河床,主要包括2009-2014年实测流量、水深(最大水深、平均水深)、流速、床沙级配、推移质级配、悬移质级配等,共计763组实测数据;其中,床沙采用挖斗式(9线、10线)方法进行取样;沙质推移质采用测验仪器为Y78-1型的推移质采样器进行取样;悬移质采用横式全断面混合、分层混合及选点法进行取样.沙市、监利站实测资料中有关水沙要素的变化范围见表 1.
| 表 1 沙市、监利站实测资料统计 Tab. 1 Statistics of the measured data at Shashi and Jianli Stations |
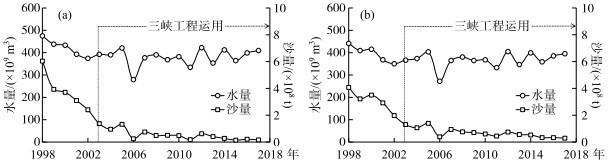
荆江河段水沙主要来源于长江上游干流及各级入汇支流,汛期集中在5-10月[27].图 2点绘了沙市、监利河段1998-2017年水量、沙量逐年(水文年)变化过程曲线.由图 2可见,三峡工程运用后(2003 2017年),沙市河段年平均水量相比于2003年之前减少了10.2 %,但沙量减少近85.9 %;沙市河段年平均水量减少7.3 %,但沙量减少近77.9 %.总之,三峡工程运用后,荆江河段水量变化较小,但沙量却大幅度减少(沙市河段较监利河段明显),这是造成坝下游河床持续冲刷的主要原因.
|
图 2 沙市(a)和监利(b)河段1998 2017年水量、沙量变化过程 Fig.2 Temporal variations in water volume and sediment load at Shashi and Jianli Reaches from 1998 to 2017 |
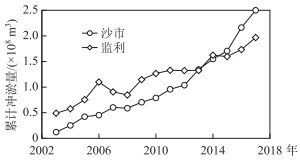
其次,三峡工程运用后,下泄沙量的大幅减少使荆江段河床处于冲刷状态,且冲刷部位集中在枯水河槽[1, 28].根据夏军强、周美蓉等[29-30]的研究,荆江河段蓄水前(1975-2002年)平滩河槽年均冲刷量为0.14 × 108 m3/a,蓄水后增加为0.37 × 108 m3/a,远大于蓄水前冲刷量;如图 3所示(冲刷为负,淤积为正),三峡工程运用后,沙市、监利河段累计冲淤量(平滩河槽)逐年增加,其中沙市河段年均冲刷量为0.167 × 108 m3,监利河段为0.131 × 108 m3,河床处于持续冲刷状态;尤其是2008年以来,沙市、监利河段河床冲刷均有所加剧,其中沙市河段较监利河段明显,原因是三峡工程下泄水流含沙量处于严重不饱和状态(图 2),下泄清水持续冲刷河床,造成长江中游河段床沙逐年粗化.
|
图 3 沙市及监利河段累计冲淤量变化过程 Fig.3 Accumulated volume of channel evolution in Shashi and Jianli Reaches process in sand bed |
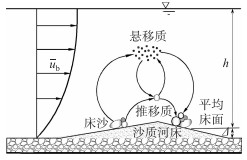
如图 4所示,在沙波运动过程中,其床面形态随着输沙强度的不同而时时变化,具有随机性及周期性[3].此外,在沙波运动的同时,床沙表面形成一个活动交换层,使得上下层床沙、沙质推移质、悬移质相互交换,促使表层床沙级配不断调整.
|
图 4 沙波运动及床沙交换过程示意图 Fig.4 Sand waves movement and sediment exchange |
王士强等[12, 15, 31]通过分析水槽试验和河流实测沙波资料,点绘了不同相对水深h/d50时,沙波运动速度Vsx(n)与沙粒阻力Θ′*的关系图,并总结出Vsx(n)的计算公式:
| $ V_{{\rm{sx}}}^{\left( n \right)} = {K_1} \cdot \mathit{\boldsymbol{\Theta }}{'_*}\sqrt {g \cdot {d_{50}}} $ | (1) |
式中,K1为与相对水深h/d50有关的系数;Θ′ *为沙粒阻力;h为水深;d50为中值粒径;g为重力加速度.
对于天然河流,沙波运动周期T及沙波波高Δ(n)可以按王士强的方法[12, 31]计算.所以,Θ′ *≤2时的Vsy(n)(活动层内床沙与运动泥沙的交换速率)为[12]:
| $ V_{{\rm{sy}}}^{\left( n \right)} = {\Delta ^{\left( n \right)}}/T $ | (2) |
但是,刘金梅等[15]通过观察水槽试验及分析实测资料,发现天然河流沙波运动周期远远大于水槽内情况,并给出了沙波运动时床沙交换速率Vsy(n)表达式.结合刘金梅等[15]的研究结果,分析可得,当Θ′ *>2时,Vsy(n)可以表示为:
| $ V_{{\rm{sy}}}^{\left( n \right)} = 1.385 \times {10^{ - 4}}{\mathit{\pmb{\Theta }}^\prime }{_*^{ - 2.6}}\sqrt {g \cdot {d_{50}}} $ | (3) |
综上,当Θ′ *>2,且h/d50≥(7000~10000)时,联立式(2)、(3)可得,Δ(n)为:
| $ {\Delta ^{\left( n \right)}} = 1.385 \times {10^4}{\mathit{\pmb{\Theta }}^\prime }{_*^{ - 2.6}}T\sqrt {g \cdot {d_{50}}} {\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\mathit{\pmb{\Theta }}{{'}_*} > 2} \right) $ | (4) |
根据已有研究可知[32],对于卵石夹沙河段来说,在床沙交换时活动层内每步被冲刷下移的沙量不能由等量的下层原始床沙来补充;这是因为在表层床沙分选输移的过程中,表层床沙逐步粗化,与底层床沙的组成差异较大,冲刷过程变得越来越慢(床沙变粗).此时,若考虑了下层原始床沙的补给,则相当于增大了活动层厚度,使粗化过程变得相对容易.
但是,沙质河床与卵石夹沙河床在床沙组成上差异较大,其上下层床沙相对来说较为均匀,粒径范围较小,床沙交换过程主要靠沙波运动来维持(河床下切);在沙波运动的同时,床沙表面形成一个活动交换层,促使表层床沙级配不断调整.因此,对于三峡工程下游沙质河段(荆江河段)来说,活动层内每步被冲刷下移的沙量应由等量的下层原始床沙来补充[33],其沙量平衡方程为:
| $ {Z^{\left( n \right)}}P_{{\rm{a}}i}^{\left( {n - 1} \right)} - H_{\rm{s}}^{\left( n \right)}\left( {\left( {P_{{\rm{b}}i}^{\left( n \right)} + p_{{\rm{s}}i}^{\left( n \right)}} \right) + H_{\rm{d}}^{\left( n \right)}\left( {P_{{\rm{b}}i}^{\left( {n - 1} \right)}\varepsilon _{21i}^{\left( n \right)} + P_{{\rm{s}}i}^{\left( {n - 1} \right)}\varepsilon _{31i}^{\left( n \right)}} \right)} \right) + {H^{\left( n \right)}}{P_{0i}} = {Z^{\left( n \right)}}P_{{\rm{a}}i}^{\left( n \right)} $ | (5) |
式中,Ζ(n)为沙质河床第n步床沙交换活动层厚度;H(n)=Hs(n)+Hd(n),为第n步总冲淤厚度,Hs(n)为冲刷厚度,Hd(n)为淤积厚度;ε31i(n)、ε21i(n)为状态转移概率;Pai(n)、Pbi(n)、Psi(n)分别为第n步床沙级配、推移质级配、悬移质级配,代表泥沙粒径小于di的沙重百分比;P0i为初始床沙级配,且存在Pai(0)=P0i;其中,等式左边第2项为冲刷项,第3项为淤积项,第4项为下层原始床沙补给项.
从而得到,沙质河床第n步床沙级配Pai(n)可以表示为:
| $ P_{{\rm{a}}i}^{\left( n \right)} = P_{{\rm{a}}i}^{\left( {n - 1} \right)} - \left( {H_{\rm{s}}^{\left( n \right)}F_{\rm{s}}^{\left( n \right)} - H_{\rm{d}}^{\left( n \right)}F_{\rm{d}}^{\left( n \right)} - {H^{\left( n \right)}}{P_{0i}}} \right)/{Z^{\left( n \right)}} $ | (6) |
式中,
王士强等[15, 31]通过分析发现,在一定的水流条件下,床沙、沙质推移质、悬移质相互交换;此时,床面表层较粗的床沙被冲走,次表层较细泥沙及落淤泥沙颗粒暴露,从而变成表层床沙,继续与沙质推移质、悬移质发生交换,循环往复,沙波逐渐向前运动.因此,在计算时段dt内,Ζ(n)与Vsy(n)有关,且最大值不超过Δ(n),其表达式为:
| $ {Z^{\left( n \right)}} = \left\{ {\begin{array}{*{20}{l}} {V_{{\rm{sy}}}^{\left( n \right)}{\rm{d}}t{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\Delta T \le T} \right)}\\ {{\Delta ^{\left( n \right)}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\Delta T > T} \right)} \end{array}} \right. $ | (7) |
式中,dt为相对于一个交换过程的计算步长,且dt=ΔT/Δt;ΔT为实际计算步长(等于相邻两组实测数据的时间间隔),Δt为完成一次床沙交换所需要的时间[30].
另外,基于以上分析,作者认为在沙质河段床沙粗化过程中,Hs(n)应与Vsy(n)及Vsx(n)有关,其表达式为:
| $ H_{\rm{s}}^{\left( n \right)} = f\left( {V_{{\rm{sy}}}^{\left( n \right)}, t} \right) \cdot V_{{\rm{sx}}}^{\left( n \right)}{\rm{d}}t $ | (8) |
式中,f(Vsy(n), t)为与Vsy(n)、dt及状态转移概率等有关的函数式;根据已有研究[32-33]及实测资料率定,
另外,在床沙交换及粗化过程中,沙质河段推移质、悬移质落淤机理与卵石夹沙河段相同,即Hd(n)与转移概率ε31i(n)、ε21i(n)有关[32],可以表示为:
| $ H_{\rm{d}}^{\left( n \right)} = {Z^{\left( n \right)}}\left( {\mathop \sum \limits_{i = 1}^{\max } P_{{\rm{s}}i}^{\left( {n - 1} \right)}\varepsilon _{31i}^{\left( n \right)} + \mathop \sum \limits_{i = 1}^{\max } P_{{\rm{b}}i}^{\left( {n - 1} \right)}\varepsilon _{21i}^{\left( n \right)}} \right) $ | (9) |
在冲淤过程中,假设冲刷为负、淤积为正,从而得到计算时段dt内总冲淤厚度H(n)为:
| $ {H^{\left( n \right)}} = H_{\rm{s}}^{\left( n \right)} + H_{\rm{d}}^{\left( n \right)} $ | (10) |
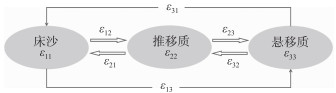
所谓三态转移概率,即在床沙调整过程中,床沙(状态1)、推移质(状态2)、悬移质(状态3)泥沙的运动状态可以相互转换,如图 5所示.在此基础上,Li等[32]对Kuai和Tsai[34]提出的Markov非齐次离散模型进行修正,得到基于隐暴效应的非均匀沙三态转移概率矩阵:
|
图 5 三态转移概率 Fig.5 Transition probabilities for three-states |
| $ \varepsilon _i^{\left( n \right)} = \left[ \begin{array}{l} 1 - P_{{\rm{T}}i}^{\left( n \right)}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_{{\rm{T}}i}^{\left( n \right)} - P_{{\rm{S}}i}^{\left( n \right)}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_{{\rm{S}}i}^{\left( n \right)}\\ 1 - P_{2i}^{\left( n \right)}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_{{\rm{R}}i}^{\left( n \right)}P_{2i}^{\left( n \right)}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_{2i}^{\left( n \right)}\left( {1 - P_{{\rm{R}}i}^{\left( n \right)}} \right)\\ 1 - P_{3i}^{\left( n \right)}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_{3i}^{\left( n \right)}\left( {1 - P_{{\rm{S}}i}^{\left( n \right)}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P_{{\rm{S}}i}^{\left( n \right)}P_{3i}^{\left( n \right)} \end{array} \right] $ | (11) |
式中,εi(n)为非均匀沙三态转移概率矩阵;εxy(n)表示泥沙颗粒由x状态转移到y状态的概率;PTi(n)为总概率,且PTi(n)=PRi(n)+PSi(n);PSi(n)为起悬概率;PRi(n)为泥沙推移概率;1-P2i(n)、1-P3i(n)分别为止滚概率、止悬概率.
综上所述,将式(8~10)代入式(6)得到长江中游沙质河段基于隐暴效应的床沙调整计算模型:
| $ P_{{\rm{a}}i}^{\left( n \right)} = \left\{ \begin{array}{l} P_{{\rm{a}}i}^{\left( {n - 1} \right)} - {\eta _1}F_{\rm{s}}^{\left( n \right)} + {\eta _3}F_{\rm{d}}^{\left( n \right)} + \left( {{\eta _1} + {\eta _3}} \right){P_{0i}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\Delta T \le T} \right)\\ P_{{\rm{a}}i}^{\left( {n - 1} \right)} - {\eta _2}F_{\rm{s}}^{\left( n \right)} + {\eta _3}F_{\rm{d}}^{\left( n \right)} + \left( {{\eta _{2 + }}{\eta _3}} \right){P_{0i}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\Delta T > T} \right) \end{array} \right. $ | (12) |
式中,
1) 根据实测流量过程及初始水沙条件(床沙、推移质、悬移质),利用插值法计算任一时刻的相对水深h/d50;若h/d50≥7000,则进行后续计算过程,否则停止计算;
2) 判断无量纲Θ′ *大小,进而计算Δ(n):若Θ′ *≤2,Δ(n)按照王士强[12]的方法计算;若Θ′ *>2,Δ(n)由式(4)计算;
3) 计算Vsx(n)及Vsy(n):Vsx(n)由式(1)计算;当Θ′ *≤2时,Vsy(n)由式(2)计算;当Θ′ *>2时,Vsy(n)由式(3)计算;
4) 判断ΔT与T的大小,运用式(7)计算Ζ(n);
5) 根据初始水沙条件,计算非均匀沙转移概率矩阵εi(n),进而运用式(10)计算H(n);根据沙市、监利站计算结果可见,矩阵εi(n)内各转移概率取值在0~1之间变化,并且各概率之间的关系与实际相符合,适用于荆江沙质河段转移概率的计算.
6) 将式(1)~(4)中各变量代入式(12),计算不同时刻床沙级配Pai(n).
3 荆江河段床沙调整及粗化计算 3.1 年内床沙级配调整本文分别采用沙市、监利站2009-2014年实测流量过程、床沙级配、推移质级配及悬移质级配资料计算分析了荆江河段年内床沙级配调整规律.
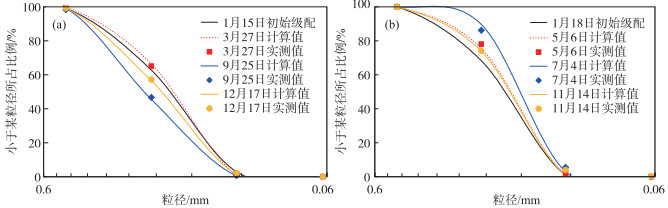
首先,沙市站选择具有代表性的2009年(平衡-粗化-细化)床沙级配计算结果来说明本文多步概率模型的计算精度.由图 6a可知,2009年床沙级配计算结果与实测资料符合较好,年内床沙级配调整过程为:平衡-粗化-细化;其中,3月27日床沙级配与1月15日初始级配相近(近似平衡态),直至汛期结束前(9月25日)完成粗化,之后床沙逐渐细化.监利站选取2011年(细化-粗化)部分计算节点,说明本文年内床沙调整过程验证结果.由图 6b可知,2011年床沙级配调整过程体现为:细化-粗化;其中,1月18日为初始床沙,至5月6日细化完成,之后床沙逐渐粗化.
|
图 6 沙市(2009年)、监利(2011年)站年内床沙变化计算结果:(a)沙市站;(b)监利站 Fig.6 Temporal variations of grain size distribution at Shashi Station (a) and Jianli Station (b) |
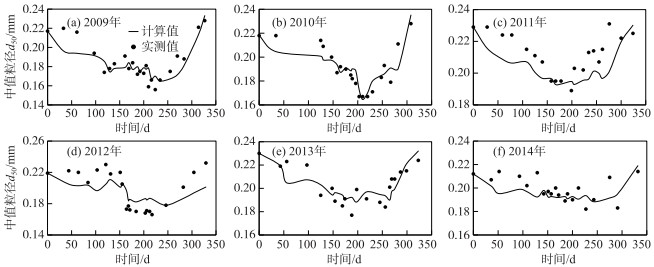
其次,为了说明本文概率模型年内床沙调整过程,将沙市、监利站年内床沙d50计算结果与实测资料进行对比.由图 7、8可见,沙市站年内床沙d50总体呈先增大后减小(先冲后淤)的变化趋势,而监利站呈先减小后增大(先淤后冲)的变化趋势,但两断面床沙d50都逐渐恢复到汛前大小.可以看出,本文模型计算结果与沙市、监利站实测资料变化趋势基本一致,能够应用于荆江河段沙质河床年内床沙调整过程的预报;但是,图中有些数据点依然存在较大误差,可能是因为床沙取样时存在随机性,模型计算时存在累计误差,亦或者水沙变化复杂,存在其他不可控因素.

|
图 7 沙市站年内床沙中值粒径计算与实测结果 Fig.7 Comparisons between the measured and calculated median particle sizes of bed material at Shashi Station |
|
图 8 监利站年内床沙中值粒径计算与实测结果 Fig.8 Comparisons between the measured and calculated median particle sizes of bed material at Jianli Station |
由实测资料分析可知,沙市、监利河段床沙分别属于中沙(0.25 mm≤d50<0.5 mm)和细沙(0.125 mm≤d50<0.25 mm)的粒径范围.为说明三峡工程下游沙质河段的床沙粗化规律及粗化程度,将沙市、监利站床沙组成按粒径范围进一步分为d<0.062 mm、0.062 mm≤d<0.25 mm以及d≥0.25 mm 3种,并用沙市、监利站2009-2014年实测流量过程、床沙级配、推移质级配、悬移质级配资料分别计算了历年荆江河段床沙组成中粒经在d<0.062 mm、0.062 mm≤d<0.25 mm、d≥0.25 mm范围内的泥沙所占百分比变化情况及年际床沙调整、粗化过程,并将计算结果与实测资料进行对比.
由表 2可见,2009 2014年,沙市站床沙组成中d<0.062 mm的泥沙所占比重始终为0;0.062 mm≤d<0.25 mm的泥沙所占比重呈逐年减少的趋势,由2009年的59.5 % (64.2 %)变为2014年的48.1 % (49.4 %),变化幅度为-11.4 %,其中在2012年变化幅度最大(-21.3 %);d≥0.25 mm的泥沙所占比重呈逐年增加的趋势,由2009年的40.5 % (35.8 %)变为2014年的51.9 % (50.6 %),变化幅度为11.4 %,同样在2012年变化幅度最大(21.3 %),床沙组成表现出明显的粗化趋势.而监利站床沙组成中粒经在d<0.062 mm、0.062 mm≤d<0.25 mm、d≥0.25 mm范围内的泥沙所占比重在2009-2014年间均存在波动性变化,床沙调整过程基本处于粗化与细化交替进行的状态,但总体上有粗化的趋势.此外,2009-2014年,沙市、监利站床沙发生不同程度的粗化,其中沙市站粗化程度较监利河段明显,监利站虽然粗化速率比较缓慢(床沙粗化与细化交替进行),但在后续时段(2014-2017年)亦有粗化趋势.
| 表 2 沙市及监利站2009-2014年床沙组成变化情况(%) Tab. 2 Temporal variations of bed material composition at Shashi and Jianli Stations from 2009 to 2014 |
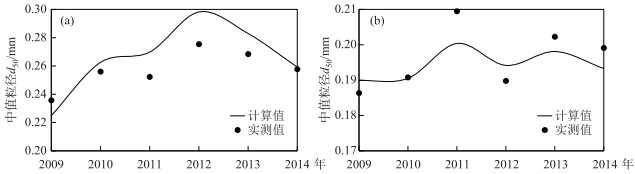
最后,将沙市、监利站年际床沙d50计算结果与2009-2014年实测资料进行比较,验证结果见图 9.结合图 7、8的计算结果,发现沙市、监利站年内床沙d50分别呈先增大后减小(先冲后淤)、先减小后增大(先淤后冲)的变化趋势,这也是造成沙市站床沙逐年粗化,监利站床沙粗化与细化交替进行的主要原因.同时,沙市站2003年床沙d50为0.236 mm(0.225 mm),2014年床沙d50为0.258 mm(0.259 mm),粗化程度为9.3 %,其中2012年粗化程度最高(16.8 %);监利河段2003年床沙d50为0.186 mm(0.190 mm),2014年床沙d50为0.199 mm(0.193 mm),粗化程度为6.9 %,其中2011年粗化程度最高(12.4 %).此外,沙市站床沙d50在2013-2014年间持续下降(图 9a),是因为该图表示汛期某时刻的床沙组成,不能完整地反映2013-2014年的床沙变化过程.
|
图 9 2009-2014年沙市站(a)和监利站(b)床沙中值粒径d50计算值与实测资料对比结果 Fig.9 Comparison of median particle sizes of bed material at Shashi Station (a) and Jianli Station (b) from 2009 to 2014 |
由以上分析可知,沙市、监利站床沙交换造成的结果分为两种:(1)年内床沙粗化与细化并存,这可能与床沙组成沿垂向变化、来水来沙过程变化及江湖水沙交换等因素有关;(2)年际床沙总体呈粗化趋势,但粗化程度不高,这也是沙质河段床沙交换的必然结果;沙质河床上、下层床沙相对来说较为均匀,粒径范围较小,而且床沙、推移质、悬移质泥沙粒径范围相当.由沙市、监利站实测资料来看,床沙的粒径在0.062~2 mm之间,沙质推移质粒径在0.002~2 mm之间(实测资料显示两水文站均无卵石推移质),悬移质泥沙粒径在0.002~1 mm之间.由于床沙粒径相对于推移质及悬移质来说较粗,所以在三者相互交换的过程中(沙波运动为床沙交换的动力):(a)如果沙波不断下切,且推移质及悬移质不断向床沙补给(淤积),就有可能会使床沙发生细化;(b)若床沙不断被水流冲刷,同时向推移质及悬移质补给,则床沙有可能发生粗化.但由于荆江河段水沙条件变化复杂,所以(a)、(b)两种情况对应的床沙调整过程也有可能产生相反的结果.这也说明在沙波运动影响下,沙质河床与卵石夹沙河床床沙交换过程的主要区别为动力驱制不同.
3.3 床沙交换方式由2.2.2节可知,在一定水流条件下,床沙可由静止状态转变为推移质或悬移质运动状态,在水流冲刷的作用下发生分选输移,使得床沙不断调整(粗化或细化).但是,当水流条件达到一定强度时,床沙交换的主要方式将是悬移或跃移[35],推移质运动状态所占比例变得越来越少.因此,为了分析长江中游沙质河段(沙市、监利)床沙调整过程中的主要交换方式,图 10给出了2009-2014年沙市及监利站汛期某时刻冲刷时状态转移概率(床沙转换为推移质的概率:ε12;床沙转换为悬移质概率:ε13)的变化规律,图 11给出了汛期某时刻淤积时状态转移概率(推移质转换为床沙的概率:ε21;悬移质转换为床沙概率:ε31)的变化规律.

|
图 10 2009-2014年沙市站(a)和监利站(b)床沙转换为推移质(B)或悬移质(S)的概率 Fig.10 Transition probability from bed material to bed load (B) or suspended load (S) at Shashi Station (a) and Jianli Station (b) from 2009 to 2014 |
|
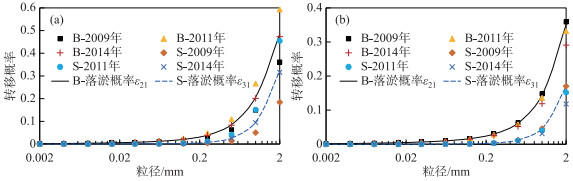
图 11 2009-2014年沙市站(a)和监利站(b)推移质(B)或悬移质(S)转换为床沙的概率 Fig.11 Transition probability from bed load (B) or suspended load (S) to bed material at Shashi Station (a) and Jianli Station (b) from 2009 to 2014 |
由图 10a可以看出,在一定水流条件下,沙市站ε12随着泥沙粒径的增大而增大.由上述床沙调整计算过程及实测床沙级配资料可知,沙市站2009 2014年床沙粒径集中在0.125~0.5 mm范围内,所占沙重百分比约为95 %,ε12在区间[0.07,0.19]内变化,即床沙转换为推移质的概率恒小于0.2;ε13随着泥沙粒径的增大而减小,并且在区间[0.73,0.89]内变化,即床沙转换为悬移质的概率恒大于0.7.监利站ε12及ε13的概率与泥沙粒径之间的变化关系与沙市站类似,ε12在区间[0.05,0.13]内变化,ε13在区间[0.81,0.93]内变化(图 10b).
在一定水流条件下,沙市、监利站推移质和悬移质转换为床沙的概率(ε21、ε31)均随着泥沙粒径的增大而增大(图 11).由前文分析可知,沙市站2009 2014年推移质泥沙粒径主要集中在0.125~1 mm范围内,悬移质泥沙粒径主要集中在0.002~0.5 mm范围内,所以沙市站ε21在区间[0.02,0.21]内变化,ε31在区间[0,0.026]内变化,即悬移质转换为床沙的概率很小.同理,监利站ε21在区间[0.016,0.14]内变化,ε31在区间[0,0.012]内变化.
4 结论三峡工程蓄水运用后,长江中游荆江河段持续冲刷,沙波运动使得床沙与推移质、悬移质泥沙不断交换(床沙调整),从而造成该河段床沙发生不同程度的粗化现象,对长江中下游河段水沙输移及河床演变规律的研究产生重要影响.为研究新水沙条件下荆江河段沙质河床年际床沙粗化及年内床沙交换过程,在总结沙波运动规律及床沙交换方式的基础上,引入三态转移概率及非均匀沙隐暴系数,进而得到基于状态转移概率的沙质河段床沙级配调整的计算模式,能够同时考虑前期水沙条件、床沙起悬及冲淤过程对床沙调整过程的影响.基于以上分析,主要结论如下:
1) 分析表明,2003-2017年,沙市、监利站床沙发生不同程度的粗化,其中沙市站粗化程度较监利河段明显;但沙市站在2010年以后有一定波动(波动幅度较小),监利站在2007年以后波动幅度较大.计算结果表明:沙市站年内床沙d50先增大后减小(先冲后淤),但年际床沙d50逐年增大;而监利站年内床沙d50则表现出先减小后增大(先淤后冲)的变化趋势;这也是造成沙市站床沙逐年粗化,监利站床沙粗化与细化交替进行的主要原因.
2) 2009 2014年,沙市站床沙组成中d<0.062 mm的泥沙所占比重始终不变;0.062 mmd<0.25 mm的泥沙所占比重呈逐年减少的趋势,变化幅度为-11.4 %,其中在2012年变化幅度最大(-21.3 %);d > 0.25 mm的泥沙所占比重呈逐年增加的趋势,变化幅度为11.4 %,同样在2012年变化幅度最大(21.3 %),床沙组成表现出明显的粗化趋势.而监利站床沙组成中3种粒径范围内的泥沙所占比重均存在波动性变化,处于粗化与细化交替进行的状态,但有粗化趋势.
3) 计算结果表明,在床沙普遍可动的情况下,床沙转换为推移质的概率随着泥沙粒径的增大而增大,床沙转换为悬移质的概率随着泥沙粒径的增大而减小,推移质和悬移质转换为床沙的概率均随着泥沙粒径的增大而增大,并呈现出一定的变化趋势;此外,在床沙交换过程中,河床发生冲刷粗化时床沙以悬移质形式发生输移的概率约为81 % ~87 %,少部分以推移质形式冲刷下移,概率约为9 % ~13 %;但是,当河床发生淤积细化时,落淤泥沙主要来源于推移质,概率约为8 % ~12 %.
| [1] |
Yu WC, Lu JY eds. Bank erosion and protection in the Yangtze River. Beijing: China Water & Power Press, 2008: 80-102. [余文畴, 卢金友. 长江河道崩岸与护岸. 北京: 水利水电出版社, 2008: 80-102.]
|
| [2] |
Changjiang Water Resources Commission (CWRC). Analysis of channel degradation downstream of the Three Gorges Dam. Scientific Report of CWRC, 2018. [长江水利委员会水文局. 2017年度三峡水库进出库水沙特性、水库淤积及坝下游河道冲刷分析.长江水利委员会水文局报, 2018. ]
|
| [3] |
Chien N, Wan ZH. Mechanics of sediment transport. Reston, VA:American Society of Civil Engineers, 1999. DOI:10.1061/9780784404003 |
| [4] |
Blom A, Parker G, Ribberink JS et al. Vertical sorting and the morphodynamics of bed-form-dominated rivers:An equilibrium sorting model. Journal of Geophysical Research Atmospheres, 2006, 111: F01006. DOI:10.1029/2004jf000175 |
| [5] |
Blom A, Ribberink JS, Parker G. Vertical sorting and the morphodynamics of bed form-dominated rivers:A sorting evolution model. Journal of Geophysical Research:Earth Surface, 2008, 113: F01019. DOI:10.1029/2006JF000618 |
| [6] |
Sun ZH, Li YT, Ge H et al. Channel erosion processes of transitional reach from gravel river bed to sand bed in middle Yangtze River. Journal of Hydraulic Engineering, 2011, 42(7): 789-797. [孙昭华, 李义天, 葛华等. 长江中游沙卵石-沙质河床过渡带冲刷趋势研究. 水利学报, 2011, 42(7): 789-797.] |
| [7] |
Zhang LH, Zhang HW, Zhao CS. Bed load graduation of sandy bed in alluvial river. Journal of Hydraulic Engineering, 2017, 48(12): 1465-1472. [张罗号, 张红武, 赵晨苏. 冲积河流沙质河床推移质级配分布规律. 水利学报, 2017, 48(12): 1465-1472.] |
| [8] |
Xu Y, Zhu DJ, Meng Z et al. Experimental study on bed load transport in the armoring process. Advances in Water Science, 2018, 29(3): 339-347. [徐元, 朱德军, 孟震等. 河床粗化过程中推移质输移特征试验研究. 水科学进展, 2018, 29(3): 339-347.] |
| [9] |
Ma DG, Dong WL, Xu JF et al. Incipient velocity of sediment on the forward slope of dunes. Journal of Sediment Research, 2016, 41(2): 46-51. [马殿光, 董伟良, 徐俊锋等. 沙波迎流面泥沙起动流速研究. 泥沙研究, 2016, 41(2): 46-51.] |
| [10] |
Yin XL. Riverbed armoring with clear water erosion. Journal of Hydraulic Engineering, 1963(1): 15-25. [尹学良. 清水冲刷河床粗化研究. 水利学报, 1963(1): 15-25.] |
| [11] |
Wang SQ. The movement of sand waves and the measurement of bed load. Journal of Sediment Research, 1988(4): 23-29. [王士强. 沙波运动与推移质测验. 泥沙研究, 1988(4): 23-29.] |
| [12] |
Wang SQ. The movement of sand waves and the exchanges of bed material. Journal of Sediment Research, 1992(4): 14-23. [王士强. 沙波运动与床沙交换调整. 泥沙研究, 1992(4): 14-23.] |
| [13] |
Gan MH, Yang GL, Wu HJ et al. Numerical simulation of 2-D coarsening of bed during riverbed erosion. Journal of Hydrodynamics, 2002, 17(6): 691-700. [甘明辉, 杨国录, 吴虹娟等. 沙质河床二维粗化数值模拟初探. 水动力学研究与进展:A辑, 2002, 17(6): 691-700. DOI:10.3969/j.issn.1000-4874.2002.06.006] |
| [14] |
Liu JM, Wang SQ, Wang GQ. Effect of coarsening surface bed material on non-equilibrium sediment transport process during river degradation. Advances in Water Science, 2000, 11(3): 229-234. [刘金梅, 王士强, 王光谦. 河流冲刷过程中表层床沙粗化对不平衡输沙的影响. 水科学进展, 2000, 11(3): 229-234. DOI:10.3321/j.issn:1001-6791.2000.03.001] |
| [15] |
Liu JM, Wang GQ, Wang SQ. Study on non-equilibrium sediment transport in the sandy river erosion. Advances in Water Science, 2003, 14(5): 563-568. [刘金梅, 王光谦, 王士强. 沙质河道冲刷不平衡输沙机理及规律研究. 水科学进展, 2003, 14(5): 563-568.] |
| [16] |
Zhong DY, Zhang HW, Wang GQ. Basic equation for variation of bed material composition in active layer of alluvial river. Journal of Hydraulic Engineering, 2004, 35(9): 24-30. [钟德钰, 张红武, 王光谦. 冲积河流混合活动层内床沙级配变化的动力学基本方程. 水利学报, 2004, 35(9): 24-30.] |
| [17] |
Zhong DY, Wang QX, Ding Y. Influence of sand wave migration on non-saturated suspended load transport in alluvial rivers. Journal of Hydraulic Engineering, 2005, 36(12): 1432-1438. [钟德钰, 王勤香, 丁贇. 沙波运动对冲积河流悬移质冲刷不平衡输沙的影响. 水利学报, 2005, 36(12): 1432-1438.] |
| [18] |
Zhong DY, Wang GQ, Ding Y. Simulation of bed loadgraing in alluvial rivers with sand bed. Advances in Water Science, 2007, 18(2): 223-229. [钟德钰, 王光谦, 丁贇. 沙质河床冲刷过程中床沙级配的模拟. 水科学进展, 2007, 18(2): 223-229.] |
| [19] |
Raubenheimer B, Elgar S, Guza RT. Estimating wave heights from pressure measured in sand bed. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1998, 124(3): 151-154. DOI:10.1061/(asce)0733-950x(1998)124:3(151) |
| [20] |
Karim F. Bed-form geometry in sand-bed flows. Journal of Hydraulic Engineering, 1999, 125(12): 1253-1261. DOI:10.1061/(ASCE)0733-9429(1999)125:12(1253) |
| [21] |
Zhan YZ, Yu MH, Deng JY et al. Research on variation law of wave height based on current intension. Engineering Journal of Wuhan University, 2006, 39(6): 10-13. [詹义正, 余明辉, 邓金运等. 沙波波高随水流强度变化规律的探讨. 武汉大学学报:工学版, 2006, 39(6): 10-13.] |
| [22] |
Raudkivi AJ. Transition from ripples to dunes. Journal of Hydraulic Engineering, 2006, 132(12): 1316-1320. DOI:10.1061/(ASCE)0733-9429(2006)132:12(1316) |
| [23] |
Zhong L, Xu GX, Zeng F. Immovable bed experiment study on the resistance of sand wave characterized by fractal dimension. Journal of Basic Science and Engineering, 2013, 21(1): 116-126. [钟亮, 许光祥, 曾锋. 沙波阻力分形表征的定床试验研究. 应用基础与工程科学学报, 2013, 21(1): 116-126.] |
| [24] |
Parker G. Surface-based bedload transport relation for gravel rivers. Journal of Hydraulic Research, 1990, 28(4): 417-436. DOI:10.1080/00221689009499058 |
| [25] |
Wilcock PR, Crowe JC. Surface-based transport model for mixed-size sediment. Journal of Hydraulic Engineering, 2003, 129(2): 120-128. DOI:10.1061/(ASCE)0733-9429(2003)129:2(120) |
| [26] |
Deng SS, Xia JQ, Zhou MR. Coupled two-dimensional modeling of bed evolution and bank erosion in theupper JingJiang Reach of middle Yangtze River. Geomorphology, 2019, 344: 10-24. DOI:10.1016/j.geomorph.2019.07.010 |
| [27] |
Cao GJ, Wang J eds. Measurements and studies of hydrological and sediment data in the Three Gorges Project. Beijing: Science Press, 2015. [曹广晶, 王俊. 长江三峡工程水文泥沙观测与研究. 北京: 科学出版社, 2015.]
|
| [28] |
Xia JQ, Zong QL eds. Study on mechanisms and process simulation of bank erosion of composite riverbank in the Jingjiang Reach. Beijing: Science Press, 2015. [夏军强, 宗全利. 长江荆江段崩岸机理及其数值模拟. 北京: 科学出版社, 2015.]
|
| [29] |
Xia JQ, Deng SS, Zhou MR et al. One-dimensional coupled modeling of bed evolution and bank erosion processes in the Middle Yangtze River. Chinese Science Bulletin, 2019, 64(7): 725-740. [夏军强, 邓珊珊, 周美蓉等. 长江中游河道床面冲淤及河岸崩退数学模型研究及其应用. 科学通报, 2019, 64(7): 725-740. DOI:10.1360/N972018-01147] |
| [30] |
Zhou MR, Xia JQ, Deng SS. One-dimensional modelling of channel evolution in an alluvial river with the effect of large-scale regulation engineering. Journal of Hydrology, 2019, 575: 965-975. DOI:10.1016/j.jhydrol.2019.05.074 |
| [31] |
Wang SQ. Sand waves in alluvial channels and their influence on sediment transport. Proc. 2nd International conference on river flood hydraulics. York:John Wiley & Sons Ltd, 1994, 301-310. |
| [32] |
Li LL, Xia JQ, Zhou MR et al. Riverbed armoring and sediment exchange process in a sand-gravel bed reach after the Three Gorges Project operation. Acta Geophysica, 2020, 68(1): 243-252. DOI:10.1007/s11600-019-00391-2 |
| [33] |
Xu QX, Zhang XF, Tan GM. Multi-step prediction modeling on riverbeds scouring and armoring. Advances in Water Science, 1999, 10(1): 42-47. [许全喜, 张小峰, 谈广鸣. 河床冲刷粗化多步预报模式研究. 水科学进展, 1999, 10(1): 42-47.] |
| [34] |
Kuai KZ, Tsai CW. Discrete-time Markov chain model for transport of mixed-size sediment particles under unsteady flow conditions. Journal of Hydrologic Engineering, 2016, 21(11): 04016039. DOI:10.1061/(ASCE)HE.1943-5584.0001392 |
| [35] |
Hui YJ, Hu CH. Saltation in water dynamics. Journal of Hydraulic Engineering, 1991, 22(12): 59-64. [惠遇甲, 胡春宏. 水流中颗粒跃移的运动学特征. 水利学报, 1991, 22(12): 59-64.] |
 2021, Vol. 33
2021, Vol. 33 


