在冲积河流上，因防洪安全及航槽稳定的需要，沿程修建了大量河道整治工程，这些工程对水沙输移及河床冲淤变形产生了显著影响^[1-5].因此，在实施了大规模河道整治工程的河段，有必要研究工程对水沙输移及河床调整的整体影响.

目前考虑河道整治工程影响的数学模型较少，且已有数学模型多是研究某一特定整治工程引起的局部影响，主要包括水流结构变化、泥沙输移及河床形态的调整^[6-10].这类模型基本为二维或三维，一部分仅考虑了工程对水流结构的影响.如Giri等^[7]采用二维模型模拟了布设有丁坝的弯道水槽中的水流运动特性；冯民权等^[8]采用平面与立面二维模型，计算了导流板周围的流速场，比较了导流板不同布置方式和尺寸对流速的影响.另一部分则进一步考虑了泥沙运动及河床变形.如潘军峰等^[9]计算了单个丁坝与丁坝群产生的流速场与涡量场，并比较了不同布置方式对局部冲刷坑范围的影响；闫军等^[4]通过二维模型计算了两种护滩工程作用下江心滩的变形过程，发现两者均可实现对心滩头部的守护，但所引起的河床局部冲淤特性上存在差异；Minor等^[10]则采用三维模型，模拟了弯道丁坝群附近的紊流结构及泥沙运动过程.但在一些情况下，了解大范围整治工程对较长河段河床调整的整体影响是十分必要的，特别是在实施了大量整治工程的重点河段.与工程附近的局部模拟不同，这类模型需考虑工程实施对整个河道的影响.

长江中下游的护岸及护滩(底)工程修建规模通常较大，对河床演变的影响尤为显著.本文将通过数学模型，重点研究这类整治工程的具体影响，主要包括悬沙输移和河床冲淤变形两个方面.守护型整治工程实施后，整治工程区域河床冲刷被限制，水流无法从这些区域冲走泥沙；一方面会影响河段整体的悬沙输移过程；另一方面可能加剧冲刷该断面其他未防护位置或影响下游河段的河床冲淤强度^[1].以往河流数学模型一般简单地通过改变局部河道边界条件或调整糙率系数的方式考虑整治工程的影响.本研究基于改进现有的一维水沙动力学模型，加强对大规模河道整治工程(护岸及护滩(底)工程)的处理，可实现定量地比较考虑和不考虑整治工程影响下的悬沙输移和河床冲淤变形过程.

1 考虑河道整治工程影响的一维水沙数学模型 1.1 模型控制方程

一维水沙数学模型的控制方程，主要包括水流连续方程、动量方程、非均匀悬沙不平衡输移方程以及河床冲淤变形方程^[11]，可分别写成如下式(1)~(4)：

$ \frac{{\partial Q}}{{\partial x}} + B\frac{{\partial Z}}{{\partial t}} = {q_l} $

(1)

$ {\left. {\frac{{\partial Q}}{{\partial t}} + \left( {g \cdot A - {\alpha _f} \cdot B\frac{{{Q^2}}}{{{A^2}}}} \right)\frac{{\partial Z}}{{\partial x}} + 2{\alpha _f}\frac{Q}{A}\frac{{\partial Q}}{{\partial x}} = \frac{{{Q^2}}}{{{A^2}}}\left( {\frac{{\partial A}}{{\partial x}}} \right)} \right|_z} - g \cdot A\left( {{J_f} + {J_l}} \right) - \frac{{{\rho _l} \cdot {q_l} \cdot {u_l}}}{{{\rho _{\rm{m}}}}} $

(2)

$ \frac{\partial }{{\partial t}}\left( {A \cdot {S_k}} \right) + \frac{\partial }{{\partial x}}\left( {A \cdot U \cdot {S_k}} \right) = B \cdot {\omega _k} \cdot {\alpha _k}\left( {{S_{*k}} - {S_k}} \right) + {S_{lk}} \cdot {q_l} $

(3)

$ \rho '\frac{{\partial {A_{\rm{b}}}}}{{\partial t}} = \sum\limits_{k = 1}^N {B \cdot {\omega _k} \cdot {\alpha _k}\left( {{S_k} - {S_{*k}}} \right)} $

(4)

式中, Q、Z分别为流量(m³/s)和水位(m)；A、B分别为过水断面面积(m²)和水面宽度(m)；x、t分别为沿程距离及时间(m和s)；g为重力加速度，取值9.81 m/s²；α_f为动量修正系数；J_f为水力坡度，可由公式J_f=(Q/A)²n²/R^4/3计算，R为水力半径(m)，在宽浅河道水力半径可近似由断面平均水深h代替(m)，n为床面的曼宁糙率系数；J_l为断面扩张与收缩引起的局部阻力；q_l、ρ_l、u_l分别为出入流的单位河长流量(m²/s)、密度(kg/m³)及流速(m/s)在主流方向的分量；ρ_m为干流浑水密度(kg/m³)；U为断面平均流速(m/s)；S_k、S_*k、ω_k分别为第k粒径组悬沙的分组含沙量(kg/m³)、水流挟沙力(kg/m³)和浑水沉速(m/s)；α_k为恢复饱和系数，其值多根据实测资料率定；S_lk为出入流的分组含沙量(kg/m³)；ρ′为床沙干密度(kg/m³)；N为悬沙分组数；A_b为冲淤可动层面积(m²).其中，分组水流挟沙力S_*k=ΔP_*k·S_*，ΔP_*k为挟沙力级配，其值可由李义天^[12]提出的方法确定，S_*为断面挟沙力(kg/m³)，本文采用张瑞瑾挟沙力公式计算^[13]：

$ {S_*} = k{\left( {\frac{{{U^3}}}{{g \cdot h \cdot {\omega _{\rm{m}}}}}} \right)^m} $

(5)

式中, k为包含量纲的系数(kg/m³)；m为指数；ω_m为非均匀悬沙的平均沉速(m/s).

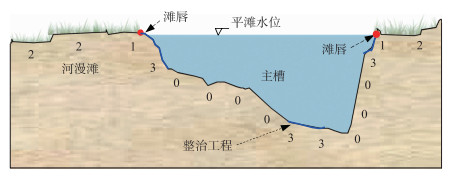
1.2 一维水沙数学模型的改进 1.2.1 确定河床边界条件

模型的第一个改进：对河漫滩、滩唇、有或无整治工程的主槽区域进行了划分.在以往的一维水沙数学模型中，通常以实测固定断面地形作为初始河床边界条件，包括断面各节点距左岸的距离及相应的河床高程.在改进后的模型中，断面上不同区域还需采用特定的代码(PC= 0、1、2、3)进行标记(图 1).首先，当洪水漫过滩地时，水力条件发生突变，因此有必要区分滩地与主槽区域；其次，整治工程对河床边界条件的影响较大，故需对有、无工程的主槽区域进行划分；最后，完成上述处理后，将所有实测固定断面地形和相应的节点代码将作为改进模型的河床边界条件.

1.2.2 改进输沙及河床变形计算模块

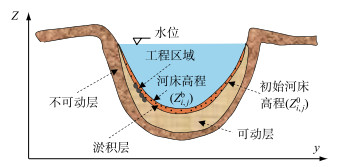
图 2给出了河道横断面形态示意图.由图可知，河床在垂向上依次可分为淤积层、可动层和不可动层；其中，淤积层定义为模拟时段内由于泥沙落淤形成的高于初始河床的沙层，$ Z_{i, j}^{\rm{b}} $代表节点河床高程，$ Z_{i, j}^0 $为节点初始河床高程(设定初始时刻实施工程的区域均无泥沙淤积).下面将详细阐述考虑河道整治工程影响时一维模型中输沙及河床变形计算模块的改进方法.

(1) 输沙模块的改进.

首先，根据公式(5)计算得到各固定断面的水流挟沙力(S_*i).但河道整治工程限制了河床的冲刷下切，对悬沙输移产生影响.故本文通过修正断面水流挟沙力来考虑所产生的影响.具体修正方法如下:

(ⅰ)当通过比较计算的含沙量与水流挟沙力的相对大小，判断出固定断面发生淤积时，其淤积过程不受整治工程的影响，故断面有效的水流挟沙力$ \left( {{{S'}_{*i}}} \right) $仍等于原始计算值(S_*i).

(ⅱ)当该断面发生冲刷时，需通过公式$ {S'_{*i}} = {S_i} + \left( {{S_{*i}} - {S_i}} \right) \cdot {r_i} \cdot {k_2} $修正原始计算的挟沙力数值，从而计算得到有效的断面水流挟沙力$ \left( {{{S'}_{*i}}} \right) $. r_i为可冲刷河床宽度L_i占整个断面湿周(χ_i)的比例. k₂为修正系数，其值设为k₂=2-r_i≥1.虽然整治工程限制了防护区域的河床冲刷，但水流可能转而冲刷该断面其他未受防护的节点，使得这些节点的冲刷强度有所增加，系数k₂一定程度上考虑了此影响.故k₂的值需大于1，且k₂还需与允许冲刷河床比例r_i相关.当r_i=1时，整个断面均会发生冲刷，不受工程限制，故k₂应等于1；当0 < r_i < 1时，随着实施工程的宽度比例增加，水流对该断面上其他未防护节点的冲刷强度愈强，故k₂的值需与可冲刷河床比例r_i呈反比关系.为了满足这些要求，k₂最终设定为2-r_i.当r_i=0时，k₂=2.该参数虽无法精确地考虑水流转移冲刷的影响，但模拟得到的结果将比不考虑这方面影响的结果更接近实际.

此外，r_i的取值在0~1之间.当r_i=0时，意味着整个断面均受到工程防护，水流无法从河床上携带起泥沙，故修正断面水流挟沙力(S_*i)等于断面含沙量(S_i)，确保整个大断面不发生冲淤变化；当r_i=1时，表示该断面未实施任何整治工程，故河床可进行自由冲刷，无需修改该断面水流挟沙力；而大多数情况下，各固定断面只有部分河床受到工程防护(0 < r_i < 1)，此时的首要任务为确定r_i的值，之后通过公式$ {S'_{*i}} = {S_i} + \left( {{S_{*i}} - {S_i}} \right) \cdot {r_i} \cdot {k_2} $进行水流挟沙力的修正.

(2) 河床变形模块的改进.

基于修正的断面挟沙力(S′_*i)，通过离散并求解河床冲淤变形方程公式(4)，得到河床冲淤面积(ΔA_{b, i}).以往一维水沙数学模型未考虑整治工程对河床变形的影响，ΔA_{b, i}通常是平均分配或根据流量加权分配到固定断面的各个节点上.而改进的模型充分考虑了整治工程的影响，对河床冲淤面积的分配模式进行了修改.具体如下：

(ⅰ)当固定断面发生淤积时，ΔA_{b, i}依据流量分配到每个节点上，从而计算得到各节点的河床冲淤厚度($ \Delta Z_{i, j}^{\rm{b}} = \frac{{\Delta {A_{{\rm{b, }}i}}}}{{\sum {0.5\left( {{q_{i, j}} + {q_{i, j + 1}}} \right)\Delta {B_{i, j}}} }}{q_{i, j}}, j $为断面上所有节点)，其中q_{i, j}为节点的单宽流量.

(ⅱ)当该断面发生冲刷时，河床形态调整只发生在无整治工程(PC= 0、1、2)或有工程但已形成可供冲刷淤积层的节点上(PC=3且$ Z_{i, j}^{\rm{b}} > Z_{i, j}^{\rm{0}} $)，故ΔA_{b, i}只在这些节点上根据流量进行分配($ \Delta Z_{i, j}^{\rm{b}} = \frac{{\Delta {A_{{\rm{b}}, i}}}}{{\sum {0.5\left( {{q_{i, j}} + {q_{i, j + 1}}} \right)\Delta {B_{i, j}}} }}{q_{i, j}}, j $为允许冲刷的断面节点).需注意的是，在实施工程的节点上(PC=3且$ Z_{i, j}^{\rm{b}} > Z_{i, j}^{\rm{0}} $)，计算得到的河床冲淤厚度$ \left| {\Delta Z_{i, j}^{\rm{b}}} \right| $应小于该时刻河床高程与初始河床高程的差值$ \left( {Z_{i, j}^{\rm{b}} - Z_{i, j}^{\rm{0}}} \right) $；若大于该值，则应修改为$ \Delta Z_{i, j}^{\rm{b}} = Z_{i, j}^{\rm{b}} - Z_{i, j}^{\rm{0}} $, 由此考虑整治工程对河床下切的限制作用.此外，在受工程防护且无淤积层提供沙源的节点上(PC=3且$ Z_{i, j}^{\rm{b}} = Z_{i, j}^{\rm{0}} $)，河床不发生进一步的冲刷，相应的$ {\Delta Z_{i, j}^{\rm{b}}} $为0.

(ⅲ)计算得到各节点的冲淤厚度后，修改各节点高程$ \left( {Z_{i, j}^{\rm{b}} = Z_{i, j}^{\rm{b}} + \Delta Z_{i, j}^{\rm{b}}} \right) $.

2 模型率定与验证

本文选取长江中游荆江段作为研究对象，利用该河段2015年的实测数据，对改进的模型进行率定，并用2016年的实测资料进行验证.总体而言，模拟得到的结果与实测过程符合较好.但需要指出的是，由于三峡工程的运用及荆江段二元结构河岸的土体特性，该河段近年来崩岸频发，故河岸崩退对该河段的泥沙输移及河床形态调整亦有显著影响.已有研究将崩岸力学模型耦合到一维水沙动力学模型中，用于计算床面冲淤与河岸崩退过程^[11].由于2015--2016年荆江段崩岸总体较弱，故模型中暂不考虑河岸崩退过程计算.如遇到河岸崩退较为显著的年份，一维水沙数学模型还需增加崩岸模块，可使计算与实测的断面形态更为吻合.

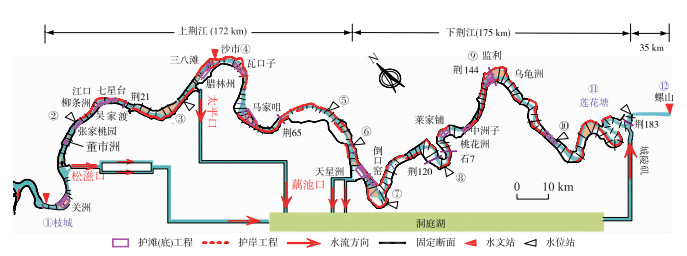
2.1 研究河段概述

荆江段全长约347 km，位于枝城和城陵矶之间，分为上、下荆江.其干流水沙通过松滋口、藕池口、太平口分流入洞庭湖(图 3)，洞庭湖再汇集湖南“四水”后又于城陵矶处重新汇入干流.该河段为典型的弯曲分汊河道，由16个河弯组成，河弯处分布着大量洲滩.进口枝城断面位于三峡大坝下游102 km，三峡及其上游水库群的运用使得该河段冲刷显著，2002--2017年累计冲刷量达10.5×10⁸ m³(平滩河槽).此外，为维护防洪及航运安全，该河段修建了大规模的整治工程.截至2016年，已完成的护滩(底)工程主要包括：枝江-江口河段航道整治一期工程、长江中游荆江河段航道整治工程(昌门溪至熊家洲段工程)、腊林洲守护工程、三八滩应急守护一、二期工程及沙市河段航道整治一期工程、瓦口子-马家咀航道整治工程等，主要工程的分布见图 3.在护岸工程方面，近60年来荆江干流完成护岸长度约252 km，上荆江实施了长达123 km的护岸工程，在下荆江守护岸线长度为129 km.

2.2 计算条件

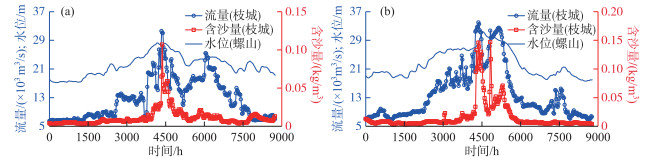
在模型的率定和验证过程中，以枝城站日均的流量、含沙量和悬沙级配资料作为进口边界条件；同时采用螺山站的日均水位过程作为出口边界条件.需指出的是，莲花塘站是荆江段的出口水位站，但该站无流量及含沙量资料.为方便模型率定，将研究范围扩展到了莲花塘下游35 km的螺山水文站. 图 4给出了2015年和2016年研究河段进、出口断面的水沙边界条件.此外，还将“三口”分流的日均流量、含沙量和悬沙级配作为侧向边界条件；荆江段汛后实测的185个固定断面地形、各节点代码作为初始河床边界条件(实测时间分别为2014年11月和2015年10月)；72个固定断面的实测床沙级配作为初始床沙资料(实测时间分别为2014年11月和2015年10月)，其余断面的初始级配由这些实测值插值求得.为研究整治工程对河床演变的影响，还需收集荆江段护岸、护滩(底)工程的分布及规模资料.首先，根据工程布置图，可大致确定护岸工程的所在位置及其沿河长方向的防护范围，以及护滩(底)工程的规模.荆江段各固定断面的间距在0.48~6.72 km之间，平均值约为2.0 km，而护岸工程覆盖长度较大(图 3).根据护岸工程布置图，将工程经过的固定断面的防护区域进行标记，并认为断面间标记位置之间的区域均为工程守护区域.然而护岸工程沿河中心方向的施工宽度无法从工程布置图获取，故采取以下方法综合确定：①采用地形套汇的方法进行估计，若河床连续3年未发生冲刷则认为这部分河床受工程防护；②主流的贴岸冲刷和迎流顶冲是造成河岸崩退的重要原因，根据护岸工程的实施原则，一般需将抛石范围延伸至深泓处，以免主流对河床的剧烈冲刷会破坏护岸结构，故可认为从岸顶到深泓范围内均受工程守护，不发生冲刷.此外，模型中水流与泥沙的计算为非耦合计算，计算时间步长为30 s.

2.3 计算步骤

(1) 模型的初始及边界条件给定；(2)水流模块计算：采用“Preissmann”隐格式离散一维水流控制方程式(1)~(2)，并用追赶法求解，计算河道内各断面的水流条件；(3)泥沙输移模块计算：基于t-1时刻修正得到的断面有效水流挟沙力，采用迎风格式离散并求解式(3)，进而计算新水流条件下(t时刻)各固定断面的悬移质含沙量(S_i)；(4)水流挟沙力计算：根据式(5)计算新水流条件下各断面的水流挟沙力(S_*i)，并对其进行修正，得到t时刻有效的断面水流挟沙力(S′_*i)；(5)河床变形模块计算：在修正的水流挟沙力条件下，采用显格式离散并求解式(4)，计算河床冲淤面积(ΔA_{b, i})并修改河床地形，其冲淤面积分配模式在有、无整治工程的区域有所不同；(6)在新河床地形条件下，重新计算水流、泥沙条件，用于下一时刻的计算.

2.4 模型率定结果及分析

本研究选取了荆江段2015年1月1日至12月31日的水沙系列，对改进的模型进行率定，模拟了该时段的水沙输移过程，从而确定模型的最优参数.

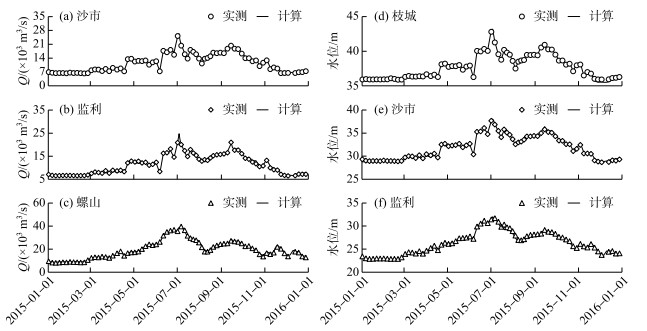
2.4.1 流量和水位变化

在改进的模型中，河漫滩和主槽的糙率将分别确定.河漫滩的曼宁糙率系数通常设为常数，在荆江段低滩及高滩糙率分别取为0.025、0.04.而主槽的糙率则通过率定得到，先假定研究河段内各水文或水位站所在断面(控制断面)的流量-糙率关系，并认为河段内其他断面某一流量下的糙率系数可由相邻两个控制断面同流量下的糙率值通过线性插值得到；然后通过调试这些控制断面的流量-糙率关系，使得研究河段内各水文站或水位站计算的水位、流量过程与实测情况能较好地符合.计算结果表明：在沙市、监利及螺山站，计算与实测的流量过程一致，平均流量的相对误差均为3 %左右(图 5a~c)；在枝城、沙市及监利站，平均水位的绝对误差则均小于0.3 m(图 5d~f).故该模型可很好地模拟典型断面流量及水位随时间的变化过程.

2.4.2 含沙量变化

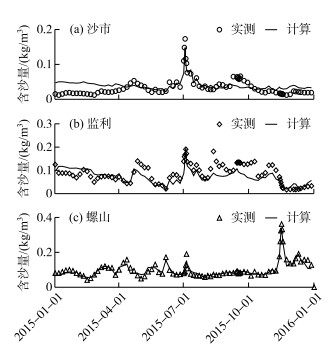
图 6给出了2015年沙市、监利及螺山站计算和实测含沙量的变化过程.由图可知，三站计算与实测的平均含沙量相对误差分别为33 %、30 %和13 %.总体而言，改进的模型可较好地模拟含沙量过程，但其误差高于流量和水位误差.此外，模型计算中张瑞瑾挟沙力公式系数k取为0.05 kg/m³，而指数m在各断面也均为常数1.55.分组泥沙恢复饱和系数α_k根据实测资料率定得到：在本次计算中，当发生淤积时，α_k取值为0.15；而发生冲刷时，α_k设为0.20.

2.5 模型验证结果

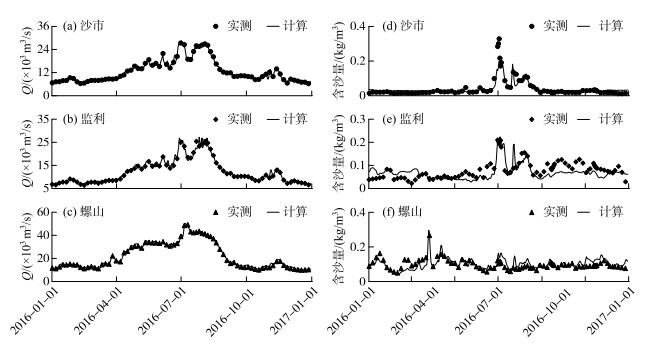
本研究验证过程选取了荆江段2016年1月1日至12月31日的水沙系列，在率定得到的最优参数条件下(如曼宁糙率系数、挟沙力公式参数、恢复饱和系数等)，验证改进模型的模拟精度.结果表明：沙市、监利和螺山站计算和实测流量的平均相对误差为3 % ~5 % (图 7a~c)，而枝城、沙市、监利站水位的平均绝对误差均在0.1~0.3 m之间.此外，沙市、监利和螺山站计算与实测悬移质含沙量的平均相对误差分别为49 %、39 %和20 %；最大计算含沙量分别为0.198、0.204和0.296 kg/m³，与实测值(0.328、0.210和0.329 kg/m³)相比，除沙市站外差别均较小(图 7d~f).

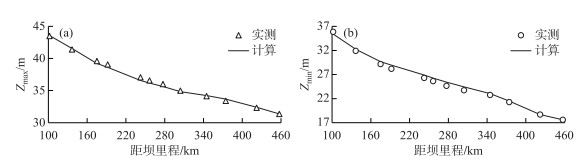
图 8给出了2016年荆江段沿程最高、最低水位(Z_max和Z_min)计算与实测值的比较结果.由图可知，模型的计算结果与实际符合较好.例如，螺山站上游3个水文站(枝城、沙市、监利)的实测最高水位分别为43.48、39.06和34.13 m，与计算值43.50、38.29、34.09 m十分接近.而最低水位计算值与实测值绝对误差均在0.2~0.7 m之间，误差亦很小.从总体上看，改进模型的计算精度较高.

3 讨论

众所周知，河道整治工程会对悬沙输移及河床冲淤变形过程产生较大的影响.故本研究基于2016年荆江段的实测资料，通过改进的一维水沙数学模型，进一步对比计算了该河段在有无考虑工程影响下的悬沙输移及河床变形过程.

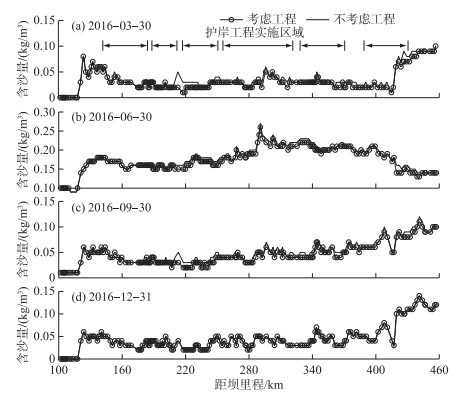
3.1 河道整治工程对悬沙输移的影响

整治工程对整个河段悬沙输移的影响主要体现在两个方面.一方面，整治工程的实施改变了河段输沙量，其限制河床冲刷的作用使得整个河段的输沙量有一定程度的减小.采用输沙率法计算的荆江段(枝城-螺山)2016年实测冲刷量为3439万t，而考虑整治工程影响时计算得到的冲刷量为4021万t，相较于不考虑工程的模拟结果(冲刷量4246万t)更接近于实测值.另一方面，整治工程的实施影响着含沙量的沿程分布.计算结果表明，未考虑工程的模型计算得到的枝城-螺山段2016年含沙量总体上大于考虑工程影响的含沙量.在计算时段内，两者的绝对差值在0~0.09 kg/m³之间. 图 9给出了4个模拟时刻有、无考虑工程影响的沿程含沙量对比图.由图可知，4个模拟时刻的含沙量平均相对差值分别为12.0 %、2.5 %、9.9 %和8.5 %.

3.2 河道整治工程对河床变形的影响

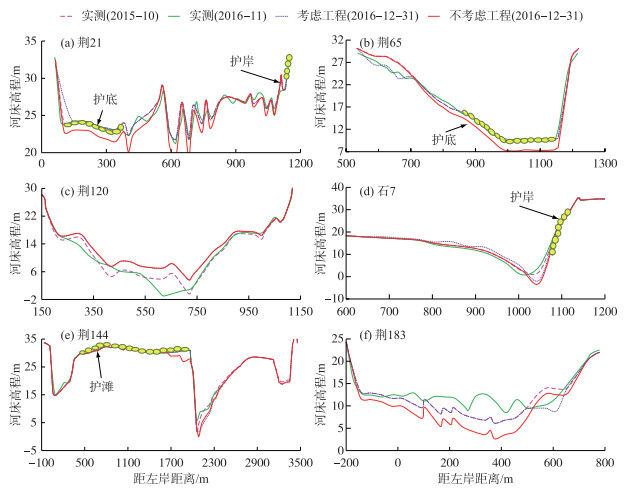
本文还分析了整治工程对河床形态调整的影响.虽然比较一维模型计算得到的横断面形态变化是不合理的，但分析考虑工程与否对模拟结果的影响是可行的.由图 10可知，考虑整治工程影响后，模拟得到的断面形态更符合实测断面形态.例如，荆21、荆65断面主槽的部分区域受工程防护，使河床无法进一步冲刷.当模型不考虑此影响时，模拟结果显示该区域(护底位置)河床继续下切，平均下切深度分别达0.67 m和1.14 m，这显然与实际情况不符(图 10a~b).如图 10e所示，护滩工程的实施亦限制了江心洲的冲刷；当不考虑工程影响时，该江心洲右缘将发生冲刷，不符合实际.此外，整治工程的实施也影响下游河段的河床变形过程.如荆120断面虽未受到工程守护，但上游河段大规模工程的实施，使得水流无法从河床携带足够的泥沙，导致该断面计算的含沙量有所减小，淤积强度减弱.当不考虑工程影响时，计算得到的河床平均淤积厚度达0.35 m；考虑工程影响后，该值减小为0.08 m(图 10c)，更符合实际发生冲刷的情况.而石7断面上游河段受到工程守护，致使该断面冲刷有所加剧.在不考虑工程影响时，计算得到的河床平均下切深度为0.14 m；而考虑工程影响时，该值为0.21 m(图 10d)，更接近实际下切深度0.38 m.同样在不考虑工程影响下，模拟结果表明荆183断面能冲刷下切0.65 m，而实际上床面淤高0.77 m；通过考虑工程影响，该断面则呈淤积状态，平均淤积厚度为0.02 m(图 10f).若不在模型中考虑整治工程，上述影响将被忽略.

4 结论

本文对一维水沙动力学模型进行了改进，用于模拟河道整治工程影响下的河床调整过程，并将该模型应用到长江中游荆江河段.结论如下：

1) 建立了考虑河道整治工程影响的一维水沙数学模型.首先在确定河床边界条件时，在横向上对有无工程的区域进行划分，在垂向上将河床分层.然后在此基础上，对模型中的输沙及河床冲淤变形模块进行改进：淤积可能发生在河床的任意区域；但冲刷只会发生在未实施整治工程或前期模拟时段内形成了可供冲刷淤积层的区域上，在有工程防护且无法为水流冲刷提供沙源的位置，河床下切则不会发生.最后分别采用2015年和2016年荆江段的实测资料，对模型进行率定和验证，结果表明改进后的模型可较准确地模拟水沙的输移过程.

2) 定量分析了河道整治工程对悬沙输移和与河床冲淤变形过程的影响. 2016年荆江段的模拟结果表明：采用输沙率法计算的荆江段(枝城-螺山)2016年实测冲刷量为3439万t，而考虑整治工程影响时计算得到的冲刷量为4021万t，相较于不考虑工程的模拟结果(冲刷量4246万t)更接近于实测值.此外，改进模型计算的河道断面形态与实测数据吻合更好.这是由于模型考虑了整治工程对河岸崩退、床面下切及洲滩冲刷的限制作用，以及水流无法从被工程防护区域攫取足够的泥沙而改变其他区域冲淤强度的影响.