(2: 宜昌市水文水资源勘测局, 宜昌 443000)
(2: Hydrology and Water Resources Survey Bureau of Yichang, Yichang 443000, P. R. China)
可靠的洪水预报是防洪决策中的重要依据[1],是减少甚至避免洪水破坏的第一道防线.在水文学研究及实际工程应用中,相较于水文资料充足的地区,更常见且更有挑战性的是对资料匮乏流域进行洪水预报.国际水文学会(IAHS)曾在20世纪初提出了水文资料匮乏流域的洪水预报(PUBs)10年计划[2],期间涌现了大量研究成果[3-5].资料匮乏流域的洪水预报研究一般被概括为以下两部分[6]:(1)直接针对径流或径流指标进行区域化;(2)针对水文模型参数进行区域化.两者都是基于回归方法或目标流域与测量流域之间的某种距离度量.首先,简单的回归模型显示出较高的应用价值,如Mazvimavi等[7-8]在非洲52个流域建立了径流指标与流域属性的多元线性回归模型,以期通过年平均降雨、流域平均坡度、河网密度和土地覆盖等流域属性估计无资料流域的年平均径流量、基流指数、历时曲线和月平均径流量等径流指标. Maréchal等[9]基于英国土壤类型水文计划(HOST)的土壤数据,使用了一个简单的回归方法较精确地预测了未测量流域的基流指数等径流指标.也有部分研究基于更复杂的回归模型,如Laaha等[10-11]揭示了根据区域特点定制回归模型而不是使用全局模型的好处,其研究表明基于按季节性分组的流域回归模型提供了鲁棒性更强的区域化结果.同样地,地质统计学方法也被用于估计资料匮乏流域的水文变量,比如Skøien等[12]提出了拓扑克里金法,可以用于解释水动力及地貌特征的空间离散性,该方法避免了输入数据的误差和参数可识别性问题.部分研究[13]认为该方法提供了比回归模型更稳健的估计.另一方面,研究者们越来越认识到,流域空间上的接近不一定导致流域产流模式的相似[14],当使用更具有水文学意义上的距离量度时,基于距离的方法的估计效果会显著提高[15].如Merz等[16]将拓扑克里金法与流域特征相结合,提高了该方法的预测性能. Dornes等[17]认为只要保证流域之间的水文相似性,水文模型的参数甚至可以传递数千千米.时至今日,资料匮乏地区的水文预报获得了长足进步,但仍有大量难题无法解决[18].
我国有防洪任务的重点中小河流(汇流面积小于3000 km2)有5186条[19].近年来,受气候变化影响,由局地强降水造成的中小河流突发性洪水频繁发生,已成为造成人员伤亡的主要灾种.据统计,我国中小流域涝灾害和山洪地质灾害损失约占全国洪涝灾害经济损失的70 % ~80 %,对人民群众的生命财产安全构成了严重的威胁[20].由于大部分中小河流源短流急,洪水具有历时短、上涨快的特点,加之水文资料短缺,传统的预报方案通常难以对这些地区的洪水做出有效的预报[21].区域化方法是解决此问题的思路之一,目前针对无资料中小流域的区域化研究较少,姚成等[22]使用区域化方法(空间临近法和回归法)将API模型和新安江模型应用于大别山区及皖南山区的29个中小流域,得到了较高的预报精度.但是在现有的区域化研究中,测量流域与目标流域大多空间分布均匀且空间距离较近.在这些地区,基于空间距离的区域化方法(以下称为空间临近法)由于操作简单且所需资料少而多被使用.同时,基于水文属性距离的区域化方法(以下称为物理相似法)和回归方法也被用来提高预测性能.在自然条件与历史因素的限制下[23],设立在我国湿润山区中小流域的水文测站分布稀疏,可能导致某一具体区域内的测量流域数量较少.是否可以通过其他资料充足但相隔较远地区的测量流域作为参证流域进行参数估计?为了回答此问题,本研究关注于目标流域与测量流域空间位置较远时,区域化方法是否可以有效估计参数.此时,测量流域与目标流域之间显著的空间差异导致空间临近法无法使用,物理相似法及回归方法是否适用,需要接下来进一步的研究.本研究将皖南山区与鄂西山区分别作为已观测区及未观测区,选用新安江模型进行洪水模拟,并验证区域化方法(物理相似法及回归法)在研究区的适用性.正如Prieto等[24]所言,单独使用参数区域化有诸多弊端,本研究基于新安江模型参数的物理意义先估算出部分参数,剩余参数使用区域化方法(物理相似法及回归法)估计,并比较不同参数估计方案的效果,提出在研究区内最为适用的参数估计方案,为长江中下游资料匮乏的山区中小流域洪水预报提供参考.
1 研究区概况及资料来源研究区域为长江中下游地区的32个山区中小流域,其中位于皖南山区的29个流域为有观测资料的测量流域,鄂西山区的3个流域被视为资料匮乏的目标流域,研究区域见图 1.各流域面积均不超过1000 km2,均为自然闭合流域,受水工建筑物的影响较小,流域平均海拔多在400~1000 m,其中雾渡河流域平均海拔最高,为1109 m.各流域年平均降水量均在1200~1500 mm,年平均蒸发量均在600~800 mm,年平均气温14~16℃.研究流域大多地势陡峭,河网密集,平均坡度大多在10~30°,河网密度大多在0.6~1.2 km/km2.研究区内土壤类型以壤土和黏土为主,土壤饱和渗透系数大多在3~12 mm/h.土地利用(LUCC)以林地为主,大部分流域林地面积占比70 %以上,甚至部分达到100 %.研究区内植被类型以木本植物为主,大多为常绿针叶林、常绿阔叶林及灌木.

|
图 1 研究区地理位置 Fig.1 Locations of the research catchments |
降雨、径流及蒸发资料来自当地水文局,时间步长均为1 h. 29个测量流域均具有至少30年的观测资料. 3个目标流域中,雾渡河有2008-2017年间共11场观测洪水,茅坪河有2016-2018年间共5场观测洪水,下牢溪仅有2016年共2场观测洪水. DEM来自中国科学院地理空间数据云,分辨率为30 m,用于提取流域地形、地貌属性;土地利用数据来自中国科学院遥感解译的2010年LUCC图,分辨率为1 km,用于提取流域土地利用属性;土壤数据来自于HWSD(世界土壤数据库)的土壤类型图,分辨率为1 km,用于提取流域土壤属性.
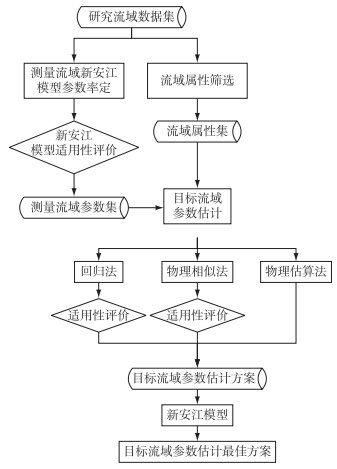
2 研究方法本研究的研究思路大致如下:首先在测量流域进行新安江模型的校准,得到测量流域的新安江模型校准参数集.然后进行流域物理属性的筛选,依据筛选出的流域物理属性集,运用区域化方法(回归法、物理相似法),将测量流域的校准参数转移至目标流域.与此同时,使用基于参数物理意义的估算方法(以下简称物理估算法),估算出部分参数.最后,将物理估算法与区域化方法相结合,提出针对目标流域的多个综合参数估计方案,并比较不同参数估计方案的效果,得到在研究区内最为适用的参数估计方案.本研究的技术路线图见附图Ⅰ.
2.1 新安江模型及物理估算法 2.1.1 新安江模型新安江模型是赵人俊[25]于1984年前后提出的概念性模型,在我国湿润及半湿润地区具有较高的预报精度,已得到广泛应用[26-28].该模型共有16个参数,各参数物理意义见文献[29],其中不敏感参数10个(WM、WUM、WLM、B、C、IMP、EX、CI、KE、XE),敏感参数7个(KC、SM、KI(KG)、CG、CS、L).根据赵人俊等[30]提出的客观优选法,不敏感参数不参与率定,直接赋予固定值.敏感参数的率定使用人工优选结合SCE-UA算法[31],这样既可以快速稳定的优选参数,又能有效避免自动优选参数可能不合理的问题.选用洪峰相对误差、峰现时间误差,纳什效率系数(NSE)对参数率定结果进行评价.依据《水文情报预报规范》[32],洪峰相对误差在20 %以内,峰现时间误差在3 h以内为合格.
在目标流域,不敏感参数同样直接赋予固定值,敏感参数需要进行估计.在敏感参数中KI与KG满足线性约束,只需估计KI即可,因此本研究在目标流域需要估计的参数为6个,见表 1.在新安江模型的待估计参数中,壤中流出流系数KI和河网水消退系数CS可以基于参数的物理意义进行估算(物理估算法).
| 表 1 目标流域待估计参数 Tab. 1 Estimated parameters of ungauged basins |
土壤质地可以用来推断土壤的性质,进而估算自由蓄水量对壤中流及地下水的出流系数(新安江模型中的KI与KG). KI和KG之和决定了自由水的排水速率,赵人俊等[29]认为KI+KG的值可固定为0.7;KI/KG决定了壤中流与地下水出流的比例,姚成等[33]在GXM模型中提出了针对栅格的KI/KG估计公式,将其修改成适用于新安江模型的形式:
| $ \left\{ \begin{array}{l} KI + KG = 0.7\\ \frac{{KI}}{{KG}} = \frac{{1 + 2\left( {1 - {\theta _{{\rm{wp}}}}} \right)}}{{{m_{\rm{r}}}}} \end{array} \right. $ | (1) |
式中,mr为自由水出流校正系数,根据前人的研究成果[33-35],在湿润流域mr可取为1;θwp为土壤凋萎含水量,以体积含水量表示,可根据土壤质地取值,见表 2[36].
| 表 2 不同质地土壤凋萎含水量 Tab. 2 Wilting moisture content of various soil textures |
李致家等[37]针对二叉树结构河网,对河链进行编号,链接河源的河链编号记为r=1,下游河链的编号等于该条河链的上游总链数+1.并根据矩形河道线性蓄泄关系(式(2)),引入一个无量纲时间tα:
| $ Q\left( {r, t} \right) = \frac{v}{L}W\left( {r, t} \right) $ | (2) |
| $ {t^\alpha } = \frac{{v \cdot t}}{L} $ | (3) |
式中,Q(r, t)为河链r的出流量,m3/s;W(r, t)为河链r的蓄量,m3;v为平均河道流速,m/s;L为平均河链长,m.
在资料匮乏地区一般没有实测流速资料,可以使用经验公式估算. Rodríguez-Iturbe等[38]基于运动波理论提出如下流速公式:
| $ v = 0.665\;{\omega ^{\frac{3}{5}}}\left( {p \cdot A} \right) $ | (4) |
| $ \omega = \frac{{{S_0}^{\frac{1}{2}}}}{{n \cdot {B^{\frac{2}{3}}}}} $ | (5) |
式中,p为次洪的平均雨强,cm/h;A为流域面积,km2;B为平均河宽,m;S0为平均河道坡度;n为河道曼宁糙率系数,根据已有研究[39],这里可取n=0.025.
李致家等[37]在此基础上推导出递推形式的河链蓄量公式:
| $ W\left( {r, {t^\alpha }} \right) = {{\rm{e}}^{ - {t^\alpha }}}\left\{ {{W_0} + \int_0^{{t^\alpha }} {{{\rm{e}}^\delta }\left[ {W\left( {{r_1}, \delta } \right) + W\left( {{r_2}, \delta } \right)} \right]{\rm{d}}\delta } } \right\} $ | (6) |
式中,r1与r2分别为河链r上游的两条河链.
河网消退系数CS表示河网退水速度,可以用河网出口处计算时段起止的流量比表示[40]:
| $ CS = \frac{{{Q_r}\left( {{t_{\rm{e}}}} \right)}}{{{Q_r}\left( {{t_{\rm{s}}}} \right)}} $ | (7) |
式中,Qr(t)为河网出口流量,m3/s;ts表示计算时段起始时刻;te表示计算时段终止时刻.
将式(2)、(3)代入式(7),得到CS与蓄量的关系[41]
| $ CS = \frac{{{W_r}\left( {t_{\rm{e}}^\alpha } \right)}}{{{W_r}\left( {t_{\rm{s}}^\alpha } \right)}} $ | (8) |
式中,Wr(tα)为河网蓄量,m3;tsα表示计算时段起始时刻的无量纲时间;teα表示计算时段终止时刻的无量纲时间.
为了避免使用单一时段造成的估计误差,通过计算N1个时段的起止蓄量,使用最小二乘法估计CS的值[41]:
| $ CS = \frac{{\sum\limits_{j = 0}^{{N_1} - 1} {{W_r}\left( {t_j^\alpha } \right){W_r}\left( {t_{j + 1}^\alpha } \right)} }}{{\sum\limits_{j = 0}^{{N_1} - 1} {W_r^2\left( {t_j^\alpha } \right)} }} $ | (9) |
式中,tjα表示时段j对应的无量纲时间.
2.2 参数区域化方法区域化是在水文资料匮乏流域进行水文预报的有效方法,所谓区域化即是将水文模型参数值从水文资料丰富的测量流域转移到水文资料匮乏的目标流域的过程[42].目前,常用的区域化方法主要有物理相似法、回归法和空间邻近法.物理相似法[43]将参数值从测量流域转移到目标流域,该测量流域的属性(气候与下垫面等)与目标流域的属性相似.回归法[44]则是在测量流域上建立校准参数与流域属性(气候与下垫面等)之间的关系,然后根据目标流域的流域属性和已建立的回归关系估计目标流域的参数值.空间邻近法[45]假定空间上邻近的流域,下垫面与气候条件也应该相似,因此目标流域的参数值通常来自一个或多个附近的测量流域.
2.2.1 物理相似法单流域物理相似法选择与目标流域水文物理相似性最高的测量流域作为参数转移的供体(以下简称参证流域),将参证流域的参数值直接移用到目标流域.利用秩累积相似性[46]作为流域物理相似性指标,对于流域属性集(区域化研究中被选择的流域属性的集合)里的每个属性,具有与目标流域最相似属性的测量流域的秩记为1,具有第二相似属性的测量流域的秩记为2,依此类推.计算流域属性集里每个属性的秩号,选择总秩最小的测量流域作为参证流域,每个用于区域化的属性在秩累积中都具有同等的权重.物理相似法要讨论的另一个重要问题是参证流域的数量,传统物理相似法仅考虑一个最相似的流域,但正如Mcintyre等[47]指出的,来自最相似流域的参数集不一定产生最佳结果. Viviroli等[48]建议选取前5个相似流域作为参证流域,可以使计算效率与模型准确性达到最佳平衡.因此本研究提出多流域物理相似法,选取秩累积最小的前n个测量流域作为参证流域,将每个参证流域的参数集分别移用至目标流域,然后在每个计算时间步长上取模拟流量的中位数,组成最终的模拟结果.使用中位数是为了避免模拟结果出现过度平滑现象.
本研究为了定量分析物理相似法的适用性,引入用户加权的欧氏距离[48]作为相似性度量,用户加权的欧氏距离越小,说明两个流域间的水文物理相似性越高:
| $ {D_\varphi }\left( {x, y} \right) = \sqrt {\sum\limits_{\alpha = 1}^{{N_2}} {{\varphi _\alpha }{{\left[ {AT{T_\alpha }\left( x \right) - AT{T_\alpha }\left( y \right)} \right]}^2}} } $ | (10) |
式中,Dφ(x, y)为x、y两流域间的用户加权的欧氏距离;N2为流域属性集里元素个数;ATTα(x)为流域x的第α个标准化流域属性;φα为用户赋予第α个标准化流域属性的权重,这里取φα=1[48].
2.2.2 回归法回归法适用于测量流域数量较多(大于10个)且流域水文物理特征相似的地区[49].回归法假设流域特征与模型参数间存在较好的相关关系,因此具有一定的局限性[50].部分模型参数可能与流域属性相关性较低,对于这类参数,难以建立可靠的回归关系,不适用回归法.另外,回归法中流域属性的选择十分重要,若流域属性选择不恰当,回归法的预测性能较差.在以往的研究中[51-53],大多根据专家经验人工选择参与回归的流域属性,具有极大的主观性;同时为了方便处理,通常使用线性回归,而线性回归很难代表实际水文情况[54],具有较大缺陷.本研究引入Boruta算法[55]进行流域属性筛选,以减少流域属性选择的主观性,并使用随机森林算法[56]进行非线性回归.
随机森林是bagging算法[57]的一个变体,以决策树为基学习器,构建多颗决策树来组成一个“森林”.随机森林使用自助采样法(bootstrap sampling)[58],以包含β个样本的数据集构建决策树的时候,依次有放回的取出一个数据放入采样集,重复取样β次,这样在创建多颗决策树时就有部分数据被多次选择,同时也有部分数据始终没有被选择,未被选择的数据大约占数据总量的36.8 % [56],这部分数据被称为袋外数据(out-of-bag data).同时,随机森林随机地从θ个自变量中选择部分自变量进行决策树节点的确定,因此每次构建的决策树都可能不一样.最终随机森林预测结果为“森林”中每决策树单独预测结果的期望值.随机森林相比于其它回归方法有以下优点:(1)可以处理变量的多元共线性问题;(2)模型结构十分灵活,不需要预先确定回归方程的形式;(3)随机性的引入使得随机森林不容易过拟合,有很好的抗噪声能力;(4)由于存在袋外数据,使随机森林没有必要进行交叉验证或单独留出验证集,袋外误差(out-of-bag error)就是模型泛化误差的一个无偏估计[59],其结果近似于k折交叉验证.
Boruta算法是一个基于随机森林的特征选择方法,使用Z分数作为特征重要性度量,考虑了随机森林中决策树之间平均准确度损失的波动.该方法将每个原始变量进行随机复制,创造出原始变量的“阴影”变量,将“阴影”变量与原始变量合并,并使用随机森林对这个扩展的信息系统分类,收集并计算出Z分数.当一个真实变量比最好的“阴影”变量具有更高的Z分数,则认为其对回归模型是有意义的.每次迭代中,不断删除不重要的特征,直到所有真实变量得到确认或拒绝. Boruta算法的具体原理可见Kursa等[60],此处不再赘述.
3 流域属性筛选及方法适用性评价 3.1 流域属性筛选选取适当的流域属性是进行区域化研究的必要前提,目前已有大量流域属性被提出[3, 15, 61-65],这些研究普遍认为流域属性必须依据不同的研究方法和研究区域进行选择,不应直接套用.流域属性的选择不宜过多[66],如英国洪水估算手册[67]推荐使用3种流域属性传递水文模型参数;Samaniego等[68]在研究中使用了7种流域属性.本研究依据研究区可获得的数据情况、新安江模型参数的物理意义及山区中小河流的特点,从气象、地形地貌特征、土地利用及土壤等方面选取25种流域属性,见表 3.首先选取流域基本属性及流域的形状属性,包括流域面积、高程,长度、宽度及形状系数等,这些属性可能影响蒸散发折算系数KC等模型参数.其次,研究流域大多地势陡峭、河网密集,反映流域坡度、河道坡度及河网密度的流域属性(如流域平均坡度、河道平均坡度、河网密度等)应该被考虑,且这些属性对流域汇流影响较大,可能影响河网水流消退系数CS、地下水消退系数CG和河网汇流滞时L等模型参数.地形指数是Beven等[69]提出的一个地形特征参数化指标,是流域径流源面积和地下水水位空间分布特征的近似表征[70],本研究将其作为一个水文综合指标.土地利用和土壤类型综合反映流域下垫面的产汇流条件,影响着自由水容量SM及壤中流出流系数KI等模型参数.
| 表 3 流域属性 Tab. 3 The watershed attributes |
通过皮尔逊相关分析剔除显著强相关的流域属性,筛选出最不相关的流域属性组成流域属性集,其中各个属性的皮尔逊相关系数P<0.7且显著性水平α>0.05[71]. Viviroli等[48, 72]研究认为,在筛选出的流域属性集里,分别选取与每个待估计水文模型参数相关性最高的两个流域属性,组成最终的流域属性集,区域化结果最优.新安江模型的待估计参数有6个(KC、SM、KI、CG、CS、L),通过皮尔逊相关分析,分别选取与待估参数相关性最高的两个流域属性,组成最终本研究使用的流域属性集(表 3中带*属性).流域属性集里包括以下7种流域属性(流域属性不足12个是因为有部分流域属性同时与多个模型参数高度相关):流域面积AREA、流域平均高程ELEVATION、河道平均坡度CSLOPE、面积坡度ASLOPE、河网密度DD、林地面积比FST和土壤饱和渗透系数SOLK.
3.2 适用性评价本研究选取的模拟时间步长为1 h. 29个测量流域的新安江模型模拟结果可见文献[22],平均洪峰合格率、平均峰现时间合格率和平均确定性系数分别为84 %、91 %和0.84,表明在本研究区域,新安江模型的次洪模拟精度较高,是适用的水文模型.
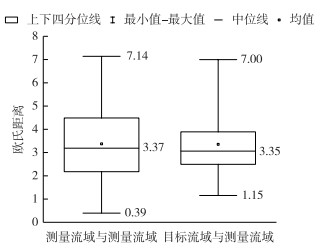
测量流域与目标流域空间距离较远,主要分为皖南和鄂西两大簇,因此空间近似法不适用.但两者具有相似的气象条件,且研究流域均是山区中小河流流域,具有相似的下垫面条件,为使用物理相似法及回归法提供了条件.根据公式(10),在流域属性的n维空间中,依次选取一个测量流域作为参证流域,分别计算与剩余的28个测量流域之间的欧氏距离,及与3个目标流域之间的欧氏距离,比较结果见图 2.可见两者的均值相近,且目标流域与测量流域之间的欧氏距离最大值未超过测量流域之间欧式距离的最大值,因此认为目标流域与测量流域之间物理相似性较高,使用物理相似法是合理的.
|
图 2 流域物理相似性分析 Fig.2 Analysis of physical similarity |
对于回归法而言,使用Boruta算法分别计算流域属性对每个敏感参数的重要性,以评估其通过随机森林建立回归关系的可靠性.结果显示,只有河网水消退系数CS及河网汇流滞时L与流域属性集里的部分属性有较密切的关系,见图 3.图中蓝色箱体代表“阴影”属性Z分数的最小值、均值与最大值,大于“阴影”属性Z分数最大值的流域属性被标记为“接受”,即绿色箱体,剩余的流域属性被标记为“拒绝”,即红色箱体.对剩余敏感参数而言,流域属性集里的所有属性的Z分数均小于“阴影”属性最大值,被Boruta算法标记为“拒绝”.即流域属性与这些参数没有明显相关性,相当于随机变量,因此无法使用回归法对这部分参数进行区域化.

|
图 3 部分新安江模型参数的Boruta分析 Fig.3 Boruta analysis about some parameters of Xin'anjiang Model |
CS与L分别与被接受的流域属性建立回归关系.在泛化误差分析中,随机森林使用袋外误差作为泛化误差,Wolpert等[59]已经证明随机森林的袋外误差结果近似于k折交叉验证.线性回归及逐步回归模型使用留一法(leave-one-out cross validation,即n折交叉验证,n为样本数)估计泛化误差.以平均绝对误差(MAD)、均方误差(MSE)及伪决定系数(RSQ)[73]作为误差评价指标,其中RSQ取值在0~1之间,表示自变量对因变量的解释程度,越接近1表示解释程度越高:
| $ RSQ = 1 - \frac{{MSE}}{{{\mathop{\rm var}} \left( y \right)}} $ | (11) |
式中,var(y)为因变量实际值的方差.
表 4统计了将流域属性集里全部流域属性作为自变量的线性回归模型、姚成等[22]在相同区域建立的逐步回归模型和本研究建立的随机森林回归模型的泛化误差.随机森林模型中CS的MAD、MSE与线性回归差别不大,但是随机森林模型中L的MAD、MSE明显低于线性回归模型.另一方面,随机森林模型中CS及L的MAD、MSE均小于逐步回归.说明在本研究区,随机森林泛化能力优秀,是较为适用的方法.且随机森林法的RSQ分别为0.46和0.58,均高于对应的线性回归方法和逐步回归方法,表明Boruta方法筛选的流域属性与CS及L关系密切,建立的回归模型较为可靠.
| 表 4 回归模型泛化误差分析 Tab. 4 The generalization error of regression model |
设计了10种不同的方案进行目标流域的参数估计:(1)所有敏感参数取29个测量流域的平均值:(2)所有敏感参数使用单流域物理相似法估计;(3)所有敏感参数使用多流域物理相似法(2个参证流域)估计;(4)所有敏感参数使用多流域物理相似法(5个参证流域)估计;(5) CS及L使用回归方法,剩余参数使用单流域物理相似法估计;(6) CS及L使用回归方法,剩余参数使用多流域物理相似法(2个参证流域)估计;(7) CS及L使用回归方法,剩余参数使用多流域物理相似法(5个参证流域)估计;(8) L使用回归方法估计,CS及KI(KG)使用物理估算法,剩余参数使用单流域物理相似法估计;(9) L使用回归方法估计,CS及KI (KG)使用物理估算法,剩余参数使用多流域物理相似法(2个参证流域)估计;(10) L使用回归方法估计,CS及KI(KG)使用物理估算法,剩余参数使用多流域物理相似法(5个参证流域)估计.方案1是不进行任何优化的基准参照组;方案2~4单独使用了物理相似法;方案5~7结合了物理相似法和回归法;方案8~10结合了物理相似法、回归法和物理估算法.方案2~4之间的区别是物理相似法中选取的参证流域数目分别为1、2、5个,方案5~7、方案8~10同理.如此设计方案的目的是:(1)比较不同方法或不同方法组合对参数估计精度的影响;(2)比较不同参证流域数量对参数估计精度的影响.
使用平均洪量相对误差、平均洪峰相对误差(为了避免正负误差抵消,均以绝对值计算)和纳什系数(NSE)作为新安江模型效率的评价指标,并将不同方案估计出的参数与率定的参数进行比较,各指标的变化即是参数估计方案导致的模型效率降低:
| $ \Delta {{E}_{\mu }}=\left( {{\widehat{EP}}_{\mu }}-EP \right)+\left( \widehat{E{{Q}_{\mu }}}-EQ \right)+\left( NSE-\widehat{NS{{E}_{\mu }}} \right) $ | (12) |
式中,ΔEμ为方案μ的模型效率损失;
表 5统计了各方案估计参数的精度.方案1作为不进行任何优化的基准参照组,参数估计效果最差,在3个目标流域NSE均远小于0,且模型效率损失最大,说明使用此方案估计参数的新安江模型不可信.方案2~10使用不同的方法进行了优化,模型效率损失均比方案1有所降低,说明这些方案不同程度的提高了资料匮乏流域的参数估计精度.比较三组选择不同参证流域数量的物理相似法(方案2、3、4;方案5、6、7及方案8、9、10),在茅坪河与雾渡河,模型效率损失为方案2<方案3<方案4,方案5<方案6<方案7,方案8<方案9<方案10.在下牢溪,除方案8模型效率损失显著较低外,其他方案差距不大.可得在本研究区,物理相似法的效果随着参证流域数量的增加而降低,与Viviroli等[48]发现的变化趋势基本一致.关注基于多流域物理相似法的方案3、6、9及方案4、7、10.这些方案的模型效率损失均较大,且使用回归法、物理估算法及其组合并不能有效提高多流域物理相似法的模型效率.可见,使用其它方法代替物理相似法估算出部分参数,不会改变参证流域数量对参数估计效果的影响趋势,不能有效弥补物理相似法参证流域数量选择不当造成的估计精度损失.基于单流域物理相似法的方案效果最优,下面聚焦于方案2、5、8.在3个目标流域,模型效率损失均是方案8<方案5<方案2,且在茅坪河与下牢溪,方案8的效率损失显著低于方案2、5.可见单独使用物理相似法的参数估计效果最差;结合回归法和物理相似法的参数估计效果与前者相比有小幅度提高;而根据模型参数特点综合使用物理相似法、回归法、物理估算法,可以显著提高模型参数估计的精度.说明在参证流域数量合适的情况下,本研究提出的综合参数估计方案可以有效估计资料匮乏流域的新安江模型参数.
| 表 5 不同参数估计方案结果统计 Tab. 5 The results of various parameter estimation schemes |
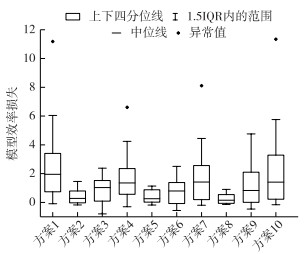
考虑不同方案在研究区的整体效果及稳定性,将3个目标流域所有洪水场次的模型效率损失统计于图 4.极少部分洪水场次存在估计参数略优于率定参数的情况,因此这部分洪水的模型效率损失可能为负值.由图可见,方案2、5、8的模型效率损失中值最接近于0,且呈现明显的负偏态分布,四分位距明显小于其他方案.说明相比于其他方案,方案2、5、8的参数估计效果更优,且结果更稳定.而方案8的四分位距又显著小于方案2、5,说明方案8的模型效率损失波动较小,估计参数的预报结果最为稳定.方案8在3个目标流域的模型效率损失仅为0.26、0.28和0.01,基于洪水场次统计的模型效率损失中值仅为0.15,说明使用方案8估计的模型参数与率定的参数相比,精度仅有略微下降.综合评比后认为,方案8是最优的模型参数估计方案,即单流域物理相似法结合回归法及物理估算法是在本研究区内进行新安江模型参数估计的最优方法,可以用于该地区资料匮乏中小流域的洪水预报.
|
图 4 不同方案模型效率损失统计 Fig.4 Model efficiency loss of different schemes for all gauged floods in target basins |
将新安江模型应用于长江中下游地区的32个山区中小流域,研究资料匮乏流域的参数估计方法.本研究提出的参数估计方案包括物理相似法、回归法、物理估算法及三者的不同组合,并同时考虑了参证流域的数量.研究结果显示:(1)在研究区内,测量流域与目标流域在空间上分为两簇,空间分布具有显著差异.在区域化方法中,空间临近法不适用,物理相似法适用,回归方法只适用于估计参数CS及L.物理估算法可以有效估计参数CS和KI;(2)目标流域与测量流域空间距离较远时,本研究提出的参数估计方案在不同程度上减少了参数估计导致的模型效率损失;(3)在本研究区,随着参证流域数目的增加,物理相似法的估计效果下降.使用回归法、物理估算法及其组合并不能有效提升多流域物理相似法的模型效率,其它方法不能弥补物理相似法参证流域数量选择不当造成的模型效率损失;(4)单独使用区域化方法往往不能得到理想效果.在参证流域数量合适的前提下,物理估算法结合区域化方法,可以显著提高模型参数估计效果;(5)提出的参数估计方案中,适用于长江中下游资料匮乏的山区中小流域的最佳方案为结合单流域物理相似法、回归法、物理估算法的方案8.
测量流域与目标流域空间距离较远可以尝试使用本研究提出的参数估计方案,但目前仅从主观上认定其空间分布具有明显差异,“较远”的距离如何量化及空间距离是否存在适用性阈值等问题还需要进一步的研究.同时,本研究中不同方案的参证流域数量仅选取了1、2、5个作为代表,多流域物理相似法的流域数目与参数估计效果的定量关系有待进一步研究.本研究仅根据参数的物理意义估算出参数CS及L,新安江模型中的其它敏感参数能否通过类似方法进行估算,进一步提高资料匮乏地区的参数估计精度,还有待继续研究.
6 附录附图Ⅰ见电子版(DOI:10.18307/2021.0223).
|
附图Ⅰ 技术路线图 AttachedFigure1 Study technique route |
| [1] |
Pilon PJ. Guidelines for reducing flood losses. United Nations International Strategy for Disaster Reduction (UNISDR), 2002. |
| [2] |
Sivapalan M, Takeuchi K, Franks SW et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003-2012: Shaping an exciting future for the hydrological sciences. Hydrological Sciences Journal, 2003, 48(6): 857-880. DOI:10.1623/hysj.48.6.857.51421 |
| [3] |
Merz R, Blöschl G. Regionalisation of catchment model parameters. Journal of Hydrology, 2004, 287(1/2/3/4): 95-123. DOI:10.1016/j.jhydrol.2003.09.028 |
| [4] |
Oudin L, Kay A, Andréassian V et al. Are seemingly physically similar catchments truly hydrologically similar?. Water Resources Research, 2010, 46(11). DOI:10.1029/2009wr008887 |
| [5] |
Samaniego L, Bárdossy A, Kumar R. Streamflow prediction in ungauged catchments using Copula-based dissimilarity measures. Water Resources Research, 2010, 46(2). DOI:10.1029/2008wr007695 |
| [6] |
He Y, Bárdossy A, Zehe E. A review of regionalisation for continuous streamflow simulation. Hydrology and Earth System Sciences, 2011, 15(11): 3539-3553. DOI:10.5194/hess-15-3539-2011 |
| [7] |
Mazvimavi D, Meijerink A, Stein A. Prediction of base flows from basin characteristics: a case study from Zimbabwe. Hydrological Sciences Journal, 2004, 49(4): 703-715. DOI:10.1623/hysj.49.4.703.54428 |
| [8] |
Mazvimavi D, Meijerink AMJ, Savenije HHG et al. Prediction of flow characteristics using multiple regression and neural networks: A case study in Zimbabwe. Physics and Chemistry Earth, Parts A/B/C, 2005, 30(11/12/13/14/15/16): 639-647. DOI:10.1016/j.pce.2005.08.003 |
| [9] |
Maréchal D, Holman IP. Development and application of a soil classification-based conceptual catchment-scale hydrological model. Journal of Hydrology, 2005, 312(1/2/3/4): 277-293. DOI:10.1016/j.jhydrol.2005.02.018 |
| [10] |
Laaha G, Blöschl G. Seasonality indices for regionalizing low flows. Hydrological Processes, 2006, 20(18): 3851-3878. DOI:10.1002/hyp.6161 |
| [11] |
Laaha G, Blöschl G. A comparison of low flow regionalisation methods—catchment grouping. Journal of Hydrology, 2006, 323(1/2/3/4): 193-214. DOI:10.1016/j.jhydrol.2005.09.001 |
| [12] |
Skøien JO, Blöschl G. Spatiotemporal topological kriging of runoff time series. Water Resources Research, 2007, 43(9). DOI:10.1029/2006WR005760 |
| [13] |
Laaha G, Skøien JO, Nobilis F et al. Spatial prediction of stream temperatures using top-kriging with an external drift. Environmental Modeling & Assessment, 2013, 18(6): 671-683. DOI:10.1007/s10666-013-9373-3 |
| [14] |
Ali G, Tetzlaff D, Soulsby C et al. A comparison of similarity indices for catchment classification using a cross-regional dataset. Advances in Water Resources, 2012, 40: 11-22. DOI:10.1016/j.advwatres.2012.01.008 |
| [15] |
Bárdossy A, Pegram GGS, Samaniego L. Modeling data relationships with a local variance reducing technique: Applications in hydrology. Water Resources Research, 2005, 41(8). DOI:10.1029/2004wr003851 |
| [16] |
Merz R, Blöschl G, Humer G. National flood discharge mapping in Austria. Natural Hazards, 2008, 46(1): 53-72. DOI:10.1007/s11069-007-9181-7 |
| [17] |
Dornes PF, Tolson BA, Davison B et al. Regionalisation of land surface hydrological model parameters in subarctic and arctic environments. Physics and Chemistry Earth, Parts A/B/C, 2008, 33(17/18): 1081-1089. DOI:10.1016/j.pce.2008.07.007 |
| [18] |
Hrachowitz M, Savenije HHG, Blöschl G et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrological Sciences Journal, 2013, 58(6): 1198-1255. DOI:10.1080/02626667.2013.803183 |
| [19] |
Liu ZY. Research and application of flash flood forecast technology. China Flood & Drought Management, 2012, 22(2): 41-45, 50. [刘志雨. 山洪预警预报技术研究与应用. 中国防汛抗旱, 2012, 22(2): 41-45, 50.] |
| [20] |
State Flood Control and Drought Relief Headquarter, Bureau of Hydrology, MW.R. Report of flood and drought disaster in China, 2010. Beijing: China Water Power Press, 2011. [国家防汛抗旱总指挥部, 中华人民共和国水利水利部水文局. 中国水旱灾害公报2010. 北京: 中国水利水电出版社, 2011.]
|
| [21] |
Liu ZY, Hou AZ, Wang XQ. Flood forecasting for small- and medium-sized rivers based on distributed hydrological modeling. Hydrology, 2015, 35(1): 1-6. [刘志雨, 侯爱中, 王秀庆. 基于分布式水文模型的中小河流洪水预报技术. 水文, 2015, 35(1): 1-6.] |
| [22] |
Yao C, Qiu ZY, Li ZJ et al. Parameter regionalization study and application of API model and Xin'anjiang model. Journal of Hohai University: Natural Sciences, 2019, 47(3): 189-194. [姚成, 邱桢毅, 李致家等. API模型和新安江模型的参数区域化研究与应用. 河海大学学报:自然科学版, 2019, 47(3): 189-194.] |
| [23] |
Zhou L, Li ZJ, Han T. Study on the parameter regularity of Nash Unit Hydrograph based on DEM and geomorphic data. J Lake Sci, 2016, 28(5): 1141-1147. [周莉, 李致家, 韩通. 基于地形地貌资料的Nash单位线参数规律研究. 湖泊科学, 2016, 28(5): 1141-1147. DOI:10.18307/2016.0525] |
| [24] |
Prieto C, Le Vine N, Kavetski D et al. Flow prediction in ungauged catchments using probabilistic random forests regionalization and new statistical adequacy tests. Water Resources Research, 2019, 55(5): 4364-4392. DOI:10.1029/2018wr023254 |
| [25] |
Zhao RJ. Hydrological modeling of watershed. Beijing: Water Resources and Electric Power Press, 1984: 1-10. [赵人俊. 流域水文模拟:新安江模型与陕北模型. 北京: 水利电力出版社, 1984: 1-10.]
|
| [26] |
Zhao RJ. The Xin'anjiang model applied in China. Journal of Hydrology, 1992, 135(1/2/3/4): 371-381. |
| [27] |
Liu JT, Chen X, Zhang JB et al. Coupling the Xinanjiang model to a kinematic flow model based on digital drainage networks for flood forecasting. Hydrological Processes, 2009, 23(9): 1337-1348. DOI:10.1002/hyp.7255 |
| [28] |
Ju Q, Yu ZB, Hao ZC et al. Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model. Neurocomputing, 2009, 72(13/14/15): 2873-2883. DOI:10.1016/j.neucom.2008.12.032 |
| [29] |
Zhao RJ, Wang PL. Analysis of parameters of Xin'anjiang model. Journal of China Hydrology, 1988(6): 4-11. [赵人俊, 王佩兰. 新安江模型参数的分析. 水文, 1988(6): 4-11.] |
| [30] |
Zhao RJ, Wang PL. Objective optimization method of hydrological model parameters. Journal of China Hydrology, 1993, 13(4): 21-24. [赵人俊, 王佩兰. 流域水文模型参数的客观优化方法. 水文, 1993, 13(4): 21-24.] |
| [31] |
Duan QY, Gupta VK, Sorooshian S. Shuffled complex evolution approach for effective and efficient global minimization. Journal of Optimization Theory and Applications, 1993, 76(3): 501-521. DOI:10.1007/bf00939380 |
| [32] |
Ministry of Water Resources of the People's Republic of China (MWR). Standard for hydrological information and hydrological forecasting. 2008. GB/T 22482-2008. [中华人民共和国水利部.水文情报预报规范. 2008. ]
|
| [33] |
Yao C, Li ZJ, Yu ZB et al. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. Journal of Hydrology, 2012, 468/469: 47-62. DOI:10.1016/j.jhydrol.2012.08.025 |
| [34] |
Koren V, Smith M, Wang D et al. Use of soil property data in the derivation of conceptual rainfall-runoff model parameters. Proceedings of the 15th Conference on Hydrology, American Meteorological Society, Long Beach, California, 2000, 103-106. |
| [35] |
Armstrong BL. Derivation of initial soil moisture accounting parameters from soil properties for the national weather service river forecast system. NOAA Technical Memorandum, NWS HYDRO 37, 1978. |
| [36] |
Anderson RM, Koren VI, Reed SM. Using SSURGO data to improve Sacramento Model a priori parameter estimates. Journal of Hydrology, 2006, 320(1/2): 103-116. DOI:10.1016/j.jhydrol.2005.07.020 |
| [37] |
Li ZJ, Laing K, Kan GY et al. A method for deriving the river network flow concentration parameter Cs of the Xin'anjiang model. Advances in Water Science, 2016, 27(5): 652-661. [李致家, 梁珂, 阚光远等. 新安江模型中河网汇流参数Cs的一种计算方法. 水科学进展, 2016, 27(5): 652-661.] |
| [38] |
Rodríguez-Iturbe I, González-Sanabria M, Bras RL. A geomorphoclimatic theory of the instantaneous unit hydrograph. Water Resources Research, 1982, 18(4): 877-886. DOI:10.1029/wr018i004p00877 |
| [39] |
Li Q, Wen K. Study on dynamic factor-velocity in general formula of geomorphic unit line. Haihe Water Resources, 1989(1): 6-12. [李琪, 文康. 地貌单位线通用公式中动力因子——流速计算的研究. 海河水利, 1989(1): 6-12.] |
| [40] |
Bao WM. Hydrological forecast. Beijing: China Water Power Press, 2006. [包为民. 水文预报. 北京: 中国水利水电出版社, 2006.]
|
| [41] |
Zang SH, Li ZJ, Huang YC et al. Calculation method and application of river network regression coefficient Cs based on self-similarity of river network structure. J Lake Sci, 2019, 31(3): 788-800. [臧帅宏, 李致家, 黄迎春等. 基于自相似河网结构的河网消退系数Cs计算方法研究. 湖泊科学, 2019, 31(3): 788-800. DOI:10.18307/2019.0317] |
| [42] |
Blöschl G, Sivapalan M. Scale issues in hydrological modelling: A review. Hydrological Processes, 1995, 9(3/4): 251-290. DOI:10.1002/hyp.3360090305 |
| [43] |
Zhang YQ, Chiew FHS. Relative merits of different methods for runoff predictions in ungauged catchments. Water Resources Research, 2009, 45(7): 4542-4548. DOI:10.1029/2008WR007504 |
| [44] |
Kokkonen TS, Jakeman AJ, Young PC et al. Predicting daily flows in ungauged catchments: Model regionalization from catchment descriptors at the Coweeta Hydrologic Laboratory, North Carolina. Hydrological Processes, 2003, 17(11): 2219-2238. DOI:10.1002/hyp.1329 |
| [45] |
Bao ZX, Zhang JY, Liu JF et al. Comparison of regionalization approaches based on regression and similarity for predictions in ungauged catchments under multiple hydro-climatic conditions. Journal of Hydrology, 2012, 466/467: 37-46. DOI:10.1016/j.jhydrol.2012.07.048 |
| [46] |
Oudin L, Andréassian V, Perrin C et al. Spatial proximity, physical similarity, regression and ungaged catchments: a comparison of regionalization approaches based on 913 French Catchments. Water Resources Research, 2008, 44(3): 893-897. DOI:10.1029/2007WR006240 |
| [47] |
Mcintyre N, Lee H, Wheater H et al. Ensemble predictions of runoff in ungauged catchments. Water Resources Research, 2005, 41(12): W1234. DOI:10.1029/2005wr004289 |
| [48] |
Viviroli D, Mittelbach H, Gurtz J et al. Continuous simulation for flood estimation in ungauged mesoscale catchments of Switzerland-Part Ⅱ: Parameter regionalisation and flood estimation results. Journal of Hydrology, 2009, 377(1/2): 208-225. DOI:10.1016/j.jhydrol.2009.08.022 |
| [49] |
Xu C. Testing the transferability of regression equations derived from small sub-catchments to a large area in central Sweden. Hydrology and Earth System Sciences, 2003, 7(3): 317-324. DOI:10.5194/hess-7-317-2003 |
| [50] |
Young AR. Stream flow simulation within UK ungauged catchments using a daily rainfall-runoff model. Journal of Hydrology, 2006, 320(1/2): 155-172. DOI:10.1016/j.jhydrol.2005.07.017 |
| [51] |
Seibert J. Regionalisation of parameters for a conceptual rainfall-runoff model. Agricultural and Forest Meteorology, 1999, 98/99: 279-293. DOI:10.1016/s0168-1923(99)00105-7 |
| [52] |
Parajka J, Merz R, Blöschl G. A comparison of regionalisation methods for catchment model parameters. Hydrology and Earth System Sciences, 2005, 9(3): 157-171. DOI:10.5194/hess-9-157-2005 |
| [53] |
Xu C. Estimation of parameters of a conceptual water balance model for ungauged catchments. Water Resources Management, 1999, 13(5): 353-368. DOI:10.1023/A:1008191517801 |
| [54] |
Bárdossy A. Calibration of hydrological model parameters for ungauged catchments. Hydrology and Earth System Sciences Discussions, 2006, 3(3): 1105-1124. DOI:10.5194/hessd-3-1105-2006 |
| [55] |
Kursa MB, Rudnicki WR. Feature selection with the Boruta Package. Journal of Statistical Software, 2010, 36(11). DOI:10.18637/jss.v036.i11 |
| [56] |
Breiman L. Random Forests. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/a:1010933404324 |
| [57] |
Breiman L. Bagging predictors. Machine Learning, 1996, 24(2): 123-140. DOI:10.1007/bf00058655 |
| [58] |
Freund Y, Schapire RE. A desicion-theoretic generalization of on-line learning and an application to boosting. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 1995: 23-37. DOI:10.1007/3-540-59119-2_166
|
| [59] |
Wolpert D, Macready W. An efficient method to estimate bagging's generalization error. Machine Learning, 1999, 35(1): 41-55. DOI:10.1023/A:1007519102914 |
| [60] |
Kursa MB, Jankowski A, Rudnicki WR. Boruta—A system for feature selection. Fundamenta Informaticae, 2010, 101(4): 271-285. DOI:10.3233/fi-2010-288 |
| [61] |
Sefton C, Howarth S. Relationships between dynamic response characteristics and physical descriptors of catchments in England and Wales. Journal of Hydrology, 1998, 211(1/2/3/4): 1-16. DOI:10.1016/s0022-1694(98)00163-2 |
| [62] |
Seibert J. Regionalisation of parameters for a conceptual rainfall-runoff model. Agricultural and Forest Meteorology, 1999, 98/99: 279-293. DOI:10.1016/s0168-1923(99)00105-7 |
| [63] |
Peel M, Chiew F, Western A et al. Extension of unimpaired monthly streamflow data and regionalisation of parameter values to estimate streamflow in ungauged catchments. National Land and Water Resources Audit Theme 1-Water Availability Extension, 2000(July): 1-37. |
| [64] |
Bárdossy A, Pegram GGS, Samaniego L. Modeling data relationships with a local variance reducing technique: Applications in hydrology. Water Resources Research, 2005, 41(8). DOI:10.1029/2004wr003851 |
| [65] |
Lamb R, Kay AL. Confidence intervals for a spatially generalized, continuous simulation flood frequency model for Great Britain. Water Resources Research, 2004, 40(7). DOI:10.1029/2003wr002428 |
| [66] |
Castellarin A, Burn DH, Brath A. Assessing the effectiveness of hydrological similarity measures for flood frequency analysis. Journal of Hydrology, 2001, 241(3/4): 270-285. DOI:10.1016/s0022-1694(00)00383-8 |
| [67] |
Institute of Hydrology (IH). Flood Estimation Handbook. UK: Wallingford, 1999.
|
| [68] |
Samaniego L, Bárdossy A. Robust parametric models of runoff characteristics at the mesoscale. Journal of Hydrology, 2005, 303(1/2/3/4): 136-151. DOI:10.1016/j.jhydrol.2004.08.022 |
| [69] |
Kirkby M, Beven K. A physically based, variable contributing area model of basin hydrology. Hydrological Sciences Journal, 1979, 24(1): 43-69. DOI:10.1080/02626667909491834 |
| [70] |
Yong B, Zhang WC, Liu CS. Analysis of the variation of topographic index spatial scale based on the modified multiple flow direction algorithm. Scientia Geographica Sinica, 2007, 27(5): 683-688. [雍斌, 张万昌, 刘传胜. 基于改进型多流向算法的地形指数空间尺度变化分析. 地理科学, 2007, 27(5): 683-688. DOI:10.3969/j.issn.1000-0690.2007.05.013] |
| [71] |
Peñas FJ, Barquín J, Snelder TH et al. The influence of methodological procedures on hydrological classification performance. Hydrology and Earth System Sciences Discussions, 2014, 11(1): 945-985. DOI:10.5194/hessd-11-945-2014 |
| [72] |
Viviroli D, Zappa M, Schwanbeck J et al. Continuous simulation for flood estimation in ungauged mesoscale catchments of Switzerland-Part Ⅰ: Modelling framework and calibration results. Journal of Hydrology, 2009, 377(1/2): 191-207. DOI:10.1016/j.jhydrol.2009.08.023 |
| [73] |
Liaw A, Wiener M. Classification and regression by Random Forest. J Food Quality, 2002, 2(3): 18-22. |
 2021, Vol. 33
2021, Vol. 33 


