(2: 金华市水利水电勘测设计院有限公司, 金华 321017)
(3: 水资源安全保障湖北省协同创新中心, 武汉 430072)
(4: 南京水利科学研究院, 水文水资源与水利工程科学国家重点实验室, 南京 210029)
(2: Jinhua Survey and Design Institute of Water Conservancy and Hydropower Co., LTD., Jinhua 321017, P. R. China)
(3: Hubei Provincial Collaborative Innovation Center for Water Resources Security, Wuhan 430072, P. R. China)
(4: State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, P. R. China)
设计洪水是防洪工程布局与规模选择的重要依据[1],也是进行洪水调度的重要基础.基于降水或径流极值序列进行水文频率分析,是目前计算设计洪水的常用方法.水文极值序列满足独立同分布是应用水文频率分析的前提条件[2-3].然而,在气候变化及人类活动的双重影响下,流域下垫面的产汇流条件和洪水的时空分布发生了改变,导致场次洪水的产汇流条件在不同时期存在不同的特征,从而使得水文极值序列不再具有一致性,水文频率分析一致性假定的前提产生了动摇,引发基于统计原理计算的设计洪峰和时段洪量等设计参数的可靠性下降[4-5].因此,迫切需要开展样本非一致性条件下的设计洪水修订研究,为水利工程的规划设计、施工及运行管理提供科学依据.
洪水事件作为一种随机水文事件,频率分析是设计洪水研究的核心内容,变化环境下非一致性洪水频率分析已成为当前水文科学的前沿问题[6-10].目前,国内非一致性水文序列频率计算方法以基于还原或还现途径为主,包括降雨径流相关分析法、时间序列分解与合成法和水文模型法等,是目前国内应用较为广泛的方法.如丛娜等[11]对海河流域王快水库的降水和洪峰序列进行了变化趋势和突变特征分析,建立了变异点前后不同时期的降雨径流关系和峰量关系,从而实现了洪水序列的一致性修订; 韩瑞光等[12]采用河北雨洪模型修正了大清河阜平站控制流域设计洪水成果,探讨了下垫面变化对流域洪水的影响; 钟栗等[13]采用新安江-海河模型,分析计算了1980年前后卫河流域自由水蓄水容量等4种模型参数的变化情况,并对设计洪量进行了修订; 姚成等[14]基于新安江-海河水文模型研究了下垫面变化对合河流域设计洪水的影响,并利用径流深的模拟结果修订了设计洪水.近年来,国外学者提出了基于非平稳序列的直接水文频率分析方法,如时变矩法、混合分布法、条件概率分布法等. Singh等[15]提出混合分布模型并应用于非一致性洪水频率的计算,取得较好效果. Strupczewski等[6]提出一种考虑统计参数均值和方差趋势性的时变矩非一致性洪水频率分析方法,从而计算得到随时间变化的设计值;Singh等[16]将条件概率分布模型应用到年内季节洪水序列的频率分析.总的来说,不同的方法有不同的适用条件和优缺点,如降雨径流相关法可以对过去、现在不同时期水文极值序列进行一致性修正,但无法反映水文序列未来的变化情况[5]; 分解与合成法在预测期较长的情况下,现有的确定性成分预测方法存在较大外延风险[5]; 水文模型法通过模型参数反映不同时期下垫面的变化,从而达到洪水序列还原/还现目的,但基于集总式水文模型的传统水文还原方法存在失真与失效问题; 基于非一致性洪水序列的直接水文频率分析方法虽已取得一些成果[17-20],但对水文过程的物理机制考虑较少[21]. SWAT(soil and water assessment tool)模型是美国农业部农业研究局开发的分布式流域水文模型,具有很强的物理基础,已被广泛应用于变化环境对流域水文过程影响的模拟与预测[22-23].与传统的集总式水文模型相比,SWAT分布式水文模型能够客观反映降水和下垫面条件空间不均性引起的产汇流过程变化,是非一致性条件下的水文过程模拟的有效方法.因此,本文利用SWAT模型模拟下垫面变化对洪水过程的影响,根据径流深的模拟结果对各设计洪水特征值进行一致性修订,为变化环境下流域设计洪水修订提供新的思路.
淮河流域地处我国南北气候的过渡地带,降水时空分布不均匀,洪涝灾害发生频繁. 20世纪以来,淮河流域发生了1921、1931、1954、1991和2007年流域性大洪水.近几10年来,由于流域大规模的水利工程、水土保持工程建设以及土地利用变化,导致流域下垫面及产汇流机制发生了显著变化,对径流及设计洪水计算成果产生了明显影响,破坏了流域洪水系列的一致性.目前,在淮河流域开展的研究侧重土地利用变化对设计洪水影响以及洪水极值非平稳性特征分析方面[24-25],而对非一致性设计洪水进行修订方面的研究尚不多见.鉴于此,本文将具有物理机制的SWAT模型引入淮河上游流域,重建具有一致性的洪水系列,修订设计洪水成果,为流域防洪规划和防灾减灾提供科学依据.
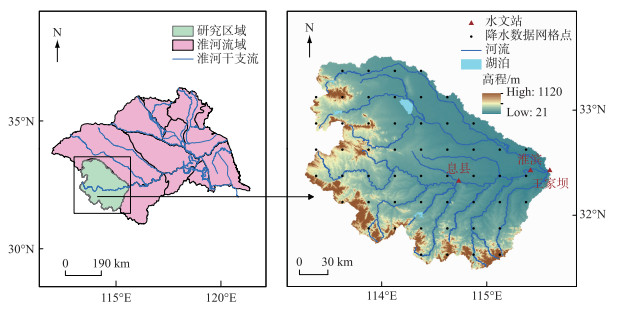
1 研究区域与数据来源 1.1 研究区域概况淮河流域(31°55′~36°36′N,111°55′~120°25′E)位于中国东部,介于长江与黄河流域之间,流域面积约为27×104 km2.淮河西起桐柏山,干流流经河南、安徽、江苏三省,全长1000 km.淮河流域属暖温带半湿润季风气候区,多年平均年降水量约920 mm.降水年内时空分配不均,冬季和春季干旱少雨,夏季和秋季炎热多雨;空间差异上,南部降水多而北部降水少,同纬度山区降水量多于平原.流域的西部、西南部和东北部是山地与丘陵地区,其余为平原,约占总面积的2/3.王家坝以上为淮河上游,王家坝至中渡为淮河中游,中渡以下为淮河下游,本文以淮河上游流域为研究区域,控制流域面积30630 km2,选择干流上的息县、淮滨和王家坝3个控制站,分别进行设计洪水修订.研究区及主要水文站位置如图 1所示.
|
图 1 研究区及主要水文站位置 Fig.1 Locations of study area and hydrological stations |
本文采用的数据包括水文、气象、数字高程模型(DEM)、土地利用、土壤等.各类数据的描述和来源如表 1所示.
| 表 1 数据描述及来源 Tab. 1 Description and source of data |
采用Mann-Kendall检验法(简称M-K法)、线性倾向估计法和滑动平均法分析年最大洪峰序列的变化趋势,运用Pettitt检验法和滑动t检验法检验洪水序列的突变特征. M-K法作为非参数的检验方法,不要求样本满足某种分布,不受少数异常值的干扰,具有计算相对简单、检测范围广的优点,因此广泛应用于水文序列趋势分析[26].采用M-K趋势检验时,统计量|Z|≥1.96、2.32时,分别表示通过了置信度95%、99%的显著检验,且Z为正值和负值时分别表示上升和下降趋势.线性倾向估计法是建立径流量与时间之间的一元线性回归方程,线性回归方程的斜率k大于0,表示径流量随时间呈增加趋势,反之,表示减少趋势; 滑动平均是用平均值来显示时间序列变化趋势的方法,它相当于低通滤波器[27]. Pettitt检验法是一种常用的非参数突变检验方法,其原理是通过检验时间序列均值变化的时间来确定系列跳跃变化的时间点[28].为了提高突变检测的可靠性,同时采用滑动t检验法[27]对洪水序列进行突变检验,并取两种检验方法相对一致的变异点作为突变年份.
2.2 SWAT模型 2.2.1 基础数据库构建SWAT模型是以日为步长进行连续模拟,能够用于流域尺度的水文过程模拟.构建SWAT模型需要处理地理空间数据和属性数据两种类型的数据,前者包括DEM、土地利用类型和土壤类型等,后者包括土壤数据库、土地利用数据库和气象水文数据库等.
1) 空间数据:利用ArcGIS对DEM原始数据进行拼接、投影变换、填洼、流向分析和流域提取,得到淮河上游流域(王家坝以上)的数字高程模型.
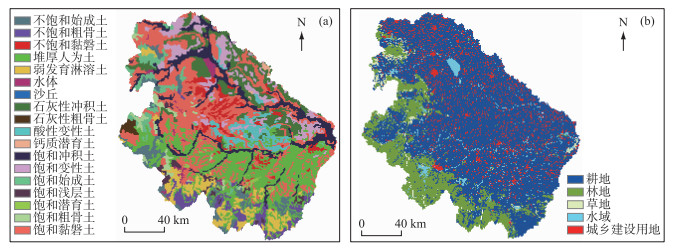
2) 土壤数据库:土壤数据库包括土壤类型数据和土壤属性数据.本文采用的HWSD数据是由栅格图和与之相关联的Access格式的属性数据库组成.在ArcGIS软件中加载原始土壤类型数据后,对其进行投影、裁剪和重分类等操作,得到研究区的土壤类型图(图 2a).由于SWAT模型内置的土壤属性数据库中只适用于北美地区,需要针对土壤数据库文件进行修改.由于本文只考虑流域的水文过程,不考虑水质等问题,因此只需修改土壤的物理属性参数.
|
图 2 淮河上游流域土壤类型和土地利用类型 Fig.2 Soil types and land use types in the upper Huaihe River Basin |
3) 土地利用数据库:本文使用的土地利用数据是中国科学院制定的两级分类系统,土地利用类型被分为水田、旱地、灌木林和城镇用地等多达16种类型,与SWAT模型内采用的由美国地质调查局指定的分类系统不一致.因此在使用ArcGIS软件对原始土地利用数据进行镶嵌拼接、投影转换和裁剪等处理后,利用Reclass模块进行重分类,将研究区的土地利用类型分为耕地、林地、草地、水域和城乡建设用地5种类型(图 2b).
4) 气象数据库:SWAT模型需要逐日降水量、最高和最低气温、相对湿度、平均风速和太阳辐射数据.这些数据可以是实测数据,也可以根据逐月数据等参数由天气发生器获得.由于气象数据中降水和气温的数据对SWAT模型的模拟影响相对更大,因此日降水、最高和最低气温采用实测数据,其他所需气象数据采用CFSR天气发生器模拟生成.
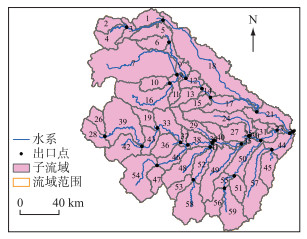
2.2.2 子流域划分首先基于流域DEM生成河网水系并进行子流域划分,然后根据土地利用、土壤和坡度等下垫面特征将各个子流域分成若干水文响应单元(HRUs).参考研究区实际情况并兼顾模型计算速度,设定最小集水面积阈值为300 km2,选择王家坝站为流域出口断面,将淮河上游流域共划分了59个子流域,如图 3所示.本文采用每个子流域划分多个HRUs的方法,根据子流域内不同土地利用、土壤和坡度占相应子流域的比例,分别设置土地利用、土壤和坡度类型的面积阈值为10%、15%和10%,最终将淮河上游流域生成427个HRUs.
|
图 3 淮河上游流域子流域划分 Fig.3 Sub-basins of the upper Huaihe River Basin |
为降低率定参数的盲目性,提高模型运行效率和模拟结果精度,需要对SWAT模型参数进行敏感性分析.本文采用SWAT模型自带的LH-OAT方法进行参数敏感性分析,该方法综合了LH(latin hypercube)抽样法和OAT(one-factor-at-a-time)敏感性分析法的优点,准确性较高.
选用SWAT-CUP的优化算法SUFI-2(sequential uncertainty fitting algorithm,ver. 2)进行参数的全局敏感性分析以及自动率定. SUFI-2是一种反演建模法.通过迭代计算确定最佳的模型参数范围.同时,选取常用的确定性系数(R2)和Nash-Sutcliffe系数(NSE)作为评价模型模拟结果好坏的指标.
2.3 设计洪水修订方法本文利用径流深R的预报结果对洪峰流量Q进行修订,具体过程如下[14]:
1) 选取1960-2010年淮河干流上游实测R与实测Q资料,点绘R与Q的相关关系图,根据它们的相关关系判断采用径流深的预报结果对洪峰流量进行修订的可行性.
2) 根据洪水变异诊断结果得到一致性变化前、后的2个洪水序列,分别通过参数率定得到2组SWAT模型参数,然后采用变化后的模型参数模拟变化前的洪水,由此计算得到变化前后预报径流深的相对变化幅度η:
| $ \eta =\left( {{R}_{2}}-{{R}_{1}} \right)/{{R}_{1}} $ | (1) |
式中,R1、R2分别表示变化前、后的参数模拟的径流深预报值,mm.
3) 将变化前的实测洪水径流深进行无量纲化,得到(0,1]区间的值α:
| $ \alpha =R/{{R}_{\max }} $ | (2) |
式中,R表示场次洪水实测径流深,mm;Rmax表示最大场次洪水实测径流深,mm.
同样的,对洪峰流量也进行归一化处理,得到相对的洪峰流量值β:
| $ \beta =Q/{{Q}_{\max }} $ | (3) |
式中,Q表示需要修订的洪峰流量,m3/s;Qmax表示洪峰流量最大值,m3/s.
4) 建立η~α的相关关系曲线图,然后把计算得到的β作为η~α曲线图的纵坐标,查询对应的横坐标值μ,则修订后的洪峰流量值为:
| $ {{Q}_{修}}=Q\left( 1-\mu \right) $ | (4) |
不同时段洪量的修订方法与洪峰流量的类似,将式(3)和式(4)中的洪峰流量Q替换为对应的洪量指标即可.
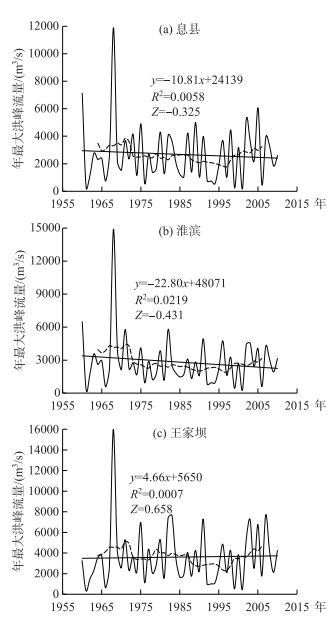
3 结果分析 3.1 洪峰流量变化趋势与突变检验结果图 4为1960-2010年淮河上游干流的息县、淮滨和王家坝站年最大洪峰序列的变化趋势.从图 4可以看出,息县和淮滨站的年最大洪峰序列在1960-2010年间整体上均呈现不显著的减少趋势,而王家坝站的年最大洪峰序列在整体上呈现不显著的增加趋势; 通过9年滑动平均曲线可以看出,3个站均以1990s中期为界,分别在该时间点以前呈现减小趋势,其后则呈现增加趋势.
|
图 4 1960-2010年淮河上游3个水文站年最大洪峰流量的变化趋势(折线为年际变化,斜线为线性趋势,虚线为9年滑动平均) Fig.4 The change trend in annual maximum peak discharge at three stations in the upper Huaihe River during 1960-2010 |
采用滑动t检验法和Pettitt法综合检测各站年最大洪峰系列的突变点,结果如表 2所示.从滑动t检验法的结果来看,王家坝站在1991年出现了明显的突变情况,并且达到了95%的显著性水平,而息县和淮滨站的突变点也出现在1991年,但并未达到95%的显著性水平.同时,Pettitt检验法的结果显示,息县站的突变点为1991年,与滑动t检验法的检验结果一致,并且达到了95%的显著性水平;淮滨站的突变点为1975年,达到了95%的显著性水平,1991年也是可能的突变点,但是未达到95%的显著性水平; 王家坝站的突变点为1968年,由于1968年是特大值点,应该排除该变异点,在排除该变异点后,可能的变异点为1985年和1991年,但是未达到95%的显著性水平.综上所述,2种方法均检测到3个站的年最大洪峰系列在1991年发生了突变,这可能由于1991年前后人类活动导致淮河上游流域下垫面发生明显变化,导致流域洪水形成过程受到了影响.
| 表 2 淮河上游3个水文站的年最大洪峰流量突变检验结果 Tab. 2 Breakpoints of annual maximum peak discharge at three stations in the upper Huaihe River |
选取对模拟结果影响比较敏感的参数进行自动率定,所选参数的敏感性分析及率定结果如表 3所示.由表 3可以看出,基流退水常数、SCS径流曲线系数、主河道水力传导度等参数最为敏感.由此可见,研究区域径流产生及模拟受地下径流变化、土壤状况和地表水与地下水转换过程的影响较大.
| 表 3 参数敏感性分析和率定的结果 Tab. 3 The results of parameters sensitivity analysis and their calibration |
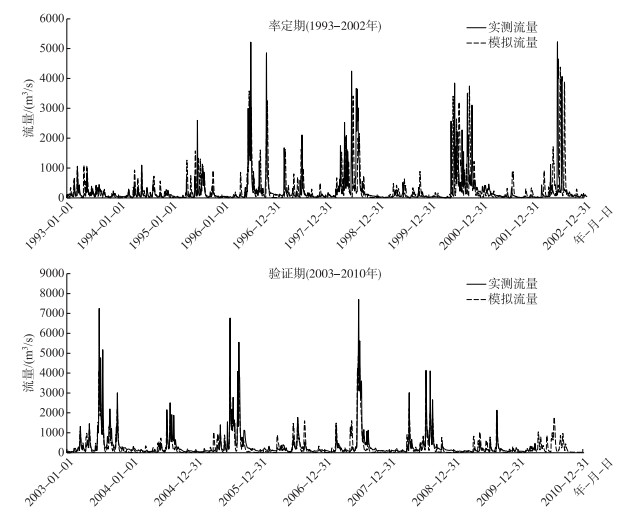
本文选定1992年为模型预热期,1993-2002年为率定期,2003-2010年为验证期. 图 5为SWAT模型在王家坝站率定期和验证期的模拟结果. 图 5显示,洪水过程线的模拟值与实测值变化趋势基本吻合,但汛期的洪峰流量模拟效果不甚理想.由3个站在率定期和验证期的确定性系数R2和NSE系数的结果可知,率定期3个站的R2与NSE的值均大于0.6,表明率定期洪水模拟精度较高;验证期除了息县站的R2与NSE的值为0.58以外,其他站点的R2与NSE值均大于0.65,表明验证期洪水模拟值与实测值基本吻合,微劣于率定期(表 4).从空间上来看,息县站的模拟效果稍逊于淮滨和王家坝站,原因可能是息县站以上为山溪性河流,洪水过程具有峰形尖瘦、陡涨陡落的特点,增加了水文模拟的不确定性.总之,从洪水过程模拟结果和评价指标值来看,3个站的洪水模拟效果整体较好,R2与NSE的值均高于评价标准,表明SWAT模型可以模拟淮河上游的洪水过程.
|
图 5 淮河上游流域王家坝站实测流量与模拟流量比较 Fig.5 Comparison of observed and simulated runoff at Wangjiaba Station in the upper Huaihe River Basin |
| 表 4 淮河上游流域3个水文站的洪水模拟结果评价 Tab. 4 Evaluation of flood simulation results at three hydrological stations in the upper Huaihe River Basin |
由于洪水过程历时相对较短,SWAT模型难以精细模拟日以下尺度的洪水事件.为避免现有模型的不足,本文将日平均流量近似处理为日最大洪峰流量,采用同一组参数对SWAT模型进行率定,利用模型模拟1993-2010年连续18年的日平均流量序列,并划分洪水场次,将日平均流量模拟值作为历年18场洪水的洪峰流量及相应的径流深模拟结果.
根据淮河上游历史洪水资料,选取息县、淮滨和王家坝站1993-2010年共18场洪水模拟结果进行误差分析,得到各站点洪峰流量和径流深的模拟统计结果,如表 5和表 6所示.结果显示,SWAT模型对于洪水径流深R的模拟效果要明显好于洪峰流量Q.根据《水文情报预报规范(GB/T 22482-2008) 》,模型在息县和王家坝站的径流深模拟达到了乙级标准,在淮滨站达到了丙级标准,参数率定的精度基本符合要求.洪峰流量模拟效果稍差的原因可能是SWAT模型没有考虑水利工程调蓄的影响,同时所选的历史洪水中多峰洪水较多,多峰洪水过程较复杂,模拟难度较高,因此导致整体洪峰流量模拟精度较低,合格率不高.由于径流深R的模拟结果较好,合格率较高,因此选择径流深R的模拟结果对淮河上游流域洪水的一致性进行修订.
| 表 5 王家坝站洪峰流量和径流深的模拟结果 Tab. 5 Simulation results of peak discharge and runoff depth at Wangjiaba Station |
| 表 6 淮河上游流域3个水文站洪水模拟的合格率 Tab. 6 The qualified rate of flood simulation in three hydrological stations in the upper Huaihe River Basin |
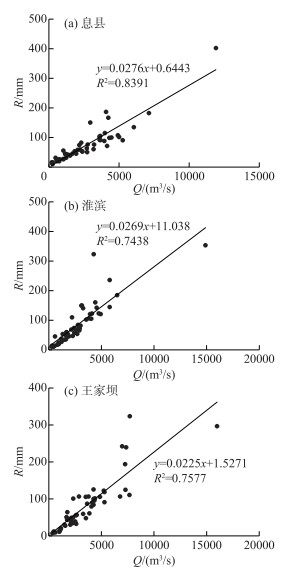
图 6为息县、淮滨和王家坝站1960-2010年的实测径流深R与实测洪峰流量Q的线性相关拟合曲线, 可以看出R与Q存在较好的线性相关关系,3个站拟合关系的确定性系数R2分别达到0.84、0.74和0.76,这表明两变量存在较为显著的相关关系.因此,使用R的预报结果对Q进行修订是可行的.
|
图 6 径流深与洪峰流量的相关关系 Fig.6 The relationship between runoff depth and peak discharge |
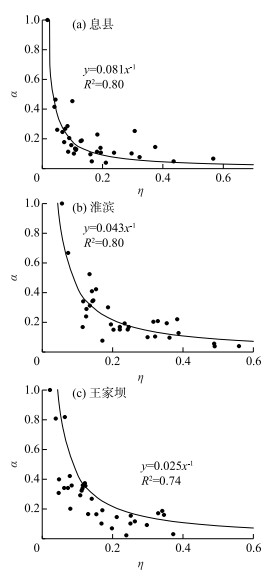
各站点相对实测径流深α与相对修订幅度η的拟合曲线如图 7所示.拟合曲线线型采用反比例函数,采用确定性系数评估拟合效果.由图 7可知,3个站拟合曲线的R2均大于0.7,因此拟合程度满足精度要求,可以进一步用于洪峰流量的修订.
|
图 7 相对实测径流深α与相对修订幅度η拟合曲线 Fig.7 The fitting curve of relative observed runoff depth α and relative revision range η |
首先根据历史洪水序列变异时间点将各站点水文序列划分为基准期(1960-1991年)和变异期(1992-2010年)两个时期,然后根据变异期的SWAT模型参数模拟基准期的洪水,最后利用式(1)~ (4)对洪峰流量和不同时段洪量进行修订,并对修订前后的洪水序列进行频率分析.本文采用皮尔逊Ⅲ型曲线作为频率分析的分布线型,其中频率曲线参数采用适线法进行估计,并将矩法估计值作为初始值.由于目估适线法主观性成分较大,为了减小目估适线法带来的误差,这里采用确定性系数最大作为最优理论频率曲线的选择标准.通过理论频率曲线,得到各站洪峰流量与不同时段洪量修订前、后的设计洪水成果,如表 7所示.
| 表 7 淮河上游流域3个水文站设计洪水修订成果* Tab. 7 Revision results of design flood of three hydrological stations in the upper Huaihe River Basin |
由表 7可知,洪峰流量修订的幅度与洪峰流量的大小呈负相关关系,即洪峰流量大的洪水修订幅度小, 洪峰流量小的洪水修订幅度大,这可能是由于发生大洪水时的流域下垫面的影响相对较小,相应的洪峰流量修订幅度也相对较小.同时,淮河上游洪水设计值较修订前略有减小.其中,洪峰流量减小幅度平均值在3.3%~6.1%之间,淮滨站的减小幅度最大;不同时段洪量的减小幅度平均值在1.4%~2.7%之间,整体修订幅度小于洪峰流量的修订幅度,并且洪量的时段越长,修订幅度越小;随着重现期的增大,各洪水指标的修订幅度逐渐减小,这表明了变化环境下淮河上游流域洪峰流量和洪量在不同频率下的设计值均有减小趋势,而小洪水较大洪水减少得更多.同时也揭示了流域下垫面对洪水的调蓄作用在小洪水中更加明显.另外,基于SWAT模型重建流域洪水序列考虑了流域下垫面变化的径流量效应,导致各站修订之后的设计值均呈现减少趋势.
4 结论与讨论本文以淮河上游流域为研究对象,采用SWAT分布式水文模型构建一致性洪水序列,对变异前的洪峰与洪量序列进行还现,得到了具有一致性的洪水序列和修订后的设计洪水.主要结论如下:
1) 采用Mann-Kendall检验法、线性倾向估计、滑动t检验法和Pettitt法分析了淮河上游流域年最大洪峰流量序列的变化趋势和突变特征.结果表明,息县和淮滨站年最大洪峰流量呈现不显著的减小趋势,王家坝站则表现出不显著增加趋势; 各站年最大洪峰流量序列在1991年发生突变,将洪水系列分为1991年前、后两个部分.
2) 基于淮河上游流域的DEM、土壤、土地利用、气象水文等数据,建立了SWAT流域水文模型,并采用SWAT-CUP软件对模型参数进行率定、验证和敏感性分析.结果显示,息县站R2和NSE相对其他站点略低,淮滨和王家坝站的率定期和验证期的R2和NSE值均大于0.65,表明模型在淮河上游流域洪水模拟具有较好的适用性.
3) 采用径流深的模拟结果对洪峰和洪量进行修订,并对修订前后的洪水序列进行频率分析.结果表明,由于气候和下垫面的变化,淮河上游洪水设计值较修订前略有减小,其中,洪峰流量减小幅度平均值在3.3%~6.1%之间,淮滨站的减小幅度最大; 不同时段洪量的减小幅度平均值在1.4%~2.7%之间,整体修订幅度小于洪峰流量的修订幅度,并且洪量的时段越长,修订幅度越小;随着重现期的增大,各洪水指标的修订幅度逐渐减小.
4) 土地利用变化、水利工程建设等人类活动改变了流域洪水过程,增加了SWAT模型在淮河上游流域洪水模拟的不确定性,但由于受资料所限,模型中没有增加水库模块,这可能会降低模型模拟的精度.同时,为避免现有模型的不足,本文将各站日平均流量近似处理为日最大洪峰流量,利用SWAT模型模拟各站场次洪水的洪峰流量及时段径流深,最后采用径流深的模拟结果对各站设计洪水特征值进行修订.将来可以考虑采用分布式VIC、DHSVM等水文模型,提高日以下时段洪水模拟效果,并采用洪峰流量的模拟结果直接对设计洪水进行修订,从而提高计算成果的精度.另外,由于资料所限,实测洪水序列中没有加入历史洪水进行频率计算,这也可能会降低设计洪水成果的精度和稳定性.
| [1] |
Guo SL, Liu ZJ, Xiong LH. Advances and assessment on design flood estimation methods. Journal of Hydraulic Engineering, 2016, 47(3): 302-314. [郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价. 水利学报, 2016, 47(3): 302-314.] |
| [2] |
Koutsoyiannis D, Montanari A. Statistical analysis of hydroclimatic time series: Uncertainty and insights. Water Resource Research, 2007, 43: W05429. DOI:10.1029/2006WR005592 |
| [3] |
Milly PCD, Betancourt J, Falkenmark M et al. Stationarity is dead: Whither water management?. Science, 2008, 319(5863): 573-574. DOI:10.1126/science.1151915 |
| [4] |
Schmocker-Fackel P, Naef F. More frequent flooding? Changes in flood frequency in Switzerland since 1850. Journal of Hydrology, 2010, 381(1/2): 1-8. DOI:10.1016/j.jhydrol.2009.09.022 |
| [5] |
Liang ZM, Hu YM, Wang J. Advances in hydrological frequency analysis of non-stationary time series. Advances in Water Science, 2011, 22(6): 864-871. [梁忠民, 胡义明, 王军. 非一致性水文频率分析的研究进展. 水科学进展, 2011, 22(6): 864-871.] |
| [6] |
Strupczewski WG, Singh VP, Feluch W. Non-stationary approach to at-site flood frequency modelling I. Maximum likelihood estimation. Journal of Hydrology, 2001, 248(1/2/3/4): 123-142. DOI:10.1016/s0022-1694(01)00397-3 |
| [7] |
Song SB, Li Y, Cai MK. Methods of frequency analysis for hydrologic data with jump up components. Journal of Hydraulic Engineering, 2012, 43(6): 734-739, 748. [宋松柏, 李扬, 蔡明科. 具有跳跃变异的非一致分布水文序列频率计算方法. 水利学报, 2012, 43(6): 734-739, 748.] |
| [8] |
Ishak EH, Rahman A, Westra S et al. Evaluating the non-stationarity of Australian annual maximum flood. Journal of Hydrology, 2013, 494: 134-145. DOI:10.1016/j.jhydrol.2013.04.021 |
| [9] |
Feng P, Li X. Bivariate frequency analysis of non-stationary flood time series based on Copula methods. Journal of Hydraulic Engineering, 2013, 44(10): 1137-1147. [冯平, 李新. 基于Copula函数的非一致性洪水峰量联合分析. 水利学报, 2013, 44(10): 1137-1147.] |
| [10] |
Xie P, Wu ZY, Zhao JY et al. Gene method for inconsistent hydrological frequency calculation Ⅰ: Inheritance, variability and evolution principles of hydrological genes. Chinese Journal of Applied Ecology, 2018, 29(4): 1023-1032. [谢平, 吴子怡, 赵江艳等. 非一致性水文频率计算的基因途径Ⅰ:水文基因遗传、变异和进化原理. 应用生态学报, 2018, 29(4): 1023-1032.] |
| [11] |
Cong N, Feng P. Revision on reservoir inflow design flood under the variation impact of underlying surface. South-to-North Water Transfers and Water Science & Technology, 2014, 12(2): 6-10. [丛娜, 冯平. 流域下垫面变化影响下入库设计洪水的修订. 南水北调与水利科技, 2014, 12(2): 6-10.] |
| [12] |
Han RG, Feng P. Effects of sublayer and land-cover change on flood in Daqinghe River Basin. Journal of Arid Land Resources and Environment, 2010, 24(8): 27-30. [韩瑞光, 冯平. 流域下垫面变化对洪水径流影响的研究. 干旱区资源与环境, 2010, 24(8): 27-30.] |
| [13] |
Zhong L, Yao C, Li ZJ et al. Effect of land surface changes on design flood using Xin'anjiang-Haihe Model. J Lake Sci, 2015, 27(5): 975-982. [钟栗, 姚成, 李致家等. 应用新安江-海河模型研究下垫面变化对设计洪水的影响. 湖泊科学, 2015, 27(5): 975-982. DOI:10.18307/2015.0525] |
| [14] |
Yao C, Sun RF, Li ZJ et al. Study of the effect of underlying surface change on design floods of Hehe River Basin. Water Power, 2015, 41(11): 9-13. [姚成, 孙如飞, 李致家等. 下垫面变化条件下合河流域设计洪水修订. 水力发电, 2015, 41(11): 9-13. DOI:10.3969/j.issn.0559-9342.2015.11.003] |
| [15] |
Singh KP, Sinclair RA. Two-distribution method for flood-frequency analysis. Journal of Hydraulics Division, 1972, 98(1): 28-44. |
| [16] |
Singh VP, Wang SX, Zhang L. Frequency analysis of nonidentically distributed hydrologic flood data. Journal of Hydrology, 2005, 307(1/2/3/4): 175-195. |
| [17] |
Cheng JQ, Song SB. Calculation of hydrological frequency parameters of inconsistent annual runoff series based on mixed distribution. Journal of Northwest A & F University: Natural Science Edition, 2010, 38(2): 229-234. [成静清, 宋松柏. 基于混合分布非一致性年径流序列频率参数的计算. 西北农林科技大学学报:自然科学版, 2010, 38(2): 229-234.] |
| [18] |
Feng P, Zeng H, Li X. Non-stationary flood-frequency analysis based on mixed distribution. Journal of Tianjin University: Science and Technology Edition, 2013, 46(4): 298-303. [冯平, 曾杭, 李新. 混合分布在非一致性洪水频率分析的应用. 天津大学学报:自然科学与工程技术版, 2013, 46(4): 298-303.] |
| [19] |
Li LJ, Kang Y, Song SB et al. Application of conditional probability model in frequency calculation of incoherent hydrologic series. Journal of Northwest A & F University: Natural Science Edition, 2016, 44(8): 119-125. [李伶杰, 康艳, 宋松柏等. 条件概率模型在非一致性水文序列频率计算中的应用. 西北农林科技大学学报:自然科学版, 2016, 44(8): 119-125.] |
| [20] |
Liu BJ, Qiu KH, Liao YY. Non-stationary flood frequency analysis of North and West River Delta with time-varying moments. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(4): 130-135. [刘丙军, 邱凯华, 廖叶颖. 基于TVM的西北江三角洲地区非一致性洪水频率分析. 中山大学学报:自然科学版, 2016, 55(4): 130-135.] |
| [21] |
Xiong LH, Jiang C, Du T et al. Review on nonstationary hydrological frequency analysis under changing environments. Journal of Water Resources Research, 2015, 4(4): 310-319. [熊立华, 江聪, 杜涛等. 变化环境下非一致性水文频率分析研究综述. 水资源研究, 2015, 4(4): 310-319.] |
| [22] |
Guo JT, Zhang ZQ, Wang SP et al. Appling SWAT model to explore the impact of changes in land use and climate on the streamflow in a Watershed of Northern China. Acta Ecologica Sinica, 2014, 34(6): 1559-1567. [郭军庭, 张志强, 王盛萍等. 应用SWAT模型研究潮河流域土地利用和气候变化对径流的影响. 生态学报, 2014, 34(6): 1559-1567. DOI:10.5846/stxb201304190746] |
| [23] |
Meaurio M, Zabaleta A, Uriarte JA et al. Evaluation of SWAT models performance to simulate streamflow spatial origin. The case of a small forested watershed. Journal of Hydrology, 2015, 525: 326-334. DOI:10.1016/j.jhydrol.2015.03.050 |
| [24] |
Wu M, Shi P, Sun Y et al. Research on the influence of land use change on the design flood of small basins in the upper reaches of Huaihe River. Journal of Xi'an University of Technology, 2015, 31(3): 366-373. [吴淼, 石朋, 孙勇等. 土地利用变化对淮河上游小流域设计洪水的影响研究. 西安理工大学学报, 2015, 31(3): 366-373. DOI:10.3969/j.issn.1006-4710.2015.03.020] |
| [25] |
Sun P, Sun YY, Zhang Q et al. Evaluation on non-stationarity assumption of annual maximum peak flows during 1956-2016 in the Huaihe River Basin. J Lake Sci, 2018, 30(4): 1123-1137. [孙鹏, 孙玉燕, 张强等. 淮河流域洪水极值非平稳性特征. 湖泊科学, 2018, 30(4): 1123-1137. DOI:10.18307/2018.0424] |
| [26] |
Burn DH, Elnur MAH. Detection of hydrologic trends and variability. Journal of Hydrology, 2002, 255(1/2/3/4): 107-122. DOI:10.1016/s0022-1694(01)00514-5 |
| [27] |
Wei FY. Modern techniques of climate statistical diagnosis and prediction. Beijing: China Meteorological Press, 1999. [魏凤英. 现代气候统计诊断预测技术. 北京: 气象出版社, 1999.]
|
| [28] |
Pettitt AN. A non-parametric approach to the change-point problem. Journal of the Royal Statistical Society, 1979, 28(2): 126-135. |
 2021, Vol. 33
2021, Vol. 33 


